Y-Combinator In Scheme, Recursion in Lambda Calcul

Programming language theorists usually develop the Y-Combinator as
a "fixed-point operator", so that for any expression X the result (Y X) is
a fixed-point of X, meaning that (X (Y X)) = (Y X). Unless you have a lot
of experience with the right sort of mathematics it is hard to see the
implications of that, so we will develop it in a different way.
Our goal will be to find a way to write recursive functions in the pure
lambda-calculus. At first glance that is impossible: how can a lambda
expression "call itself" if it doesn't have a name?? It turns out that the
Y-Combinator is the solution to this puzzle, but it will take some work
to get there.

We need a recursive function to work with. We could use almost
anything, but a particularly simple target is the recursive length
function. In Scheme this is
(define length (lambda (lat)
(cond
[(null? lat) 0]
[else (+ 1 (length (cdr lat)))])))
We are looking for a way to write this in the lambda-calculus without
assigning names to anything.

First, here is a function that loops forever:
(define eternity (lambda (x) (eternity x)))
There is no problem making this definition, but if we ever call
function eternity with any argument it will recurse forever.

Here is a function related to the length function:
(define L (lambda (f)
(lambda (lat)
(cond
[(null? lat) 0]
[else (+ 1 (f (cdr lat)))]))))
Here are some functions we can get from L:
(define L0 (L eternity))
(L0 null) is 0; (L0 lat) runs forever if lat isn't null

(define L1 (L L0)) == (L (L eternity))
(L1 lat) is the correct length of lat if lat has 0 or 1 elements; it fails if
lat has more than 1 elements
(define L2 (L L1)) == (L (L (L eternity)))
(define L3 (L L2))
(define L4 (L L3))
etc.
Function Ln finds the length of all lats that have no more than n
elements.
We are getting somewhere, but we would need L∞ to find the
length of all lats.

Here is a slightly more complicated approach:
(define M1
(let ([g (lambda (f)
(lambda (lat)
(cond
[(null? lat) 0]
[else (+ 1 ((f eternity) (cdr lat)))])))])
( g g)))
Note that (g eternity) is
(lambda (lat)
(cond
[(null? lat) 0]
[else (+ 1 ((eternity eternity) (cdr lat)))]))
which is functionally the same as L0

and (g g) is
(lambda (lat)
(cond
[(null? lat) 0]
[else (+ 1 ((g eternity) (cdr lat)))]))
This is the same as (L L0). So M1 is a stand-alone function that is
equivalent to L1. We are getting somewhere.

(define N
(let ([h (lambda (f)
(lambda (lat)
(cond
[(null? lat) 0]
[else (+ 1 ( (f f) (cdr lat)))])))])
(h h)))
N is (h h), which is
(lambda (lat)
(cond
[(null? lat) 0]
[else (+ 1 ( (h h) (cdr lat)))]))
That last line could be written [else (+ 1 (N (cdr lat)))]))
so N is exactly the recursive length function.

Don't allow the let-expression in the definition of N throw you off.
(let ([a b]) exp) is completely equivalent to ( (lambda (a) exp) b) so we
could rewrite N as a pure lambda-expression:
(define N
( (lambda (h) (h h))
(lambda (f)
(lambda (lat)
(cond
[(null? lat) 0]
[else (+ 1 ( (f f) (cdr lat)))])))))

We can write other recursive functions in this style:
The member? function is
(define member?
(let ([e (lambda (f)
(lambda (a lat)
(cond
[(null? lat) #f]
[(eq? a (car latl)) #t]
[else ( (f f) a (cdr lat))])))])
(e e)))

The factorial function is
(define Factorial
(let ([c (lambda (f)
(lambda (n)
(cond
[(= 0 n) 1]
[else (* n ( (f f) (- n 1)))] ))))])
(c c)))

There is a pattern to coding like this. Consider the following which is
an encoding of the Y-Combinator:
(define Y (lambda (exp)
(let ([a (lambda (f)
(exp (lambda (x) ( (f f) x)))))])
(a a))))
Then (Y (lambda(s)
(lambda (lat)
(cond
[(null? lat) 0]
[else (+ 1 (s (cdr lat)))]))))
is the length function

To see why, note that
(Y (lambda(s)
(lambda (lat)
(cond
[(null? lat) 0]
[else (+ 1 (s (cdr lat)))]))))
is
(lambda (lat)
(cond
[(null? lat) 0]
[else (+ 1 (lambda (x) ((f f) x))(cdr lat))))
(a a)
which is equivalent to
(lambda (lat)
(cond
[(null? lat) 0]
[else (+ 1 ((f f) (cdr lat))))
(a a)

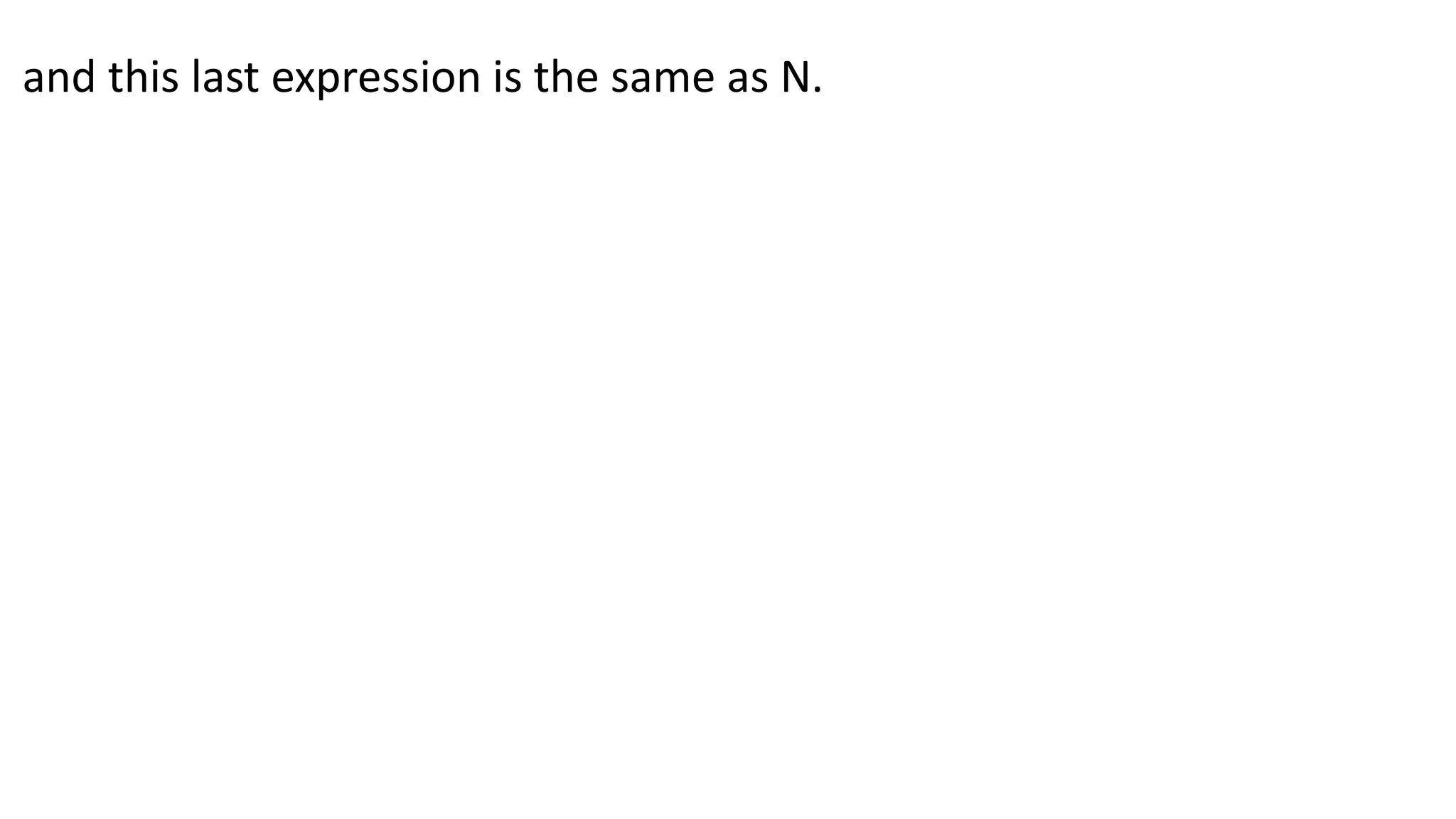
and this last expression is the same as N.

Similarly,
(Y (lambda (s)
(lambda (n)
(cond
[(= 0 n) 1]
[else (* n (s (- n 1)))]))))
is the factorial function.
In general, if you take the definition of any recursive function of one
variable, wrap a (lambda (s) ...) around it and use s as the name of the
function for the recursive call, Y takes this expression and turns it into
a recursive function.

Y converts expressions into recursive functions of 1 variable.
If we define Y2 as
(define Y2 (lambda (name)
(name (lambda (x y) ((f f) x y))))])
(a a))))
then Y2 makes recursive functions of 2 variables.

For example
(Y2 (lambda (s)
(lambda (a lat)
(cond
[(null? lat) null]
[(eq? a (car lat)) (cdr lat)]
[else (cons (car lat) (s a (cdr lat)))]))))
is the rember function and
(Y2 (lambda (s)
(lambda (a lat)
(cond
[(null? lat) null]
[(eq? a (car lat)) (s a (cdr lat))]
[else (cons (car lat) (s a (cdr lat)))]))))
is the rember-all function

The Y-Combinator shows that all recursive functions can be written in
the pure lambda- calculus. Using this fact, it can be shown that the
lambda-calculus is Turing Complete: Turing Machines, and hence any
algorithm, can be expressed in the lambda-calculus. We have seen
an algorithm for expressing any lambda-expression in terms of the
combinators S and K. This means not only that the Combinatorial
Calculus is Turing Complete, but that all possible algorithms can be
expressed as combinations of two simple combinators: S and K. This
is remarkable.
We have also shown that recursion does not require functions to be
given names. Anonymous functions can be recursive! Who knew?

Y-Combinator In Scheme, Recursion in Lambda Calcul

More Related Content

Similar to Y-Combinator In Scheme, Recursion in Lambda Calcul

Recently uploaded

Y-Combinator In Scheme, Recursion in Lambda Calcul