Tutorial Matlab 2009

Note Introduttive al Matlab © Marco Sorrentino msorrentino@unisa.it, www.macchine.unisa.it/sorrentino

Riferimenti Bibliografici e Siti Web Matlab, The Language of Technical Computing - Guida all’Uso ( Release 13 ) - The MathWorks Inc. Home page Mathworks: http://www.mathworks.com On-line Tutorial: http://www.mathworks.it/academia/student_center/tutorials/intropage.html Helpdesk: http://www.mathworks.com/access/helpdesk/help/helpdesk.shtml A. Cavallo, R. Setola, F. Vasca – Using Matlab, Simulink e Control Toolbox – A practical Approach, Prentice Hall. William J. Palm III - Introduction to MATLAB 6 for Engineers: with 6.5 Update, Mc-Graw Hill.

Corso Introduttivo al MATLAB Elementi fondamentali Operazioni Polinomi e Grafica Programmazione Funzioni avanzate Simulink Elementi Fondamentali Introduzione Avvio Ingresso da tastiera Ingresso da files esterni Manipolazione di matrici Esercizi Grafici Bidimensionali Esercizi su 2D

Elementi Fondamentali Introduzione Avvio Ingresso da tastiera Ingresso da files esterni Manipolazione di matrici Esercizi Grafici Bidimensionali Esercizi su 2D Introduzione MATrix LABoratory (ver. 5.3.1) Computation , Visualization , Programming Linguaggio di programmazione ad alto livello “ Learning by using ” Corredato da una famiglia di applicazioni specifiche ( Toolbox ): signal processing, statistics, optimization, neural networks, etc...

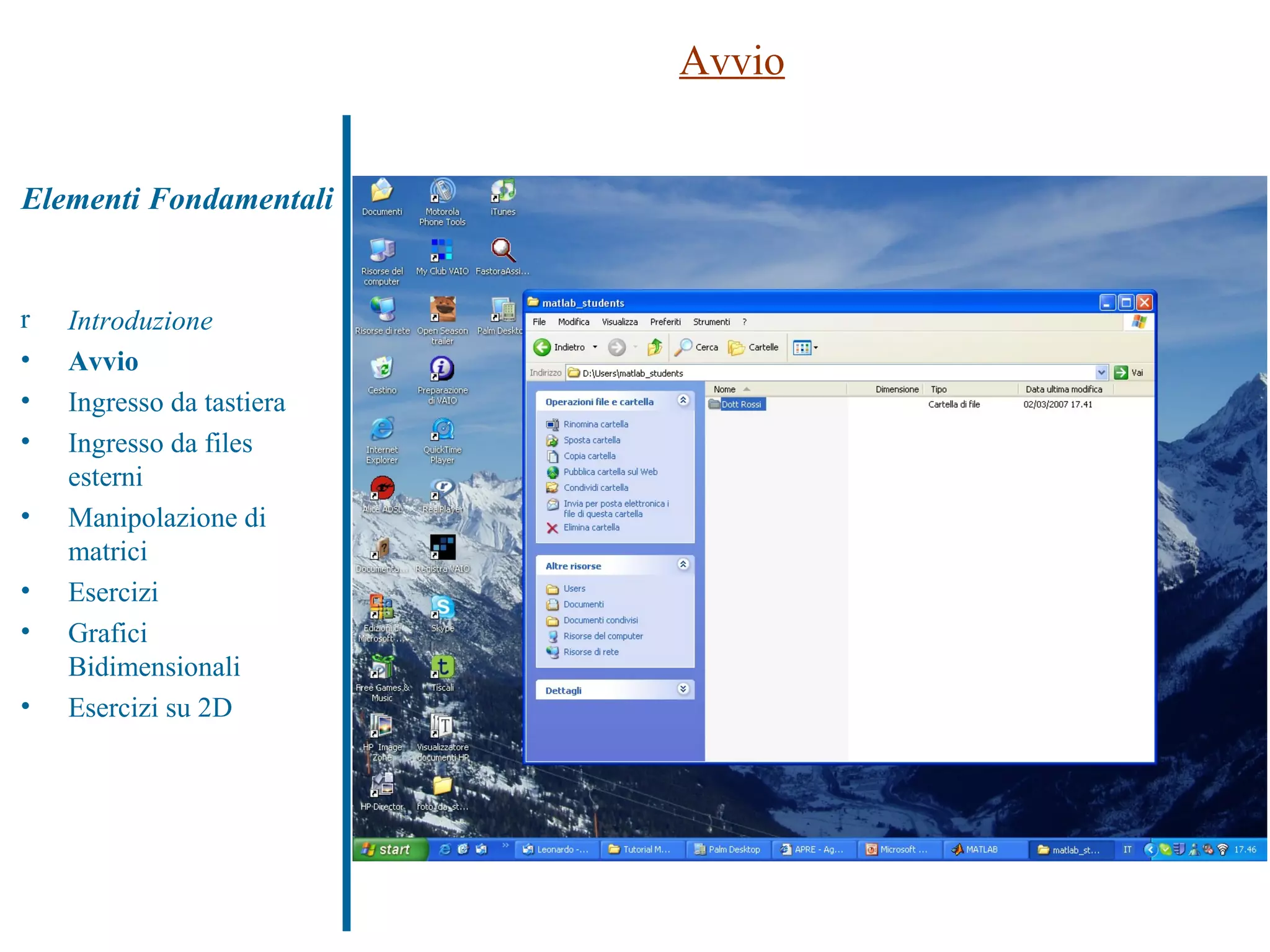
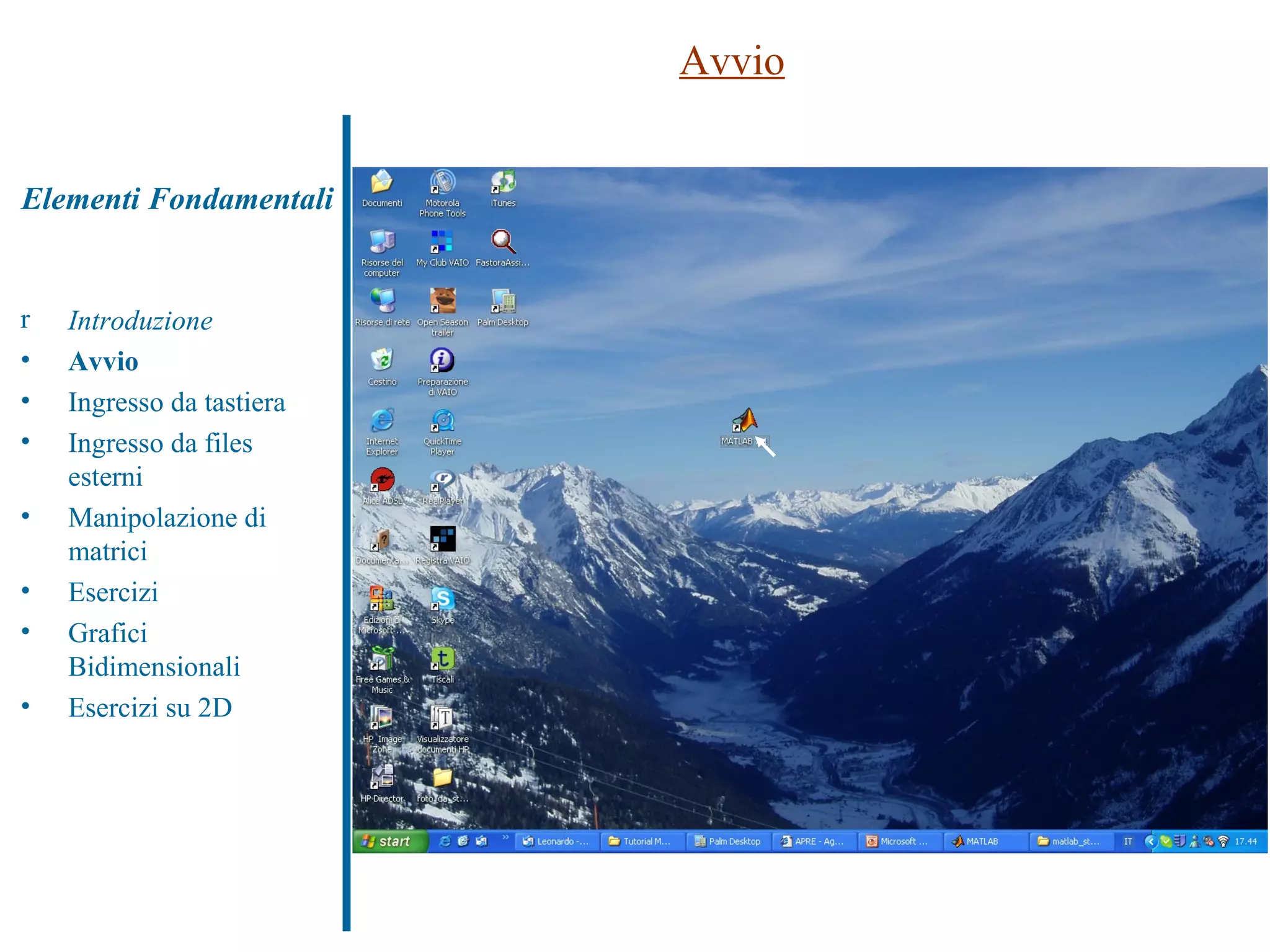
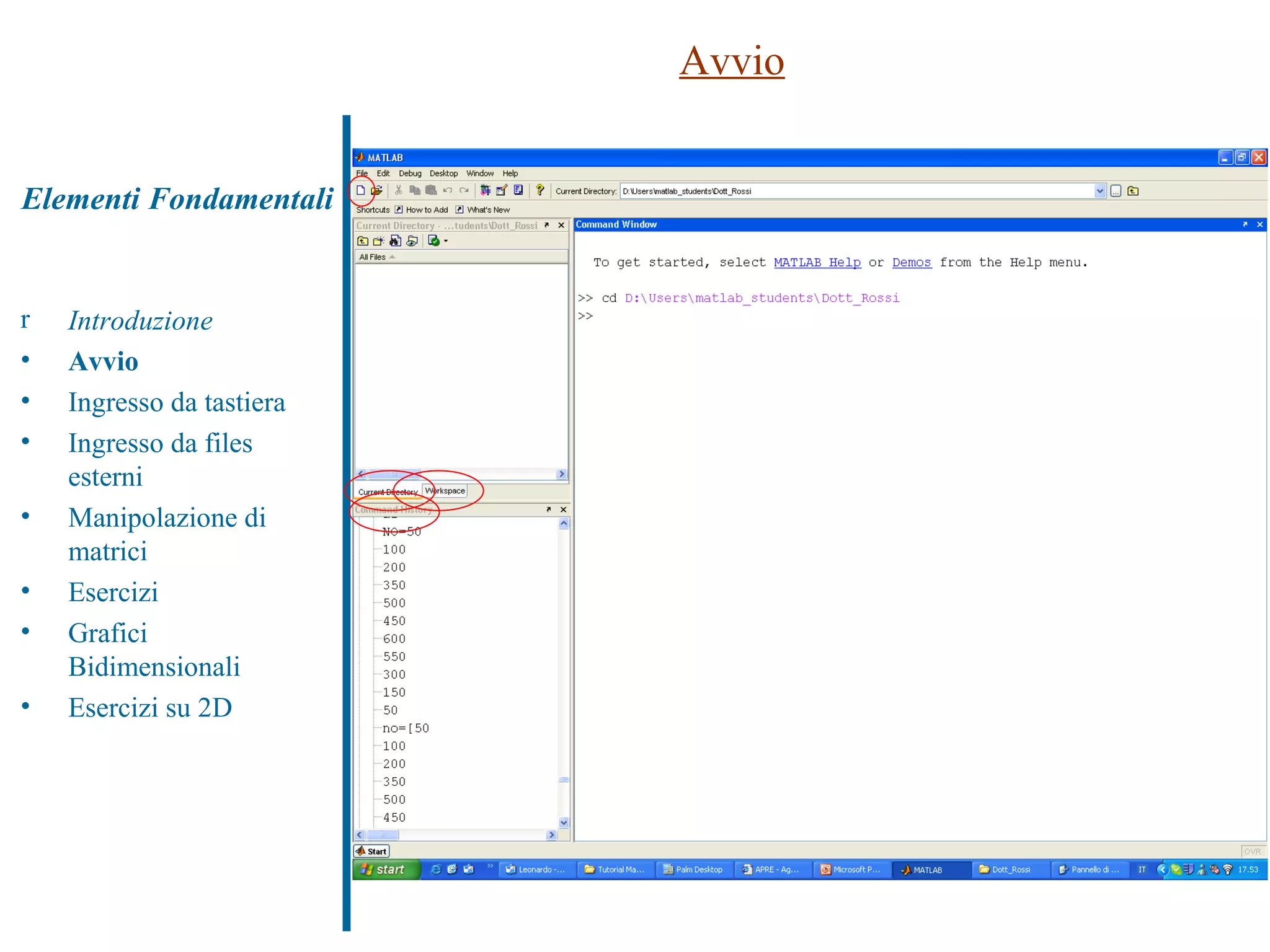
Elementi Fondamentali Avvio Introduzione Avvio Ingresso da tastiera Ingresso da files esterni Manipolazione di matrici Esercizi Grafici Bidimensionali Esercizi su 2D

Ingresso da tastiera Definizione di uno scalare e di un vettore >> A=2 >> a=[1 2 3 4] Cancellazione di un vettore (uso di ‘a’ e ‘A’) >> clear A Definizione di una matrice (uso di ‘,’ e ‘;’) >> b=[1 2 3 4 (…) 5 6 7 8] >> c=[1 2 3 4; 5 6 7 8]; … tanto per cominciare a “smanettare”... >> b=c >> b==c >> a’ >> sum (b) >> diag (c) Introduzione Avvio Ingresso da tastiera Ingresso da files esterni Manipolazione di matrici Esercizi Grafici Bidimensionali Esercizi su 2D Elementi Fondamentali

Ingresso da files esterni Un file ASCII “IN.TXT” col contenuto: 30 170 70 15 160 55 50 165 75 >> load IN.TXT >> IN Le opzioni di formato format short, long, short e, long e, hex, bank, rat , Salvataggio in un file >> save nomeFile nomeVar1 nomeVar2 Comandi di utilità … diamoci un’occhiata >> help >> help matlab\general >> help matlab\ops >> clc Introduzione Avvio Ingresso da tastiera Ingresso da files esterni Manipolazione di matrici Esercizi Grafici Bidimensionali Esercizi su 2D Elementi Fondamentali

Manipolazione di matrici Elementi di una matrice: definito un vettore x di 4 elementi si ponga >> x(5)=x(1) >> x(4)=[] >> x=[] Affiancamento di matrici >> C=[A B] >> D=[A A+3;A+3 A] Altri comandi >> [m,n]= size (C) >> h= length (b) >> who Rappresentazione di intervalli ‘:’ >> z=1:5 >> zd=1:.1:5 >> linspace ( min , max , punti ) (logspace) Operazioni sulle matrici >> B=A(1:3,2:5) >> B(:,2)=[] >> B(1,2)=[] >> B(2:2:6)=[] Introduzione Avvio Ingresso da tastiera Ingresso da files esterni Manipolazione di matrici Esercizi Grafici Bidimensionali Esercizi su 2D Elementi Fondamentali

Manipolazione di matrici Matrici speciali >> eye (3) >> eye (3,4) >> zeros (2,3) >> ones (1,2) >> diag ([4 5 6 7]) Stringhe di caratteri >> a=‘arpa’ >> b=‘un’’arpa’ >> findstr (a,’a’) (posizione di ‘a’ in a) >> int2str (123) >> num2str (1.23) >> str2num (‘1.23’) Da stringa a matrice >> A=str2mat(‘oggi’,’non’,’piove’) >> A(:,1) >> A(:,5) Introduzione Avvio Ingresso da tastiera Ingresso da files esterni Manipolazione di matrici Esercizi Grafici Bidimensionali Esercizi su 2D Elementi Fondamentali

Grafici bidimensionali Rappresentazione di un vettore di dati e uso del plot >> plot (rand(10)) >> plot(rand(1,10)) >> plot(rand(1,10),’r*:’) >> help plot >> x=[1:2:10,13:-3:-1]; y=rand(1,length(x)); >> plot(x,y) Più grafici nella stessa finestra >> subplot (2,2,1); plot(rand(1,10)) >> subplot(2,2,3); plot(3*rand(1,10)) Scalatura degli assi >> axis ([-1 5 -2 Inf]) Altri comandi: xlabel, ylabel, title, grid, gtext, ginput >> title (‘\it{alfa si scrive} \alpha’) >> t=0:.1:2*pi; plot(t,sin(t)); >> text(3*pi/4,sin(3*pi/4), ‘\leftarrow sin(t)=0.707’) Introduzione Avvio Ingresso da tastiera Ingresso da files esterni Manipolazione di matrici Esercizi Grafici Bidimensionali Esercizi su 2D Elementi Fondamentali

Grafici bidimensionali Le proprietà di una figura >> a=plot(rand(1,10)); set(a) Le opzioni sulla finestra di figura - File --> Save As - File --> Export - Tools --> Properties - Tools --> Legend - Tools --> Add … - Tools --> Zoom Grafici multipli >> plot(x1,y1,’k’,x2,y2) >> plot([1 2 3],[-1 -2 -3]) >> plot([1 2 3;-1 -2 -3]) >> teta=-pi:.1:pi; plot(teta,[sin(teta);cos(teta)]); >> legend(‘seno’,’coseno’) Elementi Fondamentali Introduzione Avvio Ingresso da tastiera Ingresso da files esterni Manipolazione di matrici Esercizi Grafici Bidimensionali Esercizi su 2D

Esercizi sui grafici bidimensionali Usando il comando patch e gli altri visti, si disegni uno spicchio di “luna rossa” Introduzione Avvio Ingresso da tastiera Ingresso da files esterni Manipolazione di matrici Esercizi Grafici Bidimensionali Esercizi su 2D Elementi Fondamentali Si costruiscano degli opportuni vettori per la rappresentazione del grafico 2 5 7 3 0

Corso Introduttivo al MATLAB Operazioni Operazioni aritmetiche Funzioni Operazioni di relazione Operazioni logiche Esercizi Elementi fondamentali Operazioni Polinomi e Grafica Programmazione Funzioni avanzate Simulink

Operazioni aritmetiche Variabili predefinite (att.ne all’unità immaginaria!) ans, eps, pi, i, j, Inf, NaN, clock, cputime, date, flops, realmax, realmin, nargin, nargout Operazioni aritmetiche su scalari +, -, *, /, ^, sqrt, \ >> 2/3 >> 2\3 >> 2*1/3 >> 1/2*3 Operazioni aritmetiche su vettori e l’operatore ‘.*’ >> sqrt([1 2 3]) >> [1:3]*[1:3] >> [1:3]*[1:3]’ >> [1:3].*[1:3] >> [1:3]^2 >> [1:3].^2 >> [1:3].^[1:3] Op aritmetiche Funzioni Op di relazione Op logiche Esercizi Operazioni

Operazioni aritmetiche Operazioni algebriche su matrici >> [1+j,1-2*j]’ >> [1+j,1-2*j].’ >> A+3 >> 2*A >> B=inv(A) >> B=A^(-1) >> X=A/B (esegue A*B -1 ) >> X=A\B (esegue A -1 *B…e se A non è quadrata?) >> B=pinv(A) ( B=(A T A) -1 A T ) Operazioni Op aritmetiche Funzioni Op di relazione Op logiche Esercizi

Operazioni aritmetiche La soluzione del problema Ax=b - se length(x)>length(b), cioè più incognite che equazioni (o meglio se rank(A)=rank([A b]) ), esistono infinite soluzioni; due possibili soluzioni sono: >> x=pinv(A)*b (soluzione a min norma) >> y=A\b (soluzione con maggior numero di zeri) - se length(x)=length(b), o meglio se la matrice A è non singolare, esiste una unica soluzione: >> y=A\b - se length(x)<length(b), cioè più equazioni che incognite (o meglio se rank(A)<rank([A b]) ), non esistono soluzioni; una soluzione approssimata è >> x=pinv(A)*b (soluzione a min norma d’errore) Operazioni Op aritmetiche Funzioni Op di relazione Op logiche Esercizi

Funzioni Arrotondamento - round arrotonda all’intero più vicino >> round(1.5) >>round(1.49…9) (15 o 16 c.d.) - fix arrotonda verso lo 0 >> fix(1.9) >> fix(1.1) >> fix(-2.1) - floor arrotonda per difetto all’intero più vicino >> foor(1.9) >> floor(-2.6) >> floor(-2.1) - ceil arrotonda per eccesso all’intero più vicino >> ceil(1.9) >> ceil(1.1) >> ceil(-2.1) Approssimazioni razionali - rem resto di una divisione intera >> rem(3,2) >> rem(2,3) >> rem(2,0) - mod risultato della a mod b >> mod(3,7) >> mod(7,3) - rats approssimazione razionale >> rats(9.22) Op aritmetiche Funzioni Op di relazione Op logiche Esercizi Operazioni

Funzioni Aritmetica complessa - real parte reale - imag parte immaginaria - conj coniugato complesso - abs valore assoluto o modulo complesso - angle angolo di fase Esempi >> 2+3i >> 2+3j >> 2+3*i >> clear i >> a=3,z=2+ai Esercizio. Si tabelli il modulo e la fase della funzione razionale fratta riportata, per s=j  ed  [10^(-2):10^2] Op aritmetiche Funzioni Op di relazione Op logiche Esercizi Operazioni

Funzioni Funzioni esponenziali e logaritmiche - pow2 esponenziale in base 2 - exp esponenziale in base e - log logaritmo naturale - log2 logaritmo in base 2 - log10 logaritmo in base 10 Esempio >> x=(1:.1:5)’; y=log(x); [x y] >> plot(x,y) … proviamo a disegnare qualche altra funzione elementare ... Op aritmetiche Funzioni Op di relazione Op logiche Esercizi Operazioni

Funzioni Funzioni trigonometriche - sin seno - cos coseno - tan tangente - asin arcoseno - acos arcocoseno - atan arcotangente - atan2 arcotangente a quattro quadranti - cart2pol da coordinate cartesiane a polari L’esempio della circonferenza >> teta=-pi:.1:pi; x=cos(teta); y=sin(teta); >> [fase,modulo]=cart2pol(x,y) >> plot(x,y) >> plot(modulo,fase) … . proviamo a rappresentare qualche altra funzione trigonometrica …. Op aritmetiche Funzioni Op di relazione Op logiche Esercizi Operazioni

Funzioni Funzioni su matrici - max funzione di massimo (e min di minimo) >> max(x) >> max(A) >> max(max(A)) >> [Y,I]=max(A) >> max(A,B) >> [m1,i1]=max(A); [m,k]=max(m1); h=i1(k); h,k - sort ordinamento in senso crescente >> R=[1,2;5,1;3,3;2,4]; A=sort(R) >> [S,i1]=sort(R); B=R(i1,:) - sum, rank, det, poly, trace, norm, eig, mean, expm, logm, sqrtm >> A=[0 1 1;0 0 1;0 0 0]; >> E1= exp (A); E2= expm (A); >> E3= eye (3)+A+A^2/2; E4= eye (3)+A+A.^2/2; >> E1, E2, E3, E4 Op aritmetiche Funzioni Op di relazione Op logiche Esercizi Operazioni

Operazioni di relazione Operatori di relazione - < minore - <= minore o uguale - > maggiore - >= maggiore o uguale - == uguale - ~= diverso Operatori logici - & and - | or - xor or esclusivo - ~ not Esempi >> 2>3 >> 2+2~=4 >> P=(rem(A,2)==0) (gli elementi di A divisibili per 2) Op aritmetiche Funzioni Op di relazione Op logiche Esercizi Operazioni

Operazioni logiche Come sempre gli operatori su matrici agiscono per colonne - any dà 1 se almeno un elemento è diverso da 0 - all dà 1 se tutti gli elementi sono diversi da 0 >> A=[0 1 1;0 0 1;0 0 0]; any(A), all(A) >> all(A<0) >> all(A>=0) >> any(A>0.5) - find trova gli indici il cui argomento è diverso da 0 >> find(A) >> [h,k]=find(A) >> t=0:.005:20; y=sin(t); (trovare i valori di t per cui y=0.5) >> tolleranza=0.05; i=find(abs(y-0.5)<tolleranza) Op aritmetiche Funzioni Op di relazione Op logiche Esercizi Operazioni

Esercizi Si rappresentino 5 periodi della funzione |sin t| Si definisca il vettore x contenente 31 valori dell’intervallo [1/2, 2 5 ] ottenuti con spaziatura logaritmica in base 2 Definito un opportuno vettore x si valutino L=(x>=2), L=(x<3), L=(x>3), L=(x<4 & x>-4) Dato il vettore x=(1, 34, 2, -12, 56, 7, 0, 9) visualizzare i valori maggiori di 5. Op aritmetiche Funzioni Op di relazione Op logiche Esercizi Operazioni

Esercizi Dati x=3+j5, y=-2+j4, z=j3, si calcolino: x+y, x-z, (x+y)z, |x|, 1/y, z 2 , log(x), e y , |x/y| Si risolva il sistema di equazioni: x+y=a 3x+2y=b per a=(1, 4, 3) e b=(1, sqrt(3), 0.5) Si rappresenti la funzione e 3t sin 5  t per t  [-2,2] con 45 punti Op aritmetiche Funzioni Op di relazione Op logiche Esercizi Operazioni

Corso Introduttivo al MATLAB Programmazione Le strutture fondamentali Script files Funzioni Esercizi sulla programmazione Elementi fondamentali Operazioni Polinomi e Grafica Programmazione Funzioni avanzate Simulink

Le strutture fondamentali La struttura if-then-else if condizione , istruzioni elseif condizione , istruzioni else istruzioni end Le strutture fondamentali Script files Funzioni Esercizi sulla programmazione Programmazione L’iterazione for for i=1:n, istruzioni end L’iterazione while while condizione , istruzioni end T=0:.1:2; for t=T, y=[y,sin(t)]; end » y=sin(T); [m,n]=size(A); for i=1:m for j=1:n if A(i,j)>10, A(i,j)=0; end, end, end » A(A>10)=0*A(A>10);

Script files Un esempio di M-file [es_scriptfile] %Un M-file per la stima approssimata della funzione coseno attraverso lo sviluppo in serie di Mc Laurin, arrestato al quinto ordine. x=0; cos_approx=0; for i=0:5 termine_par=(-1)^i*x^(2*i)/factorial(2*i); cos_approx=cos_approx+termine_par; end cos_approx Le strutture fondamentali Script files Funzioni Esercizi sulla programmazione Programmazione

Script files Un esempio sulla dipendenza dei tempi di calcolo dalla struttura di programmazione adottata [es_tempicalcolo] clear ; tic for i=1:10000 t(i)=.1*i; y(i)=t(i)^2; end ; toc clear tic t=[0:.1:1000]'; y=t.^2; toc Le strutture fondamentali Script files Funzioni Esercizi sulla programmazione Programmazione

Funzioni La struttura delle “function” [es_function] function [t,y]=es_function(x) %Una funzione per la stima approssimata della funzione coseno attraverso lo sviluppo in serie di Mc Laurin, arrestato al quinto ordine. cos_approx=0; for i=0:5 termine_parziale=(-1)^i*x^(2*i)/factorial(2*i); cos_approx=cos_approx+termine_parziale; end y=cos_approx; t=x; end >>x=[-pi:.1:pi]; >>[t,y]=es_function(x) Le strutture fondamentali Script files Funzioni Esercizi sulla programmazione Programmazione

Funzioni Un esempio con lo switch function [multipli,non_multipli]=mult(base) % Nei primi 100 interi, i numeri multipli della base data base=2; non_multipli=0; multipli=1; while n<=100 switch rem(n,base)==0 case 0 non_multipli=[non_multipli n]; case 1 multipli=[multipli n]; end n=n+1; end Le strutture fondamentali Script files Funzioni Esercizi sulla programmazione Programmazione

Esercizi sulla programmazione Programmazione Le strutture fondamentali Script files Funzioni Esercizi sulla programmazione Verificare che la funzione cos(x) nell’intorno dell’origine è approssimabile con le somme parziali del suo sviluppo in serie di Mc Laurin, tracciando i grafici della funzione cos(x) e delle prime 5 somme parziali nell’intervallo [-  , +  ] [es_taylor] : Verificare che il calcolo vettoriale consente di ridurre i tempi di elaborazione rispetto all’implementazione di una struttura classica di programmazione

Esercizi A partire dalle curve di coppia di un motore, individuare una regressione lineare del tipo [es_linreg] : x 1 + x 2 * (rpm) + x 3 * (rpm) 2 + x 4 * (throttle) = torque Operazioni Le strutture fondamentali Script files Funzioni Esercizi sulla programmazione

Operazioni Esercizi Un motore a combustione interna è caratterizzato dai seguenti valori di consumo specifico [g/kWh], in funzione del numero di giri e della coppia [es_cons_spe]: Stimare il consumo specifico nelle condizioni indicate dal simbolo “?”. Determinare il punto di minimo consumo specifico, nel campo 1000<n<6000, 10<C<100. Suggerimento: utilizzare grafici 3D. Le strutture fondamentali Script files Funzioni Esercizi sulla programmazione 6000 5000 4000 3000 2000 1000 Num giri [rpm] ? 359 389 10 346 20 365 335 30 ? 40 309 50 344 60 341 70 390 80 90 ? 314 344 100 Coppia [Nm]

Esercizi Si calcolino il lavoro utile e l’efficienza globale di un impianto con turbina a gas in cui il fluido evolve secondo il ciclo termodinamico di Joule [es_joule_id]. Ipotesi: Funzionamento ideale; Condizioni ambiente all’aspirazione; Fluido di lavoro: aria; Rapporto di compressione:  =[1:1:30]; Temp. Max ciclo: T3=[1073 1273 1573] K Si rappresentino gli andamenti dell’efficienza e del lavoro utile al variare di  e T3. Si calcolino i punti di massimo delle curve relative al lavoro utile. Si rappresentino gli andamenti di efficienza al variare del grado di rigenerazione (R=[0 0.5 0.9 1]) per T3=1273 K. Si rappresenti il ciclo termodinamico sul piano (s,T) e si valutino il lavoro utile, il calore addotto ed il rendimento in funzione dell’area del ciclo. Operazioni Le strutture fondamentali Script files Funzioni Esercizi sulla programmazione

Esercizi Le prevalenze reale ed Euleriana di una pompa possono essere espresse in funzione della portata volumetrica Q e del regime di rotazione n attraverso le seguenti relazioni: Hr = k 1 * n 2 + 2*k 2 n * Q - k 3 * Q 2 HE = k 5 * n 2 – k 6 * Q*n mentre la prevalenza esterna può essere espressa come Hest = Hu + k 4 * Q 2. A partire dai dati rilevati nelle quattro misure indicate rappresentare graficamente gli andamenti delle prevalenze Euleriana, reale ed esterna ed il rendimento al variare della portata volumetrica per vari regimi di rotazione [es_curvecaratt] . Si assuma k 4 = k 6 =1; k 5 =14; Hu=20 m 1) Q= 1 m 3 /h; n= 1000 rpm; Hr = 11 m 2) Q =2 m 3 /h; n = 2000 rpm ; Hr = 44 m 3) Q =4 m 3 /h ; n = 3000 rpm; Hr = 98 m 4) Q =10 m 3 /h; n = 3500 rpm; Hr = 92.5 m Operazioni Le strutture fondamentali Script files Funzioni Esercizi sulla programmazione

Corso Introduttivo al MATLAB Polinomi e Grafica 3D Operazioni su polinomi Interpolazione Esercizi sui polinomi Grafici tridimensionali Esercizi su 3D Elementi fondamentali Operazioni Polinomi e Grafica Programmazione Funzioni avanzate Simulink

Operazioni sui polinomi Definizione di un polinomio >> p=[1 0 -1]; (definisce il polinomio x 2 -1) Le radici di un polinomio >> roots([1 0 -1]) >> roots([1 -2 -15]) Dalle radici al polinomio >> radici=[-1,1]; poly(radici) >> radici=[-3,-5]; poly(radici) Il prodotto di polinomi >> a=[1 0 1]; b=[1 1]; c=conv(a,b) Il rapporto di polinomi a(s)=q(s)b(s)+r(s) >> [q,r]=deconv(a,b) >> [q,r]=deconv(b,a) Il valore di un polinomio in un punto >> polyval(a,3) La derivata di un polinomio >> polyder(a) Op su polinomi Interpolazione Esercizi sui polinomi Grafici tridimensionali Esercizi su 3D Polinomi e Grafica

Interpolazione Il comando polyfit per il fitting dei dati >> x=-1:.1:1; y=2*x+1+2*rand(1,length(x)); >> plot(x,y) >> p=polyfit(x,y,1); y1=polyval(p,x); >> plot(x,y,x,y1) >> p=polyfit(x,y,5); y5=polyval(p,x); >> p=polyfit(x,y,10); y10=polyval(p,x); >> plot(x,y,x,y1,x,y5,x,y10) [es_polyfit1] Polinomi e Grafica Op su polinomi Interpolazione Esercizi sui polinomi Grafici tridimensionali Esercizi su 3D

Interpolazione Il comando spline (interpolazione con cubiche) - il significato fisico (la spline usata per disegnare) - si infittisce l’intervallo tra i campioni, tra questi si cerca un’approssimazione polinomiale e si assicura la differenziabilità fino ad un certo ordine nei punti di giunzione (la cosiddetta “pp-form”): Polinomi e Grafica Op su polinomi Interpolazione Esercizi sui polinomi Grafici tridimensionali Esercizi su 3D >> x=-1:.1:1; y=2*x+1+2*rand(1,length(x)); >> xx=-1:.1/2:1; yy=spline(x,y,xx); >> plot(x,y,’o’,xx,yy)

Interpolazione Il comando interp1 per l’interpolazione monodimensionale >> x=-1:.1:1; y=2*x+1+2*rand(1,length(x)); >> xi=-1:.03:1; yi=interp1(x,y,xi,’nearest’) >> plot(x,y,’o’,xi,yi) >> yil=interp1(x,y,xi,’linear’); plot(x,y,’o’,xi,yi,xi,yil) o altre opzioni come ‘spline’ e ‘cubic’. Interpolazione bidimensionale: dati X ed Y monotoni ZI = interp2 (X, Y, Z, XI, YI, method) >> [x,y]=meshgrid(-3:1:3) >> z=x.*exp(-x.^2-y.^2) >> surf(x,y,z); >> [xi,yi]=meshgrid(-3:.25:3); >> zi=interp2(x,y,z,xi,yi); surf(xi,yi,zi) Polinomi e Grafica Op su polinomi Interpolazione Esercizi sui polinomi Grafici tridimensionali Esercizi su 3D

Esercizi sui polinomi Calcolare i punti estremali, le intersezioni con gli assi e gli eventuali punti di flesso della funzione f(x)=x 4 +5x 3 +1. [es_polinomi] Data la sequenza di punti y= [7.02 1.46 -1.55 0.94 2.21 7.95 15.56 19.22 32.80 37.72 59.79] per x= [0:10] , individuare i polinomi di interpolazione di grado (1, 2, 3) e rappresentarli graficamente. La densità dell’aria  (in g/m 3 ) varia con la quota h (in km) secondo la tabella riportata. Determinare un polinomio interpolatore di ordine n=1, 2, 3, …, 6 e la norma dell’errore commesso. Si calcolino poi i valori della densità dell’aria ai valori di quota 10, 20, 30, 40, 50 e 60. h=7, 10, 15, 21, 27, 34, 39, 43, 47, 51, 55, 59, 61  =556, 369, 191,75, 26.2, 9.9,4.4,2.3, 1.4,.8, .5,.33,.25 Polinomi e Grafica Op su polinomi Interpolazione Esercizi sui polinomi Grafici tridimensionali Esercizi su 3D

Esercizi sui polinomi Per un motore ad accensione comandata, sono state effettuate le seguenti misure di emissioni di NOx al variare del rapporto di miscela A/F [es_nox] : Polinomi e Grafica Op su polinomi Interpolazione Esercizi sui polinomi Grafici tridimensionali Esercizi su 3D Rappresentare l’andamento delle emissioni in funzione di A/F, e determinare la migliore rappresentazione polinomiale delle emissioni in funzione di A/F in termini di precisione e generalizzabilità. Stimare il valore delle emissioni per A/F=15.2

Grafici tridimensionali Un primo esempio >> t=0:pi/10:10*pi; plot3(sin(t),cos(t),t) >> x=0:.1:4; y=-2:.1:1; [X,Y]=meshgrid(x,y); >> Z=sin(X).*cos(Y); plot3(X,Y,Z); >> mesh(X,Y,Z); surf(X,Y,Z); surfc(X,Y,Z); Il colore per i grafici >> [X,Y]=meshgrid(-8:.5:8);R=sqrt(X.^2+Y.^2)+eps >> Z=sin(R)./R; surf(Z); La mappa dei colori Red Green Blue (RGB) nero 0 0 0 bianco 1 1 1 giallo 1 1 0 magenta 1 0 1 cyan 0 1 1 grigio 0.5 0.5 0.5 >> t=-pi:pi/10:pi; fi=(-pi/2:pi/20:pi/2)’; >> X=cos(fi)*cos(t); Y=cos(fi)*sin(t); >> Z=sin(fi)*ones(size(t)); surf(X,Y,Z) >> colormap([0 0 0;1 1 1]); C=rand(size(Z)); >> surf(X,Y,Z,C) Polinomi e Grafica Op su polinomi Interpolazione Esercizi sui polinomi Grafici tridimensionali Esercizi su 3D

Grafici tridimensionali Le curve di livello >> t=-2:.2:2; [X,Y,Z]=peaks(n); mesh(X,Y,Z); >> figure(2); contour(X,Y,Z,20); >> hold on; [U,V]=gradient(Z,.2); >> quiver(X,Y,U,V); hold off >> [C,h]=contour(Z,10); clabel(C,h) >> figure(3); mesh(X,Y,Z), hold on; >> contour3(X,Y,Z,[1 1],’k’); >> Az=180;El=0; view([Az El]) Polinomi e Grafica Op su polinomi Interpolazione Esercizi sui polinomi Grafici tridimensionali Esercizi su 3D x y -y z Az El

Grafici tridimensionali I solidi di rotazione ottenuti col comando cylinder - due possibili rotazioni della retta y=x: » cylinder(0:.1:2) » cylinder(-2:.1:2) - le possibili rotazioni di un coseno: » teta=0:pi/10:2*pi; » [X,Y,Z]=cylinder(4*cos(teta)); » subplot(2,2,1), mesh(X) » subplot(2,2,2), mesh(Y) » subplot(2,2,3), mesh(Z) » subplot(2,2,4), mesh(X,Y,Z) Polinomi e Grafica Op su polinomi Interpolazione Esercizi sui polinomi Grafici tridimensionali Esercizi su 3D

Esercizi su grafici tridimensionali Si rappresenti la funzione z=x 2 + 4y nel piano [z,x] al variare di y, nel piano [z,y] al variare di x e nello spazio 3D [es_grafici3d] %piano x,z x=[-10:10];hold on for y=-2:2 z=x.^2+4*y;plot(x,z) end hold off %piano y,z clear x, y;y=[-10:10];figure;hold on for x=-2:2 z=x.^2+4*y;plot(y,z) end hold off %spazio3D clear x,y;x=[-10:10];y=[-10:10]; figure [X,Y]=meshgrid(x,y); Z=X.^2+4*Y; plot3(X,Y,Z);mesh(X,Y,Z);surf(X,Y,Z); Polinomi e Grafica Op su polinomi Interpolazione Esercizi sui polinomi Grafici tridimensionali Esercizi su 3D

Esercizi su grafici tridimensionali Si risolva graficamente il problema di ottimizzazione vincolata min x 2 +y 2 +z 2 con il vincolo x 2 +2y+4z-14 Suggerimento: si disegni prima il vincolo. Ritornando all’esempio della sfera presentato in precedenza, si disegni in nero la sola semisfera inferiore e poi la sola semisfera di destra. Utilizzando il comando help e la funzione peak , si utilizzino i comandi - hist, stem, stem3, pie, light Polinomi e Grafica Op su polinomi Interpolazione Esercizi sui polinomi Grafici tridimensionali Esercizi su 3D

Corso Introduttivo al MATLAB Funzioni Avanzate Analisi Statistica Ricerca dei Minimi e degli Zeri Derivazione ed Integrazione Numerica Elementi fondamentali Operazioni Polinomi e Grafica Programmazione Funzioni avanzate Simulink

Analisi Statistica Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate Definizione di una distribuzione di variabili normale (oppure Beta, Binomiale, Chi-square, etc…) >> R=normrnd(10,1,100,1); Calcolo della probability density function in x >> y=normpdf(x,10,1) p.d.f : f(x)=Pr{x < X < x+dx} Calcolo dei momenti primo e secondo >> mean(R) >> std(R) Calcolo della matrice di covarianza e dei coefficienti di correlazione >> cov(R1,R2) >> corrcoef(R1,R2) Confronto tra distribuzioni normali al variare del momento secondo >> x=[0:20] >> y1=normpdf(x,10,1) >> y2=normpdf(x,10,2) >> plot(x,y1,x,y2)

Ricerca Minimi e Zeri Minimo e zero di una funzione function b=es_minimo(v); b=(v+1).*exp(-v.^2); return >> a= fminbnd (‘ es_minimo ’,-2,2) >> a= fzero (‘ es_minimo ’,-2) Minimo di una funzione di più variabili function b=es_minimo2(v); x=v(1); y=v(2); z=v(3); b=x^2+2.5*sin(y)-z^2*x^2*y^2; return >> a= fminsearch (‘ es_minimo2 ’,[-0.6 -1.2 0.135]) Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate

Esercizi su Ricerca Minimi e Zeri Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate Calcolare le radici dell’equazione x 2 -3sinx+0.1=0 Calcolare il minimo della funzione f(x,y)=e (x-y) +x 2 +y 2 >>minimo=fminsearch( 'es_minimo_fun' ,[-0.3 0.3]) function z=es_minimo_fun(v); x=v(1);y=v(2); z=exp(x-y)+x^2+y^2; return

Esercizi su Ricerca Minimi e Zeri Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate Assegnato il set di dati illustrato in figura e riportato nel file (es_minimo2_dati.mat), individuare i valori ottimali dei parametri lambda che ne consentano di riprodurre l’andamento attraverso la struttura funzionale seguente [es_minimo2] : y=lambda(1)*exp[-lambda(2)*t] Soluzione

Esercizi su Ricerca Minimi e Zeri Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate clear all;clc global dati load es_minimo2_dati t=dati(:,1); y=dati(:,2); plot(t,y, 'ro' ) pause; lambda0=[3 1]; lambda=fminsearch( 'es_minimo2_fun' ,lambda0) [err,z]=es_minimo2_fun(lambda); plot(t,y, 'ro' ,t,z) function [err,z] = es_minimo2_fun(lambda) global dati t = dati(:,1);y = dati(:,2); z=lambda(1)*exp(-lambda(2)*t); err = norm(z-y);plot (t,y, 'o' ,t,z) return

Esercizi su Ricerca Minimi e Zeri Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate Assegnato il set di dati illustrato in figura e riportato nel file (es_minimo2_dati.mat), individuare i valori ottimali dei parametri non lineari lambda che ne consentano di riprodurre l’andamento attraverso la struttura funzionale seguente [es_minimo3] : y=c(1)*exp[-lambda(1)*t]+c(2)*exp[-lambda(2)*t]

Esercizi su Ricerca Minimi e Zeri Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate Nel modello economico semplificato di mercato perfettamente concorrenziale , grande rilievo assumono le curve di domanda ed offerta, che in ascissa hanno la quantità di bene prodotto o richiesto in un prefis s ato periodo di tempo ed in ordinata il prezzo unitario del bene. L’intersezione delle curve determina il prezzo di equilibrio della merce. Assumendo i seguenti dati per la produzione e richiesta del grano in un ipotetico mercato si calcoli il prezzo di equilibrio e si traccino le curve di domanda ed offerta utilizzando almeno 30 punti [es_minimo4] .

Si calcoli il minimo della funzione x 4 +6xy+xy 3 -6xz 3 -yz+4z 3 Una fabbrica decide di iniziare la produzione di un nuovo tipo di caramelle dietetiche. Il costo di produzione è di L. 1000 per confezione e l’ufficio di marketing prevede una richiesta settimanale di 100000/p 2 confezioni dove p è il prezzo complessivo al quale ogni confezione è venduta. Si calcoli il prezzo al quale sarà messa in vendita una confezione di caramelle per massimizzare il profitto [ es_max_prof ] . Esercizi su Ricerca Minimi e Zeri Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate

Le prevalenze reale ed Euleriana di una pompa possono essere espresse in funzione della portata volumetrica Q e del regime di rotazione n attraverso le seguenti relazioni: Hr = k 1 * ( n/1000) 2 + 2*k 2 (n/1000) * Q - k 3 * Q 2 HE = k 5 * ( n/1000) 2 – k 6 * Q*(n/1000) mentre la prevalenza esterna può essere espressa come Hest = Hu + k 4 * Q 2. Si assuma k 1 =10; k 2 = k 3 = k 4 = k 6 =1; k 5 =14; Hu =20 Calcolare il punto ottimale di funzionamento corrispondente al massimo rendimento con il vincolo di uguaglianza tra caratteristica interna ed esterna. Eseguire l’ottimizzazione sia con un metodo di minimizzazione non vincolata impiegando una penalty function , sia con un metodo di minimizzazione vincolata [es_curvecaratt]: 1 – max [  - k * ( Hr - Hest ) 2 ] 2 – max  con Hr =Hest e dHr/dQ <0 Esercizi su Ricerca Minimi e Zeri Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate

Carico termico ed elettrico Cogeneratore Utenza termica Utenza elettrica Ausiliario (caldaia) ENEL Serbatoio Esercizi su Ricerca Minimi e Zeri Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate [es_ cogenerazione ]

Integrazione Numerica Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate La risoluzione delle equazioni differenziali ordinarie in Matlab viene eseguita con due metodi: 1 - ode23 usa il metodo di Runge-Kutta del 2°-3° ordine; 2 - ode45 usa il metodo di Runge-Kutta del 4°-5° ordine; La sintassi è identica per le due funzioni e richiede che l’equazione da integrare sia espressa come sistema di equazioni ordinarie del primo ordine: >> [t,x]=ode23(‘xpunto’,t0,tf,x0)

Esercizi sulla Integrazione Numerica Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate Le equazioni di Volterra-Lokta descrivono un modello semplificato dell’evoluzione di due specie in competizione tra loro (noto come modello preda-predatore ): Si studi la soluzione di queste equazioni a partire dai parametri nominali a=2.7, b=0.7, c=1, d=3 [es_loktavolterra] . preda Soluzione predatore

Esercizi sulla Integrazione Numerica Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate clear all % Modello Lokta-Volterra (preda-predatore) global a b c d a=2.7;b=0.7;c=1;d=3; x0=[2,3]'; timerange=[0: .1:10]; [t,x]=ode45( 'loktavolterra' ,timerange,x0); plot(t,x) function xpunto=loktavolterra(t,x) global a b c d xpunto(1)=a*x(1)-b*x(1)*x(2); xpunto(2)=c*x(1)*x(2)-d*x(2); xpunto=xpunto'; return

Esercizi sulla Integrazione Numerica Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate Simulare il modello preda-predatore rappresentato dalle equazioni di Volterra - Lokta in presenza dell’effetto ‘pesca’: 1) Si studi la soluzione di queste equazioni a partire dai parametri nominali a=2.7, b=0.7, c=1, d=3, h=0.5 nell’intervallo t = [0:.1:10] [es_loktavolterra2] . 2) Si identifichi il valore ottimale del parametro ‘h’ che consenta di riprodurre attraverso il sistema di equazioni l’andamento preda/tempo riportato nel file loktavolterra.mat, lasciando invariati i valori degli altri parametri [es_loktavolterra2min] . preda predatore

Esercizi sulla Integrazione Numerica Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate Partendo dalla legge rappresentativa di una trasformazione adiabatica: P v K = cost. riprodurre la fase di compressione ideale per un motore ad accensione comandata [es_compr_id] .

Esercizi sulla Integrazione Numerica Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate Un impianto di pompaggio è costituito da una pompa che preleva acqua da un bacino per alimentare un serbatoio in pressione situato ad una quota di 20 m rispetto al bacino. Simulare l’andamento della pressione nel serbatoio nelle seguenti condizioni [es_serbatoio]: Volume serbatoio = 10 m 3 ; Pressione iniziale serbatoio = 1 bar; Temperatura aria = 300 K; Regime rotazione pompa = 2000 rpm; Hr = 10* ( n/1000) 2 + 2* (n/1000) * Q - Q 2; Hest = Hu + k 4 * Q 2 Hu =  z +  P/  Soluzione

Esercizi sulla Integrazione Numerica Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate %----------------------------------------------------------------------------- % calcolo pressione serbatoio %----------------------------------------------------------------------------- global k4 k5 k6 hu k1 k2 k3 n gamma pamb mair rair tamb g k1=10;k2=1;k3=1;k4=1;k5=14;k6=1; hu=20;vserb=10;rair=287;pamb=1e5;tamb=300; mair=pamb*vserb/rair/tamb; rpm=2000;n=rpm*1e-3;g=9.807; timespan=[0:5000]; p0=pamb; %[Pa] [t,p]=ode45('dpserb',timespan,p0); plot(t,p) -------------------------------------------------------------------------- % funzione calcolo pressione serbatoio function dp = dpserb(t,p) global k4 k5 k6 hu k1 k2 k3 n gamma pamb mair rair tamb g gamma=g*1000; AA=k4+k3;BB=-2*k2*n;CC=hu+(p-pamb)/gamma-k1*n^2; qvol=(-BB+sqrt(BB^2-4*AA*CC))/(2*AA) dp=p^2*qvol/3600/mair/rair/tamb; return

Corso Introduttivo al MATLAB Simulink Come costruire uno schema Sources e Sinks La simulazione Esercizi Elementi fondamentali Operazioni Polinomi e Grafica Programmazione Funzioni avanzate Simulink

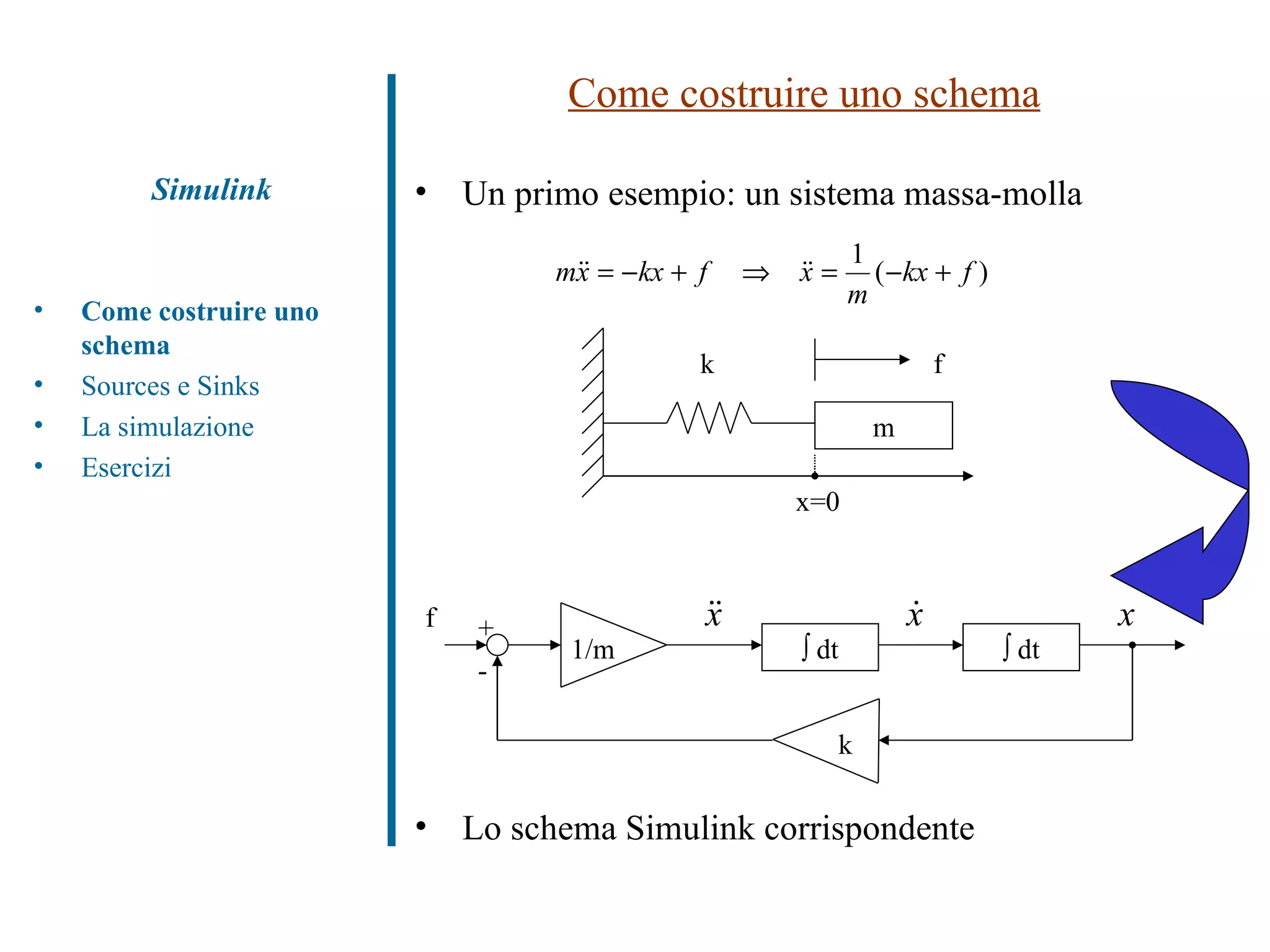
Come costruire uno schema Un primo esempio: un sistema massa-molla Simulink Come costruire uno schema Sources e Sinks La simulazione Esercizi Lo schema Simulink corrispondente m k f x=0  dt 1/m  dt k f + -

Come costruire uno schema L’uso del mouse: Sui blocchi: bottone sin per selezionare e spostare blocchi bottone dex per duplicare il blocco bottone dex su selezione per le proprietà doppio click sin per selezionare i parametri Sulle linee bottone sin per selezionare e spostare linee bottone sin su vertice per spostare il vertice bottone dex per creare una diramazione Sullo schermo bottone sin per creare una nuova linea in ingresso o uscita ad un blocco bottone dex per le proprietà dello schema doppio click sin per inserire testo Simulink Come costruire uno schema Sources e Sinks La simulazione Esercizi

Sources e Sinks Sources: Il clock per il tempo simulato La costante anche definibile dal workspace Una generica variabile temporale definita col From Workspace (è necessario anche il tempo) Un segnale periodico con il Repeating Sequence La sinusoide e il gradino Sinks: Per assegnare il valore ad una variabile con il To Workspace (occhio ai parametri!) Stop Simulation per fermare la simulazione Lo Scope per visualizzare la variabile durante la simulazione Simulink Come costruire uno schema Sources e Sinks La simulazione Esercizi

La simulazione I parametri della simulazione: Istante di tempo iniziale < Istante di tempo finale I metodi di risoluzione a passo fisso: * il metodo di Eulero (rapporto incrementale) * il metodo di Runge Kutta * l’opzione Mode/MultiTasking per consentire la verifica di incoerenza nella connessione di blocchi con diversi periodi di campionamento Simulink Come costruire uno schema Sources e Sinks La simulazione Esercizi

La simulazione I parametri della simulazione: I metodi di risoluzione a passo variabile sulla differenza di due successive iterazioni: * la predizione e la correzione * il max (per default (t_fin-t_in)/50) e min passo * la tolleranza relativa (percentuale della norma dello stato) e assoluta (quando lo stato si avvicina a zero): * per modificare la tolleranza assoluta sulla singola variabile, usare i parametri dell’integratore L’opzione Refine Output per valutare le uscite del sistema in un numero maggiore di punti (di un fattore e questa opzione non cambia l’intervallo di integrazione), o in un numero prefissato di punti. Simulink Come costruire uno schema Sources e Sinks La simulazione Esercizi

Esercizi Costruire lo schema Simulink per un sistema massa-molla-smorzatore ed analizzare la risposta ad una forzante sinusoidale (m=1, k=10, sigma=0.1, F0=10) [es_pendoloforzato] . Simulare la risposta dinamica di un autoveicolo ad una variazione a gradino della coppia motrice [es_dynvehicle] . Simulink Come costruire uno schema Sources e Sinks La simulazione Esercizi

Esercizi sulla Integrazione Numerica Analisi Statistica Ricerca Minimi e Zeri Derivazione ed Integrazione Numerica Funzioni Avanzate Il modello semplificato di un satellite in orbita circolare intorno a un pianeta è: dove r è la distanza del satellite dal centro del pianeta,  è l’angolo di azimut (detto in altri termini anomalia, se pensiamo al riferimento che giace nel piano dell’orbita e un sistema di coordinate polari per individuare la posizione del satellite) e k la costante di gravitazione relativa al pianeta (per la terra k=9.807). Si studi il moto del satellite in orbita intorno alla terra per quote variabili tra 350 e 500 km. [es_satellite]

La simulazione I parametri della simulazione: I metodi di risoluzione a passo variabile sulla differenza di due successive iterazioni: * la predizione e la correzione * il max (per default (t_fin-t_in)/50) e min passo * la tolleranza relativa (percentuale della norma dello stato) e assoluta (quando lo stato si avvicina a zero): * per modificare la tolleranza assoluta sulla singola variabile, usare i parametri dell’integratore Simulink Come costruire uno schema Sources e Sinks La simulazione Esercizi

Tutorial Matlab 2009

More Related Content

What's hot

Viewers also liked

Similar to Tutorial Matlab 2009

More from Andrea Della Corte

Recently uploaded

Tutorial Matlab 2009