Downloaded 458 times
Uploaded byCarlo Magno
Teaching and learning framework in mathematics
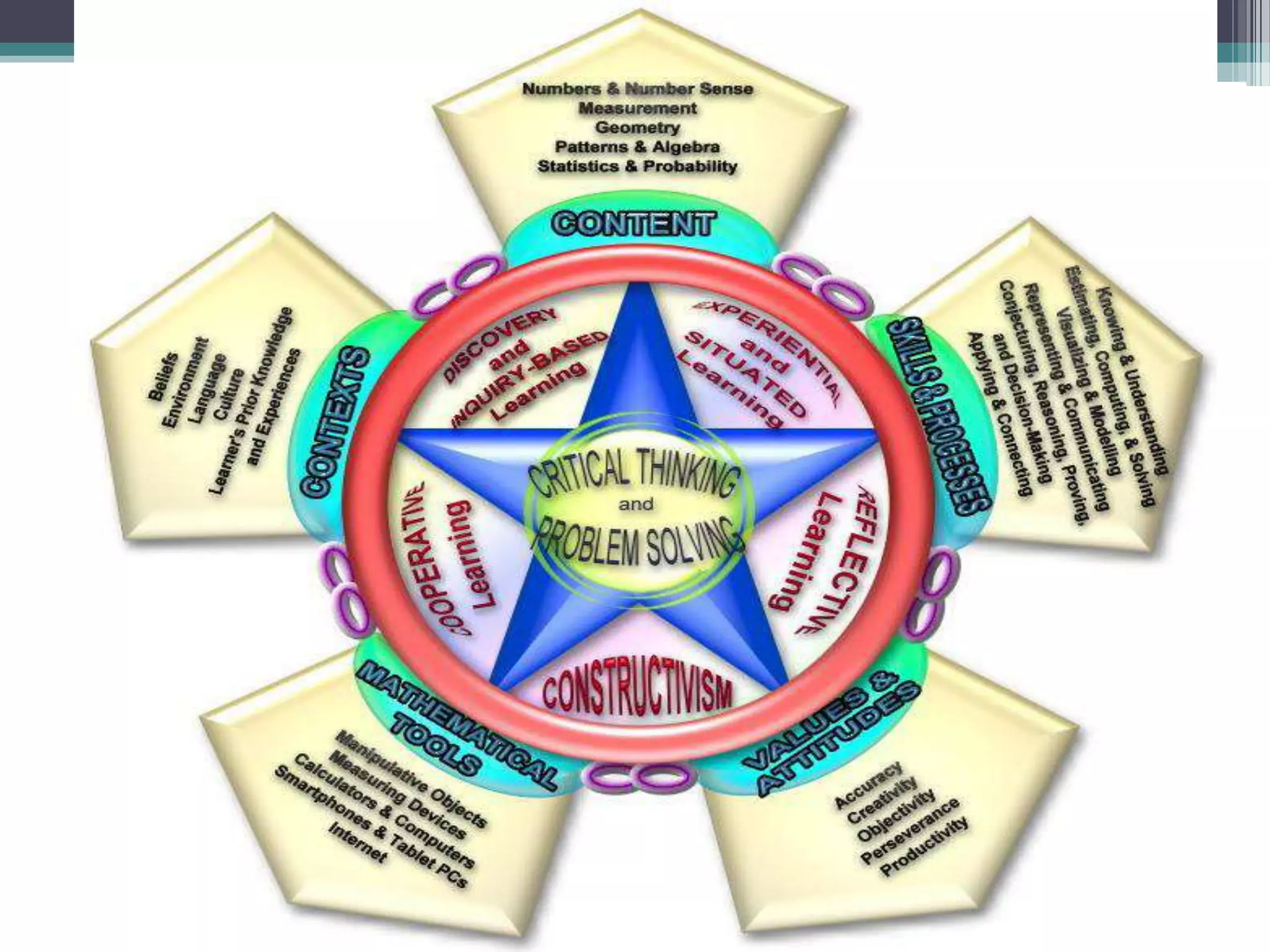
This document outlines a teaching and learning framework for mathematics education. It discusses important skills like critical thinking and problem solving. It also covers key content areas and processes to develop, like numbers, measurement, geometry, and representing and communicating. Principles for both teaching and learning mathematics are provided, such as the need for active engagement and using a variety of tools. Learning theories like constructivism, cooperative learning, and discovery-based learning are also referenced. Examples of experiential and reflective learning activities are given to help students learn mathematics concepts through real-world experiences and reflection.
More Related Content
![Approaches, methods and_techniques_in_edukasyon_sa[1]](https://cdn.slidesharecdn.com/ss_thumbnails/approachesmethodsandtechniquesinedukasyonsa1-160416051040-thumbnail.jpg?width=640&height=640&fit=bounds)
Similar to Teaching and learning framework in mathematics
More from Carlo Magno
Teaching and learning framework in mathematics
- 1. Teaching and Learning Frameworkin Mathematics Carlo Magno, PhD De La Salle University, Manila
- 2. • What doyou think are the important skills that students needs to learn in mathematics?
- 3. Goals of Mathematicseducation in the K to 12 Critical Thinking Problem Solving
- 4. Critical Thinking • Intellectuallydisciplined process of actively and skillfully conceptualizing, applying, analyzing, synthesizin g, and/or evaluating information gathered from, or generated by, observation, experience, reflection, reasoning , or communication, as a guide to belief and action (Scriven & Paul, 1987).
- 5. Problem solving • Findinga way around a difficulty, around an obstacle, and finding a solution to a problem that is unknown (Polya, 1945 & 1962).
- 6. Content areas inthe curriculum • Numbers and Number Sense • Measurement • Geometry • Patterns and Algebra • Probability and Statistics
- 7. Skills and processesto be developed • Knowing and Understanding • Estimating • Computing and Solving • Visualizing and Modelling • Representing and Communicating • Conjecturing • Reasoning • Proving and Decision-making • Applying and Connecting
- 8. values and attitudes •Accuracy • Creativity • Objectivity • Perseverance • Productivity
- 9. Tools in teachingmathematics • manipulative objects • measuring devices • calculators and computers • Smartphones and tablet PCs • Internet
- 11. Teaching Principles inMathematics • Principle 1: While the ability to explain and solve a problem is evidence in good understanding of mathematical ideas, teaching mathematics requires more than this. • Principle 2: Mathematics must be real to students and therefore, mathematics teachers should be mindful of students contexts an when teaching mathematics.
- 12. Teaching Principles inMathematics • Principle 3: Mathematics is best learned when students are actively engaged. • Principle 4: Mathematics can never be learned in an instant, but rather requires lots of work and the right attitude. • Principle 5: All students regardless of gender, culture, socio0economic status, religion, and educational background have the right and be taught good and correct mathematics.
- 13. Teaching Principles inMathematics • Principle 6: Assessment must be an integral part of the mathematics instruction. • Principle 7: Mathematics as a field continues to develop and evolve. Therefore, the teaching if it must keep up with development in the field.
- 14. Teaching Principles inMathematics • Principle 8: Technology plays an important role in the teaching and learning of mathematics. Mathematics teachers must learn to use and manage technological tools and resources well. • Principle 9: Mathematics teachers must never stop learning.
- 15. Learning Principles inMathematics • Principle 1: Being mathematically competent means more than having the ability to compute and perform algorithms and mathematical procedures. • Principle 2: The physical and social dimension of a mathematical environment contribute to one’s success in learning mathematics.
- 16. Learning Principles inMathematics • Principle 3: Mathematics is best learned when students are actively engaged. • • Principle 4: A deep understanding of mathematics requires a variety of tools for learning.
- 17. Learning Principles inMathematics • Principle 5: Assessment in mathematics must be valued for the sake of knowing what and how students learn or fail to learn mathematics. • Principle 6: Students’ attitudes and beliefs about mathematics affect their learning. • Principle 7: Mathematics learning needs the support of both parents and other community groups.
- 18. Learning Principles andTheories • Experiential and Situated Learning • Reflective Learning • Constructivism • Cooperative Learning • Discovery and Inquiry-based Learning
- 19. Experiential and SituatedLearning • Experiential learning as advocated by David Kolb is learning that occurs by making sense of direct everyday experiences. • Experiential learning theory defines learning as "the process whereby knowledge is created through the transformation of experience. “ • Knowledge results from the combination of grasping and transforming experience" (Kolb, 1984, p. 41).
- 20. Experiential and SituatedLearning • Situated learning, theorized by Lave and Wenger, is learning in the same context on which concepts and theories are applied.
- 21. Reflective Learning • Reflectivelearning refers to learning that is facilitated by reflective thinking. • It is not enough that learners encounter real-life situations. • Deeper learning occurs when learners are able to think about their experiences and process these allowing them the opportunity to make sense and meaning of their experiences.
- 22. Constructivism • Constructivism isthe theory that argues that knowledge is constructed when the learner is able to draw ideas from his own experiences and connects them to new ideas that are encountered.
- 23. Cooperative Learning • CooperativeLearning puts premium on active learning achieved by working with fellow learners as they all engage in a shared task.
- 24. Discovery and Inquiry-basedlearning • The mathematics curriculum allows for students to learn by asking relevant questions and discovering new ideas. • Discovery and Inquiry-based learning (Bruner, 1961) support the idea that students learn when they make use of personal experiences to discover facts, relationships and concepts.
- 25. Experiential and Situatedlearning • Ask students to record the time it takes them to travel from home to school in minutes for one week. • Tabulate the results • Ask students to make interpretation ▫ Which days took the longest time? Why is this so? ▫ Which days took the shortest time? Why is this so? • Open google maps and see how many kilometers is the distance from your house to school. • What is the average time required to get to school? • How many minutes per kilometer does it take you to travel?
- 26. Experiential and Situatedlearning • Watch your favorite cartoons. ▫ Count all the words being said in the cartoons. ▫ How long is the cartoon in minutes? ▫ If the time of the cartoon is doubled, can you predict the number of words that can be mentioned? • If you talk in the telephone for a 10 minutes, what is the estimated number if words you can use? • If you need to tell your friend an important message with 50 words, how much time will it require you to tell him/her?
- 27. Experiential and Situatedlearning • Measure how much volume can your bathroom pail contain water. • Determine the time it takes you to fill the pail. • If you double the size of your pail, how much time will you fill it? • Take the time in consuming the one pail of water when taking a bath. How many pails do you consume? • Given the pails of water you consume, estimate how long you take a bath.
- 28. Experiential and Situatedlearning • Ask students to collect their own data such as: ▫ weight of children in their barangay, ▫ number of people working in the community ▫ Students who had fever over the last month ▫ Number of households where things are stolen • Summarize the data by reporting the: ▫ Histogram, line graph ▫ Mean, Median, mode ▫ Standard deviation, range, quartile deviation • Ask students to make interpretation
- 29. Experiential and Situatedlearning • Count the number of people who joined “hueteng” in your community. • Compute the chance of winning for each person. • Judge whether there is a big chance of winning. • Estimate the number of people who joins the lotto each day. • Compute the chance of winning for each person. • Which game will give you a greater chance of winning?
- 30. Experiential and Situatedlearning • Count the set of pants and set of shirts you have at home. • Compute the number of combinations that you can make each? • Report how many days can you wear each combination. • Take a picture of each combination and put it in a portfolio. Plan when you will wear each pair. • When you ran out of combination how many pairs do you still need to buy for the rest of the occasion you need to wear a new set.
- 31. Experiential and Situatedlearning • Participants will give their own example
- 32. Reflective Learning • Usegoogle maps and estimate the kilometers from your house to where your father is working. • Ask for the total amount spent when commuting. • Ask for the total amount spent when driving your won car. • Show your data to your father and recommend which mode of transportation is better.
- 33. Reflective Learning • Getthe weight of each of your family members. • Determine their ages and check who is underweight and overweight. • Given your data make recommendations on the following: ▫ Money spent on food ▫ Menu for the week ▫ Exercise activities for the family
- 34. Reflective Learning • Keepa journal and take note of all your travels via plane. • Jot down in the journal the time you spent in the plane and the places you went. • Summarize the following: ▫ What places took the longest plane ride? Why? ▫ What places took the shorted plane ride? Why? ▫ What is the relationship between time and distance?
- 35. Reflective Learning • Getthe square meter of your land area. • How much does your land cost? • Get the square meter of other land areas. • How much do they cost? • Get the square meter of residential lands in the city. How much do they cost. • Compare the cost of equal land areas in the city and in the province? • Is there a difference? Why is this so? • What do you need to do if you want to live in the city?
- 36. Reflective Learning • Countthe total number of days your parents played for the lotto. Compute how much money did they spend for it? • If they have not won anything, how much could they have saved if they had not joined? • Where could this money be spent? • Provide a set of recommendations for your parents given your predictions.
- 37. Reflective Learning • Geta graph of the Philippine’s GDP from 2000 until 2013. • What years is the GDP high? Years it is low? • What inferences can you make about the present situation compared to the past years? • What events made the GDP high in those years? • What events made the GDP low in those years? • What projects should be engaged in order to increase the GDP again?
- 38. Reflective Learning • Participantswill give their own example
- 39. Constructivism • Students willidentify a problem in their community in the following areas: ▫ Waste management ▫ Overcrowding ▫ Increased air temperature • Collect data to serve as evidence to these problems by: ▫ Measure the weight of garbage produced by each household each day for 4 weeks ▫ Count the number of people living in each household and the floor area of their house. Report the ratio. ▫ Get the temperature each day and tabulate it. • Provide recommendations given the severity of the problem (reflective learning)
- 40. Constructivism • What typeof body pains did you experience as the most painful? Why did you had such pain? • List them down. • For each pain indicate how painful it is using a scale from 0 (no pain) to 10 (very painful) • Ask your classmates to rate the list of pain you have. • Get the average of the rating for each pain. • Report the standard deviation. • Given the SD are you all having a similar feeling for each pain? (reflective learning)
- 41. Constructivism • Measure thetemperature for the months of April and May. • Go to the malls and ask some sales person which types of clothes are bought and the quantity. • Tabulate the number of purchases for each type of clothes for each day and the temperature? • What does the temperature got to do with the type of clothes sold?
- 42. Constructivism • What typeof body pains did you experience as the most painful? Why did you had such pain? • List them down. • For each pain indicate how painful it is using a scale from 0 (no pain) to 10 (very painful) • Ask your classmates to rate the list of pain you have. • Get the average of the rating for each pain. • Report the standard deviation. • Given the SD are you all having a similar feeling for each pain? (reflective learning)
- 43. Constructivism • Make yourown portfolio of the clothes you will wear this summer. • Which of these clothes is your favorite? • Go to the malls and ask some sales person which types of clothes are bought and the quantity. • Tabulate the number of purchases for each type of clothes. Report into percentage. • Make a pie chart.
- 44. Constructivism • Which modelof cell phone do you have? • What do you think is the best cell phone model? • List down different cell phone models and count the number of people in your community who has it. • Make a bar graph for each model of cell phone? • Which one is the most in demand?
- 45. Constructivism • Participants willprovide their own example.
- 46. Cooperative Learning • Forma group and each one will be assigned to a place to take the air temperature for 7 days. • Compare the temperature for each person. • Why is there variation in the temperature? • Report the findings.
- 47. Cooperative Learning • Studentsform three groups and are assigned to measure the floor area of the classroom. • One group will only use a one inch paper clip. • One group will use an 8 inches pencil. • One group will use a 15 inches long stick. • Which group do you think will measure the floor area the fastest? Why?
- 48. Cooperative Learning • Participantswill provide their own example
- 49. Discovery and Inquiry-based •Students will ask their parents at home the different tools they use to measure length of objects. • The students will bring this material and demonstrate to their classmates how the tools are used.
- 50. Discovery and Inquiry-based •Self-study on the procedure to convert oC to oF. • Show how it is done in class
- 51. Discovery and Inquiry-based •Self-study on the procedure to compute for the mean, median and mode. • Show how it is done in class
- 52. Discovery and Inquiry-based •Participants will provide their own example
- 53.