![9
9
Numerical Integration
Definite integral of f(t) on
interval [a,b]
Analytic method: anti-
derivative
F where F’(t) = f(t)
Iab = F(b) – F(a)
( ) ( ) ( ) ( )
b
ab
a
F t I f t dt F b F a
](https://image.slidesharecdn.com/03integral-211013005136/75/SPSF03-Numerical-Integrations-9-2048.jpg)
![32
The Integral
2
2
1
5 sin ( )
x
x
I x x dx
Gnuplot
set xrange [0:10]
set xrange [0:20]
plot x*(sin(x))**2](https://image.slidesharecdn.com/03integral-211013005136/75/SPSF03-Numerical-Integrations-32-2048.jpg)
Uploaded bySyeilendra Pramuditya
SPSF03 - Numerical Integrations
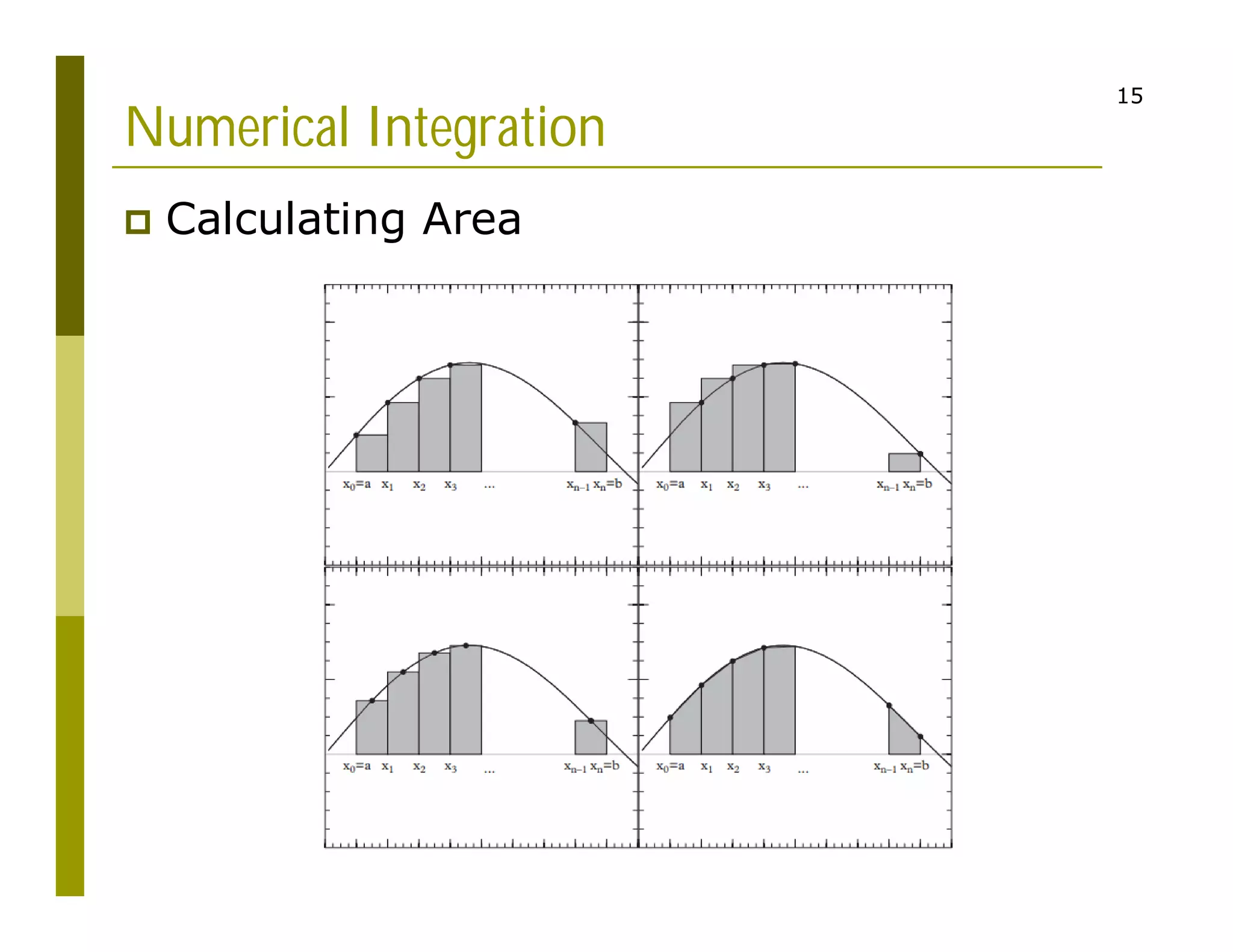
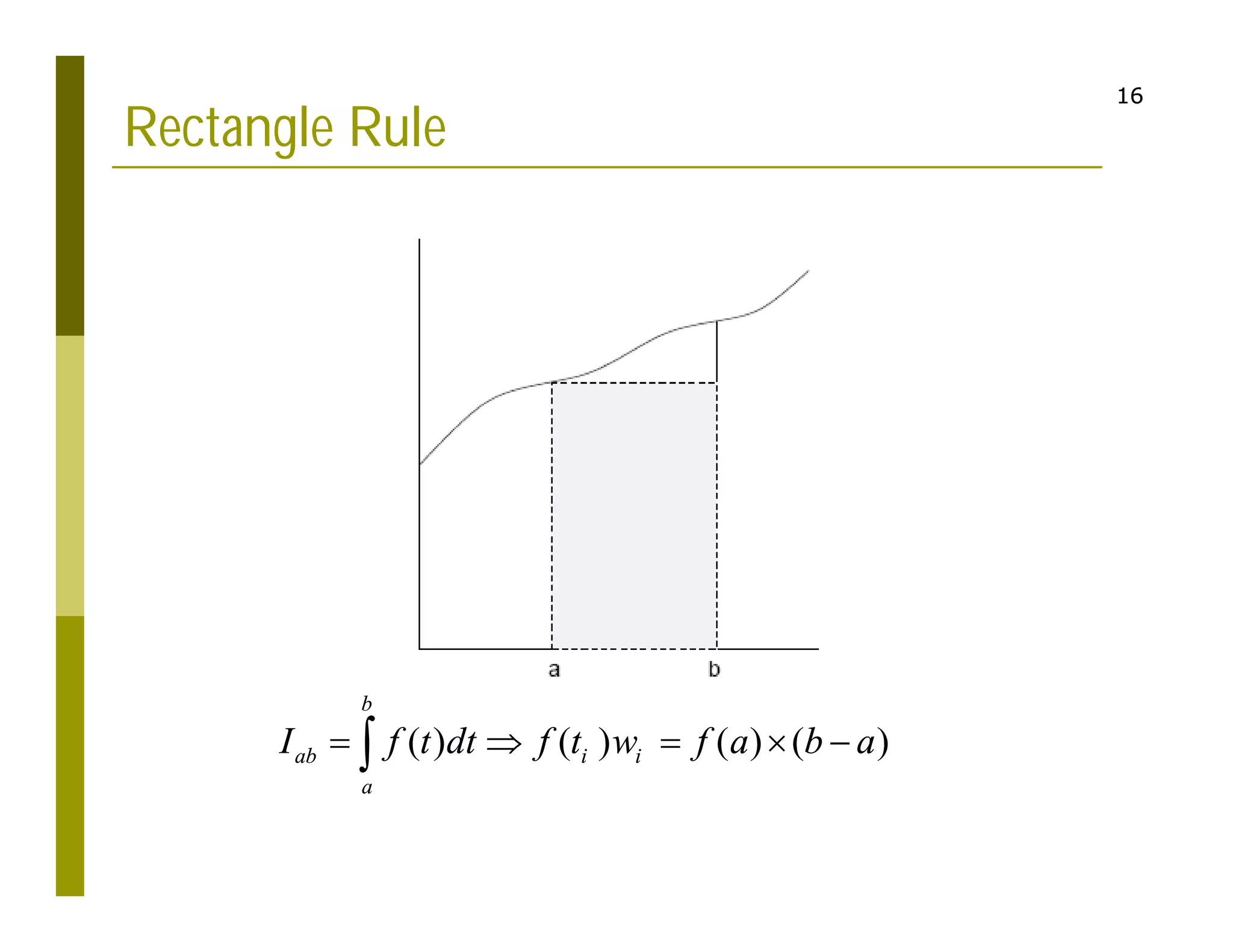
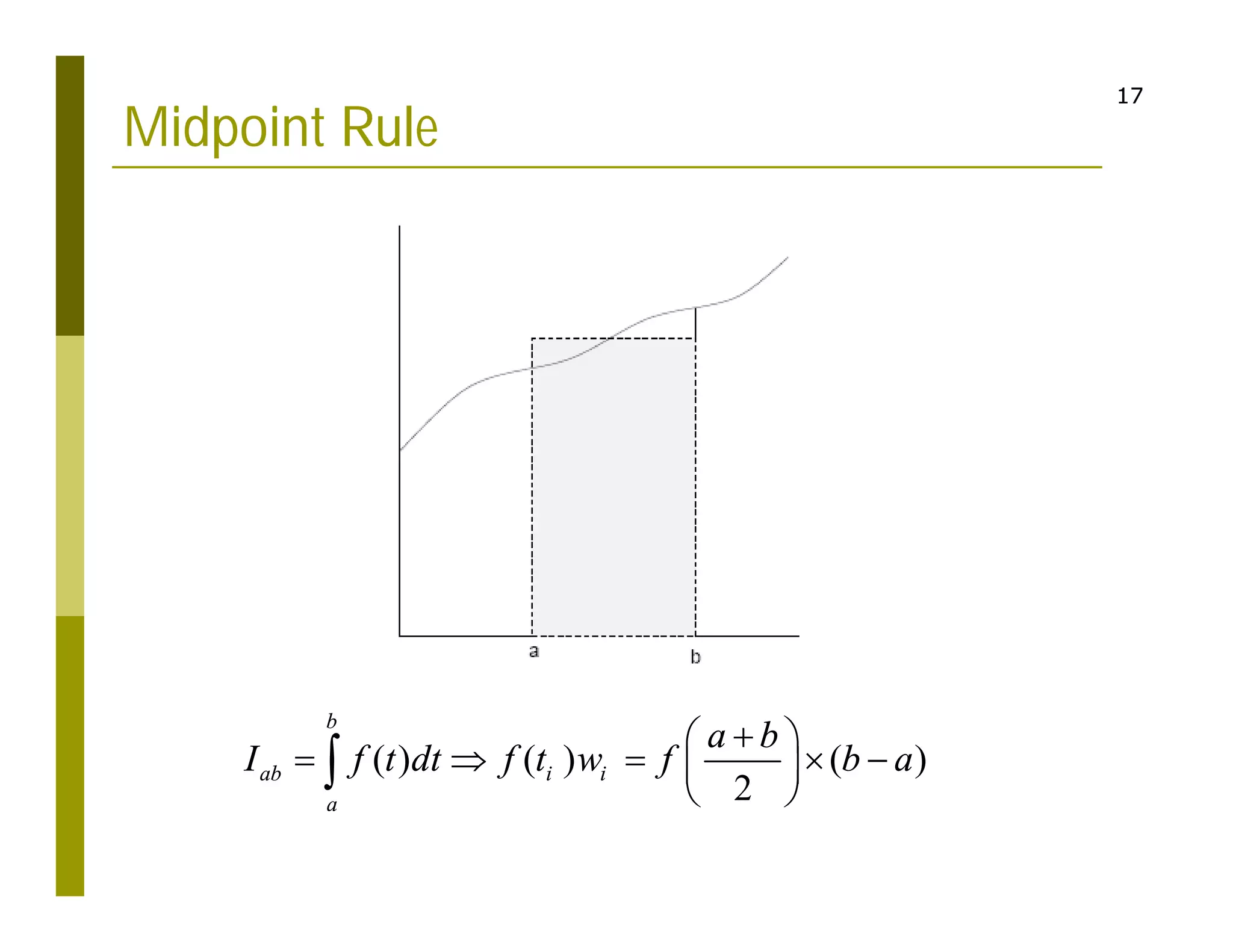
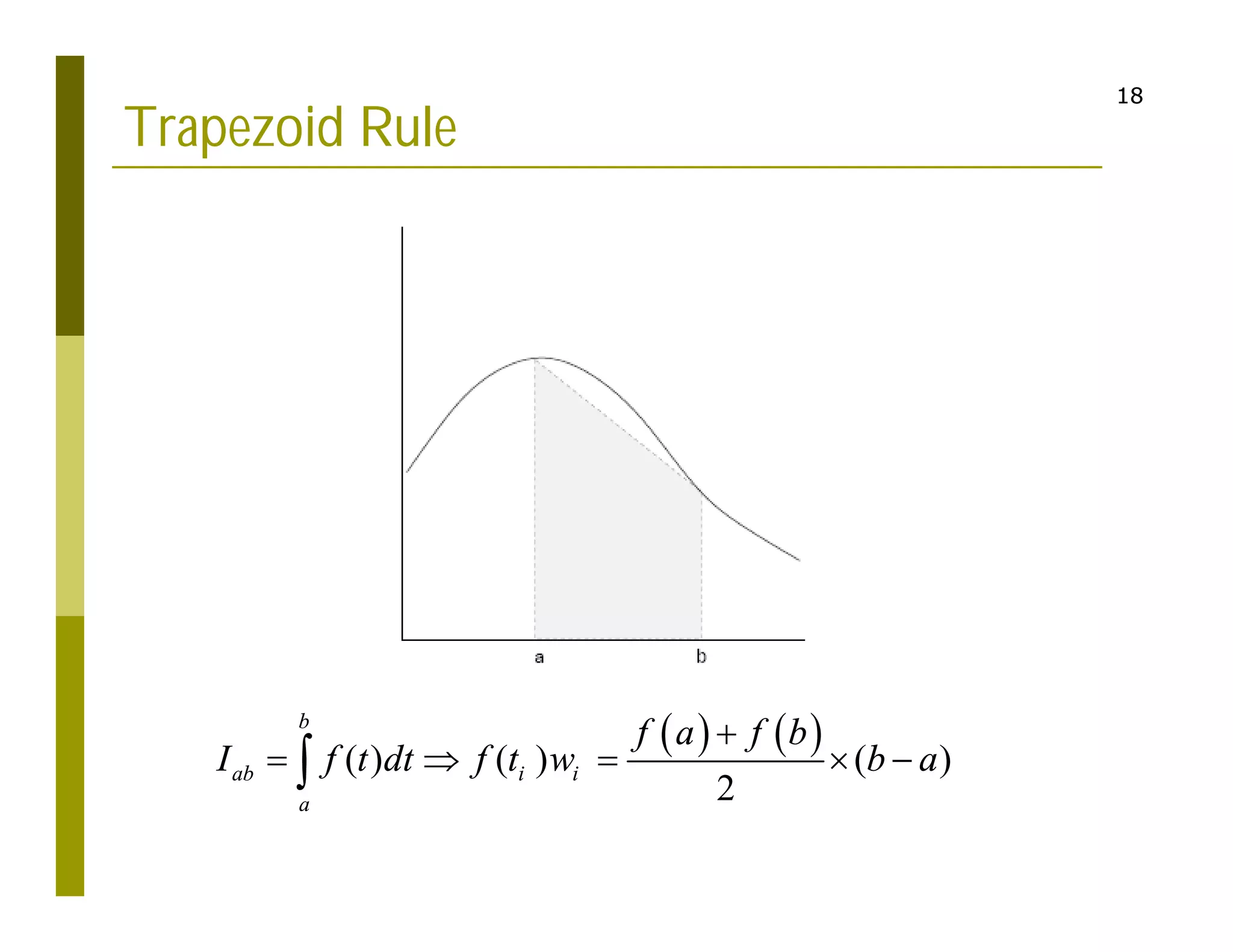
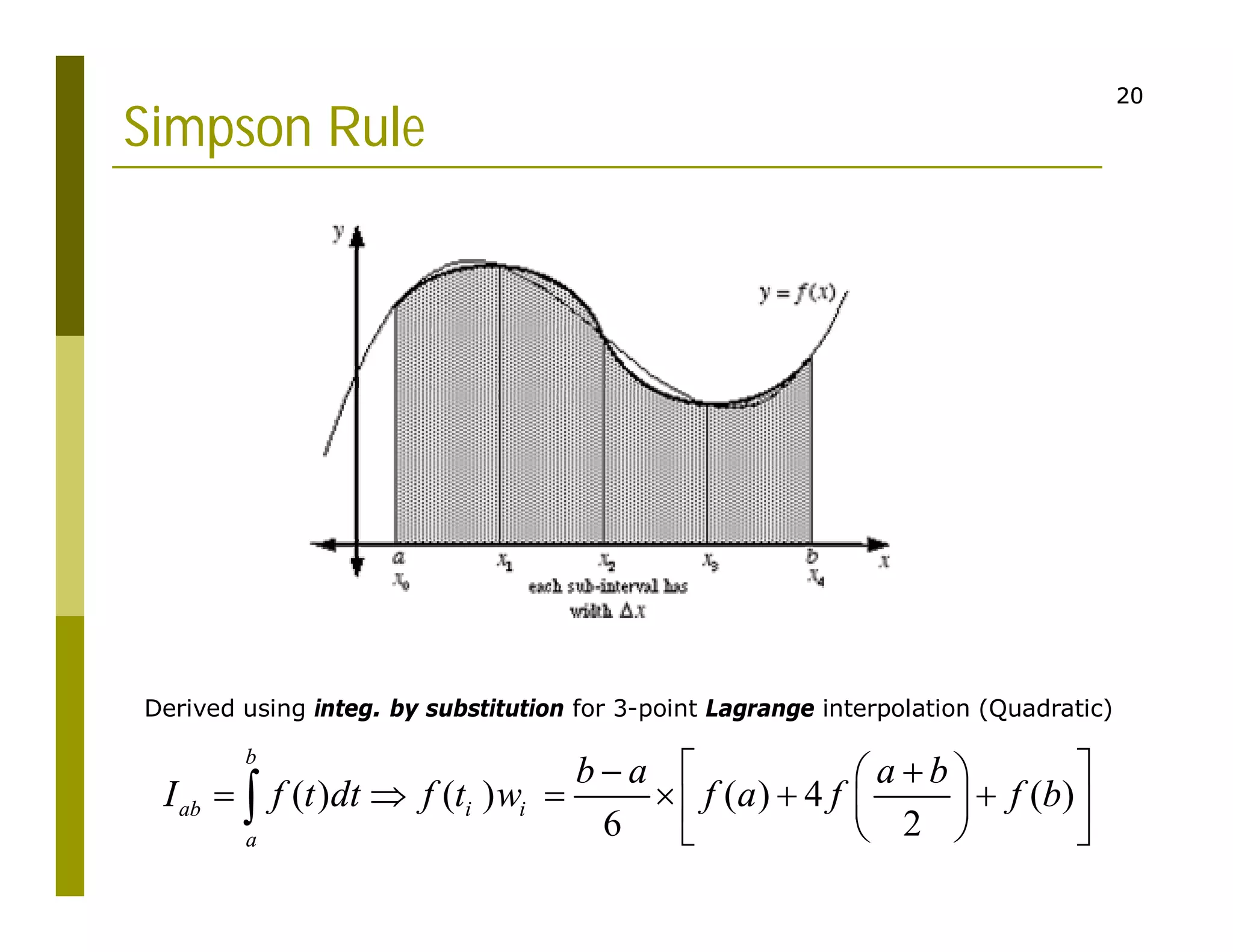
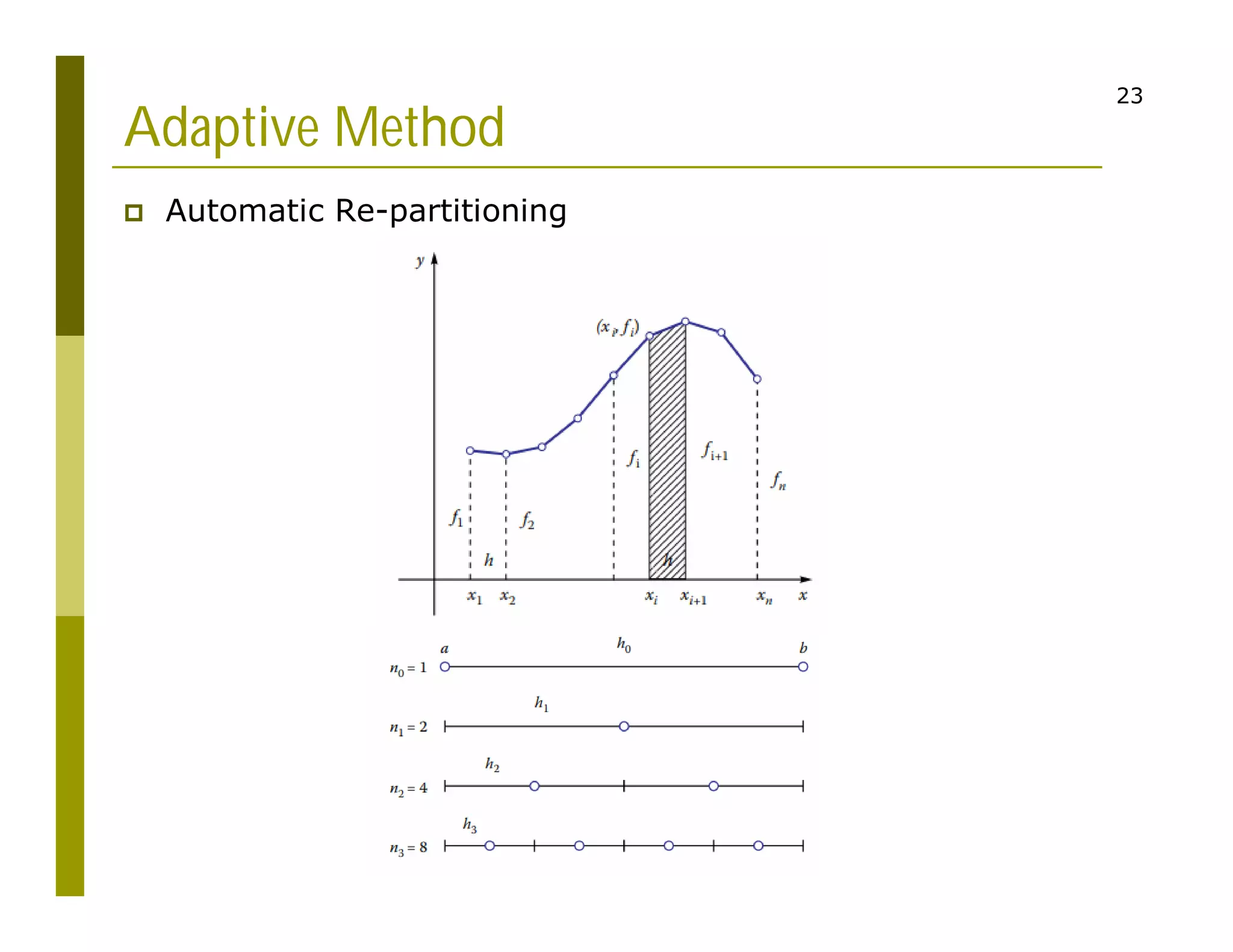
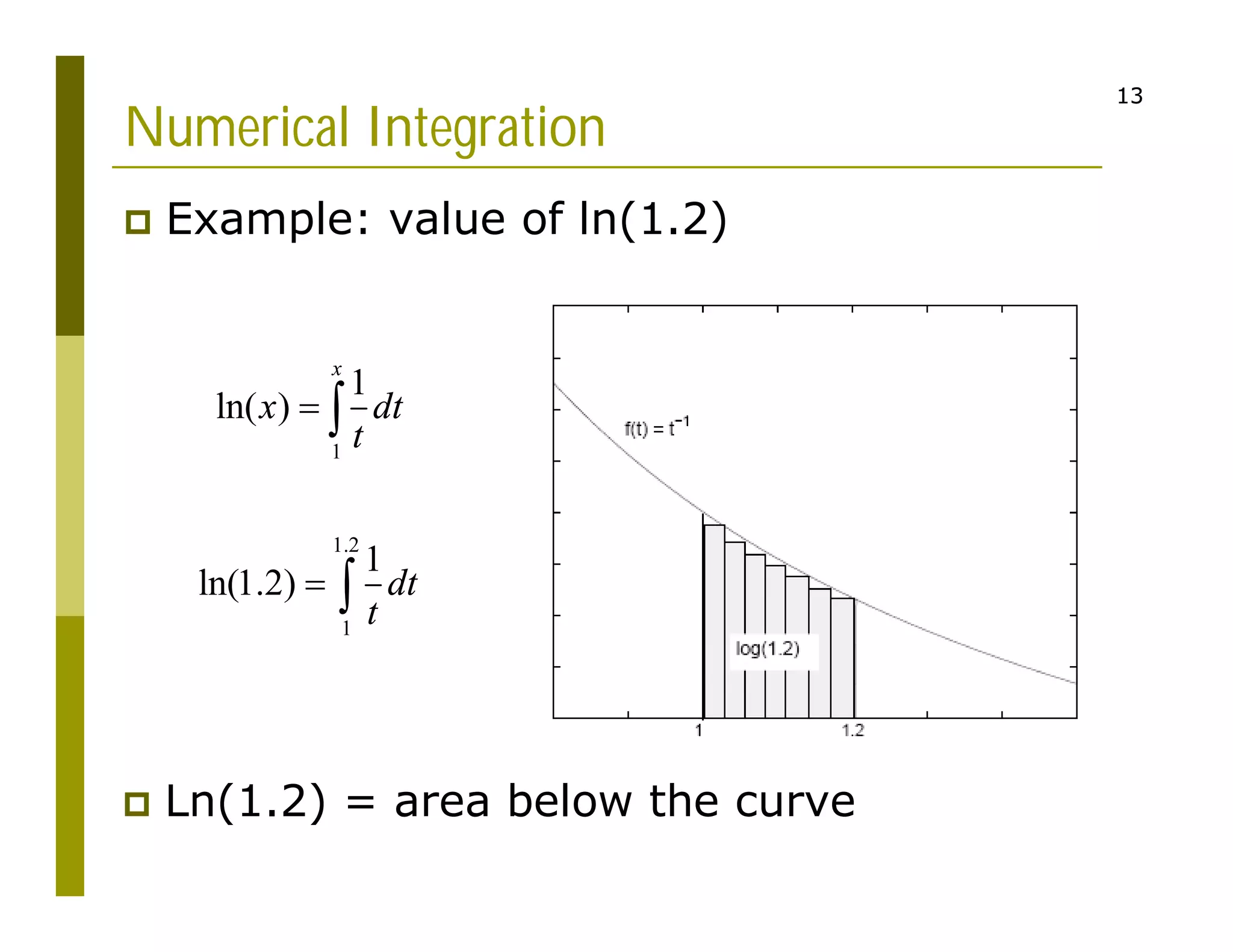
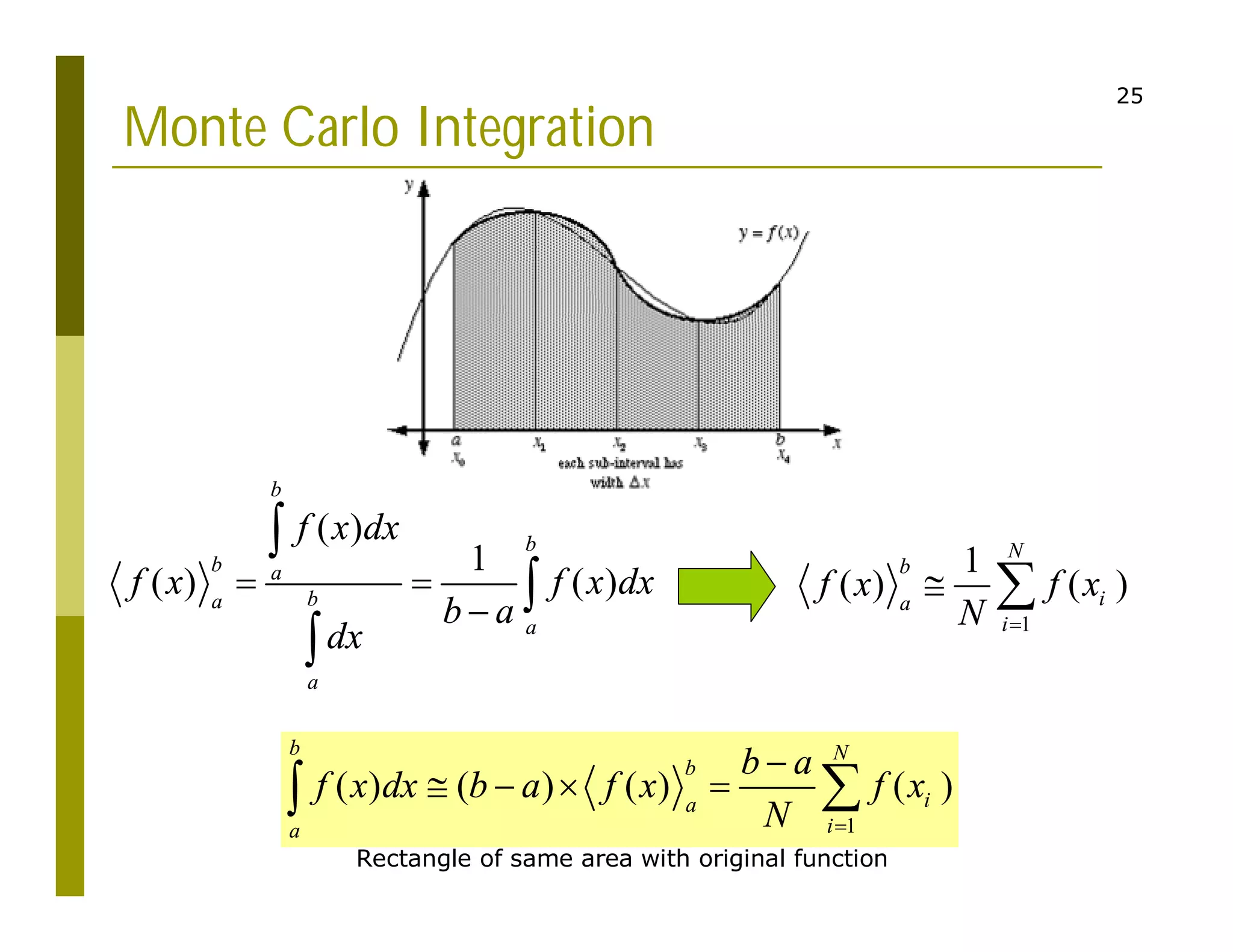
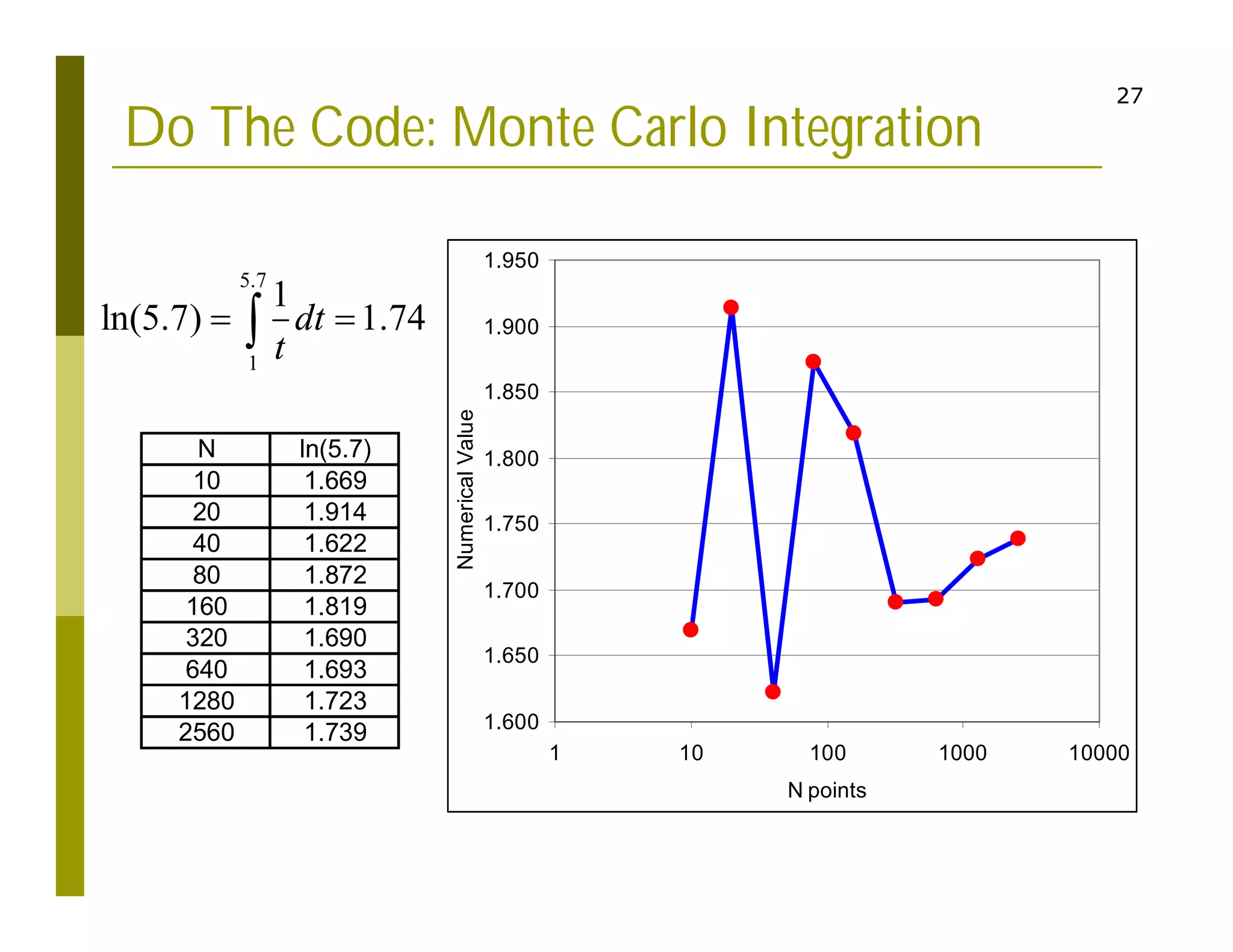
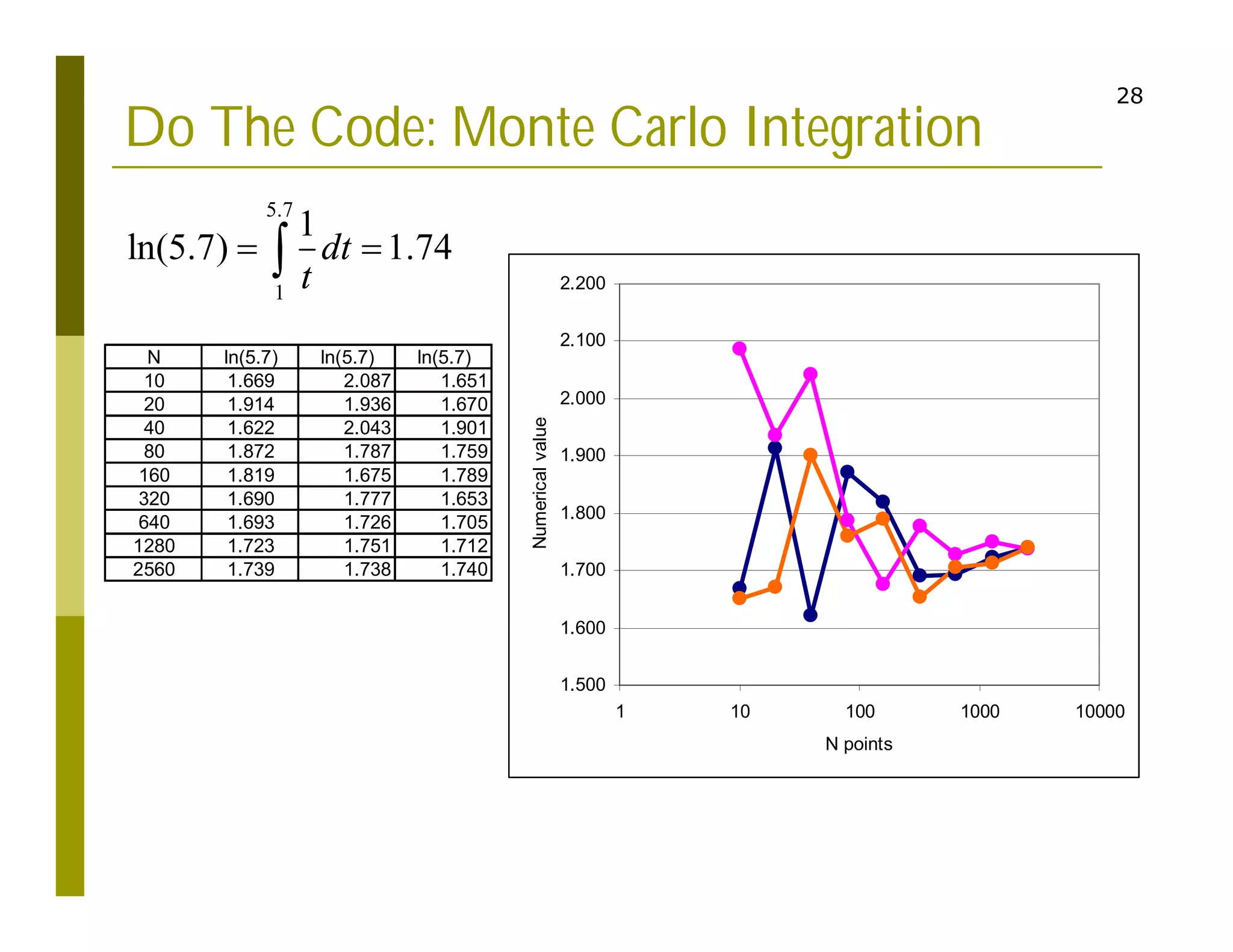
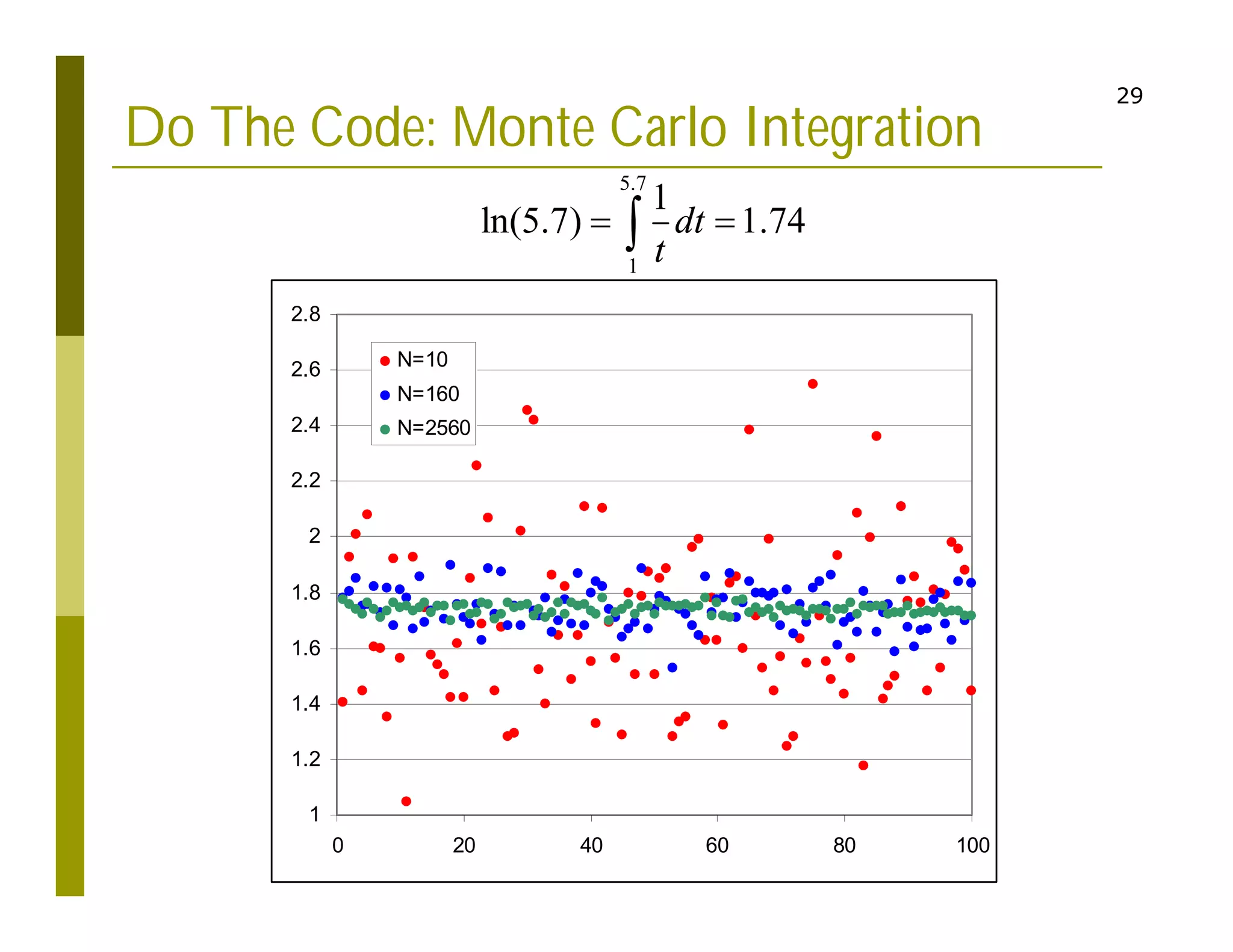
1. The document discusses numerical integration techniques for approximating definite integrals that cannot be solved analytically. It covers basic techniques like the rectangle, midpoint, and trapezoid rules as well as more accurate techniques like Simpson's rule. 2. Examples are provided to demonstrate calculating definite integrals numerically to approximate values like the natural logarithm of numbers. The document also introduces Monte Carlo integration techniques using random sampling. 3. As an example problem, the document calculates the final speed of a box moving under a time-varying force using numerical integration over the integral expression for work. The Simpson's rule is identified as an approach to implement in a programming code to solve this example.
SPSF03 - Numerical Integrations
- 1. 1 1 Programming, Computation, Simulation Applicationsin Math & Physics Numerical Integrations Syeilendra Pramuditya Department of Physics Institut Teknologi Bandung
- 2. 2 Physics Problem Periodof Pendulum How Easy! 2 2 ( ) ( ) 2 1 2 d t t SHM dt g f l l T f g
- 3. 3 Physics Problem LargeAmplitude Pendulum..?
- 4. 4 Physics Problem LargeAmplitude Pendulum..? sin g d d l
- 5. 5 Large Amplitude Pendulum Problem:Division by zero
- 6. 6 Large Amplitude Pendulum LegendreComplete Elliptic Integral of the First Kind Trigonometric identities, change of variable, etc…
- 7. 7 Large Amplitude Pendulum Input g, l, 0 Process Evaluate the integral Output Period of the pendulum Small Amplitude 1 2 l T f g Solution by series expansion Check your result
- 8. 8 Do The Code Benchmark your integrator code first 0 1 0 sin(30 ) 0.5 sin (0.5) 30
- 9. 9 9 Numerical Integration Definiteintegral of f(t) on interval [a,b] Analytic method: anti- derivative F where F’(t) = f(t) Iab = F(b) – F(a) ( ) ( ) ( ) ( ) b ab a F t I f t dt F b F a
- 10. 10 Hand Calculation? Calculateuntil 2 decimal numbers? a = 88/17 b = square-root of 23 c = ln(7)
- 11. 11 11 Numerical Integration ln7= .. ? ln5 = .. ? 7 5 1 ( ) 1 ln 7 ln5 ab f t t I dt t Need to somehow calculate the numerical value of natural logarithm Real-world functions don’t have anti derivatives Direct calculation of definite integrals is needed
- 12. 12 Numerical Integration Newton-CotesFormula Composite Method Quadrature Method Riemann Sum Etc…
- 13. 13 13 Numerical Integration Example:value of ln(1.2) 1 1 ln( ) x x dt t 1.2 1 1 ln(1.2) dt t Ln(1.2) = area below the curve
- 14. 14 14 Numerical Integration GeneralFormula 0 ( ) ( ) b n ab i i i a I f t dt f t w f(ti) : function f evaluated at ti wi : weighting factor
- 15.
- 16. 16 16 Rectangle Rule ( )( ) ( ) ( ) b ab i i a I f t dt f t w f a b a
- 17. 17 17 Midpoint Rule ( )( ) ( ) 2 b ab i i a a b I f t dt f t w f b a
- 18. 18 18 Trapezoid Rule ( ) ( ) ( ) 2 b ab i i a f a f b I f t dt f t w b a
- 19. 19 19 Non-Linear Rule (Simpson) Approx.by 3-point Lagrange interpolation (Quadratic) 2 ( ) p x ax bx c
- 20. 20 20 Simpson Rule ( )( ) ( ) 4 ( ) 6 2 b ab i i a b a a b I f t dt f t w f a f f b Derived using integ. by substitution for 3-point Lagrange interpolation (Quadratic)
- 21. 21 21 Simpson Rule 1 1 1 ( )( ) 4 ( ) 6 2 b N i i ab i i i a x x x I f x dx f x f f x Derived using integ. by substitution for 3-point Lagrange interpolation (Quadratic) N partitions
- 22. 22 More Complex Integral 7.6 3.2 2 () ln( ) ( ) 5 ab I f t dt x f t x
- 23. 23 Adaptive Method AutomaticRe-partitioning
- 24. 24 Monte Carlo Integration 1 Averageof 2, 8, 5, 12, 4 2 8 5 12 4 Average 5 1 ( ) ( ) ( ) 1 ( ) ( ) N b i a i b b b a b a a a f x f x N f x dx f x f x dx b a dx Discrete Functions Continuous Functions
- 25. 25 Monte Carlo Integration () 1 ( ) ( ) b b b a b a a a f x dx f x f x dx b a dx 1 1 ( ) ( ) N b i a i f x f x N 1 ( ) ( ) ( ) ( ) b N b i a i a b a f x dx b a f x f x N Rectangle of same area with original function
- 26. 26 Do The Code:Monte Carlo Integration 5.7 1 1 ln(5.7) 1.74 dt t
- 27. 27 Do The Code:Monte Carlo Integration N ln(5.7) 10 1.669 20 1.914 40 1.622 80 1.872 160 1.819 320 1.690 640 1.693 1280 1.723 2560 1.739 1.600 1.650 1.700 1.750 1.800 1.850 1.900 1.950 1 10 100 1000 10000 N points Numerical Value 5.7 1 1 ln(5.7) 1.74 dt t
- 28. 28 Do The Code:Monte Carlo Integration 5.7 1 1 ln(5.7) 1.74 dt t N ln(5.7) ln(5.7) ln(5.7) 10 1.669 2.087 1.651 20 1.914 1.936 1.670 40 1.622 2.043 1.901 80 1.872 1.787 1.759 160 1.819 1.675 1.789 320 1.690 1.777 1.653 640 1.693 1.726 1.705 1280 1.723 1.751 1.712 2560 1.739 1.738 1.740 1.500 1.600 1.700 1.800 1.900 2.000 2.100 2.200 1 10 100 1000 10000 N points Numerical value
- 29. 29 Do The Code:Monte Carlo Integration 5.7 1 1 ln(5.7) 1.74 dt t 1 1.2 1.4 1.6 1.8 2 2.2 2.4 2.6 2.8 0 20 40 60 80 100 N=10 N=160 N=2560
- 30. 30 Do The Code:Monte Carlo Integration 7.6 3.2 2 ( ) ln( ) ( ) 5 ab I f t dt x f t x
- 31. 31 Sample Problem A variableforce is applied to an initially stationary box of mass 2.35 kg at x= 0 m. The box moves in +x direction due to the applied force. What is the speed of the box when its position is at x = 7.53 m? The surface is frictionless. 2 ˆ ( ) 5 sin ( rad) F x x x i N 2 2 1 1 2 2 2 2 1 1 ( ) ( )cos(0) 1 ( ) 5 sin ( ) 2 f i x x f x x x x f x x K K K W K F x dx F x dx mv F x dx x x dx
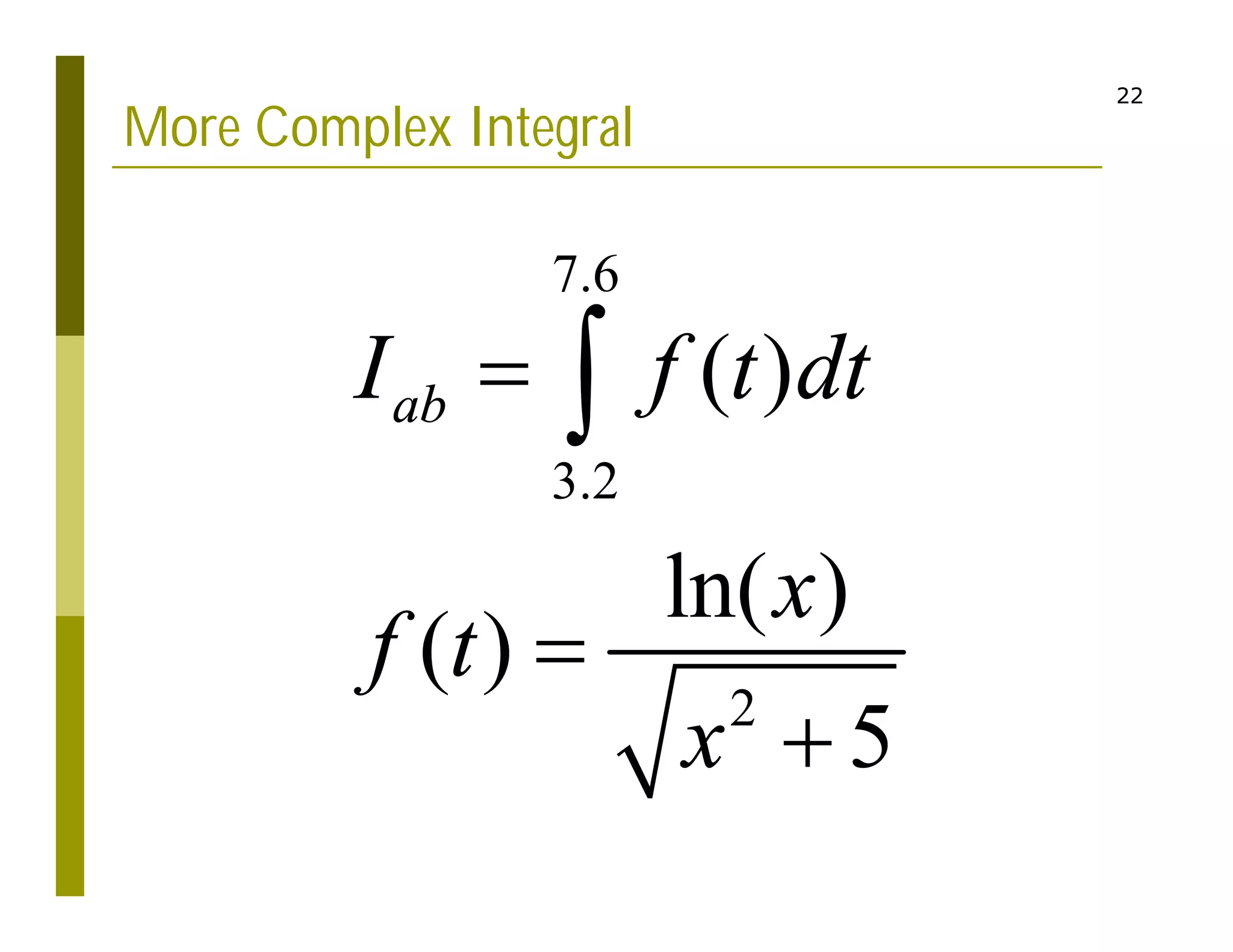
- 32. 32 The Integral 2 2 1 5 sin( ) x x I x x dx Gnuplot set xrange [0:10] set xrange [0:20] plot x*(sin(x))**2
- 33. 33 Practice Develop yourintegrator code using Simpson rule in Pascal language The code mainly evaluates numerically: What is the final speed of the box? Using 75 partitions 2 2 1 5 sin ( ) x x I x x dx