Uploaded bySyeilendra Pramuditya
SPSF02 - Graphical Data Representation
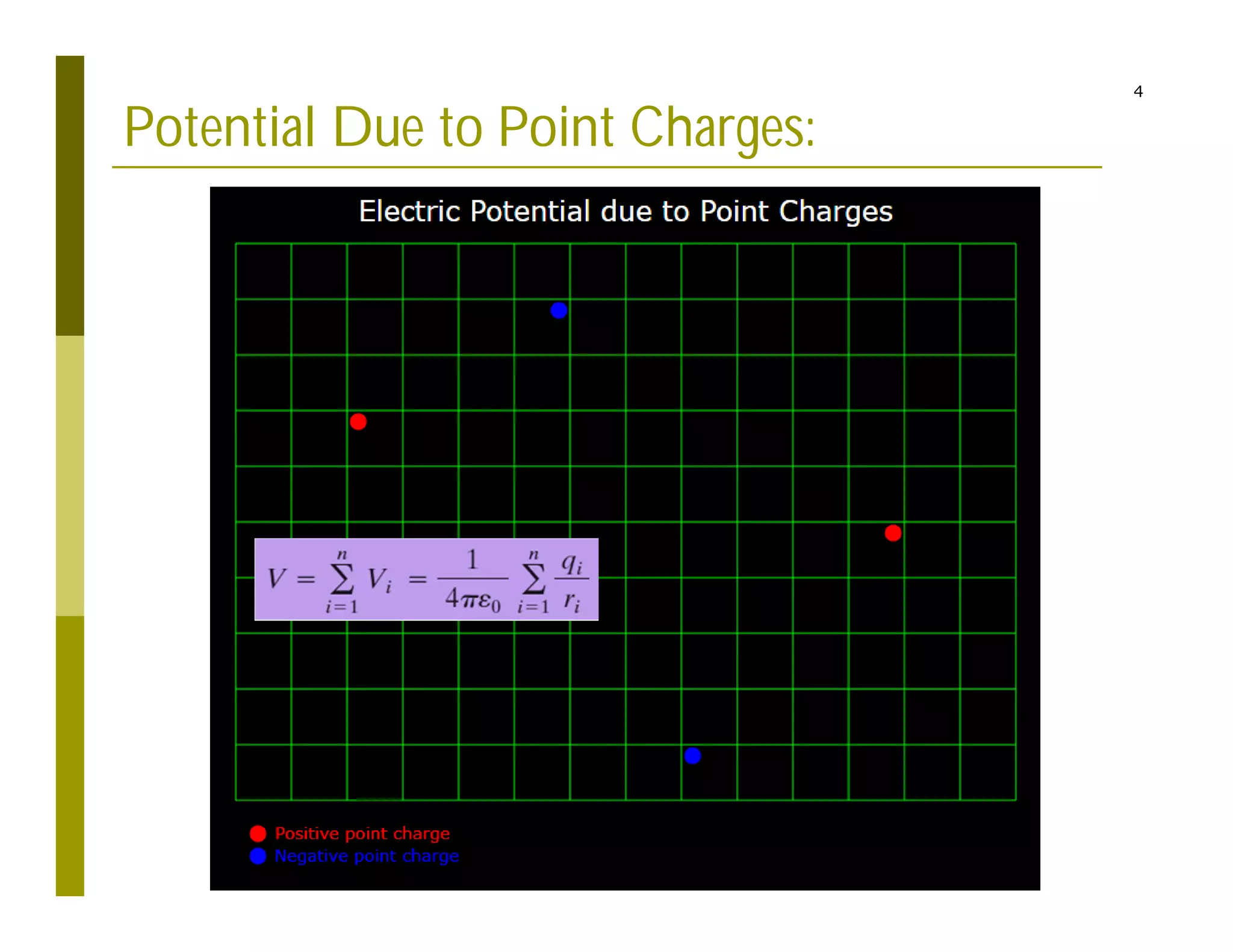
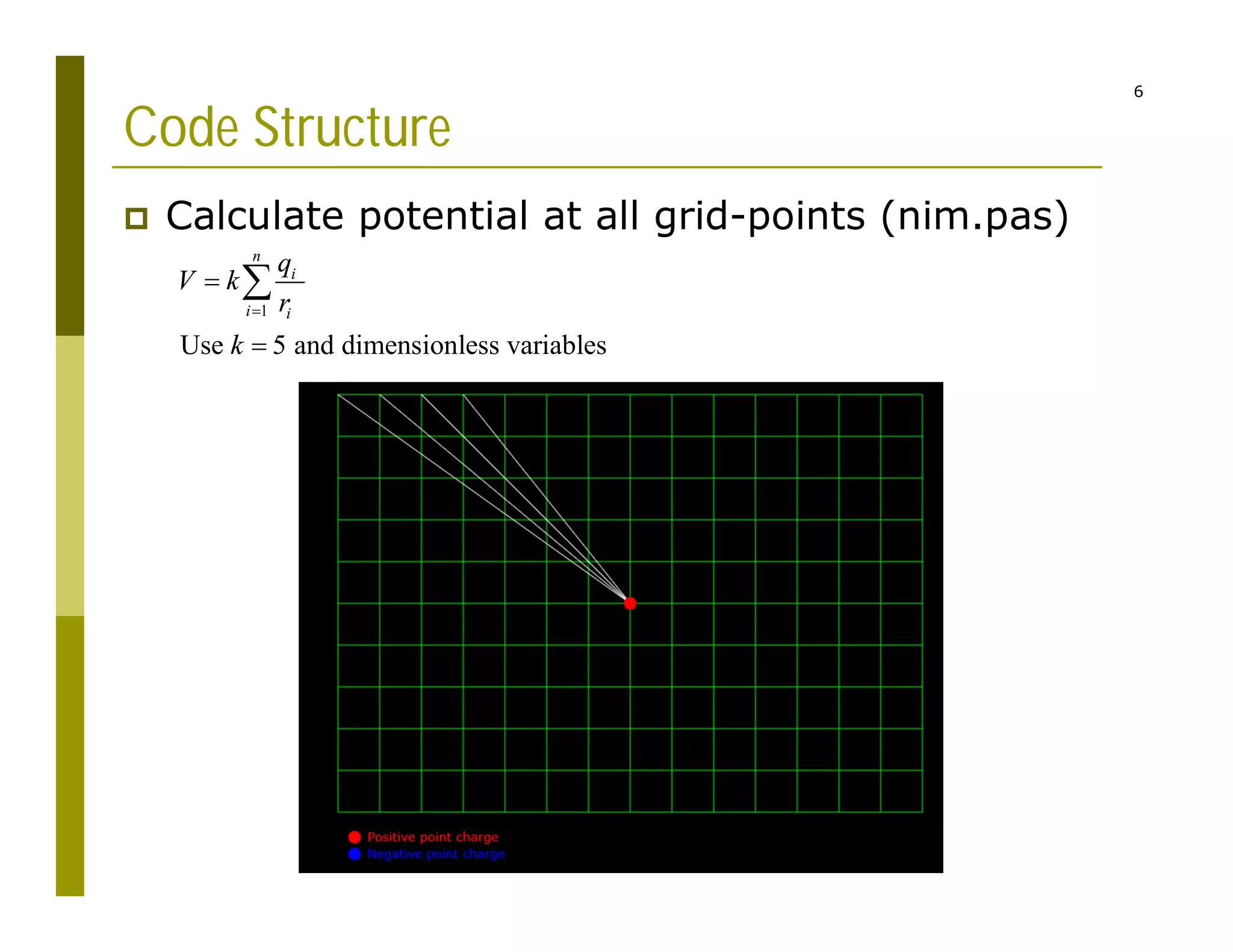
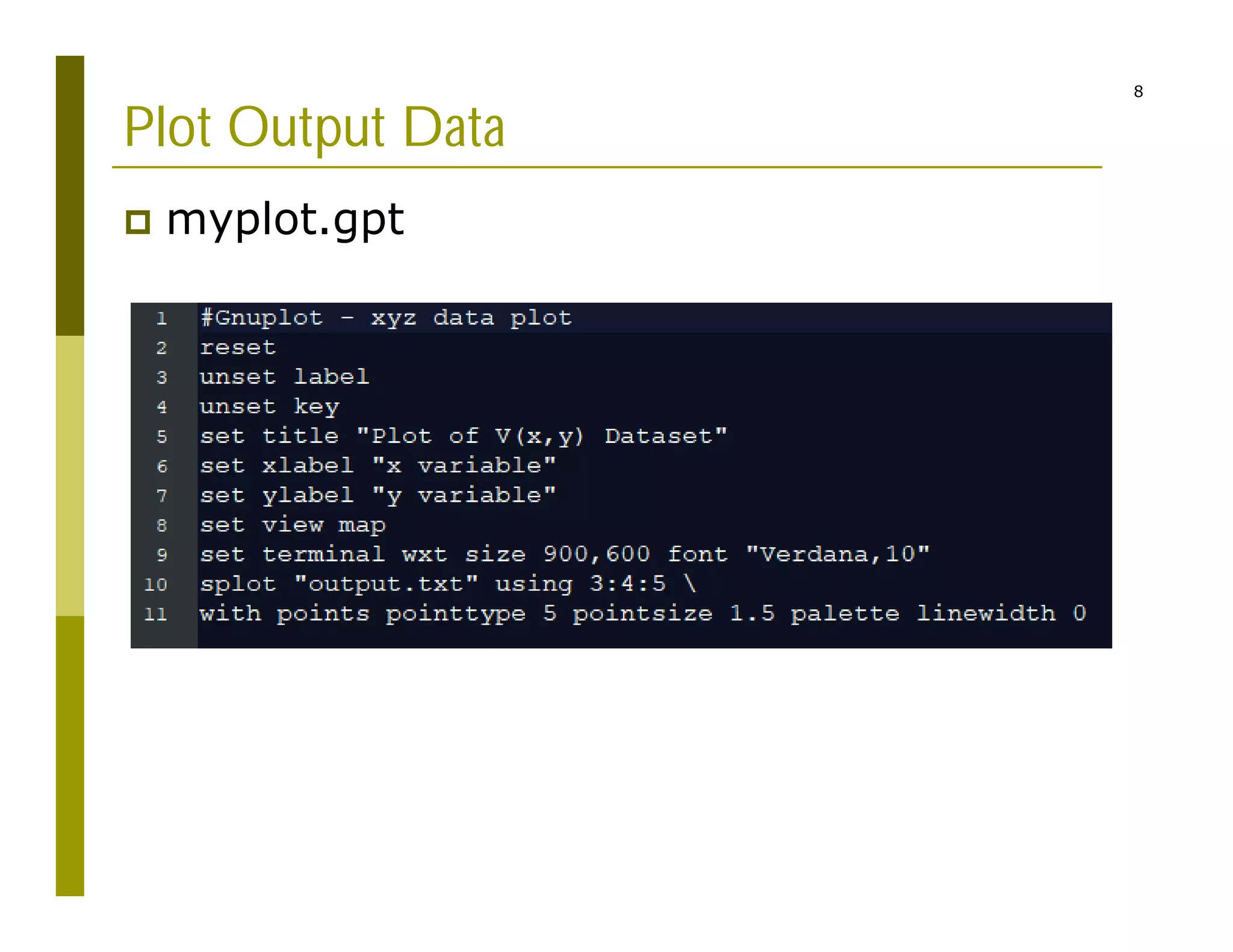
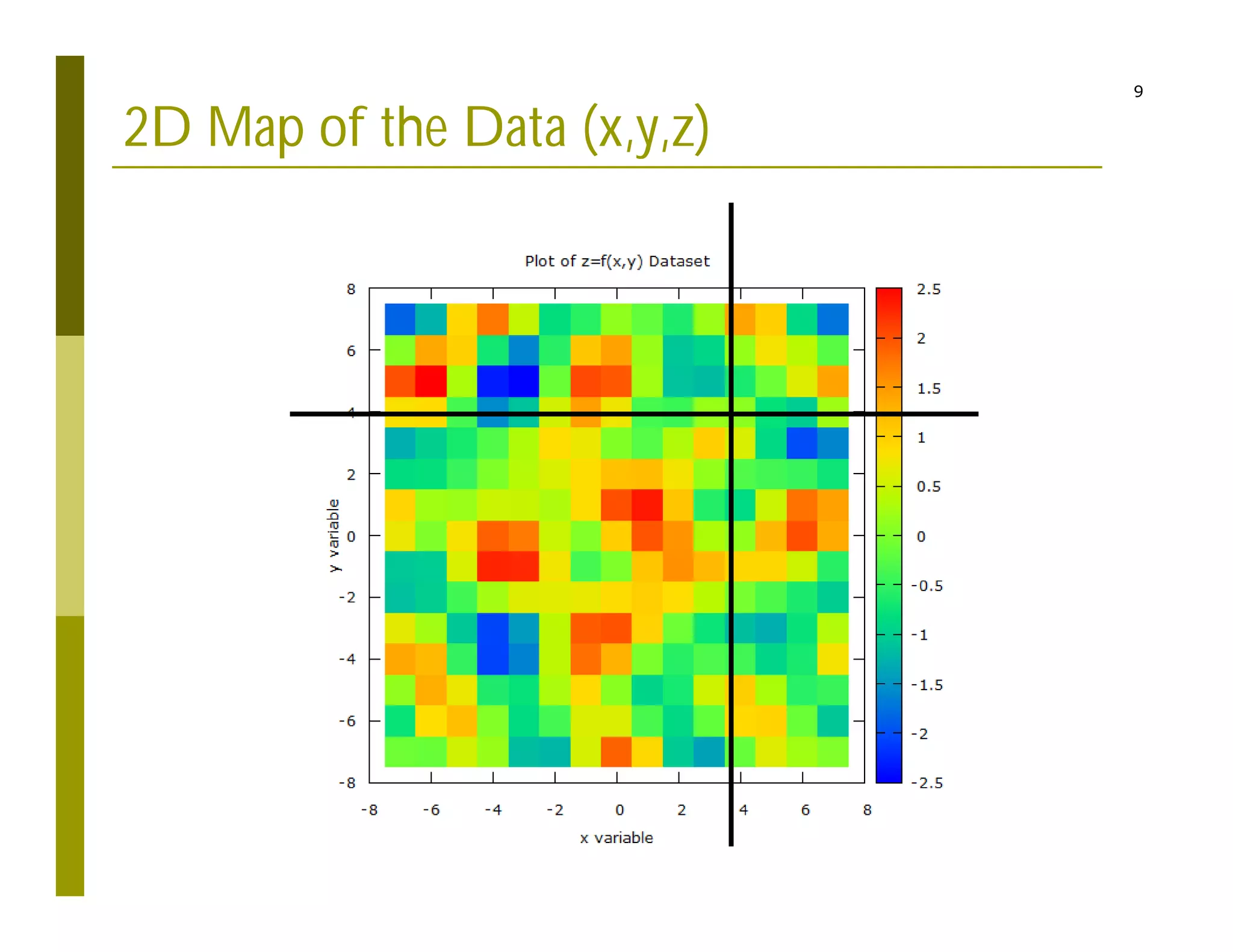
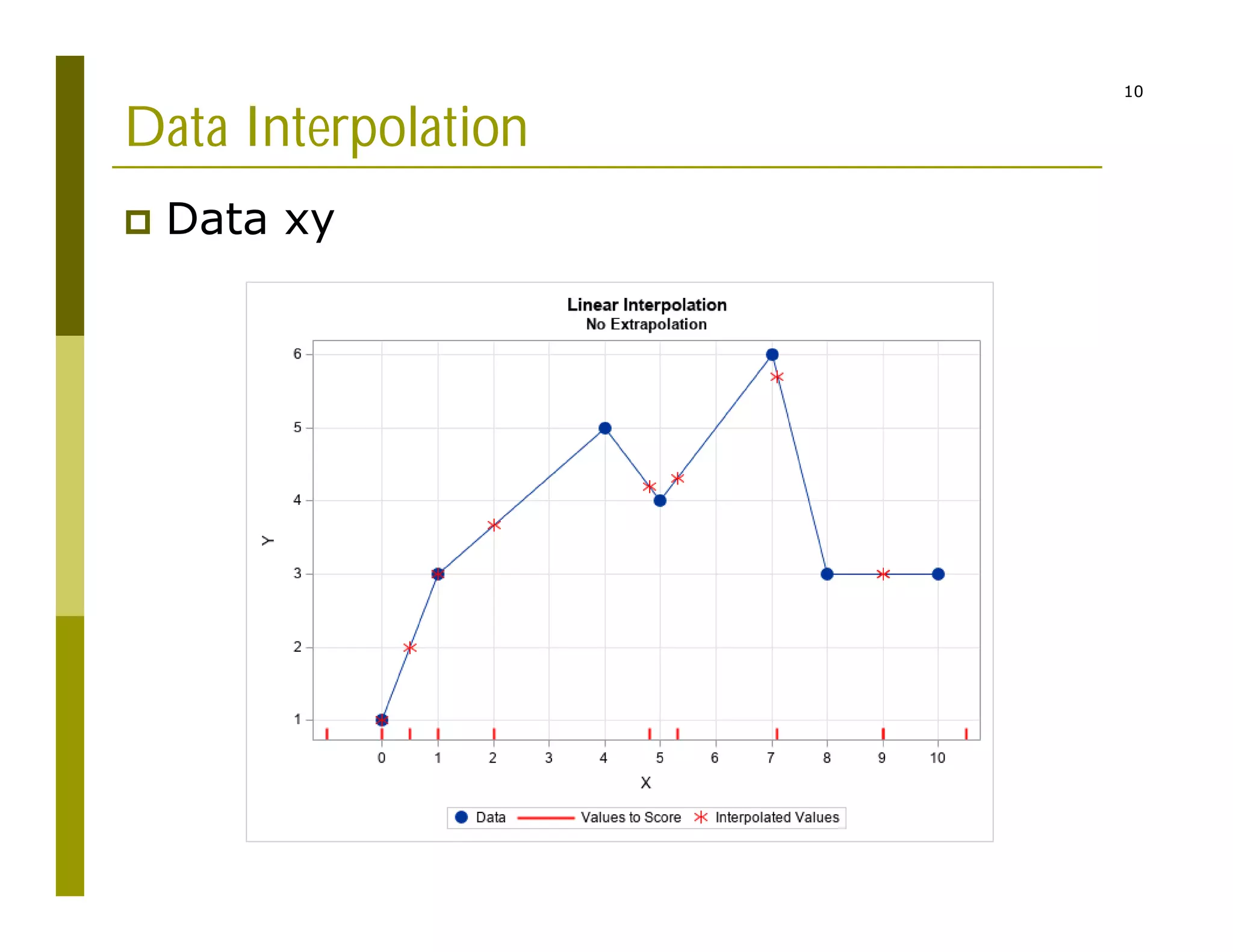
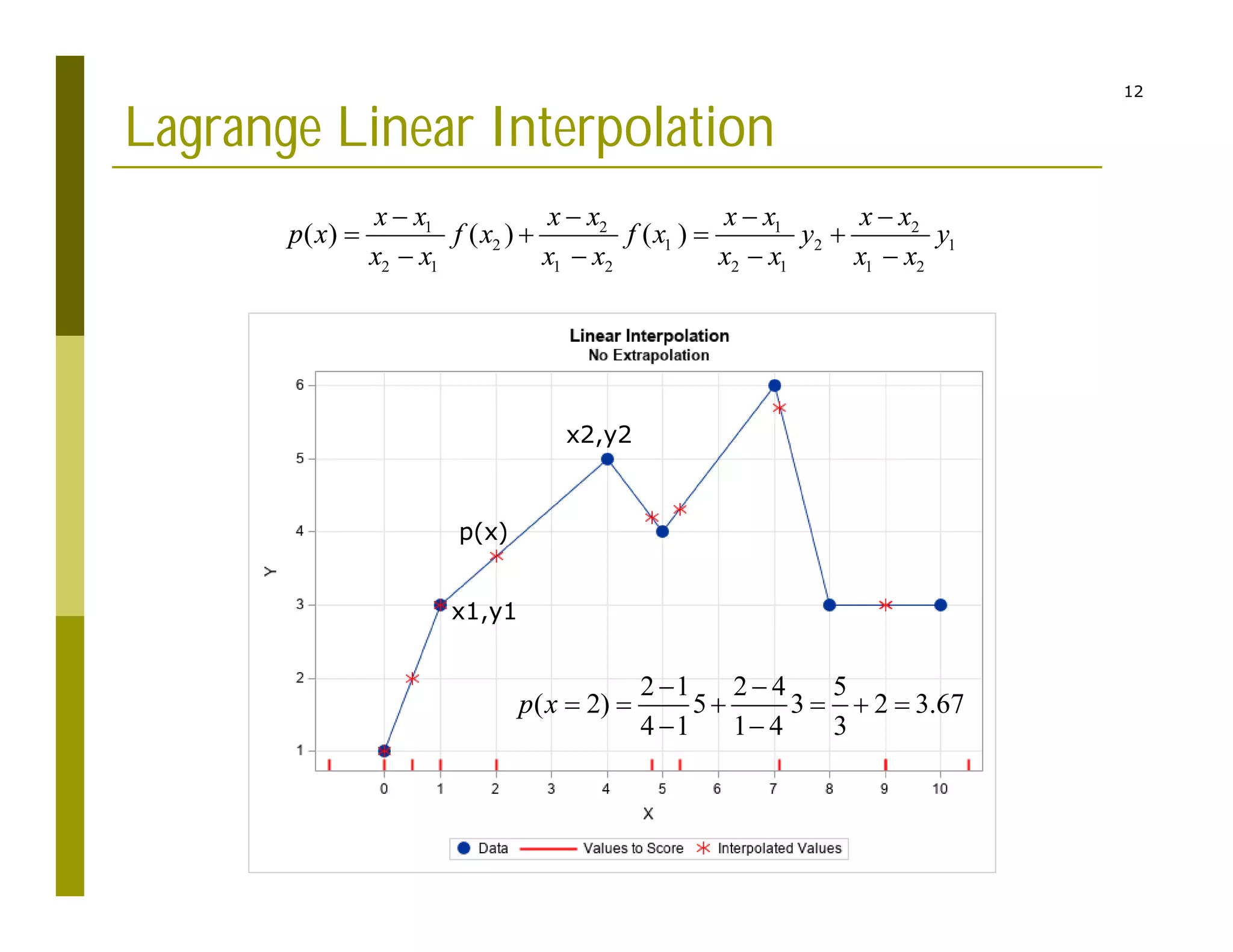
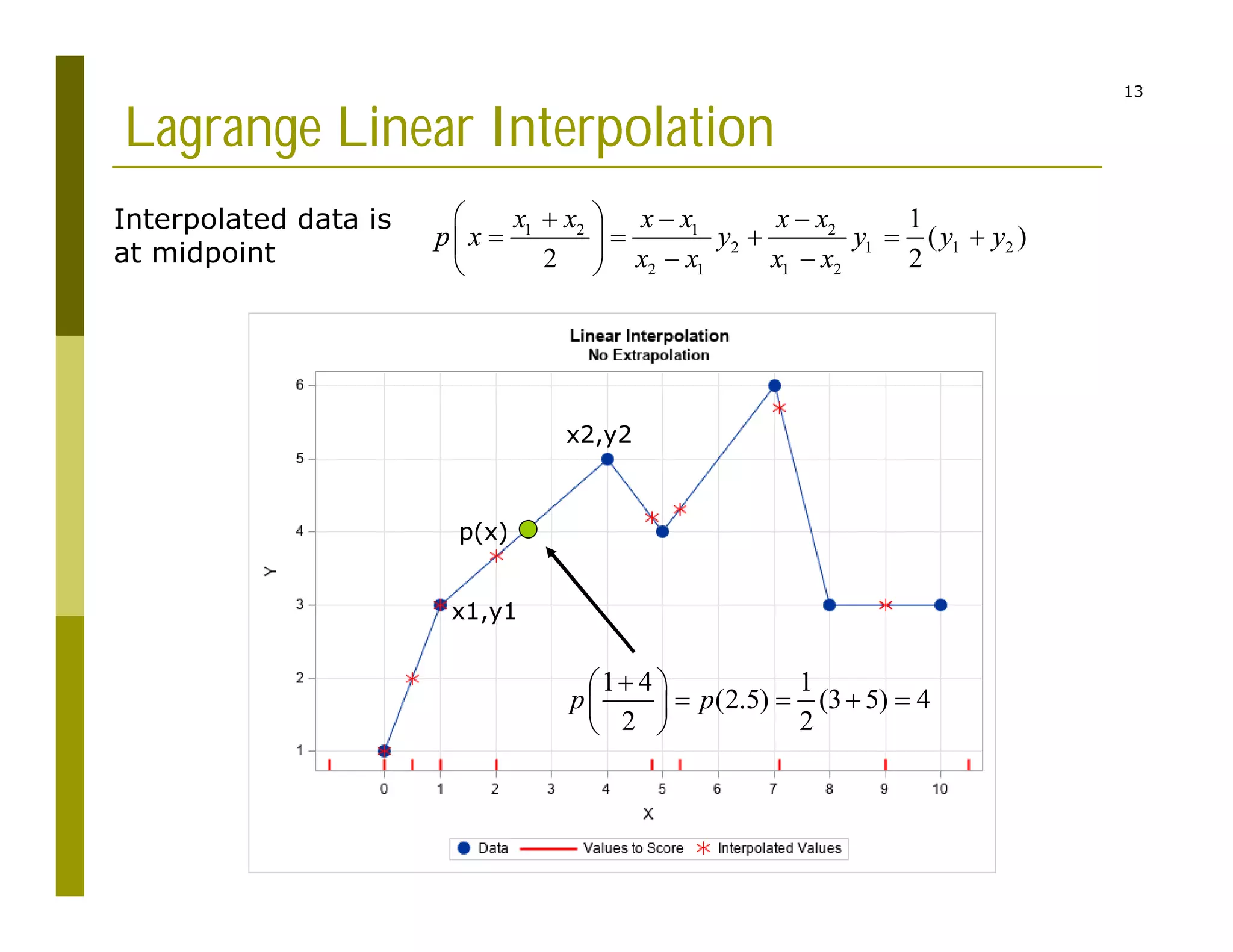
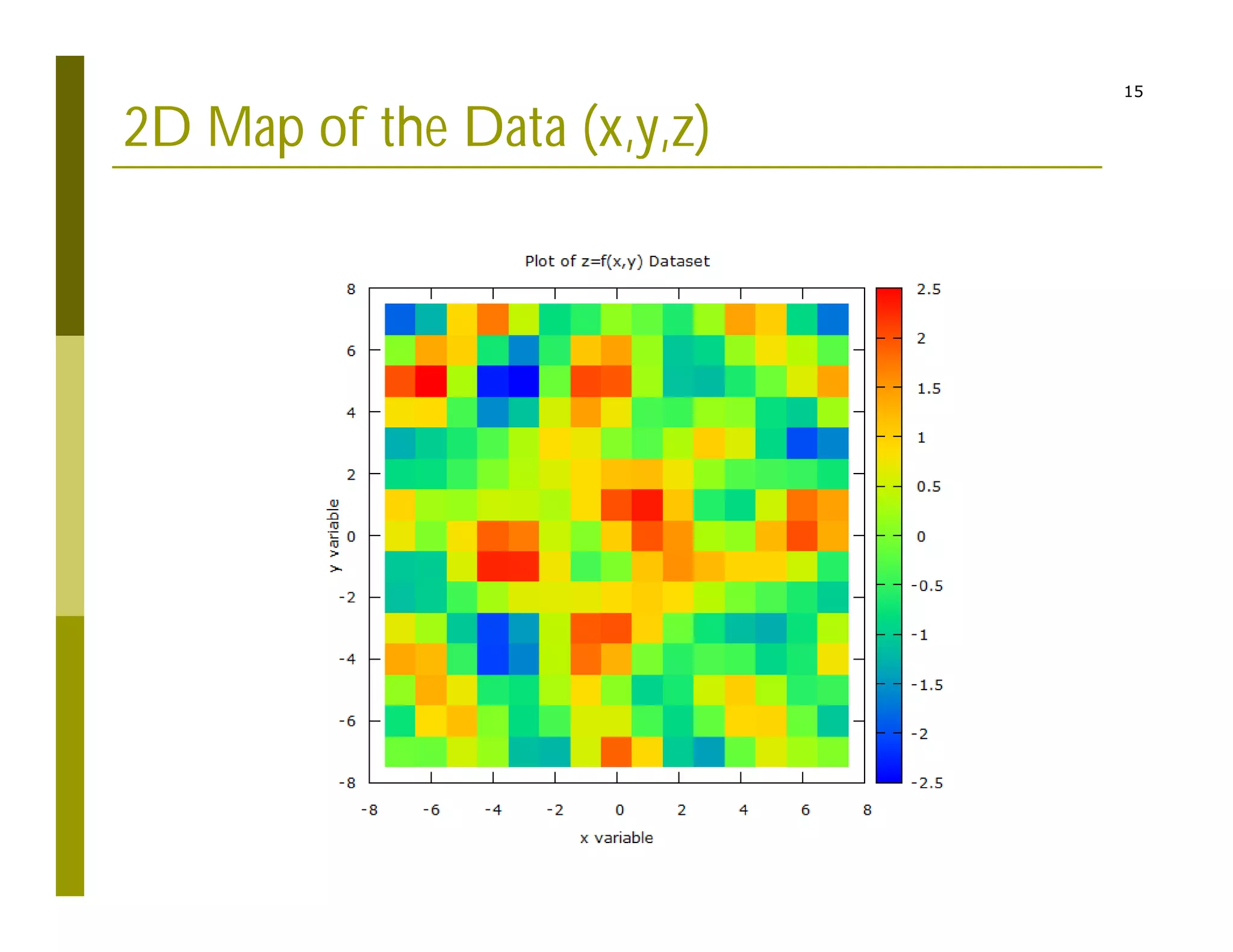
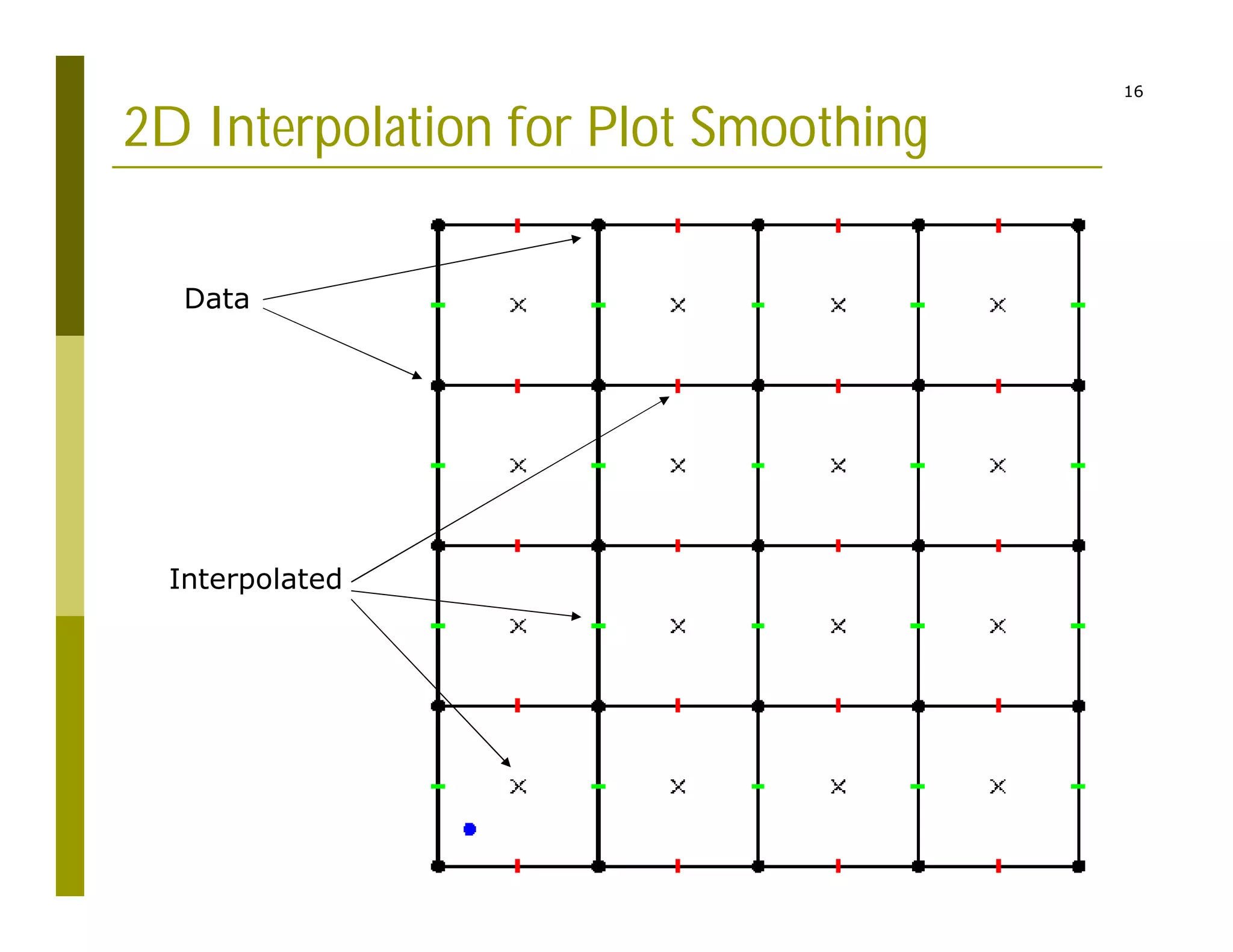
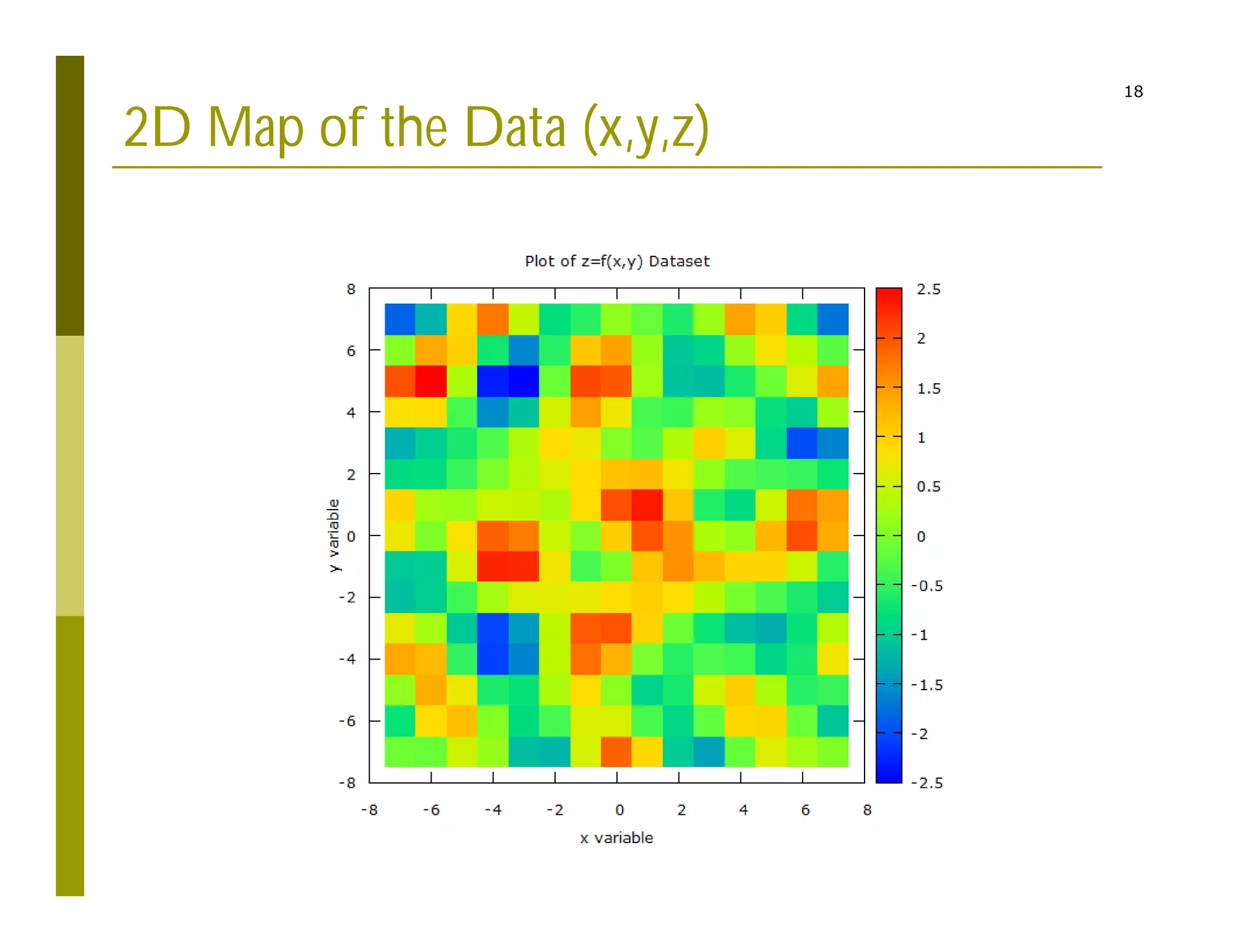
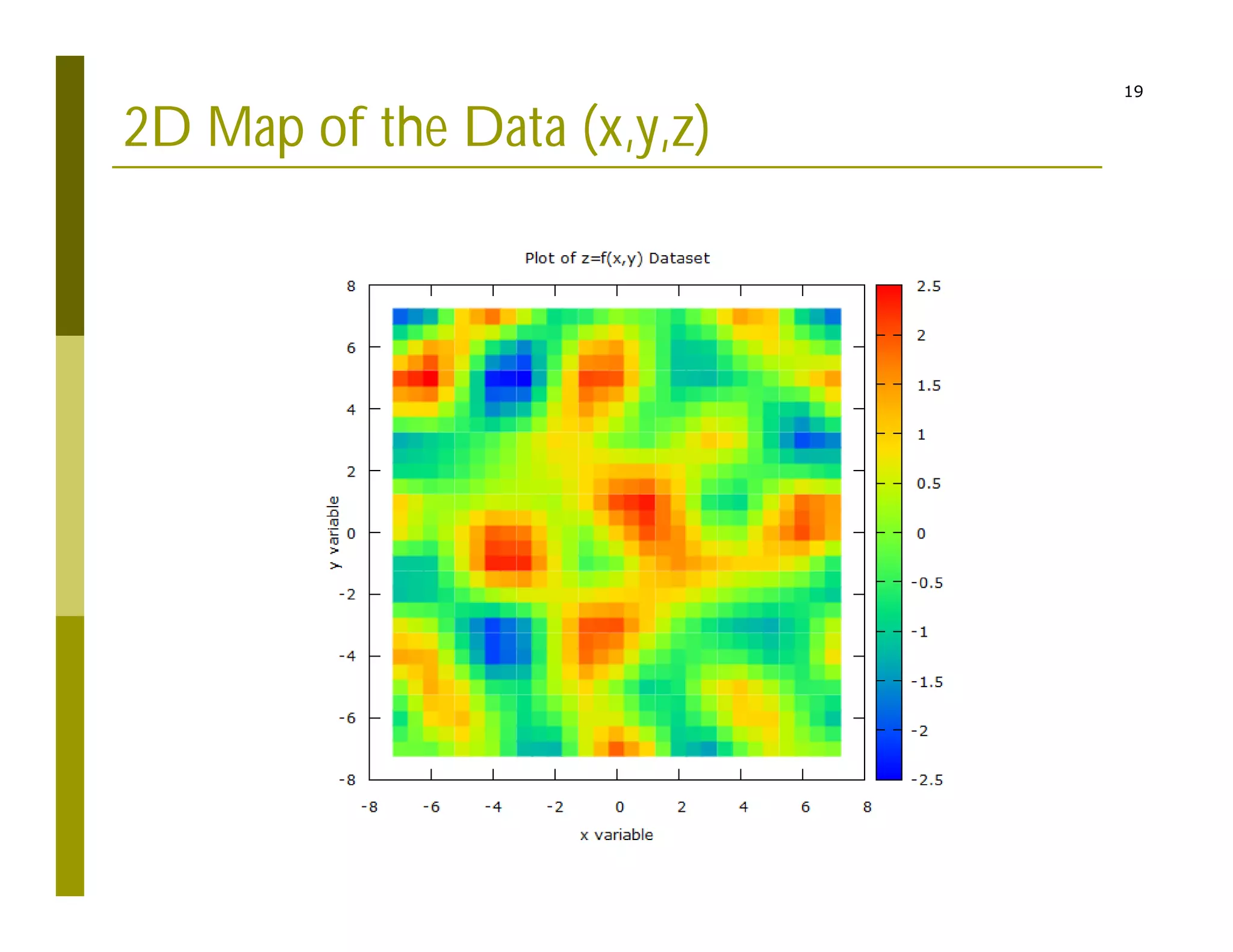
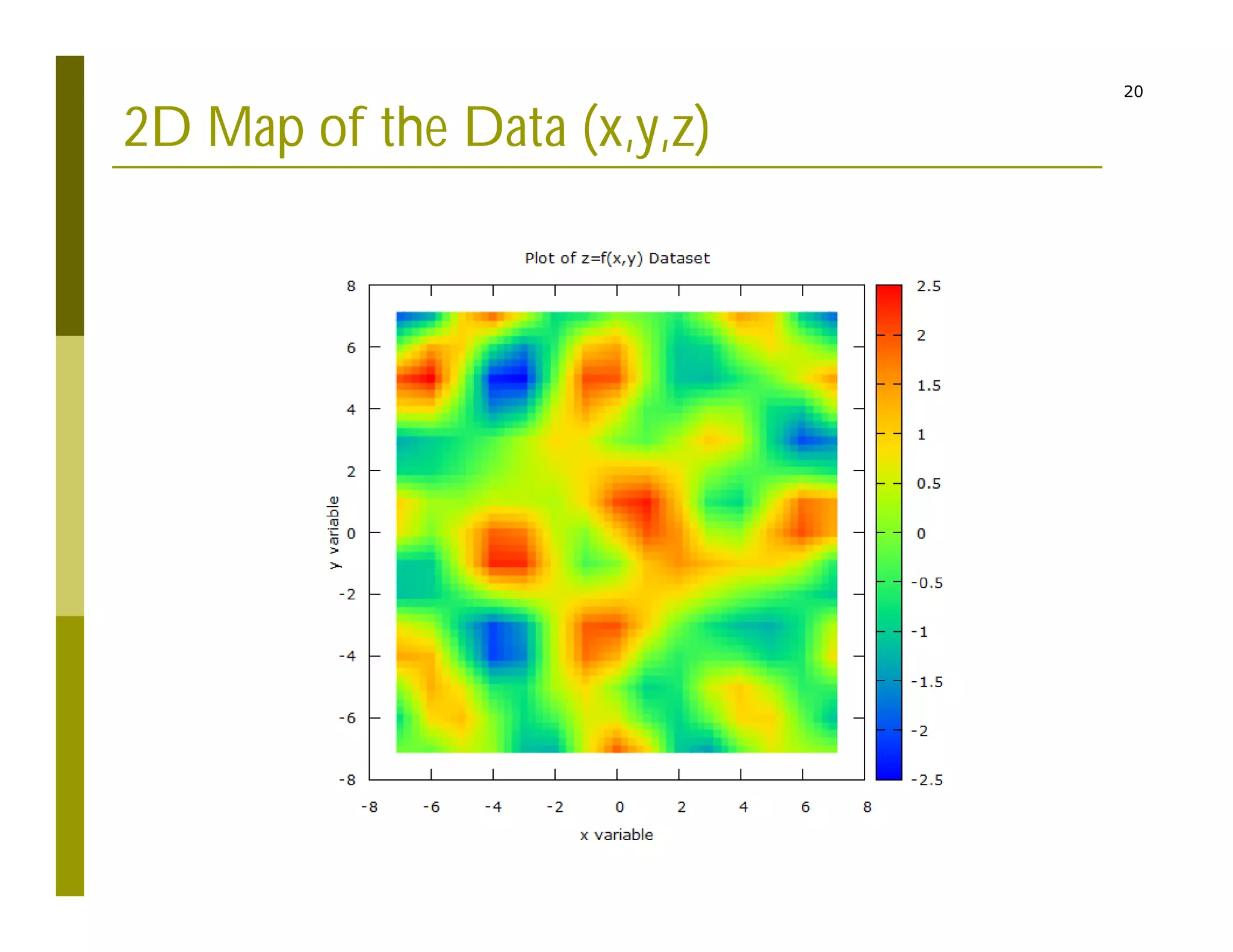
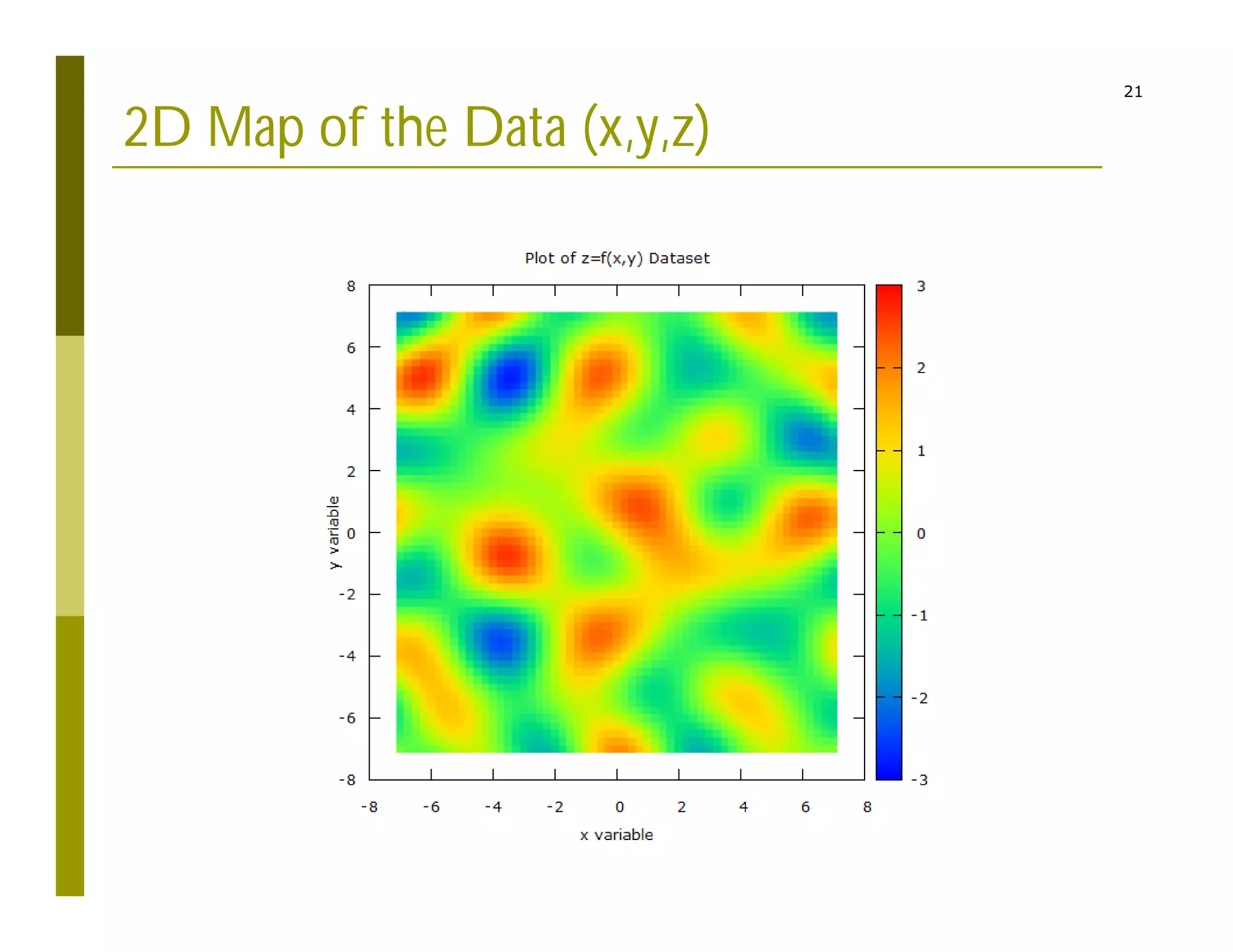
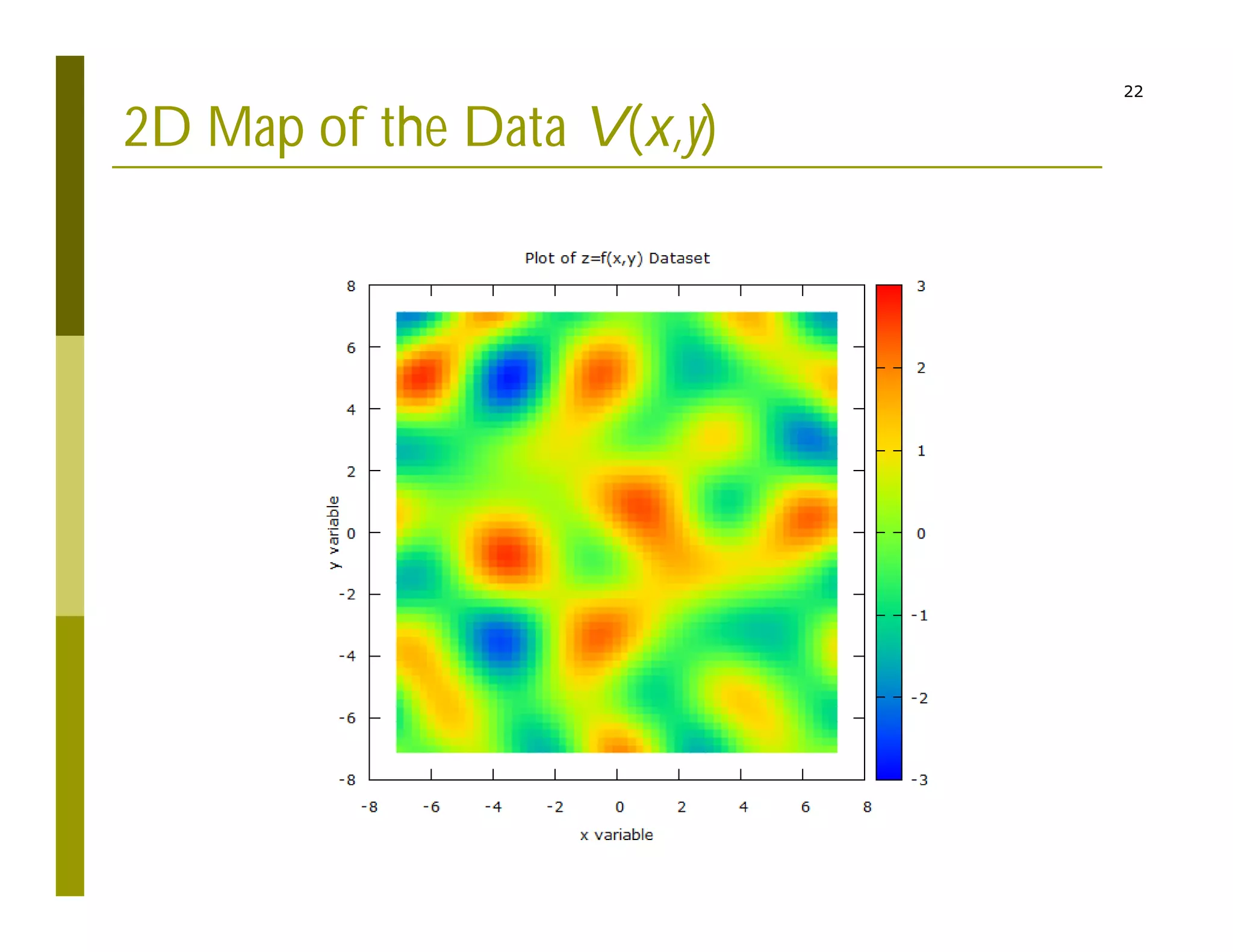
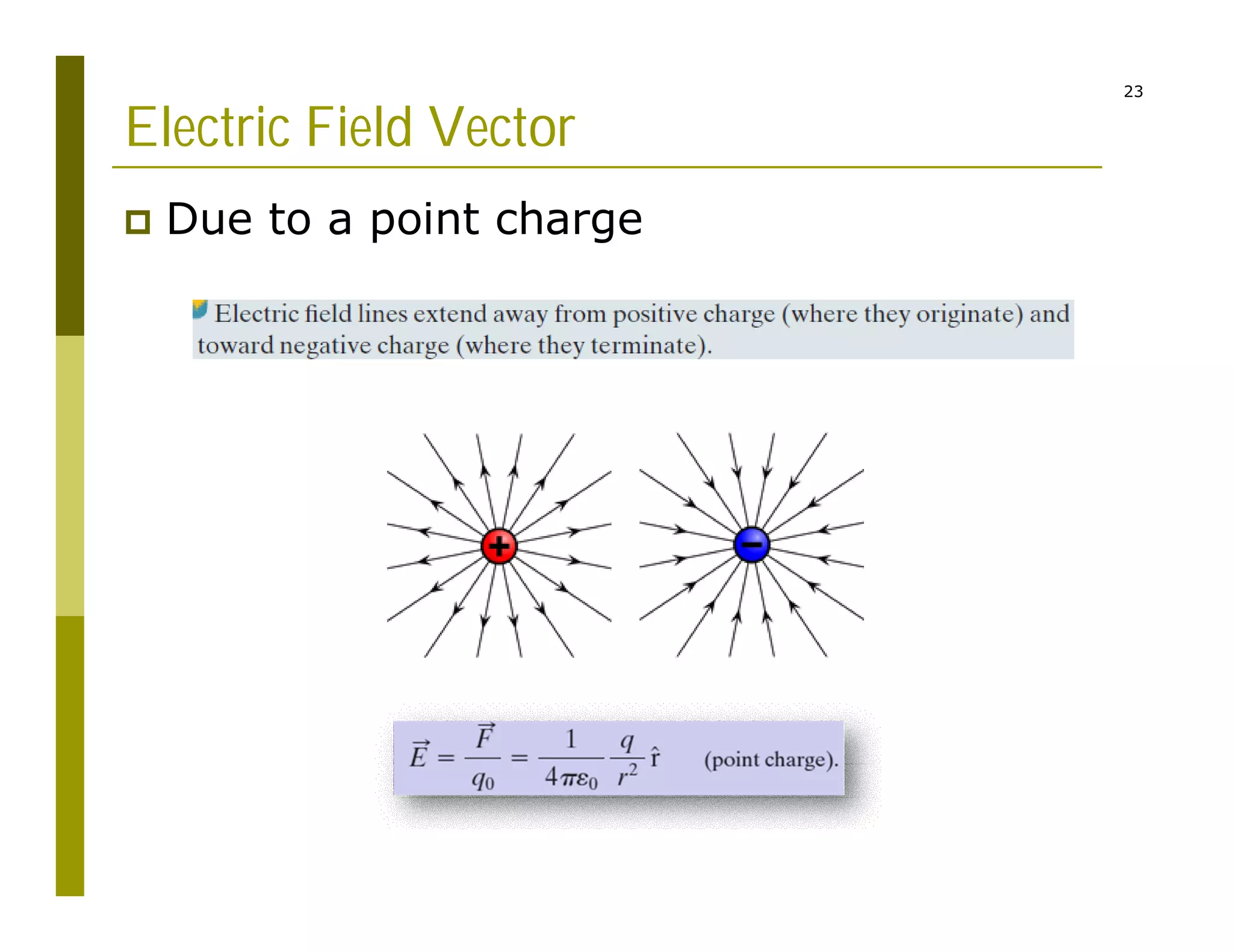
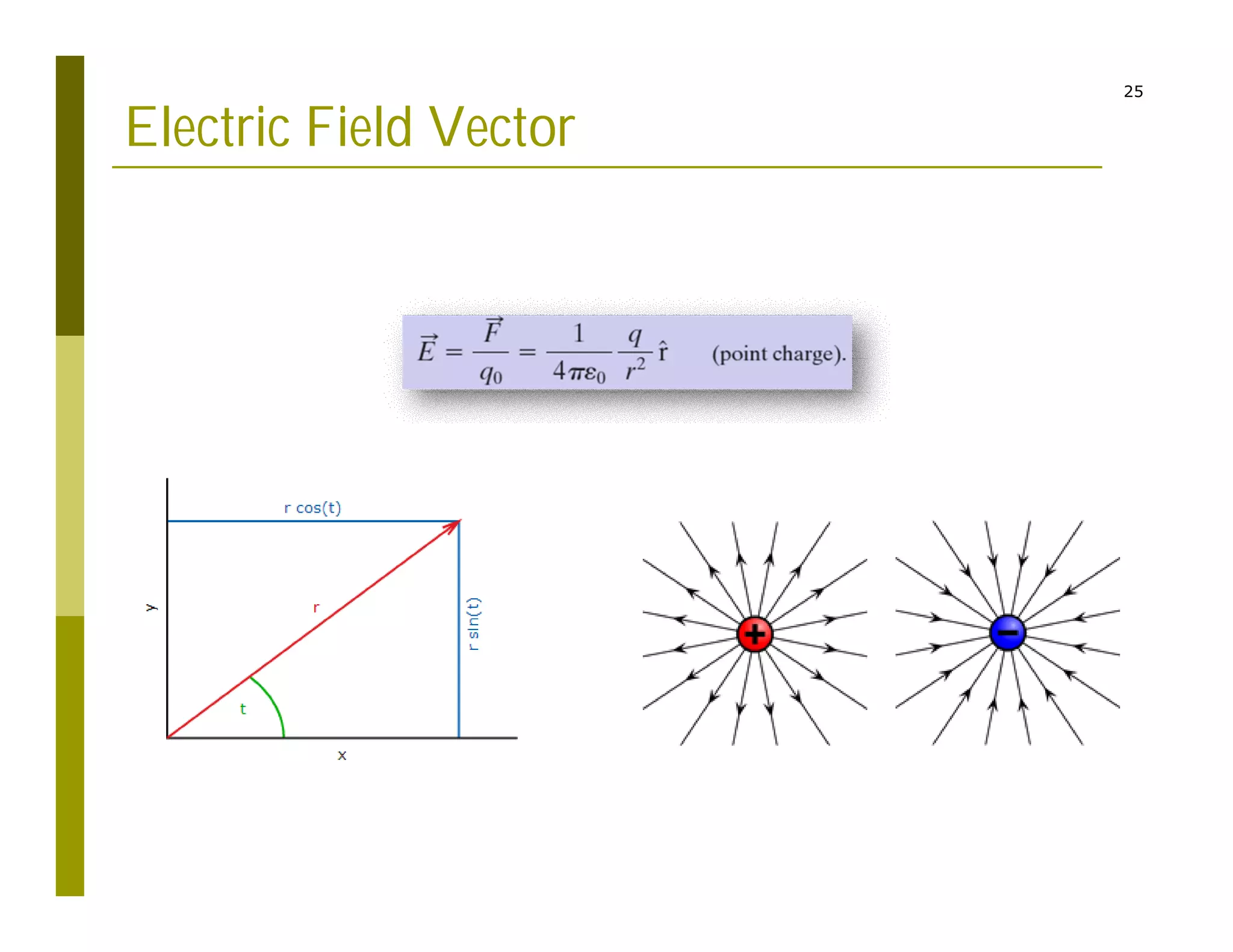
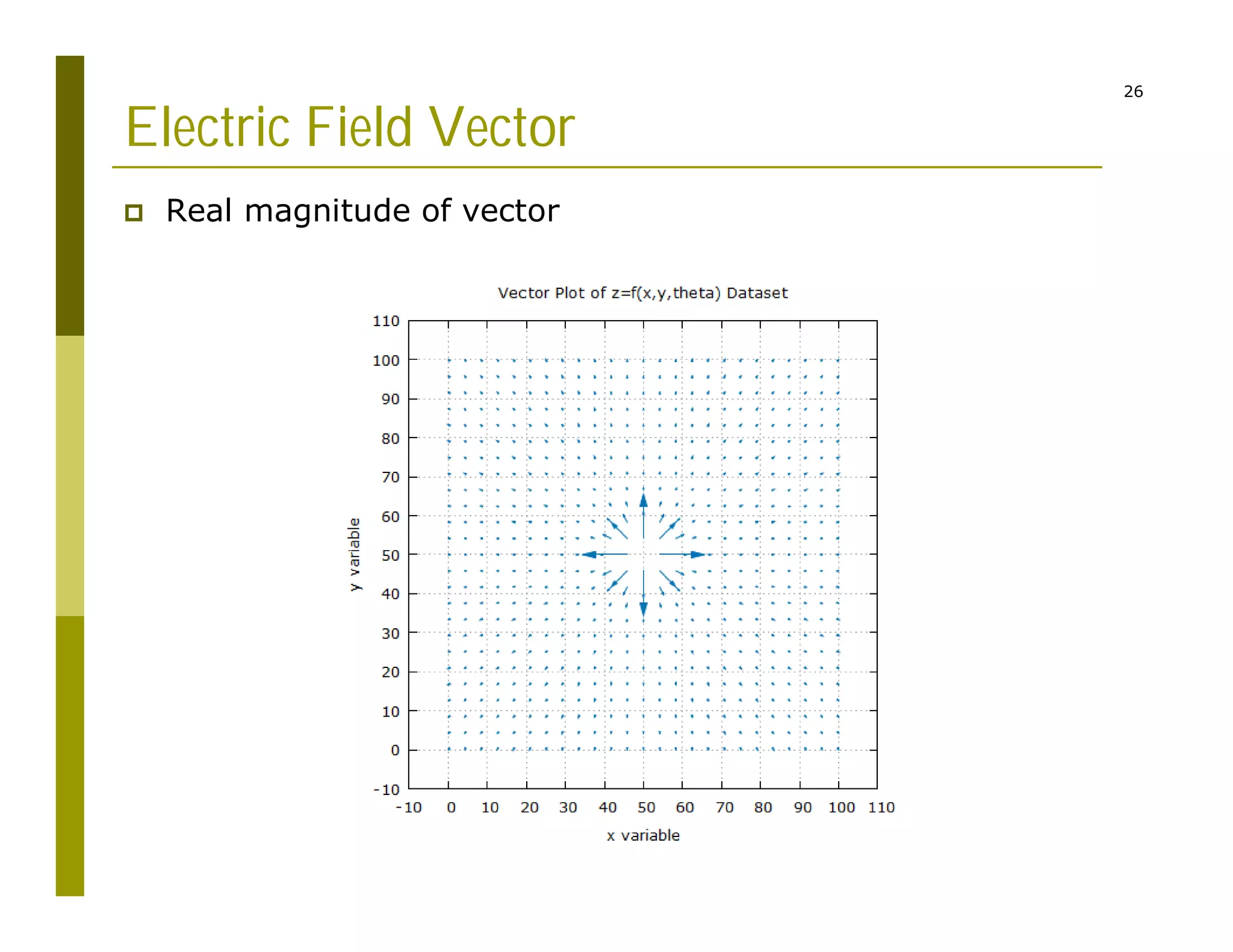
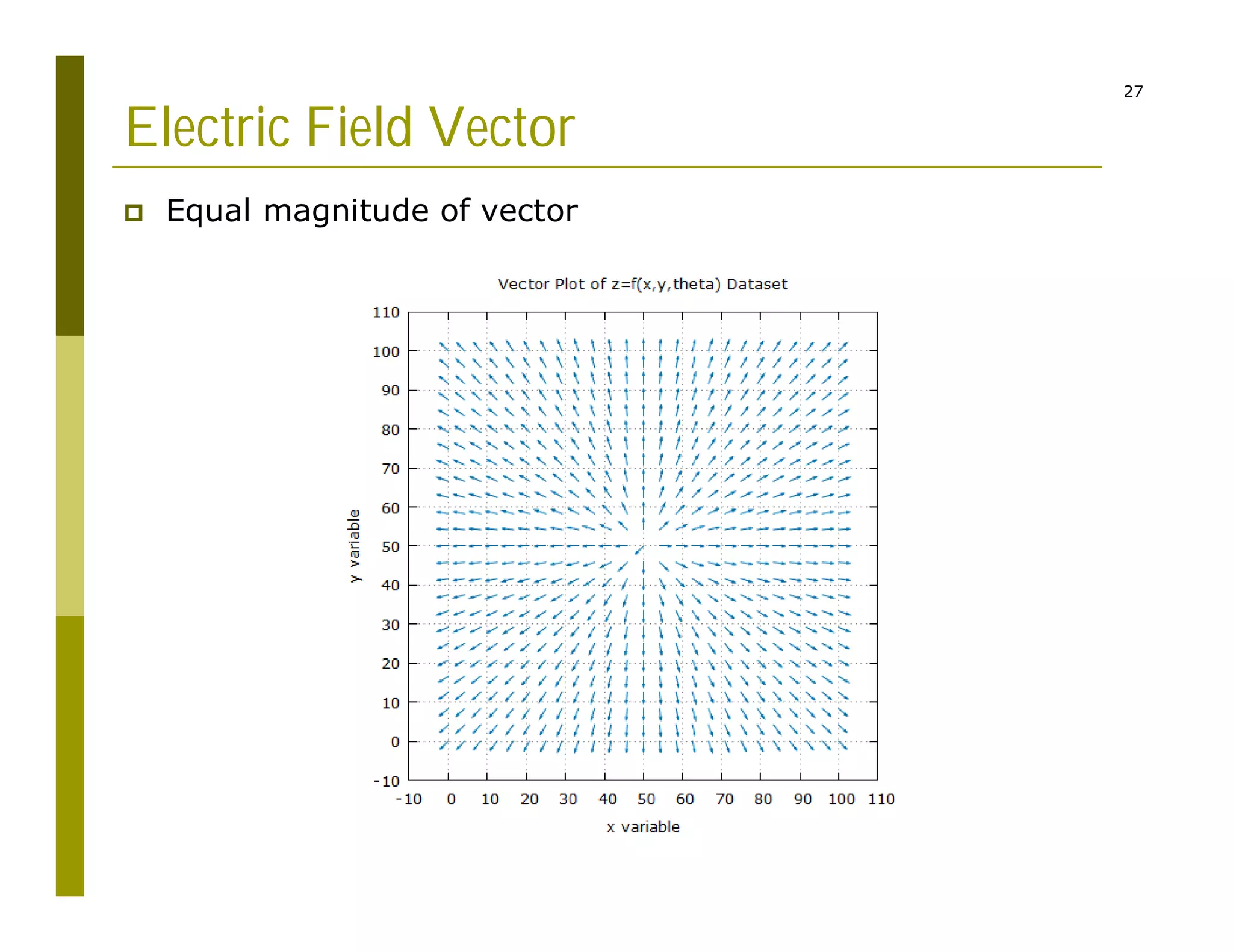
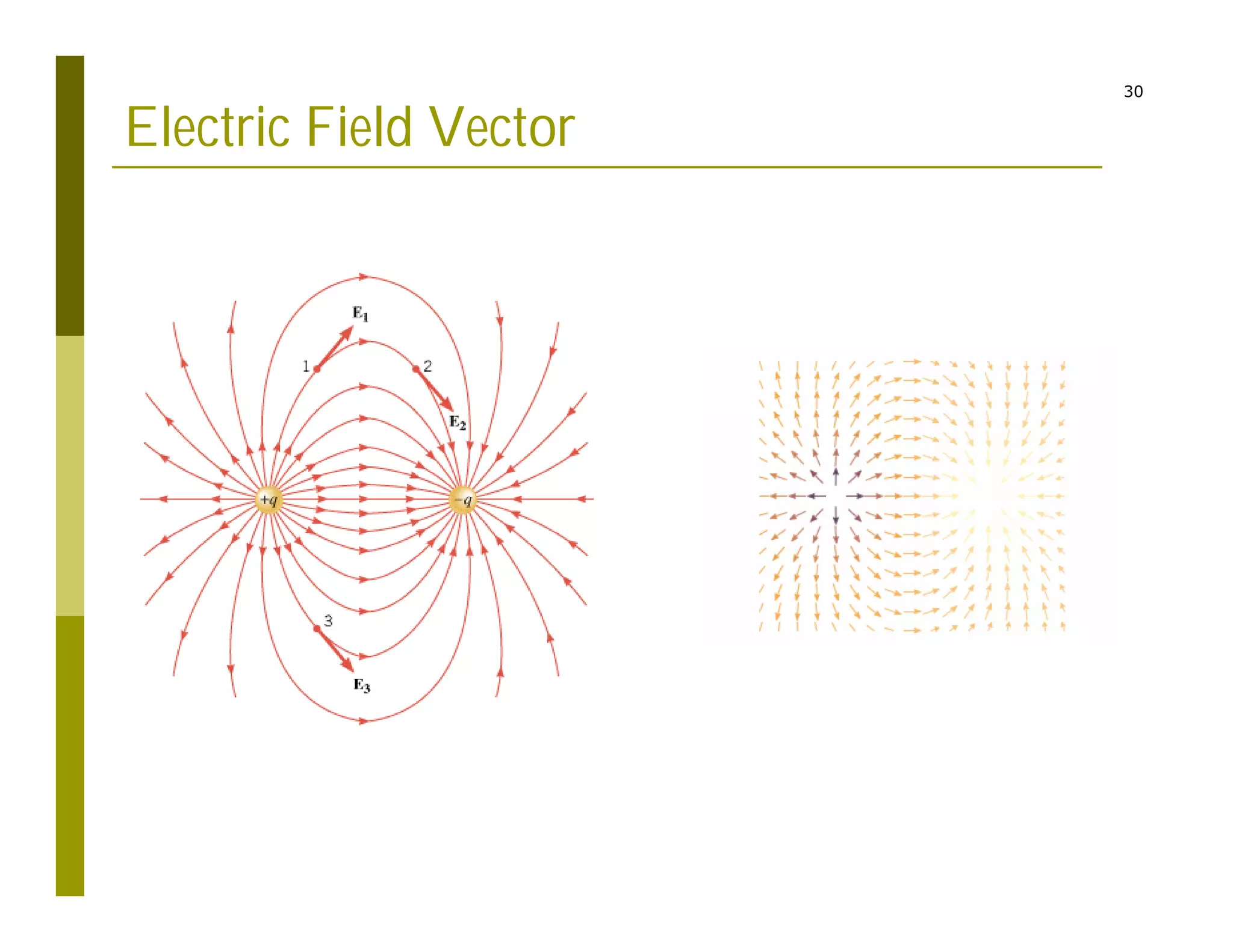
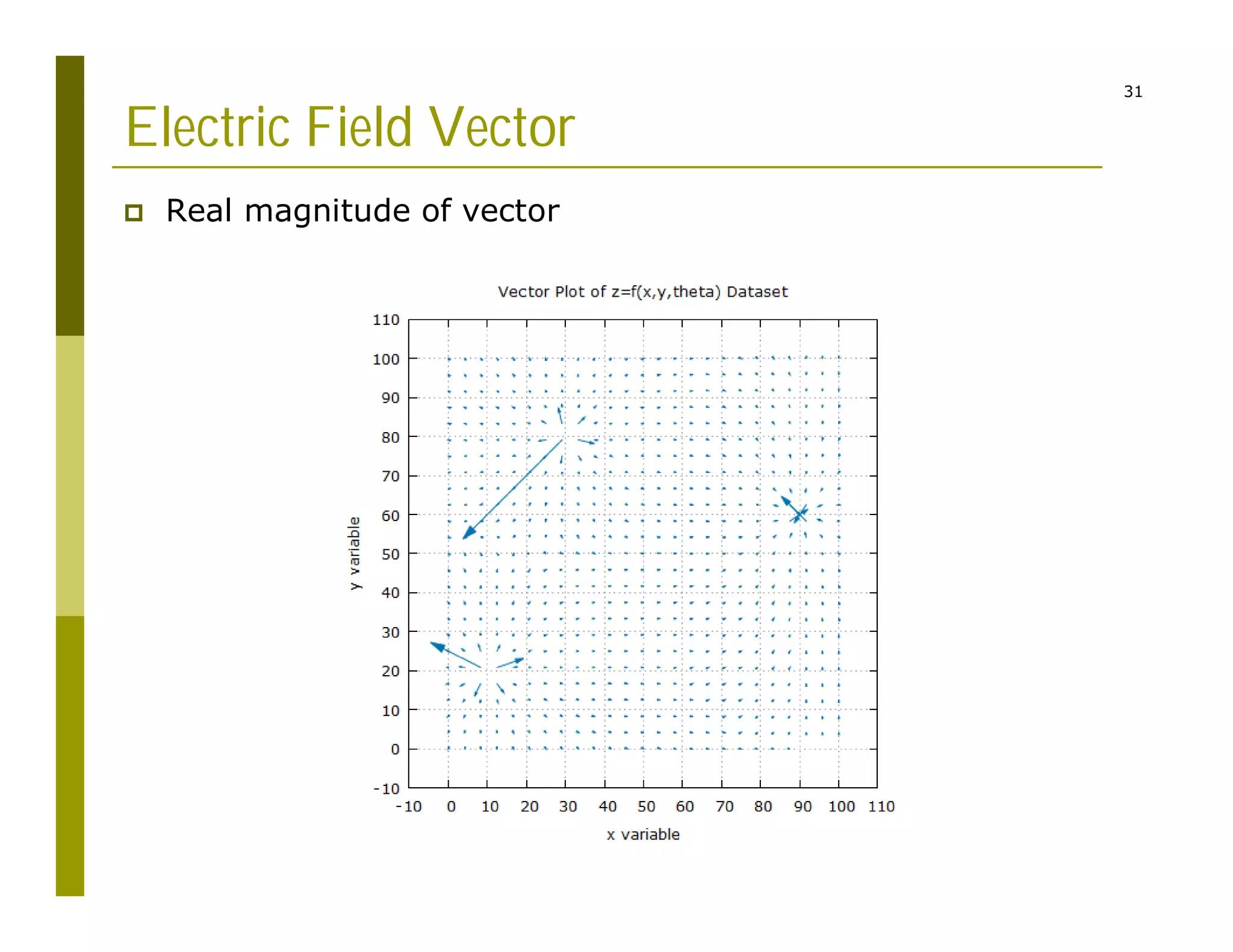
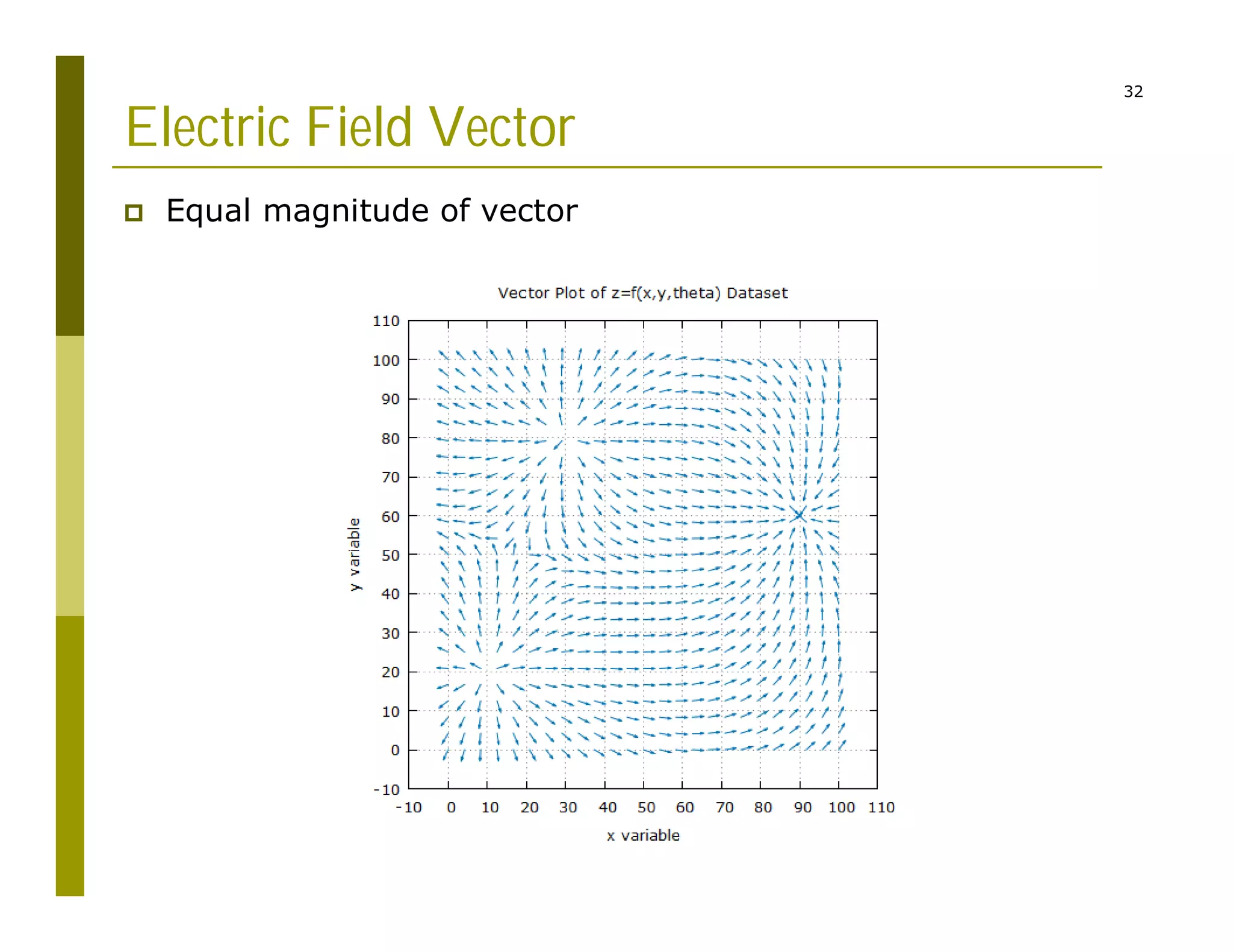
This document describes a code structure for calculating and visualizing electric potential and field from point charges. It discusses: 1) Calculating the potential and electric field at grid points due to multiple point charges using superposition principles. 2) Interpolating sparse potential data to generate smooth 2D potential maps. 3) Representing the electric field as vectors showing position, magnitude, and direction originating from point charges. The code reads charge and position inputs, calculates potentials and fields on a grid, interpolates the potential data, and outputs files to generate vector maps visualizing the electric potential and field.
More Related Content
Similar to SPSF02 - Graphical Data Representation
SPSF02 - Graphical Data Representation
- 1. 1 1 Programming, Computation, Simulation Applicationsin Math & Physics Graphical Data Representation Syeilendra Pramuditya Department of Physics Institut Teknologi Bandung
- 2. 2 Potential Due toa Point Charge Consider a point P at distance R from a fixed particle of positive charge q. Imagine that we move a positive test charge q0 from point P to infinity. The path chosen can be the simplest one— a line that extends radially from the fixed particle through P to infinity. If Vf =0 (at ∞) and Vi =V (at R). Then, for the magnitude of the electric field at the site of the test charge, That gives: Switching R to r, A positively charged particle produces a positive electric potential. A negatively charged particle produces a negative electric potential.
- 3. 3 Potential Due toPoint Charges: The net potential at a point due to a group of point charges can be found with the help of the superposition principle. First the individual potential resulting from each charge is considered at the given point. Then we sum the potentials. For n charges, the net potential is Scalar Equation (Easy) r
- 4. 4 Potential Due toPoint Charges:
- 5. 5 Code Structure ReadInput (input.txt) How many particles? Charge of each particle Location of each particle Calculation domain (xmin, ymin, xmax, ymax) Grid resolution
- 6. 6 Code Structure Calculatepotential at all grid-points (nim.pas) 1 Use 5 and dimensionless variables n i i i q V k r k
- 7. 7 Code Structure WriteOutput to Datafile (output.txt)
- 8. 8 Plot Output Data myplot.gpt
- 9. 9 2D Map ofthe Data (x,y,z)
- 10.
- 11. 11 Data Interpolation LagrangeInterpolation Based on Taylor series General: Polynomial Simplest: Linear, y = ax + b And many more methods.. Ref.: A First Course in Computational Physics, Chapter 3, Paul DeVries
- 12. 12 Lagrange Linear Interpolation 12 1 2 2 1 2 1 2 1 1 2 2 1 1 2 ( ) ( ) ( ) x x x x x x x x p x f x f x y y x x x x x x x x x1,y1 x2,y2 p(x) 2 1 2 4 5 ( 2) 5 3 2 3.67 4 1 1 4 3 p x
- 13. 13 Lagrange Linear Interpolation 12 1 2 2 1 1 2 2 1 1 2 1 ( ) 2 2 x x x x x x p x y y y y x x x x x1,y1 x2,y2 p(x) 1 4 1 (2.5) (3 5) 4 2 2 p p Interpolated data is at midpoint
- 14. 14 Tabular Data File(x,y,z) Contoh file output data
- 15. 15 2D Map ofthe Data (x,y,z)
- 16. 16 2D Interpolation forPlot Smoothing Data Interpolated
- 17. 17 Code Structure ReadInput Data File Interpolate Data Write (File/Array) Interpolated Output Data Generate 2D map of the data
- 18. 18 2D Map ofthe Data (x,y,z)
- 19. 19 2D Map ofthe Data (x,y,z)
- 20. 20 2D Map ofthe Data (x,y,z)
- 21. 21 2D Map ofthe Data (x,y,z)
- 22. 22 2D Map ofthe Data V(x,y)
- 23. 23 Electric Field Vector Due to a point charge
- 24.
- 25.
- 26. 26 Electric Field Vector Real magnitude of vector
- 27. 27 Electric Field Vector Equal magnitude of vector
- 28. 28 Electric Field Vector Multiple Charged Particles The net, or resultant, electric field due to more than one point charge can be found by the superposition principle. The net electric field at the position of the test charge is
- 29.
- 30.
- 31. 31 Electric Field Vector Real magnitude of vector
- 32. 32 Electric Field Vector Equal magnitude of vector
- 33. 33 Code Structure ReadInput How many particles? Location of each particle Charge of each particle Calculation domain (xmin, ymin, xmax, ymax) Grid resolution Calculate electric field vector at all nodes/grid- points Write Output to Datafile (depends on your graphic tools) Position, magnitude, angle x1, y1, x2, y2 Generate vector map of the output data