The document discusses solving large sparse linear systems on GPUs, emphasizing the efficiency of using GPUs for computations in cosmology, particularly in the context of dark matter and the universe's expansion. It covers GPU architecture, programming techniques, and performance benchmarks that showcase significant speed improvements over CPUs. Additionally, it details methods for scaling computations, including hardware upgrades and algorithmic advancements for optimal transport and preconditioning strategies.








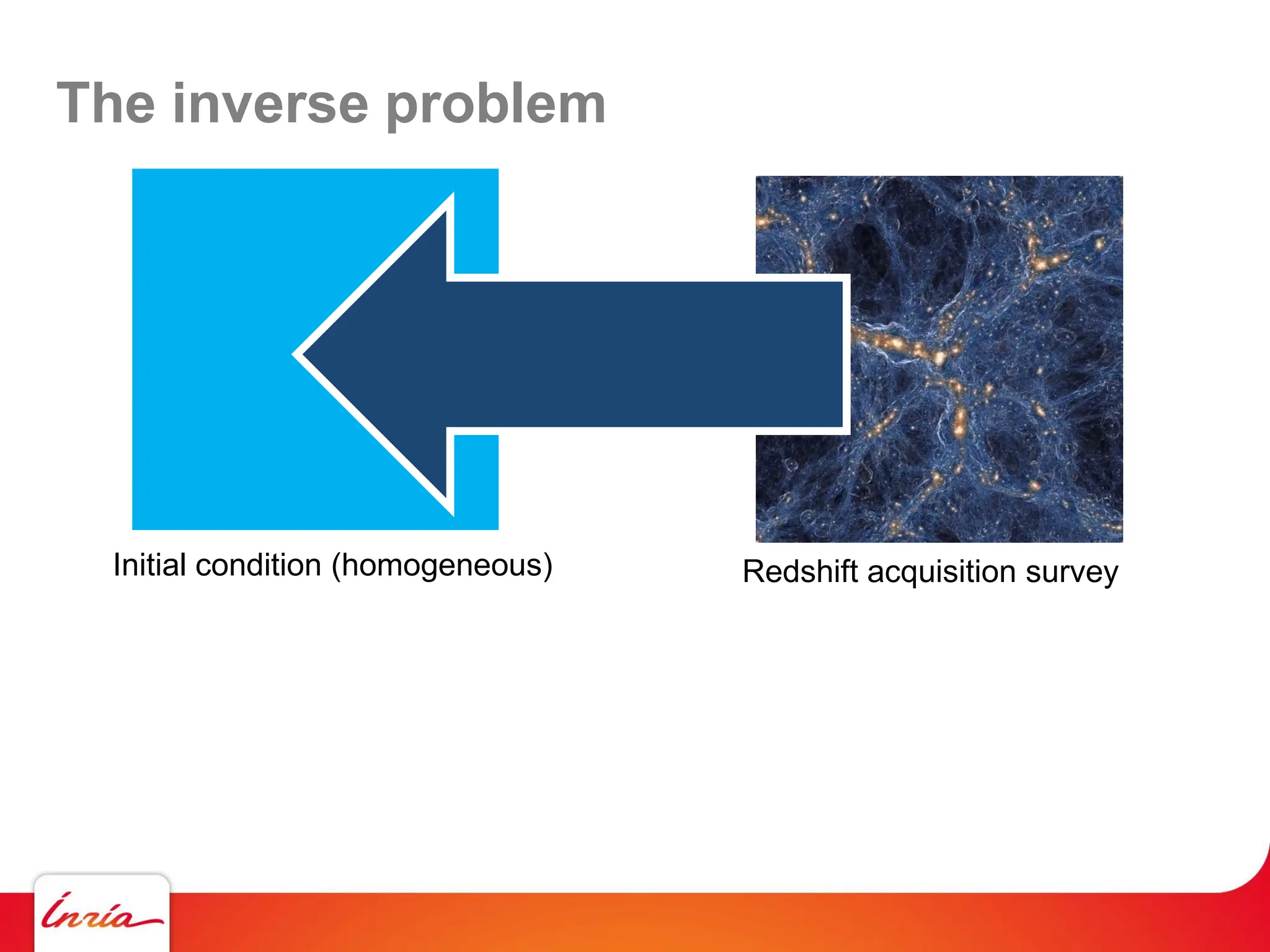
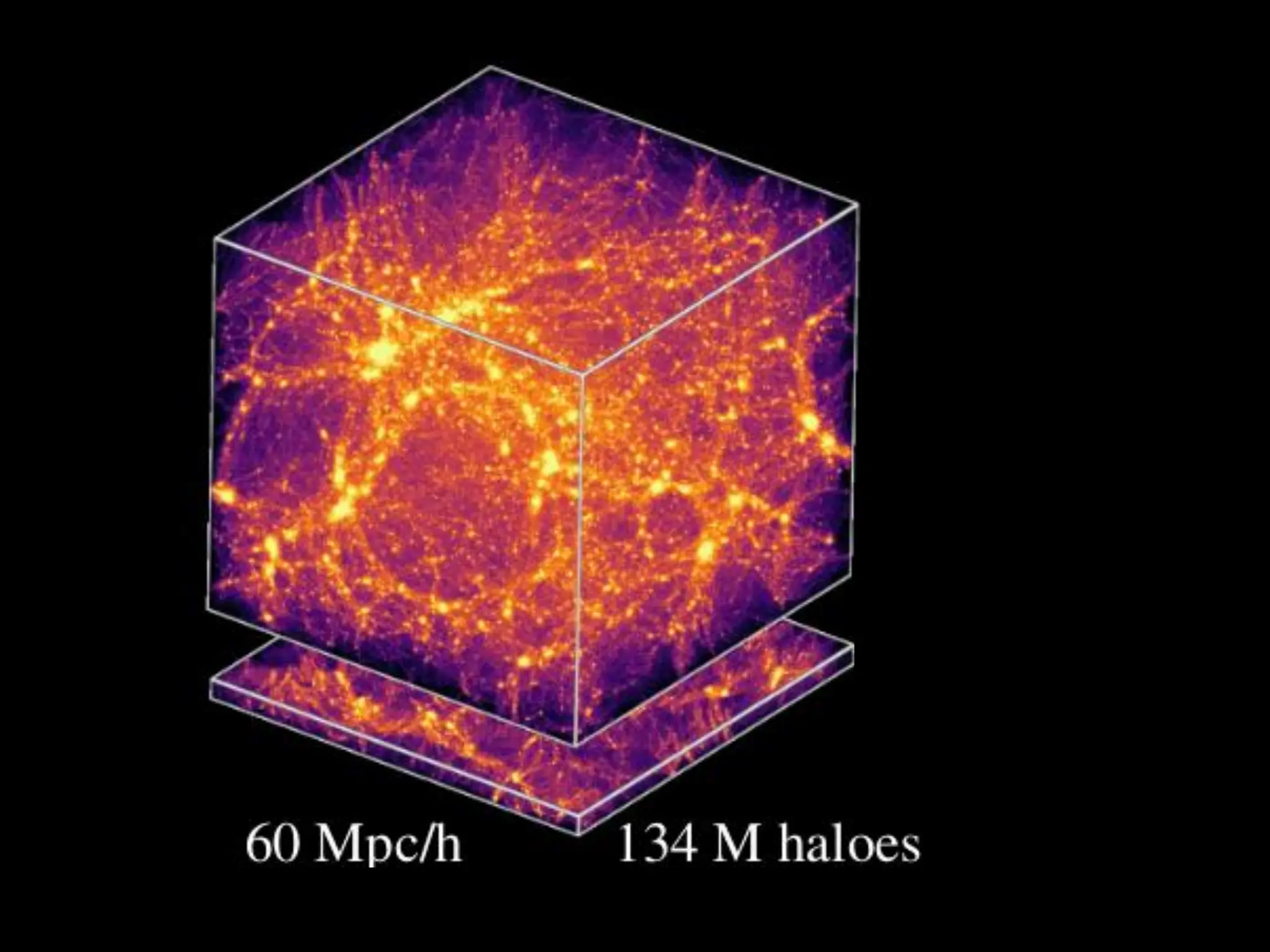
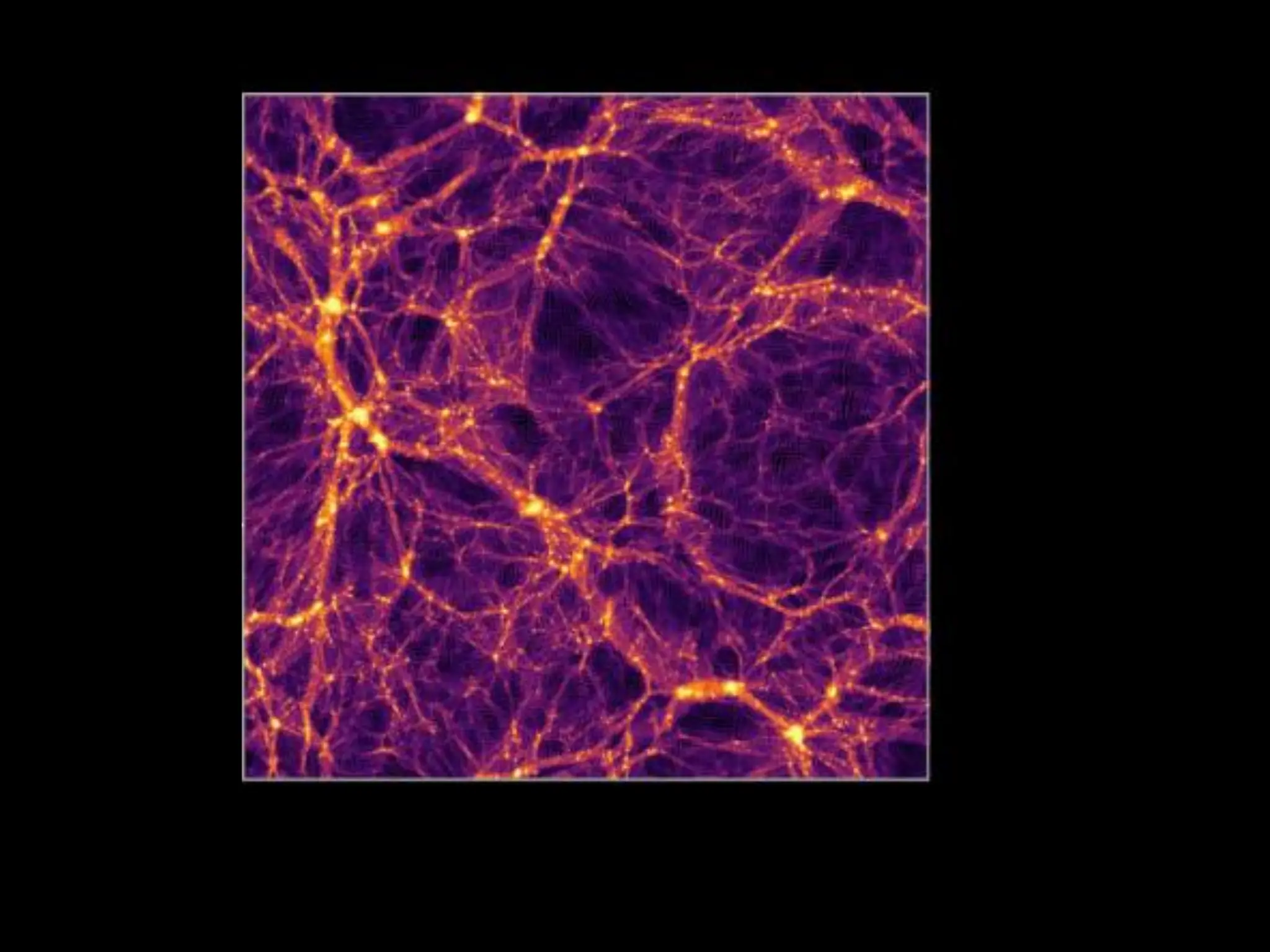
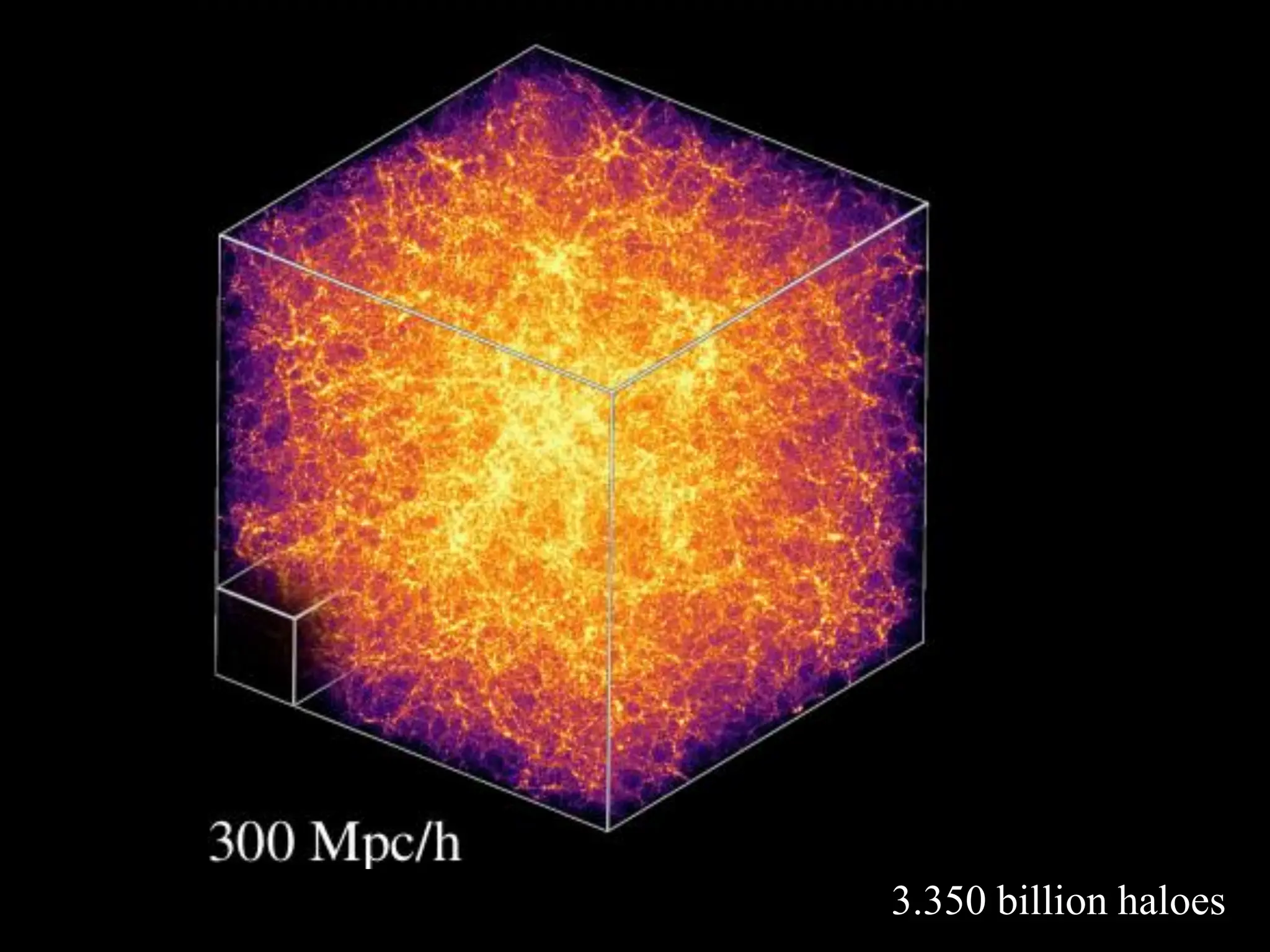

![The inverse problem – Benamou-Brenier thm
Initial condition (homogeneous) Redshift acquisition survey
T(x)
[Frisch, Matarrese, Mohayaee, Sobolevski 2002 (Nature)]
[Brenier, Frisch, Henon, Loeper, Matarrese, Mohayaee, Sobolevskii 2003]](https://image.slidesharecdn.com/gpunl-241218081309-df2bd1bb/75/Solving-large-sparse-linear-systems-on-the-GPU-17-2048.jpg)
![The inverse problem – Benamou-Brenier thm
Initial condition (homogeneous) Redshift acquisition survey
T(x)
∫t1
t2
(t2-t1)
∫V
ρ(x,t) ||v(t,x)||2
dxdt
s.t. ρ(t1,.) = ρ1 ; ρ(t2,.) = ρ2 ; d ρ
dt
= - div(ρv)
Minimize
A(ρ,v) =
[Frisch, Matarrese, Mohayaee, Sobolevski 2002 (Nature)]
[Brenier, Frisch, Henon, Loeper, Matarrese, Mohayaee, Sobolevskii 2003]](https://image.slidesharecdn.com/gpunl-241218081309-df2bd1bb/75/Solving-large-sparse-linear-systems-on-the-GPU-18-2048.jpg)
![The inverse problem – Benamou-Brenier thm
Initial condition (homogeneous) Redshift acquisition survey
T(x)
∫t1
t2
(t2-t1)
∫V
ρ(x,t) ||v(t,x)||2
dxdt
s.t. ρ(t1,.) = ρ1 ; ρ(t2,.) = ρ2 ; d ρ
dt
= - div(ρv)
Minimize C(T) =
∫V
|| x – T(x) ||2 dx
s.t. T is measure-preserving
ρ1(x)
Minimize
A(ρ,v) =
Optimal transport
[Frisch, Matarrese, Mohayaee, Sobolevski 2002 (Nature)]
[Brenier, Frisch, Henon, Loeper, Matarrese, Mohayaee, Sobolevskii 2003]](https://image.slidesharecdn.com/gpunl-241218081309-df2bd1bb/75/Solving-large-sparse-linear-systems-on-the-GPU-19-2048.jpg)
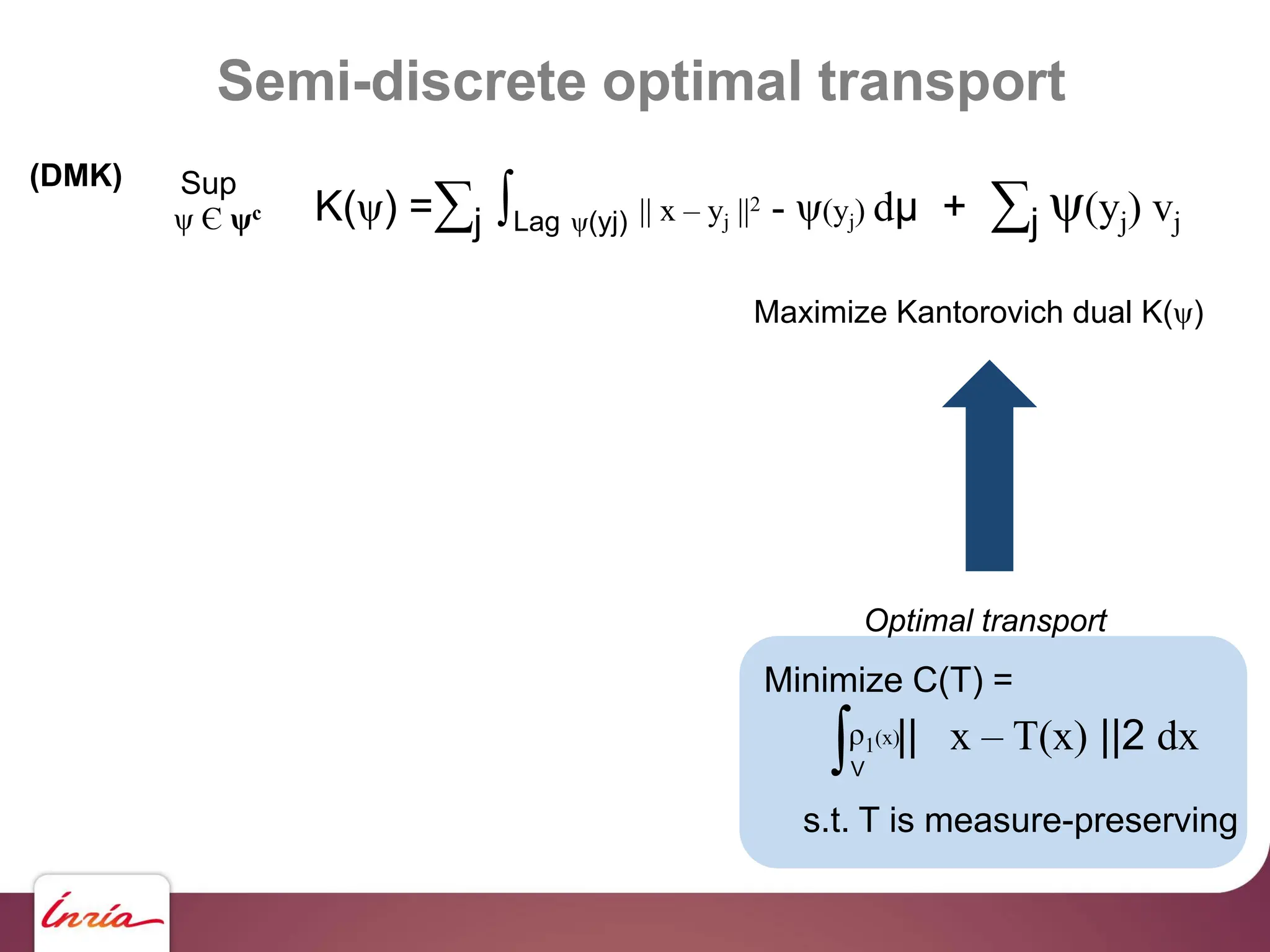
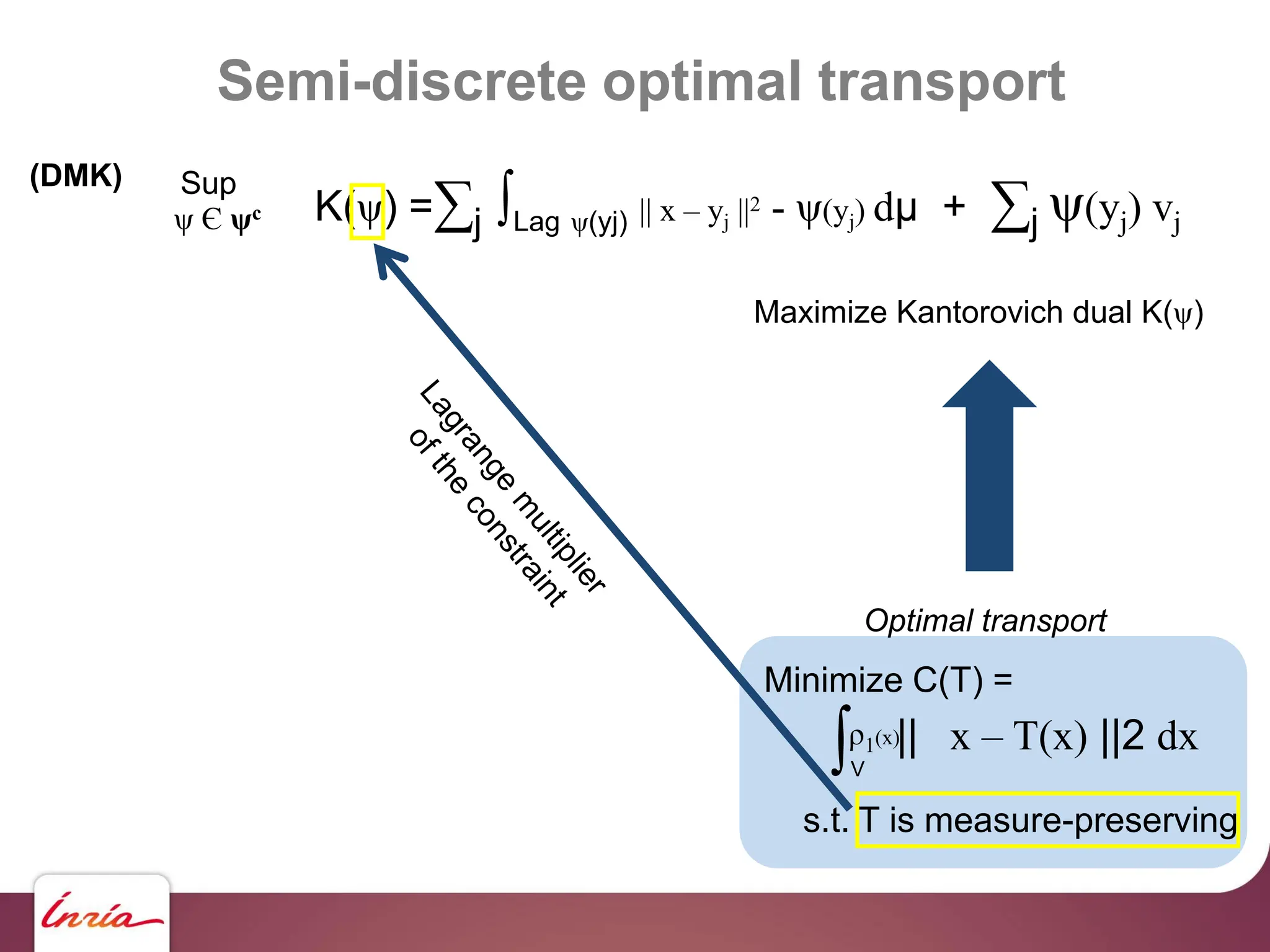

![K(ψ) =∑j ∫Lag ψ(yj) || x – yj ||2 - ψ(yj) dμ + ∑j ψ(yj) vj
Sup
ψ Є ψc
(DMK)
Where: Lag ψ(yj) = { x | || x – yj ||2 – ψ(yj) < || x – yj ||2 - ψ(yj’) } for all j’ ≠ j
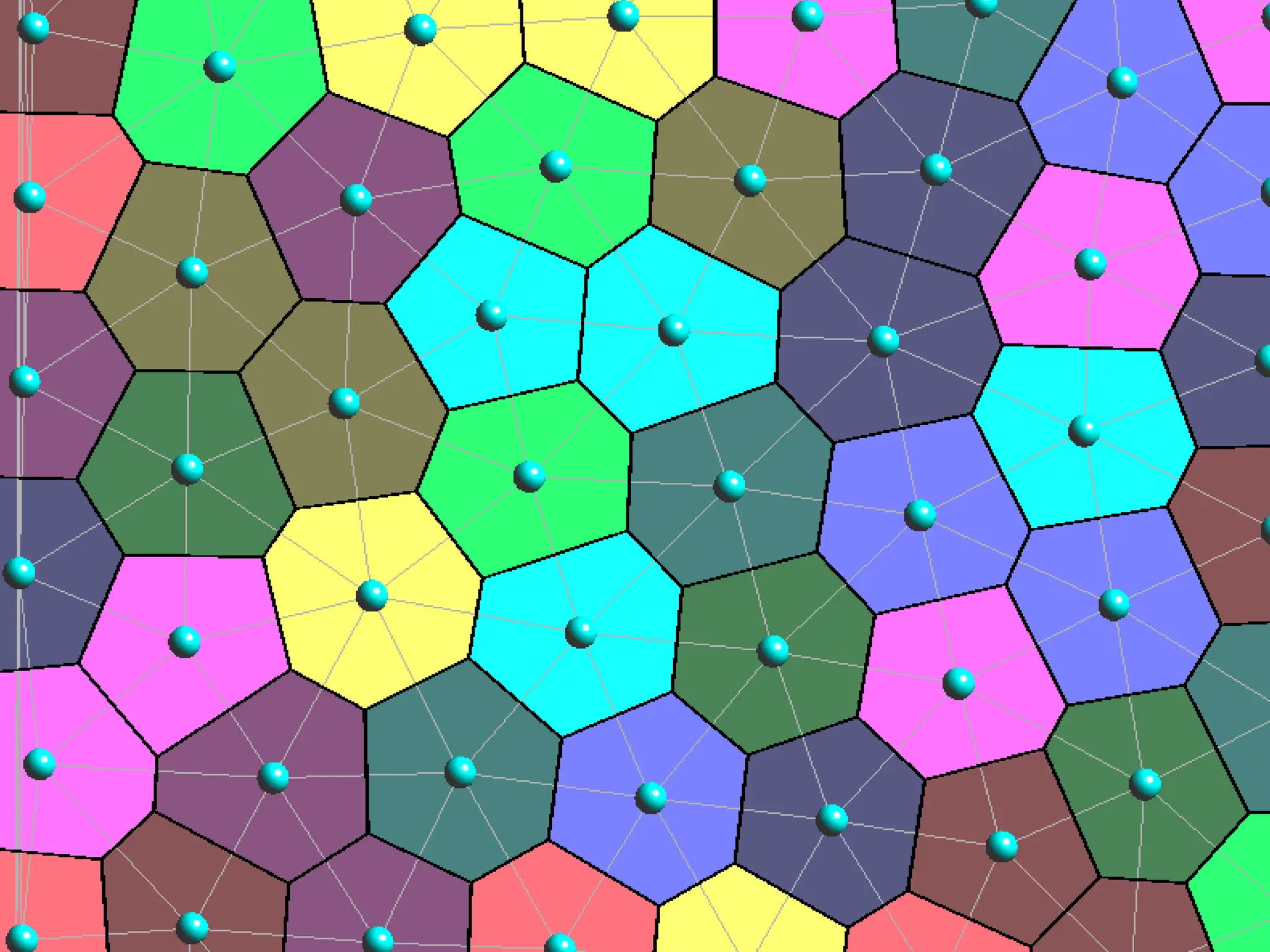
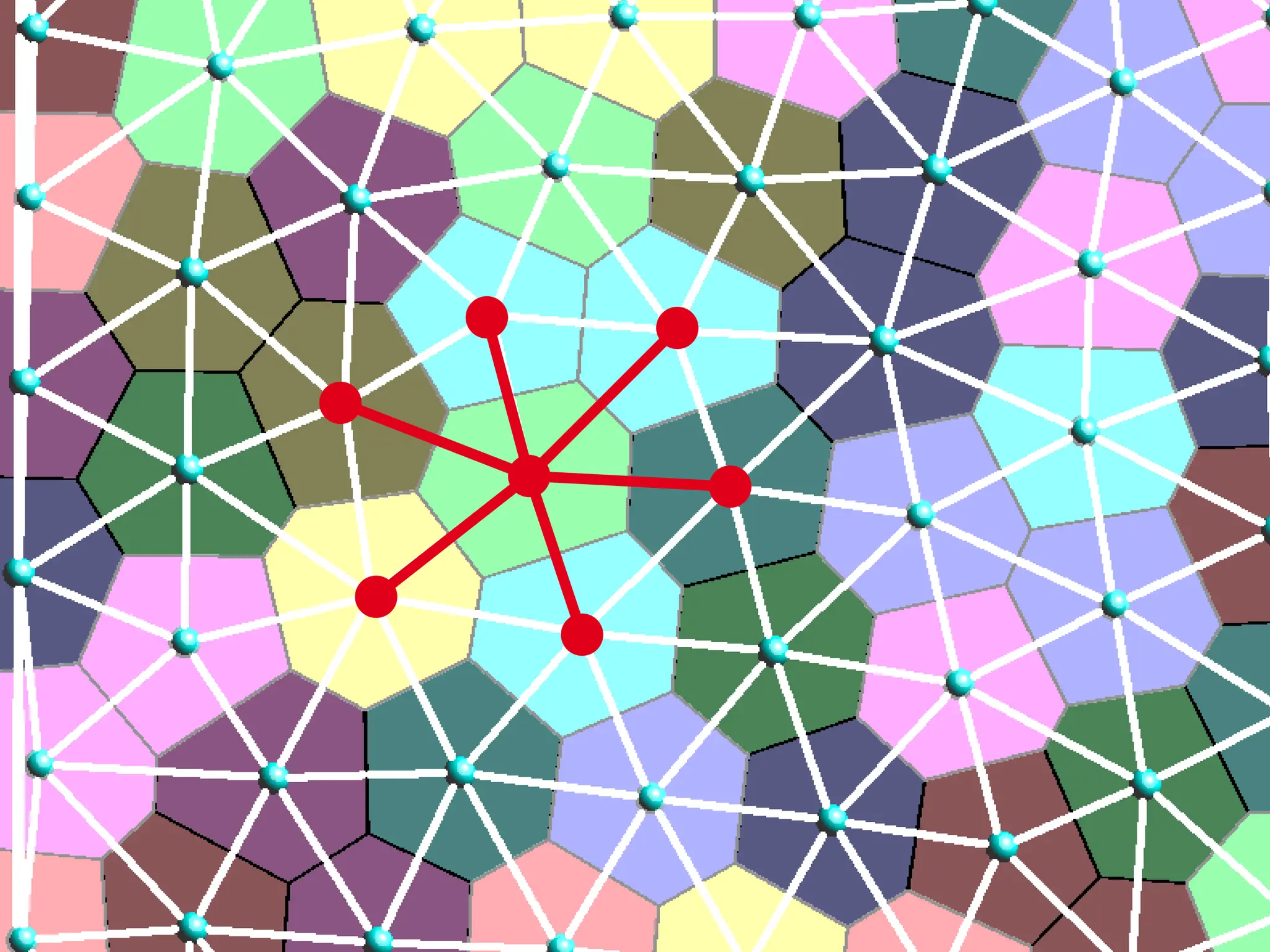
Laguerre diagram of the yj’s
(with the L2 cost || x – y ||2 used here, Power diagram)
Weight of yj in the power diagram
ψ is determined by the
weight vector [ψ(y1) ψ(y2) … ψ(ym)]
Semi-discrete optimal transport](https://image.slidesharecdn.com/gpunl-241218081309-df2bd1bb/75/Solving-large-sparse-linear-systems-on-the-GPU-23-2048.jpg)
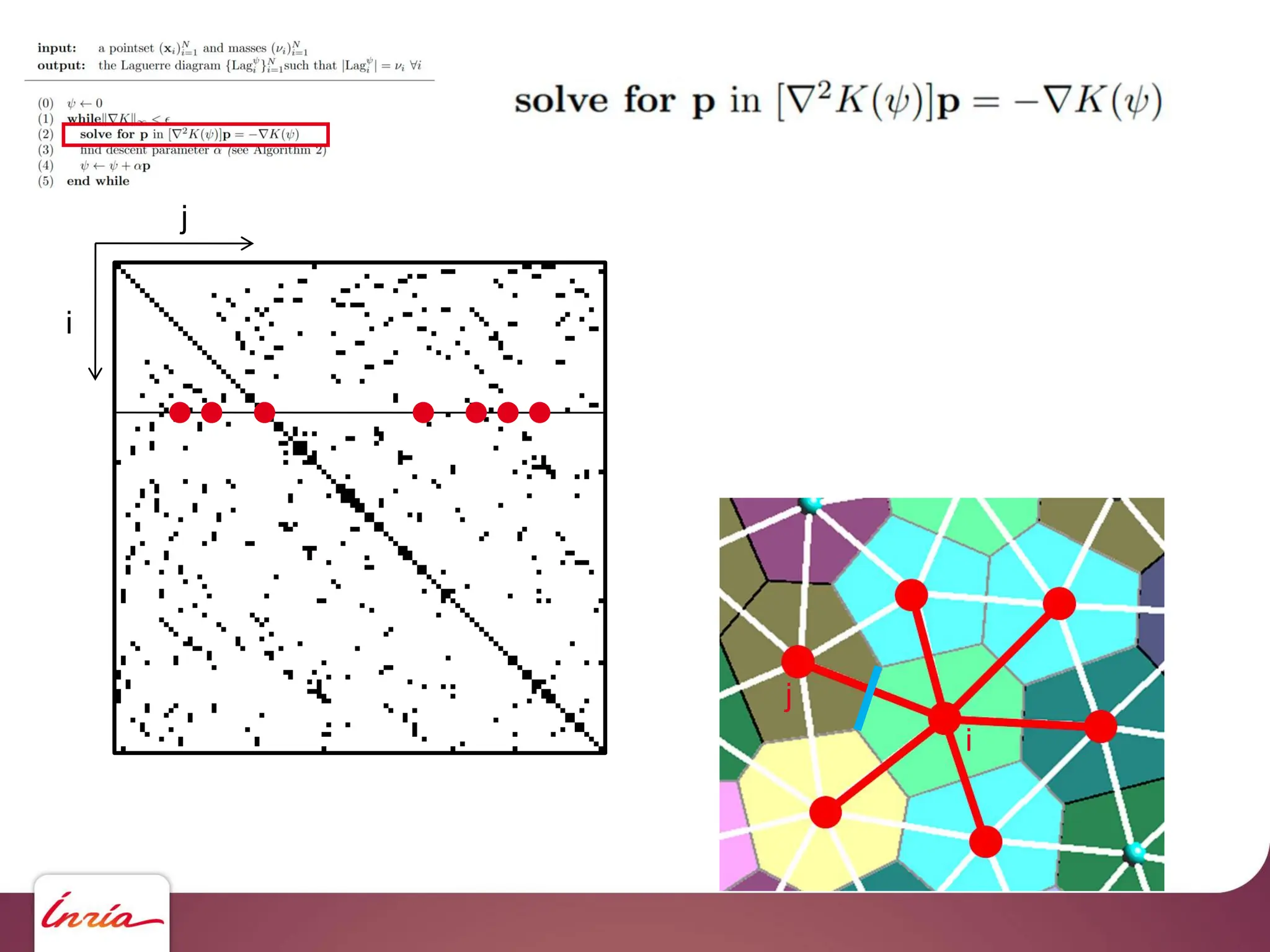
![Semi-discrete optimal transport
[Kitagawa Merigot Thibert 2019, JEMS]
[L 2015, M2AN]
[L 2021, JCP]
[Nikhaktar, Seth, L, Mohayaee 2022, PRL]
[von Hausseger, L, Mohayaee 2021, PRL]
[L, Ray, Merigot, Leclerc, JCP (pend. rev.)]](https://image.slidesharecdn.com/gpunl-241218081309-df2bd1bb/75/Solving-large-sparse-linear-systems-on-the-GPU-24-2048.jpg)



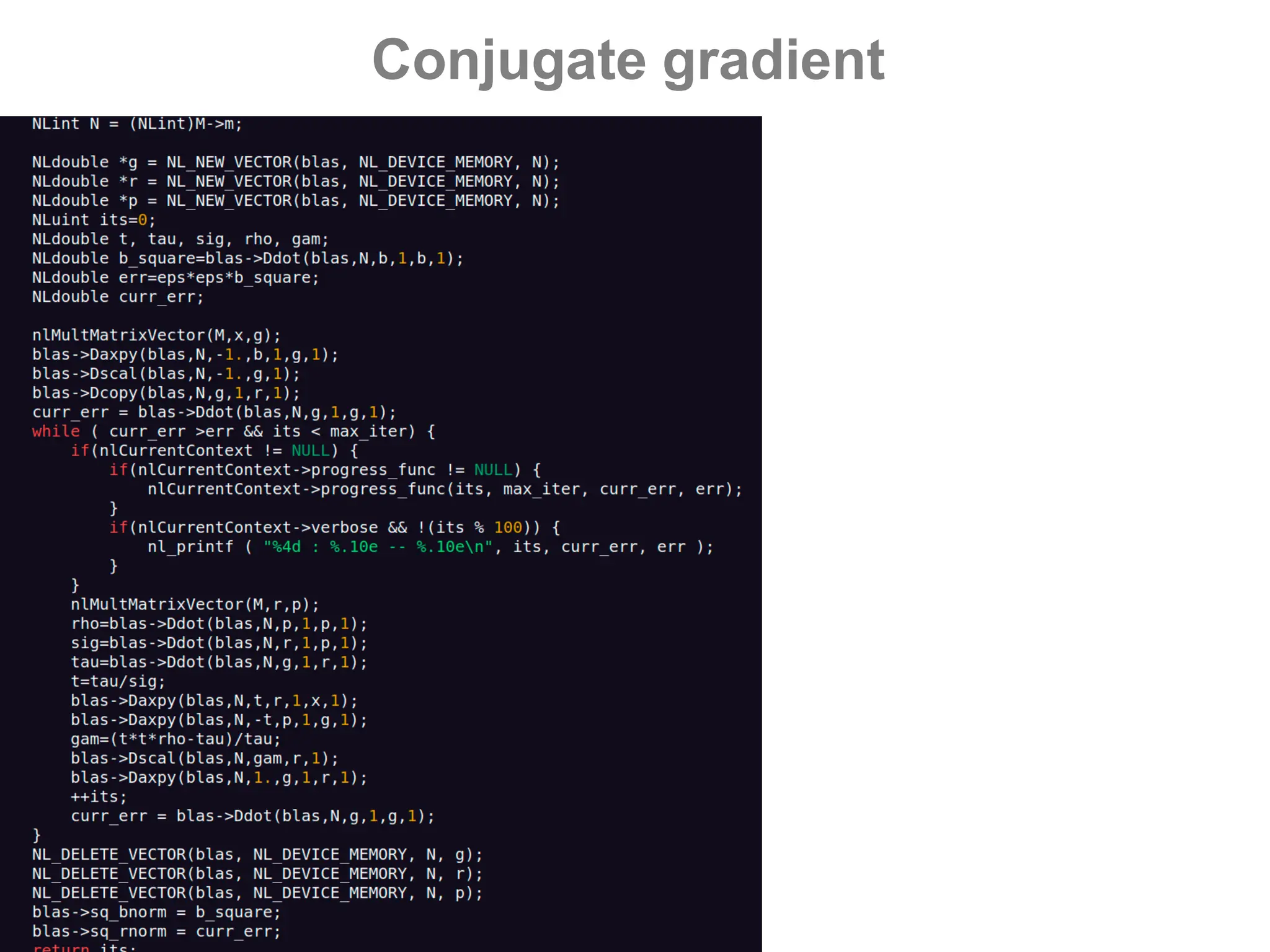
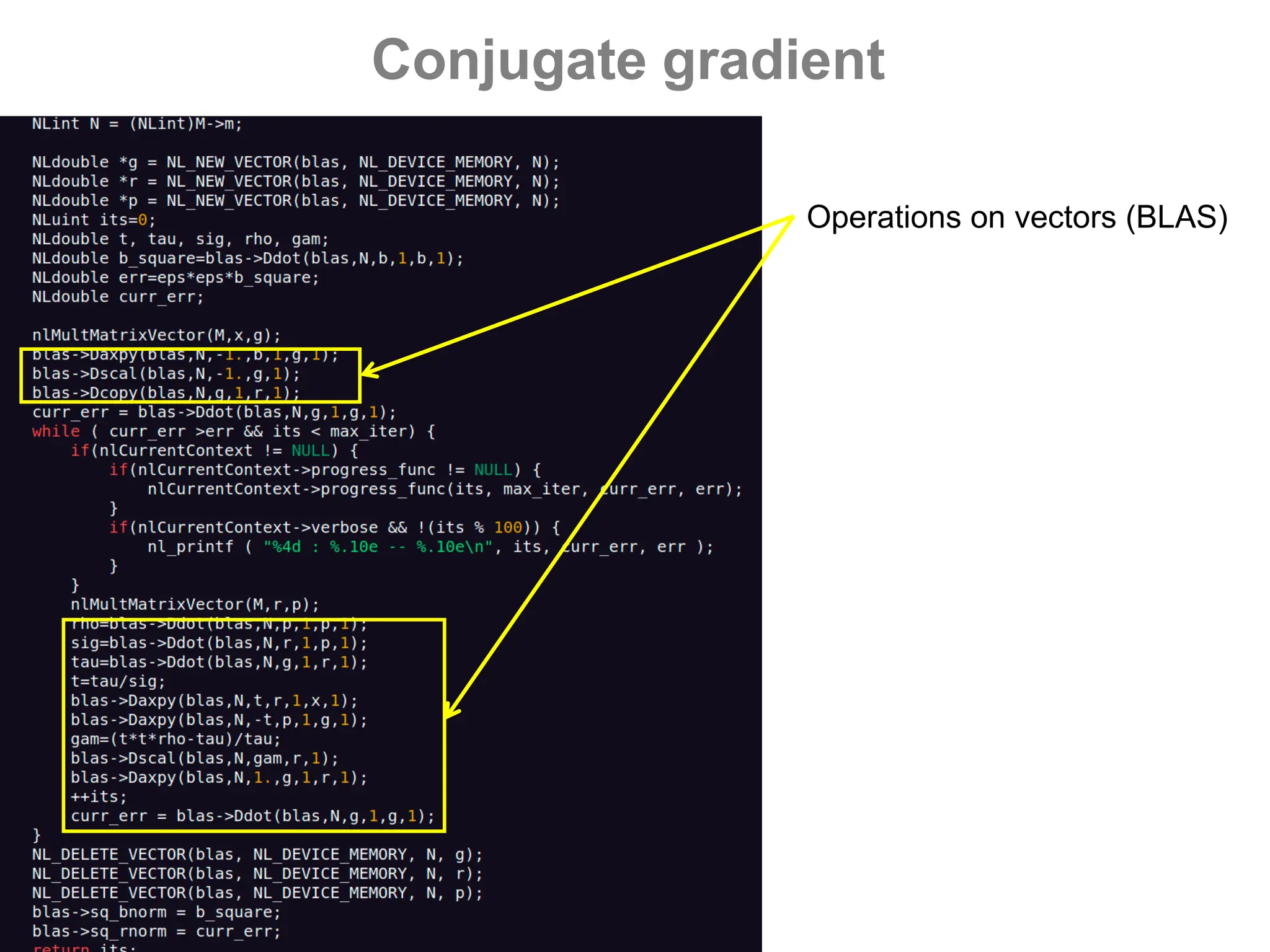




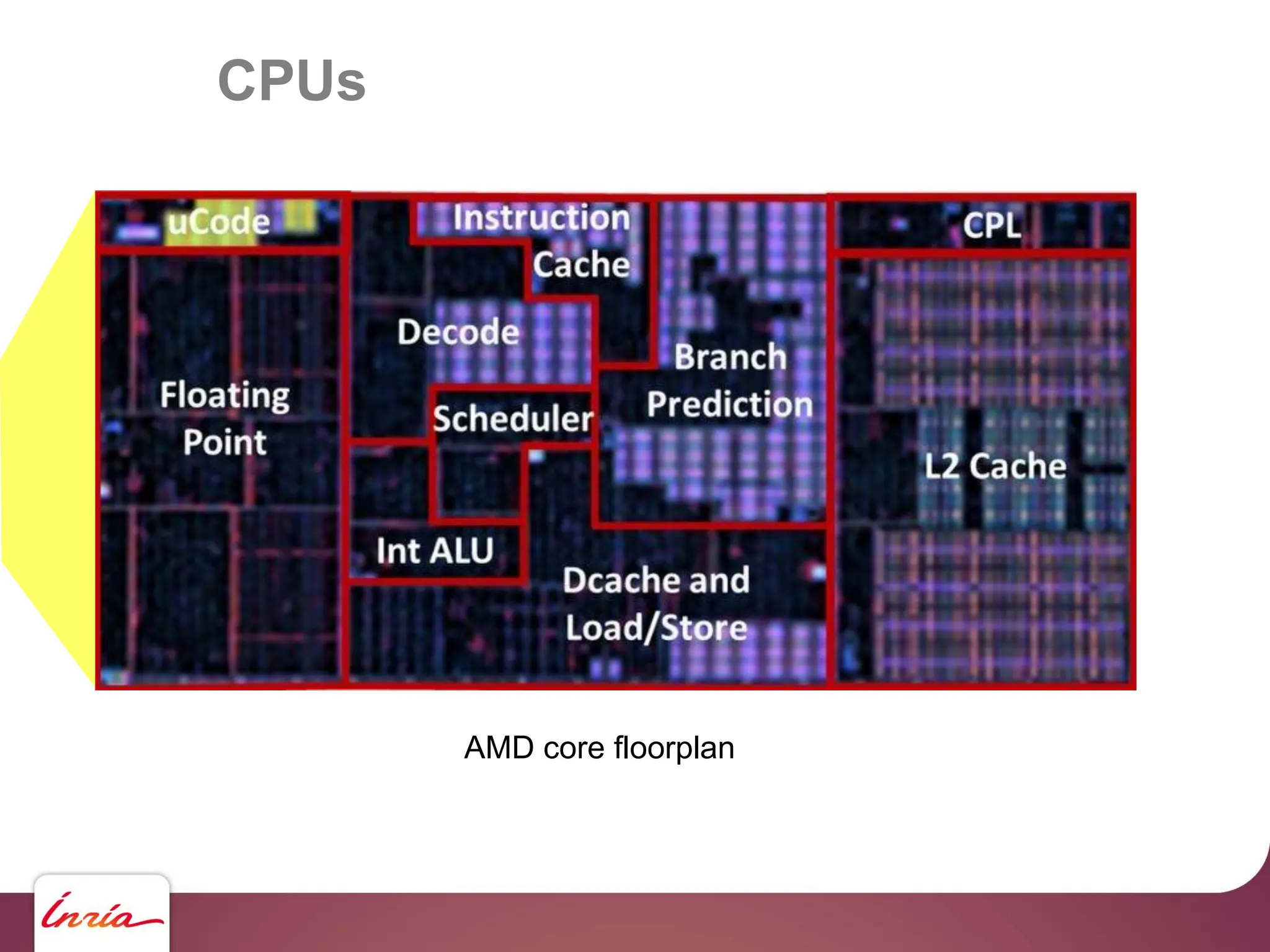
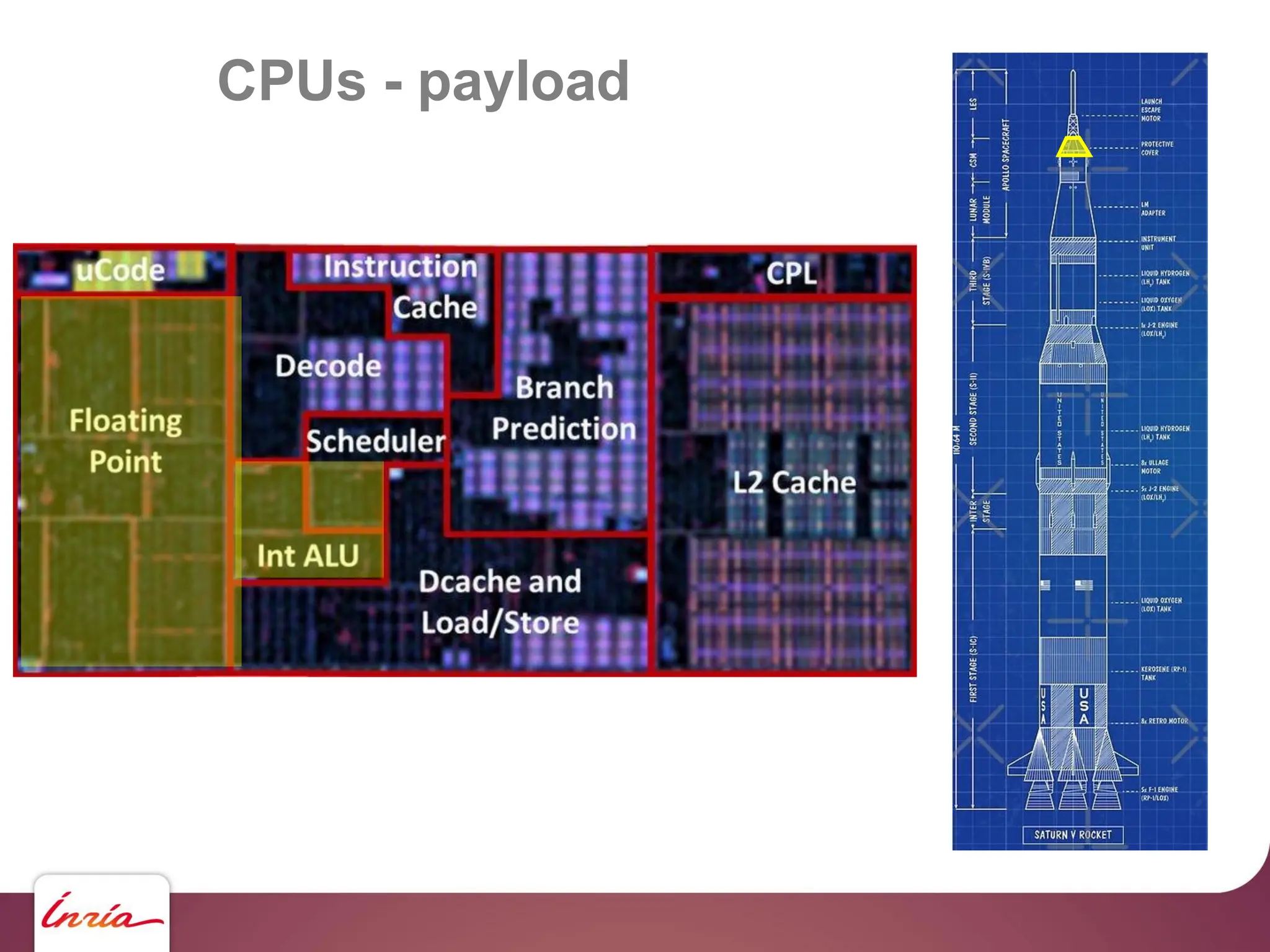
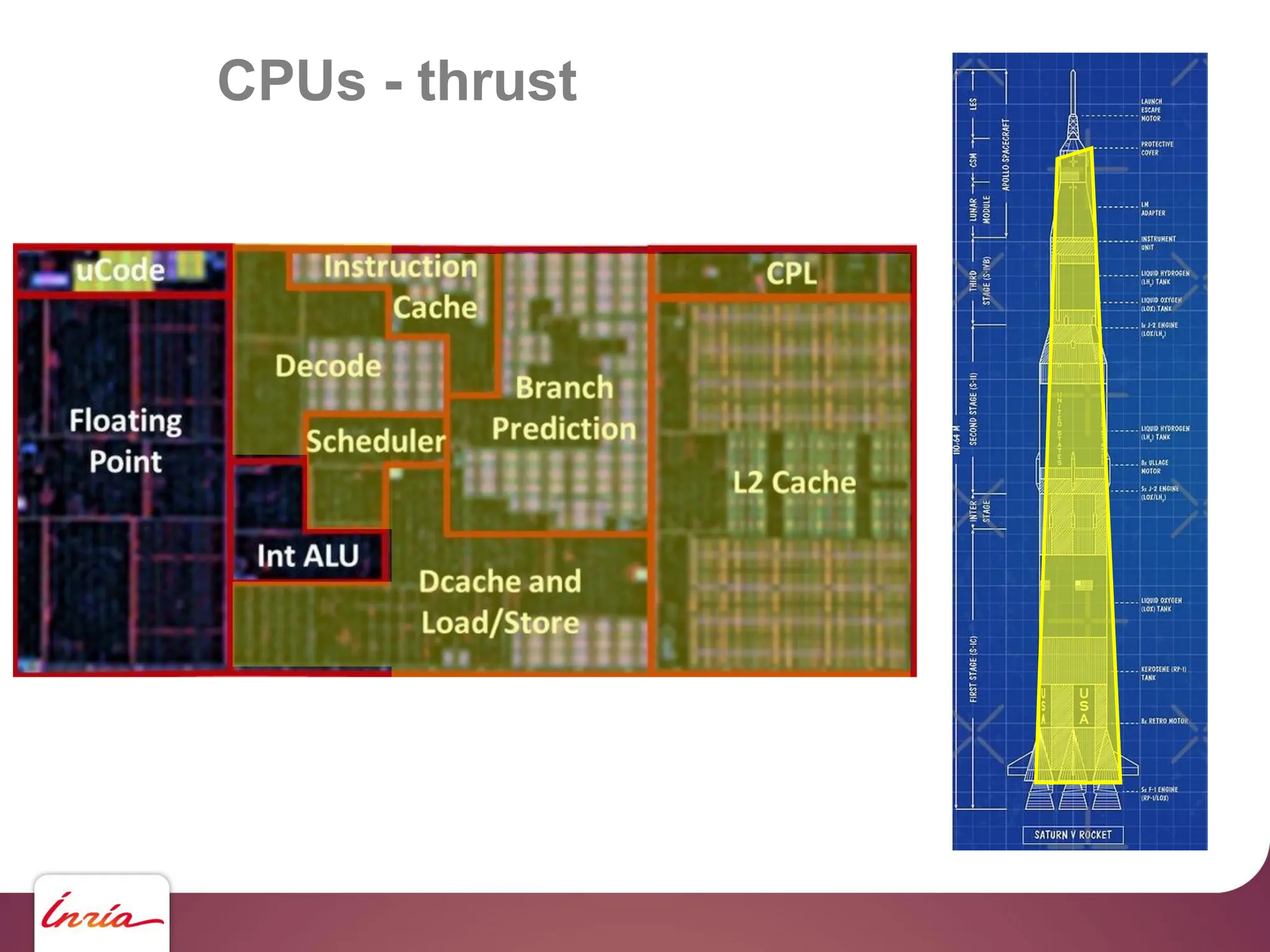

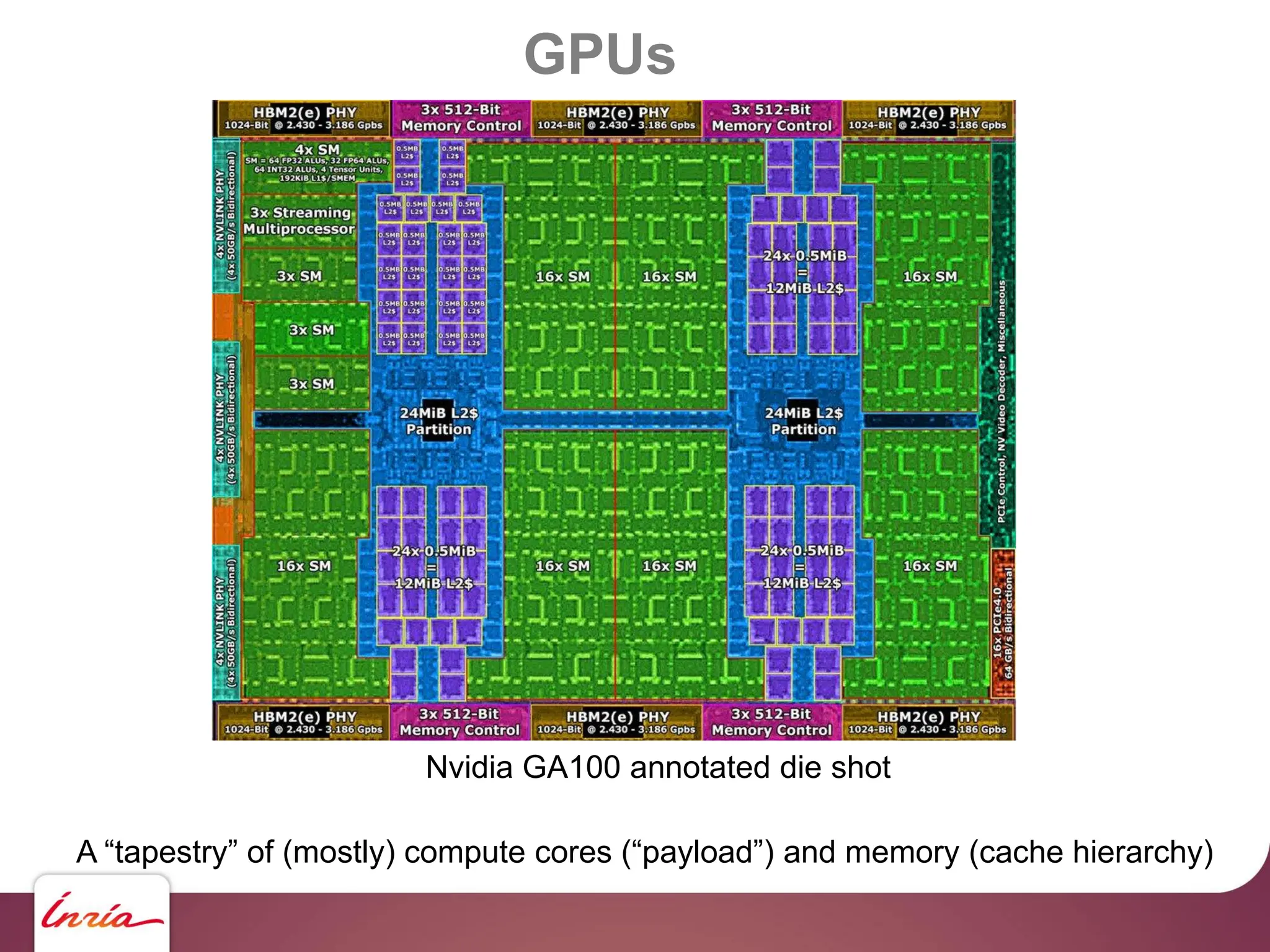







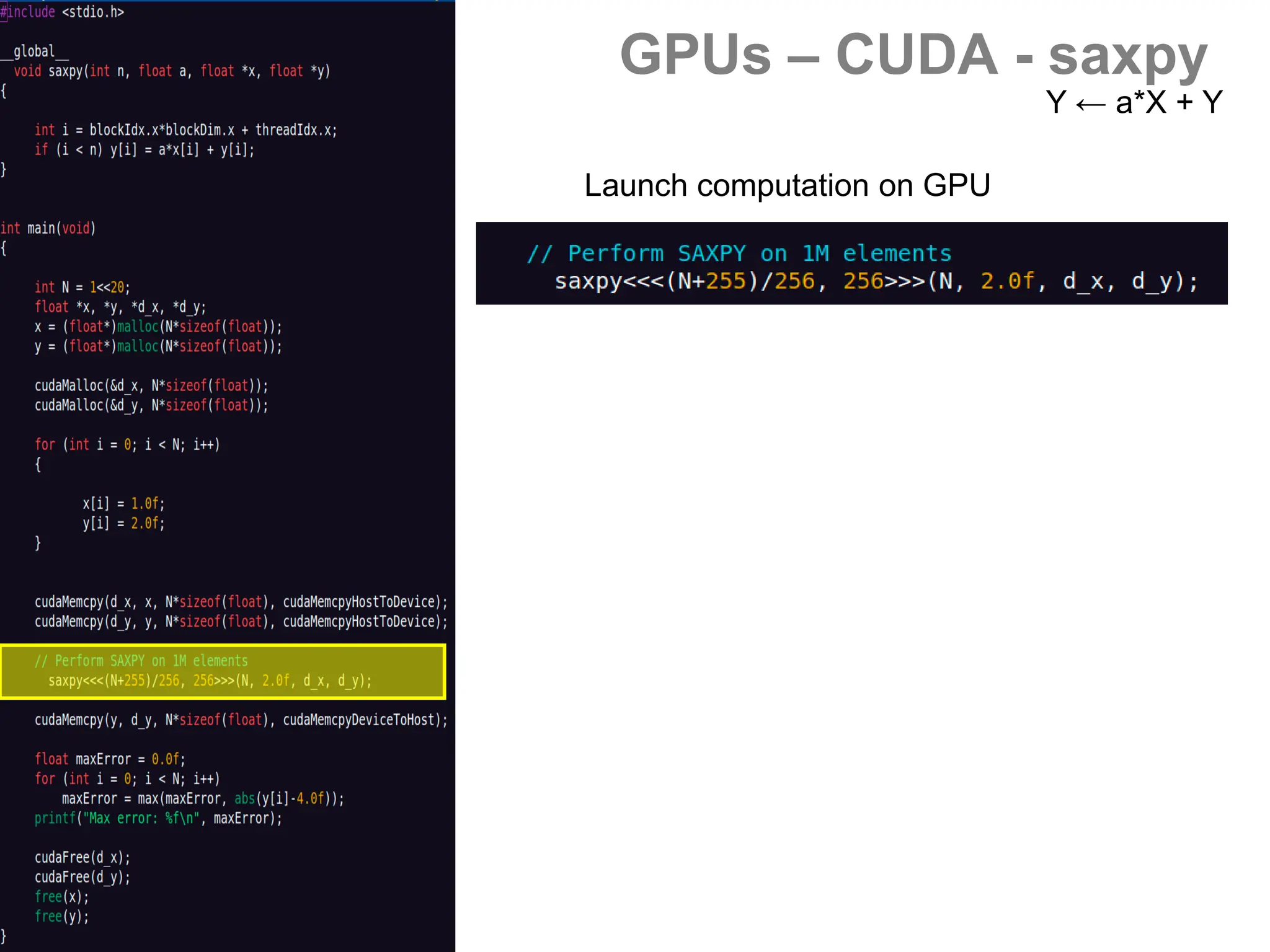
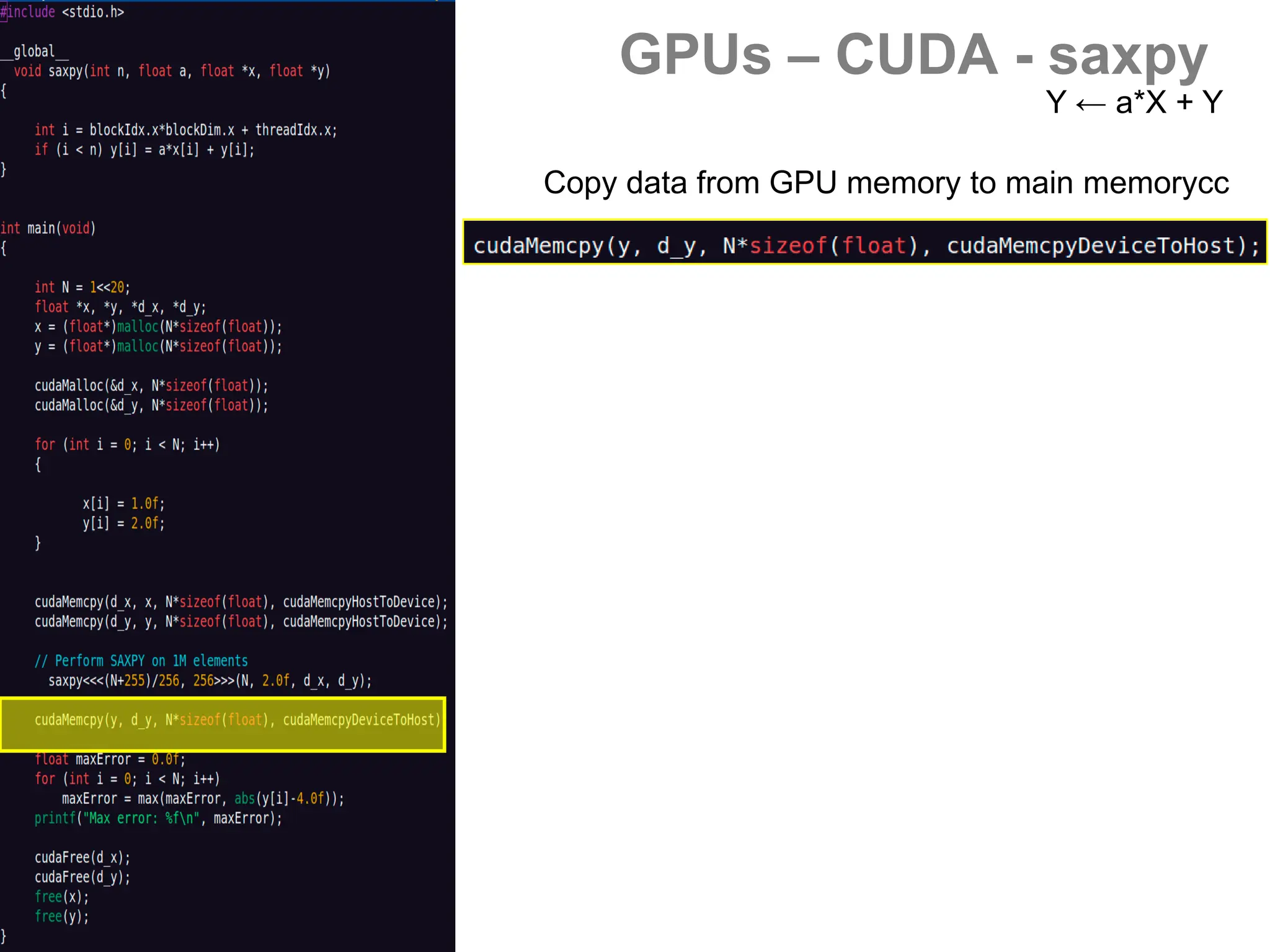
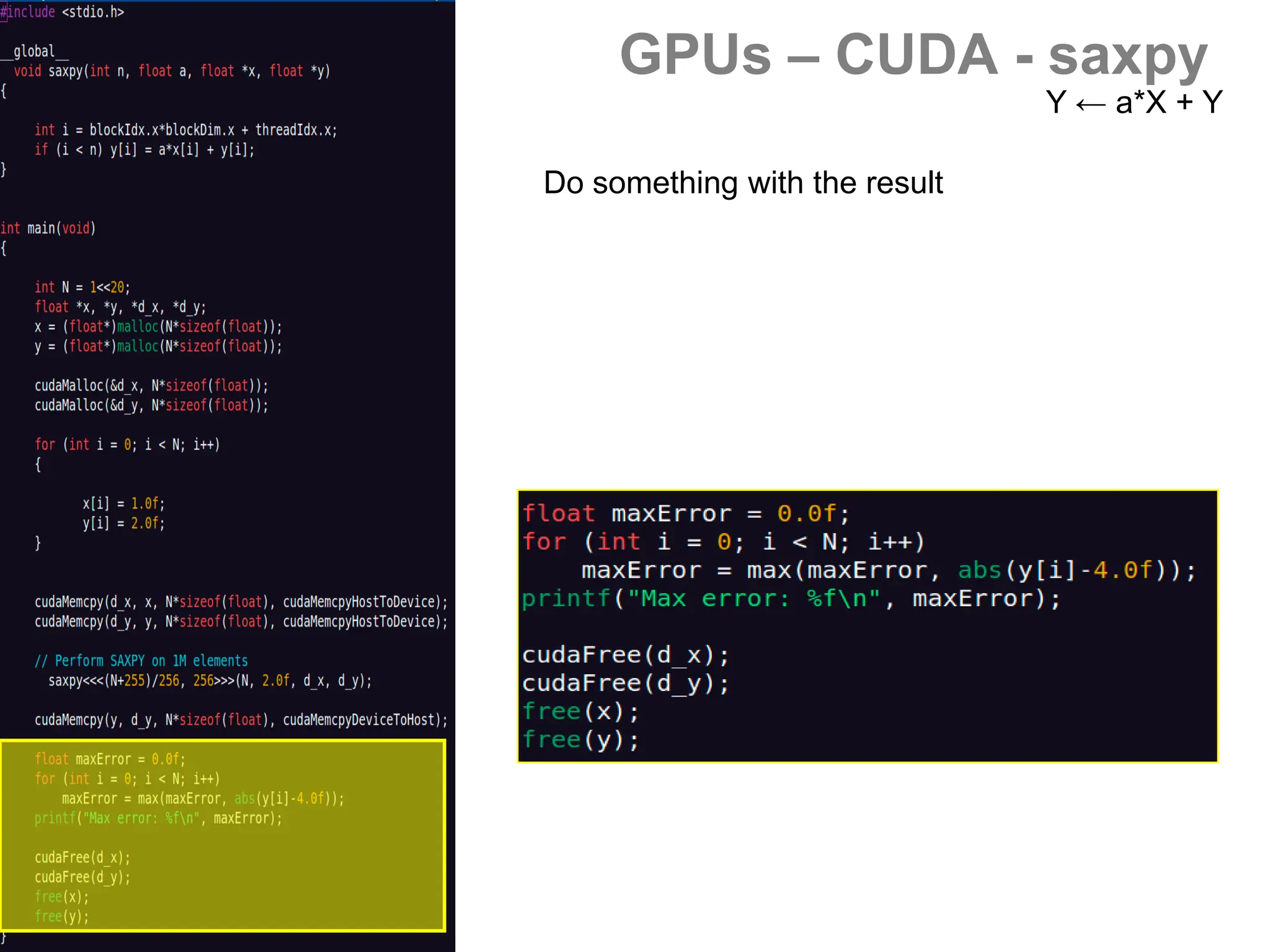
![GPUs – CUDA - saxpy
- Vector operations (BLAS)
[s/d]axpy Y ← a*X + Y
[s/d]dot a ← X.Y
[s/d]scal X ← a*X](https://image.slidesharecdn.com/gpunl-241218081309-df2bd1bb/75/Solving-large-sparse-linear-systems-on-the-GPU-54-2048.jpg)
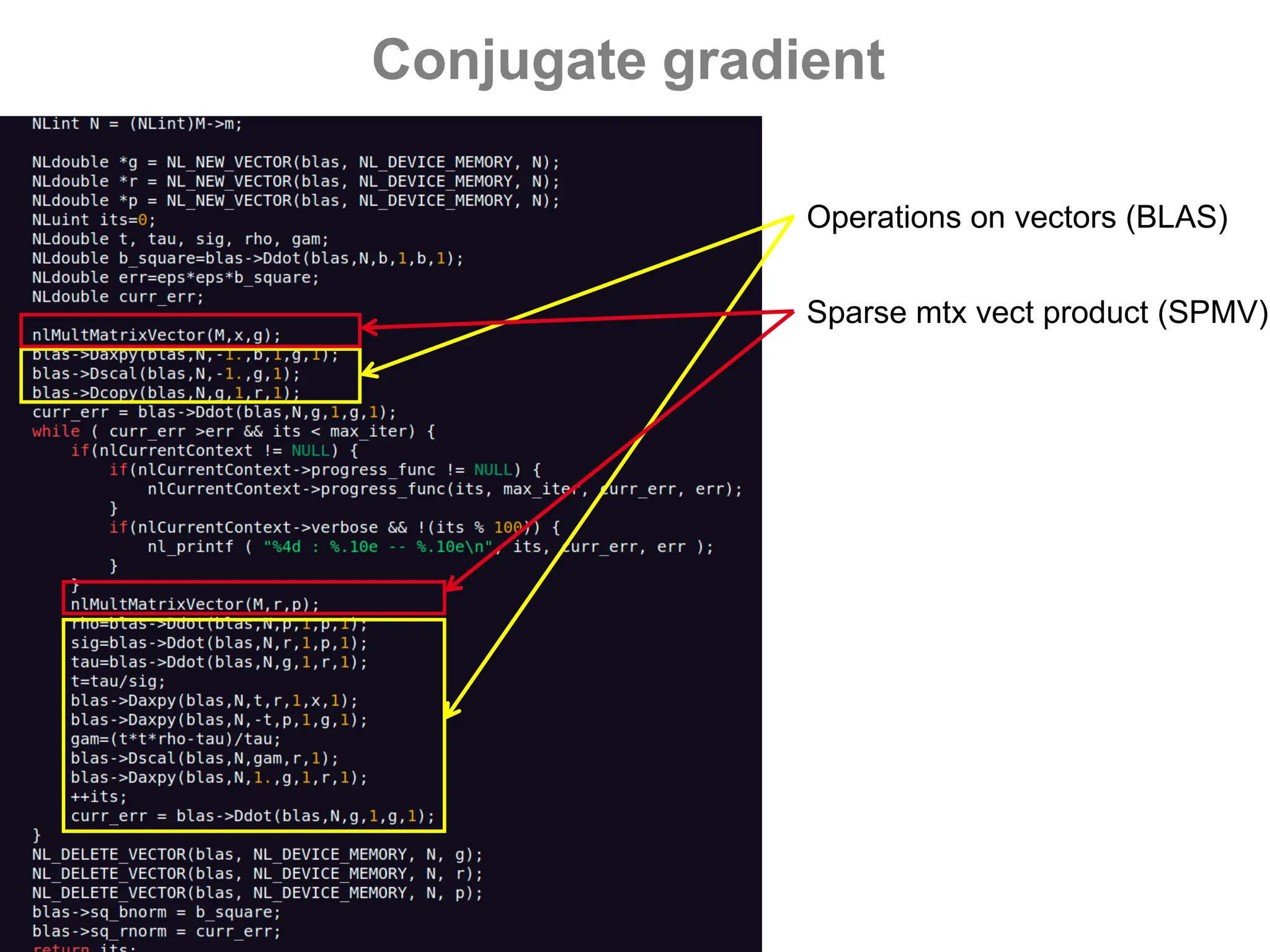
![GPUs – CUDA - spmv
- Vector operations (BLAS)
- Sparse matrix-vector product
[Buatois, Caumon, L 2009]
“Concurrent Number Cruncher”
OpenNL (github, part of geogram),
CUDA backend
Y ← M*X](https://image.slidesharecdn.com/gpunl-241218081309-df2bd1bb/75/Solving-large-sparse-linear-systems-on-the-GPU-55-2048.jpg)
![GPUs – CUDA - spmv
- Vector operations (BLAS)
- Sparse matrix-vector product
[Buatois, Caumon, L 2009]
“Concurrent Number Cruncher”
OpenNL (github, part of geogram),
CUDA backend
Y ← M*X](https://image.slidesharecdn.com/gpunl-241218081309-df2bd1bb/75/Solving-large-sparse-linear-systems-on-the-GPU-56-2048.jpg)




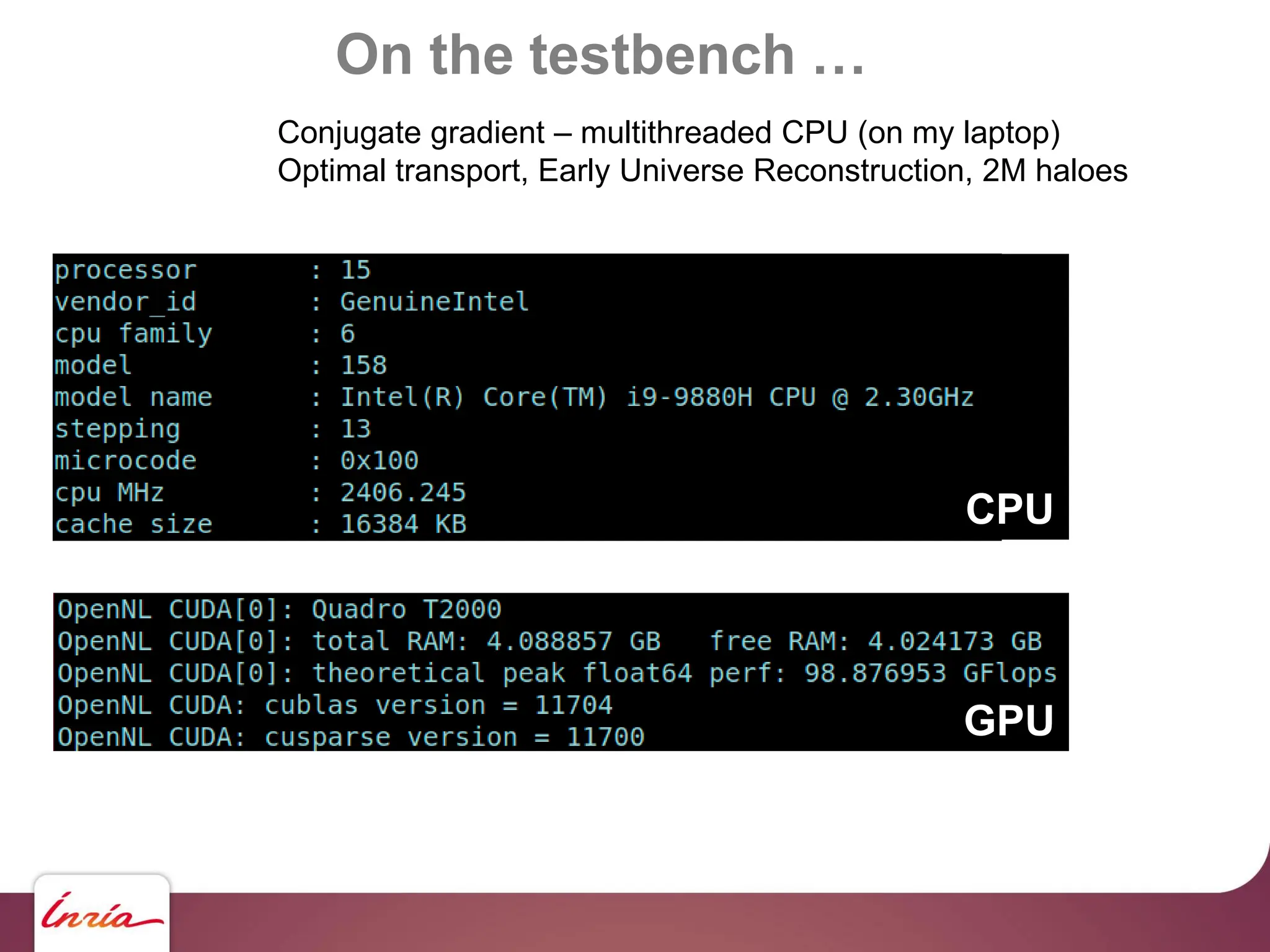
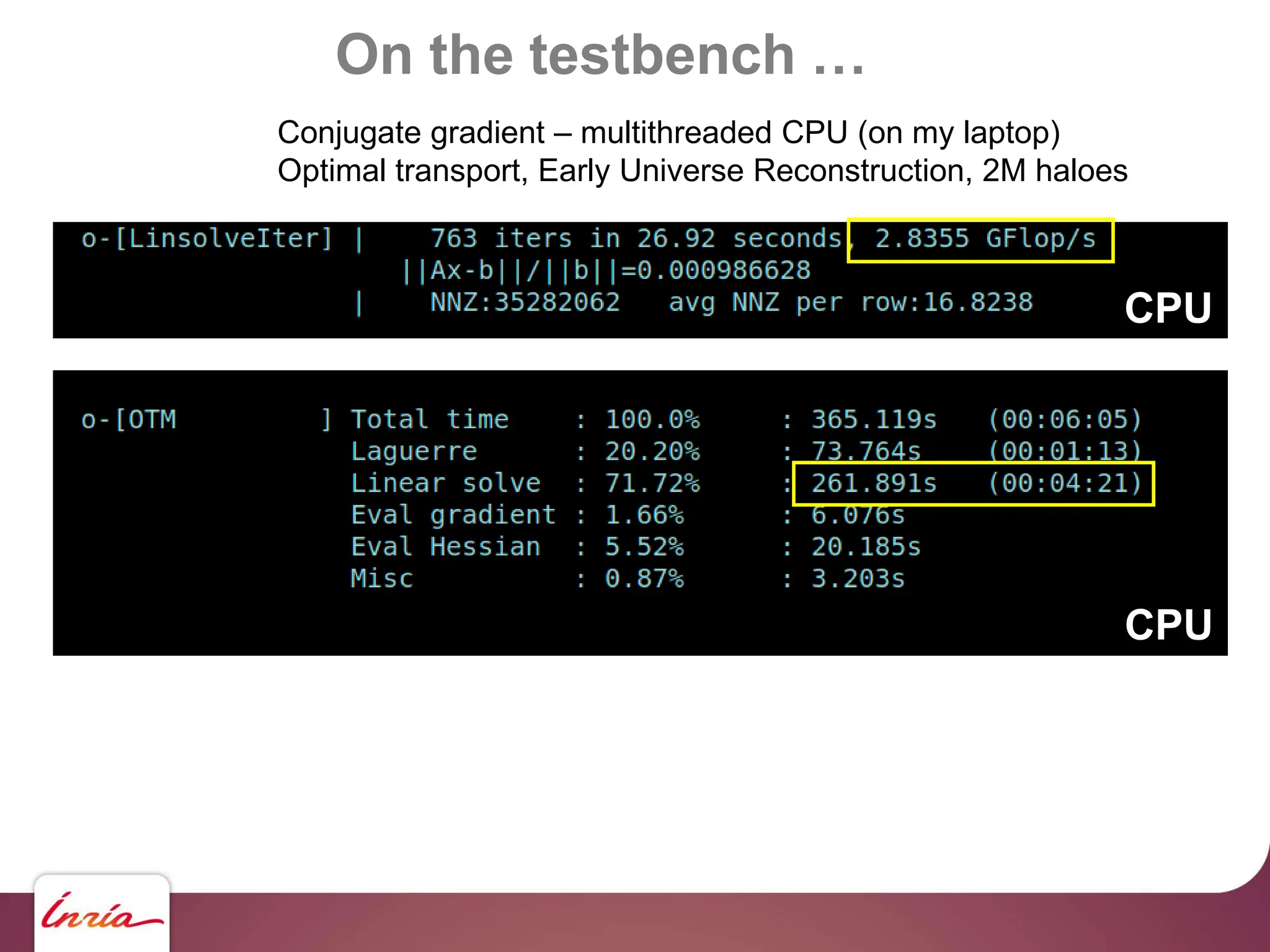
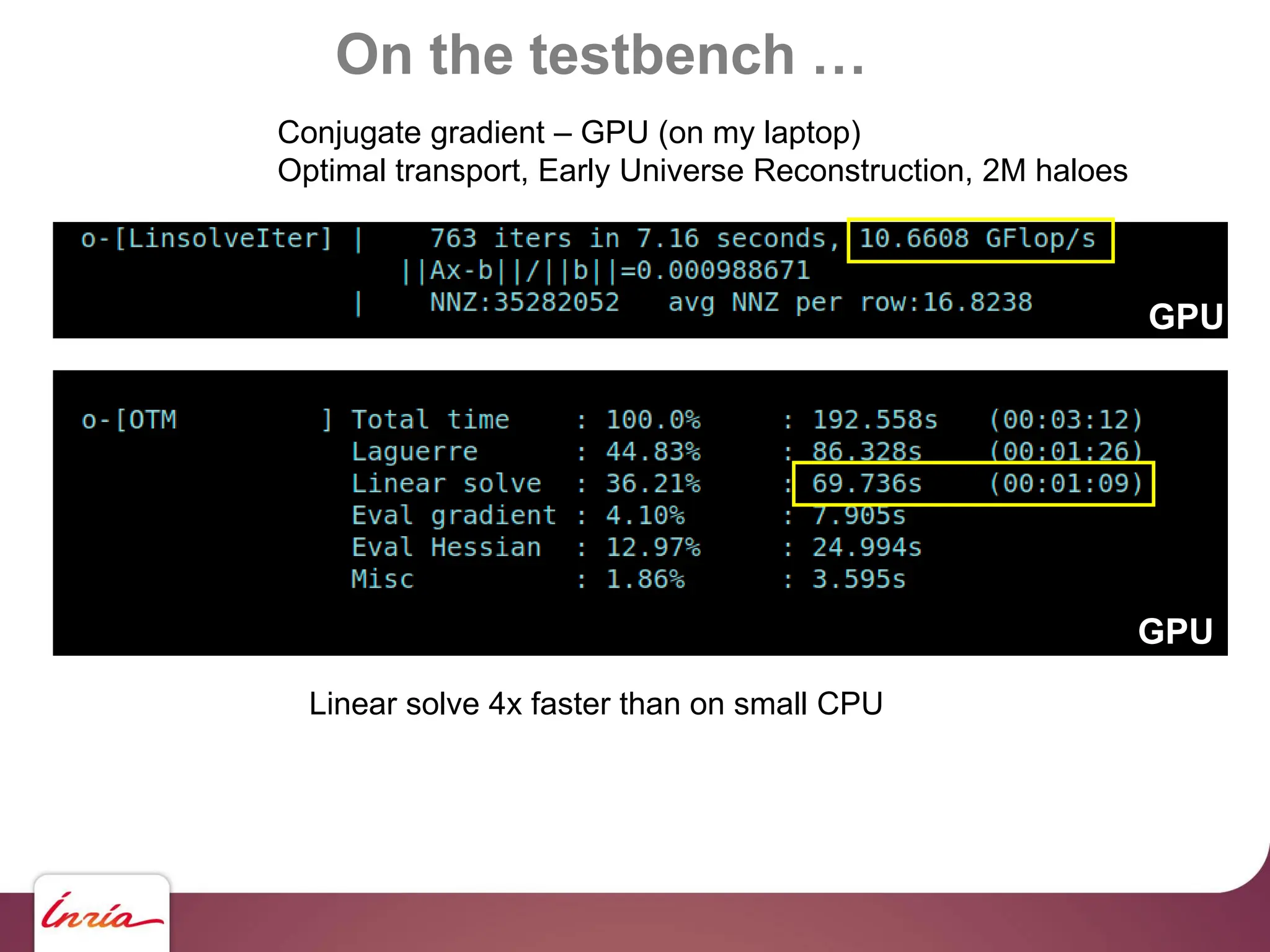




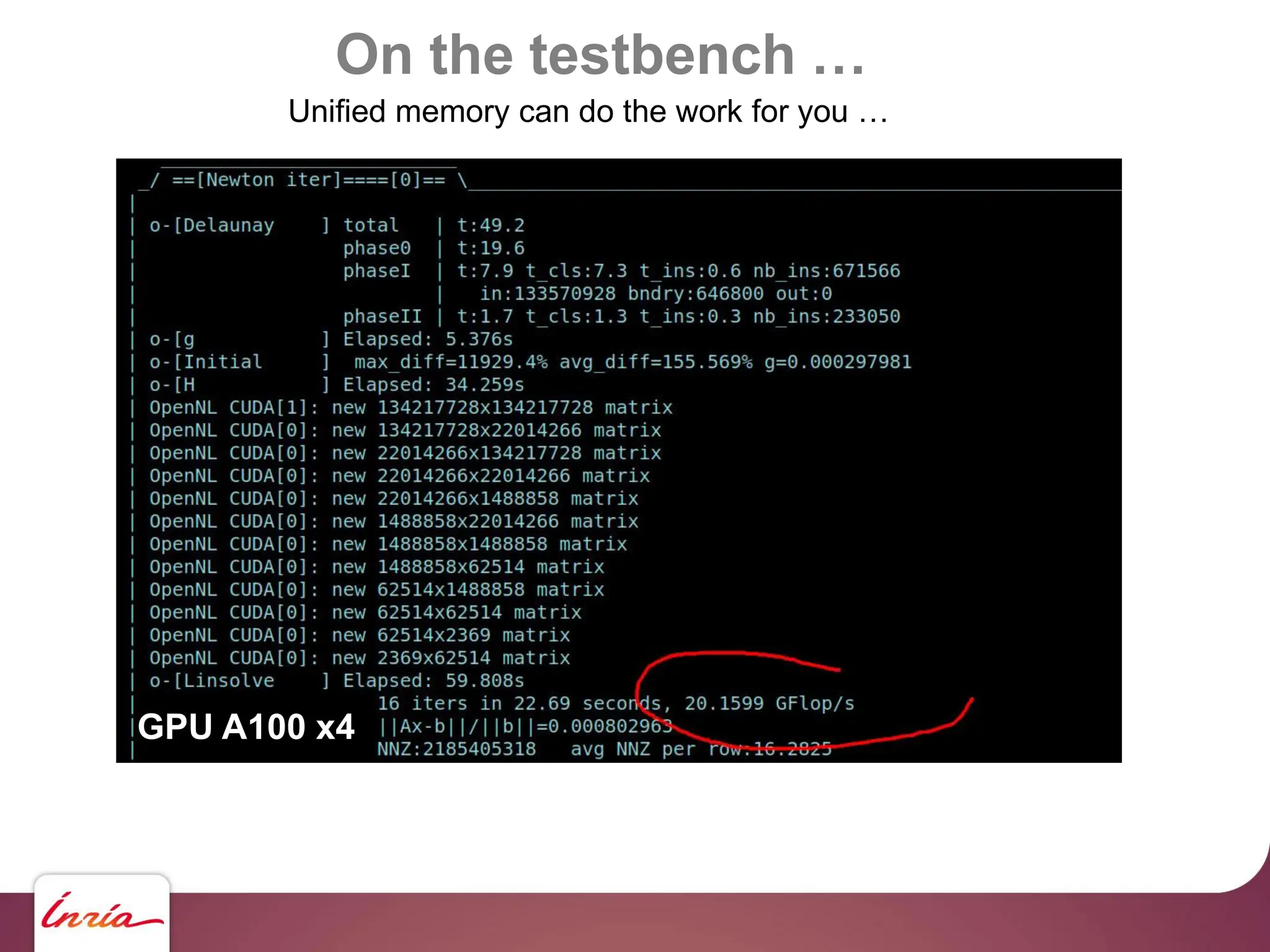
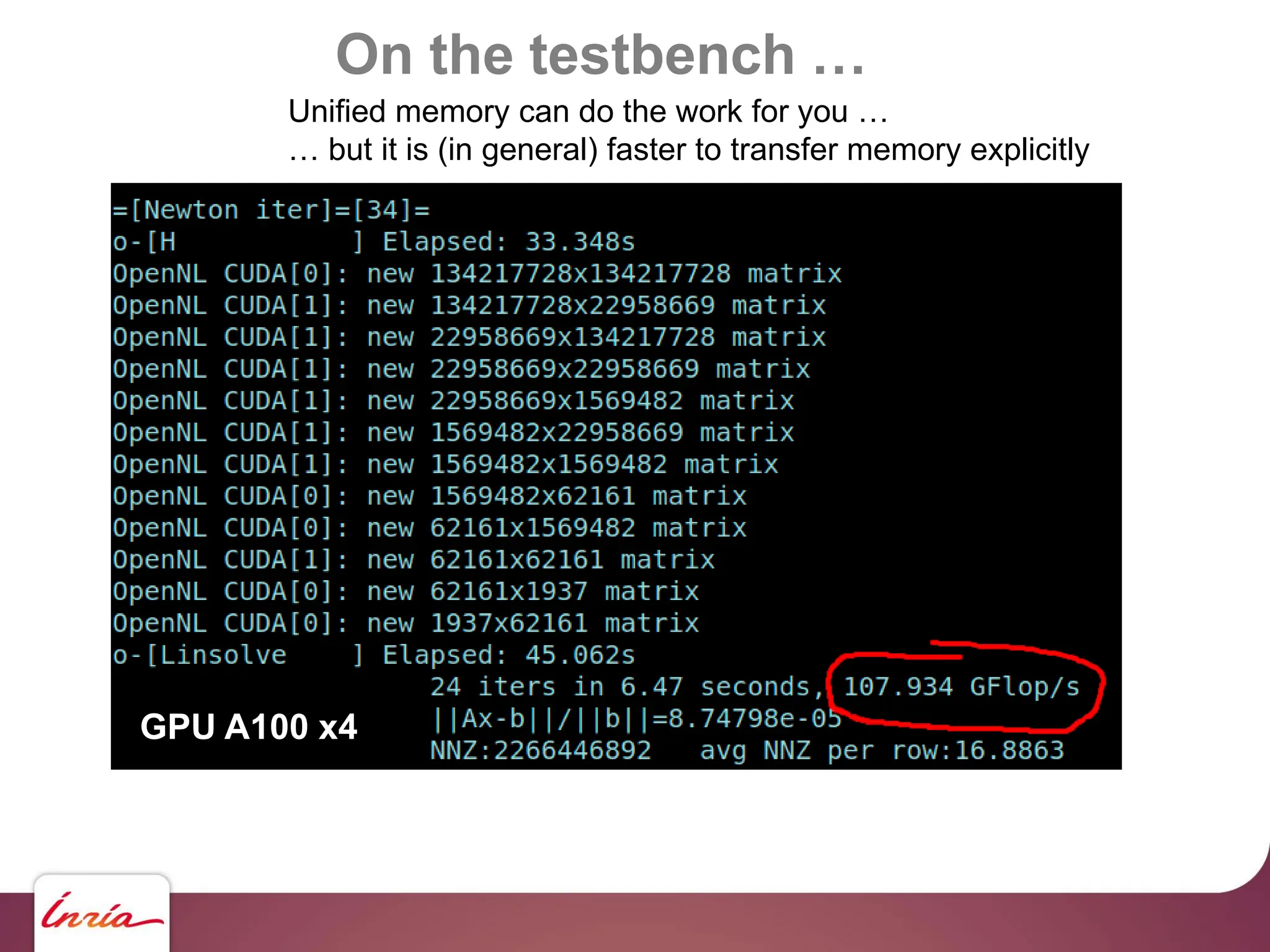
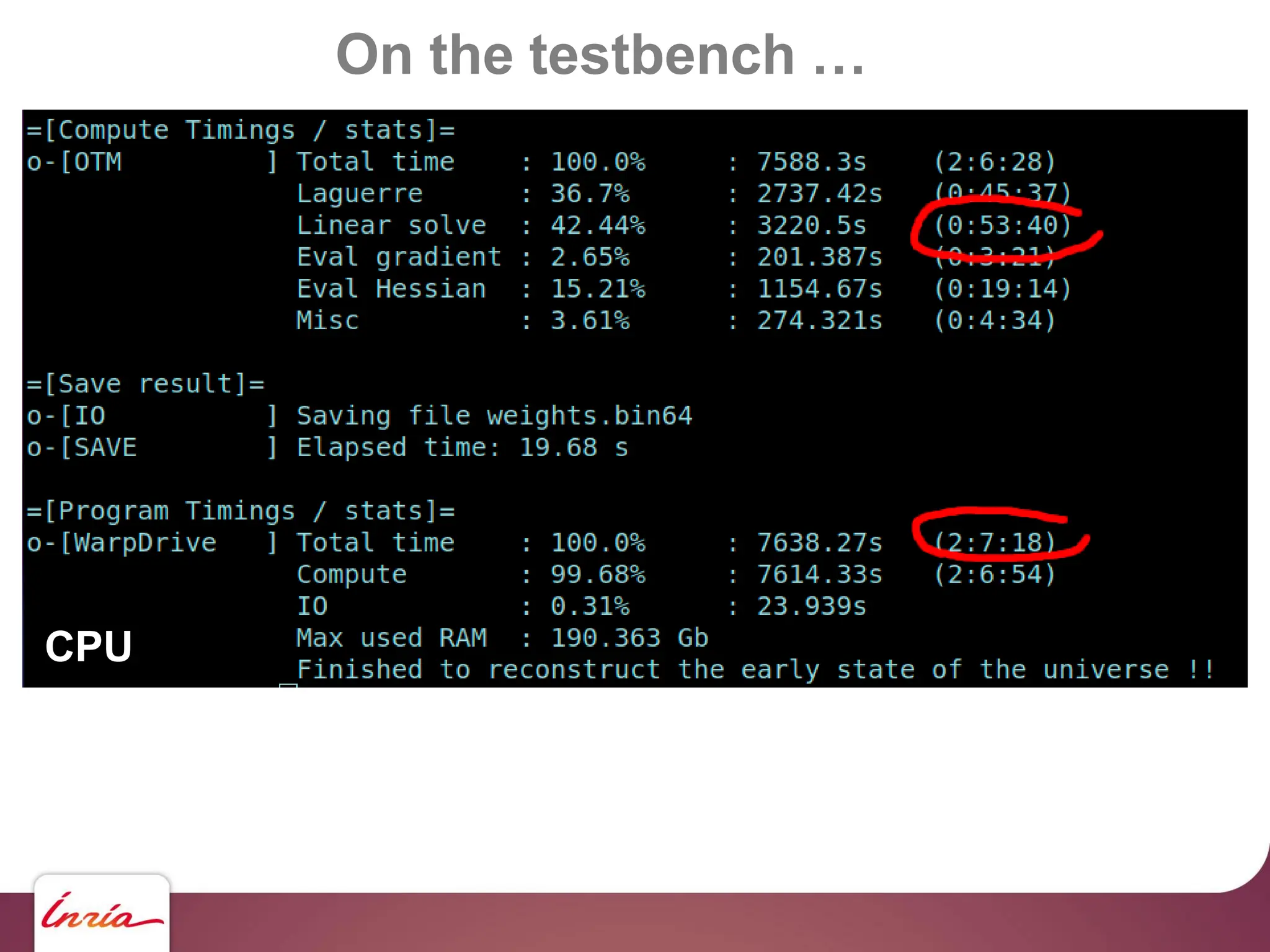
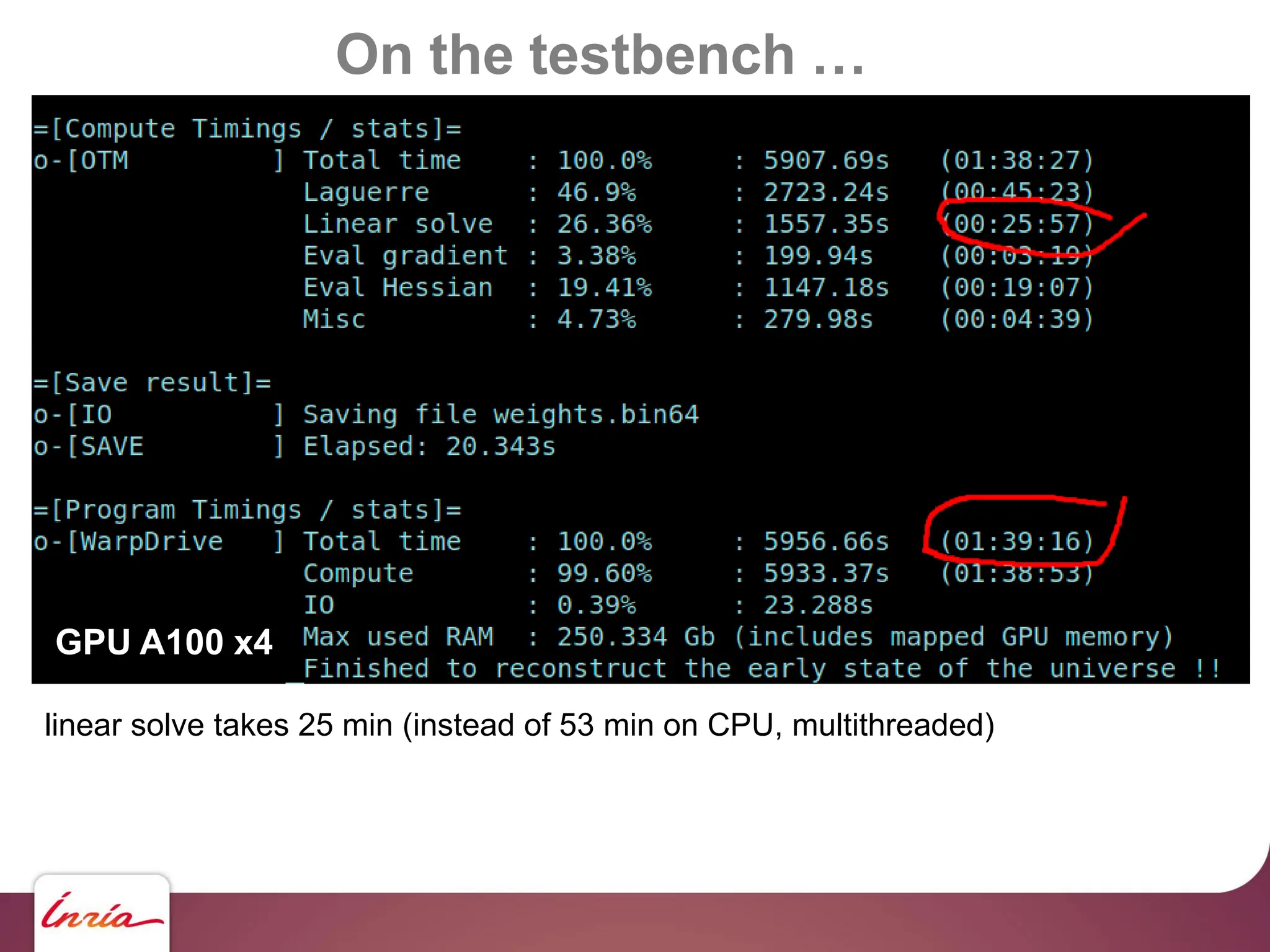
![On the testbench …
… scaling up !!
130 M haloes … we need to upgrade !!!
- Hardware side: 4x Nvidia A100
- Algorithmic side:
algebraic multigrid preconditioner
- Sofware side: AMGCL [Demidov] +
custom backend for multi-GPU (OpenNL/geogram), Object-oriented C
- BLAS abstraction layer
- Sparse Matrix abstraction layer
- Matrix assembly helper https://github.com/BrunoLevy/geogram](https://image.slidesharecdn.com/gpunl-241218081309-df2bd1bb/75/Solving-large-sparse-linear-systems-on-the-GPU-68-2048.jpg)
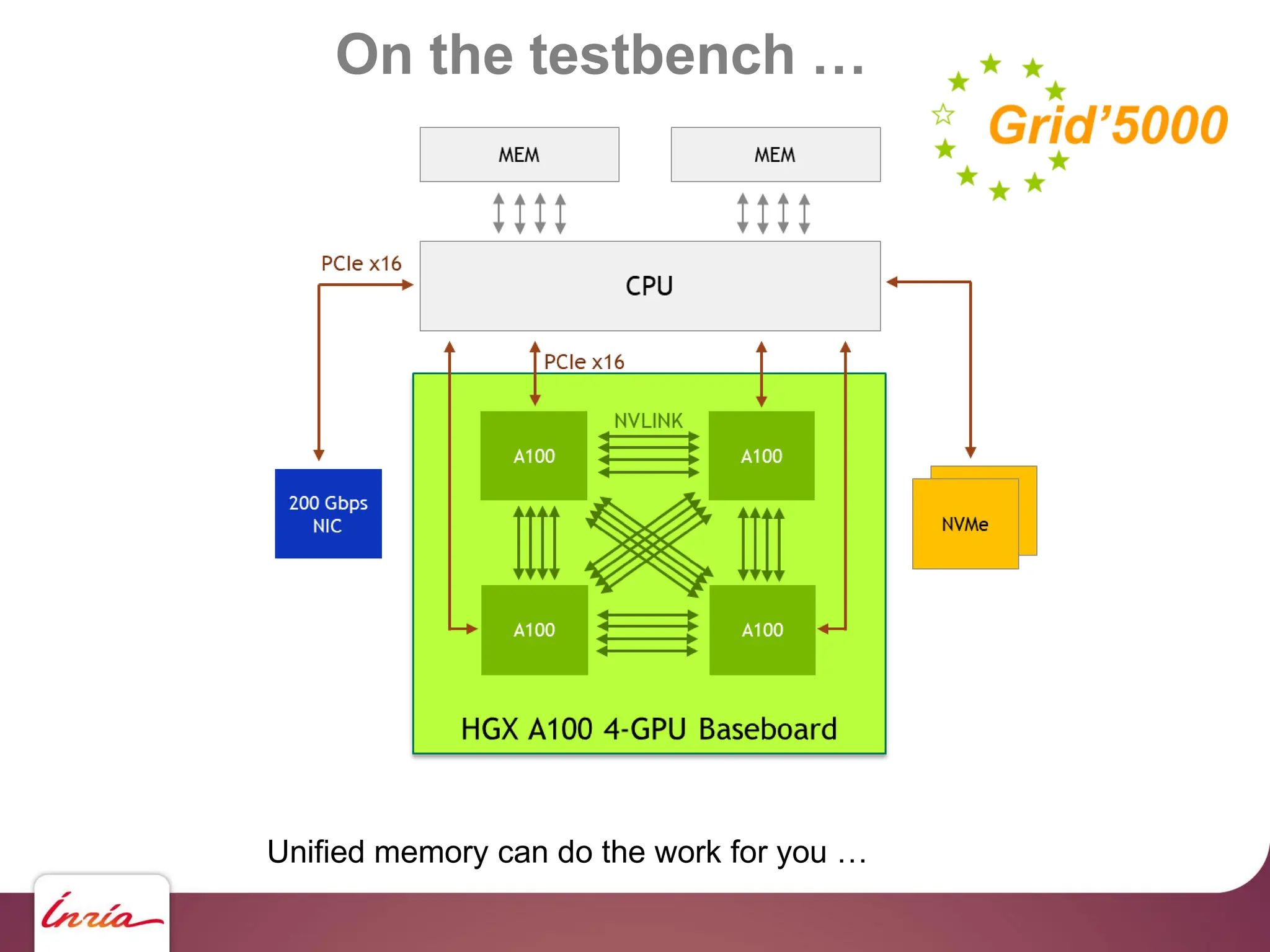
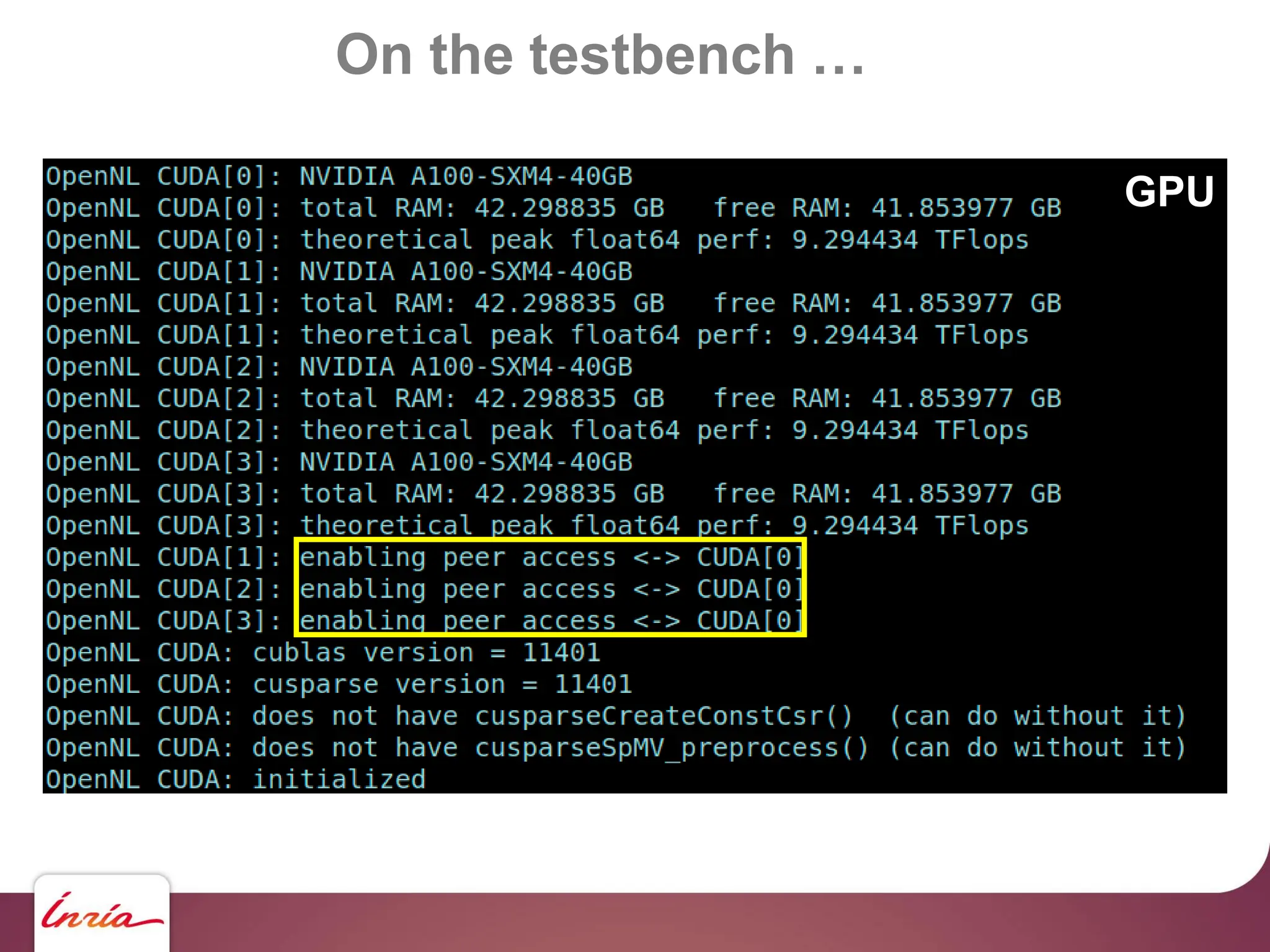
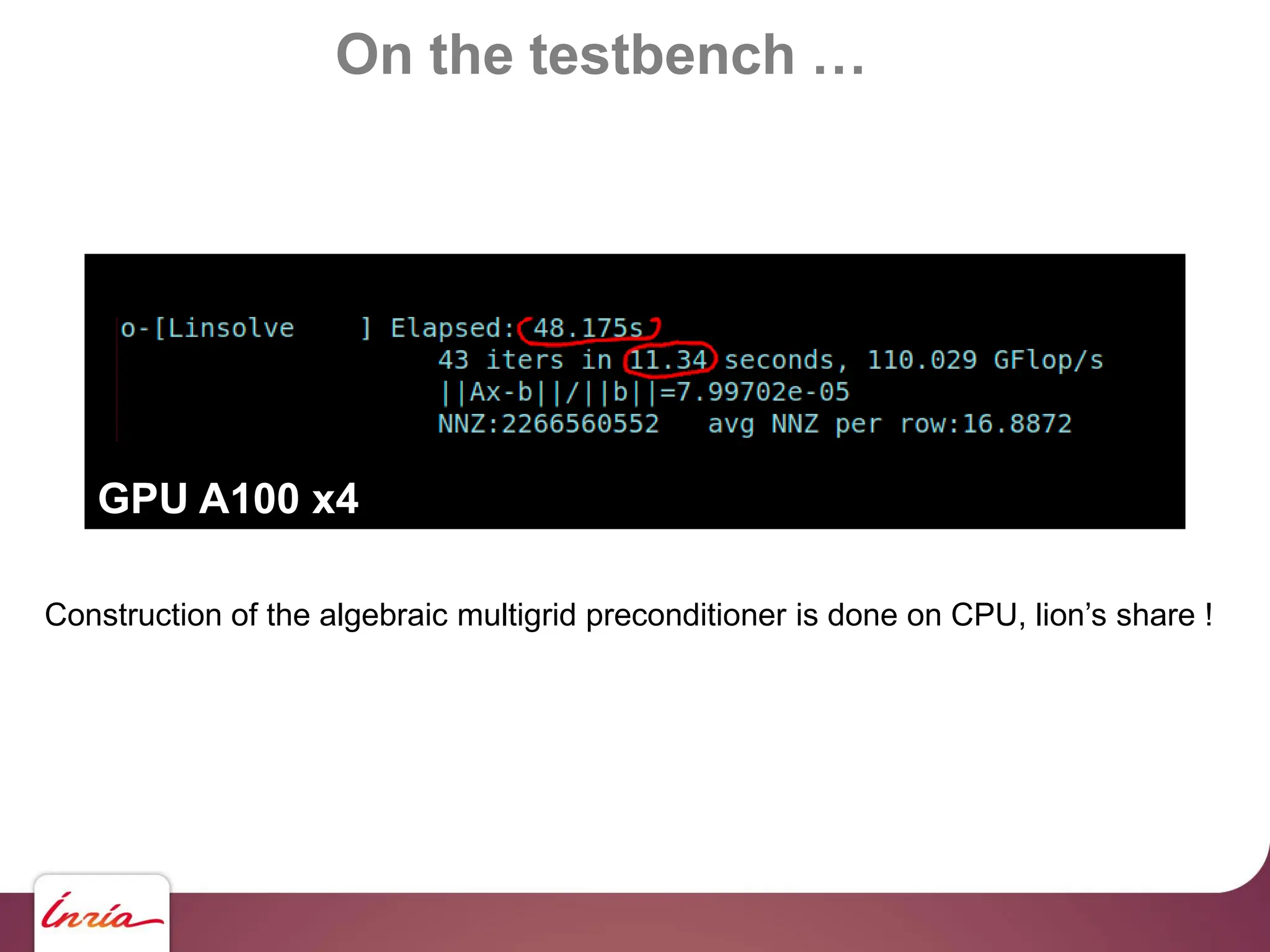
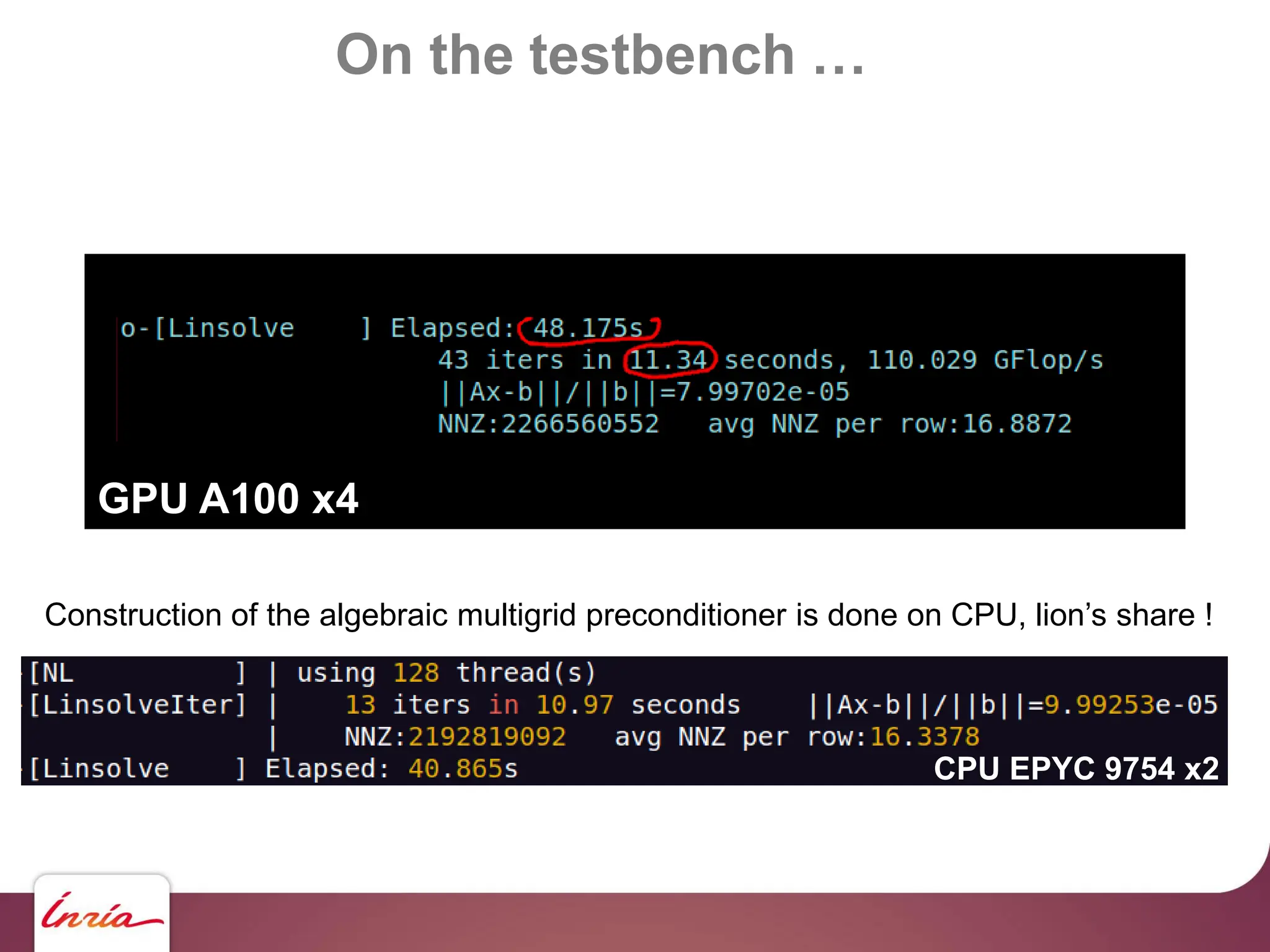
![Coming Next …
Coming next: construction of preconditioner on GPU too.
Laguerre diagram on GPU ?
possible but harder… [Ray, Basselin, Alonso, Sokolov, L, Lefebvre]](https://image.slidesharecdn.com/gpunl-241218081309-df2bd1bb/75/Solving-large-sparse-linear-systems-on-the-GPU-77-2048.jpg)
