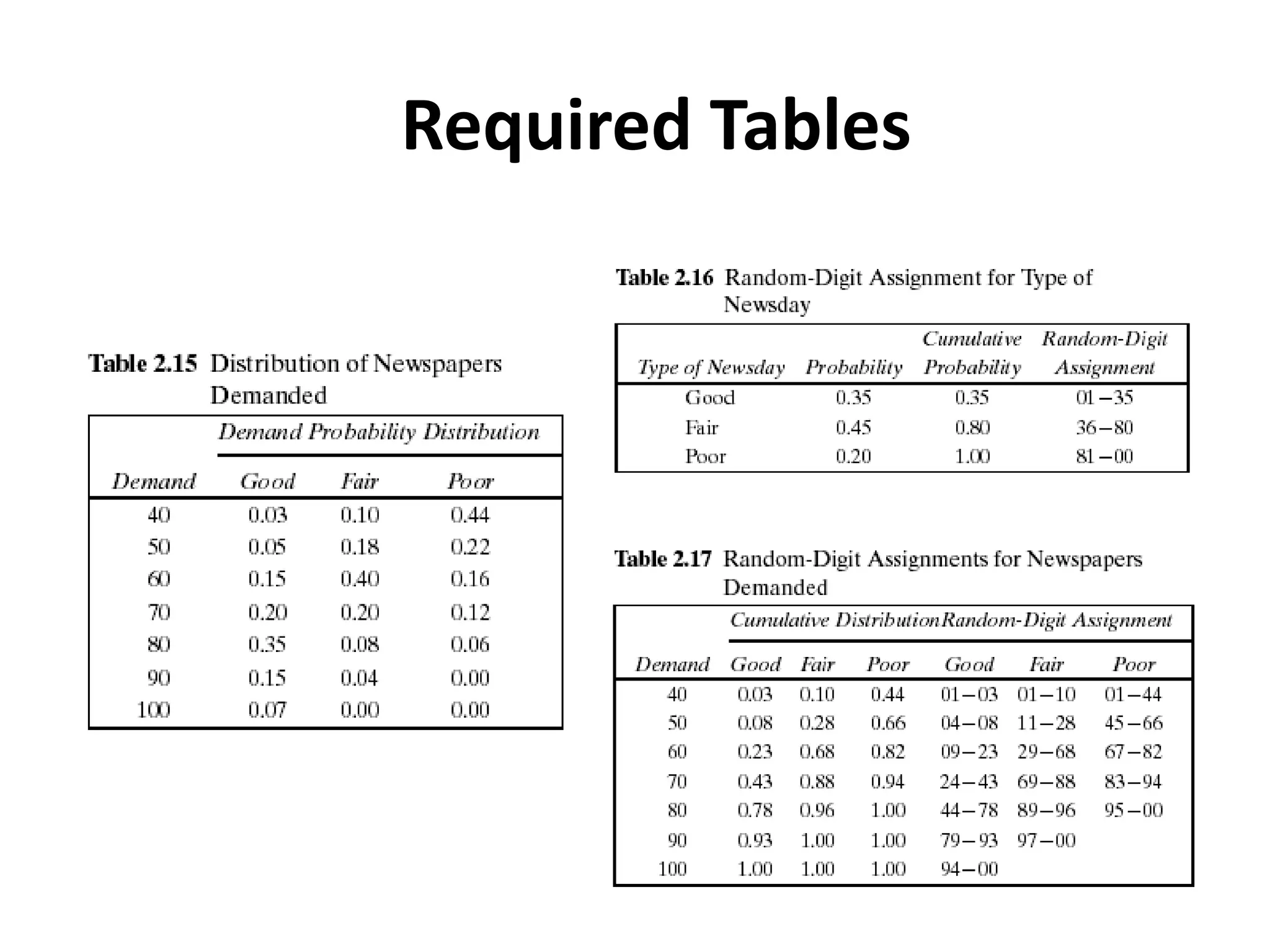
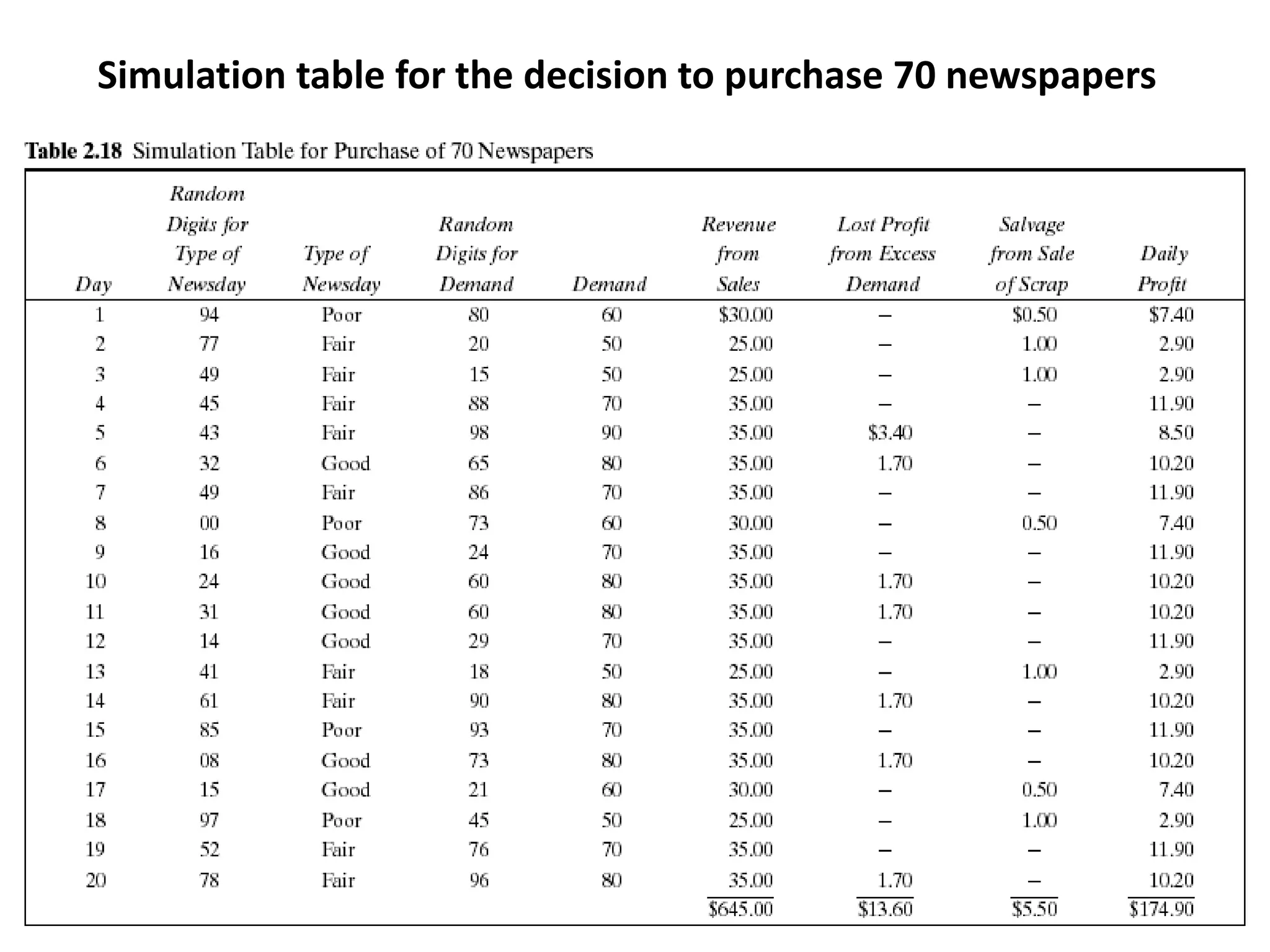
The document presents a simulation of an inventory system for a newspaper seller determining the optimal number of papers to purchase. It outlines the demand variability over 20 days and calculates profits based on sales, excess demand, and salvage value, ultimately finding a total profit of $174.90. The paper seller's purchasing decisions are iteratively tested and adjusted for optimal outcomes.