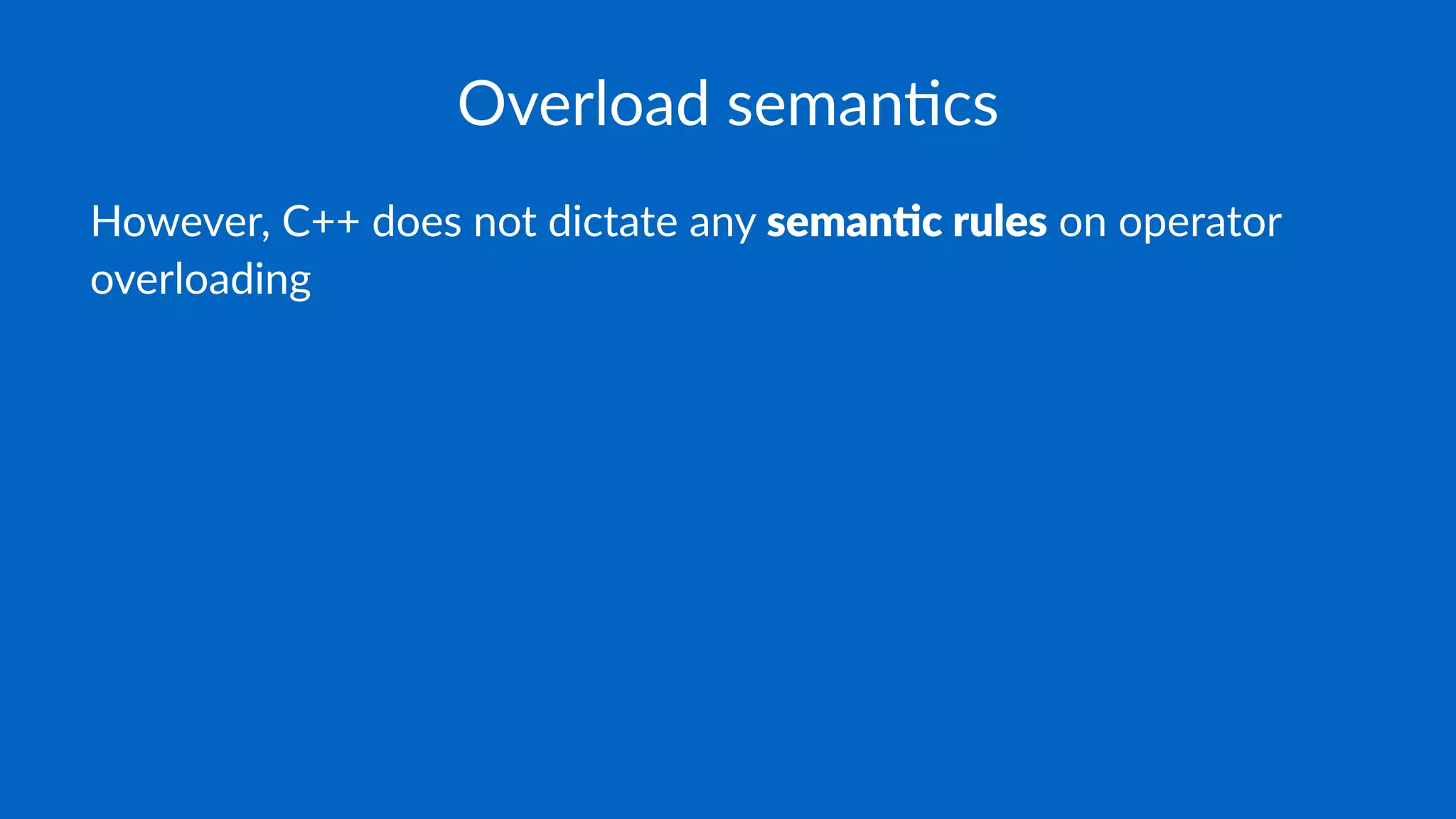
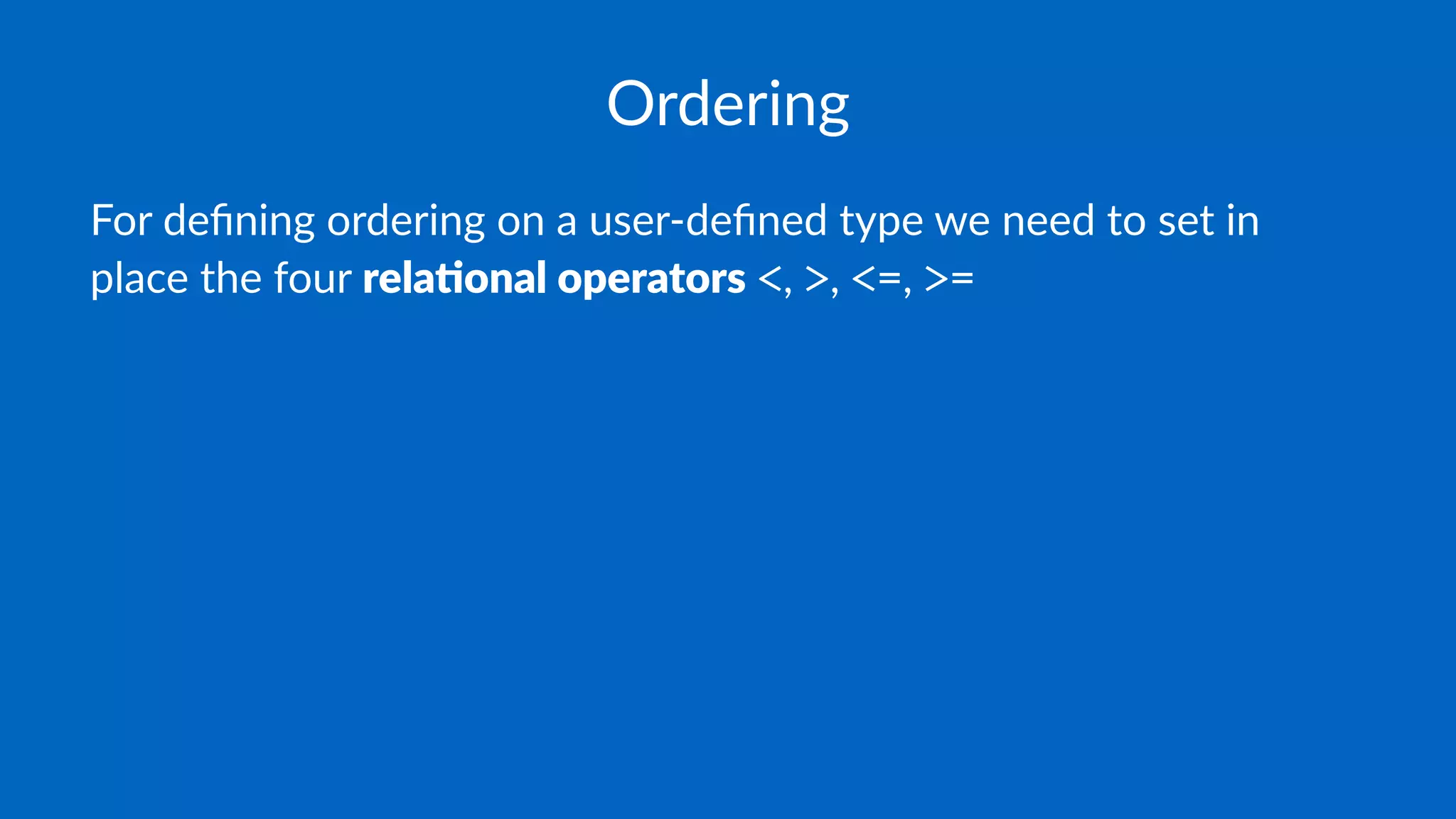
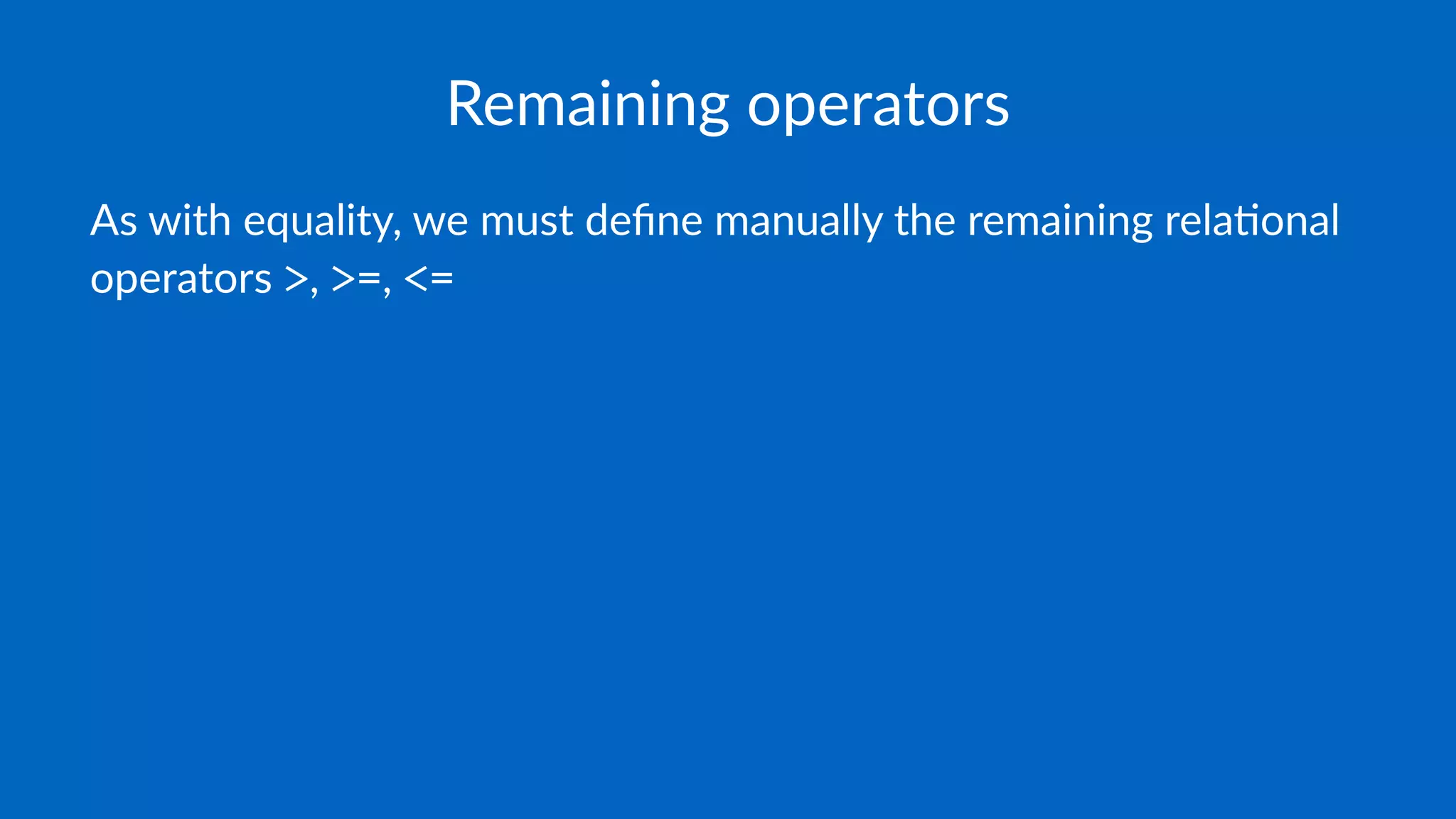
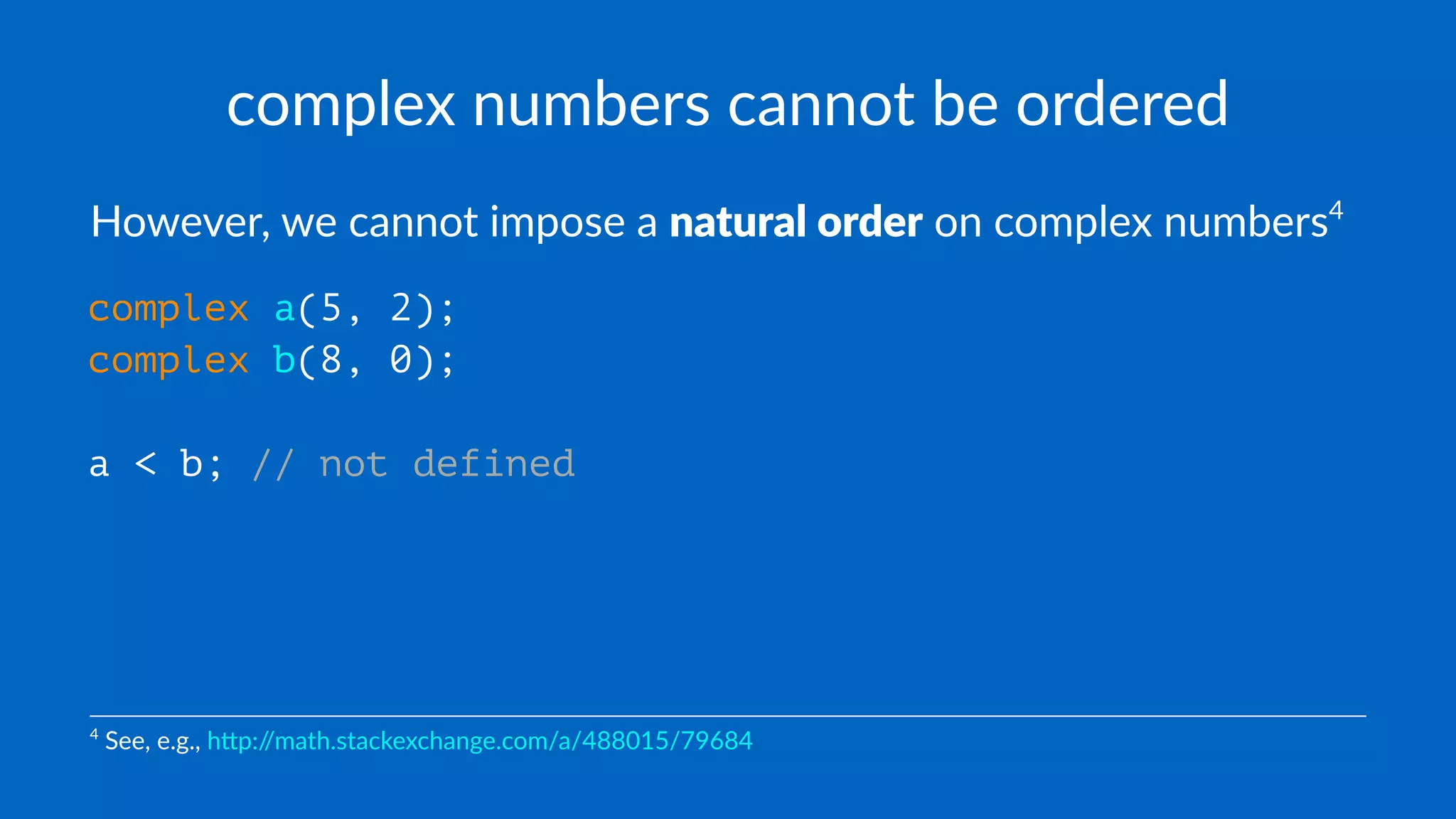
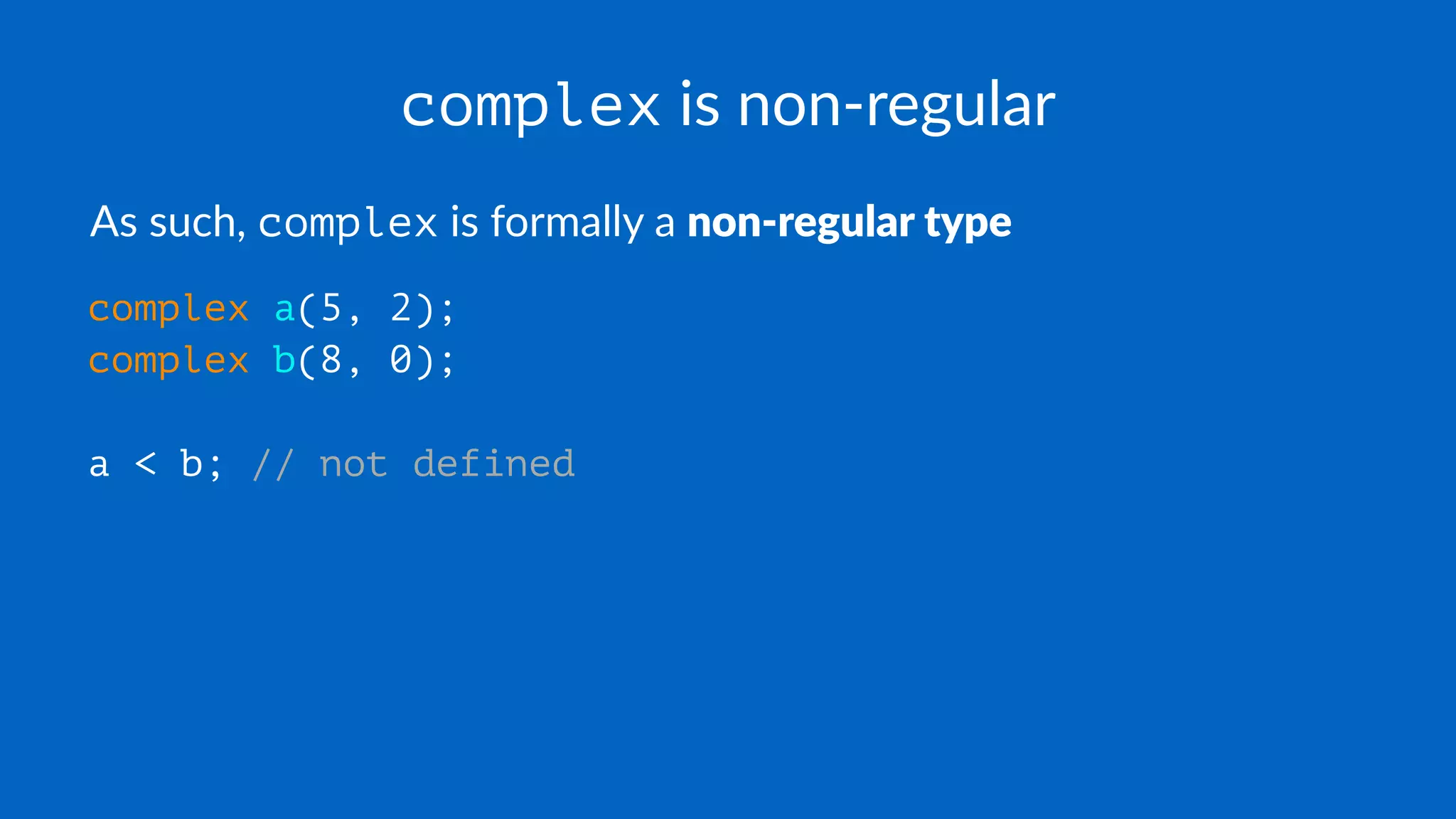
The document discusses the characteristics of regular types in C++, emphasizing their similarity to built-in types in terms of operations like assignment, copy construction, and equality. It explains the importance of defining user-defined types (UDTs) in a way that preserves the behaviors of standard operations while introducing fundamental operations consistent across built-in types. Additionally, the text highlights the need for strict and transitive definitions of ordering and equality in UDTs.















































































































![vector_int
class vector_int {
public:
vector_int(): sz(0), elem(nullptr) {}
vector_int(std::size_t sz): sz(sz), elem(new int[sz]) {...}
vector_int(vector_int const& v): sz(v.sz), elem(new int[v.sz]) {...}
~vector_int() {...}
std::size_t size() const {...}
int operator[](std::size_t i) const {...}
int& operator[](std::size_t i) {...}
vector_int& operator=(vector_int const& v) {...}
private:
std::size_t sz;
int* elem;
};](https://image.slidesharecdn.com/regulartypes-160130133044/75/Regular-types-in-C-118-2048.jpg)

![Equality
class vector_int {
public:
...
bool operator==(vector_int const& v) const {
if (sz != v.sz) return false;
for (std::size_t i = 0; i < sz; ++i)
if (elem[i] != v.elem[i]) return false;
return true;
}
};](https://image.slidesharecdn.com/regulartypes-160130133044/75/Regular-types-in-C-120-2048.jpg)
![Less-than operator
class vector_int {
public:
...
bool operator<(vector_int const& v) const {
std::size_t min_size = std::min(sz, v.sz);
std::size_t i = 0;
while (i < min_size && elem[i] == v.elem[i]) ++i;
if (i < min_size)
return elem[i] < v.elem[i];
else
return sz < v.sz;
}
};](https://image.slidesharecdn.com/regulartypes-160130133044/75/Regular-types-in-C-121-2048.jpg)


