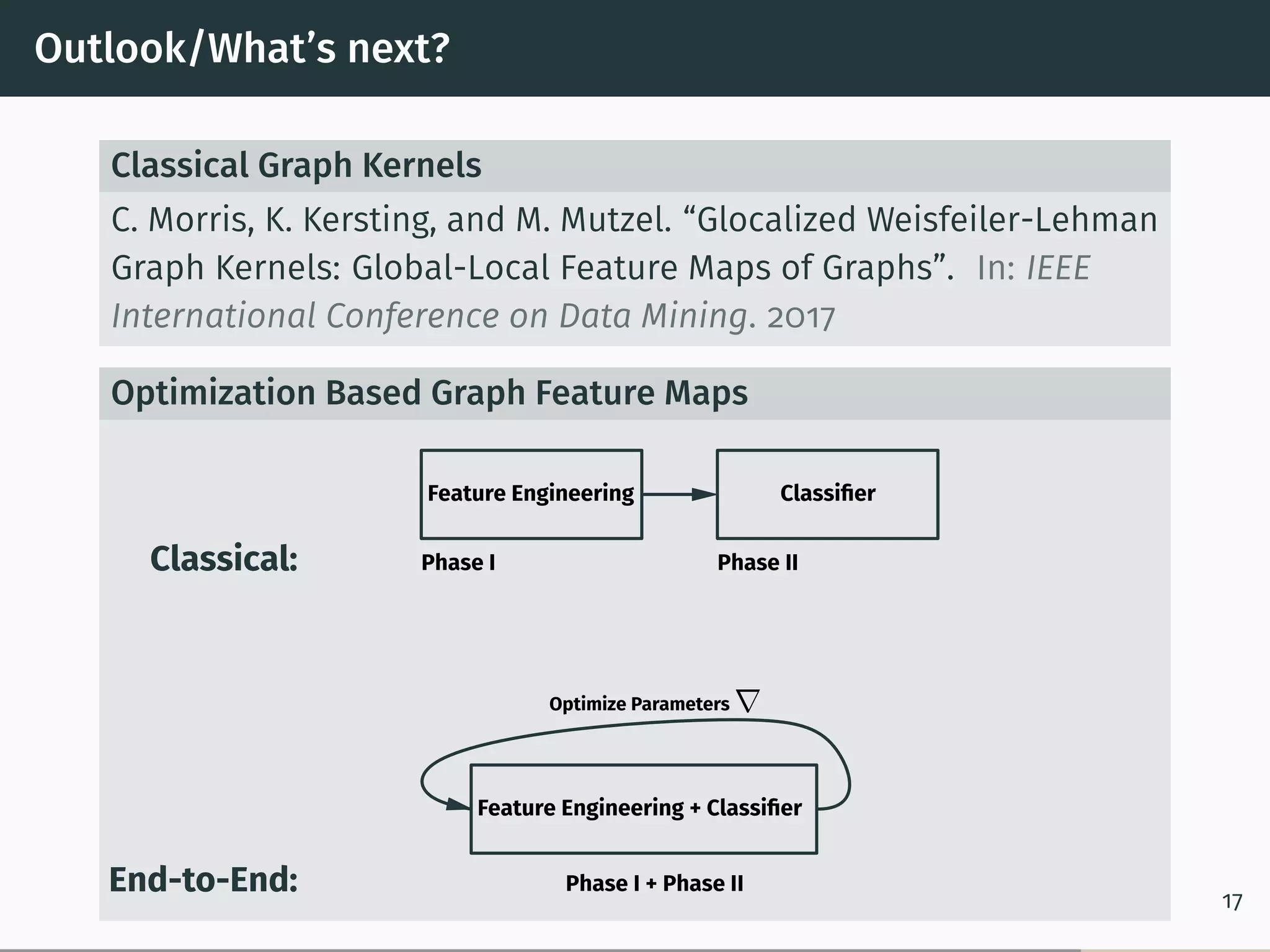
The document discusses recent advancements in kernel-based graph classification, particularly focusing on explicit versus implicit graph kernels and their computational properties. It covers various methods and frameworks, including explicit feature maps for convolution kernels, the hash graph kernel framework for continuous labels, and optimal assignment kernels. The findings suggest that explicit kernels can outperform implicit ones in certain scenarios, offering significant improvements in classification accuracy and runtime efficiency.



![Part I: Explicit vs. Implicit Graph Kernels
𝜑 Cont. Labels Run time
Random Walk [Gärtner et al., 2003] IM 𝒪(n2𝜔
)
Shortest-Path [Borgwardt et al., 2005] IM 𝒪(n4
)
Subgraph Matching [Kriege, Mutzel, 2012] IM 𝒪(kn2k+2
)
GraphHopper [Feragen et al., 2013] IM 𝒪(n2
m)
Graphlet [Shervashidze et al., 2009] EX
NSPDK [Costa et al., 2010] EX
Weisfeiler-Lehman [Shervashidze et al., 2011] EX 𝒪(hm)
Propagation [Neumann et al., 2016] EX
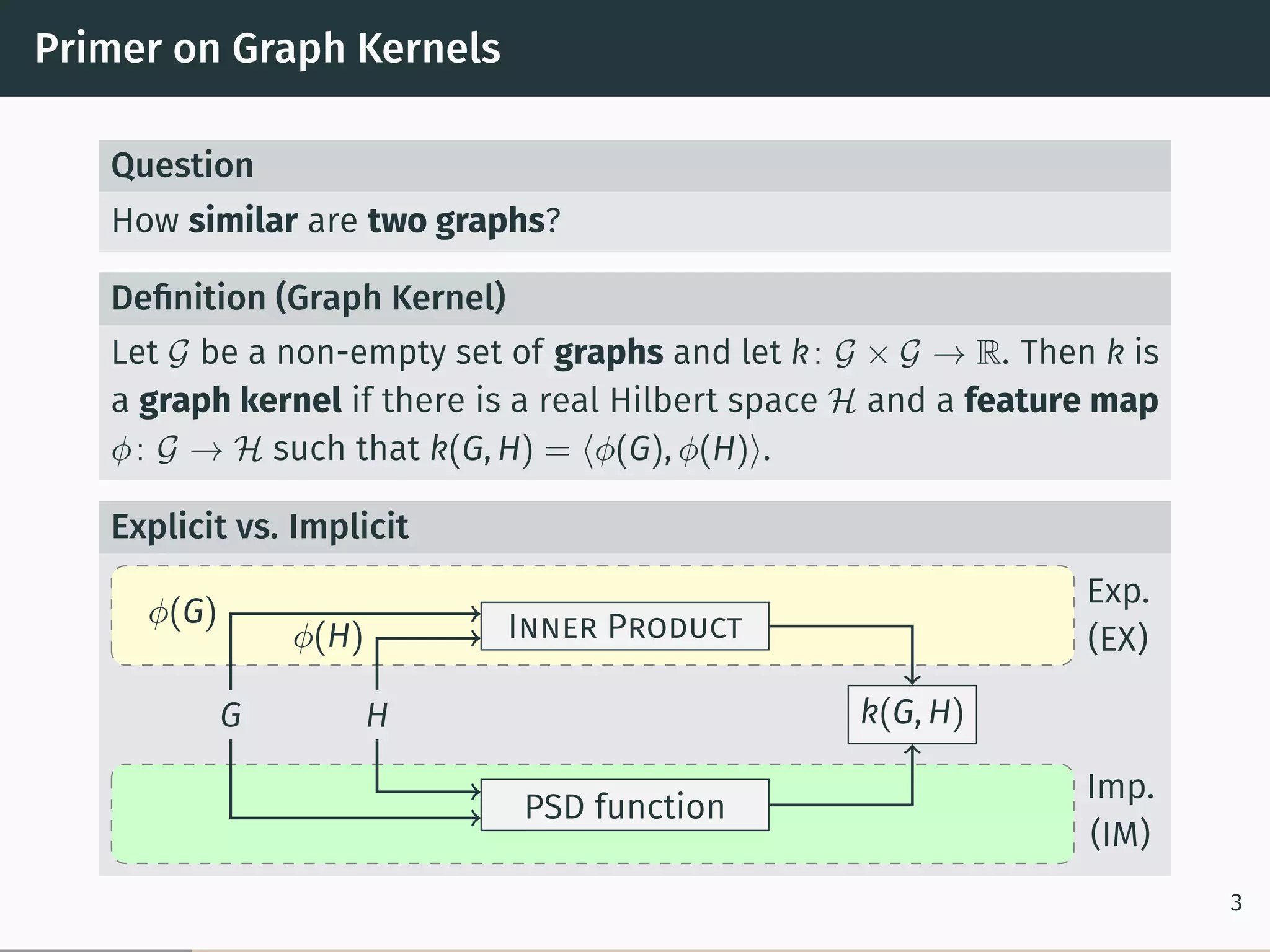
Implicit vs. Explicit
• Implicit Kernels: do not scale, extendable to continuous labels
• Explicit Kernels: do scale, only discrete labels
6](https://image.slidesharecdn.com/main-170928123404/75/Recent-Advances-in-Kernel-Based-Graph-Classification-7-2048.jpg)





![Part I: Explicit vs. Implicit Graph Kernels
implicit
explicit
100
150
200
250
300
Data set size
0
1020
30
40
50
60
Label diversity
0
2
4
6
8
10
Runtime [s]
Experimental Results
Discrete Labels: explicit feature maps outperform implicit kernels
(for most kernels and benchmark data sets)
8](https://image.slidesharecdn.com/main-170928123404/75/Recent-Advances-in-Kernel-Based-Graph-Classification-13-2048.jpg)
![Part I: Explicit vs. Implicit Graph Kernels
implicit
explicit
100
150
200
250
300
Data set size
0
1020
30
40
50
60
Label diversity
0
2
4
6
8
10
Runtime [s]
Experimental Results
Discrete Labels: explicit feature maps outperform implicit kernels
(for most kernels and benchmark data sets)
Continuous Labels: approximation by explicit feature maps not
competitive for complex kernels
8](https://image.slidesharecdn.com/main-170928123404/75/Recent-Advances-in-Kernel-Based-Graph-Classification-14-2048.jpg)
![Part II: Hash Graph Kernel Framework
Challenge
Design fast, explicit graph kernels that can handle continuous
labels.
C. Morris, N. M. Kriege, K. Kersting, and P. Mutzel. “Faster Kernel for
Graphs with Continuous Attributes via Hashing”. In: IEEE
International Conference on Data Mining. 2016, pp. 1095–1100
[ 1.2
0.3 ]
[ 9.1
0.9 ]
[ 1.6
0.7 ]
[ 5.2
1.0 ]
[ 5.1
0.2 ]
[ 1.0
0.2 ]
9](https://image.slidesharecdn.com/main-170928123404/75/Recent-Advances-in-Kernel-Based-Graph-Classification-15-2048.jpg)
![Part II: Hash Graph Kernel Framework
Challenge
Design fast, explicit graph kernels that can handle continuous
labels.
𝜑 Cont. Labels Run time
Random Walk [Gärtner et al., 2003] IM 𝒪(n2𝜔
)
Shortest-Path [Borgwardt et al., 2005] IM 𝒪(n4
)
Subgraph Matching [Kriege, Mutzel, 2012] IM 𝒪(kn2k+2
)
GraphHopper [Feragen et al., 2013] IM 𝒪(n2
m)
Graphlet [Shervashidze et al., 2009] EX
NSPDK [Costa et al., 2010] EX
Weisfeiler-Lehman [Shervashidze et al., 2011] EX 𝒪(hm)
Propagation [Neumann et al., 2016] EX
HGK Framework [Morris et al., 2016] EX Linear in BK
10](https://image.slidesharecdn.com/main-170928123404/75/Recent-Advances-in-Kernel-Based-Graph-Classification-16-2048.jpg)
![Part II: Hash Graph Kernel Framework
(G, a)
(G, l1)
(G, l2)
Hash
φ(G, l1)
φ(G, l2)
1/I[φ(G,l1),...,φ(G,lI)]
Feat. Vectors
(G, lI) φ(G, lI)
11](https://image.slidesharecdn.com/main-170928123404/75/Recent-Advances-in-Kernel-Based-Graph-Classification-17-2048.jpg)



![Part III: Positive-semidefinite Optimal Assignments
Intuition
Optimal Assignments are a “natural” measure of similarity.
Definition (Optimal Assignment Kernel)
Let ℬ(X, Y) be the bijections between X, Y in [𝒮]n
, the optimal
assignment kernel on [𝒮]n
is defined as
Kk
ℬ(X, Y) = max
B∈ℬ(X,Y)
W(B), where W(B) =
∑︁
(x,y)∈B
k(x, y)
and k is a base kernel on 𝒮.
14](https://image.slidesharecdn.com/main-170928123404/75/Recent-Advances-in-Kernel-Based-Graph-Classification-24-2048.jpg)
![Part III: Positive-semidefinite Optimal Assignments
Previous Work:
• Optimal assignment kernels for attributed molecular graphs
[Fröhlich, Wegner, Sieker, Zell, 2005], ICML
• The optimal assignment kernel is not positive definite
[Vert, 2008], CoRR, abs/0801.4061
Problem
Optimal assignments yield indefinite functions.
15](https://image.slidesharecdn.com/main-170928123404/75/Recent-Advances-in-Kernel-Based-Graph-Classification-25-2048.jpg)