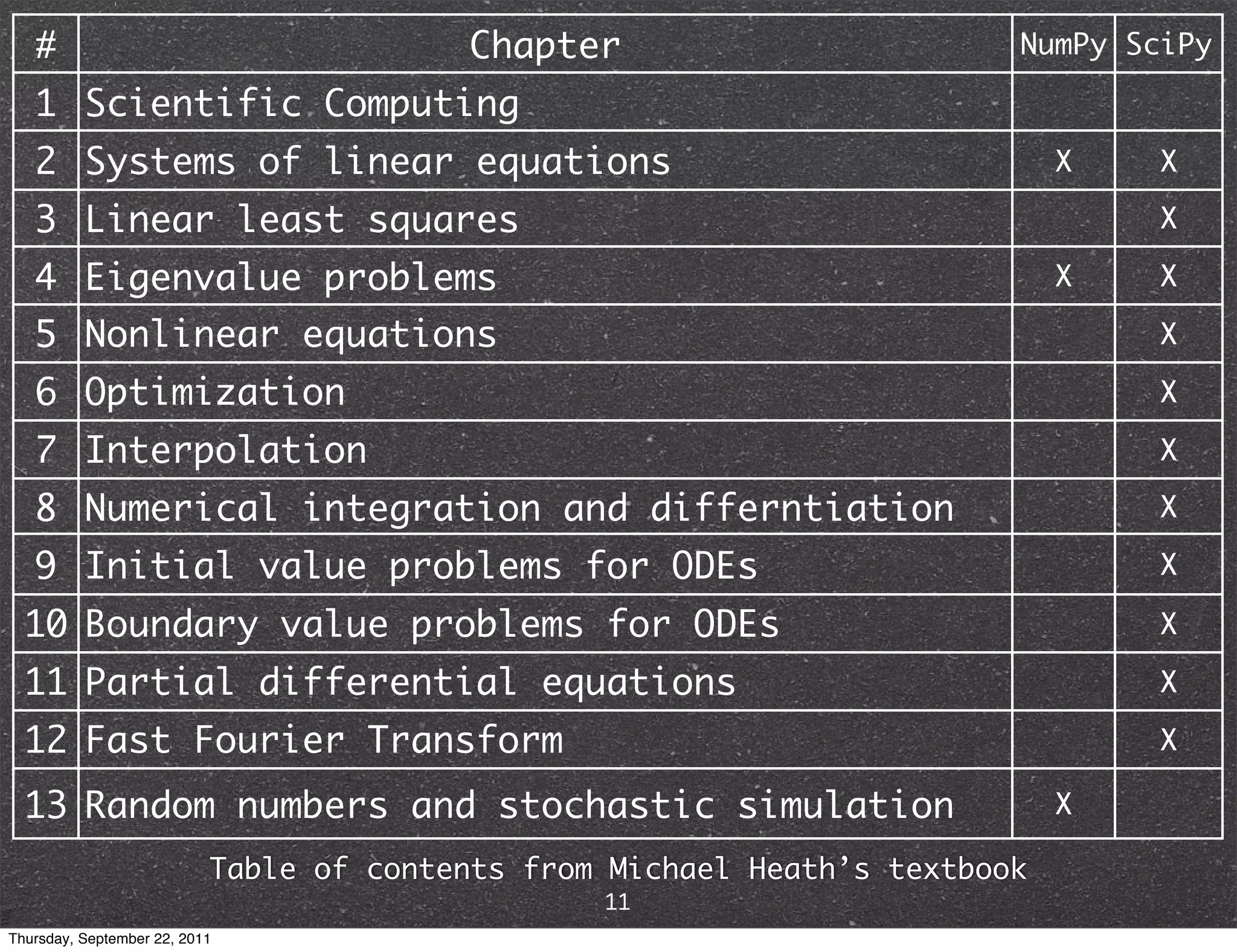
The document discusses NumPy and SciPy, two popular Python packages for scientific computing. NumPy adds support for large, multi-dimensional arrays and matrices to Python. It also introduces data types and affords operations like linear algebra on array objects. SciPy builds on NumPy and contains modules for optimization, integration, interpolation and other tasks. Together, NumPy and SciPy provide a powerful yet easy to use environment for numerical computing in Python.






![Using numpy can make code cleaner
import numpy as np
a = range(10000000) a = np.arange(10000000)
b = range(10000000) b = np.arange(10000000)
c = [] c = a + b
for i in range(len(a)):
c.append(a[i] + b[i])
What’s different??
6
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-7-2048.jpg)
![What’s different?creates list of creates ndarray of
dynamically typed int statically typed int
import numpy as np
a = range(10000000) a = np.arange(10000000)
b = range(10000000) b = np.arange(10000000)
c = [] #a+b is concatenation c = a + b #vectorized addition
for i in range(len(a)):
c.append(a[i] + b[i])
Using numpy can save lots of time
7.050s 0.333s (21x)
a convenient interface to compiled C/Fortran
libraries: BLAS, LAPACK, FFTW, UMFPACK,...
7
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-8-2048.jpg)


![The most fundamental object in NumPy is the
ndarray (N-dimensional array)
v[:] vector
M[:,:] matrix
x[:,:,...,:] higher order tensor
unlike built-in Python data types,
ndarrays are designed for
homogeneous, explicitly typed data
13
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-15-2048.jpg)

![Structured array: ndarray of data structure
>>> mol = np.zeros(3, dtype=('uint8, 3float64'))
>>> mol[0] = 8, (-0.464, 0.177, 0.0)
>>> mol[1] = 1, (-0.464, 1.137, 0.0)
>>> mol[2] = 1, (0.441, -0.143, 0.0)
>>> mol
array([(8, [-0.46400000000000002, 0.17699999999999999, 0.0]),
(1, [-0.46400000000000002, 1.137, 0.0]),
(1, [0.441, -0.14299999999999999, 0.0])],
dtype=[('f0', '|u1'), ('f1', '<f8', (3,))])
Recarray: ndarray of data structure
with named fields (record)
>>> mol = np.array(mol,
dtype={'atomicnum':('uint8',0), 'coords':('3float64',1)})
>>> mol['atomicnum']
array([8, 1, 1], dtype=uint8)
15
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-17-2048.jpg)

![Creating ndarrays
• from Python iterable: lists, tuples,...
e.g. array([1, 2, 3]) == asarray((1, 2, 3))
• from intrinsic functions
empty() allocates memory only
zeros() initializes to 0
ones() initializes to 1
arange() creates a uniform range
rand() initializes to uniform random
randn() initializes to standard normal random
...
• from binary representation in string/buffer
• from file on disk
18
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-20-2048.jpg)
![Generating ndarrays
fromfunction() creates an ndarray whose
entries are functions of its indices
e.g. the Hilbert matrix
1..n
>>> np.fromfunction(lambda i,j: 1./(i+j+1), (4,4))
array([[ 1. , 0.5 , 0.33333333, 0.25 ],
[ 0.5 , 0.33333333, 0.25 , 0.2 ],
[ 0.33333333, 0.25 , 0.2 , 0.16666667],
[ 0.25 , 0.2 , 0.16666667, 0.14285714]])
19
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-21-2048.jpg)
![Generating ndarrays
arange(): like range() but accepts floats
>>> import numpy as np
>>> np.arange(2, 2.5, 0.1)
array([ 2. , 2.1, 2.2, 2.3, 2.4])
linspace(): creates array with specified
number of elements, spaced equally between
the specified beginning and ending.
>>> np.linspace(2.0, 2.4, 5)
array([ 2. , 2.1, 2.2, 2.3, 2.4])
20
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-22-2048.jpg)



![Indexing
>>> x = np.arange(12).reshape(3,4); x
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> x[1,2]
6
>>> x[2,-1] row, then column
11
>>> x[0][2]
2
>>> x[(2,2)] #tuple
10
>>> x[:1] #slices return views, not copies
array([[0, 1, 2, 3]])
>>> x[::2,1:4:2]
array([[ 1, 3],
[ 9, 11]])
24
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-26-2048.jpg)
![Fancy indexing
>>> x = np.arange(12).reshape(3,4); x
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
>>> x[(2,2)]
array index
10
>>> x[np.array([2,2])] #same as x[[2,2]]
array([[ 8, 9, 10, 11],
[ 8, 9, 10, 11]])
>>> x[np.array([1,0]), np.array([2,1])]
array([6, 1])
>>> x[x>8] Boolean mask
array([ 9, 10, 11])
>>> x>8
array([[False, False, False, False],
[False, False, False, False],
[False, True, True, True]], dtype=bool)
25
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-27-2048.jpg)
![Fancy indexing II
>>> y = np.arange(1*2*3*4).reshape(1,2,3,4); y
array([[[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]]])
>>> y[0, Ellipsis, 0] # == y[0, ..., 0] == [0,:,:,0]
array([[ 0, 4, 8],
[12, 16, 20]])
>>> y[0, 0, 0, slice(2,4)] # == y[(0, 0, 0, 2:4)]
array([2, 3])
26
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-28-2048.jpg)
![Broadcasting
What happens when you multiply ndarrays of
different dimensions?
Case I: trailing dimensions match
>>> x #.shape = (3,4)
array([[ 0, 1, 2, 3],
>>> y * x
[ 4, 5, 6, 7],
array([[[[ 0, 1, 4, 9],
[ 8, 9, 10, 11]])
[ 16, 25, 36, 49],
>>> y #.shape = (1,2,3,4)
[ 64, 81, 100, 121]],
array([[[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[[ 0, 13, 28, 45],
[ 8, 9, 10, 11]],
[ 64, 85, 108, 133],
[160, 189, 220, 253]]]])
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]]])
27
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-29-2048.jpg)
![Broadcasting
What happens when you multiply ndarrays of
different dimensions?
Case II: trailing dimension is 1
>>> b.shape = 4,1
>>> a + b
>>> a = np.arange(4); a array([[3, 4, 5, 6],
array([0, 1, 2, 3]) [2, 3, 4, 5],
>>> b = np.arange(4)[::-1]; b [1, 2, 3, 4],
array([3, 2, 1, 0]) [0, 1, 2, 3]])
>>> a + b
array([3, 3, 3, 3])
>>> b.shape = 1,4
>>> a + b
array([[3, 3, 3, 3]])
28
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-30-2048.jpg)

![Matrix functions
You can apply a function elementwise to a
matrix...
>>> from numpy import array, exp
>>> X = array([[1, 1], [1, 0]])
>>> exp(X)
array([[ 2.71828183, 2.71828183],
[ 2.71828183, 1.]])
...or a matrix version of that function
>>> from scipy.linalg import expm
>>> expm(X)
array([[ 2.71828183, 7.3890561 ],
[ 1. , 2.71828183]])
other functions in scipy.linalg.matfuncs
30
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-32-2048.jpg)

![Least-squares curve fitting
from scipy import *
fit data to model from scipy.optimize import leastsq
from matplotlib.pyplot import plot
#Make up data x(t) with Gaussian noise
num_points = 150
t = linspace(5, 8, num_points)
x = 11.86*cos(2*pi/0.81*t-1.32) + 0.64*t
+4*((0.5-rand(num_points))*
exp(2*rand(num_points)**2))
# Target function
model = lambda p, x:
p[0]*cos(2*pi/p[1]*x+p[2]) + p[3]*x
# Distance to the target function
error = lambda p, x, y: model(p, x) - y
# Initial guess for the parameters
p0 = [-15., 0.8, 0., -1.]
p1, _ = leastsq(error, p0, args=(t, x))
t2 = linspace(t.min(), t.max(), 100)
plot(t, x, "ro", t2, model(p1, t2), "b-")
raw_input()
32
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-34-2048.jpg)



![From math to code
import numpy
#Make up some data
N = 30000
idx = 24700
size = 300
data = numpy.random.rand(N)
frag_pad = numpy.zeros(N)
frag = data[idx:idx+size]
frag_pad[:size] = frag
#Compute phase correlation
data_ft = numpy.fft.rfft(data)
frag_ft = numpy.fft.rfft(frag_pad)
phase = data_ft * numpy.conj(frag_ft)
phase /= abs(phase)
cross_correlation = numpy.fft.irfft(phase)
offset = numpy.argmax(cross_correlation)
print 'Input offset: %d, computed: %d' % (idx, offset)
from matplotlib.pyplot import plot
plot(cross_correlation)
raw_input() #Pause
35
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-38-2048.jpg)
![From math to code
import numpy
#Make up some data
N = 30000
idx = 24700
size = 300
data = numpy.random.rand(N)
frag_pad = numpy.zeros(N)
frag = data[idx:idx+size]
frag_pad[:size] = frag
#Compute phase correlation
data_ft = numpy.fft.rfft(data)
frag_ft = numpy.fft.rfft(frag_pad)
phase = data_ft * numpy.conj(frag_ft)
phase /= abs(phase)
cross_correlation = numpy.fft.irfft(phase)
offset = numpy.argmax(cross_correlation)
print 'Input offset: %d, computed: %d' % (idx, offset)
from matplotlib.pyplot import plot
plot(cross_correlation)
raw_input() #Pause
35
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-39-2048.jpg)



![From math to code
B G from numpy import linspace
from scipy.integrate import odeint
P = 0 # birth rate
d = 0.0001 # natural death rate
S Z R B = 0.0095 # transmission rate
+ A G = 0.0001 # resurrection rate
A = 0.0001 # destruction rate
r d def f(y, t):
Si, Zi, Ri = y
return [P - B*Si*Zi - d*Si,
B*Si*Zi + G*Ri - A*Si*Zi,
d*Si + A*Si*Zi - G*Ri]
y0 = [500, 0, 0] # initial conditions
t = linspace(0, 5., 1000) # time grid
soln = odeint(f, y0, t) # solve ODE
S, Z, R = soln[:, :].T
http://www.scipy.org/Cookbook/Zombie_Apocalypse_ODEINT
39
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-43-2048.jpg)



![scipy.weave.inline
python on-the-fly
scipy distutils compiled
weave core C/C++
program
inline Extension
>>> from scipy.weave import inline
>>> x = 4.0
>>> inline('return_val = 1./sqrt(x));',
['x'])
0.5
see: https://github.com/scipy/scipy/blob/
master/scipy/weave/doc/tutorial.txt
43
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-47-2048.jpg)
![scipy.weave.blitz
Uses the Blitz++ numerical library for C++
Converts between ndarrays and Blitz arrays
>>> # Computes five-point average using numpy and weave.blitz
>>> import numpy import empty
>>> from scipy.weave import blitz
>>> a = numpy.zeros((4096,4096)); c = numpy.zeros((4096, 4096))
>>> b = numpy.random.randn(4096,4096)
>>> c[1:-1,1:-1] = (b[1:-1,1:-1] + b[2:,1:-1] + b[:-2,1:-1] + b
[1:-1,2:] + b[1:-1,:-2]) / 5.0
>>> blitz("a[1:-1,1:-1] = (b[1:-1,1:-1] + b[2:,1:-1] + b
[:-2,1:-1] + b[1:-1,2:] + b[1:-1,:-2]) / 5.")
>>> (a == c).all()
True
see:
https://github.com/scipy/scipy/blob/master/scipy/weave/doc/
tutorial.txt
44
Thursday, September 22, 2011](https://image.slidesharecdn.com/numpyscipy-110922225541-phpapp01/75/Python-as-number-crunching-code-glue-48-2048.jpg)