(chapter 6) A Concise and Practical Introduction to Programming Algorithms in Java

1A Concise and Practical Introduction to Programming Algorithms in Java © 2009 Frank Nielsen
Frank NIELSEN
nielsen@lix.polytechnique.fr
A Concise and
Practical
Introduction to
Programming
Algorithms in Java
Chapter 6: Searching and sorting

Agenda
● Answering a few questions
● Searching (sequential, bisection)
● Sorting for faster searching
● Recursive sort
● Hashing

Swapping
Java is pass-by-value only.
Arrays and objects: pass-by-reference (=memory `value')
0 y
Memory for
main
class FunctionCallSample
{
public static void f(double x)
{
x=1;
System.out.println(x);//1
return;
}
public static void main(String[] args)
{
int y=0;
f(y);
System.out.println(y);//y is still 0
}}
Memory for
f
x1

Swapping & Strings
public static void Swap(String p, String q)
{ String tmp;
tmp=p;
p=q;
q=tmp;}
public static void Swap(String [] t, int i, int j)
{ String tmp;
tmp=t[i];
t[i]=t[j];
t[j]=tmp;}
String s1="toto";
String s2="titi";
String [] s=new String[2];
s[0]=new String("toto");
s[1]=new String("titi");
System.out.println(s1+" "+s2);
Swap(s1,s2);
System.out.println(s1+" "+s2);
Swap(s,0,1);
System.out.println(s[0]+" "+s[1]);
Result

Swapping using wrapped integers
// Wrapping integers into an object
class IntObj {
private int x;
public IntObj(int x)
{ this.x = x; }
public int getValue()
{ return this.x; }
public void insertValue(int newx)
{ this.x = newx;}
}
Let us wrap integers into a tailored object named IntObj

public class SwapInt {
// Pass-by-value (= pass-by-reference for objects)
static void swap(IntObj p, IntObj q)
{
// interchange values inside objects
int t = p.getValue();
p.insertValue(q.getValue());
q.insertValue(t);
}
public static void main(String[] args) {
int a = 23, b = 12;
System.out.println("Before| a:" + a + ", b: " + b);
IntObj aObj = new IntObj(a);
IntObj bObj = new IntObj(b);
swap(aObj, bObj);
a = aObj.getValue();
b = bObj.getValue();
System.out.println("After| a:" + a + ", b: " + b);
}
} Java wrapper class for int is Integer BUT
it doesn't allow you to alter the data field inside.

class SwapInteger
{
public static void main(String args[])
{
Integer a, b;
a = new Integer(10);
b = new Integer(50);
System.out.println("before swap...");
System.out.println("a is " + a);
System.out.println("b is " + b);
swap(a, b); // References did not change (PASS-BY-VALUE)
System.out.println("after swap...");
System.out.println("a is " + a);
System.out.println("b is " + b);
}
public static void swap(Integer a, Integer b)
{
Integer temp = a;
a = b;
b = temp;
}
}

Searching: Problem statement
● Objects are accessed via a corresponding key
● Each object stores its key and additional fields
● One seeks for information stored in an object from its key
(key= a handle)
● All objects are in the main memory (no external I/O)
More challenging problem:
Adding/removing or changing object attributes dynamically

Searching: Basic examplesSearching: Basic examplesSearching: Basic examples
Dictionary
Key: word
Object:
(word, definition)
class DictionaryEntry
{
String word;
String definition;
}

Dictionary
class DictionaryEntry
{
String word;
String definition;
DictionaryEntry(String w, String def)
{
this.word=new String(w); // Clone the strings
this.definition=new String(def);
}
}
class TestMyDictionary
{public static void main(String[] args){
DictionaryEntry [] Dico =new DictionaryEntry[10];
Dico[0]=new DictionaryEntry("INF311","Cours d'informatique");
Dico[1]=new DictionaryEntry("ECO311","Cours d'economie");
}
}

Searching: Basic examples
● Objects denote people: Each object represents an individual
● The key (handle) is the lastname, firstname, ...
● Additional information fields are:
address, phone number, etc.
class Individual {
String Firstname;
String Lastname;
String Address;
String Phonenumber;
int Age;
boolean Sex;
}
Object
Firstname
Lastname
Phonenumber
int Age

Searching: Basic examples
● Objects denote 2D point sets: Each object is a 2D point
● The key (handle) is the name, or x- or y- ordinate, etc.
● Additional information fields are:
color, name, etc.
class Color {int Red, Green, Blue;}
class Point2D
{
double x;
double y;
String name;
Color color;
}
x
y
name
color

Sequential (linear) search
● Objects are stored in an array (of objects):
Any order is fine (= not necessarily sorted)
● To seek for an object, we browse sequentially the array until
we find the object, or that we report that it is not inside
● Compare the keys of the query with object keys

class Person{
String firstname, lastname; // key for searching
String phone; // additional fields go here
// Constructor
Person(String l, String f, String p)
{firstname=f; lastname=l; phone=p;}
};
static Person[] array=new Person[5];
static String LinearSearch(String lastname, String firstname)
{
for(int i=0;i<array.length;i++)
{
if ((lastname.equals(array[i].lastname) &&
(firstname.equals(array[i].firstname))))
{return array[i].phone;}
}
return "Not found in my dictionary";
}

class LinearSearch{
static Person[] array=new Person[5];
{...}
public static void main (String [] args)
{
array[0]=new Person("Nielsen","Frank","0169364089");
array[1]=new Person("Nelson","Franck","04227745221");
array[2]=new Person("Durand","Paul","0381846245");
array[3]=new Person("Dupond","Jean","0256234512");
array[4]=new Person("Tanaka","Ken","+81 3 1234 4567");
System.out.println(LinearSearch("Durand","Paul"));
System.out.println(LinearSearch("Tanaka","Ken"));
System.out.println(LinearSearch("Durand","Jean"));
}
}
Array is class variable, here

● In the worst case, we need to scan the full array
● On average, we scan half the array size (if object is inside)
Donald Knuth. The Art of Computer Programming, Volume 3:
Sorting and Searching, Third Edition. Addison-Wesley, 1997.
ISBN 0-201-89685-0. Section 6.1: Sequential Searching, pp.396–408.
Complexity of sequential search

Adding an element (object)
● To add dynamically an element, we first build a bigger array
● Then we use an index for storing the position of the
last stored element
● When added an element, we increment the position of the
'end of array'
● Of course, we should check whether the array there is
overflow or not
● Notice that it is difficult to erase elements...

Adding an element to the corpus
public static final int MAX_ELEMENTS=100;
static int nbelements=0;
static Person[] array=new Person[MAX_ELEMENTS];
{
for(int i=0;i<nbelements;i++)
{
if ((lastname.equals(array[i].lastname) &&
(firstname.equals(array[i].firstname))))
return array[i].phone;
}
return "Not found in my dictionary";
}
static void AddElement(Person obj)
{if (nbelements<MAX_ELEMENTS)
array[nbelements++]=obj; // At most MAX_ELEMENTS-1 here
// nbelements is at most equal to MAX_ELEMENTS now
}

Adding elements to the corpus
public static void main (String [] args)
{
AddElement(new Person("Nielsen","Frank","0169334089"));
AddElement(new Person("Nelson","Franck","04227745221"));
AddElement(new Person("Durand","Paul","0381846245"));
AddElement(new Person("Dupond","Jean","0256234512"));
AddElement(new Person("Tanaka","Ken","+81 3 1234 4567"));
System.out.println(LinearSearch("Durand","Paul"));
System.out.println(LinearSearch("Tanaka","Ken"));
AddElement(new Person("Durand", "Jean","0199989796"));
}
Check if a person already belongs to the array before adding it
Under or oversaturated memory
(not convenient for non-predictable array sizes)

Dichotomic search (in sorted arrays)
● Assume all elements (keys) are totally sorted in the array
● For example, in increasing order
array[0] < array[1] < ... <
(any lexicographic order would do)
● To find information, use a dichotomic search on the key
● Compare the key of the middle element with the query key:
● If identical, we are done since we found it
● If the key is greater, we search in the rightmost array part
● If the key is less, we search in the leftmost array part
● If the range [left,right] is <=1 and element not inside then...
.....conclude it is not inside the array

Dichotomic search/Bisection search
Think recursion!
static int Dichotomy(int [] array, int left, int right, int key)
{
if (left>right) return -1;
int m=(left+right)/2; // !!! Euclidean division !!!
if (array[m]==key) return m;
else
{
if (array[m]<key) return Dichotomy(array,m+1, right, key);
else return Dichotomy(array,left,m-1, key);
}
}
static int DichotomicSearch(int [] array, int key)
{
return Dichotomy(array,0,array.length-1, key);
}
Result is the index of the element position
Does it always terminate? Why?

Dichotomic search/Bisection search
public static void main (String[] args)
{
int [] v={1, 6, 9, 12 , 45, 67, 76, 80, 95};
System.out.println("Seeking for element 6: Position "+DichotomicSearch(v,6));
}
1, 6, 9, 12 , 45, 67, 76, 80, 95
9 elements [0,8] m=4 6<45
1, 6, 9, 12
4 elements [0,3] m=1 6=6 Found it return 1

We halve by 2 the array range at every recursion call
n => n/2 => (n/2)/2 => ((n/2)/2)/2 => ...etc... => 1 or 0
How many recursion calls?
2**k=n => k=log(n)
(Execution stack (memory) is also of order log n)
Big O(.)-notation of ALGORITHMSALGORITHMS & complexity
Requires a logarithmic number of operations: O(log n)
t(1024)=10,
t(2048)=11,
t(65556)=16
=> (exponentially more) Efficient compare to sequential search
!!! SORTING HELPS A LOT !!!
Complexity of bisection search

static int Dichotomy(int [] array, int left, int right, int key)
{
if (left>right)
{throw new RuntimeException("Terminal state reached");
//return -1;
}
int m=(left+right)/2;
if (array[m]==key)
{throw new RuntimeException("Terminal state reached");
//return m;
}
else
{
if (array[m]<key) return Dichotomy(array,m+1, right, key);
else return Dichotomy(array,left,m-1, key);
}
}

Sorting: A fundamental procedure
● Given an (unsorted) array of elements
● We are asked to get a sorted array in, say increasing order
● The only primitive operations (basic operations) are
● comparisons and
● element swappings
static boolean GreaterThan(int a, int b)
{return (a>b);}
static void swap (int [] array, int i, int j)
{
int tmp=array[i];
array[i]=array[j];
array[j]=tmp;
}

Sorting: Sorting by selectionselection
Many different sorting techniques (endless world)
● First, seek for the smallest element of the array
(=SELECTION)
● Put it at the front (using a swapping operation)
● Iterate for the remaining part:
array[1], ..., array[n-1]
=> we seek for the smallest elements for all (sub)arrays
array[j], array[j+1], ..., array[n-1]

for i ← 0 to n-2 do
min ← i
for j ← (i + 1) to n-1 do
if A[j] < A[min]
min ← j
swap A[i] and A[min]
Sorting by selectionselection
Pseudo-code: 2 NESTED LOOPS

min ← i
if A[j] < A[min]
min ← j
The inner loop (i=0)
min ← i
if A[j] < A[min]
min ← j
22 is my first min

min ← i
if A[j] < A[min]
min ← j
35 is my first min

min ← i
if A[j] < A[min]
min ← j
The outer loop:
min of respective subarrays

Sorting by selection
Two nested loops:
● Select and put the smallest element in front of the array (inner loop)
● Repeat for all subarrays (at the right)
{return (a>b);}
{int tmp=array[i];array[i]=array[j];array[j]=tmp;}
static void SelectionSort(int [] array)
{
int n=array.length;
for(int i=0;i<n-1;i++){
for(int j=i+1;j<n;j++){
if (GreaterThan(array[i],array[j]))
swap(array,i,j);}
}
}

{
int [] array={22,35,19,26,20,13,42,37,11,24};
SelectionSort(array);
System.out.print(array[i]+" ");
System.out.println("");
}
Sorting by selection

From sorting integers to objects
● Array array contains objects of the same type
● Define a predicate that returns whether an object
is greater than another one or not
● Adjust the swap procedure
In Java 1.5, there are generics, beyond the scope of this course
Generic algorithms for sorting any kind (=type) of elementsGeneric algorithms for sorting any kind (=type) of elements

For example, sorting events
class EventObject
{
int year, month, day;
EventObject(int y, int m, int d)
{year=y; month=m; day=d;}
static void Display(EventObject obj)
{System.out.println(obj.year+"/"+obj.month+"/"+obj.day);}
}
static boolean GreaterThan(EventObject a, EventObject b)
{return (( a.year>b.year) ||
( (a.year==b.year) && (a.month>b.month)) ||
((a.year==b.year) && (a.month==b.month) && (a.day>b.day)) ) ;}
static void swap (EventObject [] array, int i, int j)
{
EventObject tmp=array[i];
array[i]=array[j];
array[j]=tmp;
}

sorting events
static void SelectionSort(EventObject [] array)
{
int n=array.length;
for(int i=0;i<n-1;i++)
for(int j=i+1;j<n;j++)
if (GreaterThan(array[i],array[j]))
swap(array,i,j);
}
{
EventObject [] array=new EventObject[5];
array[0]=new EventObject(2008,06,01);
EventObject.Display(array[i]);
System.out.println("");
}
2005/4/1
2005/4/3
2005/4/15
2005/5/27
2008/6/1

Worst-case complexity of selection sort
Quadratic time: O(n^2)
= number of elementary operations
= number of comparisons+swap operations
...Try sorting a reversed sorted array...
16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1
1, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2
1, 2, 16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3
...
nb=2*array.length*(array.length-1)/2
( 2 times n choose 2)

class SelectionSort
{
static int nboperations;
{nboperations++; return (a>b);}
{
nboperations++;
int tmp=array[i];array[i]=array[j];array[j]=tmp;}
{
int [] array={16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1};
nboperations=0;
System.out.println("Number of operations:"+nboperations);
int nb=2*array.length*(array.length-1)/2;
System.out.println("Number of operations:"+nb);
}

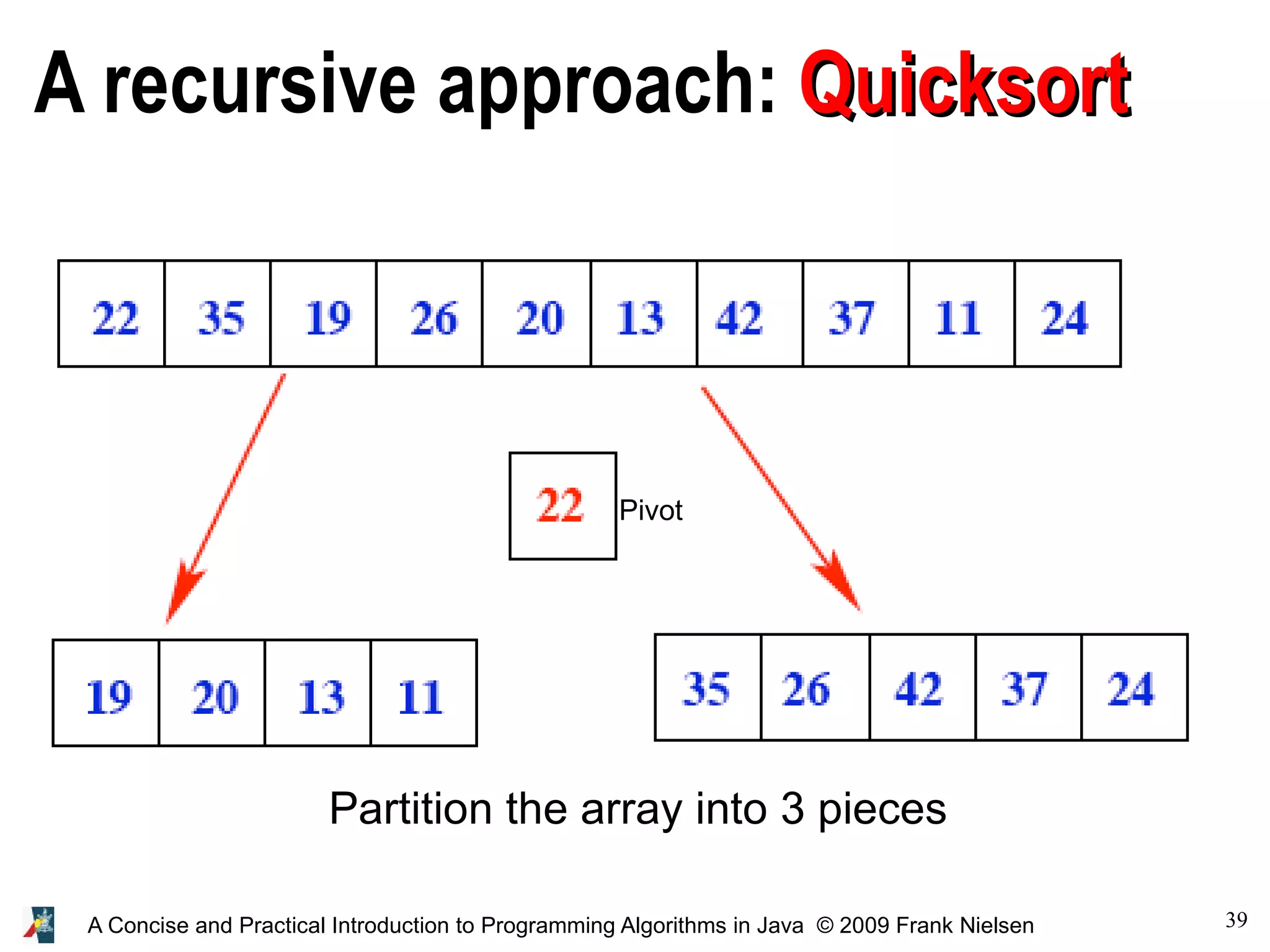
● Classify the elements according to array[0] (the pivot):
- those smaller than the pivot: arrayleft
- those greater than the pivot: arrayright
- those equal to the pivot (in case of ties): arraypivot
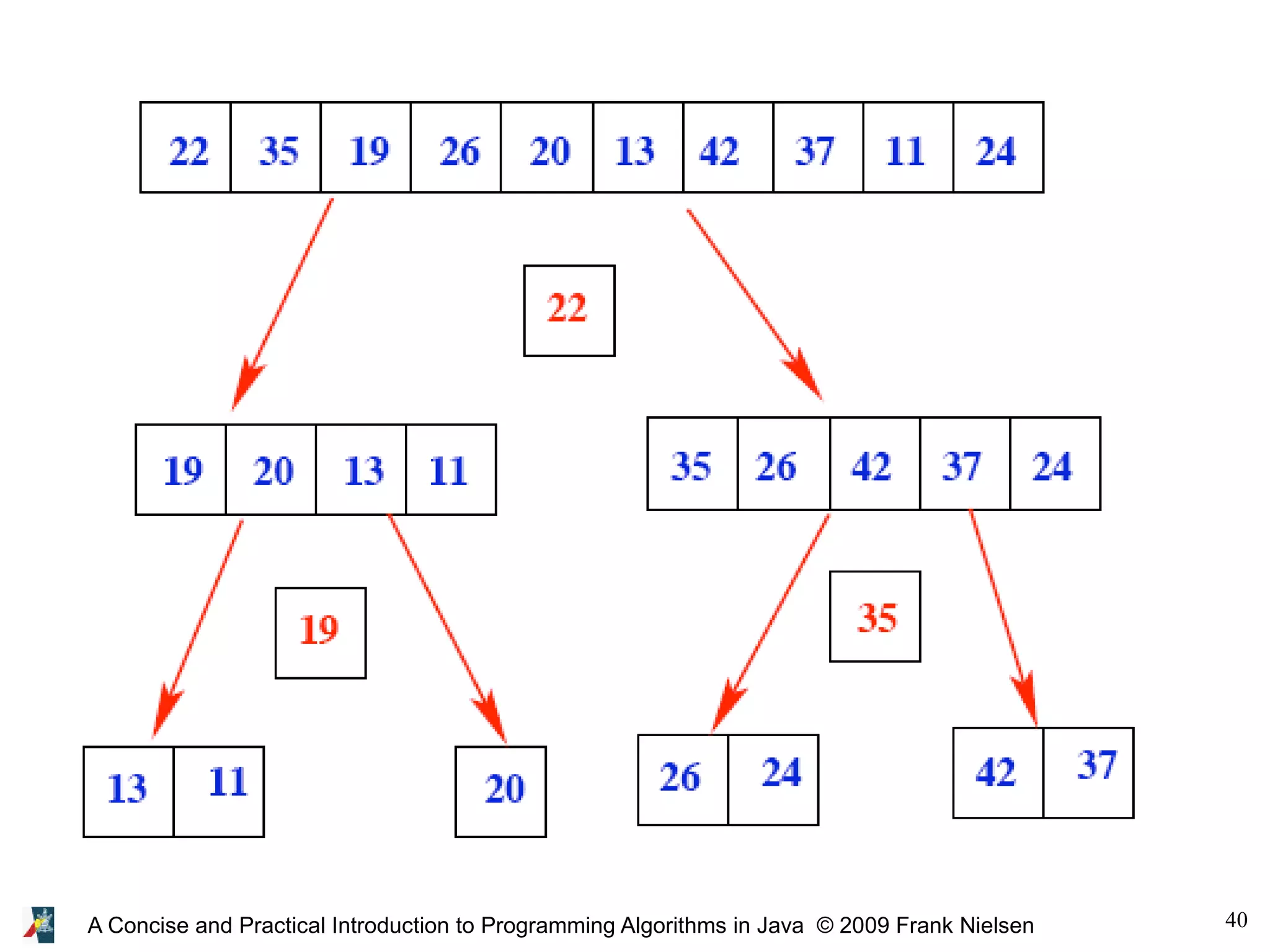
● Solve recursively the sorting in arrayleft / arrayright,
and recompose as
arrayleft arraypivot arrayright
● Note that a single element is sorted (=terminal case)

Pivot
A recursive approach: QuicksortQuicksort
Partition the array into 3 pieces

static int partition(int [] array, int left, int right)
{
int m=left;// pivot
for(int i=left+1; i<=right;i++)
{
if (GreaterThan(array[left],array[i]))
{
swap(array,i,m+1);
m++;// we extend left side array
}
}
// place pivot now
swap(array,left,m);
return m;
}
Sorting is in-place
(require no extre memory storage)
Pivot

static void quicksort(int [] array, int left, int right)
{
if (right>left)
{
int pivot=partition(array,left,right);
quicksort(array,left,pivot-1);
quicksort(array,pivot+1,right);
}
}
static void QuickSort(int [] array)
{
quicksort(array,0, array.length-1);
}

Quicksort: Analyzing the running time
● Worst-case running time is quadratic O(n^2)
● Expected running time is O(n log n)
● Best case is linear O(n) (all elements are identical)
● Lower bound is n log n: Any algorithm sorting
n numbers require n log n comparison operations
Las Vegas complexity analysis, tail bounds (how much deviation), etc...
http://www.cs.ubc.ca/~harrison/Java/sorting-demo.html

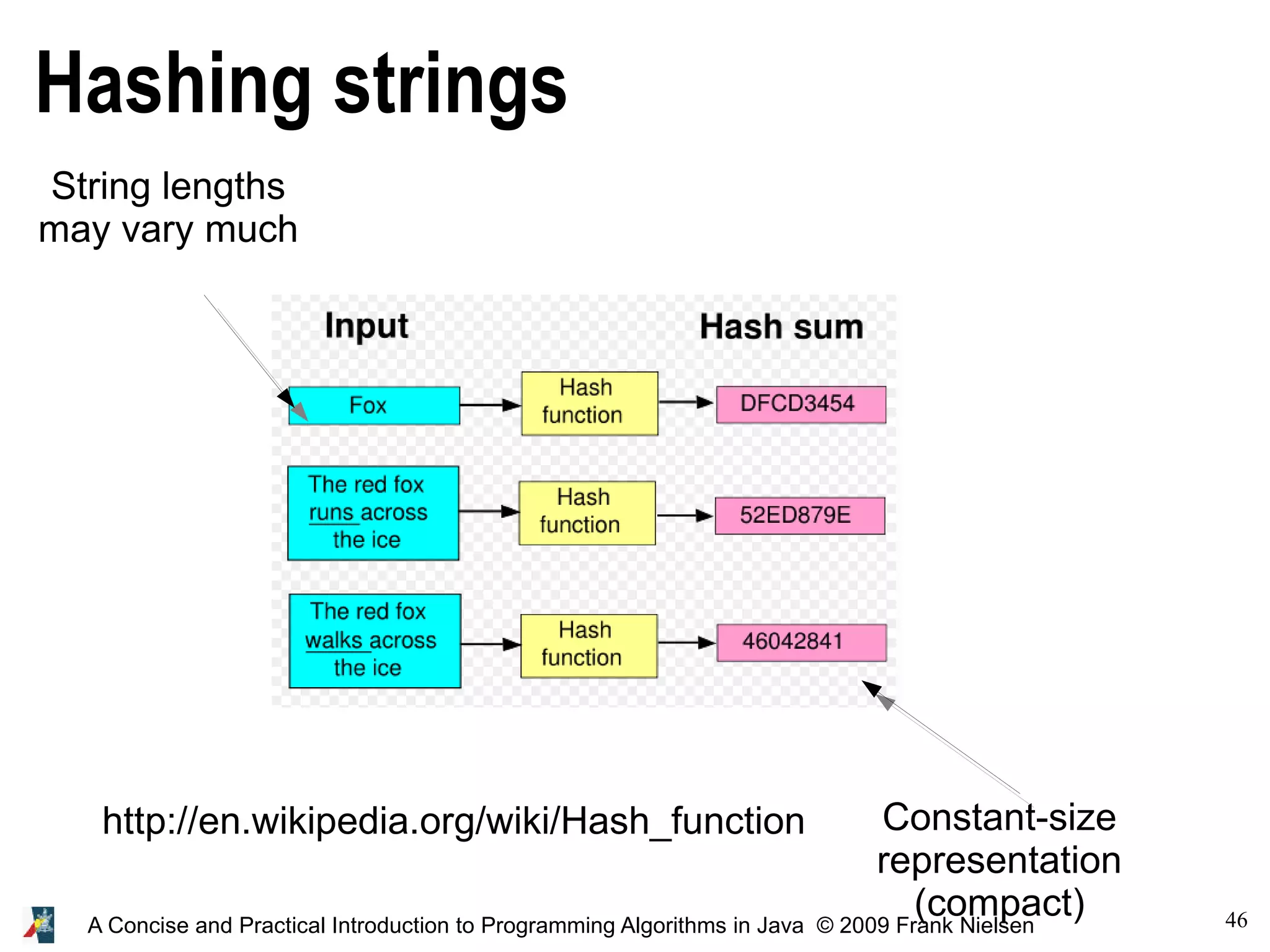
Hashing: Principle and techniques
● Hashing: fundamental technique in computer science
(see INF 421.a')
● Store object x in position h(x) (int) in an array
● Problem occurs if two objects x and y
are stored on the same cell: Collision.
● Finding good hashing functions that minimize collisions, and
adopting a good search policy in case of collisions are
key problems of hashing.
int i;
array[i]
Object Obj=new Object();
int i;
i=h(Obj);// hashing function
array[i]

Hashing functions
● Given a universe X of keys and for any x in X,
we need to find an integer h(x) between 0 and m
● Usually easy to transform the object into an integer:
For example, for strings just add the ASCII codes of characters
● The problem is then to transform
a set of n (sparse) integers
into a compact array of size m<<N.
(<< means much less than)

http://en.wikipedia.org/wiki/Hash_function
Hashing strings
Constant-size
representation
(compact)
String lengths
may vary much

Hashing functions
Key idea is to take the modulo operation
h(k) = k mod m where m is a prime number.
static int m=23;
static int String2Integer(String s)
{
int result=0;
for(int j=0;j<s.length();j++)
result+=(int)s.charAt(j);
return result;
}
// Note that m is a static variable
static int HashFunction(int l)
{return l%m;}

public static void main (String[] args)
{
String [] animals={"cat","dog","parrot","horse","fish",
"shark","pelican","tortoise", "whale", "lion",
"flamingo", "cow", "snake", "spider", "bee", "peacock",
"elephant", "butterfly"};
int i;
String [] HashTable=new String[m];
for(i=0;i<m;i++)
HashTable[i]=new String("-->");
for(i=0;i<animals.length;i++)
{int pos=HashFunction(String2Integer(animals[i]));
HashTable[pos]+=(" "+animals[i]);
}
for(i=0;i<m;i++)
System.out.println("Position "+i+"t"+HashTable[i]);
}

Position 0 --> whale
Position 1 --> snake
Position 2 -->
Position 3 -->
Position 4 -->
Position 5 -->
Position 6 -->
Position 7 --> cow
Position 8 --> shark
Position 9 -->
Position 10 -->
Position 11 -->
Position 12 --> fish
Position 13 --> cat
Position 14 -->
Position 15 --> dog tortoise
Position 16 --> horse
Position 17 --> flamingo
Position 18 -->
Position 19 --> pelican
Position 20 --> parrot lion
Position 21 -->
Position 22 -->

(chapter 6) A Concise and Practical Introduction to Programming Algorithms in Java

More Related Content

What's hot

Viewers also liked

Similar to (chapter 6) A Concise and Practical Introduction to Programming Algorithms in Java

Recently uploaded

(chapter 6) A Concise and Practical Introduction to Programming Algorithms in Java