Numpy Talk at SIAM

SciPy and NumPy

Travis Oliphant
SIAM 2011

Mar 2, 2011

Magnetic Resonance Elastography 1997
Richard Ehman

Armando Manduca
Raja Muthupillai

2
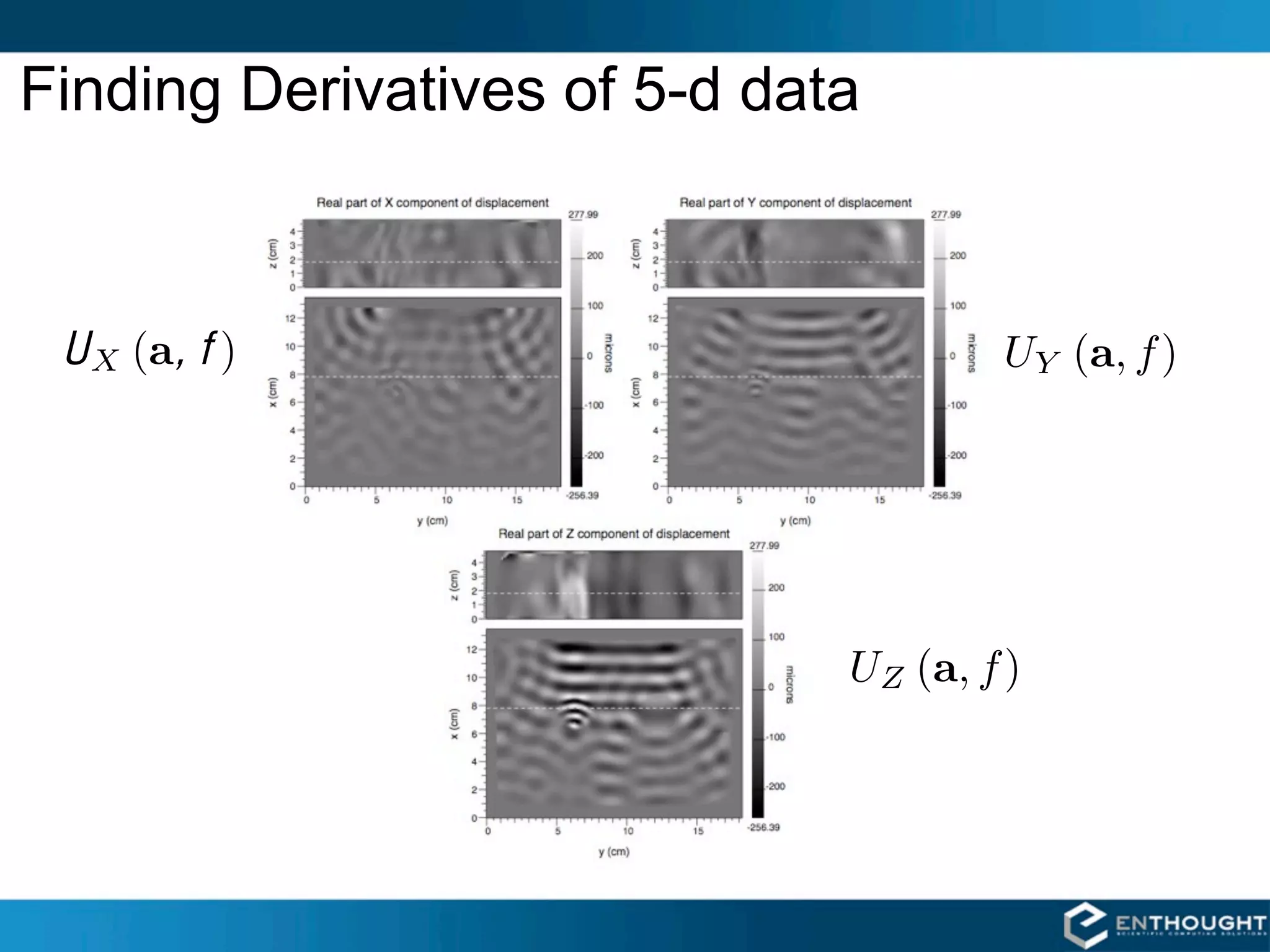
ρ0 (2πf ) Ui (a, f ) = [Cijkl (a, f ) Uk,l (a, f )],j

Finding Derivatives of 5-d data

U X (a, f ) UY (a, f )

UZ (a, f )

Finding Derivatives of 5-d data
Ξ= ×U

ΞX (a, f ) ΞY (a, f )

ΞZ (a, f )

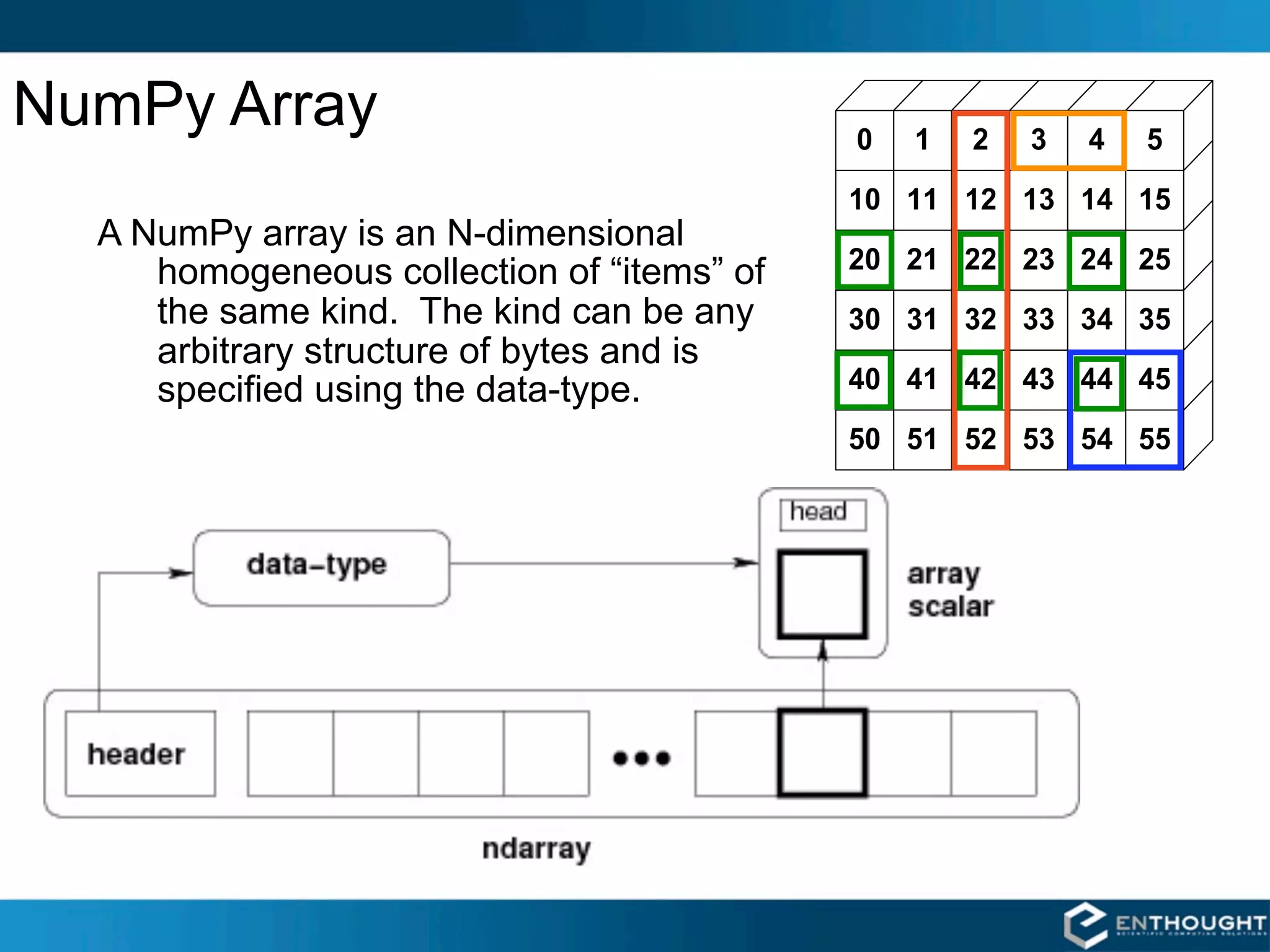
NumPy Array
A NumPy array is an N-dimensional
homogeneous collection of “items” of
the same kind. The kind can be any
arbitrary structure of bytes and is
specified using the data-type.

SciPy [ Scientific Algorithms ]
linalg stats interpolate

cluster special maxentropy

io fftpack odr

ndimage sparse integrate

signal optimize weave

NumPy [ Data Structure Core ]
fft random linalg

NDArray UFunc
multi-dimensional fast array
array object math operations

Python

SciPy is a
community
Project

A great way to
get involved with
Python

Community effort
• Chuck Harris many, many others --- forgive me!
• Pauli Virtanen
• Mark Wiebe
• David Cournapeau
• Stefan van der Walt
• Jarrod Millman
• Josef Perktold
• Anne Archibald
• Dag Sverre Seljebotn
• Robert Kern
• Matthew Brett
• Warren Weckesser
• Ralf Gommers
• Joe Harrington --- Documentation effort
• Andrew Straw --- www.scipy.org

Optimization: Data Fitting
NONLINEAR LEAST SQUARES CURVE FITTING
>>> from scipy.optimize import curve_fit
>>> from scipy.stats import norm
# Define the function to fit.
>>> def function(x, a , b, f, phi):
... result = a * exp(-b * sin(f * x + phi))
... return result

# Create a noisy data set.
>>> actual_params = [3, 2, 1, pi/4]
>>> x = linspace(0,2*pi,25)
>>> exact = function(x, *actual_params)
>>> noisy = exact + 0.3*norm.rvs(size=len(x))

# Use curve_fit to estimate the function parameters from the noisy data.
>>> initial_guess = [1,1,1,1]
>>> estimated_params, err_est = curve_fit(function, x, noisy, p0=initial_guess)
>>> estimated_params
array([3.1705, 1.9501, 1.0206, 0.7034])

# err_est is an estimate of the covariance matrix of the estimates
# (i.e. how good of a fit is it)

2D RBF Interpolation
EXAMPLE
>>> from scipy.interpolate import
... Rbf
>>> from numpy import hypot, mgrid
>>> from scipy.special import j0
>>> x, y = mgrid[-5:6,-5:6]
>>> z = j0(hypot(x,y))
>>> newfunc = Rbf(x, y, z)
>>> xx, yy = mgrid[-5:5:100j,
-5:5:100j]
# xx and yy are both 2-d
# result is evaluated
# element-by-element
>>> zz = newfunc(xx, yy)
>>> from enthought.mayavi import mlab
>>> mlab.surf(x, y, z*5)
>>> mlab.figure()
>>> mlab.surf(xx, yy, zz*5)
>>> mlab.points3d(x,y,z*5,
scale_factor=0.5)

Brownian Motion
Brownian motion (Wiener process):
2
X (t + dt) = X (t) + N 0, σ dt, t, t + dt
where N (a, b, t1 , t2 ) is normal with mean a
and variance b, and independent on
disjoint time intervals.

>>> from scipy.stats import norm
>>> x0 = 100.0
>>> dt = 0.5
>>> sigma = 1.5
>>> n = 100
>>> steps = norm.rvs(size=n,
scale=sigma*sqrt(dt))
>>> steps[0] = x0 # Make i.c. work
>>> x = steps.cumsum()
>>> t = linspace(0, (n-1)*dt, n)
>>> plot(t, x)

Image Processing
# Edge detection using Sobel filter
>>> from scipy.ndimage.filters import sobel
>>> imshow(lena)
>>> edges = sobel(lena)
>>> imshow(edges)

LENA IMAGE FILTERED IMAGE

NumPy : so what? (speed and expressiveness)

• Data: the array object
– slicing
– shapes and strides
– data-type generality

• Fast Math:
– vectorization
– broadcasting
– aggregations

Array Slicing
SLICING WORKS MUCH LIKE
STANDARD PYTHON SLICING

>>> a[0,3:5]
array([3, 4])

>>> a[4:,4:]
array([[44, 45],
[54, 55]])

>>> a[:,2]
array([2,12,22,32,42,52])

STRIDES ARE ALSO POSSIBLE
>>> a[2::2,::2]
array([[20, 22, 24],
[40, 42, 44]])

14

Fancy Indexing in 2-D

>>> a[(0,1,2,3,4),(1,2,3,4,5)]
array([ 1, 12, 23, 34, 45])

>>> a[3:,[0, 2, 5]]
array([[30, 32, 35],
[40, 42, 45],
[50, 52, 55]])

>>> mask = array([1,0,1,0,0,1],
dtype=bool)
>>> a[mask,2]
array([2,22,52])

Unlike slicing, fancy indexing
creates copies instead of a
view into original array.

Fancy Indexing with Indices
INDEXING BY POSITION
# create an Nx3 colormap
# grayscale map -- R G B
>>> cmap = array([[1.0,1.0,1.0],
[0.9,0.9,0.9],
...
[0.0,0.0,0.0]])
>>> cmap.shape
(10,3)

>>> img = array([[0,10],
[5,1 ]])
>>> img.shape
(2,2)

# use the image as an index into
# the colormap
>>> rgb_img = cmap[img]
>>> rgb_img.shape
(2,2,3)

16

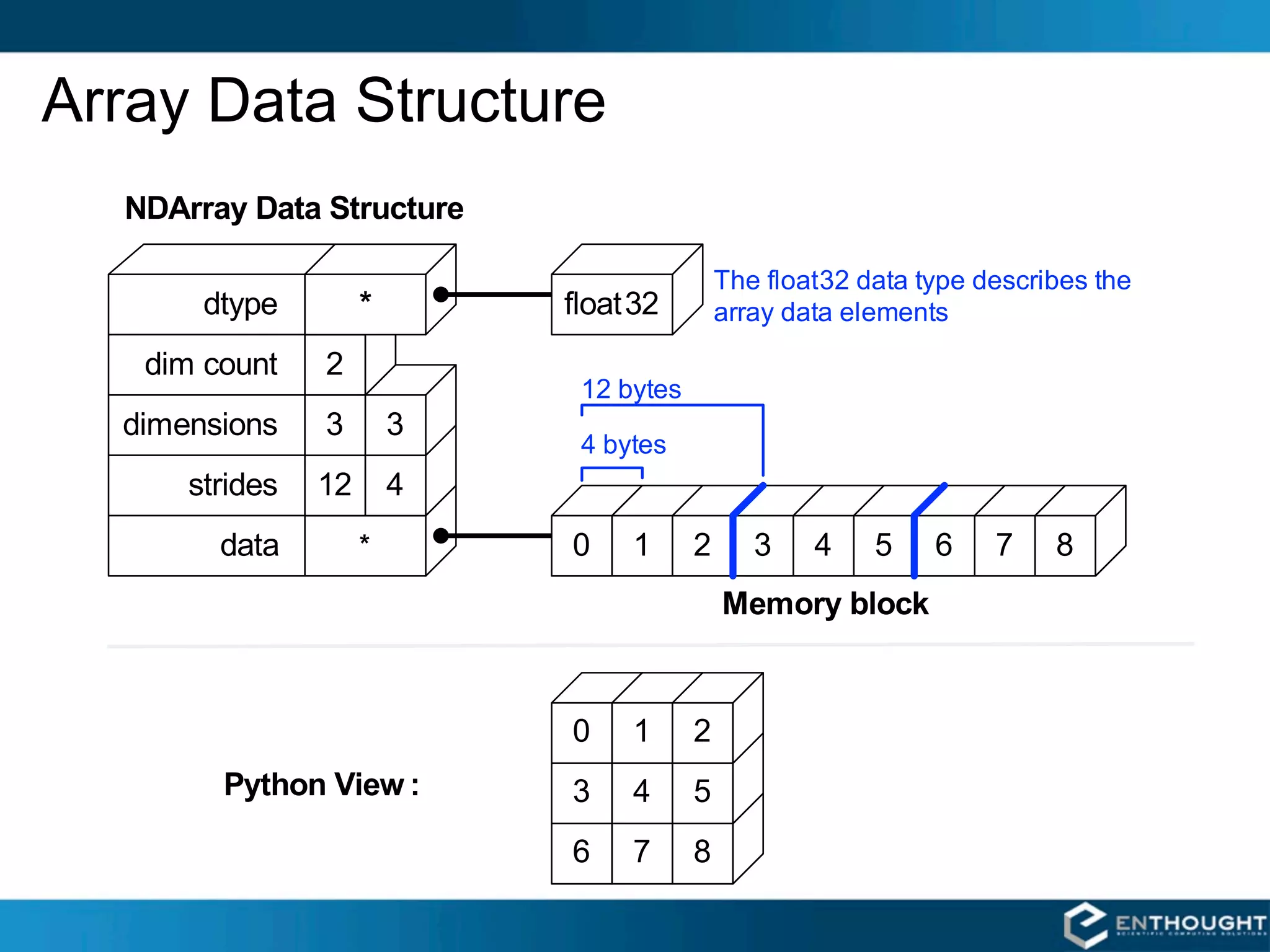
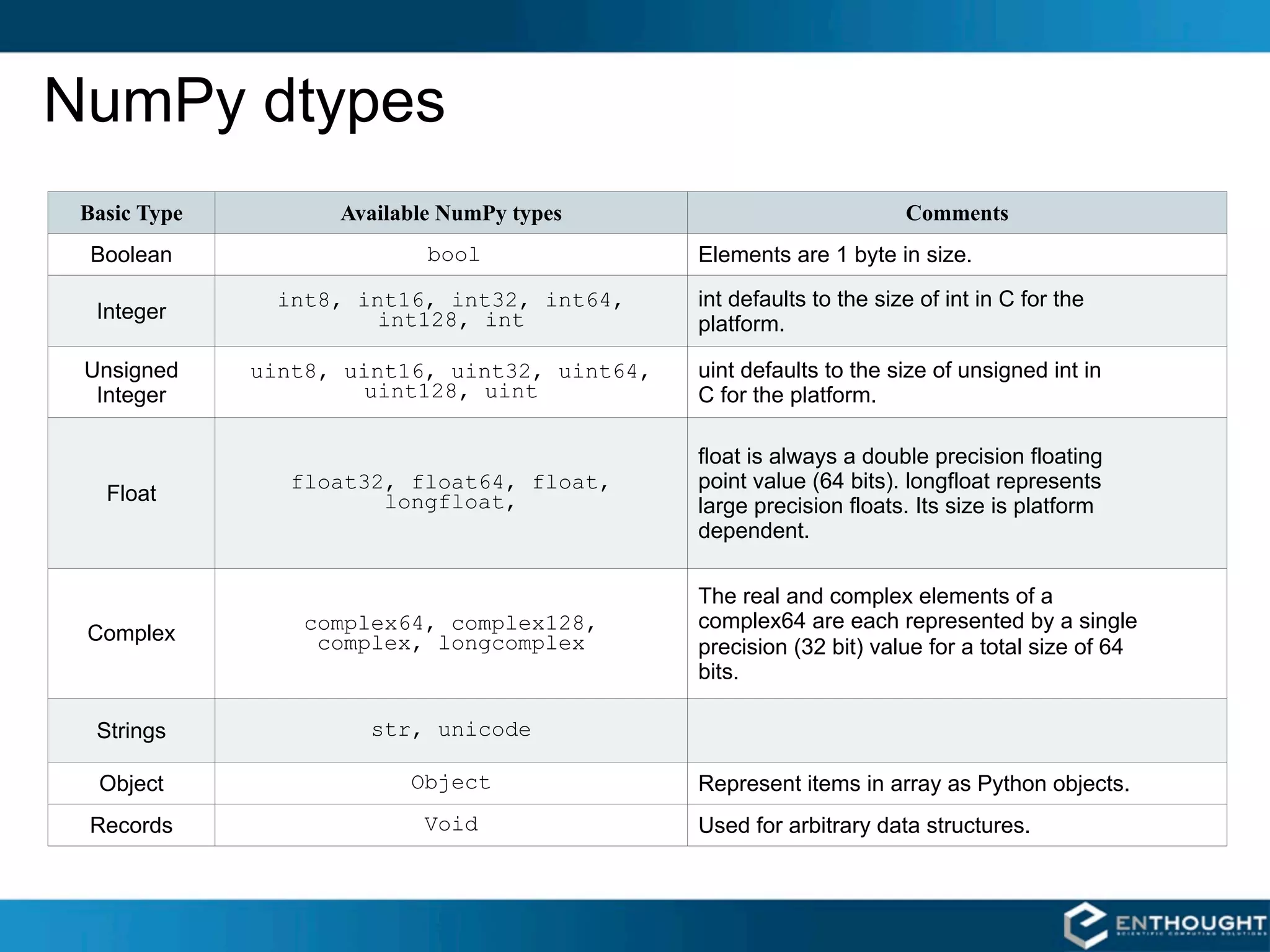
NumPy dtypes
Basic Type Available NumPy types Comments
Boolean bool Elements are 1 byte in size.
int8, int16, int32, int64, int defaults to the size of int in C for the
Integer int128, int platform.

Unsigned uint8, uint16, uint32, uint64, uint defaults to the size of unsigned int in
Integer uint128, uint C for the platform.

float is always a double precision floating
float32, float64, float, point value (64 bits). longfloat represents
Float longfloat, large precision floats. Its size is platform
dependent.

The real and complex elements of a
complex64, complex128, complex64 are each represented by a single
Complex complex, longcomplex precision (32 bit) value for a total size of 64
bits.

Strings str, unicode

Object Object Represent items in array as Python objects.
Records Void Used for arbitrary data structures.

“Structured” Arrays
Elements of an array can be EXAMPLE
any fixed-size data structure! >>> from numpy import dtype, empty
# structured data format
name char[10] >>> fmt = dtype([('name', 'S10'),
age int ('age', int),
weight double ('weight', float)
])
>>> a = empty((3,4), dtype=fmt)
Brad Jane John Fred >>> a.itemsize
22
33 25 47 54
>>> a['name'] = [['Brad', … ,'Jill']]
135.0 105.0 225.0 140.0 >>> a['age'] = [[33, … , 54]]
Henry George Brian Amy >>> a['weight'] = [[135, … , 145]]
>>> print a
29 61 32 27 [[('Brad', 33, 135.0)
154.0 202.0 137.0 187.0 …
Ron Susan Jennifer Jill
('Jill', 54, 145.0)]]
19 33 18 54
188.0 135.0 88.0 145.0

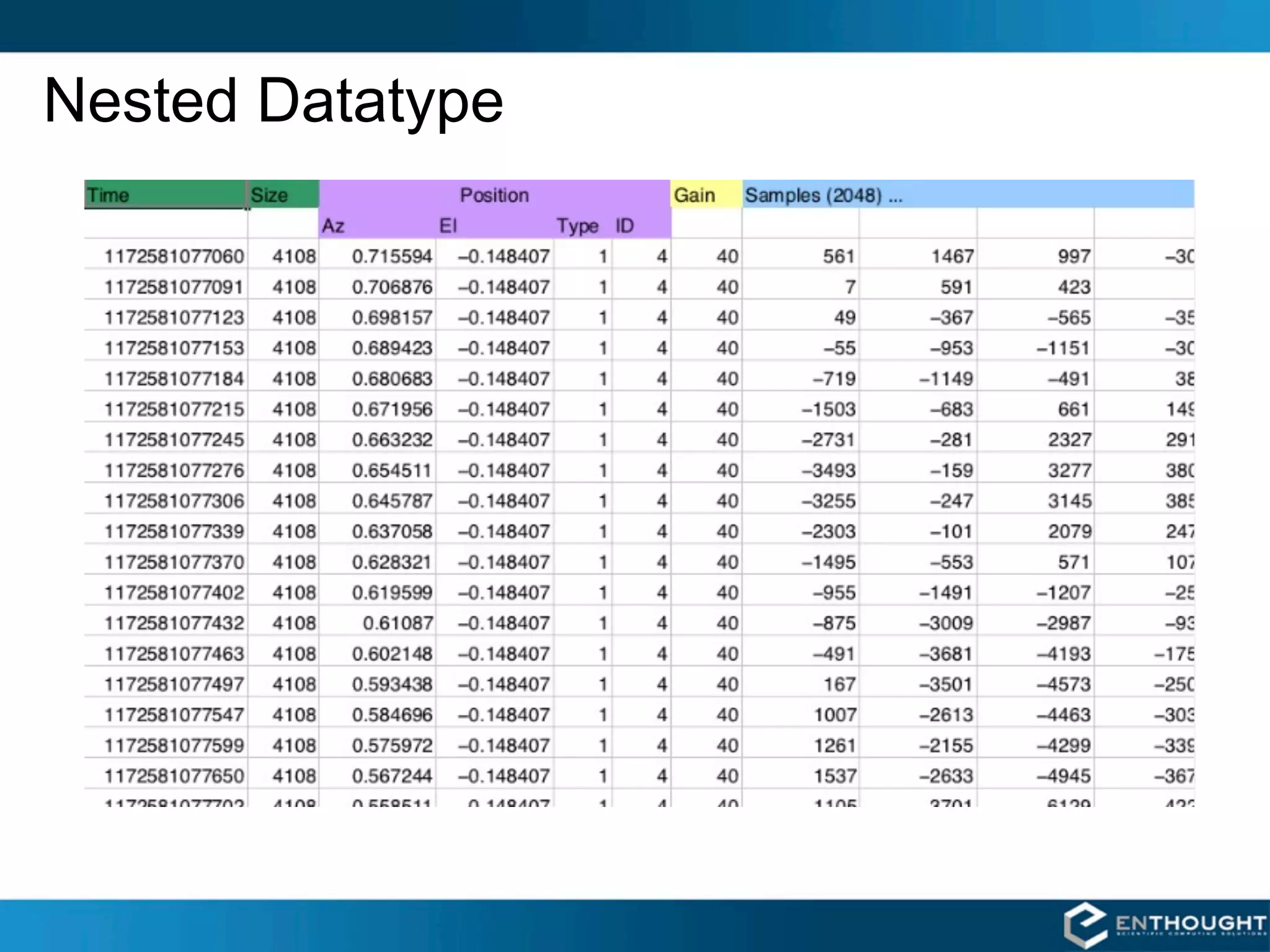
Nested Datatype
dt = dtype([('time', uint64),
('size', uint32),
('position', [('az', float32),
('el', float32),
('region_type', uint8),
('region_ID', uint16)]),
('gain', np.uint8),
('samples', np.int16, 2048)])

data = np.fromfile(f, dtype=dt)

Memory Mapped Arrays
• Methods for Creating:
–memmap: subclass of ndarray that manages the
memory mapping details.
–frombuffer: Create an array from a memory mapped
buffer object.
– ndarray constructor: Use the buffer keyword to
pass in a memory mapped buffer.
• Limitations:
–Files must be < 2GB on Python 2.4 and before.
–Files must be < 2GB on 32-bit machines.
–Python 2.5 on 64 bit machines is theoretically "limited"
to 17.2 billion GB (17 Exabytes).

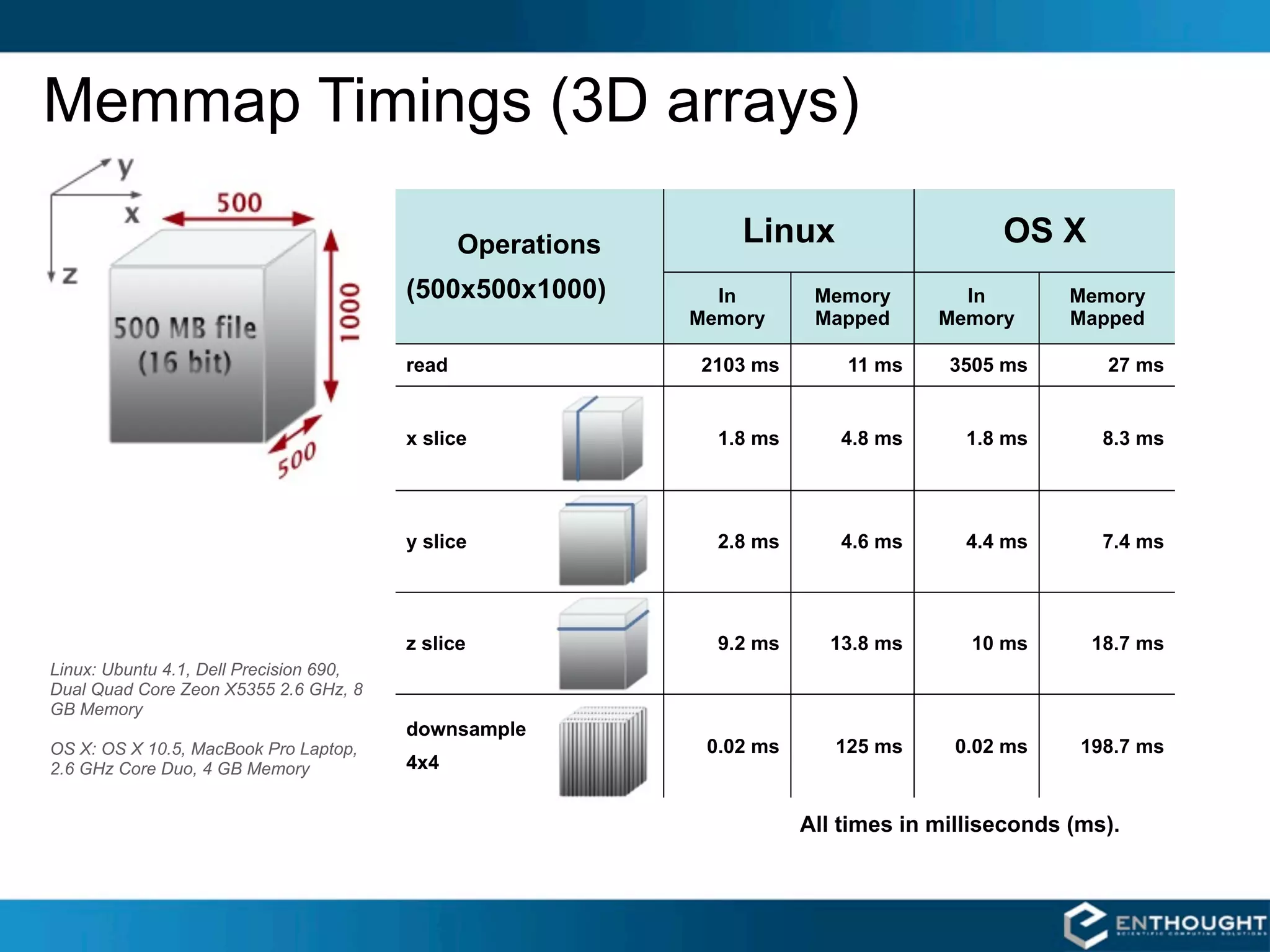
Memmap Timings (3D arrays)

Operations Linux OS X
(500x500x1000) In Memory In Memory
Memory Mapped Memory Mapped

read 2103 ms 11 ms 3505 ms 27 ms

x slice 1.8 ms 4.8 ms 1.8 ms 8.3 ms

y slice 2.8 ms 4.6 ms 4.4 ms 7.4 ms

z slice 9.2 ms 13.8 ms 10 ms 18.7 ms
Linux: Ubuntu 4.1, Dell Precision 690,
Dual Quad Core Zeon X5355 2.6 GHz, 8
GB Memory
downsample
OS X: OS X 10.5, MacBook Pro Laptop, 0.02 ms 125 ms 0.02 ms 198.7 ms
2.6 GHz Core Duo, 4 GB Memory 4x4

All times in milliseconds (ms).

Structured Arrays
char[12] int64 float32 Elements of array can be any
fixed-size data structure!
Name Time Value
MSFT_profit 10 6.20 Example
GOOG_profit 12 -1.08 >>> import numpy as np
>>> fmt = np.dtype([('name', 'S12'),
MSFT_profit 18 8.40 ('time', np.int64),
('value', np.float32)])
>>> vals = [('MSFT_profit', 10, 6.20),
INTC_profit 25 -0.20 ('GOOG_profit', 12, -1.08),

…
('INTC_profit', 1000385, -1.05)
('MSFT_profit', 1000390, 5.60)]
GOOG_profit 1000325 3.20
>>> arr = np.array(vals, dtype=fmt)
GOOG_profit 1000350 4.50 # or
>>> arr = np.fromfile('db.dat', dtype=fmt)
INTC_profit 1000385 -1.05 # or
>>> arr = np.memmap('db.dat', dtype=fmt,
mode='c')
MSFT_profit 1000390 5.60

MSFT_profit 10 6.20 GOOG_profit 12 -1.08 INTC_profit 1000385 -1.05 MSFT_profit 1000390 5.60

Mathematical Binary Operators
a + b  add(a,b) a * b  multiply(a,b)
a - b  subtract(a,b) a / b  divide(a,b)
a % b  remainder(a,b) a ** b  power(a,b)

MULTIPLY BY A SCALAR ADDITION USING AN OPERATOR
FUNCTION
>>> a = array((1,2))
>>> a*3. >>> add(a,b)
array([3., 6.]) array([4, 6])

ELEMENT BY ELEMENT ADDITION IN-PLACE OPERATION

# Overwrite contents of a.
>>> a = array([1,2])
# Saves array creation
>>> b = array([3,4])
# overhead.
>>> a + b
>>> add(a,b,a) # a += b
array([4, 6])
array([4, 6])
>>> a
array([4, 6])

Comparison and Logical Operators
equal (==) not_equal (!=) greater (>)
greater_equal (>=) less (<) less_equal (<=)
logical_and logical_or logical_xor
logical_not
2-D EXAMPLE
Be careful with if statements
>>> a = array(((1,2,3,4),(2,3,4,5))) involving numpy arrays. To
>>> b = array(((1,2,5,4),(1,3,4,5))) test for equality of arrays,
>>> a == b don't do:
array([[True, True, False, True], if a == b:
[False, True, True, True]])
# functional equivalent Rather, do:
>>> equal(a,b) if all(a==b):
array([[True, True, False, True],
[False, True, True, True]]) For floating point,
if allclose(a,b):
is even better.

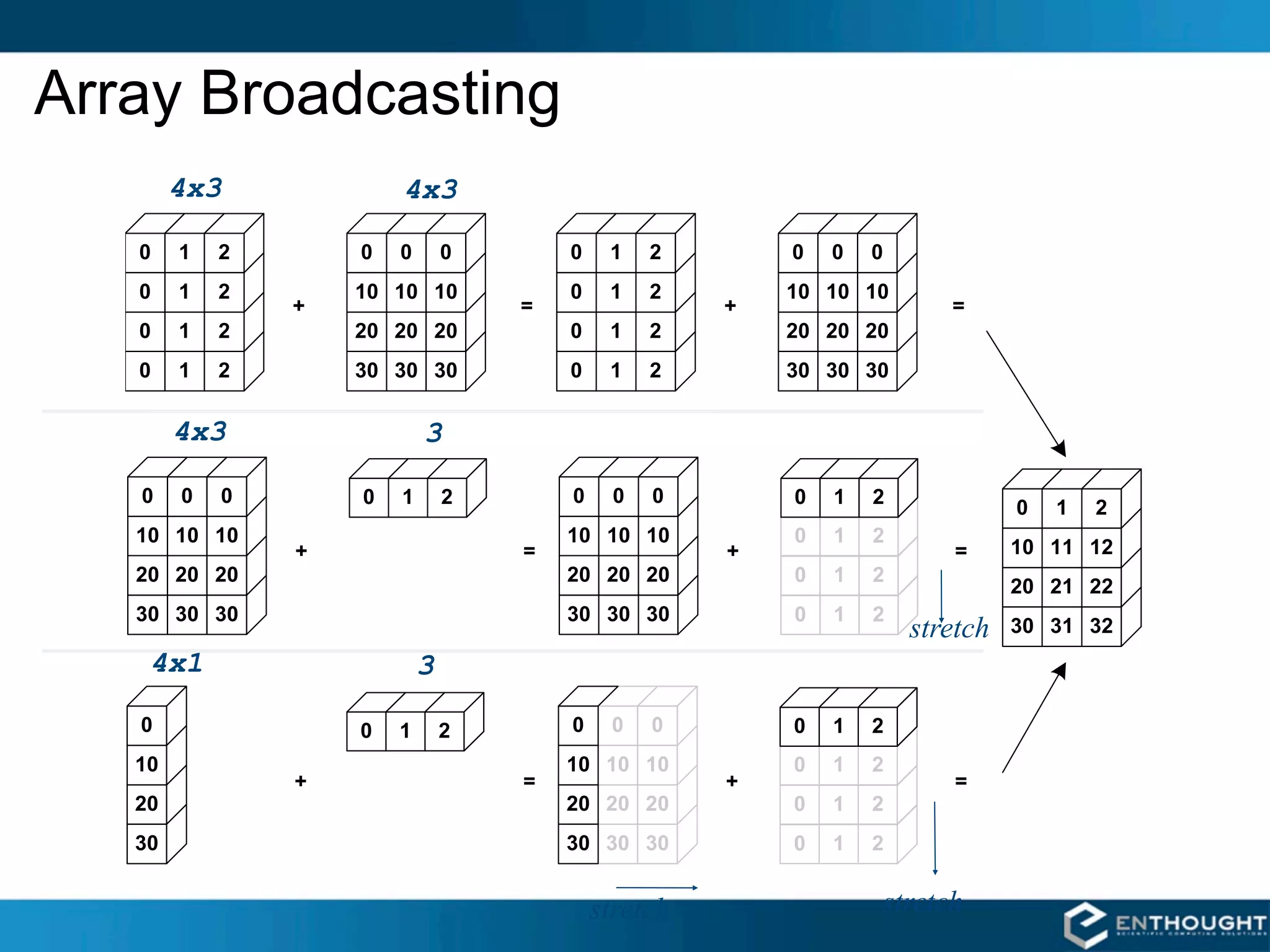
Array Broadcasting
4x3 4x3

4x3 3

stretch
4x1 3

stretch stretch

Broadcasting Rules

                             
         
"ValueError: shape mismatch: objects cannot be
broadcast to a single shape"    

!
4x3 4

Broadcasting in Action

>>> a = array((0,10,20,30))
>>> b = array((0,1,2))
>>> y = a[:, newaxis] + b

Universal Function Methods

           
               
         

op.reduce(a,axis=0)
op.accumulate(a,axis=0)
op.outer(a,b)
op.reduceat(a,indices)

op.reduce()
For multidimensional arrays, op.reduce(a,axis)applies op to the elements of a
along the specified axis. The resulting array has dimensionality one less than a. The
default value for axis is 0.

SUM COLUMNS BY DEFAULT SUMMING UP EACH ROW

>>> add.reduce(a) >>> add.reduce(a,1)
array([60, 64, 68]) array([ 3, 33, 63, 93])

Array Calculation Methods
SUM FUNCTION SUM ARRAY METHOD
>>> a = array([[1,2,3], # a.sum() defaults to adding
[4,5,6]], float) # up all values in an array.
>>> a.sum()
# sum() defaults to adding up 21.
# all the values in an array.
>>> sum(a) # supply an axis argument to
21. # sum along a specific axis
>>> a.sum(axis=0)
# supply the keyword axis to array([5., 7., 9.])
# sum along the 0th axis
>>> sum(a, axis=0)
array([5., 7., 9.]) PRODUCT
# product along columns
# supply the keyword axis to >>> a.prod(axis=0)
# sum along the last axis array([ 4., 10., 18.])
>>> sum(a, axis=-1)
array([6., 15.]) # functional form
>>> prod(a, axis=0)
array([ 4., 10., 18.])

Min/Max
MIN MAX
>>> a = array([2.,3.,0.,1.]) >>> a = array([2.,3.,0.,1.])
>>> a.min(axis=0) >>> a.max(axis=0)
0. 3.
# Use NumPy's amin() instead
# of Python's built-in min()
# for speedy operations on
# multi-dimensional arrays. # functional form
>>> amin(a, axis=0) >>> amax(a, axis=0)
0. 3.

ARGMIN ARGMAX
# Find index of minimum value. # Find index of maximum value.
>>> a.argmin(axis=0) >>> a.argmax(axis=0)
2 1
# functional form # functional form
>>> argmin(a, axis=0) >>> argmax(a, axis=0)
2 1

Statistics Array Methods
MEAN STANDARD DEV./VARIANCE
>>> a = array([[1,2,3], # Standard Deviation
[4,5,6]], float) >>> a.std(axis=0)
array([ 1.5, 1.5, 1.5])
# mean value of each column
>>> a.mean(axis=0) # variance
array([ 2.5, 3.5, 4.5]) >>> a.var(axis=0)
>>> mean(a, axis=0) array([2.25, 2.25, 2.25])
array([ 2.5, 3.5, 4.5]) >>> var(a, axis=0)
>>> average(a, axis=0) array([2.25, 2.25, 2.25])
array([ 2.5, 3.5, 4.5])

# average can also calculate
# a weighted average
>>> average(a, weights=[1,2],
... axis=0)
array([ 3., 4., 5.])

Zen of NumPy (version 0.1)

• strided is better than scattered
• contiguous is better than strided
• descriptive is better than imperative (e.g. data-types)
• array-oriented is better than object-oriented
• broadcasting is a great idea -- use where possible
• vectorized is better than an explicit loop
• unless it’s complicated --- then use Cython or numexpr
• think in higher dimensions

Recent Developments in NumPy / SciPy
• Community growth (github)
• Addition of .NET (IronPython) support
– NumPy as a core C-library
– NumPy and SciPy using Cython to build all
extension modules
– better tests and bugs closed
• Re-factoring of the ufunc-implementation as
iterators (Mark Wiebe)
– expose the pipeline that was only previously used
in “worst-case” scenario.
– first stages of calculation structure refactoring

NumPy next steps (1.6, 2.0 and beyond)
• Calculation Frame-work
– basic generic function mechanism needs to be extended to allow other objects
to participate more seamlessly
– test on distributed arrays, generated arrays, masked arrays, etc.
– add better support for run-time code-generation
– more optimized algorithms (e.g. add special-case versions of low-level loops)

• Addition of an “indirect array”
– could subsume sparse arrays, distributed arrays, etc.
– add compressed arrays, lazy-evaluation arrays, generator arrays

• Data-base integration
– data-base integration: please give me a structured array from a fetchall
command
– SQL front end for NumPy table

NumPy next steps (1.6, 2.0, ...)

• Catching up
– Dropping support for <2.5 (in NumPy 2.0)
– Addition of “with-statement” contexts (error handling, print-options, lazy-
evaluation, etc.)
– Finish datetime NEP
– Finish reduce-by NEP
– Add “geometry” information to NumPy (dimension and index labels).

• Core library growth
– Eliminate extra indirection where possible
– Optimizations for small-arrays
– Addition of additional front-ends: Jython, Ruby, Javascript

SciPy next steps
• Roadmap generation (move to github)
• Finish Cython migration
• Module cleanup continues
• Lots of work happening...
– errorbars in polyfit
– spectral algorithms in signal
– improvements to ode and sparse
– addition of pre-conditioners to sparse
– ..., ...

Numpy Talk at SIAM

More Related Content

What's hot

Viewers also liked

Similar to Numpy Talk at SIAM

More from Enthought, Inc.

Recently uploaded

Numpy Talk at SIAM

Editor's Notes