Modular Macros for OCaml

Modular Macros for OCaml

• 1.
  Modular Macros forOCaml Olivier Nicole ENSTA ParisTech nicole@ensta.fr 1 / 16
• 2.
  Macros? 2 / 16
• 3.
  Safety Expressiveness CPP Lisp macros Racket macros OCamlmacros 3 / 16
• 4.
  Why should wecare? Domain-specific optimisations 4 / 16
• 5.
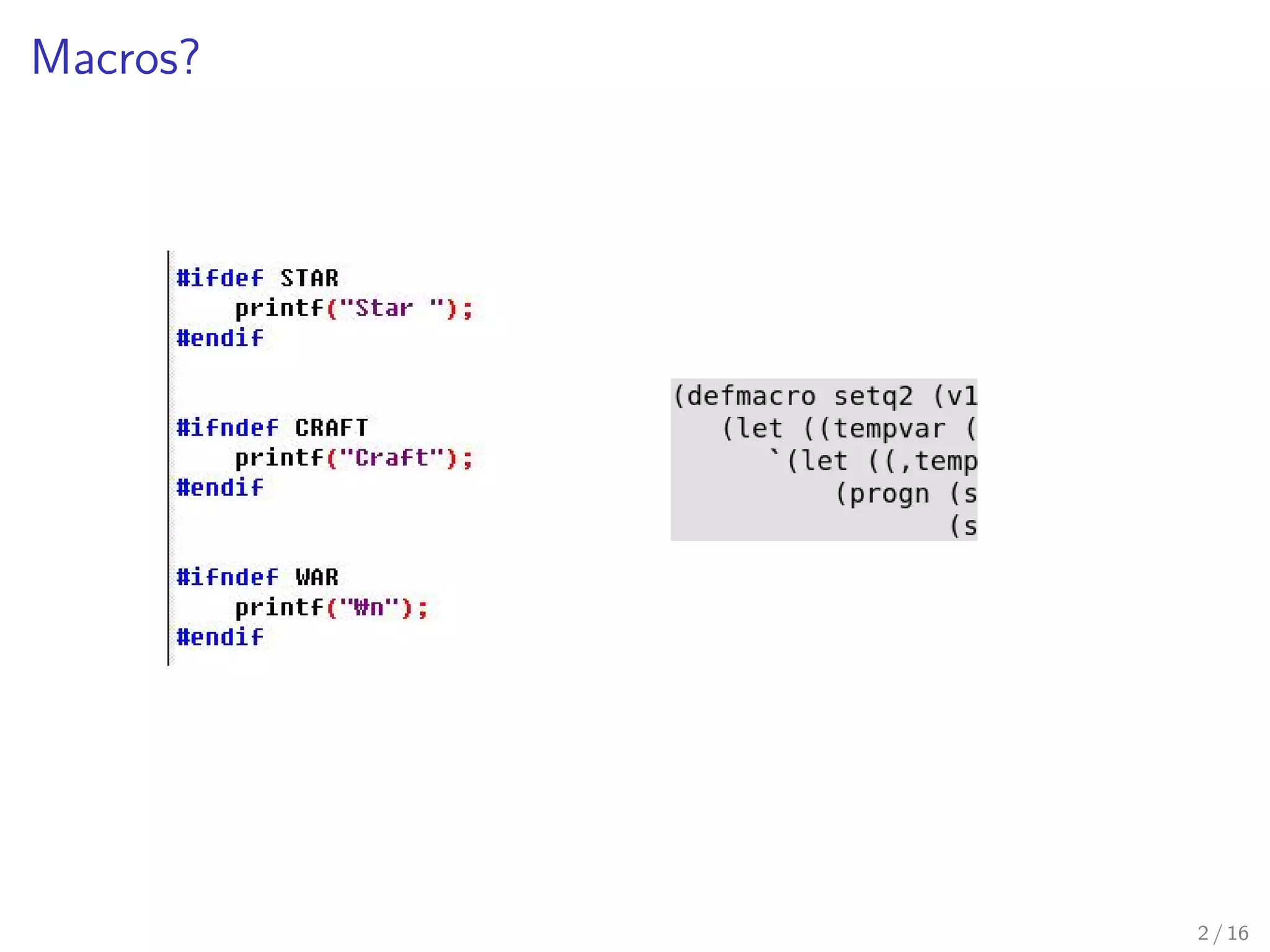
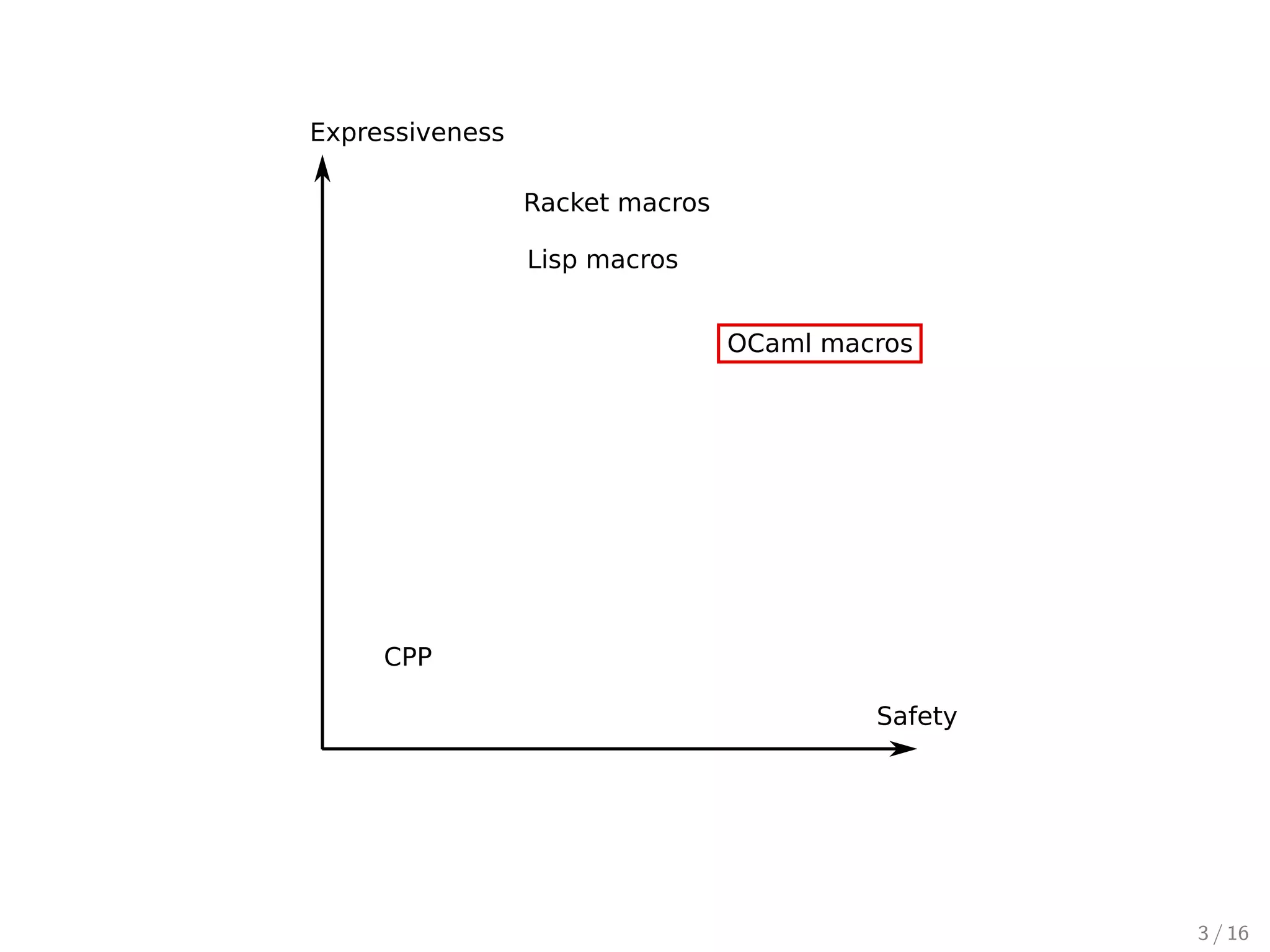
  Why should wecare? Domain-specific optimisations strymonas: optimal stream processing [Kiselyov et al., POPL’17] of_arr << arr >> |> map (fun x → << $x * $x >>) |> fold (fun z a → << $a + $z >>) << 0 >> 5 / 16
• 6.
  Why should wecare? Domain-specific optimisations strymonas: optimal stream processing [Kiselyov et al., POPL’17] of_arr << arr >> |> map (fun x → << $x * $x >>) |> fold (fun z a → << $a + $z >>) << 0 >> let s_1 = ref 0 in let arr_2 = arr in for i_3 = 0 to Array.length arr_2 -1 do let el_4 = arr_2.(i_3) in let t_5 = el_4 * el_4 in s_1 := t_5 + !s_1 done; !s_1 6 / 16
• 7.
  Principle ▶ quoting << >>: α → α expr ▶ antiquoting $ : α expr → α 7 / 16
• 8.
  Principle ▶ quoting << >>: α → α expr ▶ antiquoting $ : α expr → α e.g.: macro x = << 42 >> macro y = << $x + 1 >> 8 / 16
• 9.
  Power function let squarex = x * x let rec power n x = if n = 0 then 1 else if n mod 2 = 0 then square (power (n / 2) x) else x * (power (n - 1) x) 9 / 16
• 10.
  Power function let squarex = x * x macro rec power n x = if n = 0 then << 1 >> else if n mod 2 = 0 then << square $(power (n / 2) x) >> else << $x * $(power (n - 1) x) >> 10 / 16
• 11.
  Power function let squarex = x * x macro rec power n x = if n = 0 then << 1 >> else if n mod 2 = 0 then << square $(power (n / 2) x) >> else << $x * $(power (n - 1) x) >> Usage: $(power 9 << 2 >>) expands to: 2 * square (square (square (2 * 1))) 11 / 16
• 12.
  The environment matters letsquare x = x * x macro power n x = (* ... *) let square = "a rectangle with equal sides" $(power 9 << 2 >>) 12 / 16
• 13.
  The environment matters letsquare x = x * x let square = "a rectangle with equal sides" 2 * square (square (square (2 * 1))) (* Oops! *) 13 / 16
• 14.
  The environment matters letsquare x = x * x let power = [| square |] let square = "a rectangle with equal sides" 2 * power.(0) (power.(0) (power.(0) (2 * 1))) 14 / 16
• 15.
  Summary ▶ powerful macrosystems are useful ▶ staging is a good way to achieve that ▶ in OCaml, correctness is achieved by using path closures. 15 / 16
• 16.
  References ▶ Yallop andWhite, Modular Macros. OCaml Workshop ’15 ▶ Kiselyov et al., Stream Fusion, to Completeness. POPL’17 Thanks! 16 / 16