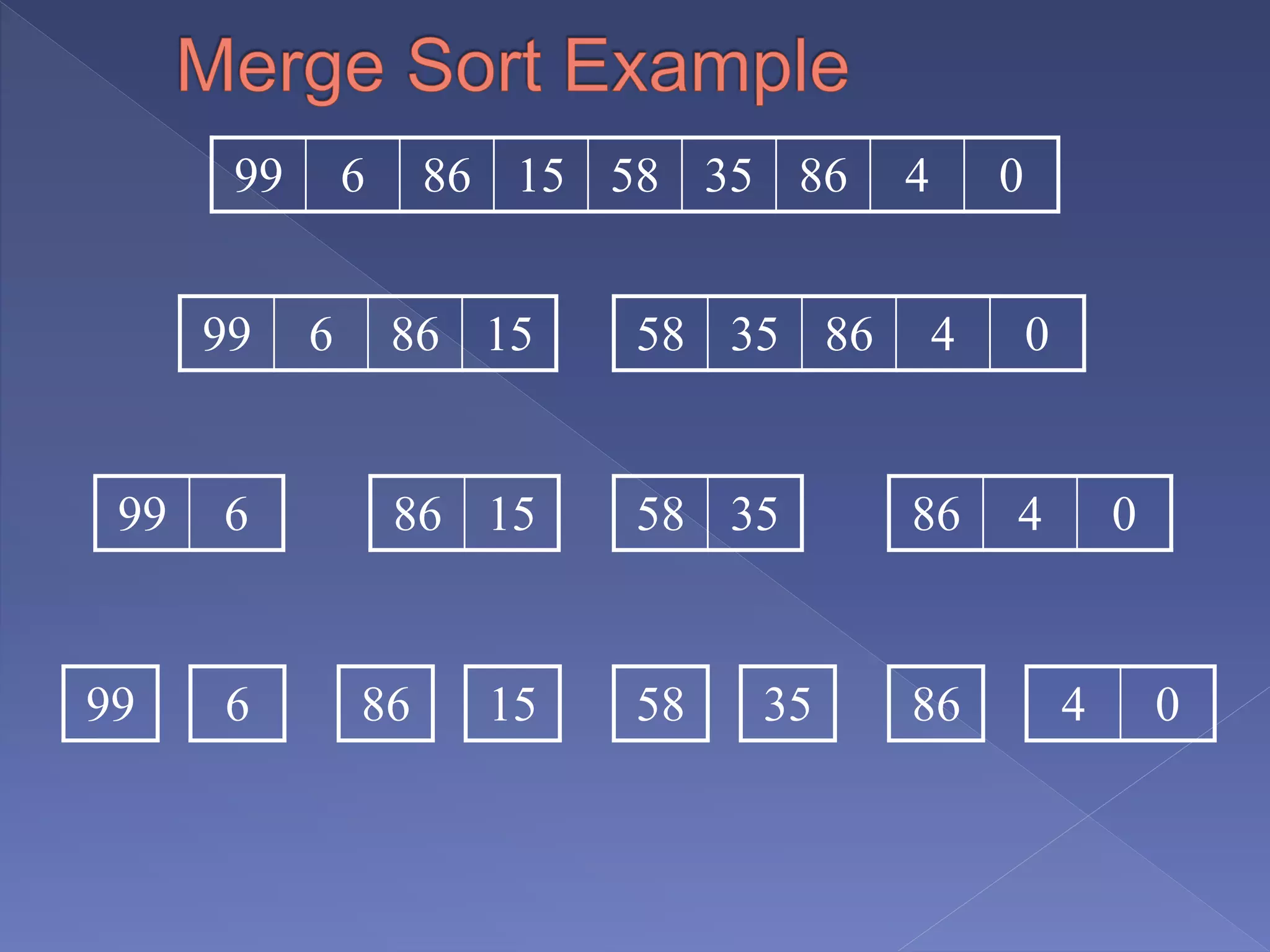
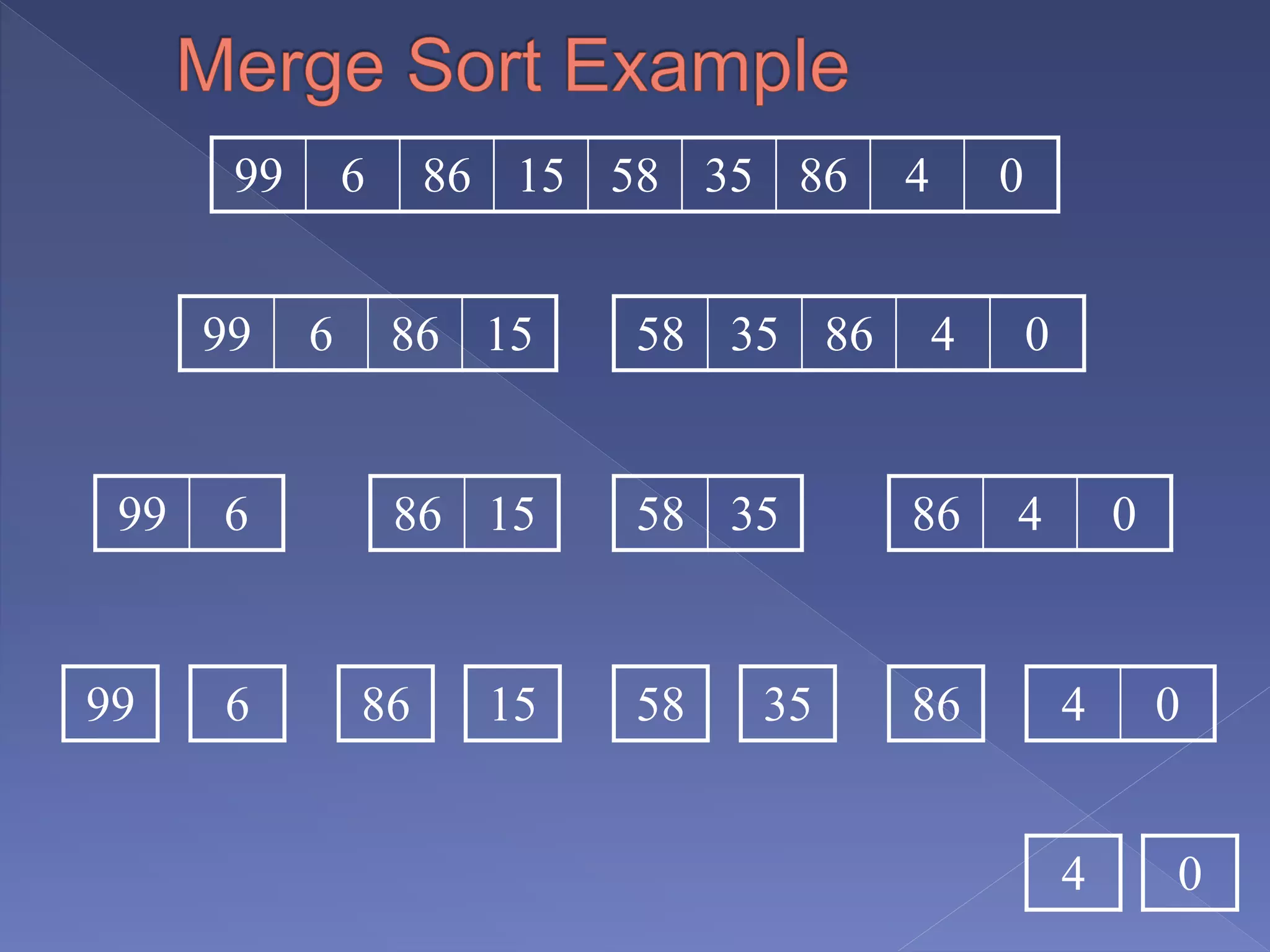
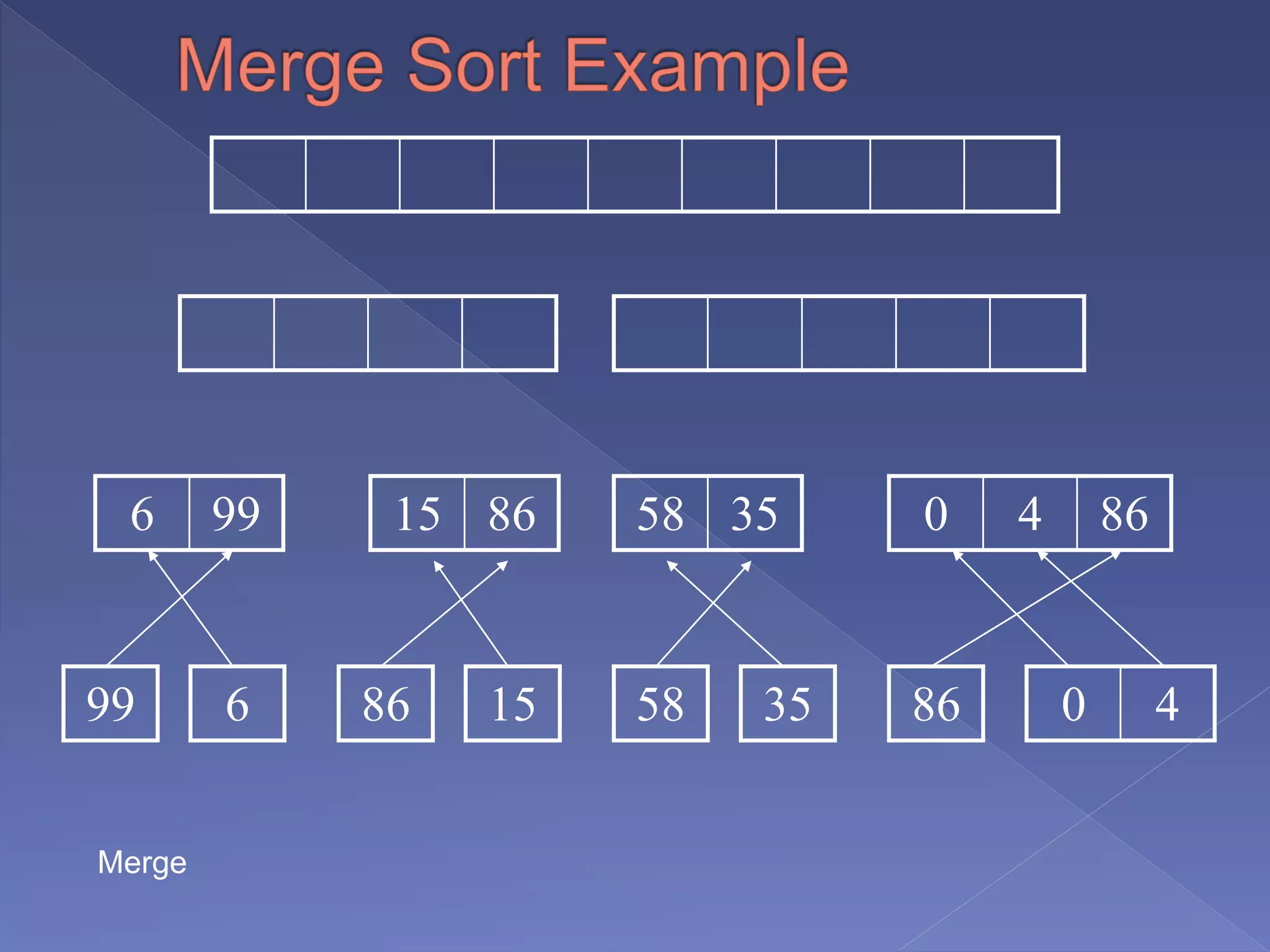
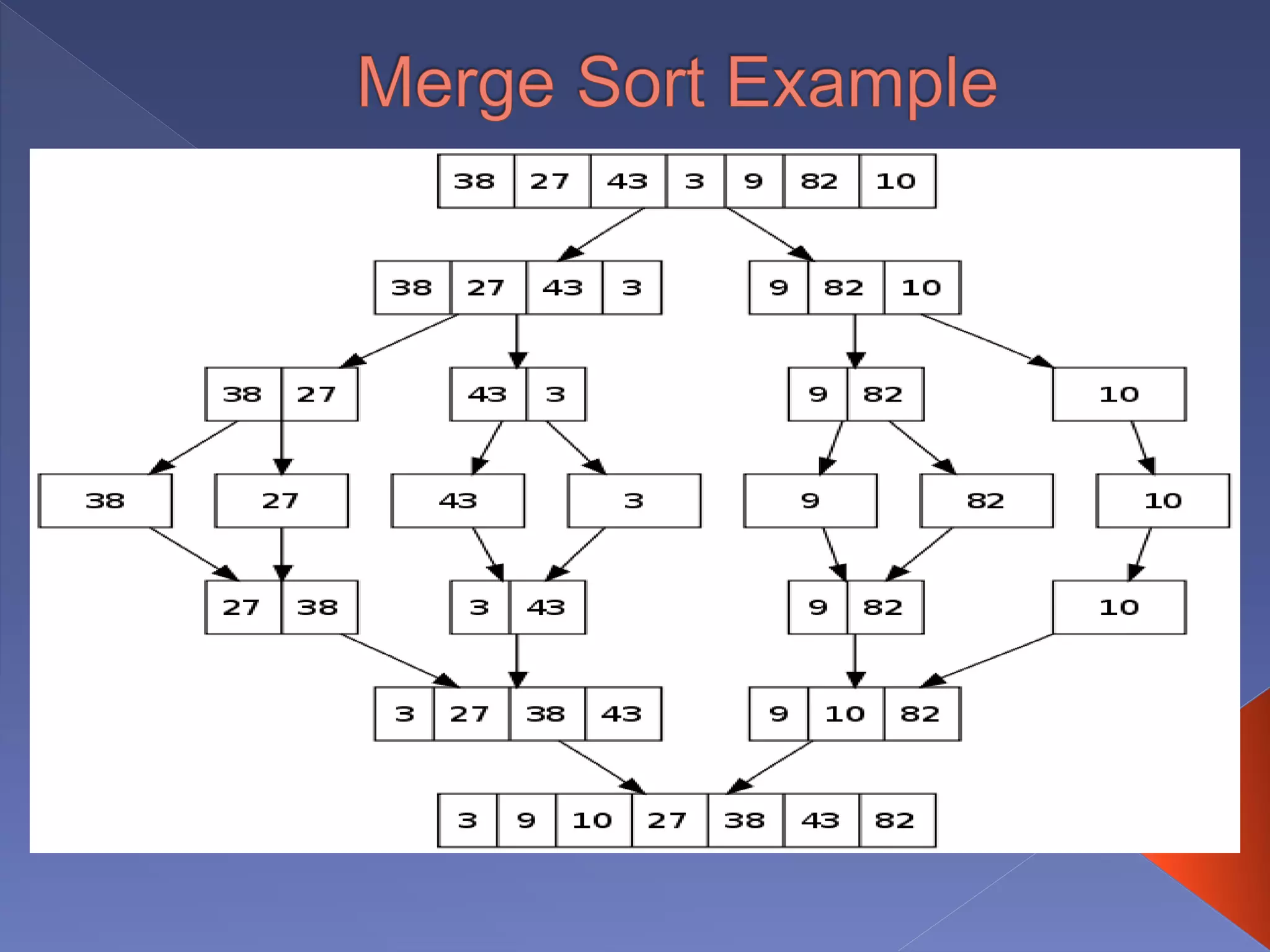
Merge sort algorithm

 Merge sort is a sorting technique based on
divide and conquer technique. With worst-
case time complexity being Ο(n log n), it is
one of the most respected algorithms.
 Merge sort first divides the array into equal
halves and then combines them in a sorted
manner.

Invented by
John von Neumann
(1903-1957)
 Follows divide and
conquer paradigm.
 Developed merge
sort for EDVAC in
1945

1.Divide: Divide the unsorted list into two sub lists
of about half the size.
2.Conquer: Sort each of the two sub lists
recursively until we have list sizes of length 1,in
which case the list itself is returned.
3.Combine: Merge the two-sorted sub lists back
into one sorted list.

 MERGE SORT (A,p,r) //divide
if p < r
then q= [ (p + r) / 2 ]
MERGE SORT(A,p,q)
MERGER SORT(A,q + 1,r)
MERGE(A,p,q,r)

Merge(array A, int p, int q, int r)
{
array B[p..r] //temp array taken
i = k = p // initialize pointers
j = q+1
while (i <= q and j <= r)
{
if (A[i] <= A[j]) B[k++] = A[i++]
else B[k++] = A[j++]
}
while (i <= q)
B[k++] = A[i++] // copy any leftover to B
while (j <= r)
B[k++] = A[j++]
for i = p to r
A[i] = B[i] // copy B back to A
}

99 6 86 15 58 35 86 4 0
99 6 86 15 58 35 86 4 0

99 6 86 15 58 35 86 4 0
99 6 86 15 58 35 86 4 0
86 1599 6 58 35 86 4 0

99 6 86 15 58 35 86 4 0
99 6 86 15 58 35 86 4 0
86 1599 6 58 35 86 4 0
99 6 86 15 58 35 86 4 0

99 6 86 15 58 35 86 4 0
99 6 86 15 58 35 86 4 0
86 1599 6 58 35 86 4 0
99 6 86 15 58 35 86 4 0
4 0

99 6 86 15 58 35 86 0 4
4 0Merge

15 866 99 58 35 0 4 86
99 6 86 15 58 35 86 0 4
Merge

6 15 86 99 0 4 35 58 86
15 866 99 58 35 0 4 86
Merge

0 4 6 15 35 58 86 86 99
6 15 86 99 0 4 35 58 86
Merge

Merge sort algorithm

More Related Content

What's hot

Viewers also liked

Similar to Merge sort algorithm

More from Shubham Dwivedi

Recently uploaded

Merge sort algorithm