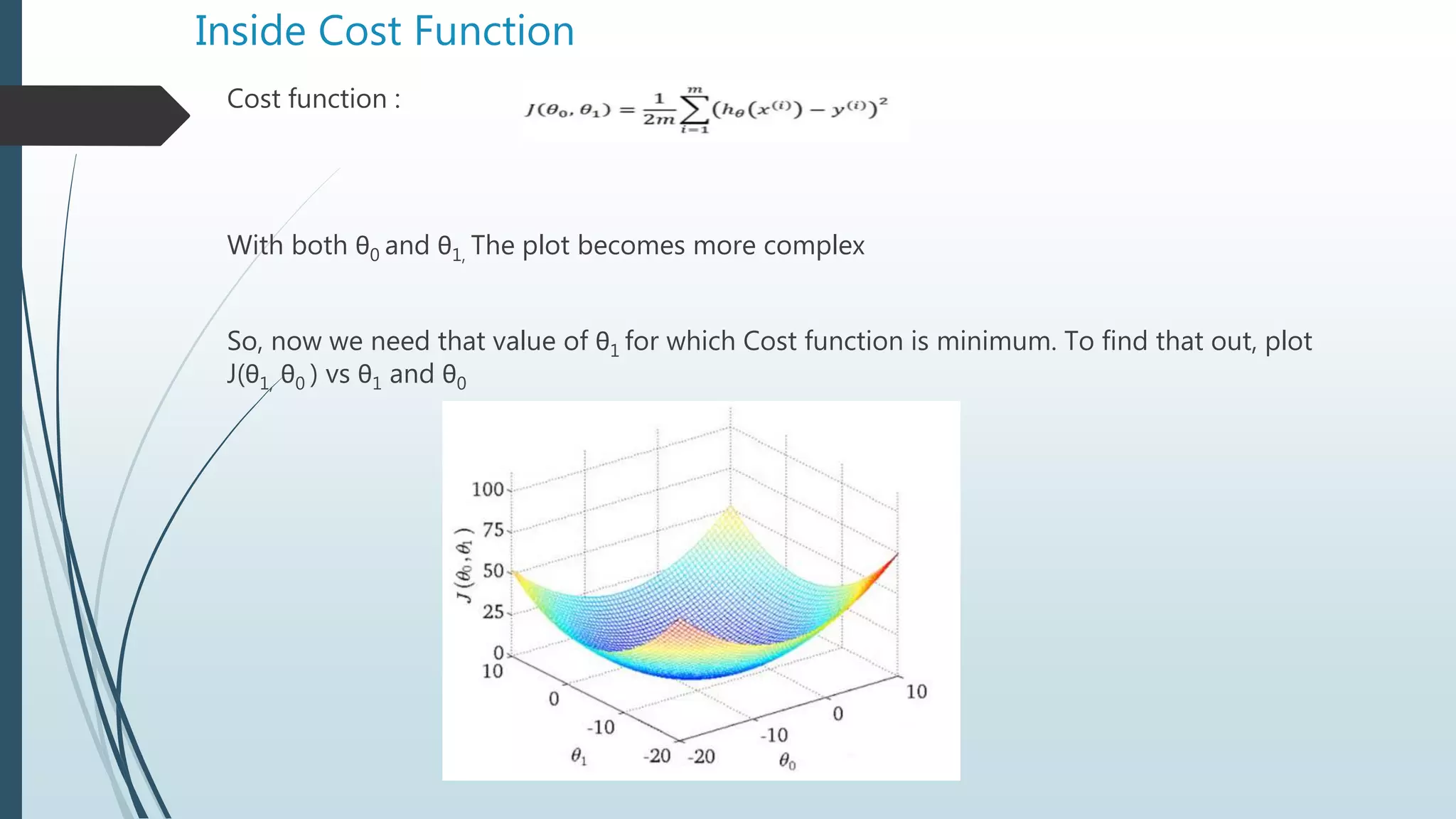
The document provides an overview of linear regression using Python, emphasizing the calculation of the best-fit line and its application in predicting outcomes. It discusses methods for minimizing errors, metrics for evaluating model performance such as mean absolute error and R-squared, and introduces concepts like polynomial regression and the potential pitfalls of overfitting and underfitting. Additionally, it briefly covers the bias-variance trade-off and explains how to adjust the R-squared value to assess model accuracy considering the number of predictors.