Machine learning introduction lecture notes

CS 179: LECTURE 13
INTRO TO MACHINE LEARNING

GOALS OF WEEKS 5-6
 What is machine learning (ML) and when is it useful?
 Intro to major techniques and applications
 Give examples
 How can CUDA help?
 Departure from usual pattern: we will give the
application first, and the CUDA later

HOW TO FOLLOW THIS LECTURE
 This lecture and the next one will have a lot of math!
 Don’t worry about keeping up with the derivations 100%
 Important equations will be boxed
 Key terms to understand: loss/objective function, linear
regression, gradient descent, linear classifier
 The theory lectures will probably be boring for those of
you who have done some machine learning (CS156/155)
already

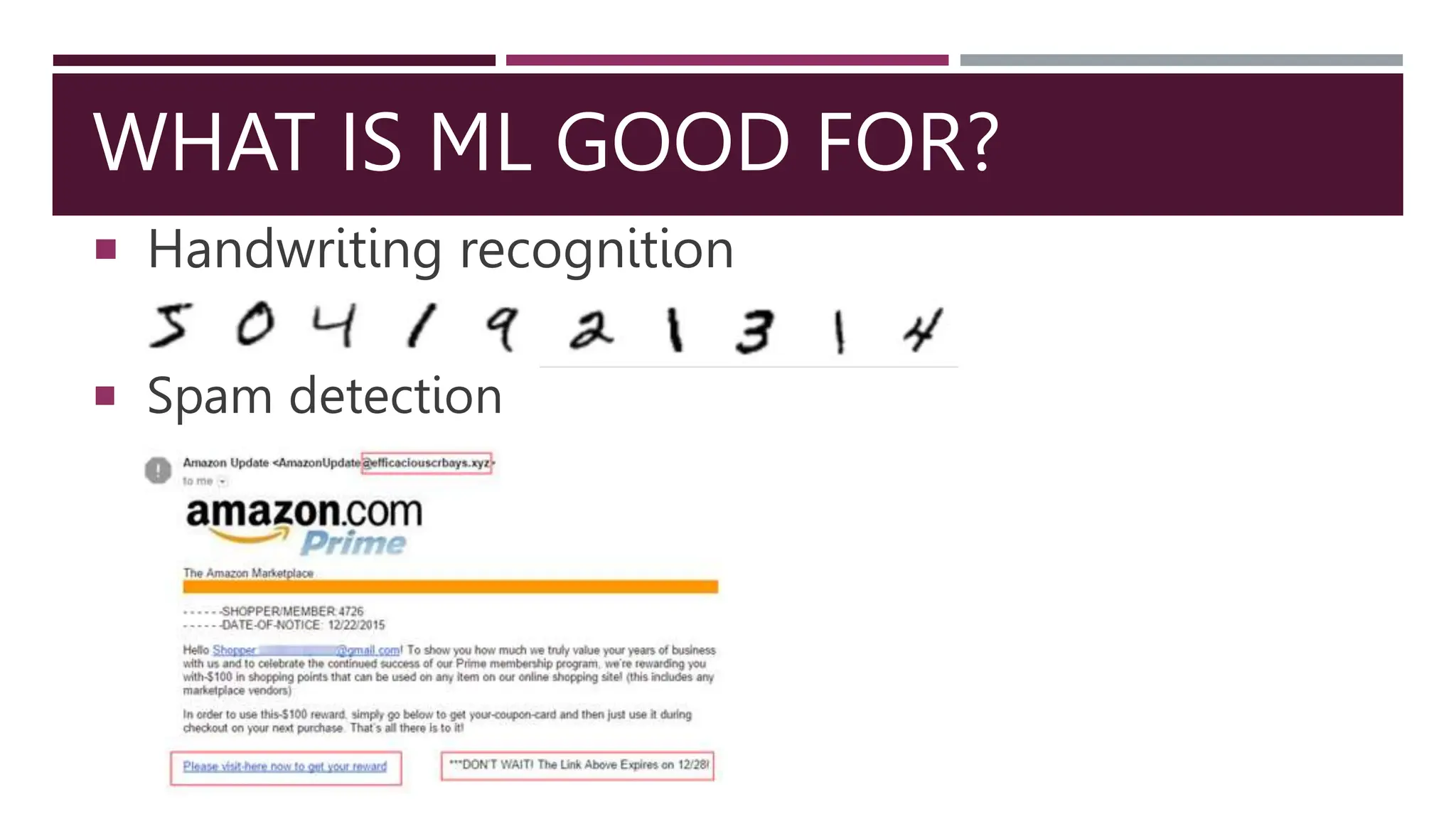
WHAT IS ML GOOD FOR?
 Handwriting recognition
 Spam detection

WHAT IS ML GOOD FOR?
 Teaching a robot how to do a backflip
 https://youtu.be/fRj34o4hN4I
 Predicting the performance of a stock portfolio
 The list goes on!

WHAT IS ML?
 What do these problems have in common?
 Some pattern we want to learn
 No good closed-form model for it
 LOTS of data
 What can we do?
 Use data to learn a statistical model for
the pattern we are interested in

DATA REPRESENTATION
 One data point is a vector 𝑥 in ℝ𝑑
 A 30 × 30 pixel image is a 900-dimensional
vector (one component per pixel intensity)
 If we are classifying an email as spam or not
spam, set 𝑑 = number of words in dictionary
 Count the number of times 𝑛𝑖 that a word 𝑖
appears in an email and set 𝑥𝑖 = 𝑛𝑖
 The possibilities are endless 

WHAT ARE WE TRYING TO DO?
 Given an input 𝑥 ∈ ℝ𝑑
, produce an output 𝑦
 What is 𝑦?
 Could be a real number, e.g. predicted return
of a given stock portfolio
 Could be 0 or 1, e.g. spam or not spam
 Could be a vector in ℝ𝑚
, e.g. telling a robot
how to move each of its 𝑚 joints
 Just like 𝑥, 𝑦 can be almost anything 

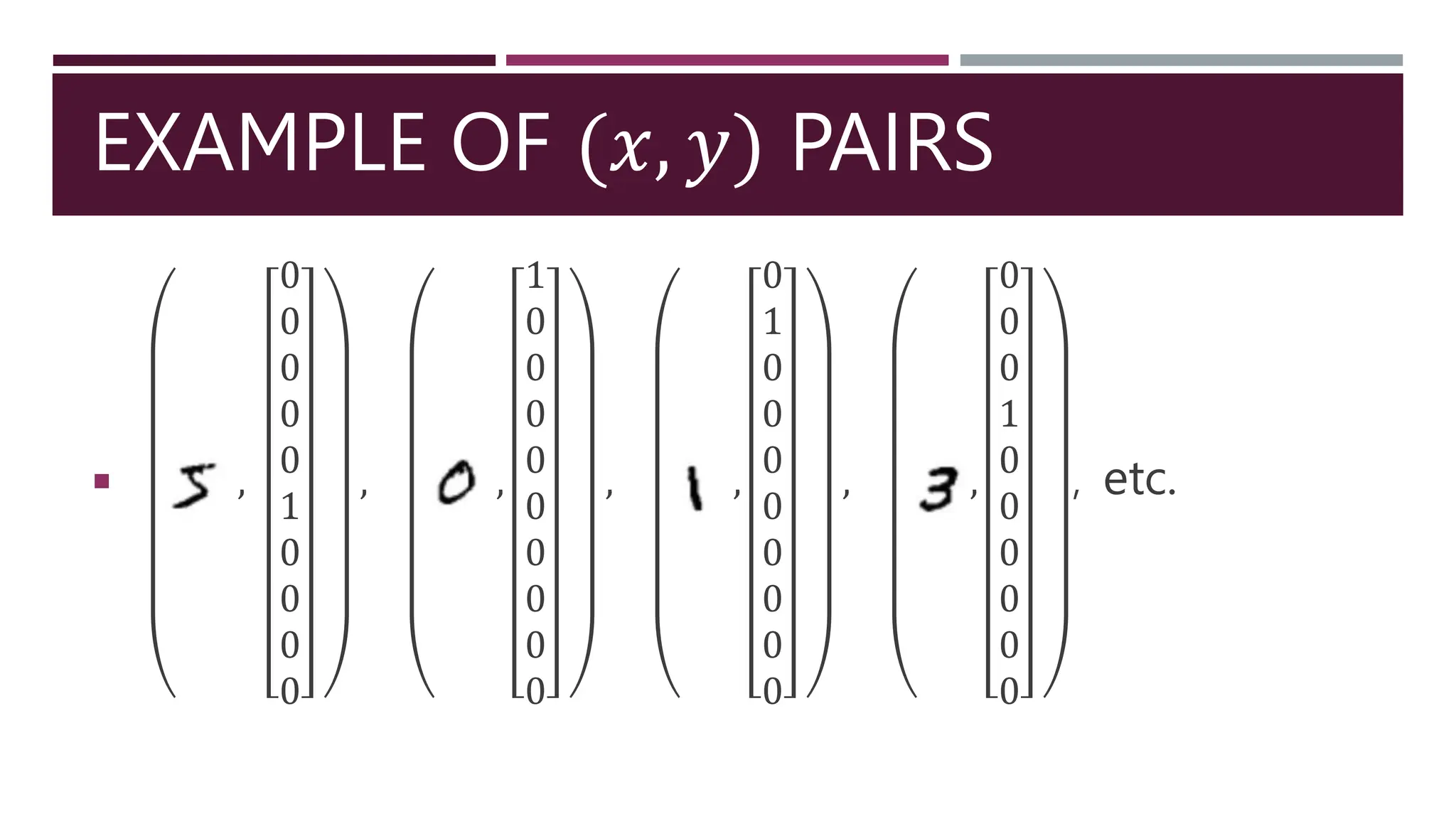
EXAMPLE OF (𝑥, 𝑦) PAIRS
 ,
0
0
0
0
0
1
0
0
0
0
, ,
1
0
0
0
0
0
0
0
0
0
, ,
0
1
0
0
0
0
0
0
0
0
, ,
0
0
0
1
0
0
0
0
0
0
, etc.

NOTATION
𝑥′
=
1
𝑥
∈ ℝ𝑑+1
𝐗 = 𝑥 1
, … , 𝑥 𝑁
∈ ℝ𝑑×𝑁
𝐗′
= 𝑥 1 ′
, … , 𝑥 𝑁 ′
∈ ℝ 𝑑+1 ×𝑁
𝐘 = 𝑦 1
, … , 𝑦 𝑁 𝑇
∈ ℝ𝑁×𝑚
𝕀 𝑝 =
1
0
𝑝 is true
otherwise

STATISTICAL MODELS
 Given (𝐗, 𝐘) (𝑁 pairs of 𝑥 𝑖
, 𝑦 𝑖
data), how
do we accurately predict an output 𝑦 given
an input 𝑥?
 One solution: a model 𝑓(𝑥) parametrized by
a vector (or matrix) 𝑤, denoted as 𝑓 𝑥; 𝑤
 The task is finding a set of optimal
parameters 𝑤

FITTING A MODEL
 So what does optimal mean?
 Under some measure of closeness, we want
𝑓(𝑥; 𝑤) to be as close as possible to the true
solution 𝑦 for any input 𝑥
 This measure of closeness is called a loss
function or objective function and is
denoted 𝐽 𝑤; 𝐗, 𝐘 -- it depends on our data
set (𝐗, 𝐘)!
 To fit a model, we try to find parameters 𝑤∗
that minimize 𝐽(𝑤; 𝐗, 𝐘), i.e. an optimal 𝑤

FITTING A MODEL
 What characterizes a good loss function?
 Represents the magnitude of our model’s
error on the data we are given
 Penalizes large errors more than small ones
 Continuous and differentiable in 𝑤
 Bonus points if it is also convex in 𝑤
 Continuity, differentiability, and convexity are
to make minimization easier

LINEAR REGRESSION
 𝑓 𝑥; 𝑤 = 𝑤0 + 𝑖=1
𝑑
𝑤𝑖𝑥𝑖 = 𝑤𝑇
𝑥′
 Below: 𝑑 = 1. 𝑤𝑇
𝑥′ is graphed.

LINEAR REGRESSION
 What should we use as a loss function?
 Each 𝑦 𝑖
is a real number
 Mean-squared error is a good choice 
 𝐽 𝑤; 𝐗, 𝐘 =
1
𝑁 𝑖=1
𝑁
𝑓 𝑥 𝑖
; 𝑤 − 𝑦 𝑖 2
=
1
𝑁 𝑖=1
𝑁
𝑤𝑇
𝑥 𝑖 ′
− 𝑦 𝑖
2
=
1
𝑁
𝑤𝑇
𝐗′ − 𝐘 𝑇
𝑤𝑇
𝐗′
− 𝐘

GRADIENT DESCENT
 How do we find 𝑤∗
= argmin
𝑤∈ℝ𝑑+1
𝐽(𝑤; 𝐗, 𝐘)?
 A function’s gradient points in the direction
of steepest ascent, and its negative in the
direction of steepest descent
 Following the gradient downhill will cause us
to converge to a local minimum!

GRADIENT DESCENT
 Fix some constant learning rate 𝜂 (0.03 is usually a
good place to start)
 Initialize 𝑤 randomly
 Typically select each component of 𝑤 independently
from some standard distribution (uniform, normal, etc.)
 While 𝑤 is still changing (hasn’t converged)
 Update 𝑤 ← 𝑤 − 𝜂∇𝐽 𝑤; 𝐗, 𝐘

GRADIENT DESCENT
 For mean squared error loss in linear regression,
∇𝐽 𝑤; 𝐗, 𝐘 =
2
𝑁
𝑤𝑇
𝐗′
𝐗′𝑇
− 𝐗′
𝐘
 This is just linear algebra! GPUs are good at this kind of
thing 
 Why do we care?
 𝑓 𝑥; 𝑤∗ = 𝑤∗𝑇
𝑥′ is the model with the lowest possible
mean-squared error on our training dataset (𝐗, 𝐘)!

STOCHASTIC GRADIENT DESCENT
 The previous algorithm computes the gradient over the
entire data set before stepping.
 Called batch gradient descent
 What if we just picked a single data point 𝑥 𝑖
, 𝑦 𝑖
at
random, computed the gradient for that point, and
updated the parameters?
 Called stochastic gradient descent

STOCHASTIC GRADIENT DESCENT
 Advantages of SGD
 Easier to implement for large datasets
 Works better for non-convex loss functions
 Sometimes faster
 Often use SGD on a “mini-batch” of 𝑘 examples rather
than just one at a time
 Allows higher throughput and more parallelization

BINARY LINEAR CLASSIFICATION
 𝑓 𝑥; 𝑤 = 𝕀 𝑤𝑇
𝑥′
> 0
 Divides ℝ𝑑
into two half-spaces
 𝑤𝑇
𝑥′
= 0 is a hyperplane
 A line in 2D, a plane in 3D, and so on
 Known as the decision boundary
 Everything on one side of the hyperplane is
class 0 and everything on the other side is
class 1

BINARY LINEAR CLASSIFICATION
 Below: 𝑑 = 2. Black line is the decision boundary
𝑤𝑇
𝑥′ = 0

MULTI-CLASS GENERALIZATION
 We want to classify 𝑥 into one of 𝑚 classes
 For each input 𝑥, 𝑦 is a vector in ℝ𝑚
with 𝑦𝑘 = 1 if class 𝑥 =
𝑘 and 𝑦𝑗 = 0 otherwise (i.e. 𝑦𝑘 = 𝕀 class 𝑥 = 𝑘 )
 Known as a one-hot vector
 Our model 𝑓(𝑥; 𝐖) is parametrized by a 𝑚 × (𝑑 + 1) matrix
𝐖 = 𝑤 1
, … , 𝑤 𝑚
 The model returns an 𝑚-dimensional vector (like 𝑦) with
𝑓𝑘 𝑥; 𝐖 = 𝕀 arg max
𝑖
𝑤 𝑖 𝑇
𝑥′
= 𝑘

 𝑤 𝑗 𝑇
𝑥′
= 𝑤 𝑘 𝑇
𝑥′
describes the intersection of 2
hyperplanes in ℝ𝑑+1
(where 𝑥 ∈ ℝ𝑑
)
 Divides ℝ𝑑
into half-spaces; 𝑤 𝑗 𝑇
𝑥′ > 𝑤 𝑘 𝑇
𝑥′ on one side,
vice versa on the other side.
 If 𝑤 𝑗 𝑇
𝑥′
= 𝑤 𝑘 𝑇
𝑥′
= max
𝑖
𝑤 𝑖 𝑇
𝑥′
, this is a decision
boundary!
 Illustrative figures follow

 Below: 𝑑 = 1, 𝑚 = 4. max
𝑖
𝑤 𝑖 𝑇
𝑥′
is graphed.

 Below: 𝑑 = 2, 𝑚 = 3. Lines are decision
boundaries 𝑤 𝑗 𝑇
𝑥 = 𝑤 𝑘 𝑇
𝑥 = max
𝑖
𝑤 𝑖 𝑇
𝑥

 For 𝑚 = 2 (binary classification), we get the
scalar version by setting 𝑤 = 𝑤 1
− 𝑤 0
 𝑓1 𝑥; 𝐖 = 𝕀 arg max
𝑖
𝑤 𝑖 𝑇
𝑥′
= 1
= 𝕀 𝑤 1 𝑇
𝑥′
> 𝑤 0 𝑇
𝑥′
= 𝕀 𝑤 1
− 𝑤 0 𝑇
𝑥′
> 0

FITTING A LINEAR CLASSIFIER
 𝑓 𝑥; 𝑤 = 𝕀 𝑤𝑇
𝑥′
> 0
 How do we turn this into something continuous and
differentiable?
 We really want to replace the indicator function 𝕀 with a
smooth function indicating the probability of whether
𝑦 is 0 or 1, based on the value of 𝑤𝑇
𝑥′

PROBABILISTIC INTERPRETATION
 Interpreting 𝑤𝑇
𝑥′
 𝑤𝑇
𝑥′ large and positive
 ℙ 𝑦 = 0 ≪ ℙ[𝑦 = 1]
 𝑤𝑇
𝑥′ large and negative
 ℙ 𝑦 = 0 ≫ ℙ[𝑦 = 1]
 𝑤𝑇
𝑥′ small
 ℙ 𝑦 = 0 ≈ ℙ[𝑦 = 1]

 We therefore use the probability functions
 𝑝0 𝑥; 𝑤 = ℙ 𝑦 = 0 =
1
1+exp(𝑤𝑇𝑥′)
 𝑝1 𝑥; 𝑤 = ℙ 𝑦 = 1 =
exp(𝑤𝑇𝑥′)
1+exp(𝑤𝑇𝑥′)
 If 𝑤 = 𝑤 1
− 𝑤 0
as before, this is just
𝑝𝑘 𝑥; 𝑤 = ℙ 𝑦 = 𝑘 =
exp 𝑤 𝑘 𝑇
𝑥′
exp 𝑤 0 𝑇
𝑥′ +exp 𝑤 1 𝑇
𝑥′

 In the more general 𝑚-class case, we have
𝑝𝑘 𝑥; 𝐖 = ℙ 𝑦𝑘 = 1 =
exp 𝑤 𝑘 𝑇
𝑥′
𝑖=1
𝑚
exp 𝑤 𝑖 𝑇
𝑥′
 This is called the softmax activation and will be used
to define our loss function

THE CROSS-ENTROPY LOSS
 We want to heavily penalize cases where 𝑦𝑘 = 1 with
𝑝𝑘 𝑥; 𝐖 ≪ 1
 This leads us to define the cross-entropy loss as
follows:
𝐽 𝐖; 𝐗, 𝐘 = −
1
𝑁
𝑖=1
𝑁
𝑘=1
𝑚
𝑦𝑘
𝑖
ln 𝑝𝑘 𝑥 𝑖
; 𝐖

MINIMIZING CROSS-ENTROPY
 As with mean-squared error, the cross-entropy loss is
convex and differentiable 
 That means that we can use gradient descent to
converge to a global minimum!
 This global minimum defines the best possible linear
classifier with respect to the cross-entropy loss and the
data set given

SUMMARY
 Basic process of constructing a machine learning model
 Choose an analytically well-behaved loss function that
represents some notion of error for your task
 Use gradient descent to choose model parameters that
minimize that loss function for your data set
 Examples: linear regression and mean squared error,
linear classification and cross-entropy

NEXT TIME
 Gradient of the cross-entropy loss
 Neural networks
 Backpropagation algorithm for gradient
descent

Machine learning introduction lecture notes

More Related Content

Similar to Machine learning introduction lecture notes

Recently uploaded

Machine learning introduction lecture notes

Editor's Notes