Embed presentation
Downloaded 17 times






![Formula:
0 1 2 3 4
1 0 4 8(1)
2 0 2 10(3
)
3 0 6
4 0 3
5 0
C[1,2]=
K=1
C[1,0]+C[2,2]=0+2=2---------
ROOT(1)
K=2
C[1,1]+C[3,2]=4+0=4
+ 6===8
C[2,3]=
I=2
J=3
K=2
C[2,1]+C[3,3]=0+6=6
K=3
C[2,2]+C[4,3]=2+0=2
+8===10](https://image.slidesharecdn.com/lecture-optimalbinarysearchtreeautosaved-200424135015/75/Lecture-optimal-binary-search-tree-13-2048.jpg)
![0 1 2 3 4
1 0 4 8(1) 20(3
)
26(3
)
2 0 2 10(3
)
16(3
)
3 0 6 12(3
)
4 0 3
5 0
C[3,4]
k=3
C[3,2]+C[4,4]=0+3=3
i=3,j=4 k=4
C[3,3]+C[5,4]=6+0=6
Frequency=9
=====12ROOT(3)
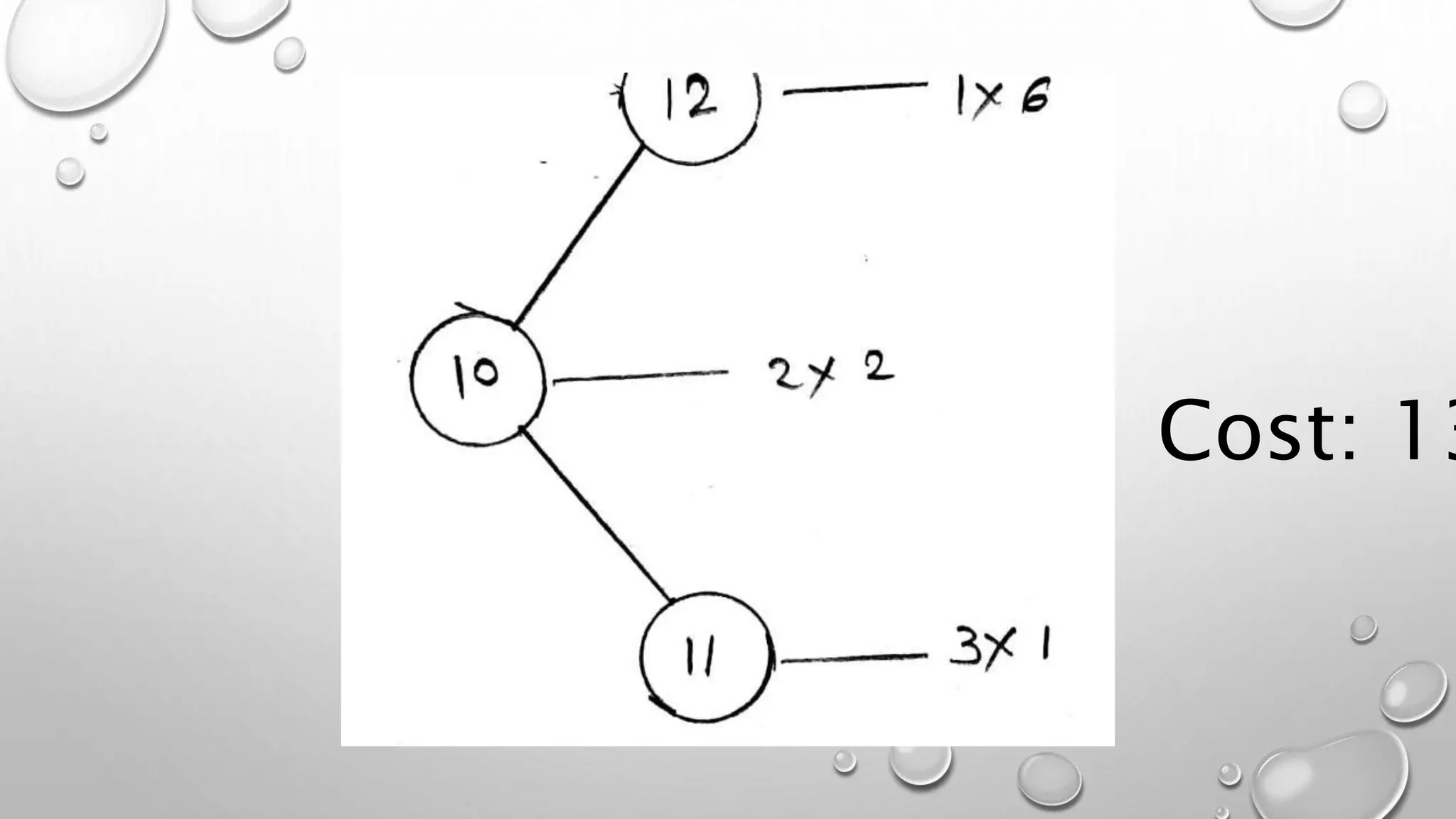
Minimum cost =2
16
10 21
12 Optimal Binary search
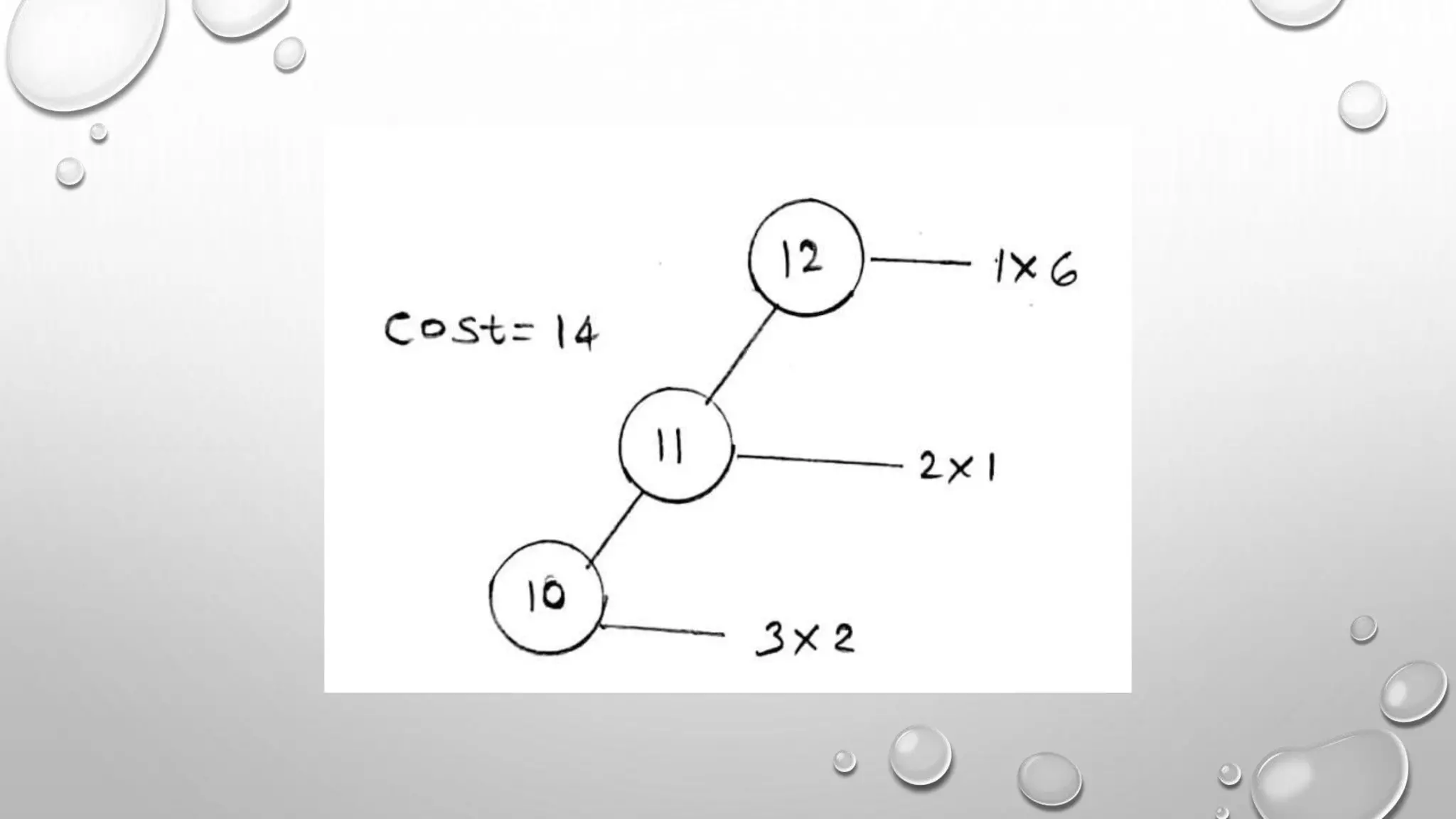
1*6=6
2*4+2*3=14
3*2=6](https://image.slidesharecdn.com/lecture-optimalbinarysearchtreeautosaved-200424135015/75/Lecture-optimal-binary-search-tree-14-2048.jpg)


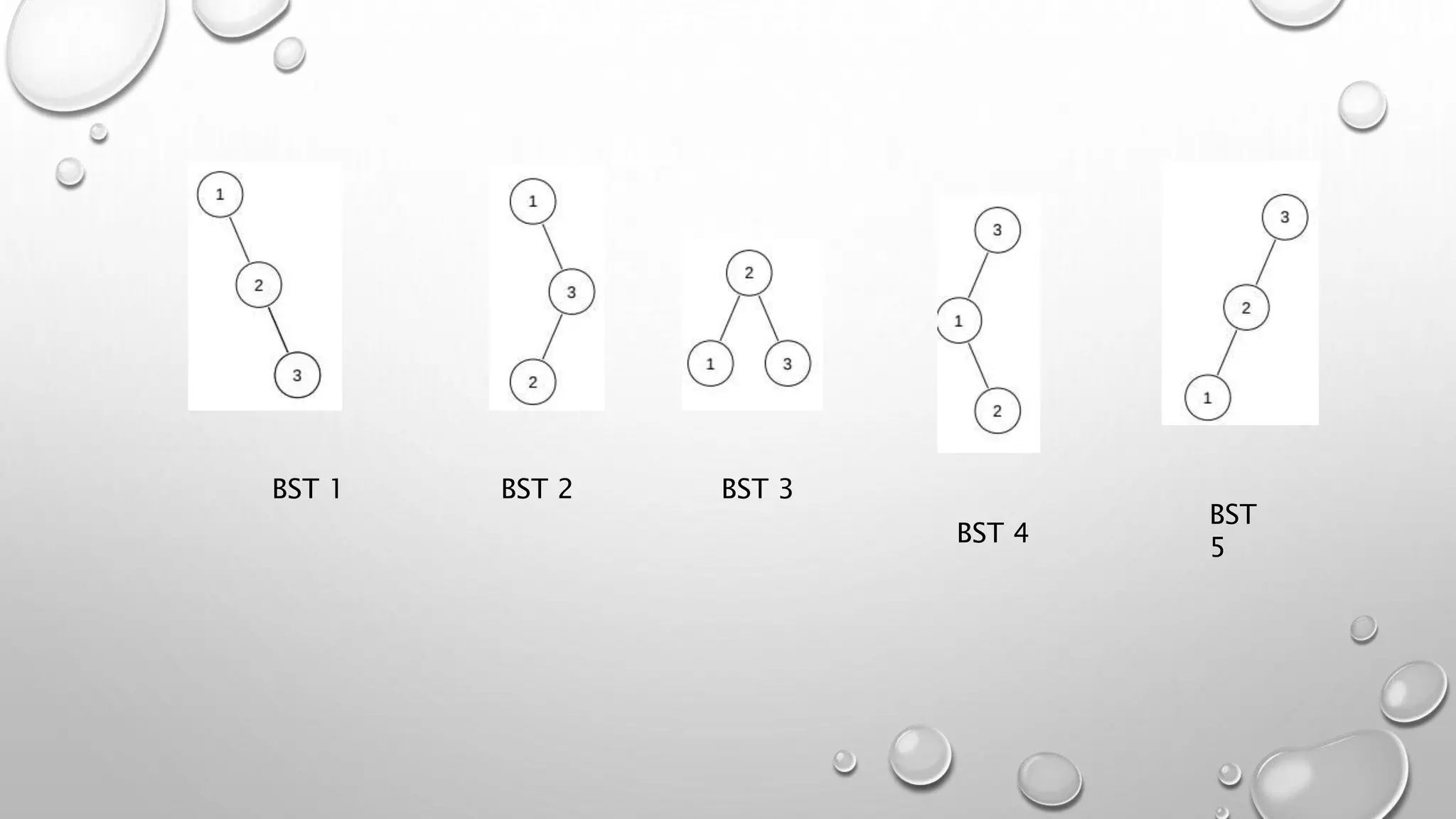
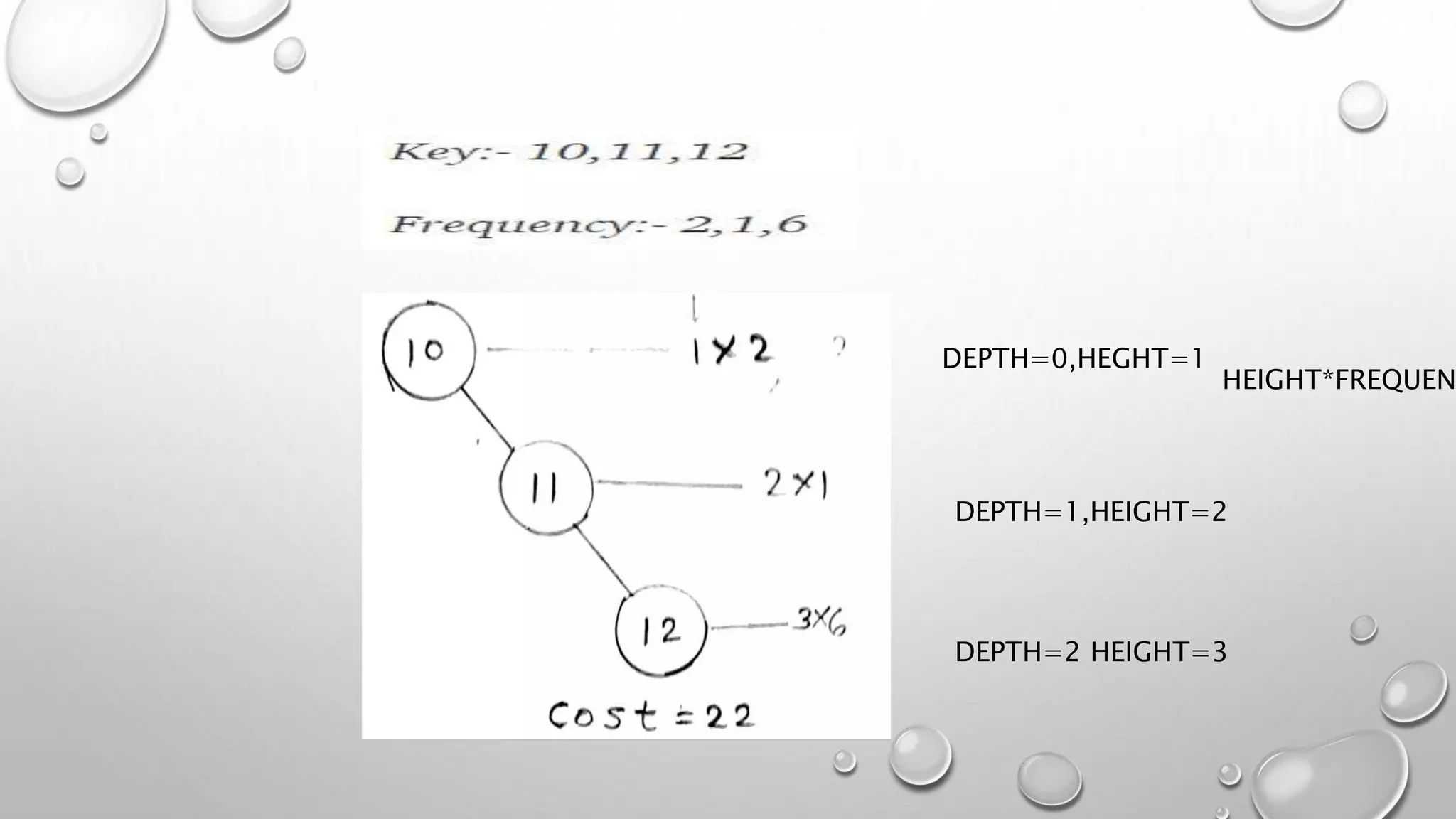
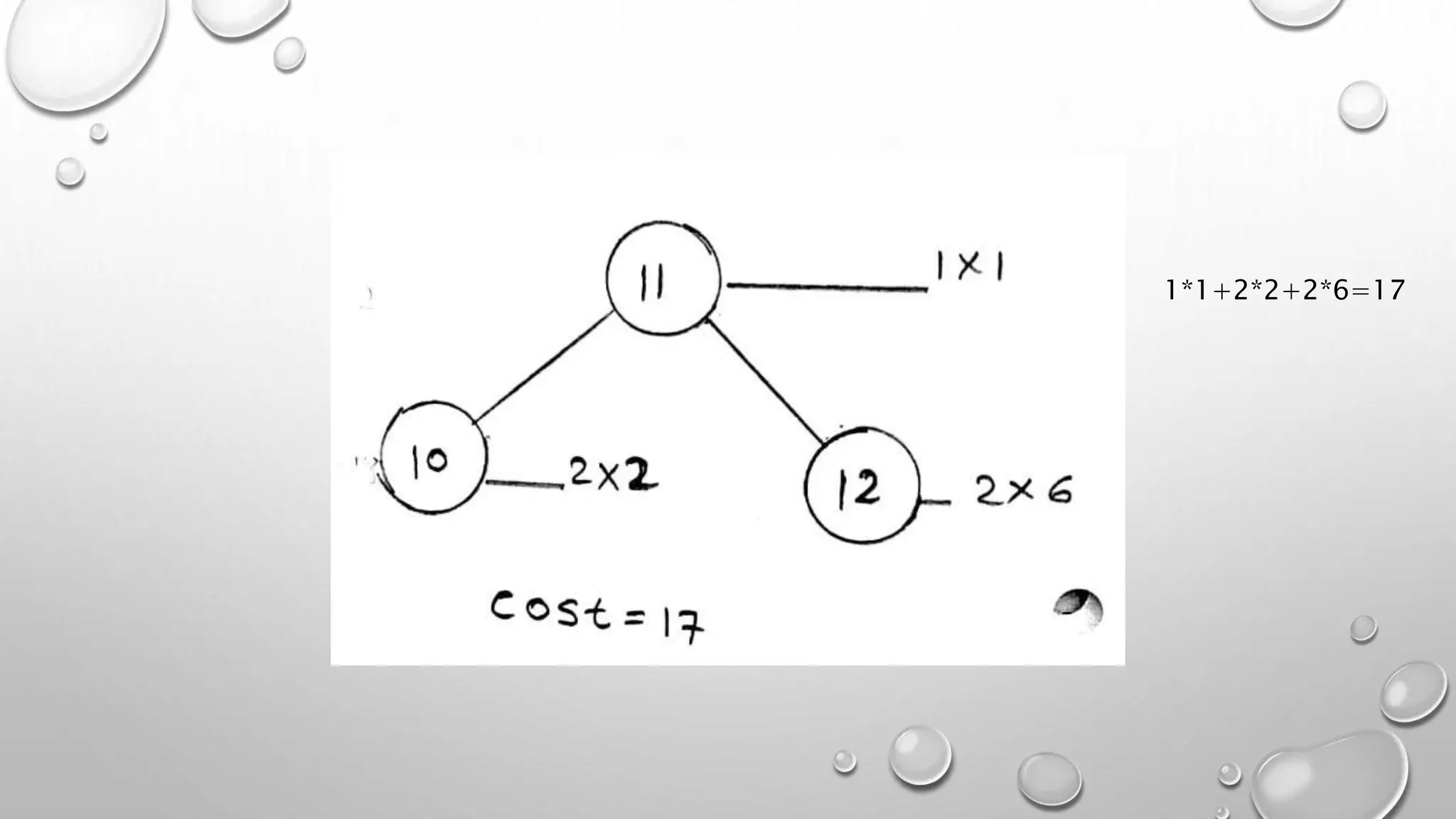
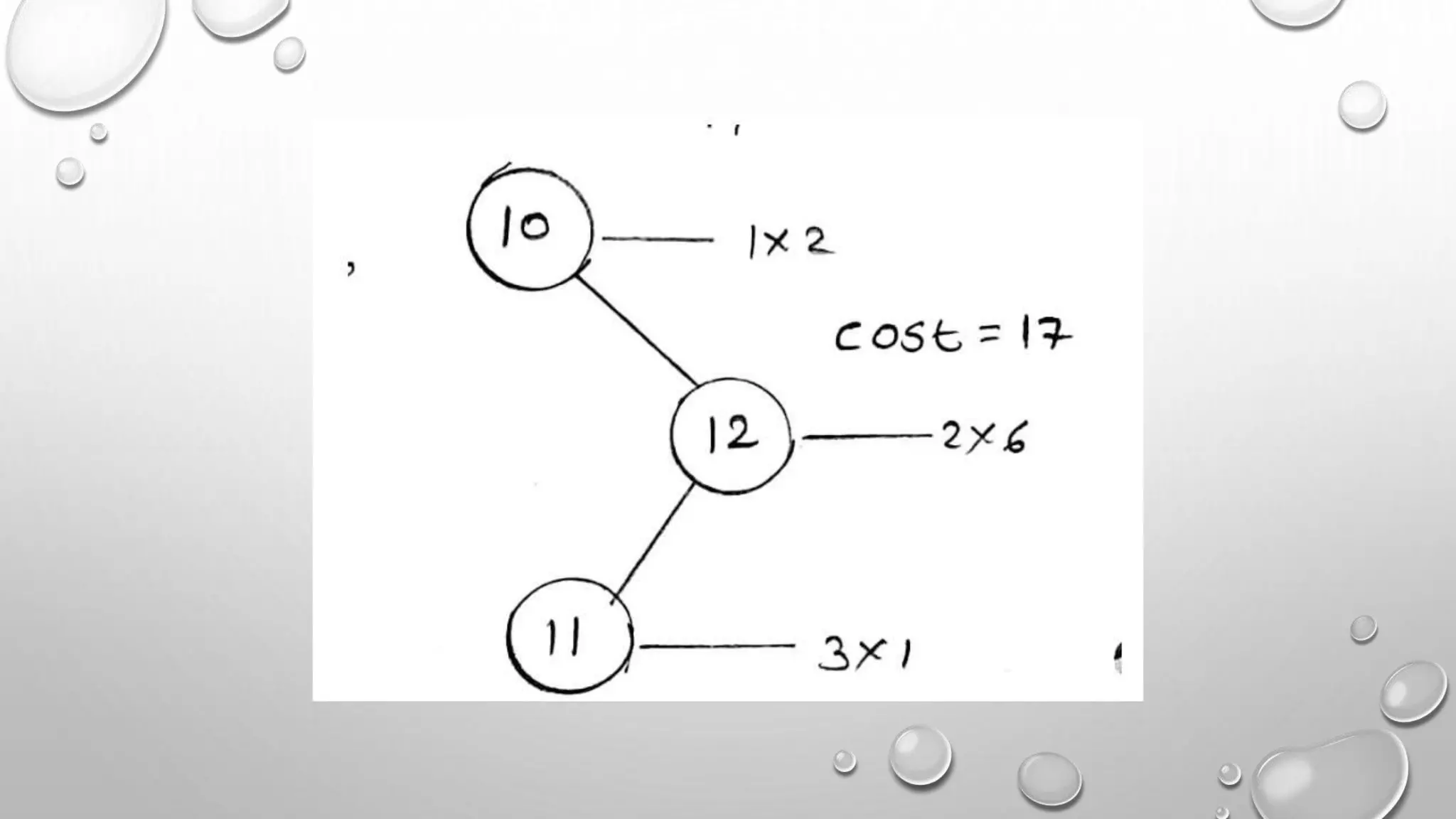
This document discusses optimal binary search trees and provides an example problem. It begins with basic definitions of binary search trees and optimal binary search trees. It then shows an example problem with keys 1, 2, 3 and calculates the cost as 17. The document explains how to use dynamic programming to find the optimal binary search tree for keys 10, 12, 16, 21 with frequencies 4, 2, 6, 3. It provides the solution matrix and explains that the minimum cost is 2 with the optimal tree as 10, 12, 16, 21.












![Formula:
0 1 2 3 4
1 0 4 8(1)
2 0 2 10(3
)
3 0 6
4 0 3
5 0
C[1,2]=
K=1
C[1,0]+C[2,2]=0+2=2---------
ROOT(1)
K=2
C[1,1]+C[3,2]=4+0=4
+ 6===8
C[2,3]=
I=2
J=3
K=2
C[2,1]+C[3,3]=0+6=6
K=3
C[2,2]+C[4,3]=2+0=2
+8===10](https://image.slidesharecdn.com/lecture-optimalbinarysearchtreeautosaved-200424135015/75/Lecture-optimal-binary-search-tree-13-2048.jpg)
![0 1 2 3 4
1 0 4 8(1) 20(3
)
26(3
)
2 0 2 10(3
)
16(3
)
3 0 6 12(3
)
4 0 3
5 0
C[3,4]
k=3
C[3,2]+C[4,4]=0+3=3
i=3,j=4 k=4
C[3,3]+C[5,4]=6+0=6
Frequency=9
=====12ROOT(3)
Minimum cost =2
16
10 21
12 Optimal Binary search
1*6=6
2*4+2*3=14
3*2=6](https://image.slidesharecdn.com/lecture-optimalbinarysearchtreeautosaved-200424135015/75/Lecture-optimal-binary-search-tree-14-2048.jpg)

