L1 intro2 supervised_learning

Some slides were adapted/taken from various sources, including Prof. Andrew Ng’s Coursera Lectures,
Stanford University, Prof. Kilian Q. Weinberger’s lectures on Machine Learning, Cornell University, Prof.
Sudeshna Sarkar’s Lecture on Machine Learning, IIT Kharagpur, Prof. Bing Liu’s lecture, University of
Illinois at Chicago (UIC), CS231n: Convolutional Neural Networks for Visual Recognition lectures,
Stanford University and many more. We thankfully acknowledge them. Students are requested to use
this material for their study only and NOT to distribute it.

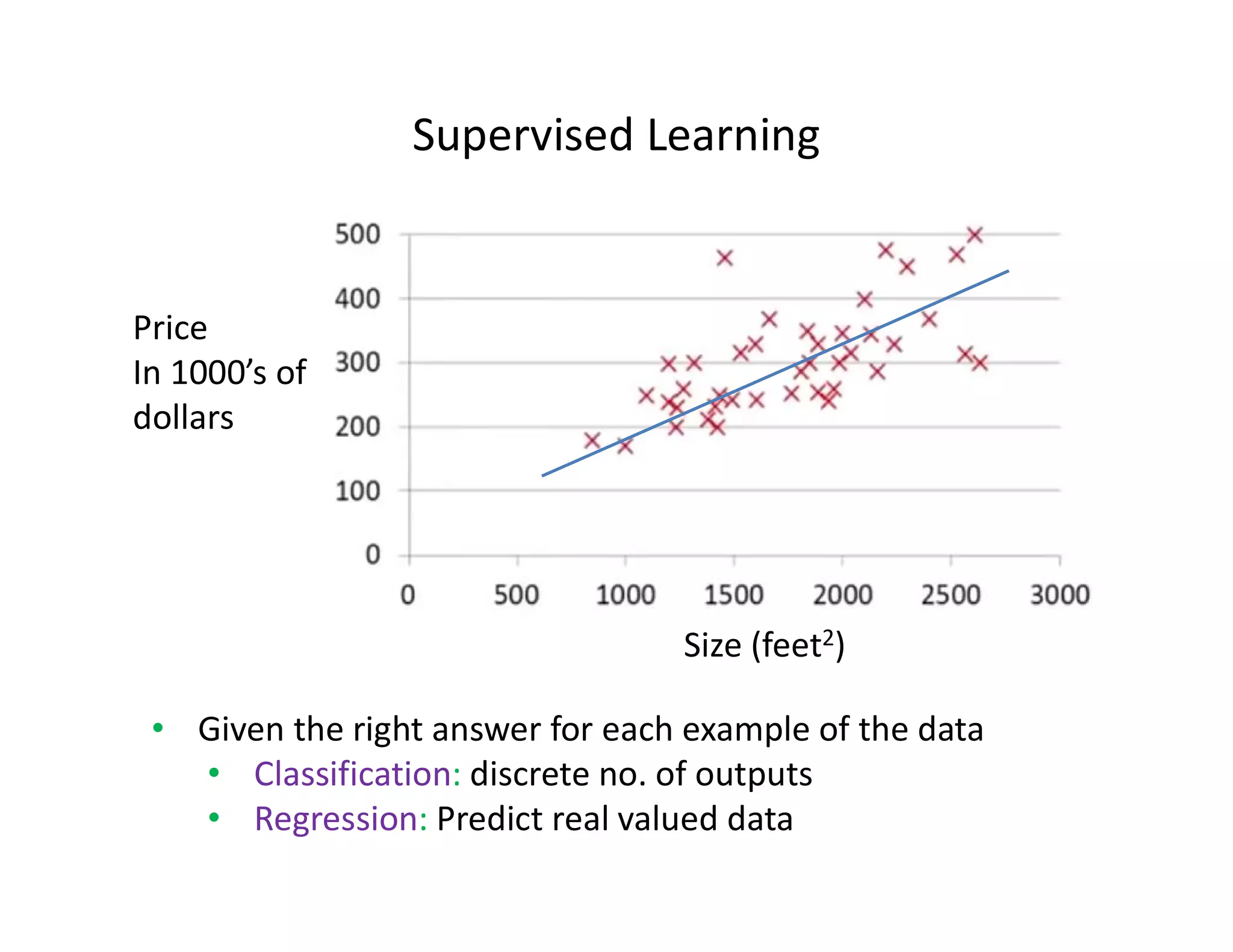
Supervised Learning
Size (feet2)
Price
In 1000’s of
dollars
• Given the right answer for each example of the data
• Classification: discrete no. of outputs
• Regression: Predict real valued data

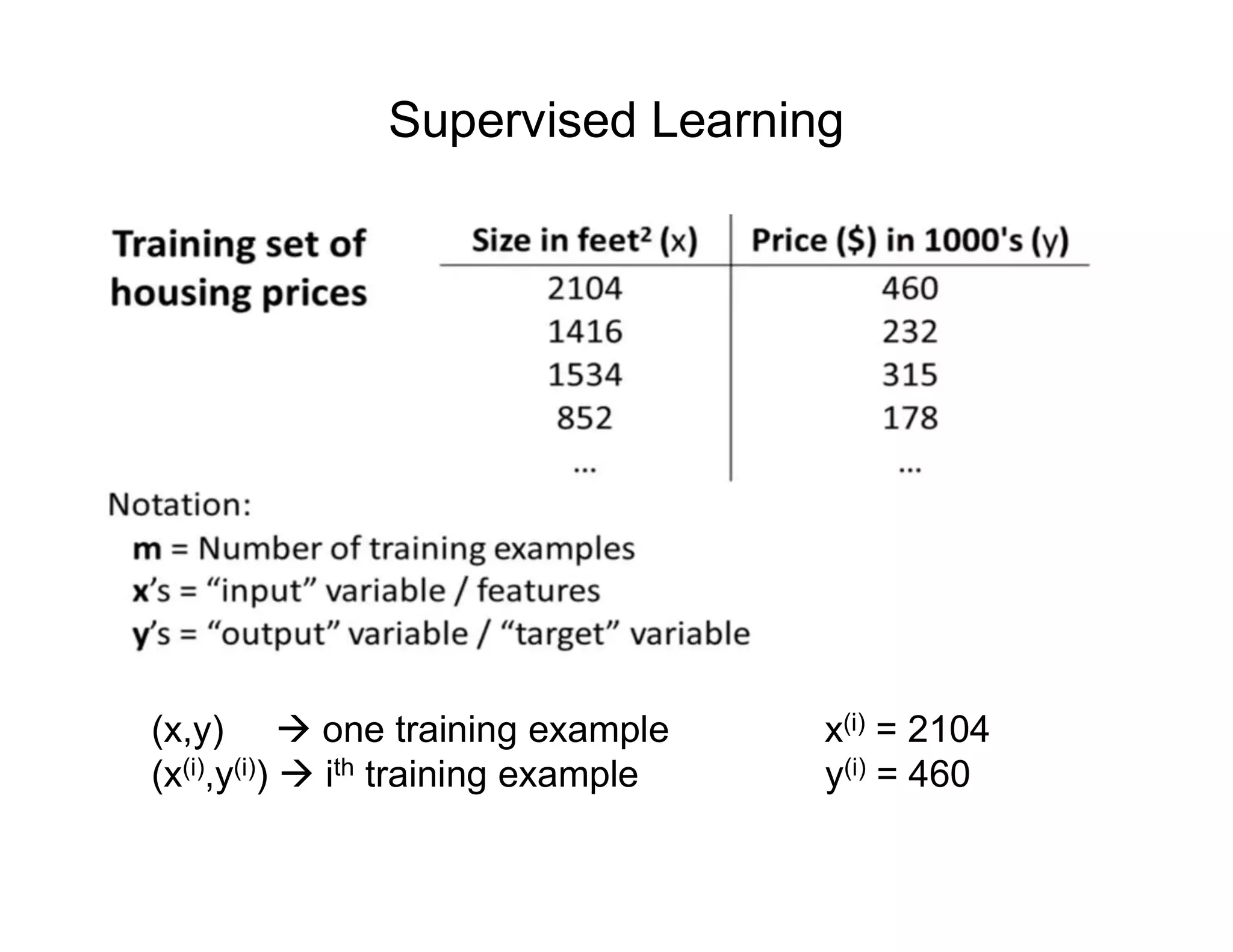
(x,y)  one training example x(i) = 2104
(x(i),y(i))  ith training example y(i) = 460
Supervised Learning

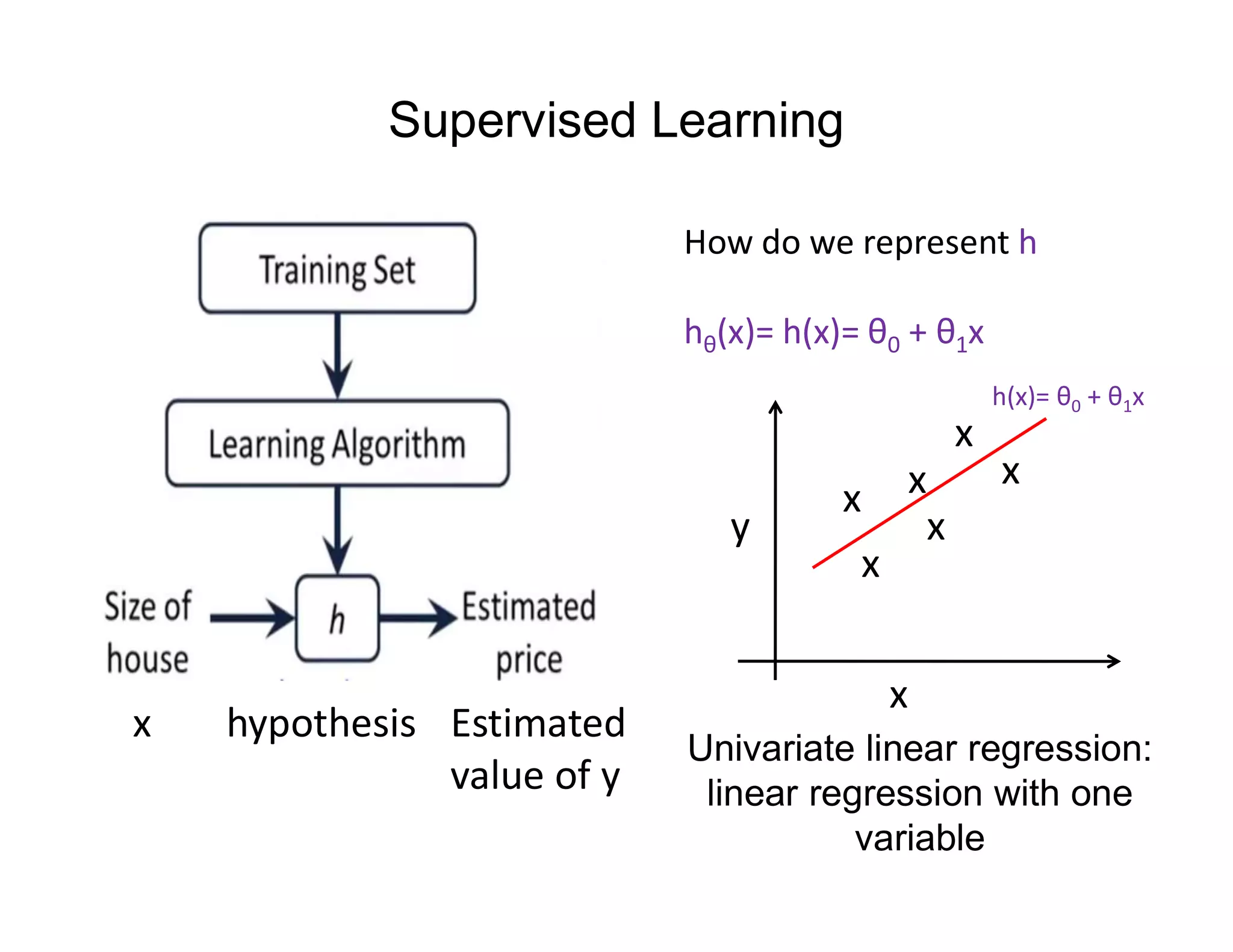
x hypothesis Estimated
value of y
How do we represent h
hθ(x)= h(x)= θ0 + θ1x
x
x
x
x x
x
x
y
h(x)= θ0 + θ1x
Univariate linear regression:
linear regression with one
variable
Supervised Learning

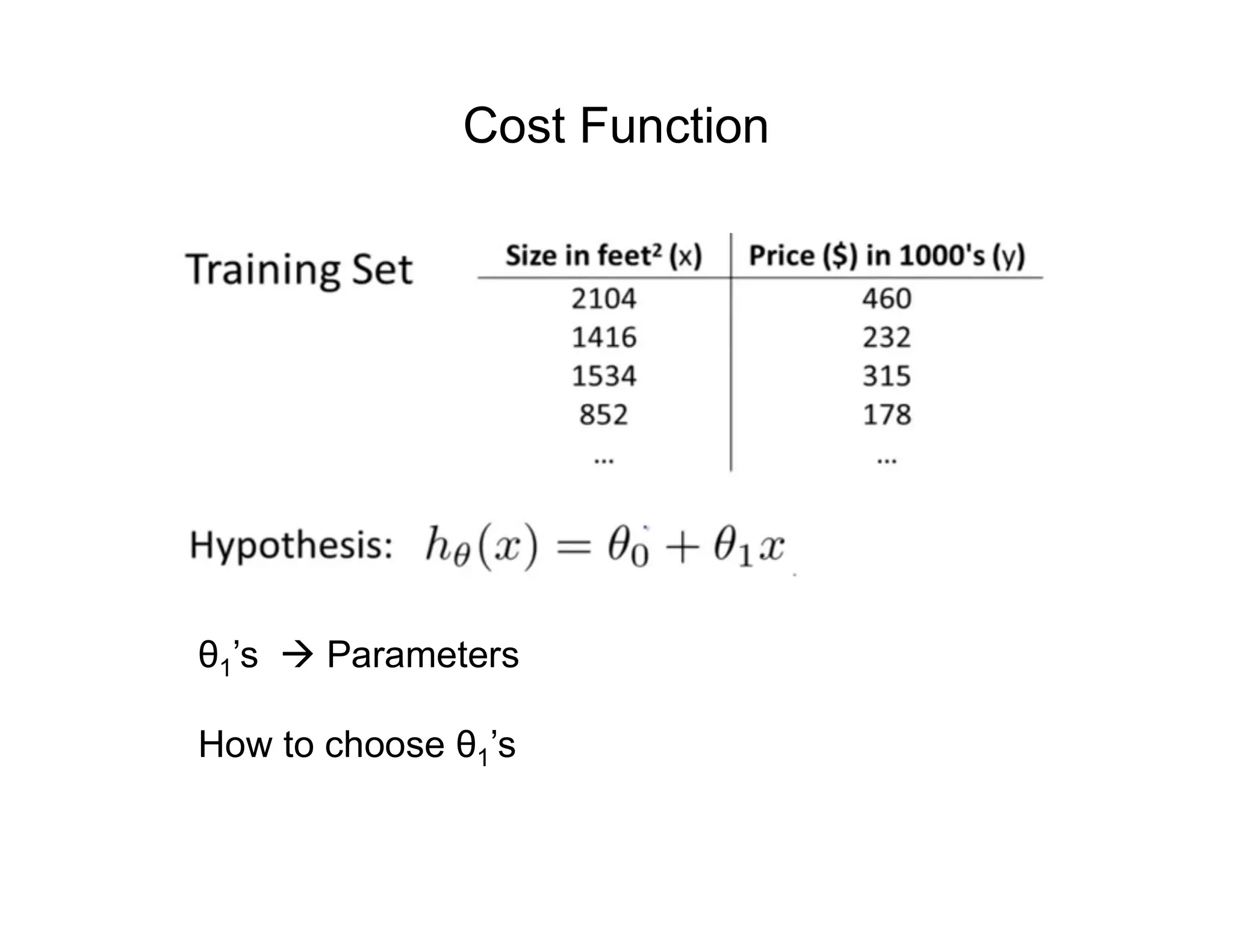
Cost Function
θ1’s  Parameters
How to choose θ1’s

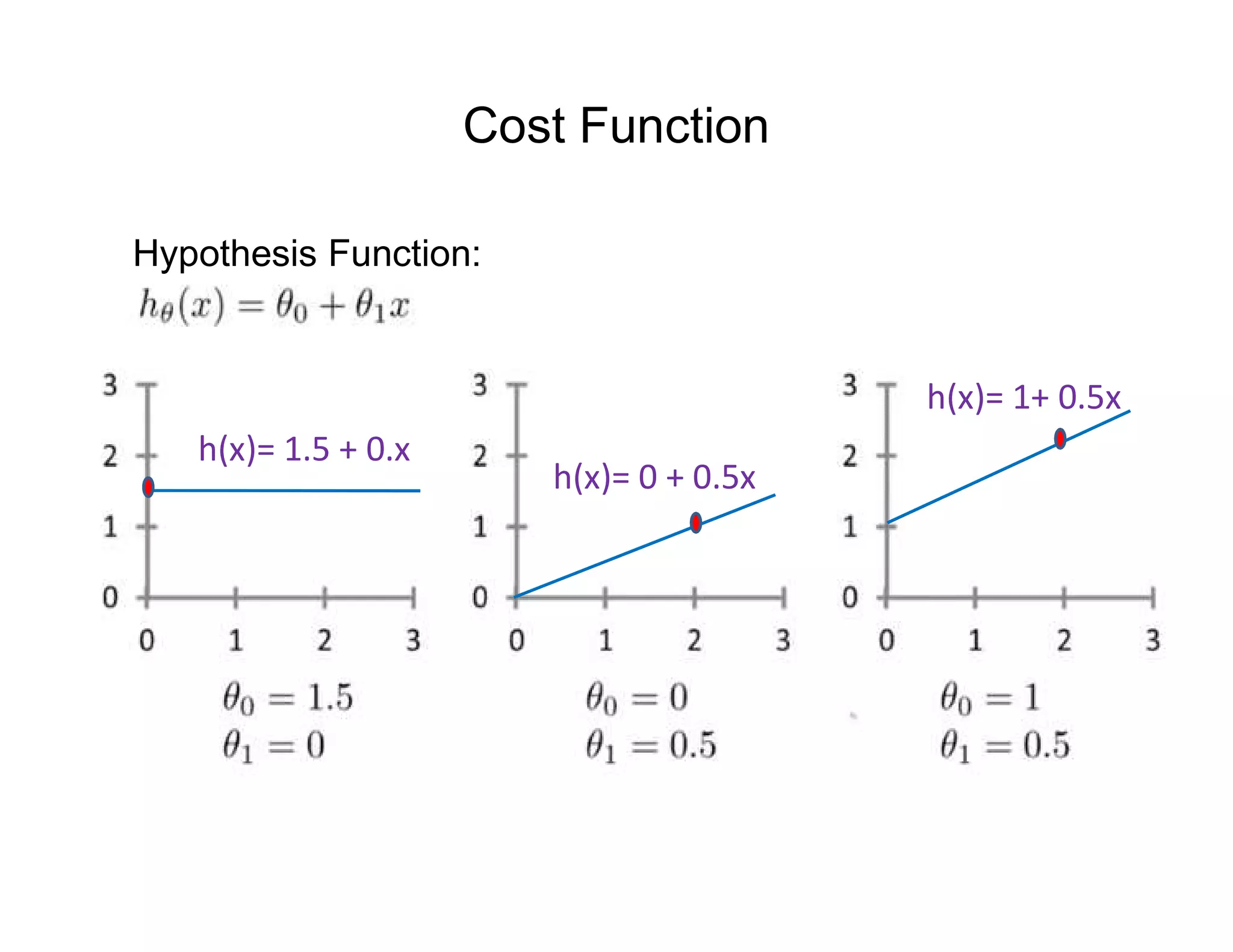
Cost Function
h(x)= 1.5 + 0.x
h(x)= 0 + 0.5x
h(x)= 1+ 0.5x
Hypothesis Function:

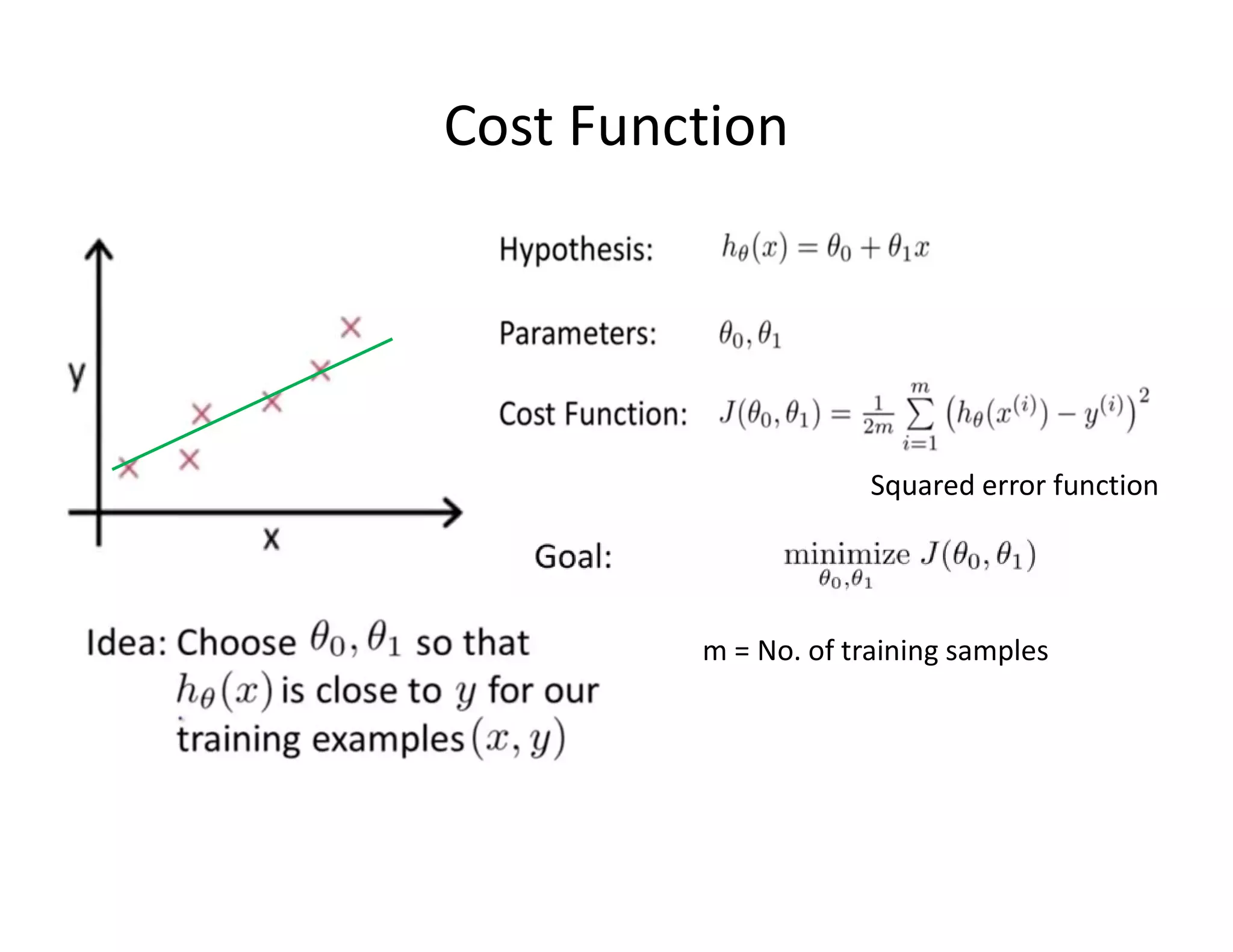
Cost Function
m = No. of training samples
Squared error function

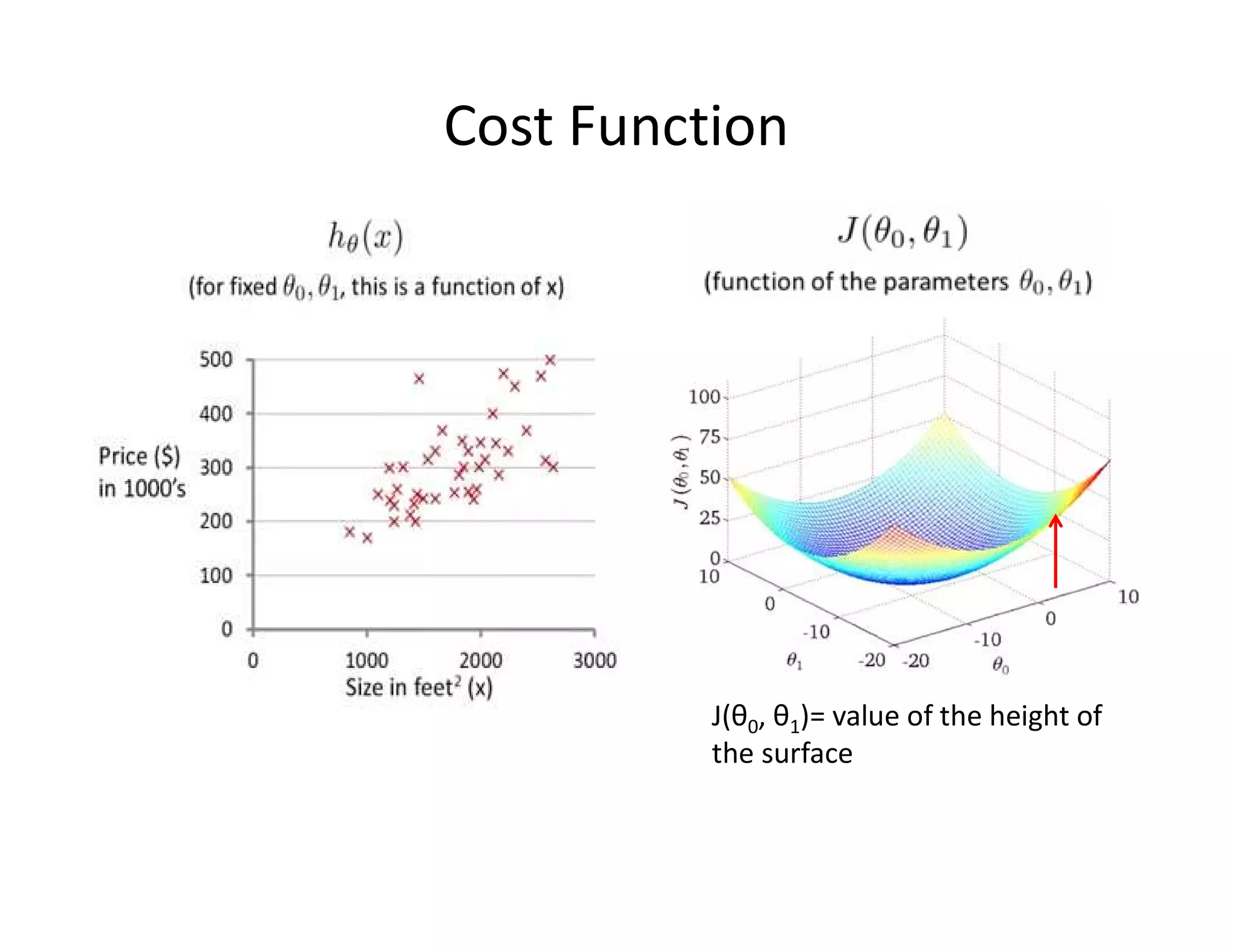
J(θ0, θ1)= value of the height of
the surface
Cost Function

Contour Plots / Figures
J(θ0, θ1)
X
X
X
(θ0, θ1) = (800, - 0.125)

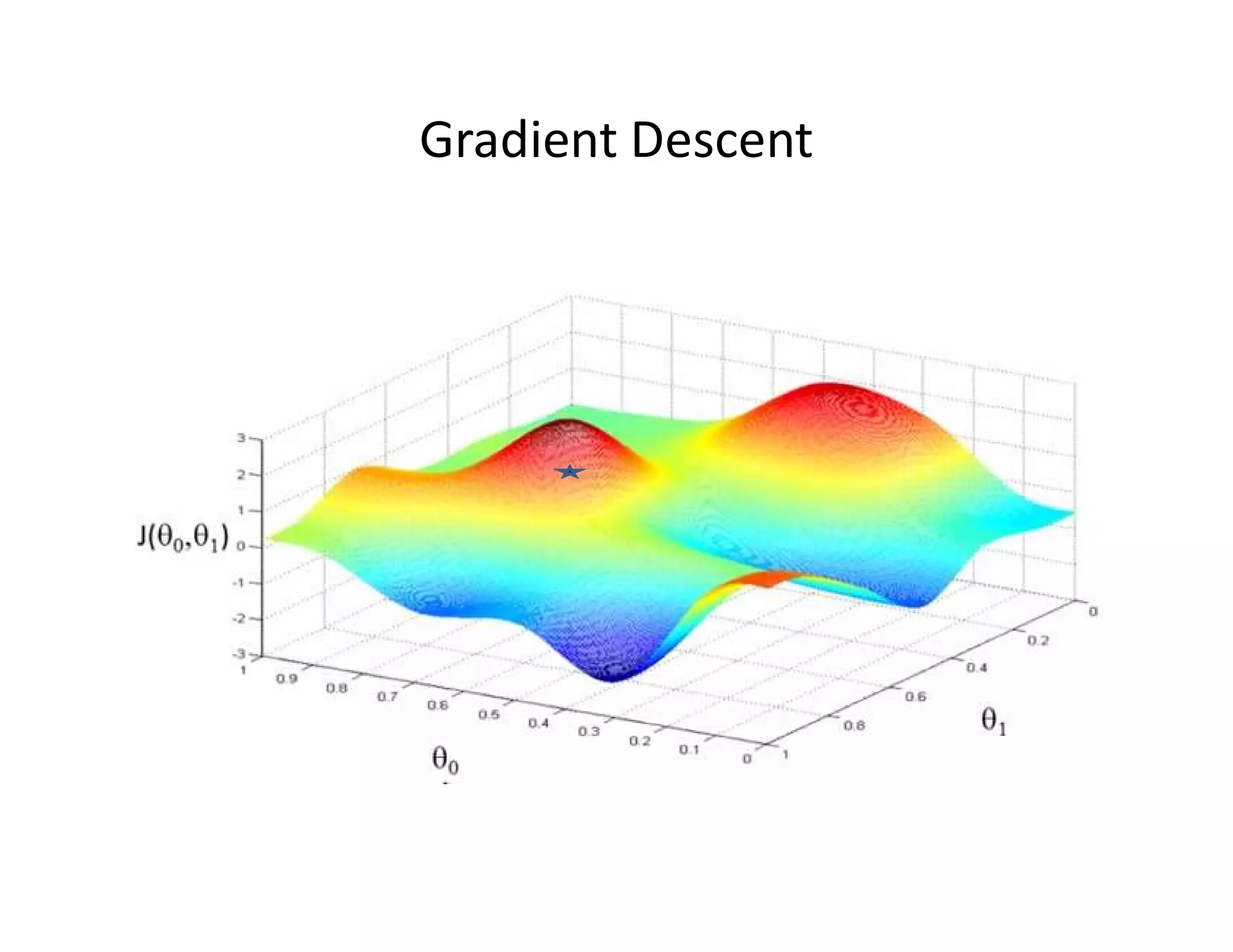
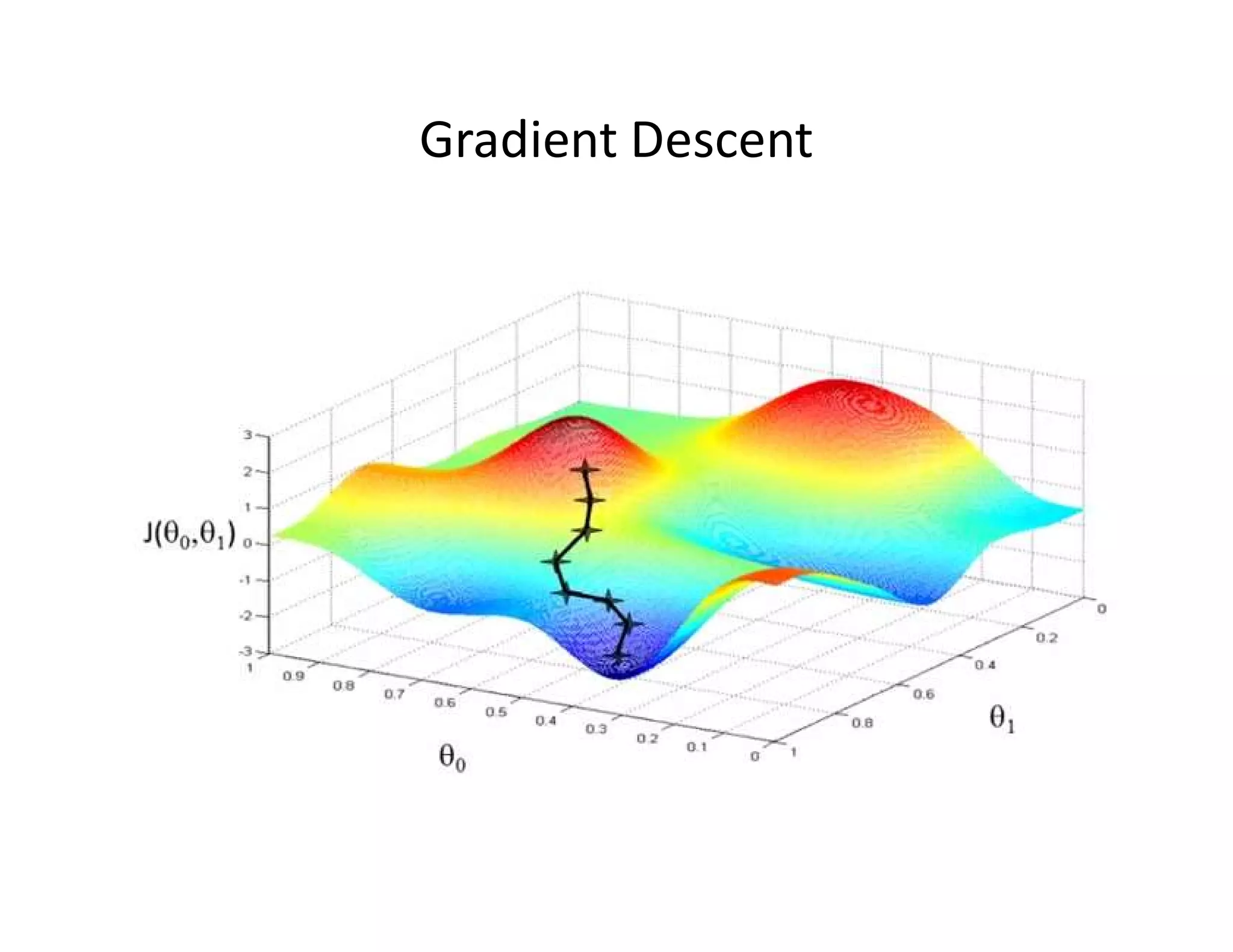
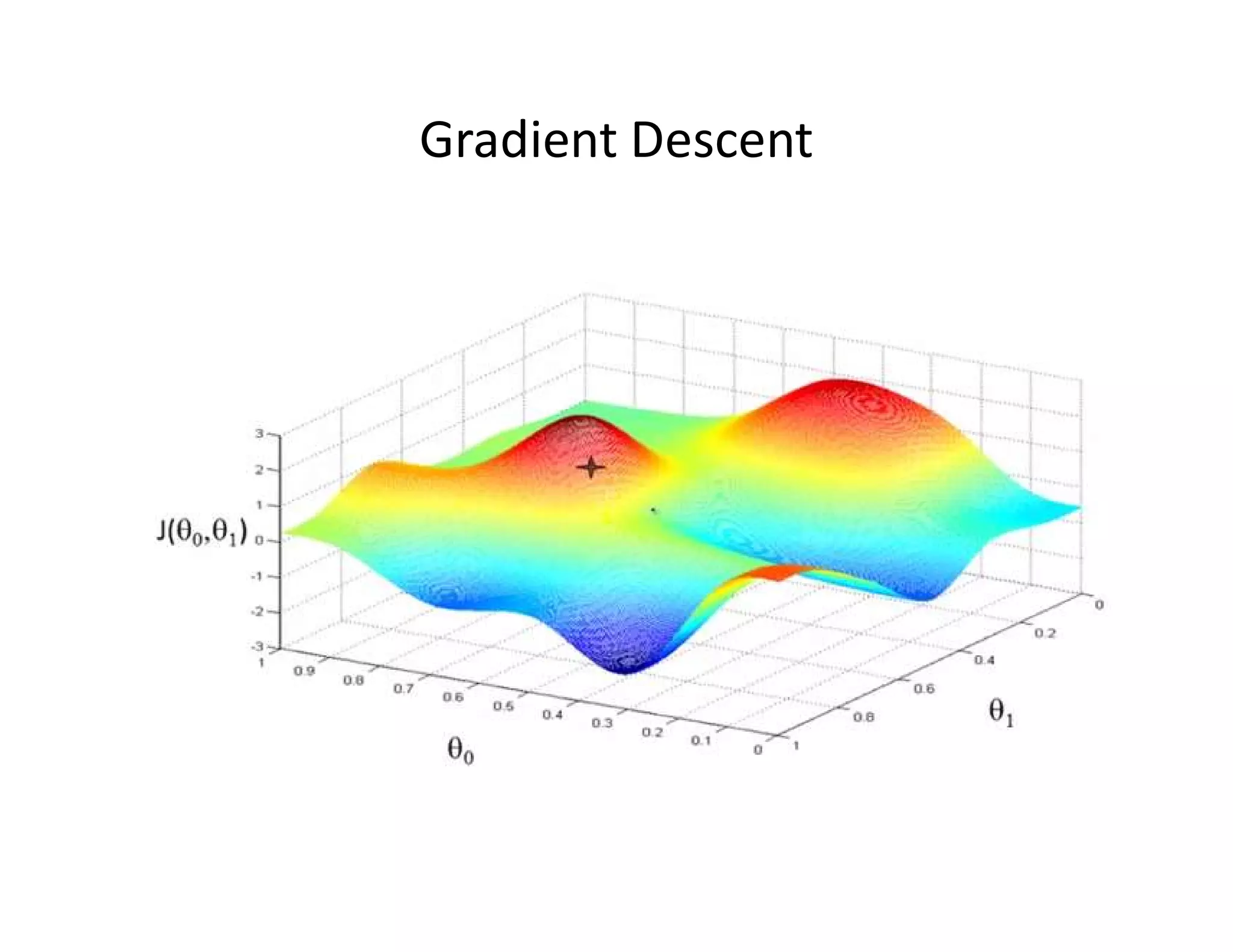
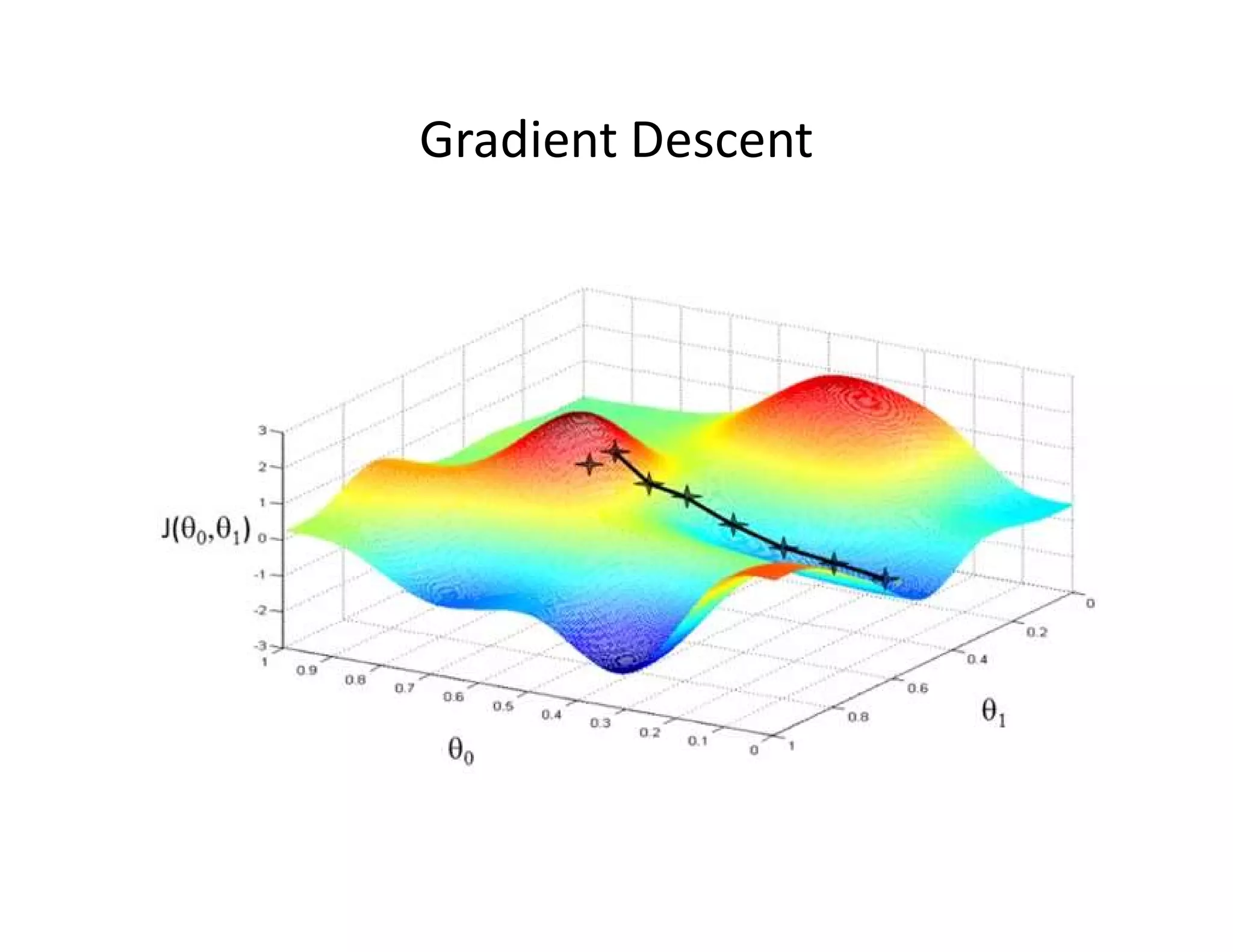
Gradient Descent
• Let some function
• We have to find
• Start with some (θ0, θ1) (let say θ0=0, θ1=0)
• Keep changing θ0, θ1 to reduce
until we hopefully end up at a minimum

Gradient Descent Algorithm
α = learning rate
Implication of α = it controls how bigger steps we are taking over
gradient descent

• Let take a single variable
• we have to minimize
where θ1 ϵ R
• So the GD algorithm becomes

≥ 0
(slope is positive)
θ1 is reduced
≤ 0
(slope is negative)
θ1
Local minima
Local minima

θ1
Local minima
Local minima

Multivariate Linear Regression
Univariate Hypothesis function:
Multivariate Hypothesis function:
where x0 = 1

Multivariate Gradient Descent
J(Ɵ)
Ɵ : n+1 dimensional vector
J(Ɵ)

Feature Scaling
θ1
θ2
θ1
θ2
J(θ)
J(θ)
0 ≤ x1 ≤ 1 0 ≤ x2 ≤ 1

Logistic Regression: Classification
hθ(x)= θTx
hθ(x)= θTx
0.5

Logistic Regression
0.5
Linear regression for classification problem is not always good

Logistic Regression Model
g(z)
Sigmoid Function or Logistic function
Linear Regression:
Logistic Regression:
hθ(x)= θTx

Hypothesis Representation
estimated probability that y=1 on input x
Example: if
0.7
There is 70% chance that the object is salient
p(y=1|x, Ɵ)
i.e. “probability that y=1, given x, parameterized by Ɵ”
p(y=0|x; Ɵ) + p(y=1|x; Ɵ) = 1
p(y=0|x; Ɵ) = 1 - p(y=1|x; Ɵ)

Decision Boundary
Predict “y = 0” if
Decision boundary is a property of hypothesis function NOT of a data set

Non-Linear Decision Boundary
Decision Boundary
y0
y1
y1
y1
y1
Again, decision boundary is a property of hypothesis function NOT
of a data set

Cost Function
• Optimization objective of the cost function

So,
Let,
where, for logistic regression
Cost Function

Non convex
J(Ɵ)
J(Ɵ)
Logistic Regression Linear Regression
Cost Function
Ɵ
Ɵ

Cost Function: Logistic Regression
0 1
If y = 1
Cost

0 1
If y = 0
Cost
It can be shown that the overall cost function is convex function and local optimum
free. But details of such convexity analysis is beyond of the scope of this course.
Cost =0 if y=0, hƟ(x) = 0
But as hƟ(x)  1
Cost  ꝏ
Captures intuition that if hƟ(x) = 1,
(predict P(y=0|x; Ɵ) = 1), but y = 0,
We will penalize learning algorithm
by a very large cost.

Principle of Maximum Likelihood Estimation
Output:
Obtain
and get Ɵ
For p(y=1|x; Ɵ)
How to minimize J(Ɵ) ?

=
Cost Function and Gradient Descent

For Linear Regression:
For Logistic Regression:
Cost Function and Gradient Descent

• Problems:
– Choosing step size
• too small  convergence is slow and inefficient
• too large  may not converge
– Can get stuck on “flat” areas of function
– Easily trapped in local minima
Gradient descent optimization

Stochastic (definition):
1. involving a random variable
2. involving chance or probability; probabilistic
Stochastic gradient descent

• Application to training a machine learning model:
1. Choose one sample from training set
2. Calculate loss function for that single sample
3. Calculate gradient from loss function
4. Update model parameters a single step based on gradient and
learning rate
5. Repeat from 1) until stopping criterion is satisfied
• Typically entire training set is processed multiple
times before stopping.
• Order in which samples are processed can be fixed or
random.
Stochastic gradient descent

One vs. All (One vs. Rest)
Ɵ
Ɵ
Ɵ

Overfitting
• A hypothesis function h is said to overfit the training data if there is
another hypothesis h’ such that h’ has more error than h on training
data but h’ has less error than h on testing data.
• Learning a classifier that classifies a training data perfectly may not
lead to the classifier with best generalization performance
– There may be noise in training data
– Training data set is too small
• Simplistically, overfitting occurs when model is too complex
whether underfitting occurs when model is too simple.
• Note: Training error is not a good predictor for the testing error.

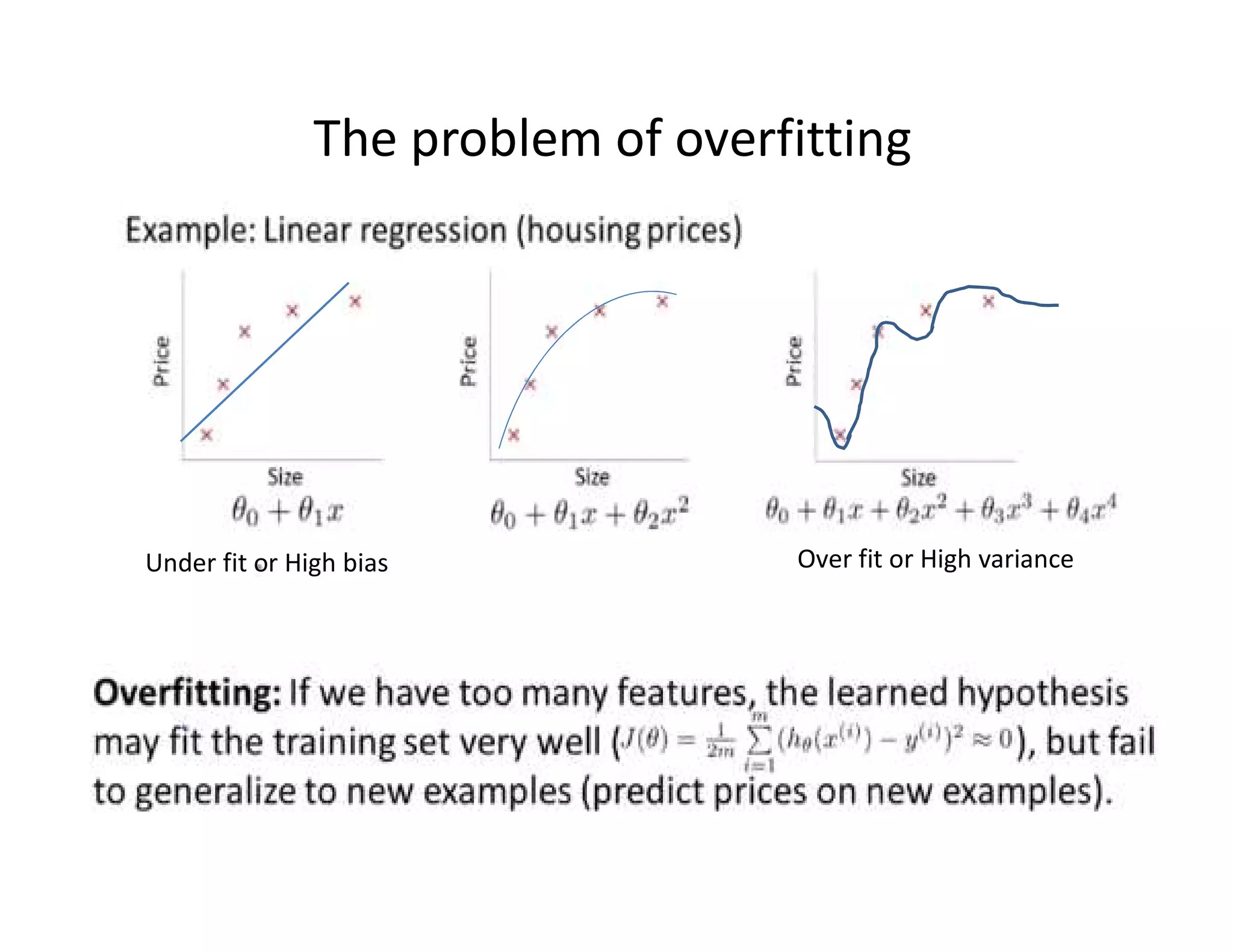
The problem of overfitting
Under fit or High bias Over fit or High variance

Under fit or High bias Over fit or High variance

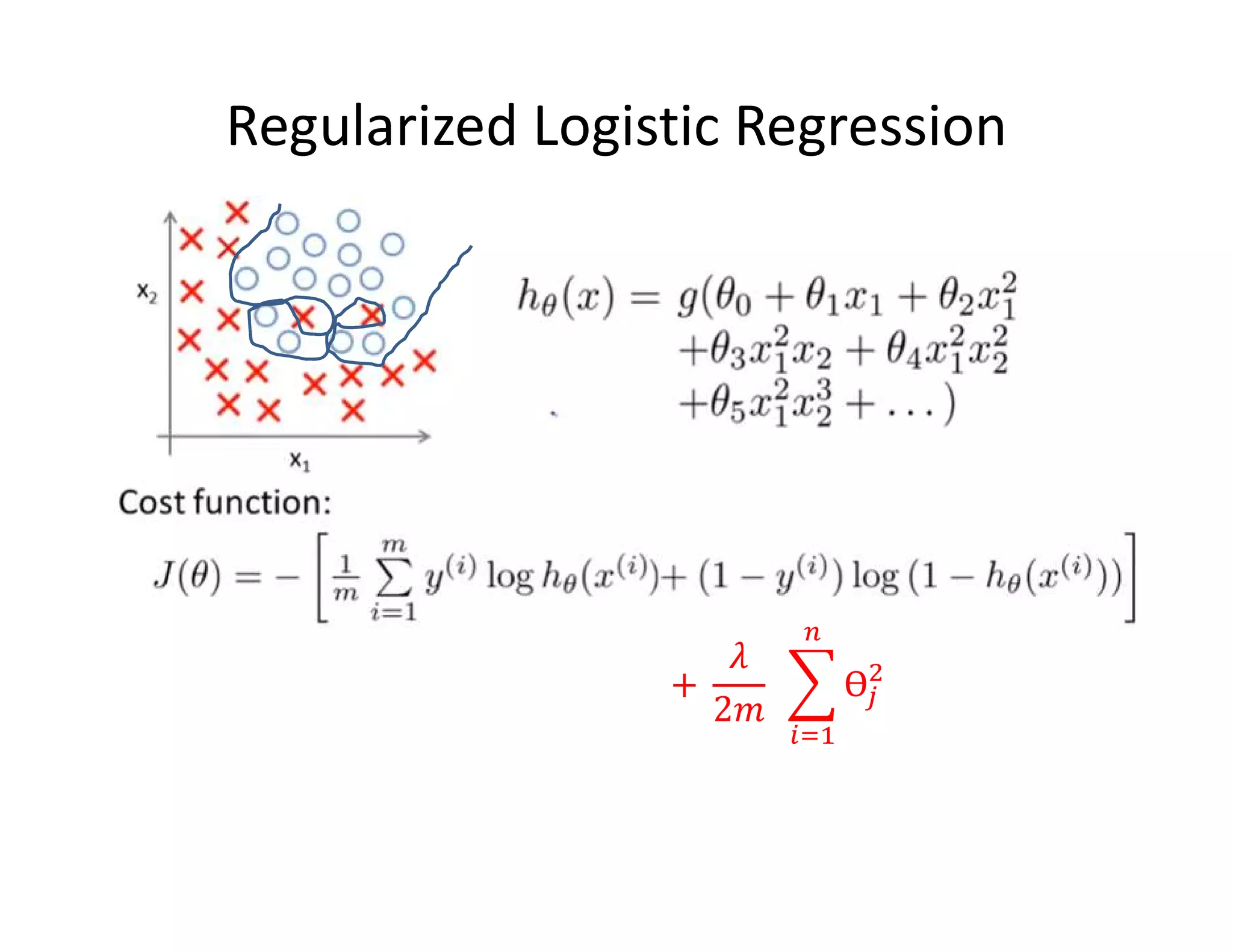
• Let’s consider D, the entire distribution of data, and T, the training
set.
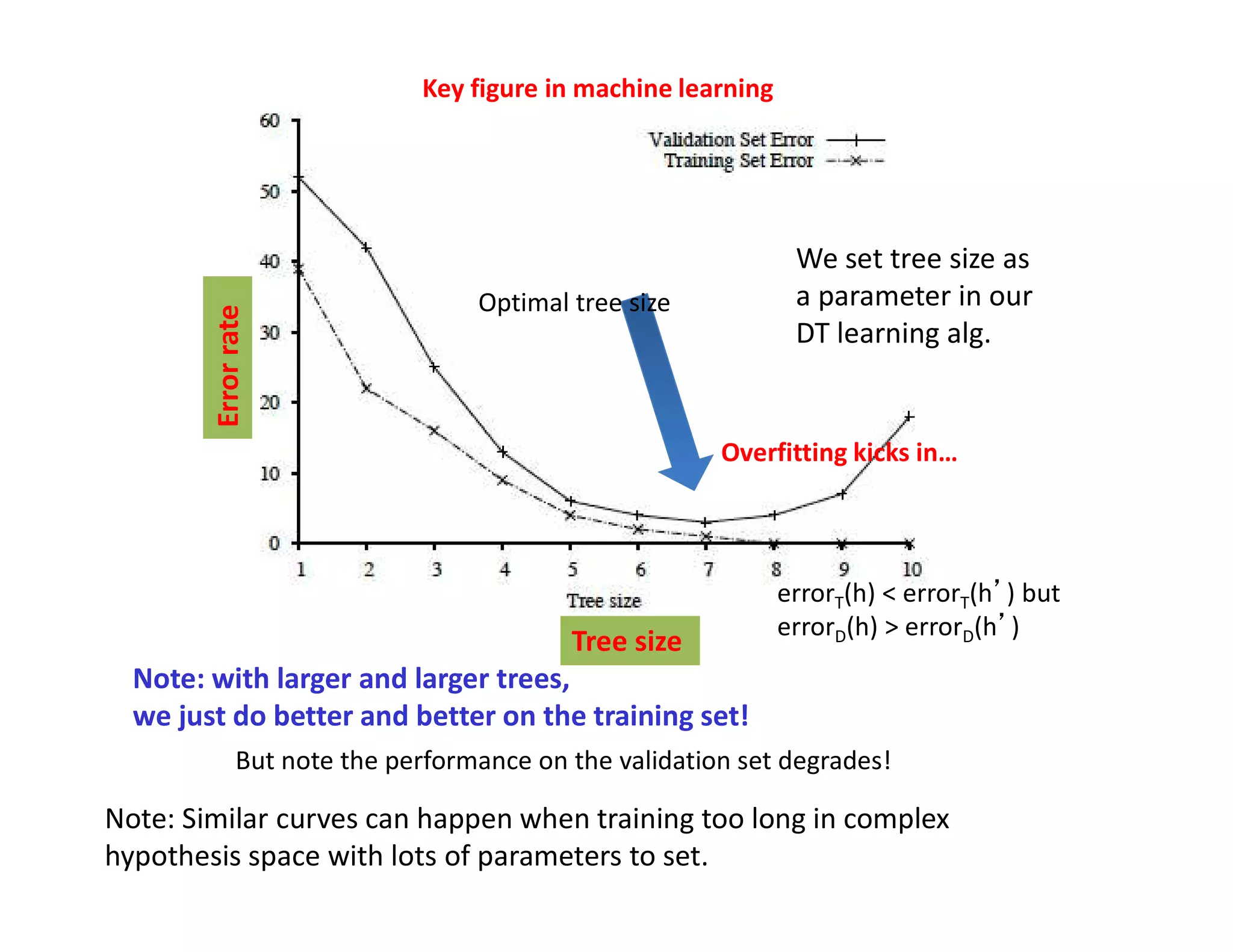
• Hypothesis h  H overfits D if
 h’ h  H such that
(1) errorT(h) < errorT(h’) [i.e. doing well on training set]
but
(2) errorD(h) > errorD(h’)
•What do we care about most (1) or (2)?
•Estimate error on full distribution by using test data set.
Error on test data: Generalization error (want it low!!)
•Generalization to unseen examples/data is what we care about.

• Data overfitting is the arguably the most common pitfall in machine
learning.
• Why?
• Temptation to use as much data as possible to train on. (“Ignore test
till end.” Test set too small.) Data “peeking” not noticed.
• Temptation to fit very complex hypothesis (e.g. large decision tree). In
general, the larger the tree, the better the fit to the training data.
• It’s hard to think of a better fit to the training data as a “worse”
result. Often difficult to fit training data well, so it seems that
“a good fit to the training data means a good result.”

Key figure in machine learning
Note: with larger and larger trees,
we just do better and better on the training set!
We set tree size as
a parameter in our
DT learning alg.
But note the performance on the validation set degrades!
Tree size
Error
rate
Overfitting kicks in…
Optimal tree size
errorT(h) < errorT(h’) but
errorD(h) > errorD(h’)
Note: Similar curves can happen when training too long in complex
hypothesis space with lots of parameters to set.

• K- fold Cross Validation
• Regularization
• Early stopping
• Drop-out
• Pre or post pruning for decision tree
• Minimum description length (MDL) principle
Solutions for Overfitting

K- fold Cross Validation
Training Set Testing Set
Training Set Testing Set
Validation Set
S1 S2 S3 … Sk
Training Set = S
Round Training Set Testing Set
1 S1 S – S1
2 S2 S – S2
i Si S-Si
Average test score = 1/k ( ∑Si)
• Trade-off:
• Complex hypothesis fit the data well  may tend to overfitting
• Simple hypothesis may generalize better  may tend to underfitting
• As the training data samples increase, generalization error decreases.

• Fitting the data points well
• Keeping the no. of parameters (Ɵs) small
Regularization parameter
Regularization

Regularization
Ɵ
0
Under fitting

< 1
Shrinkage Parameter updation
Regularized Linear Regression

Regularized Logistic Regression

For Logistic Regression:
Regularized Logistic Regression

L1 intro2 supervised_learning

More Related Content

What's hot

Similar to L1 intro2 supervised_learning

Recently uploaded

L1 intro2 supervised_learning