The document describes the k-means++ seeding algorithm for initializing k-means clustering. It presents the k-means++ algorithm, provides an implementation in MLDemos, and evaluates it on test and real datasets. The results show k-means++ yields a significant reduction in clustering error compared to random initialization, providing better separation of clusters. However, the document also notes there are many seeding techniques and some may work better than k-means++ for certain datasets.


![K-means++!
• A seeding technique for k-means
from Arthur and Vassilvitskii [2007]!
• Idea: spread the k initial cluster centers away from
each other.!
• O(log k)-competitive with the optimal clustering"
• substantial convergence time speedups (empirical)!](https://image.slidesharecdn.com/kmeanspp1-120605042854-phpapp02/75/Kmeans-plusplus-3-2048.jpg)

![Implementation!
• Based on Apache Commons Math’s
KMeansPlusPlusClusterer and
Arthur’s [2007] implementation!
• Implemented directly in MLDemos’ core!](https://image.slidesharecdn.com/kmeanspp1-120605042854-phpapp02/75/Kmeans-plusplus-5-2048.jpg)
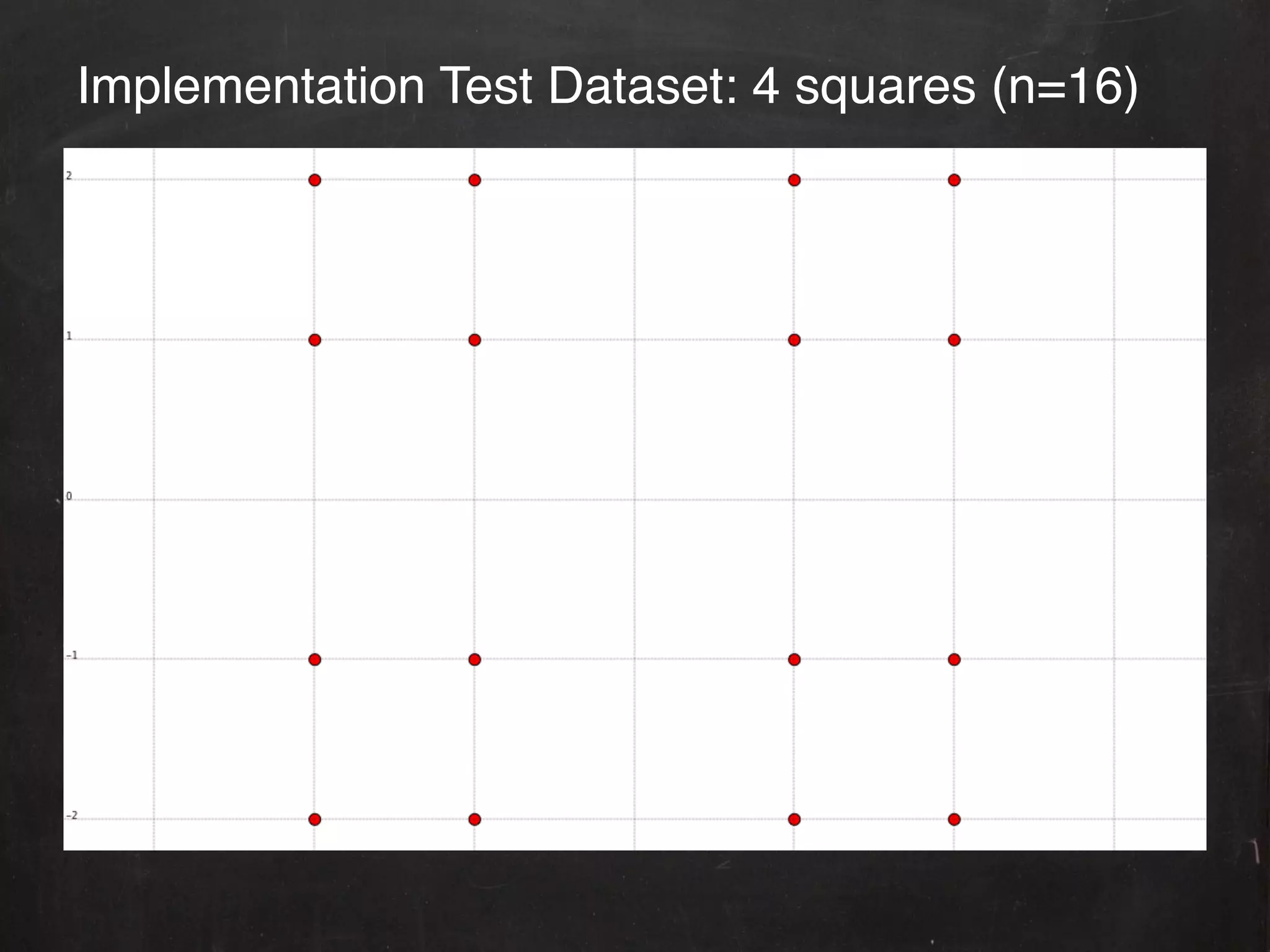

![Sample Output!
1:
first
cluster
center
0
at
rand:
x=4
[-‐2.0;
2.0]
1:
initial
minDist
for
0
[-‐1.0;-‐1.0]
=
10.0
1:
initial
minDist
for
1
[
2.0;
1.0]
=
17.0
1:
initial
minDist
for
2
[
1.0;-‐1.0]
=
18.0
1:
initial
minDist
for
3
[-‐1.0;-‐2.0]
=
17.0
1:
initial
minDist
for
5
[
2.0;
2.0]
=
16.0
1:
initial
minDist
for
6
[
2.0;-‐2.0]
=
32.0
1:
initial
minDist
for
7
[-‐1.0;
2.0]
=
1.0
1:
initial
minDist
for
8
[-‐2.0;-‐2.0]
=
16.0
1:
initial
minDist
for
9
[
1.0;
1.0]
=
10.0
1:
initial
minDist
for
10[
2.0;-‐1.0]
=
25.0
1:
initial
minDist
for
11[-‐2.0;-‐1.0]
=
9.0
[…]
2:
picking
cluster
center
1
-‐-‐-‐-‐-‐-‐-‐-‐-‐-‐-‐-‐-‐-‐
3:
distSqSum=3345.0
3:
random
index
1532.706909
4:
new
cluster
point:
x=6
[2.0;-‐2.0]](https://image.slidesharecdn.com/kmeanspp1-120605042854-phpapp02/75/Kmeans-plusplus-8-2048.jpg)
![Sample Output (2)!
4:
updating
minDist
for
0
[-‐1.0;-‐1.0]
=
10.0
4:
updating
minDist
for
1
[
2.0;
1.0]
=
9.0
4:
updating
minDist
for
2
[
1.0;-‐1.0]
=
2.0
4:
updating
minDist
for
3
[-‐1.0;-‐2.0]
=
9.0
4:
updating
minDist
for
5
[
2.0;
2.0]
=
16.0
4:
updating
minDist
for
7
[-‐1.0;
2.0]
=
25.0
4:
updating
minDist
for
8
[-‐2.0;-‐2.0]
=
16.0
4:
updating
minDist
for
9
[
1.0;
1.0]
=
10.0
4:
updating
minDist
for
10[2.0
;-‐1.0]
=
1.0
4:
updating
minDist
for
11[-‐2.0;-‐1.0]
=
17.0
[…]
2:
picking
cluster
center
2
-‐-‐-‐-‐-‐-‐-‐-‐-‐-‐-‐-‐-‐-‐-‐-‐-‐
3:
distSqSum=961.0
3:
random
index
103.404701
4:
new
cluster
point:
x=1
[2.0;1.0]
4:
updating
minDist
for
0
[-‐1.0;-‐1.0]
=
13.0
[…]](https://image.slidesharecdn.com/kmeanspp1-120605042854-phpapp02/75/Kmeans-plusplus-9-2048.jpg)

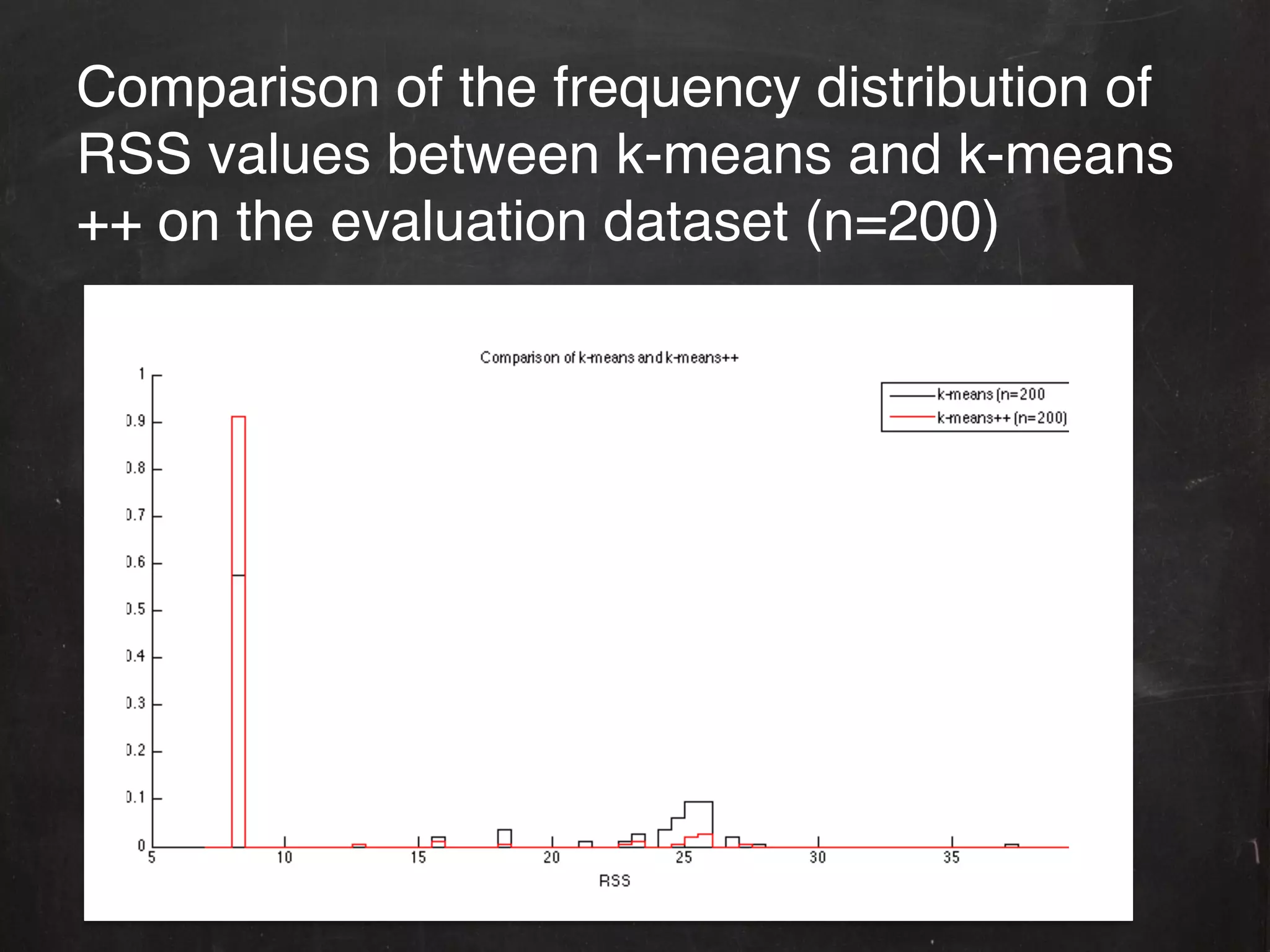

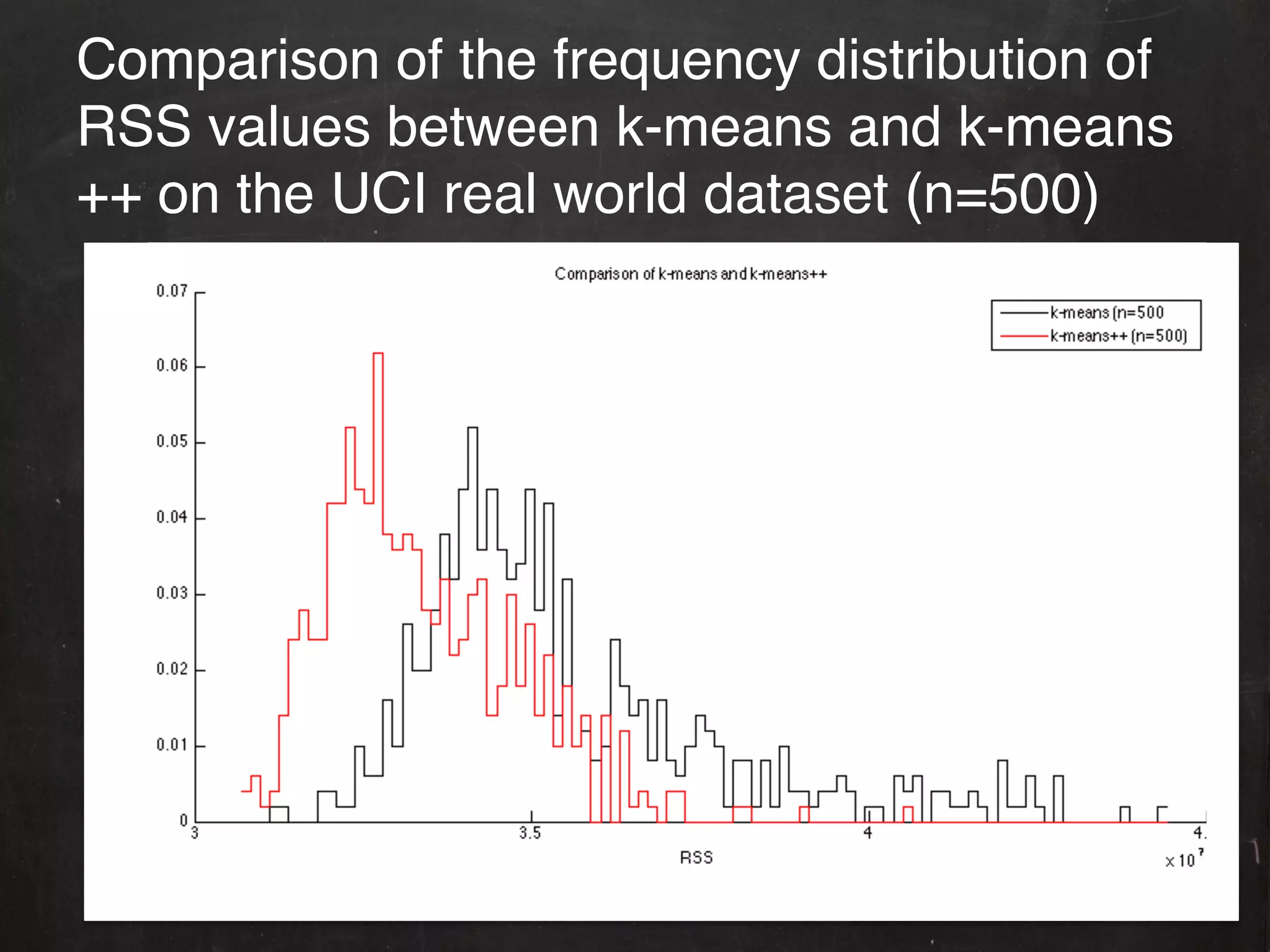
![Alternatives Seeding Algorithms!
• Extensive research into seeding techniques for k-
means.!
• Steinley [2007]: evaluated 12 different techniques
(omitting k-means++). Recommends multiple
random starting points for general use.!
• Maitra [2011] evaluated 11 techniques (including k-
means++). Unable to provide recommendations
when evaluating nine standard real-world datasets. !
• Maitra analyzed simulated datasets and
recommends using Milligan’s [1980] or Mirkin’s
[2005] seeding technique, and Bradley’s [1998]
when dataset is very large.!](https://image.slidesharecdn.com/kmeanspp1-120605042854-phpapp02/75/Kmeans-plusplus-14-2048.jpg)

