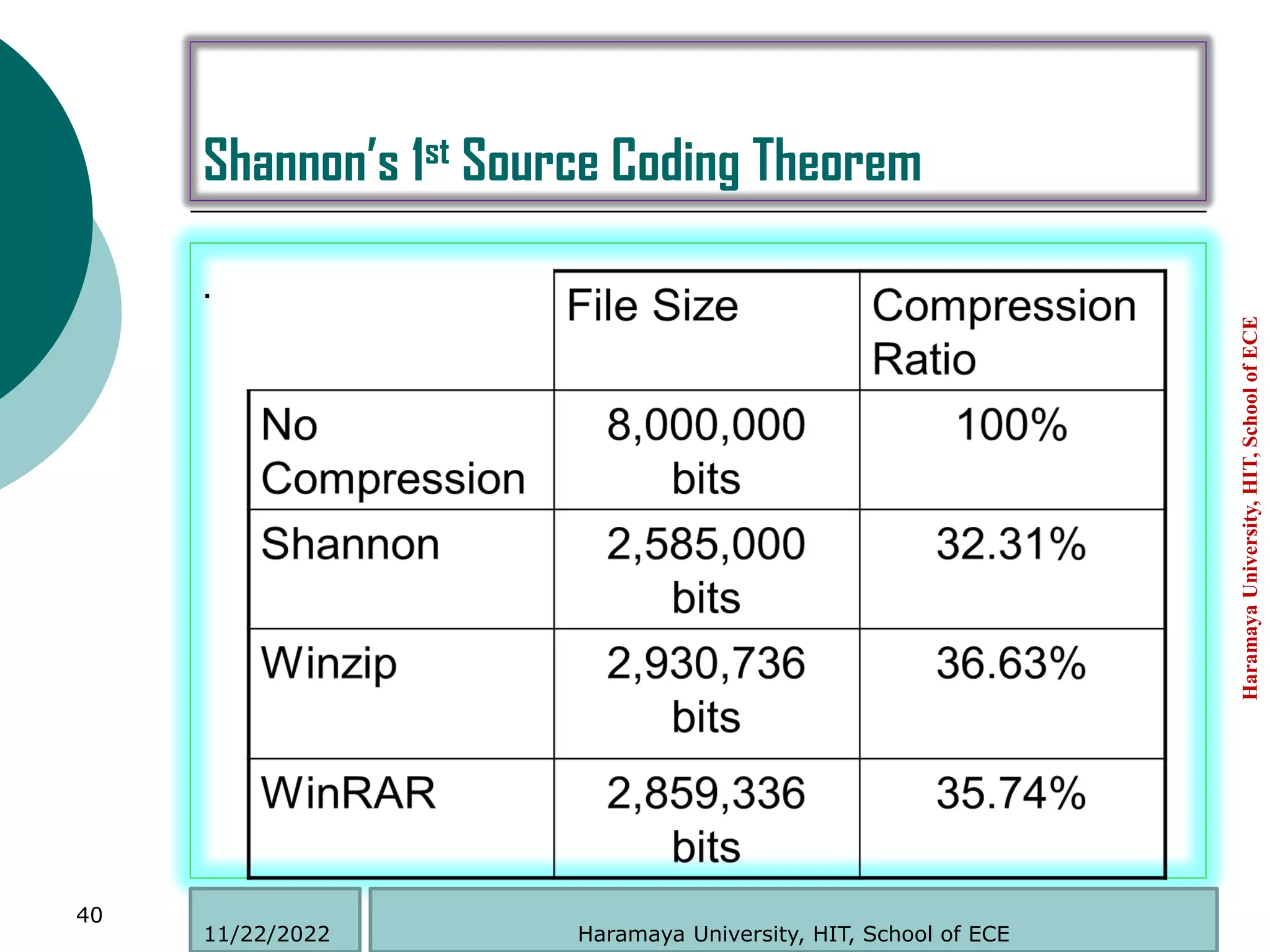
This document discusses information theory and entropy. It defines information as something that reduces uncertainty and provides new knowledge. Entropy is defined as the average amount of information contained in a message. The entropy of a probability distribution measures the uncertainty in the distribution. It is calculated as the expected value of the information contained in each symbol of the distribution. A higher entropy means more uncertainty in the distribution. Logarithms are used to measure information and entropy because they allow the properties of non-negativity, additivity, and continuity.



















![ “The fundamental problem of communication is that of reproducing at
one point either exactly or approximately a message selected at
another point.”
Haramaya University, HIT, School of ECE 20
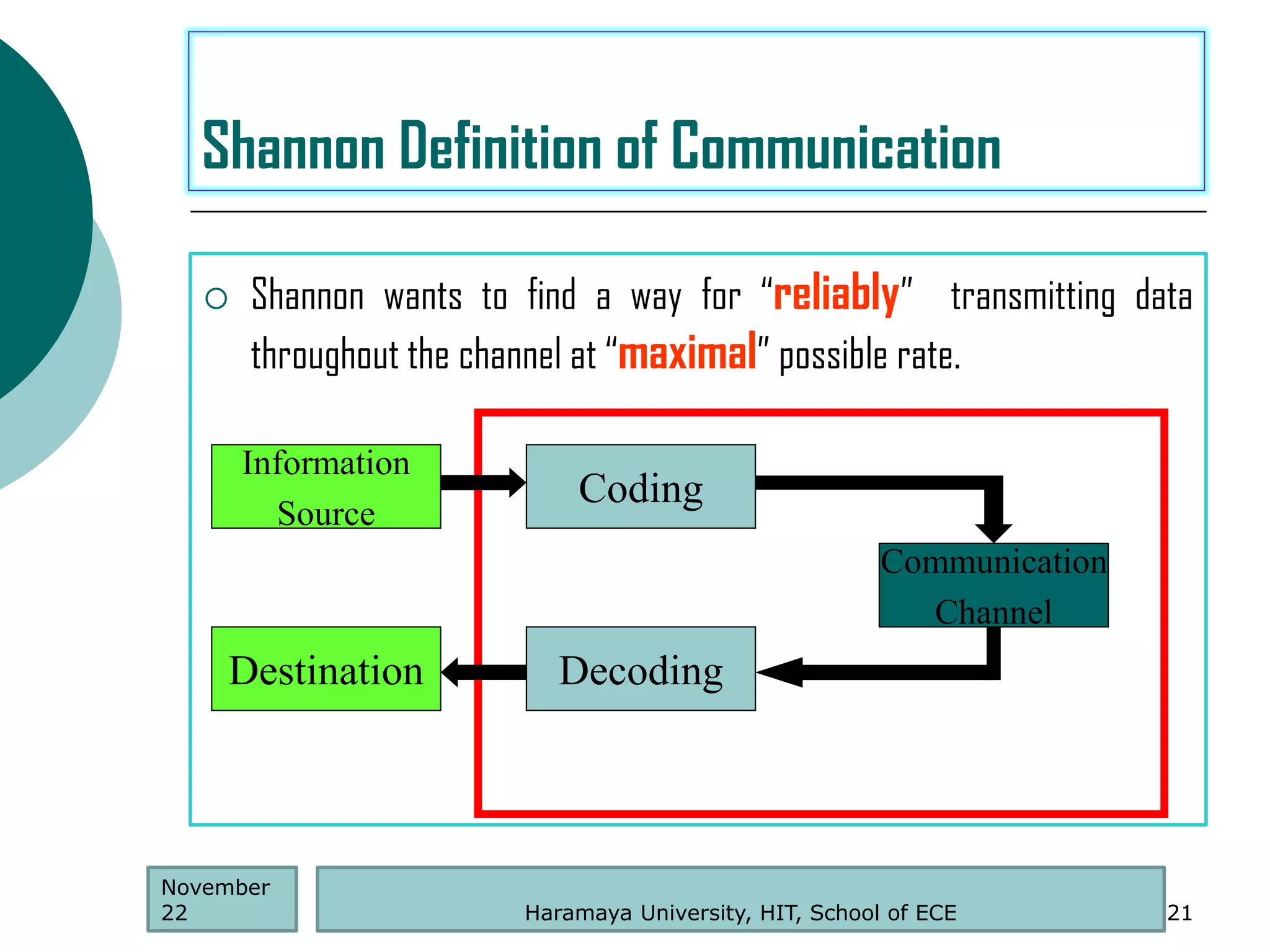
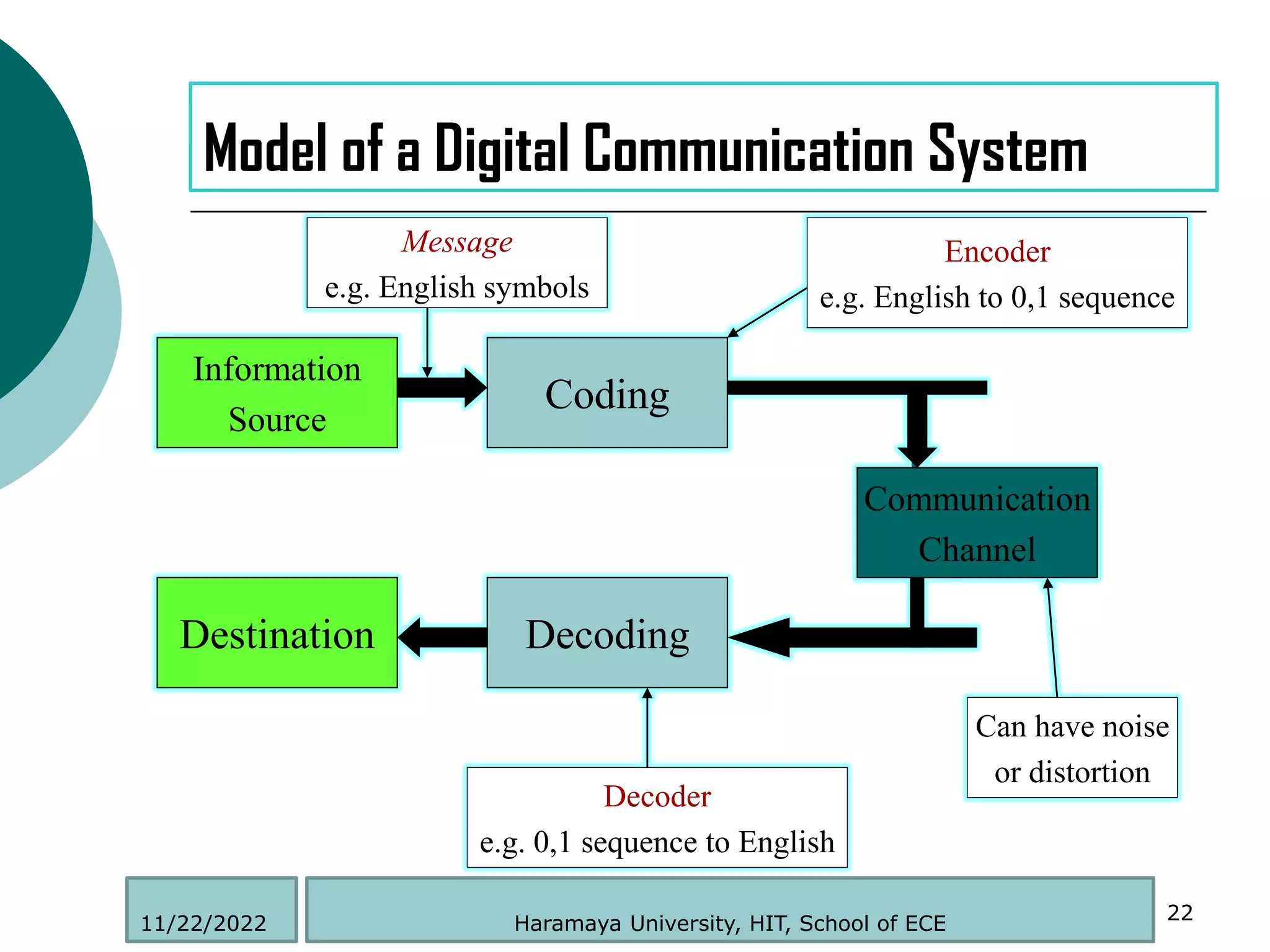
Shannon Definition of Communication
November
22
“Frequently the messages have meaning”
“... [which is] irrelevant to the engineering problem.”](https://image.slidesharecdn.com/introductiontoinformationtheoryandcoding-230101205551-92963318/75/Introduction-to-Information-Theory-and-Coding-pdf-20-2048.jpg)