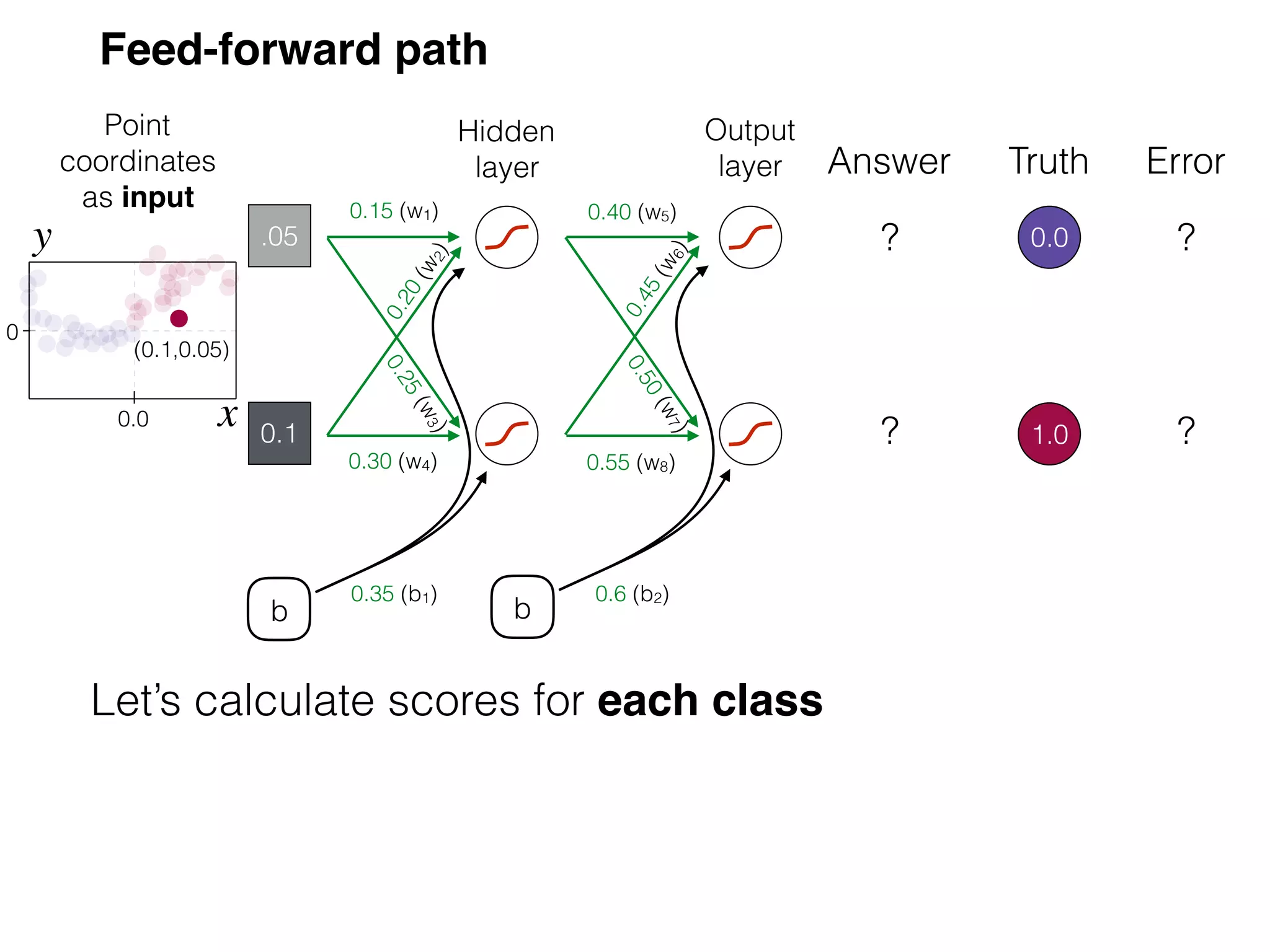
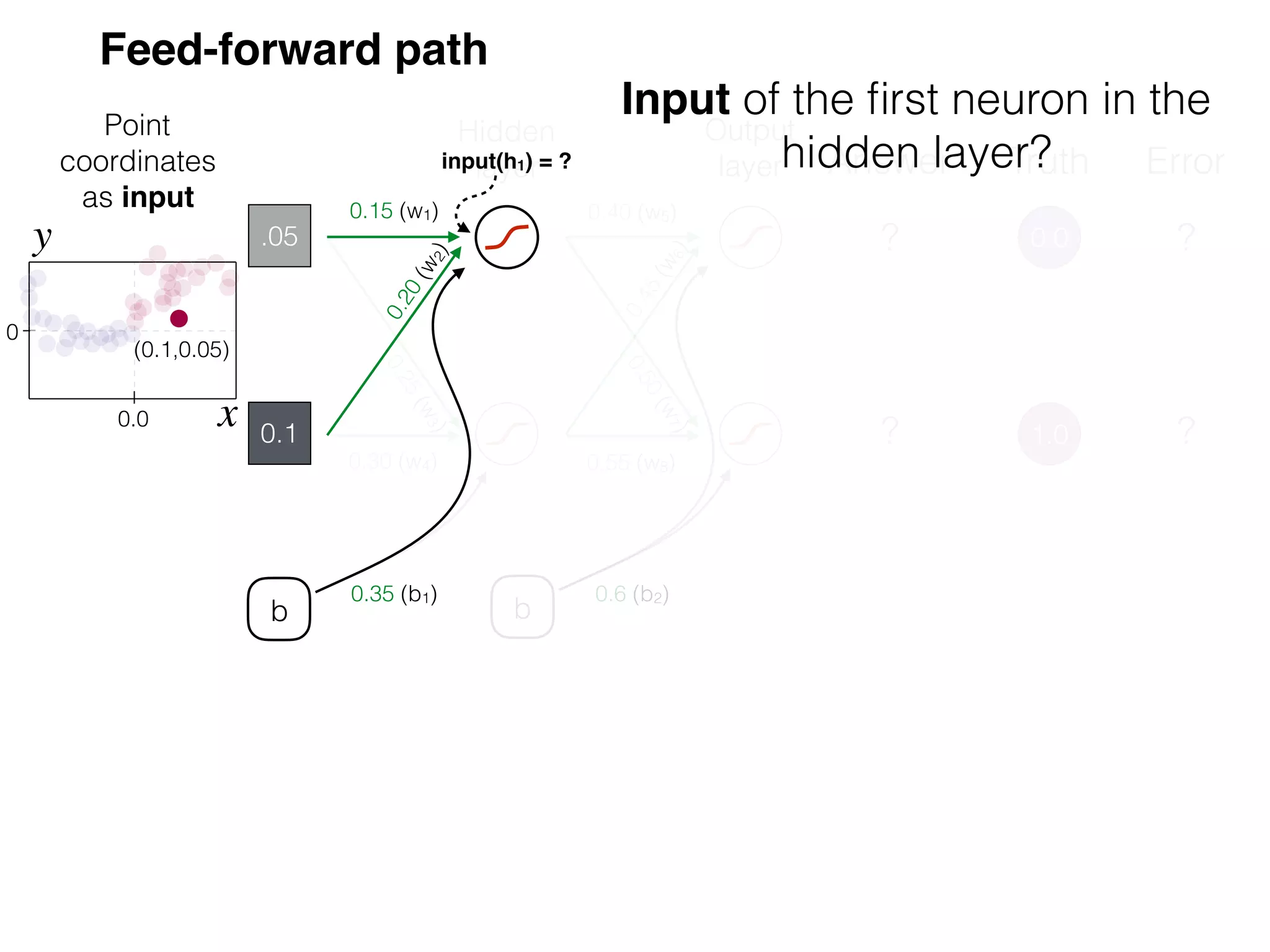
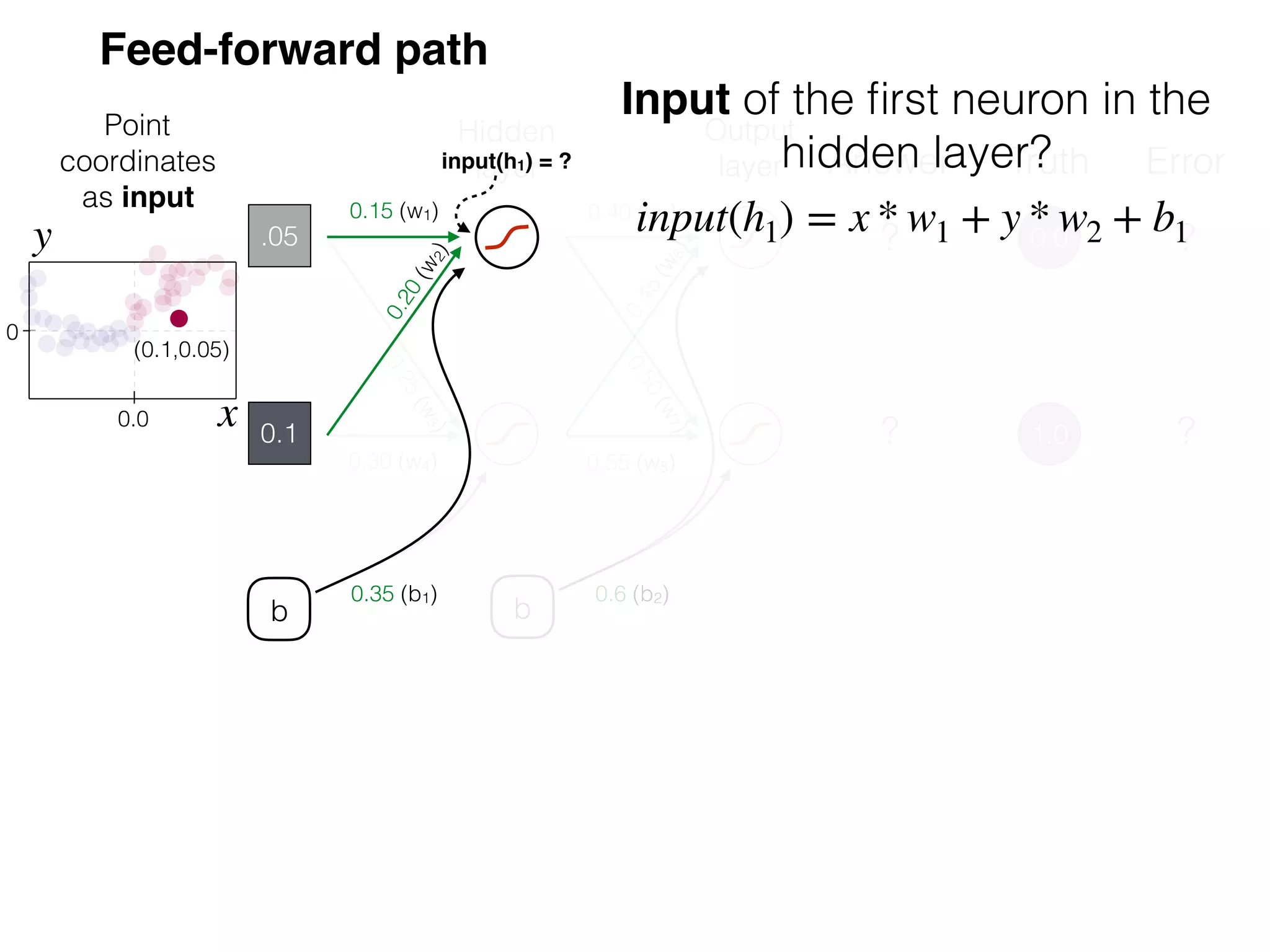
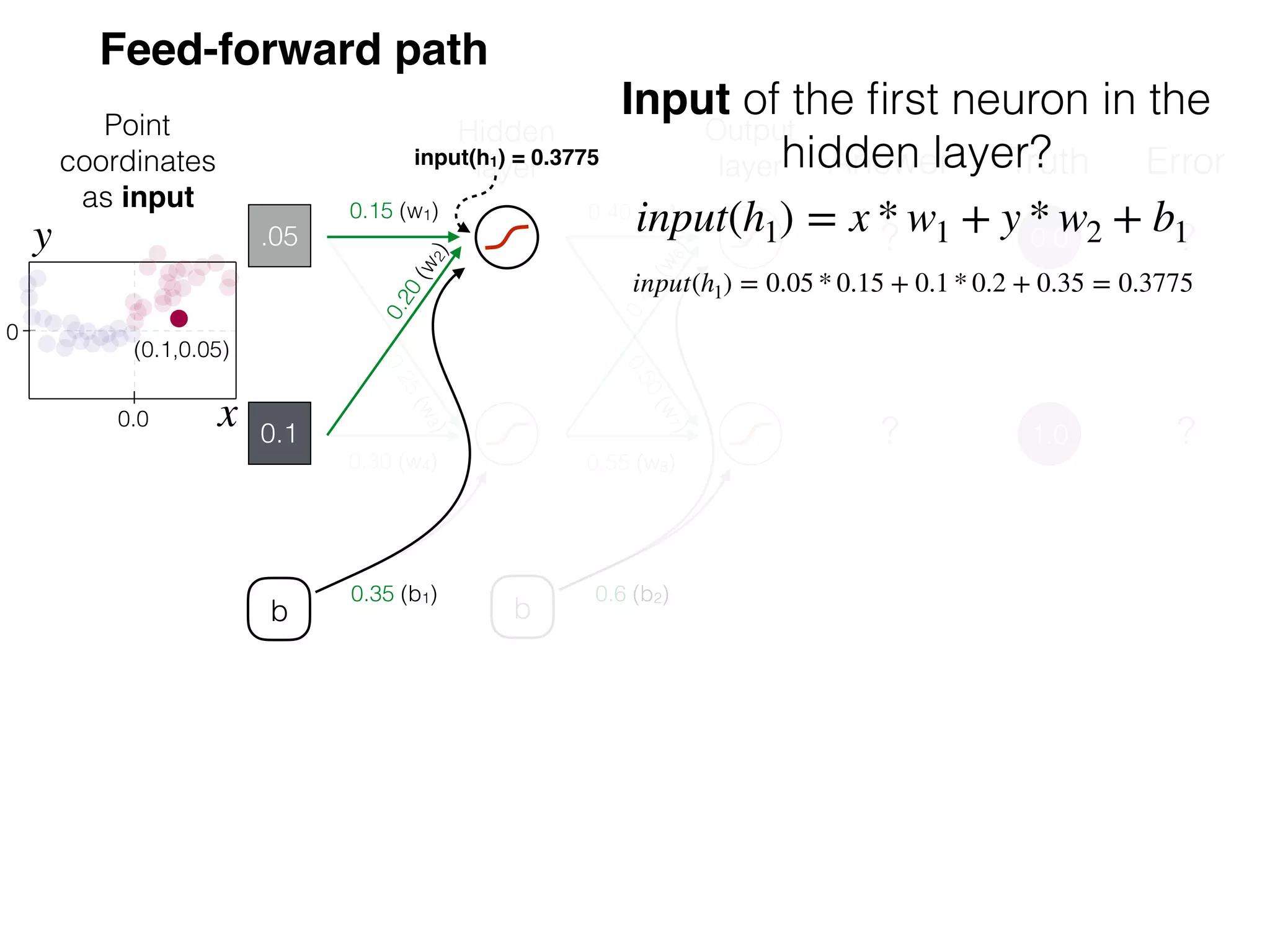
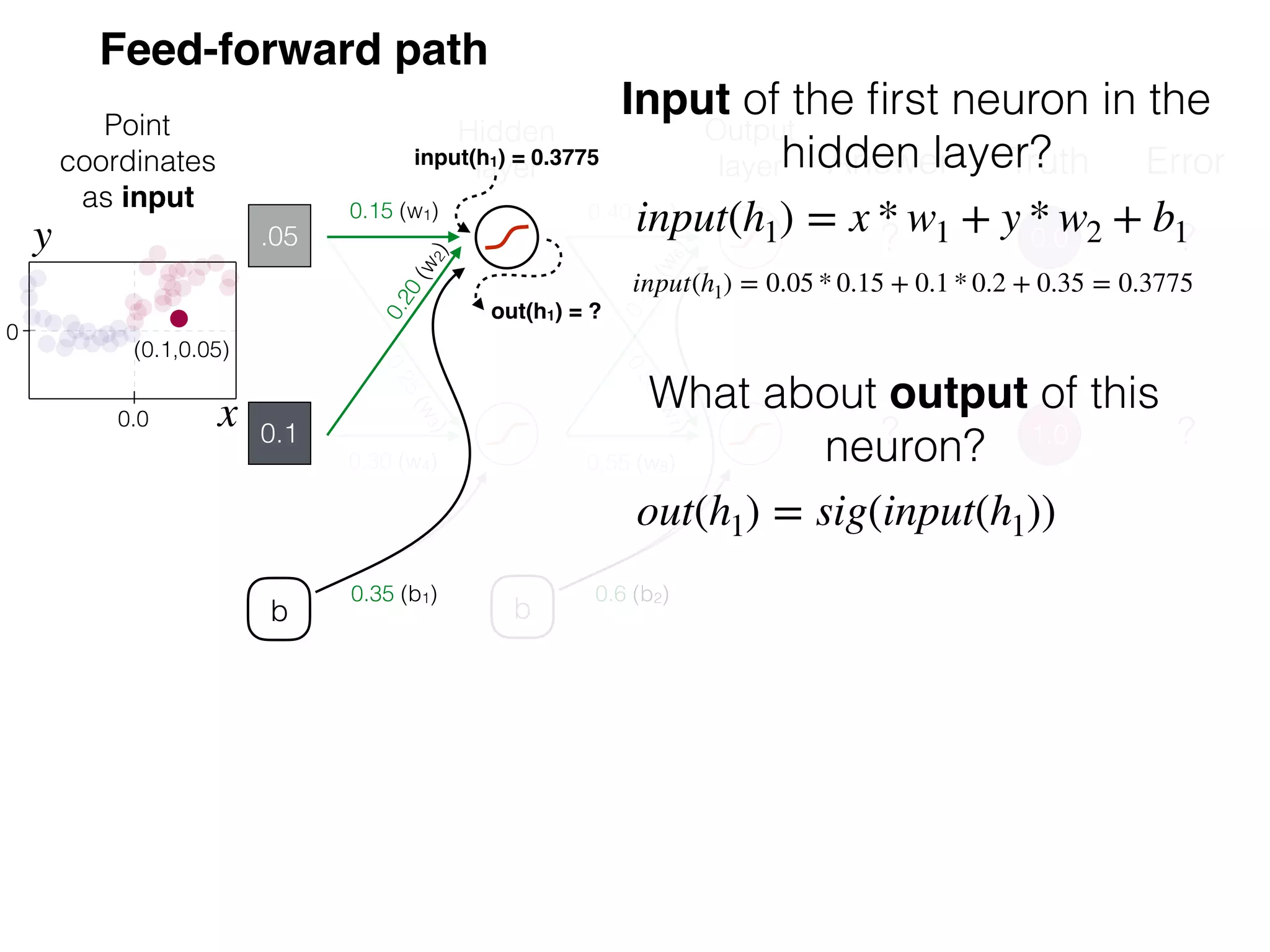
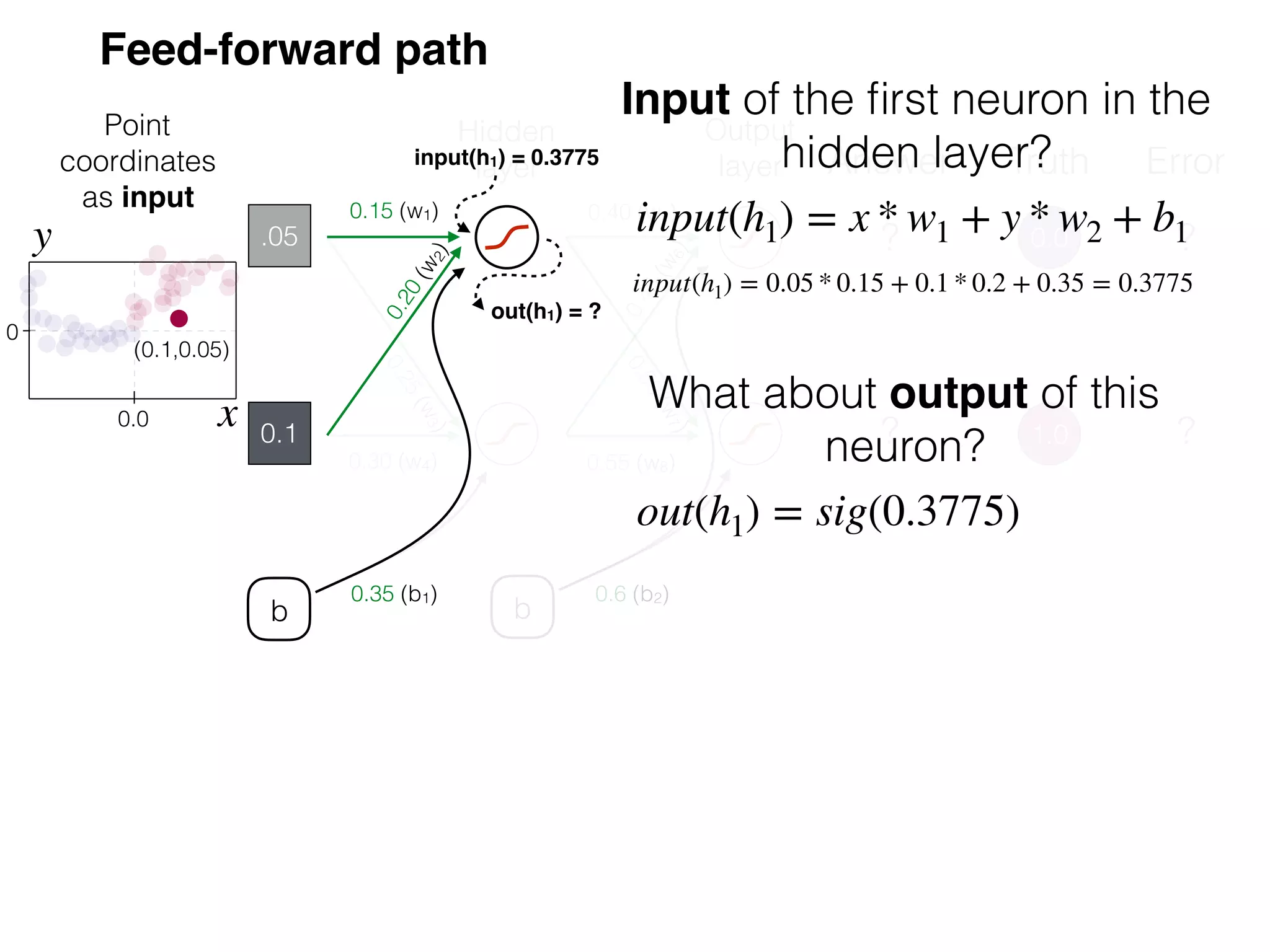
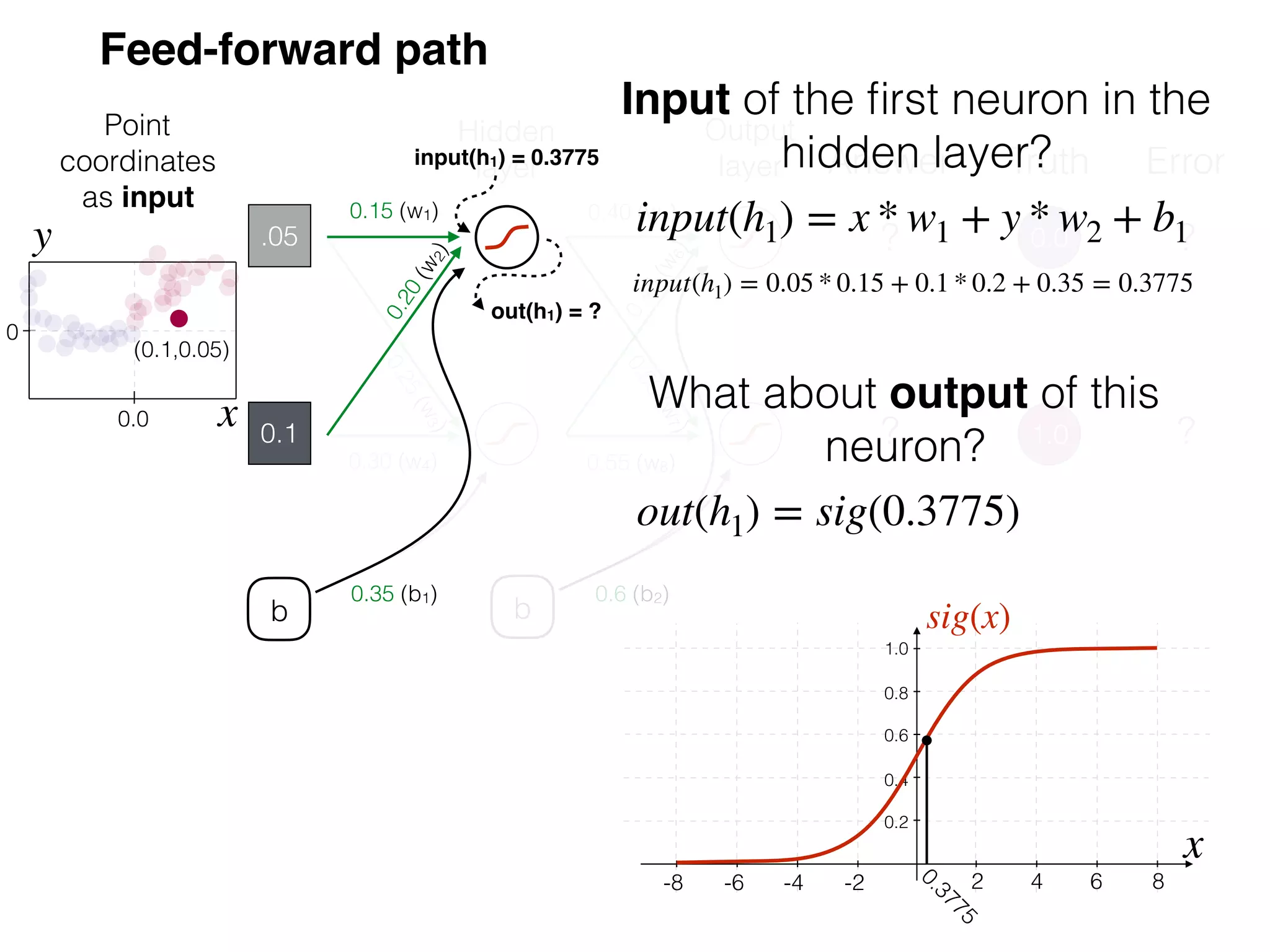
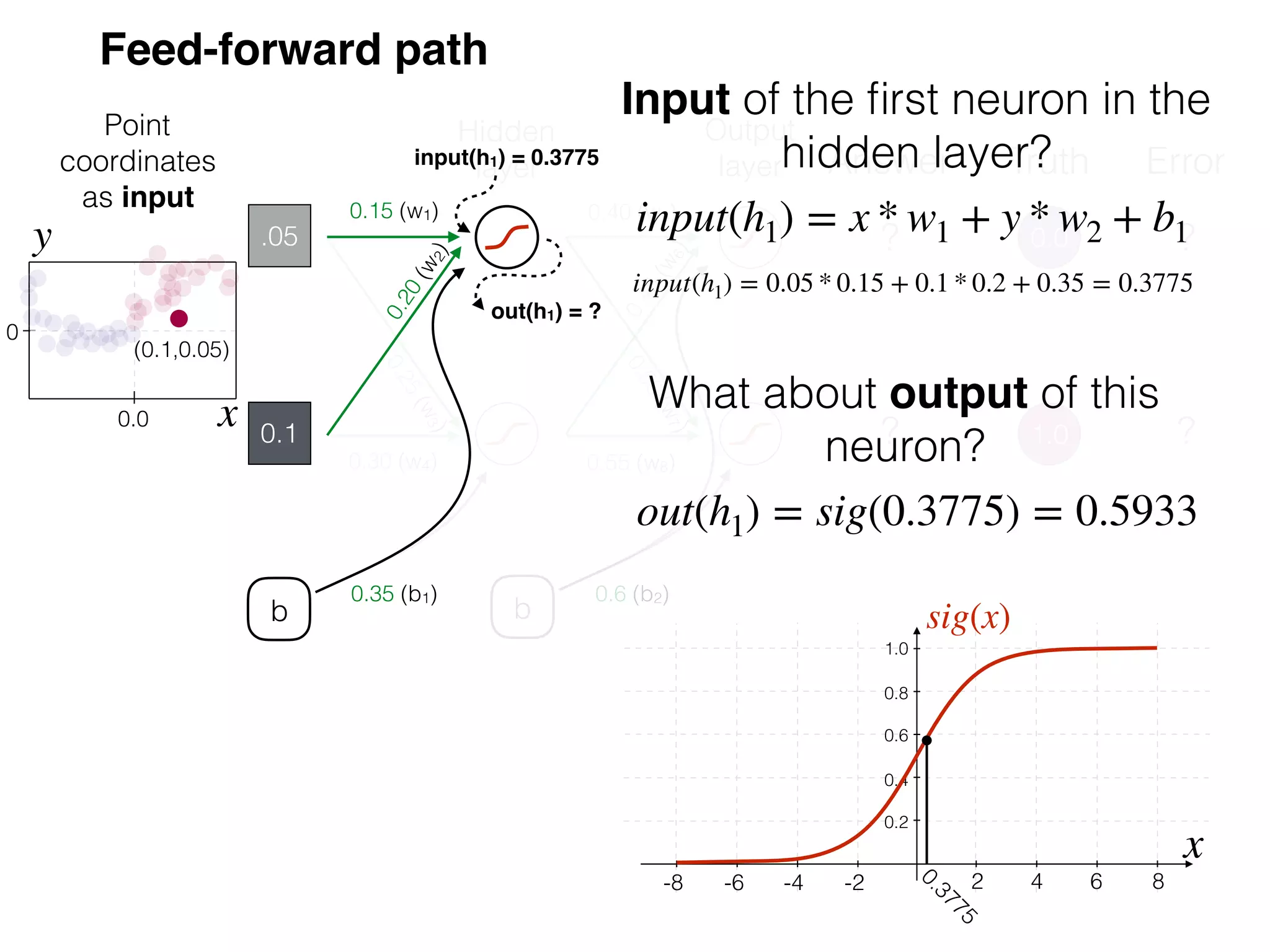
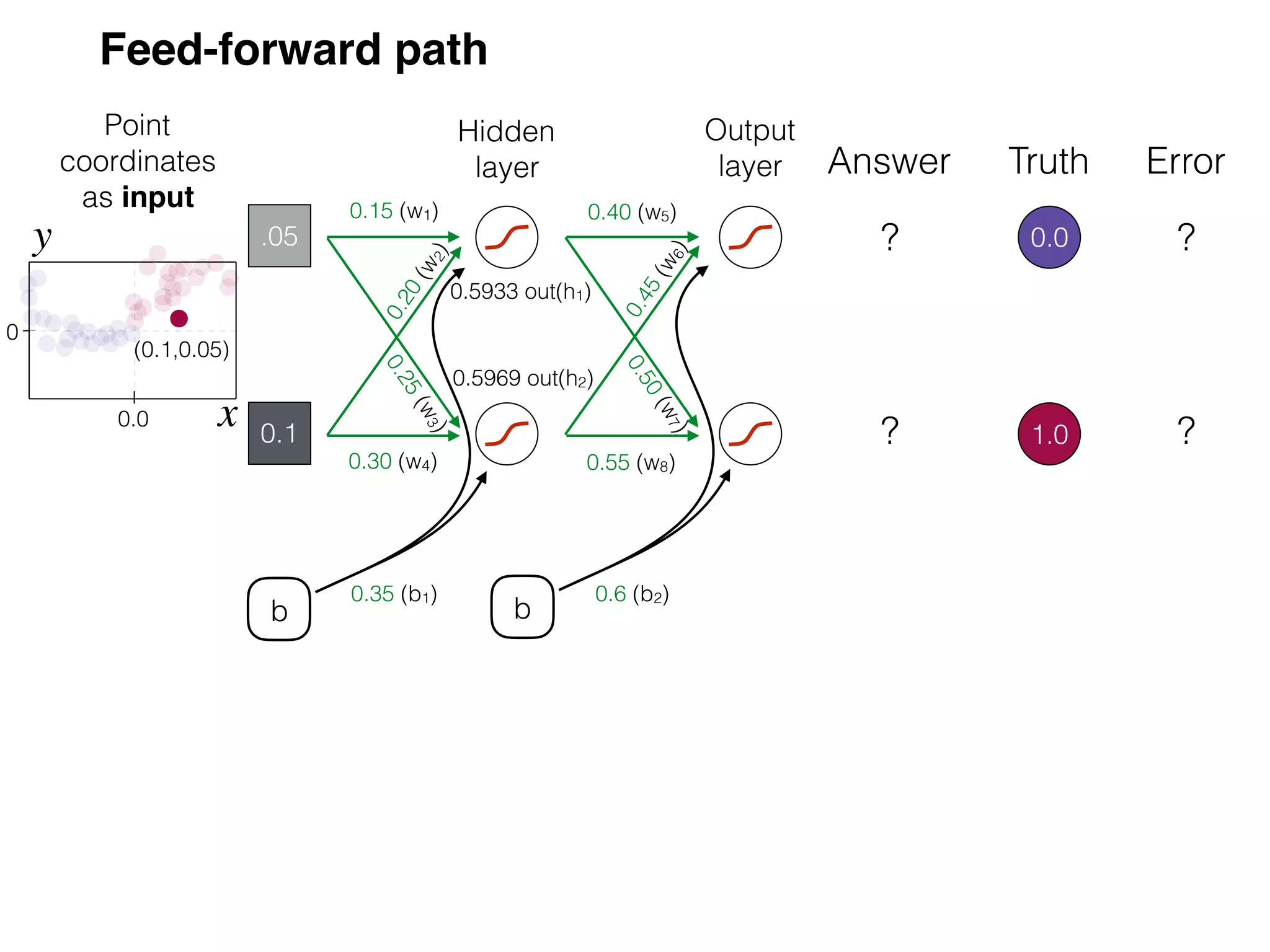
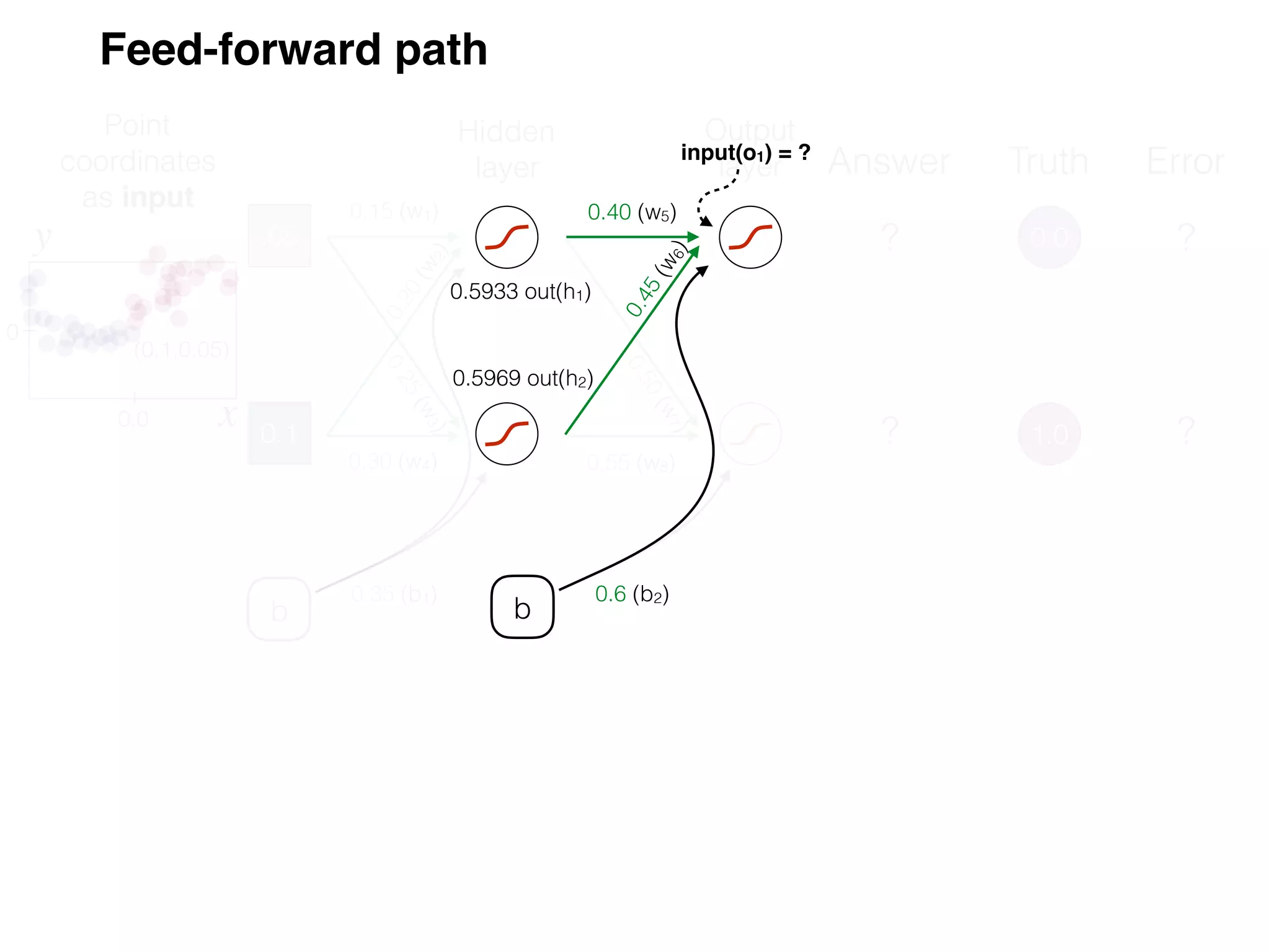
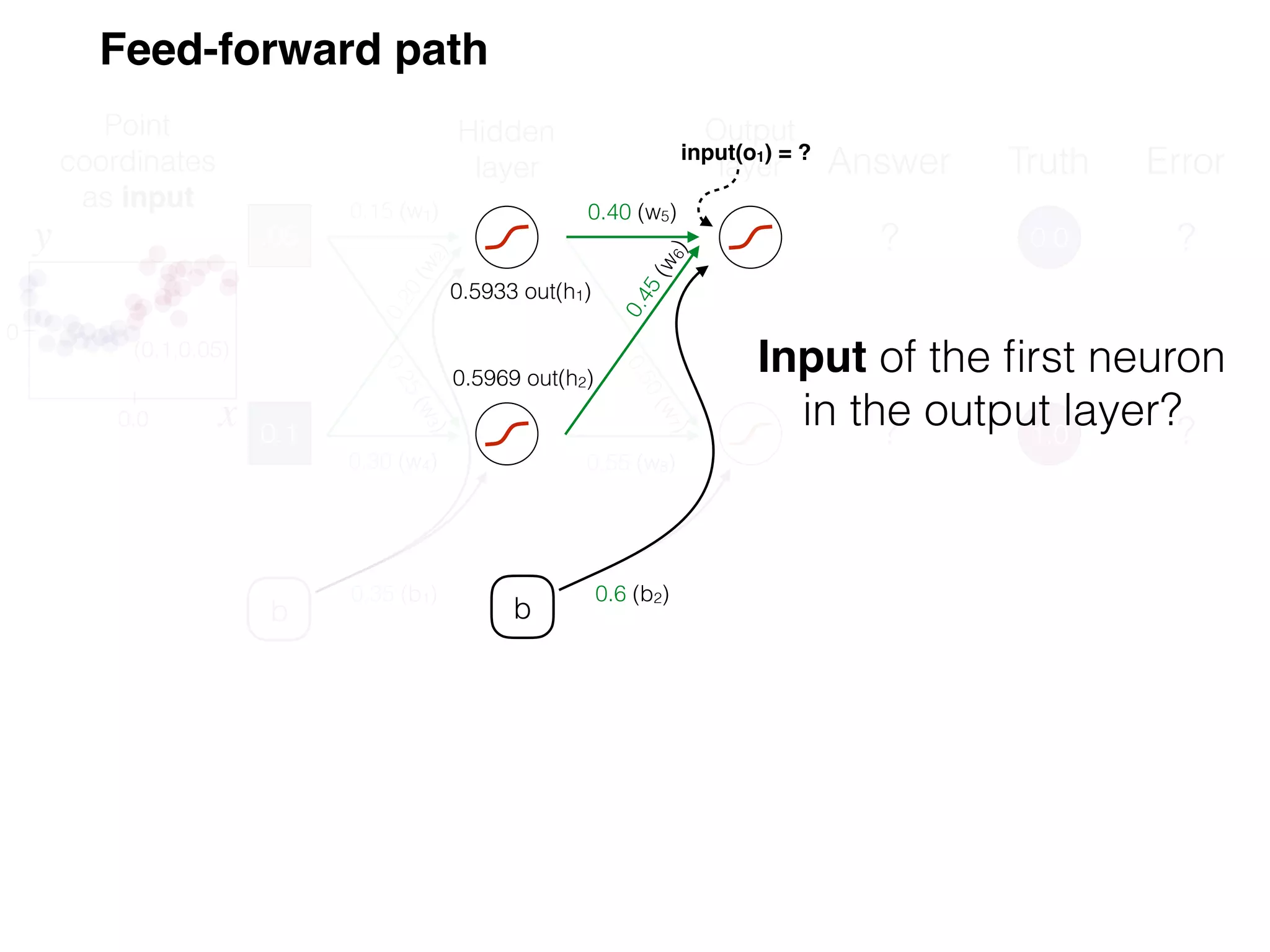
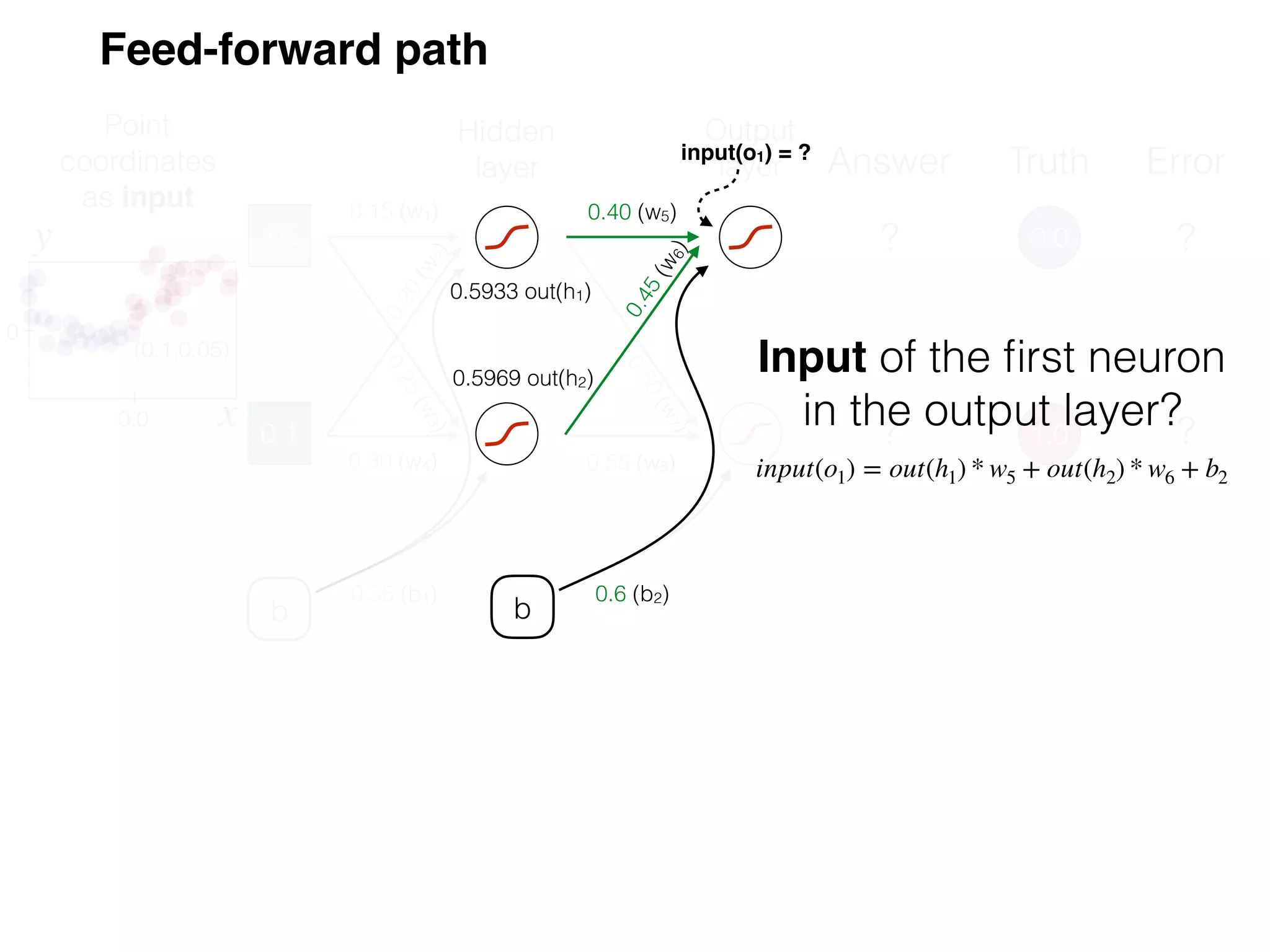
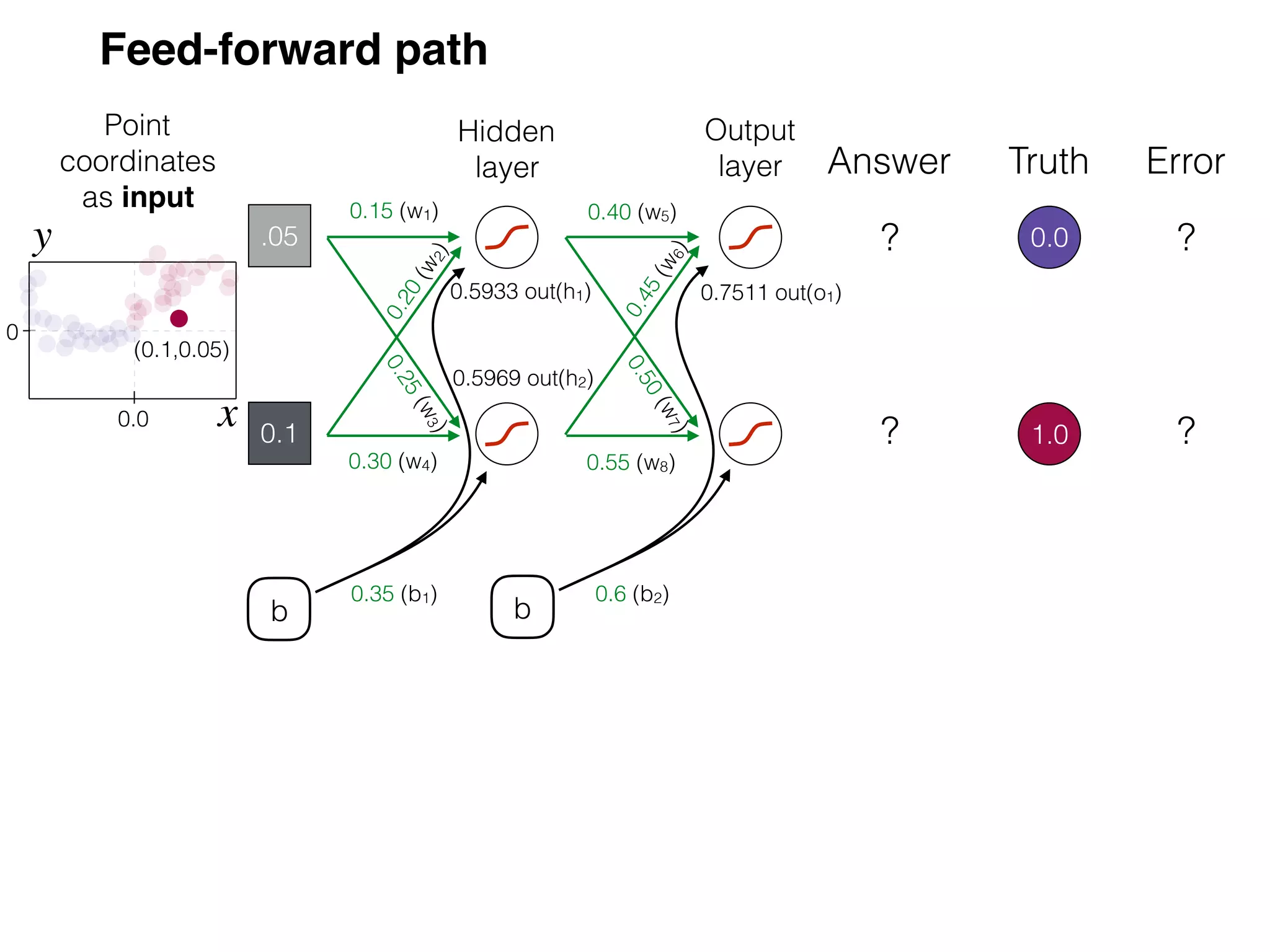
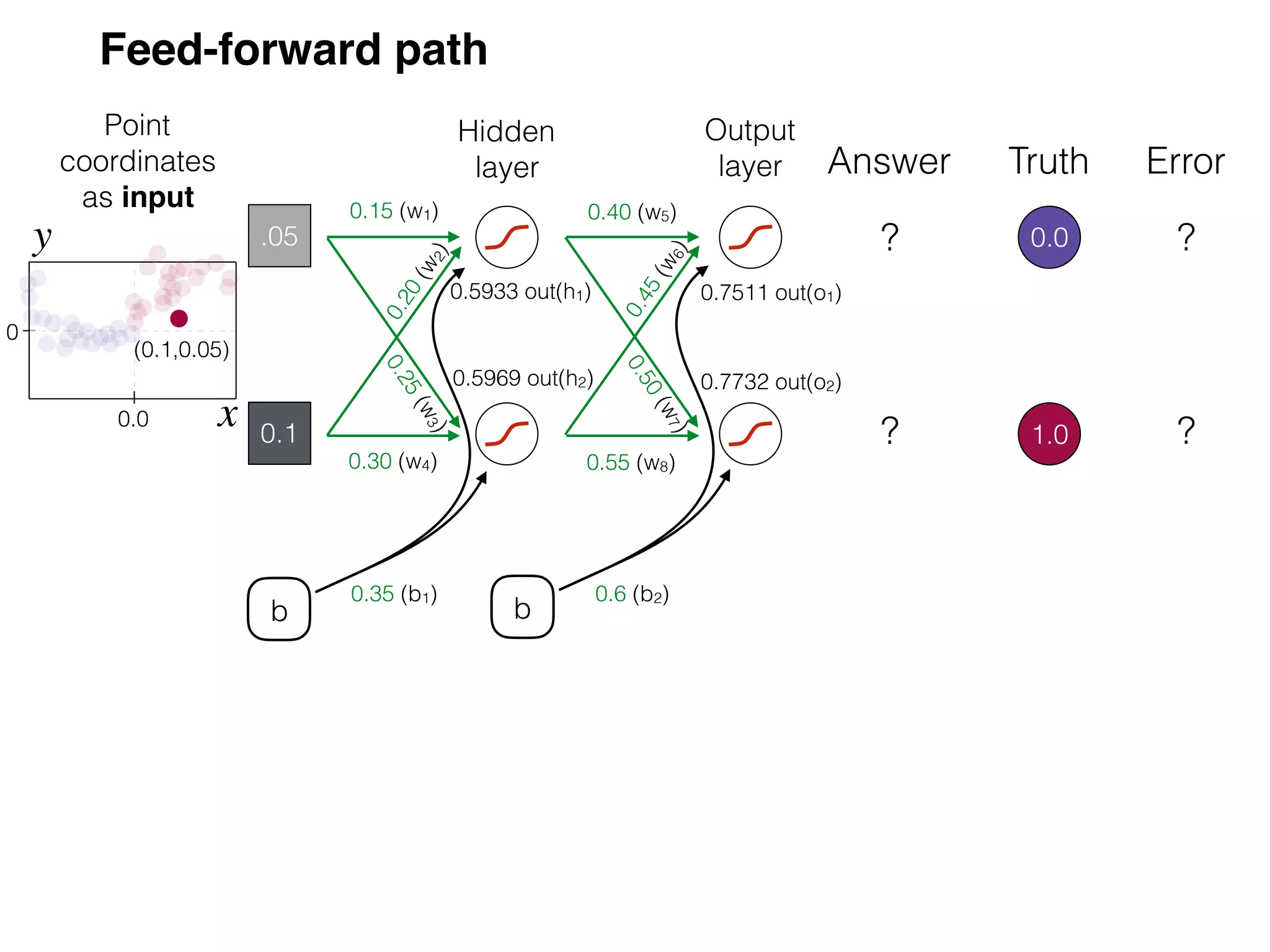
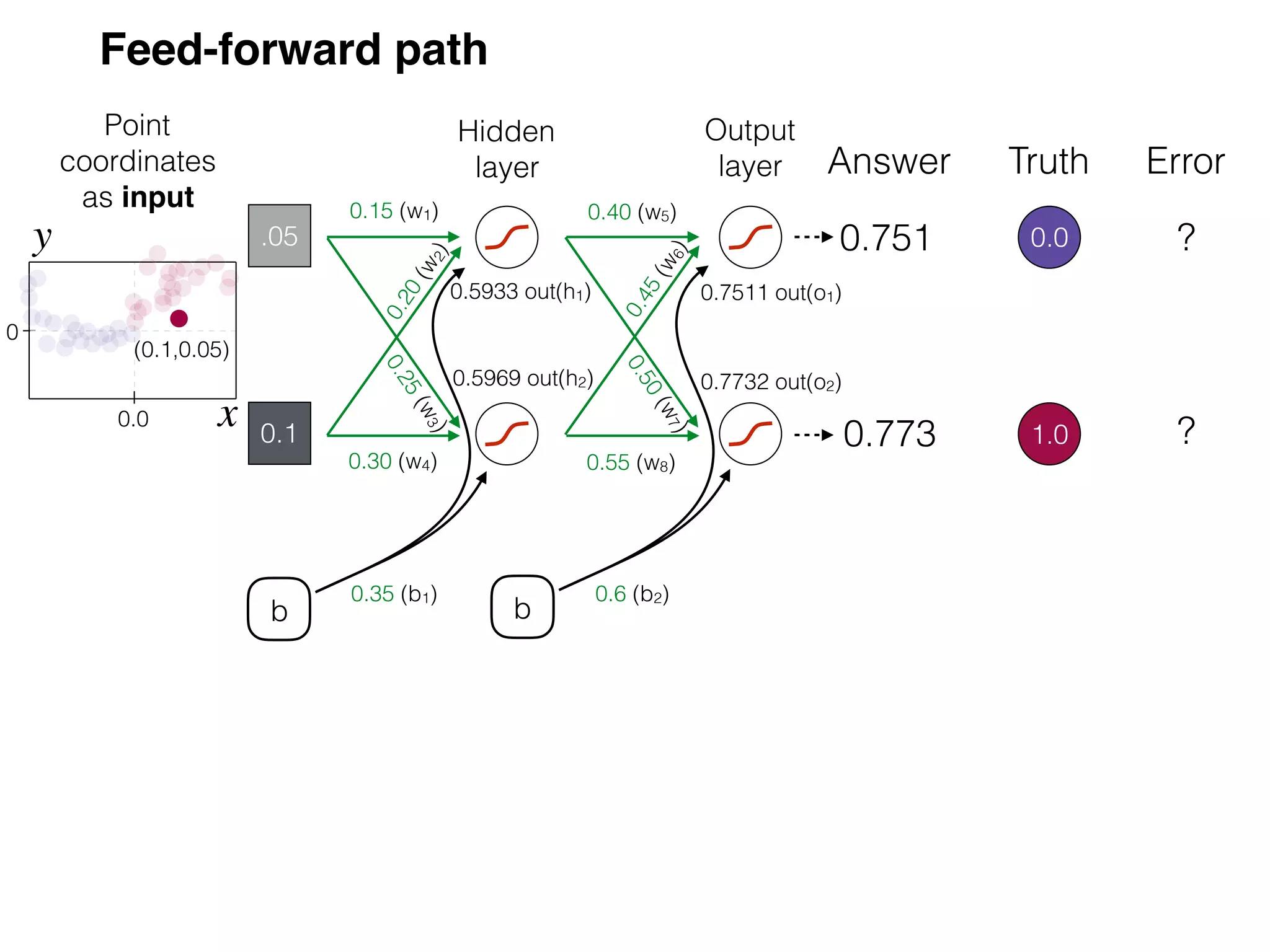
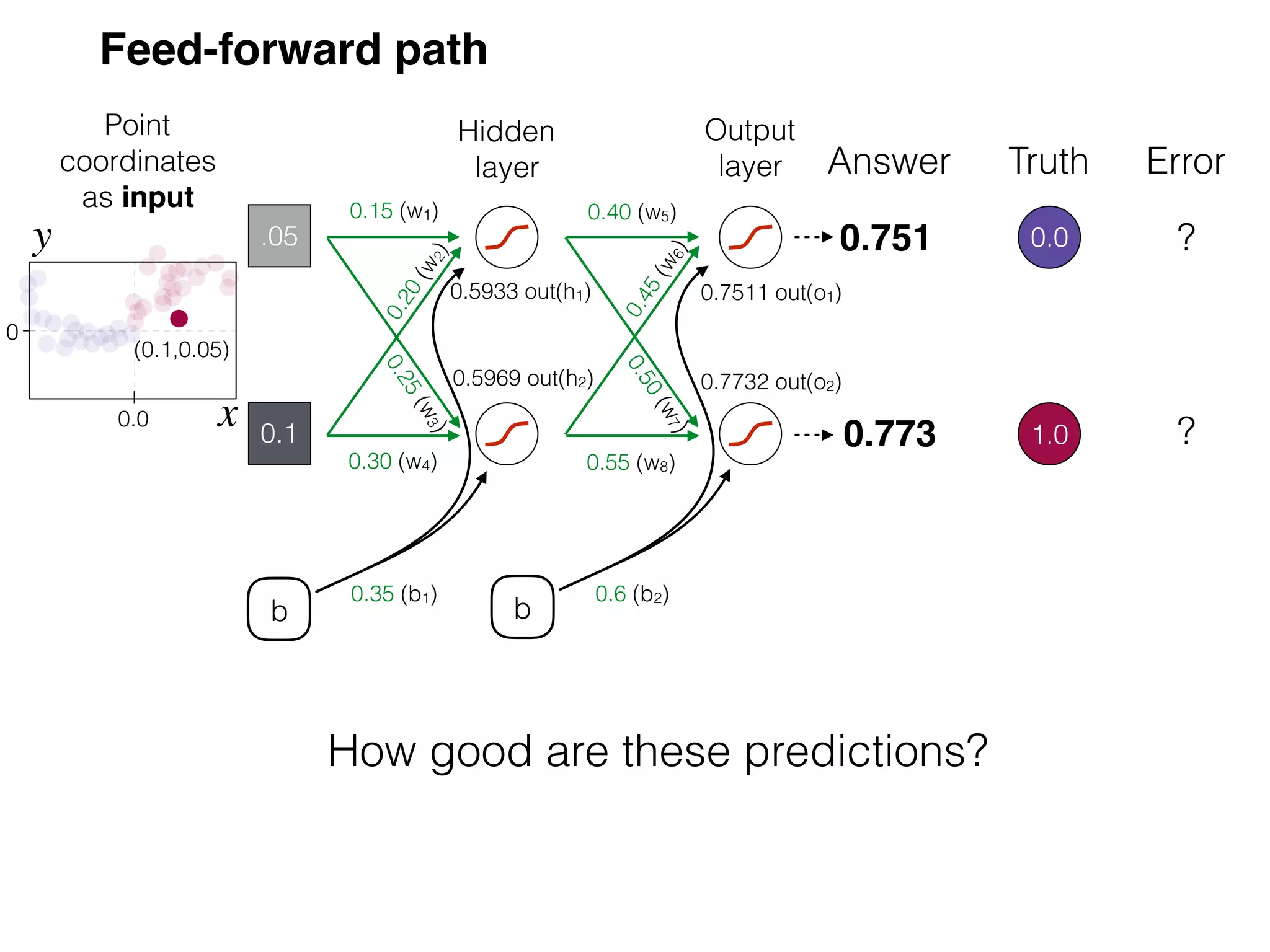
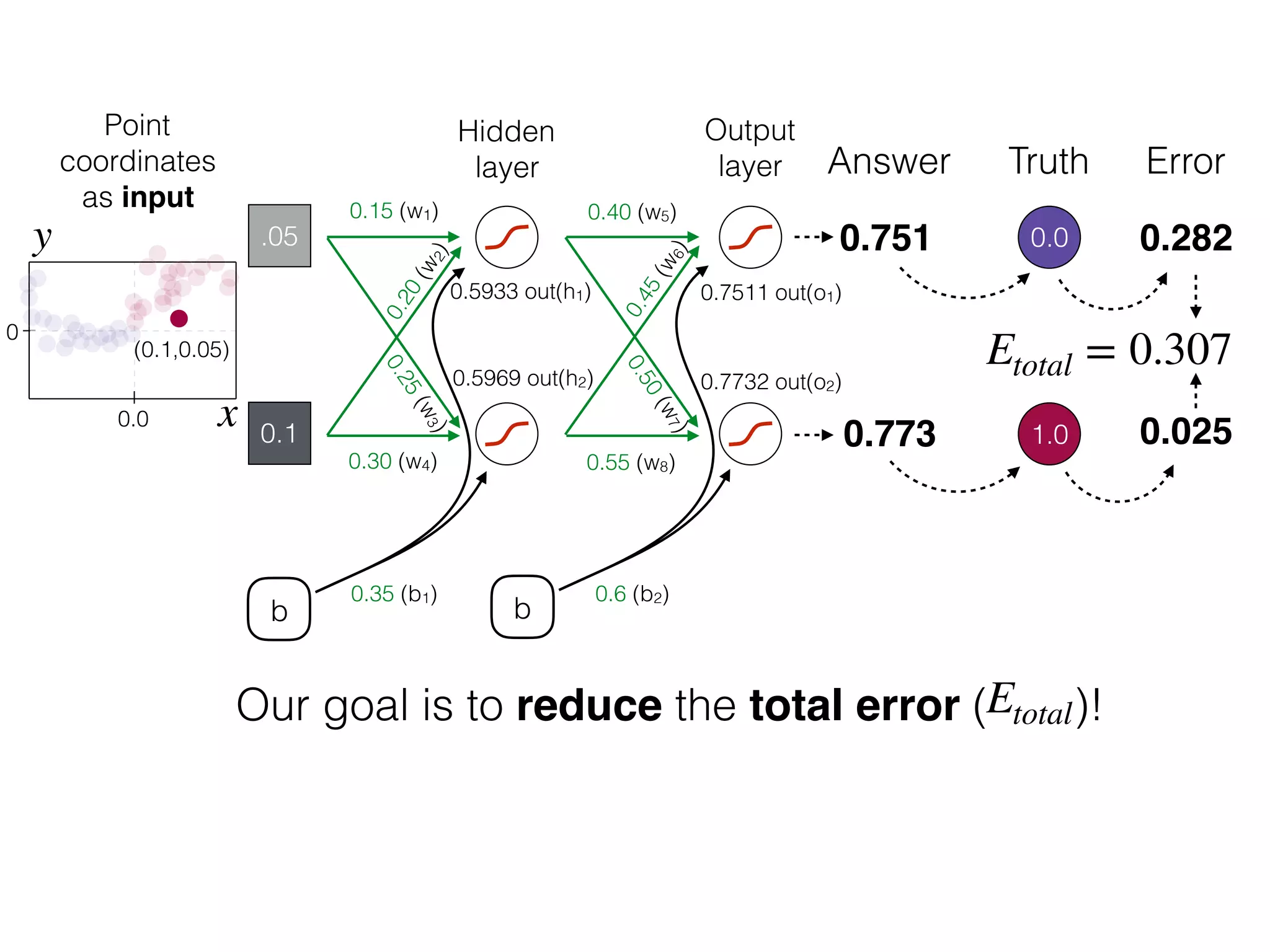
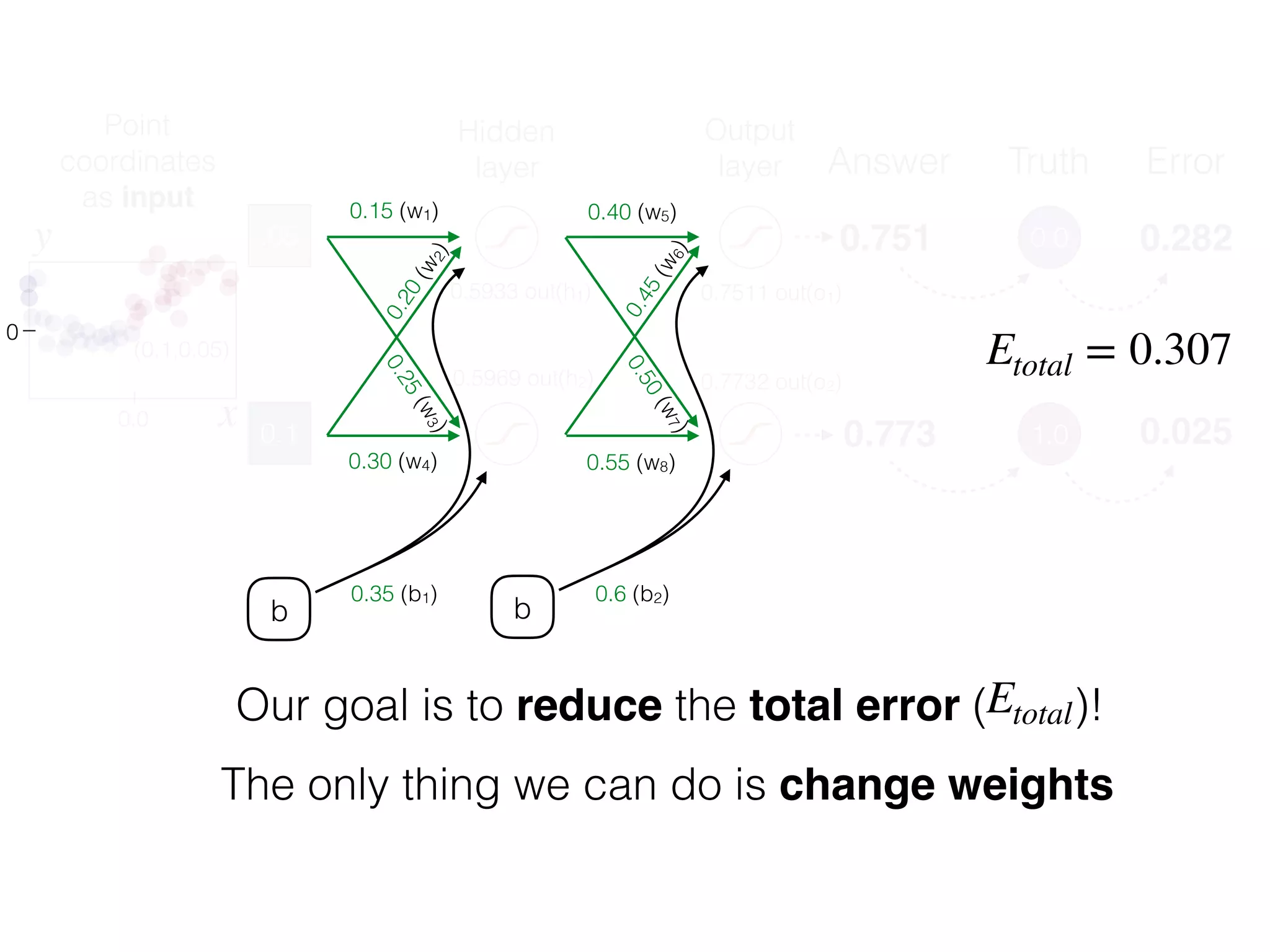
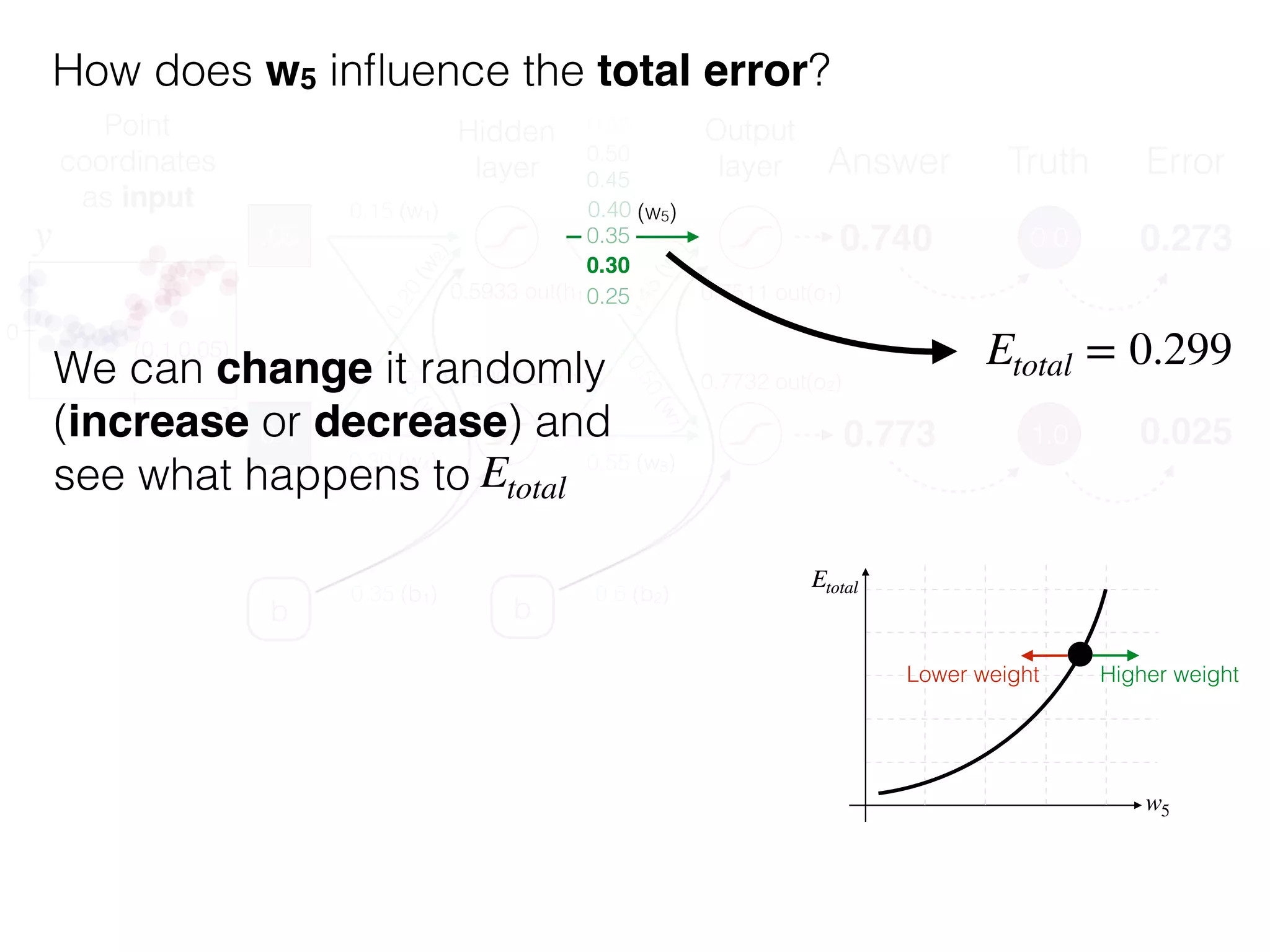
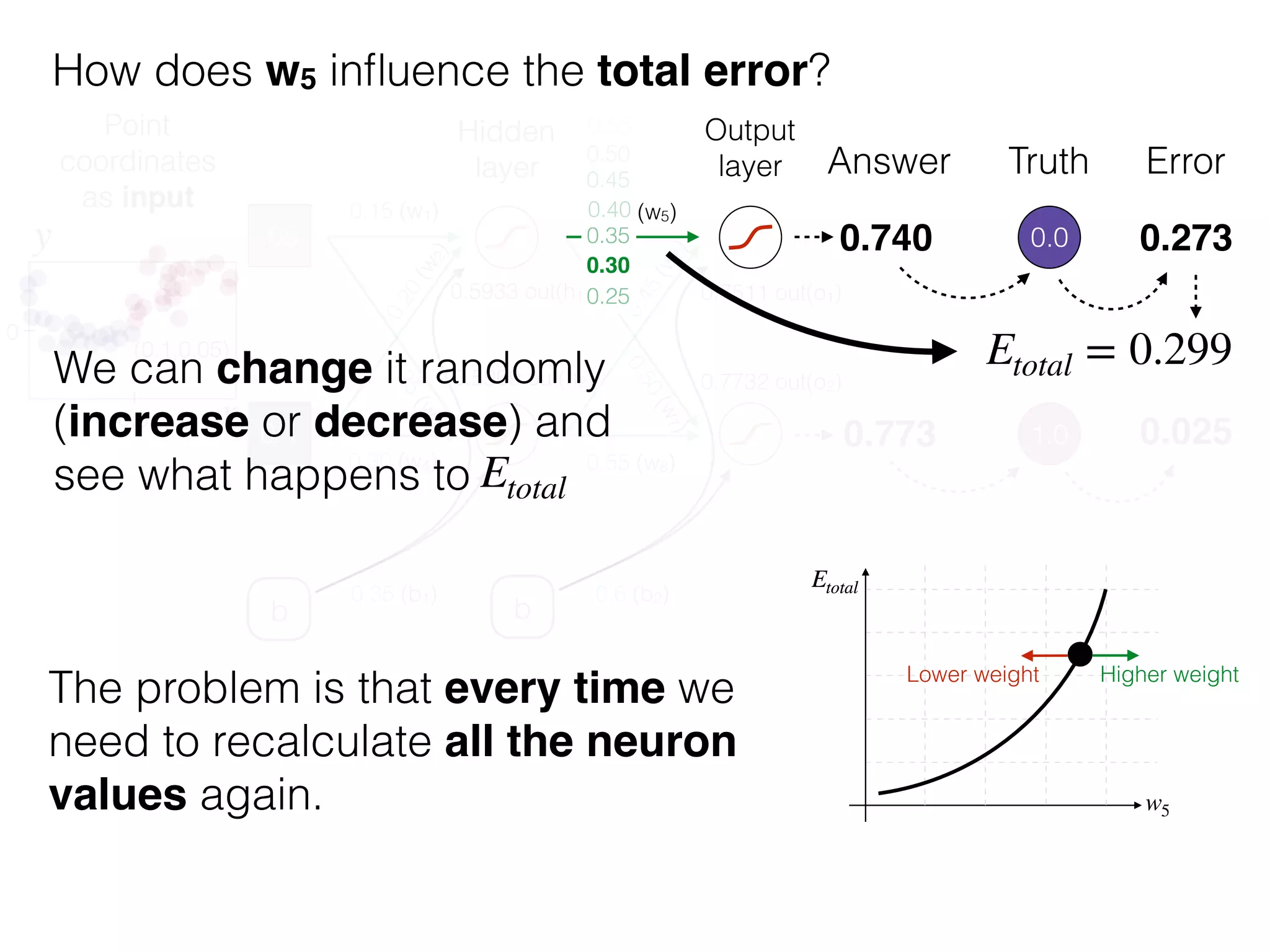
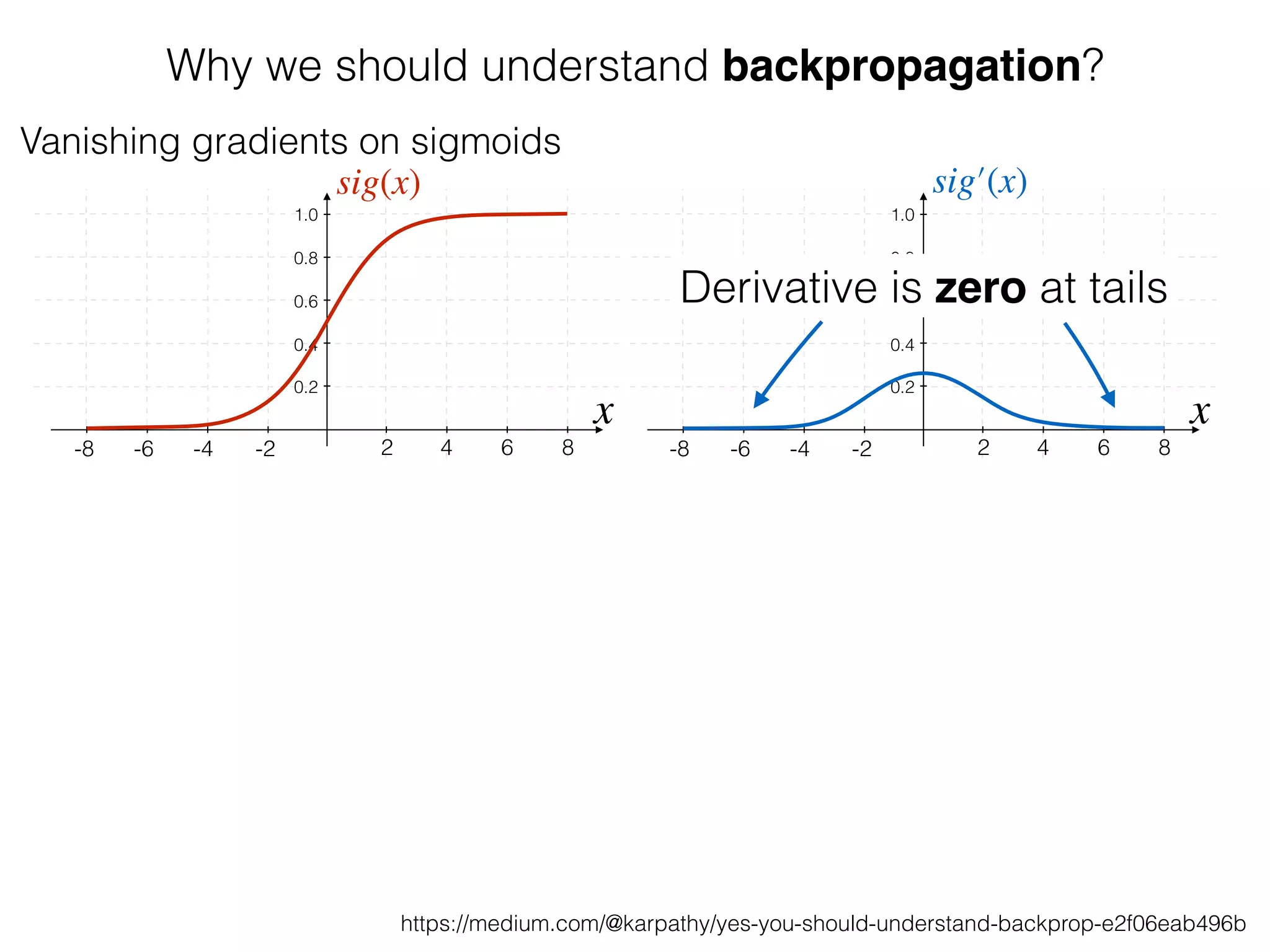
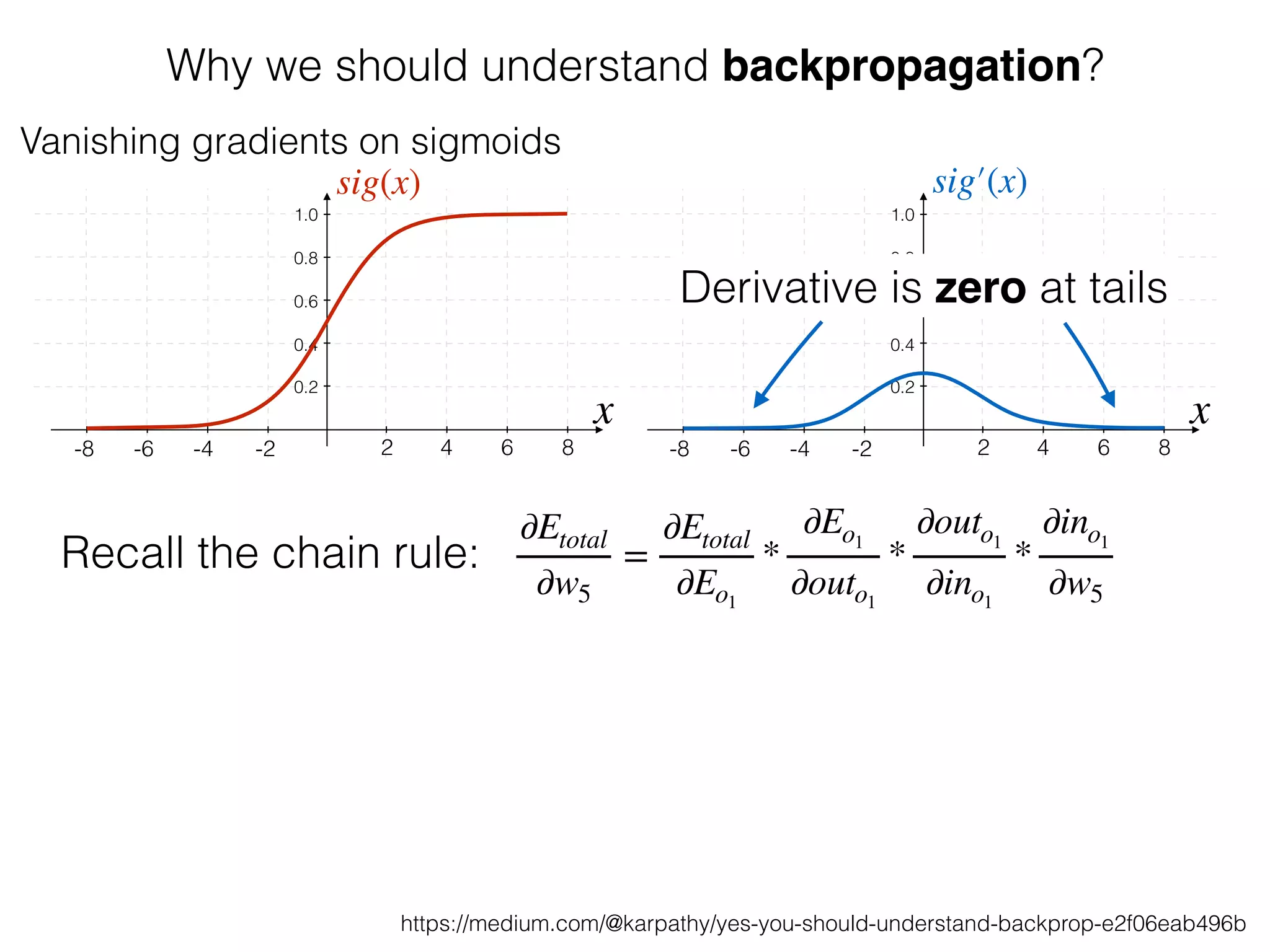
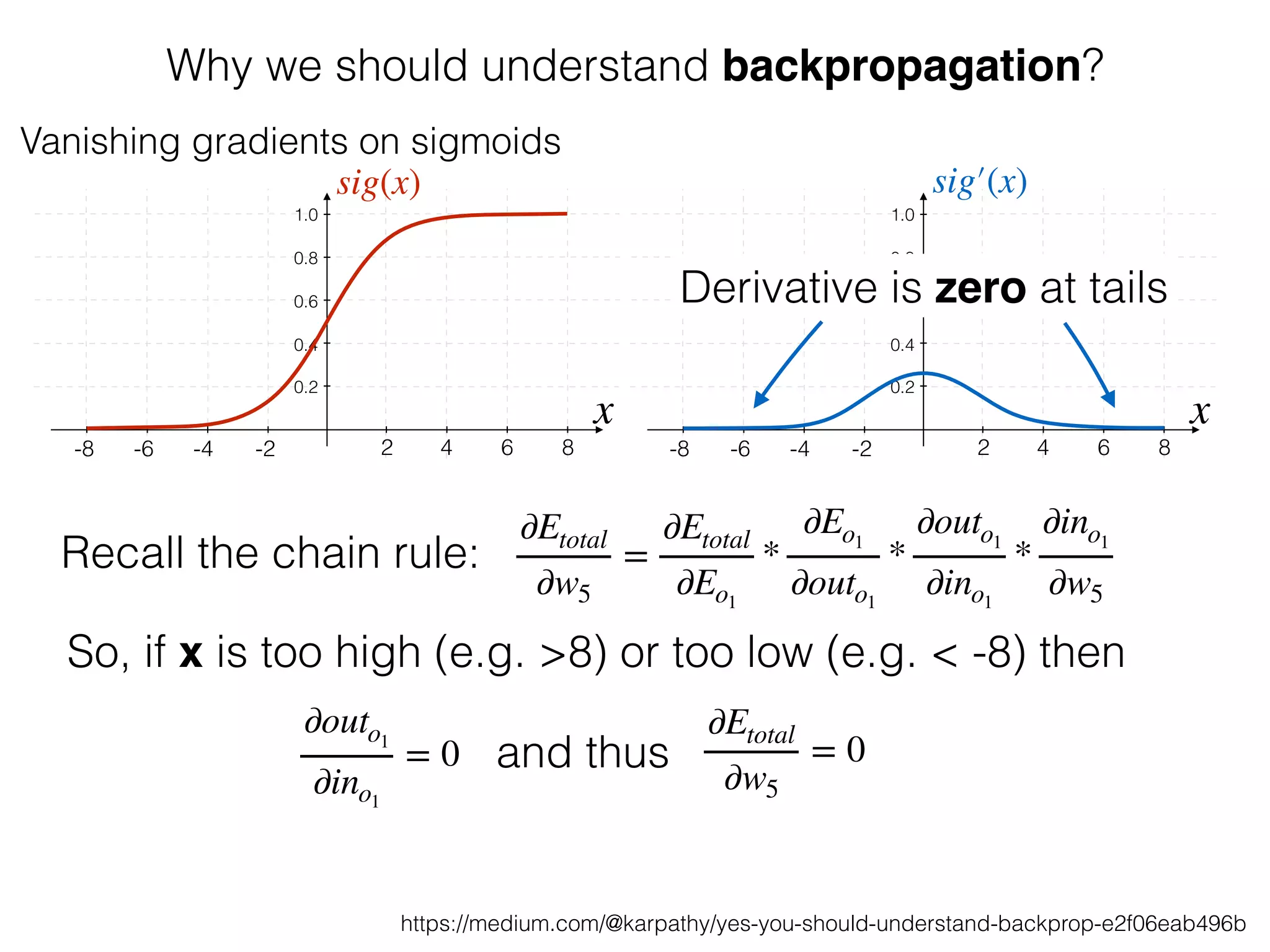
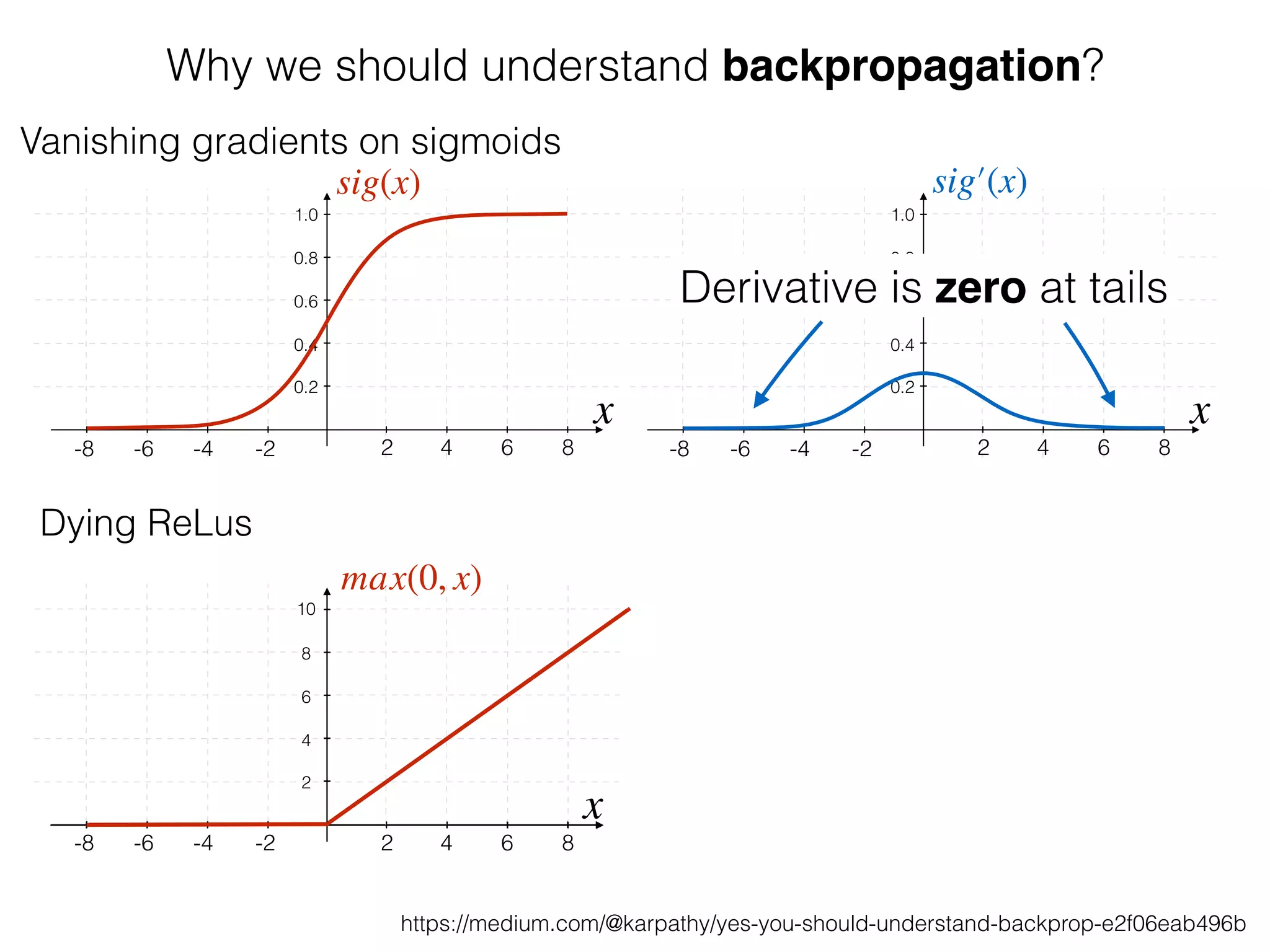
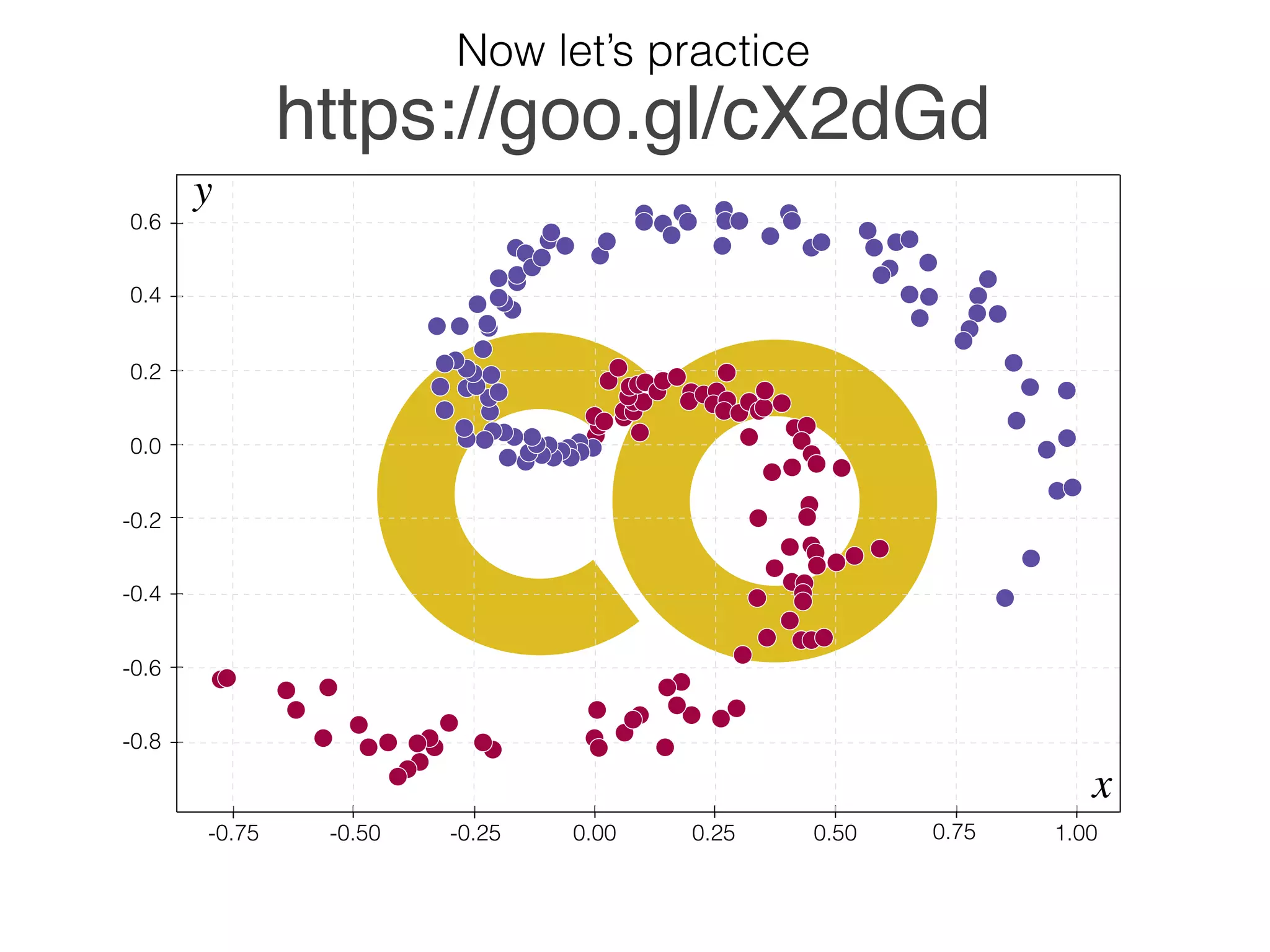
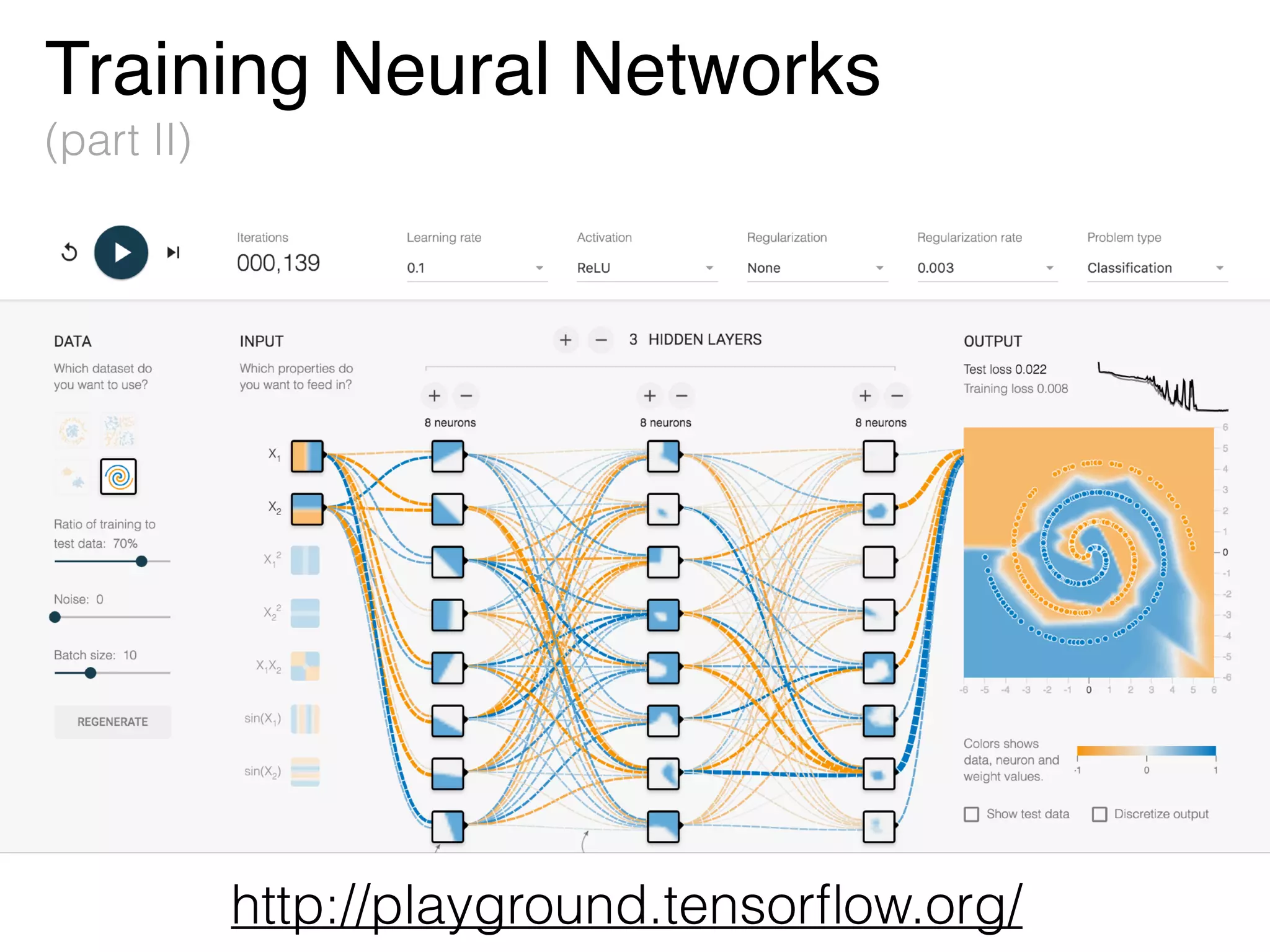
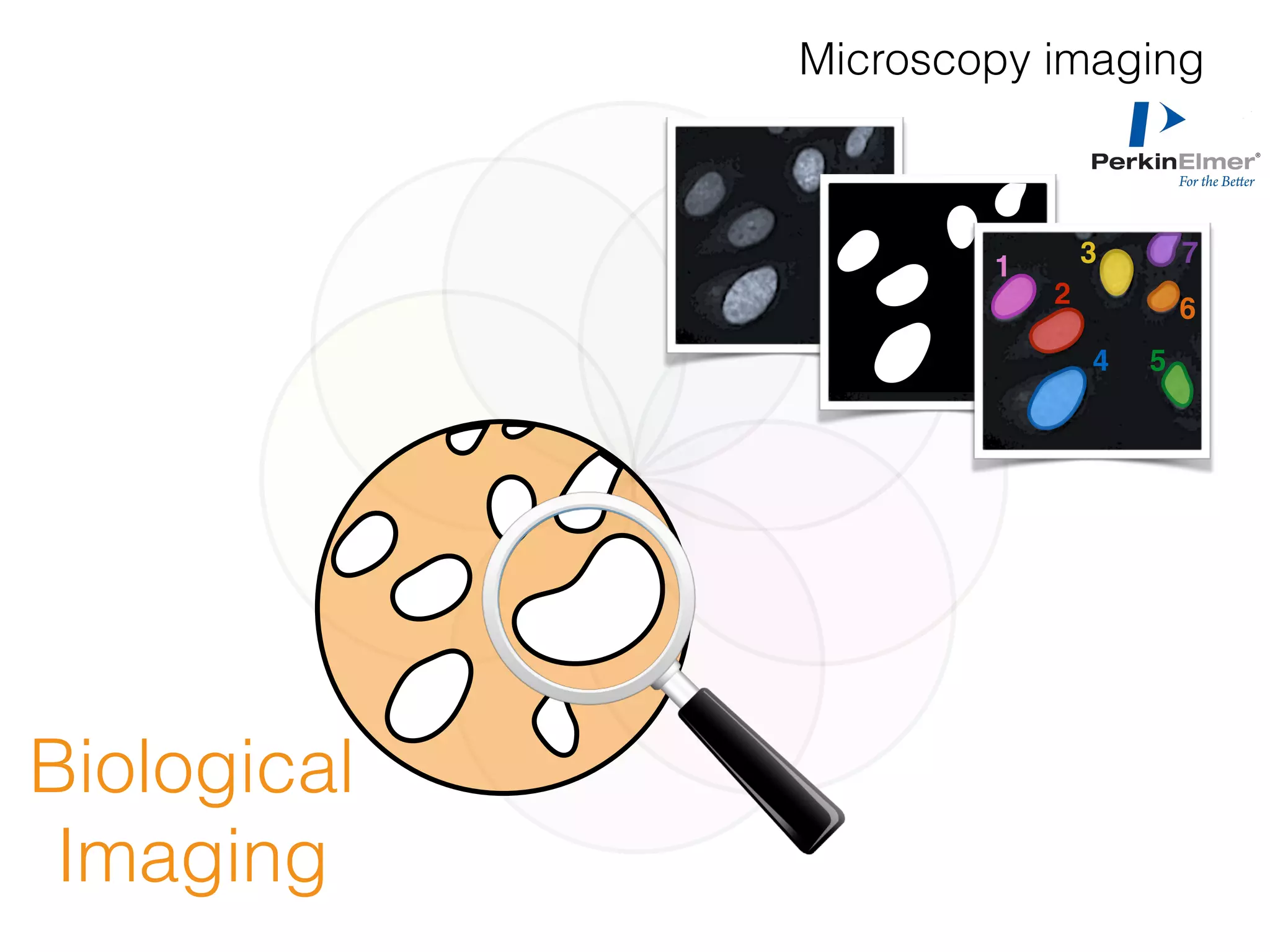
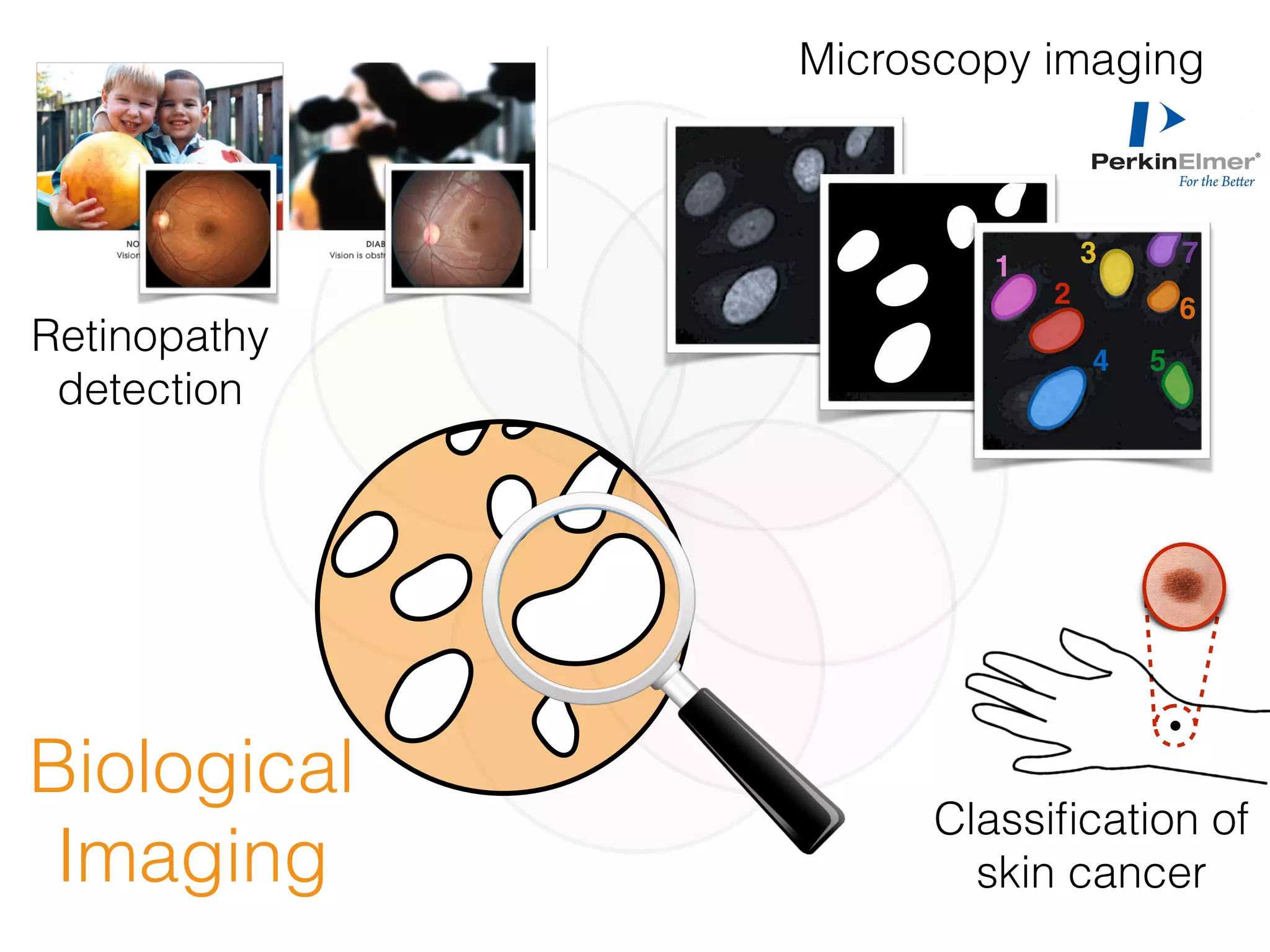
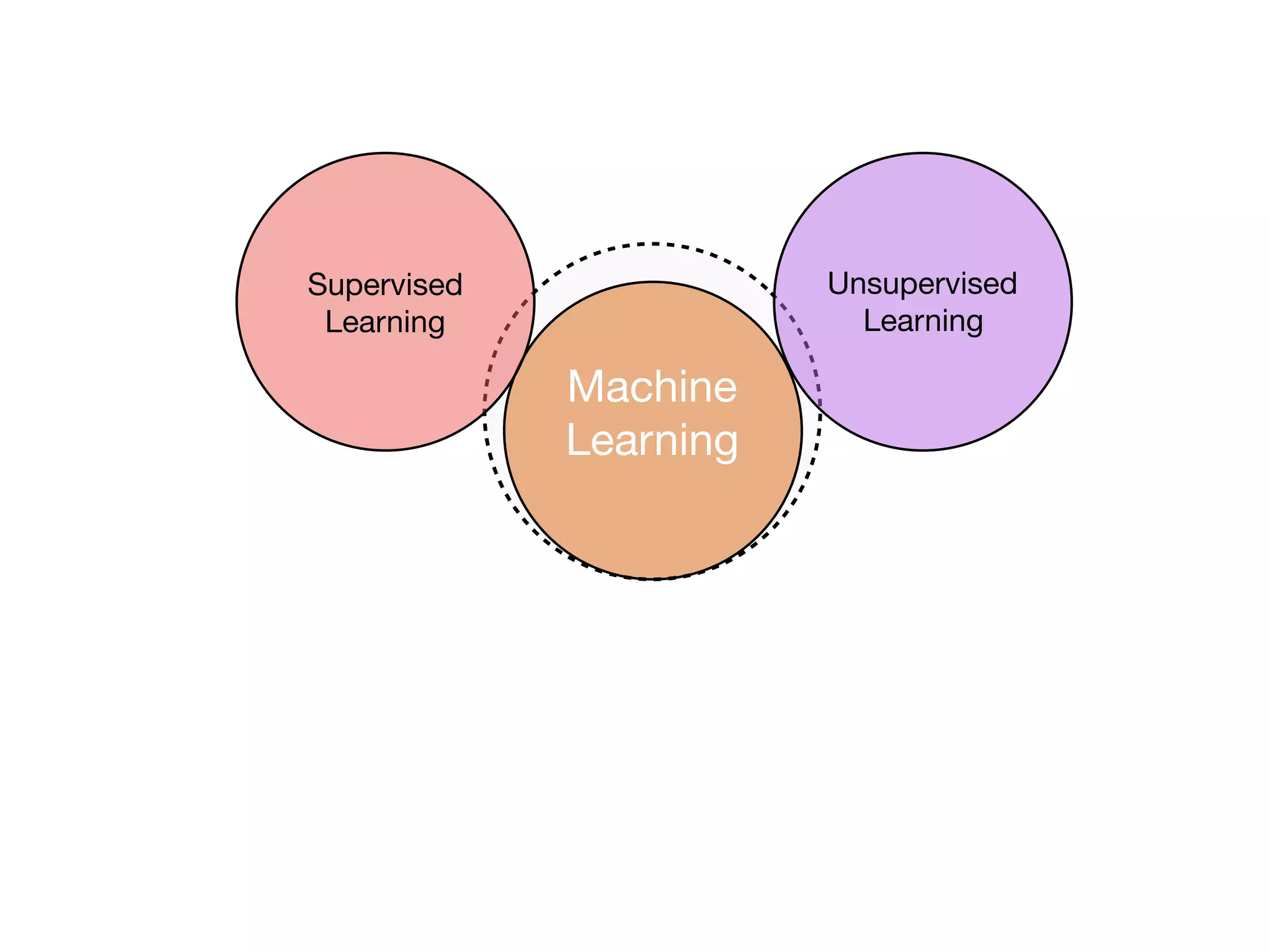
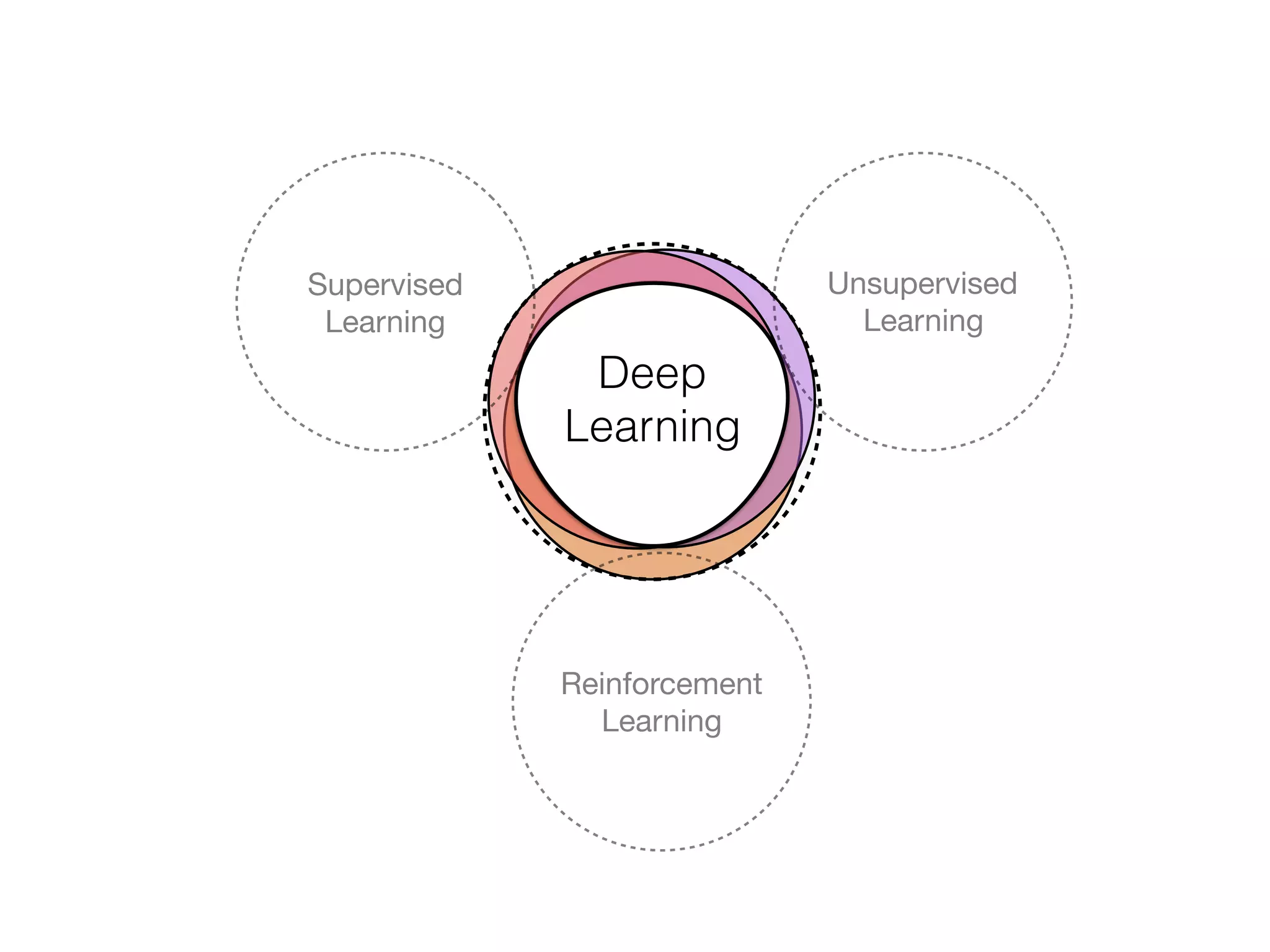
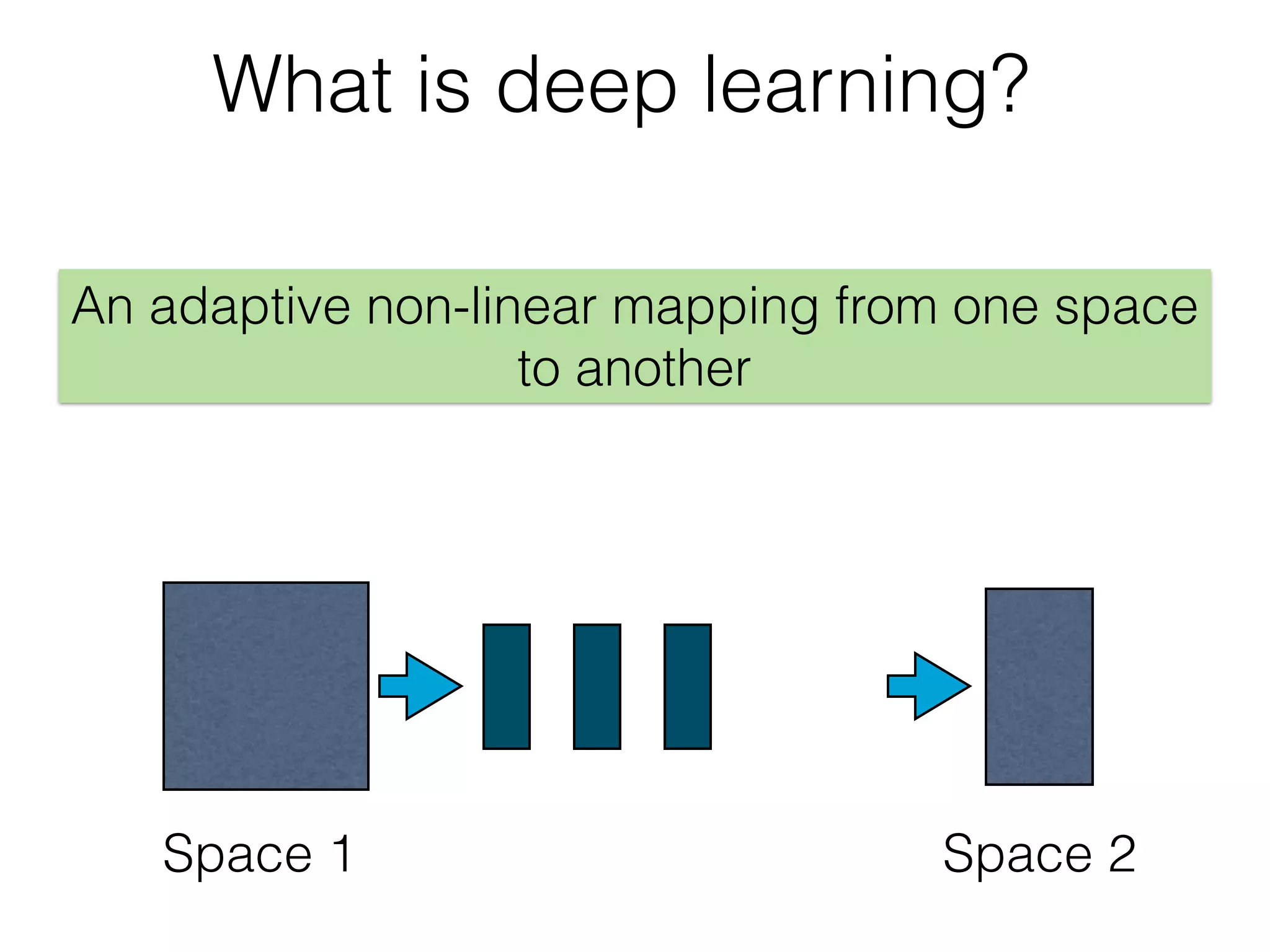
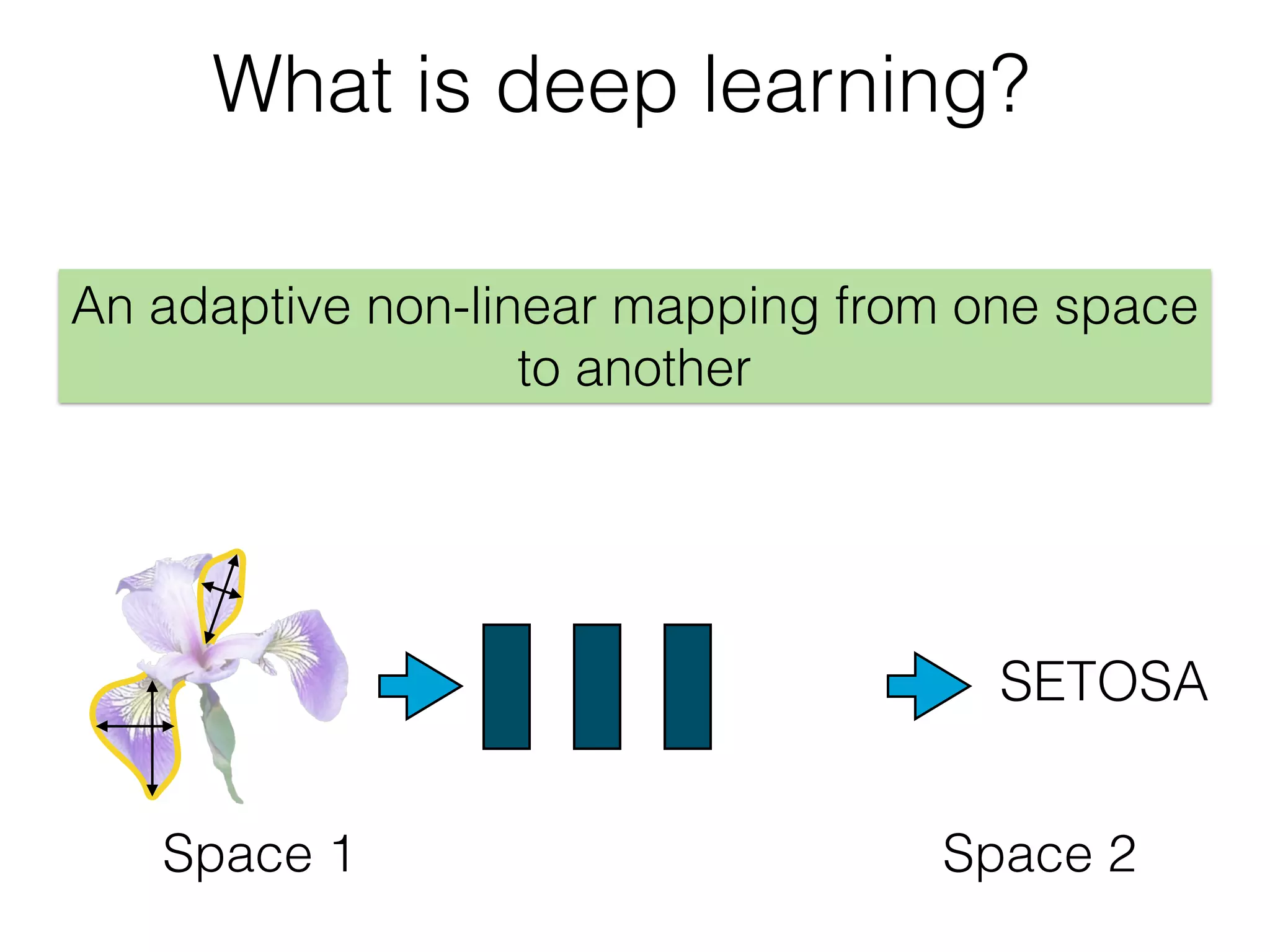
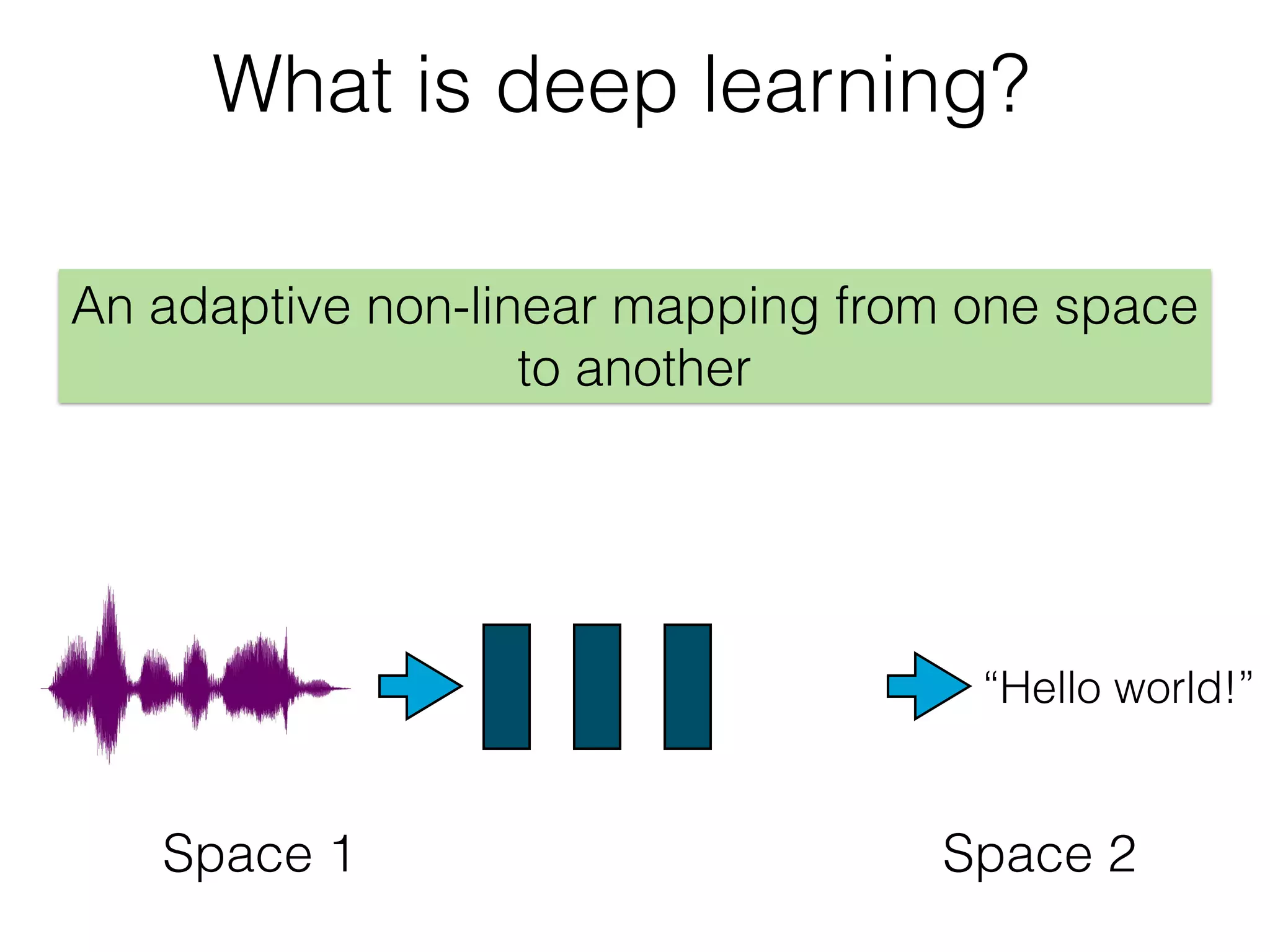
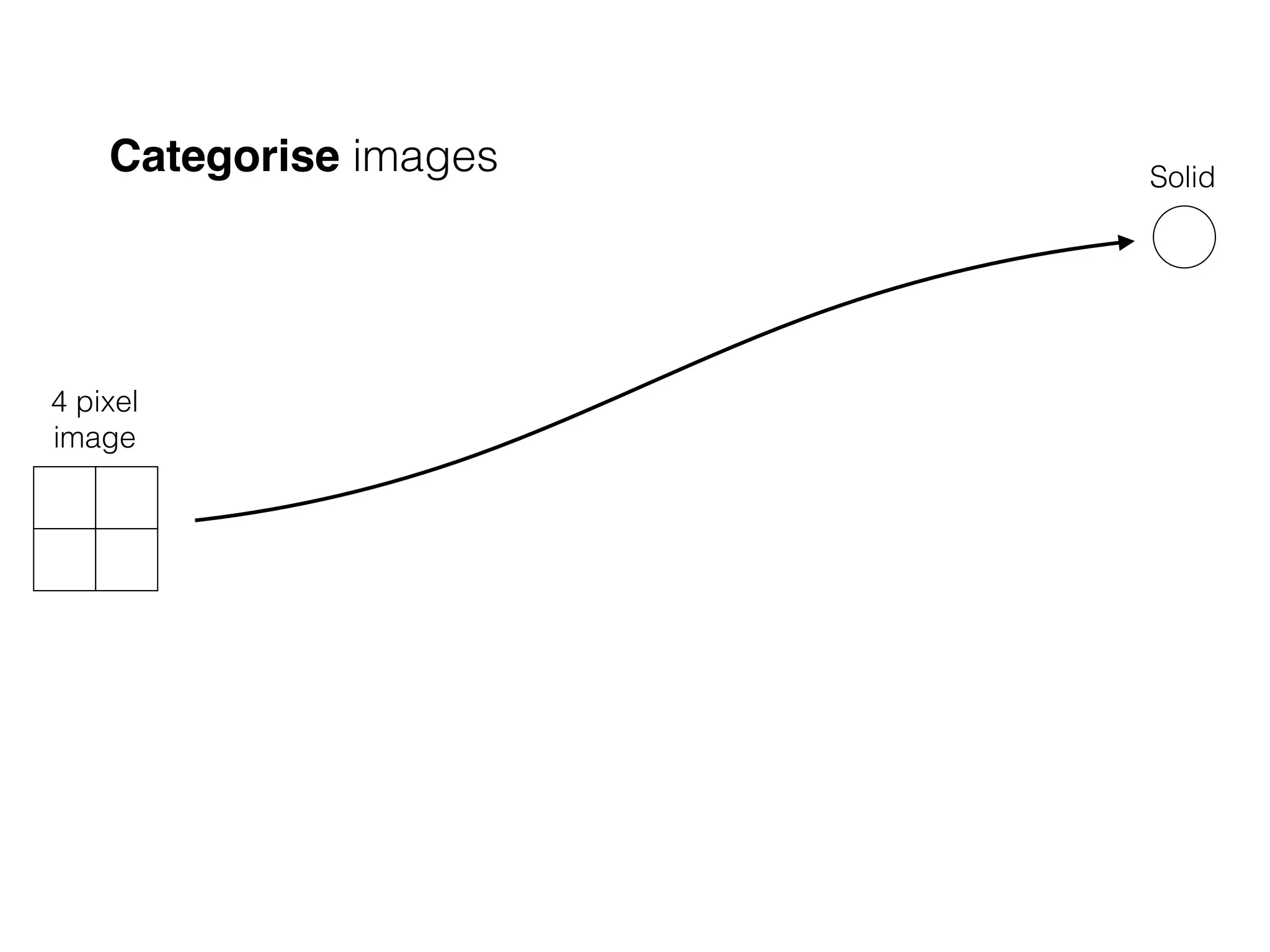
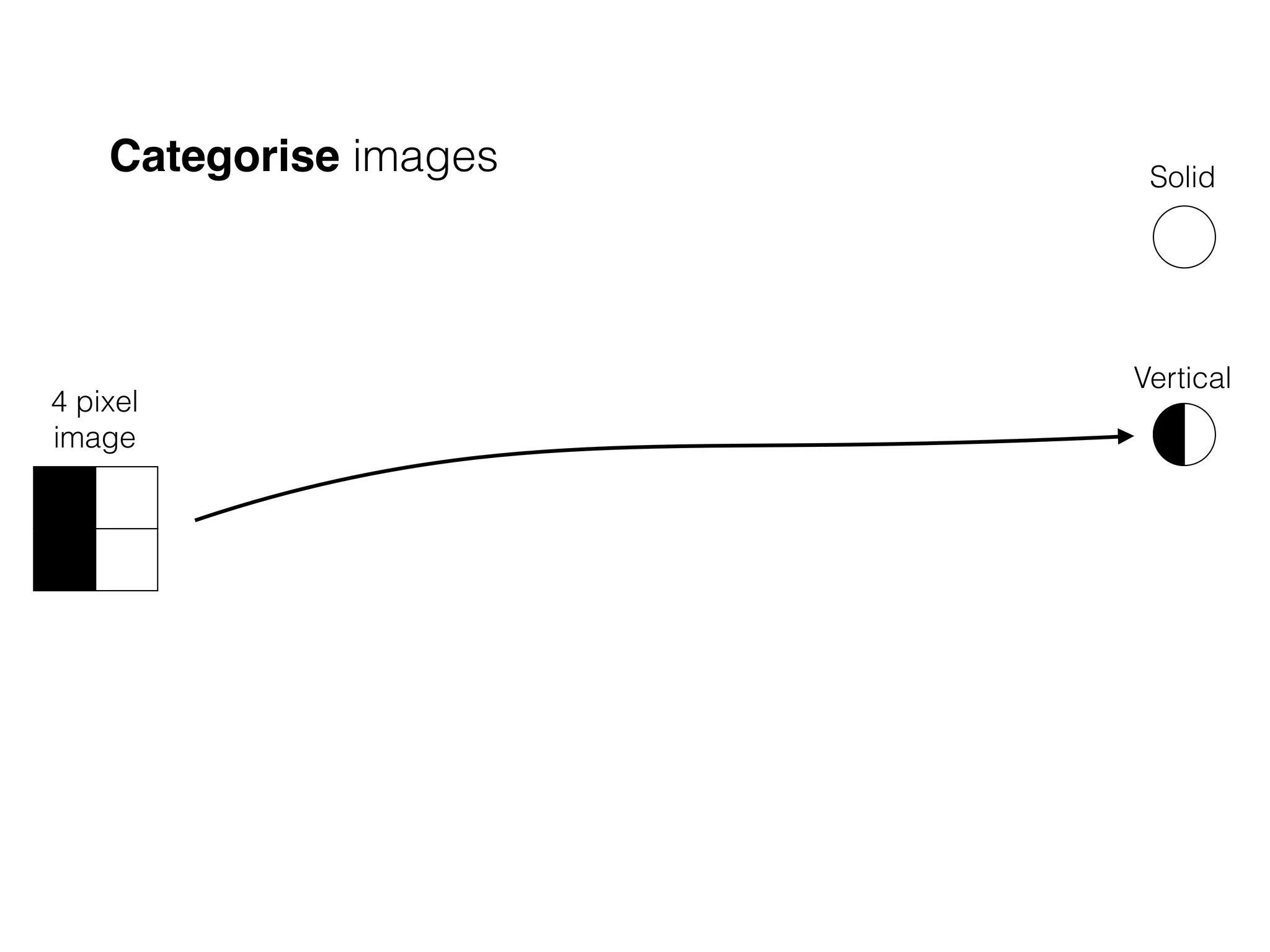
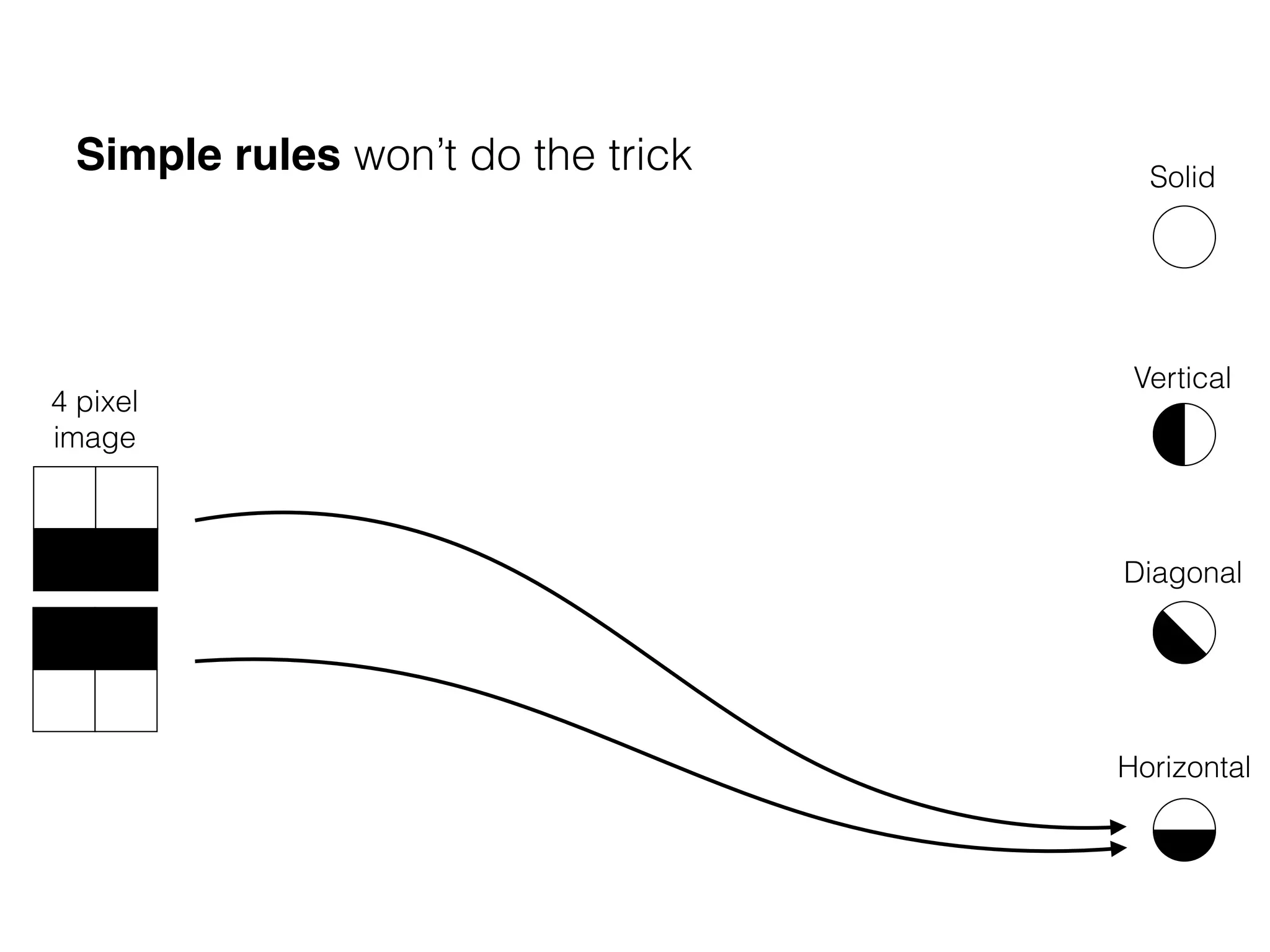
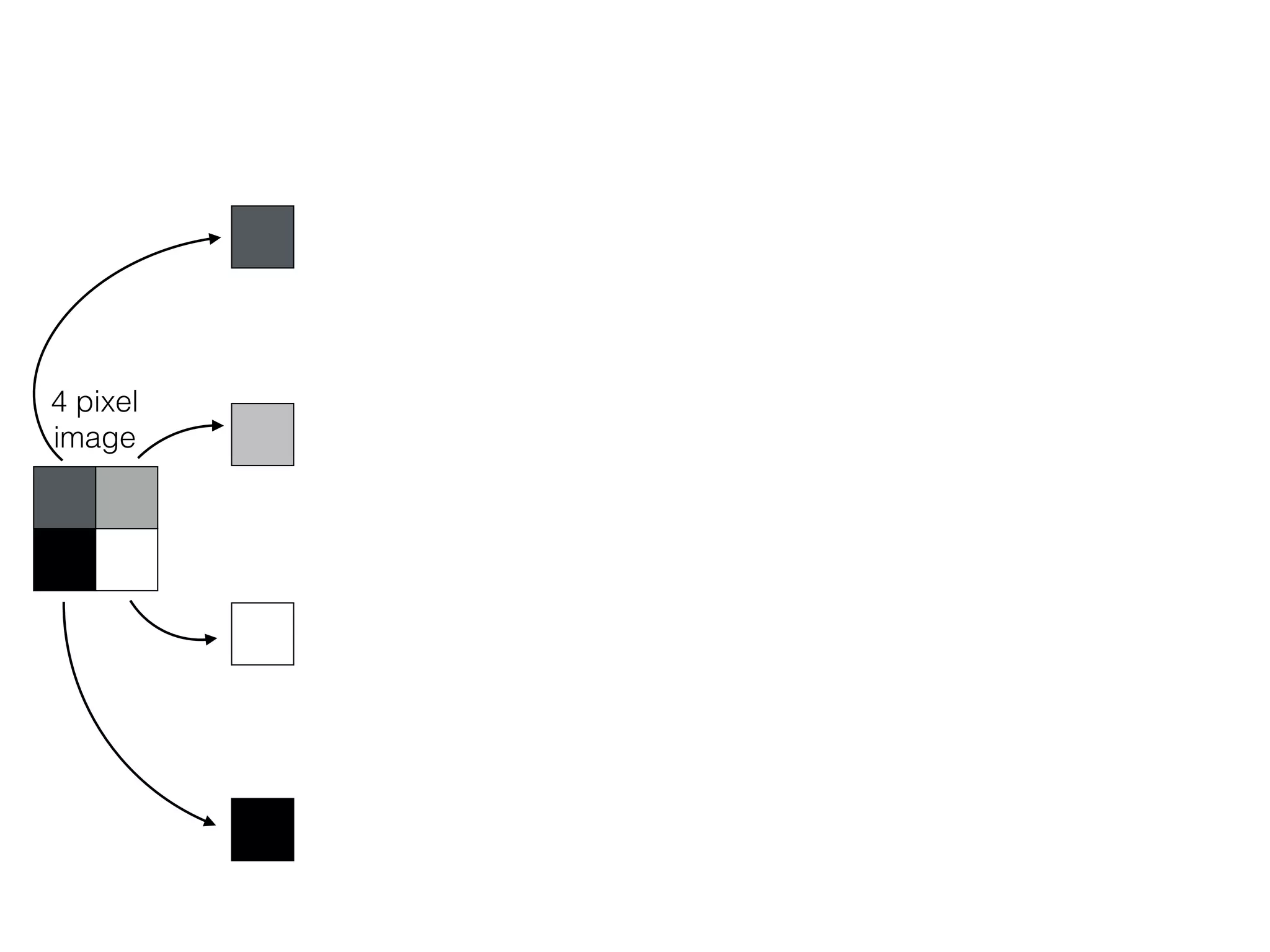
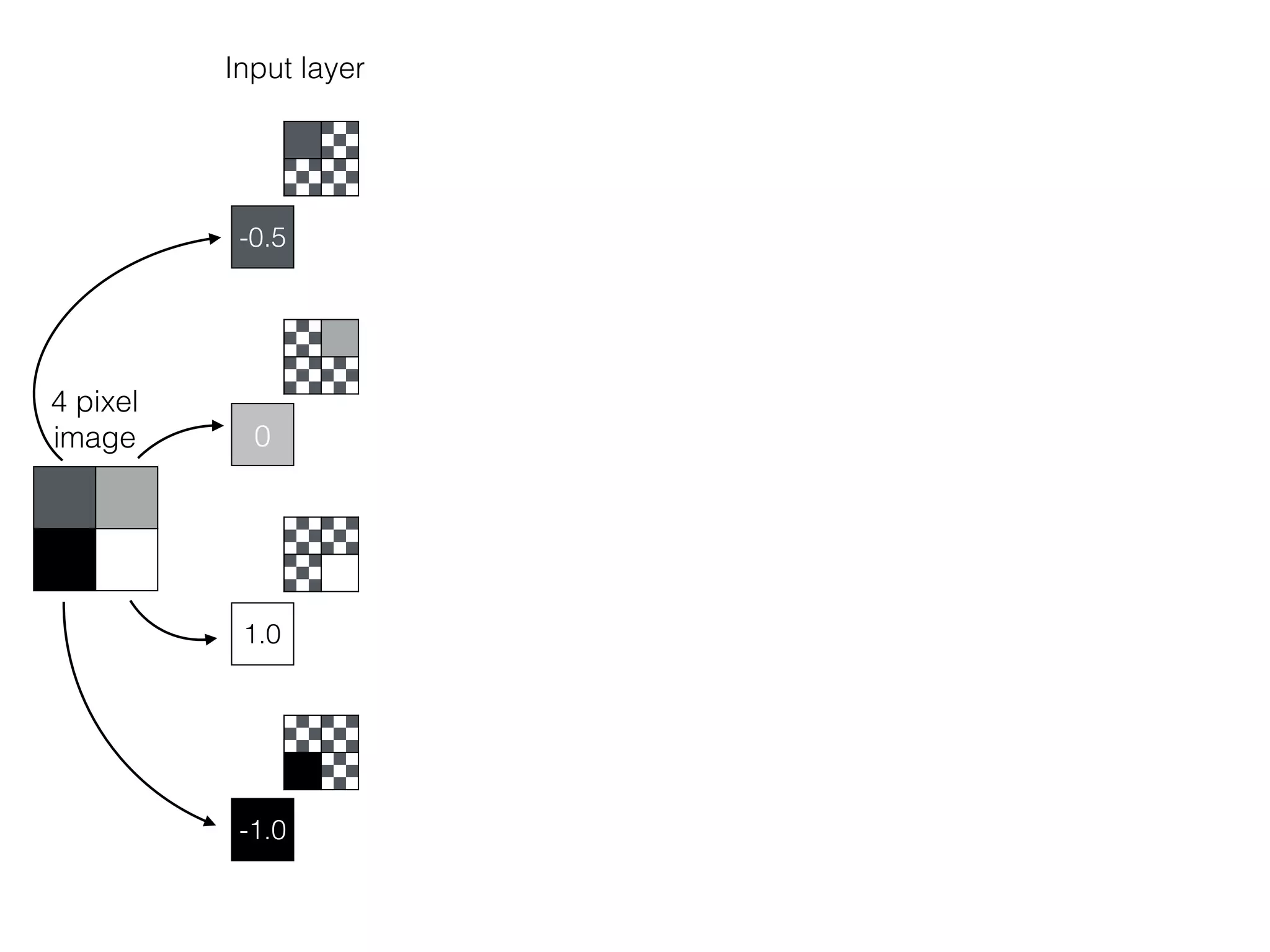
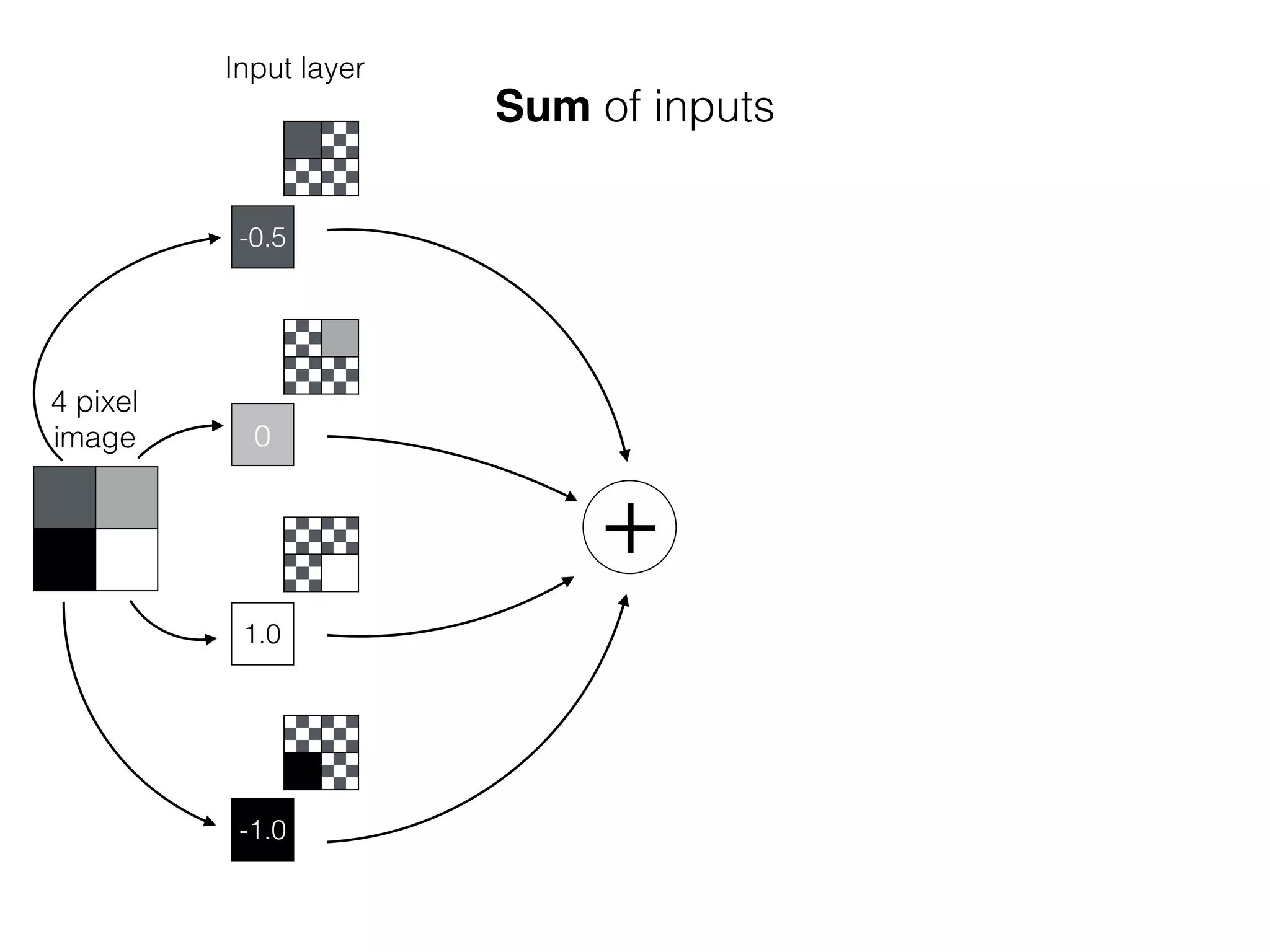
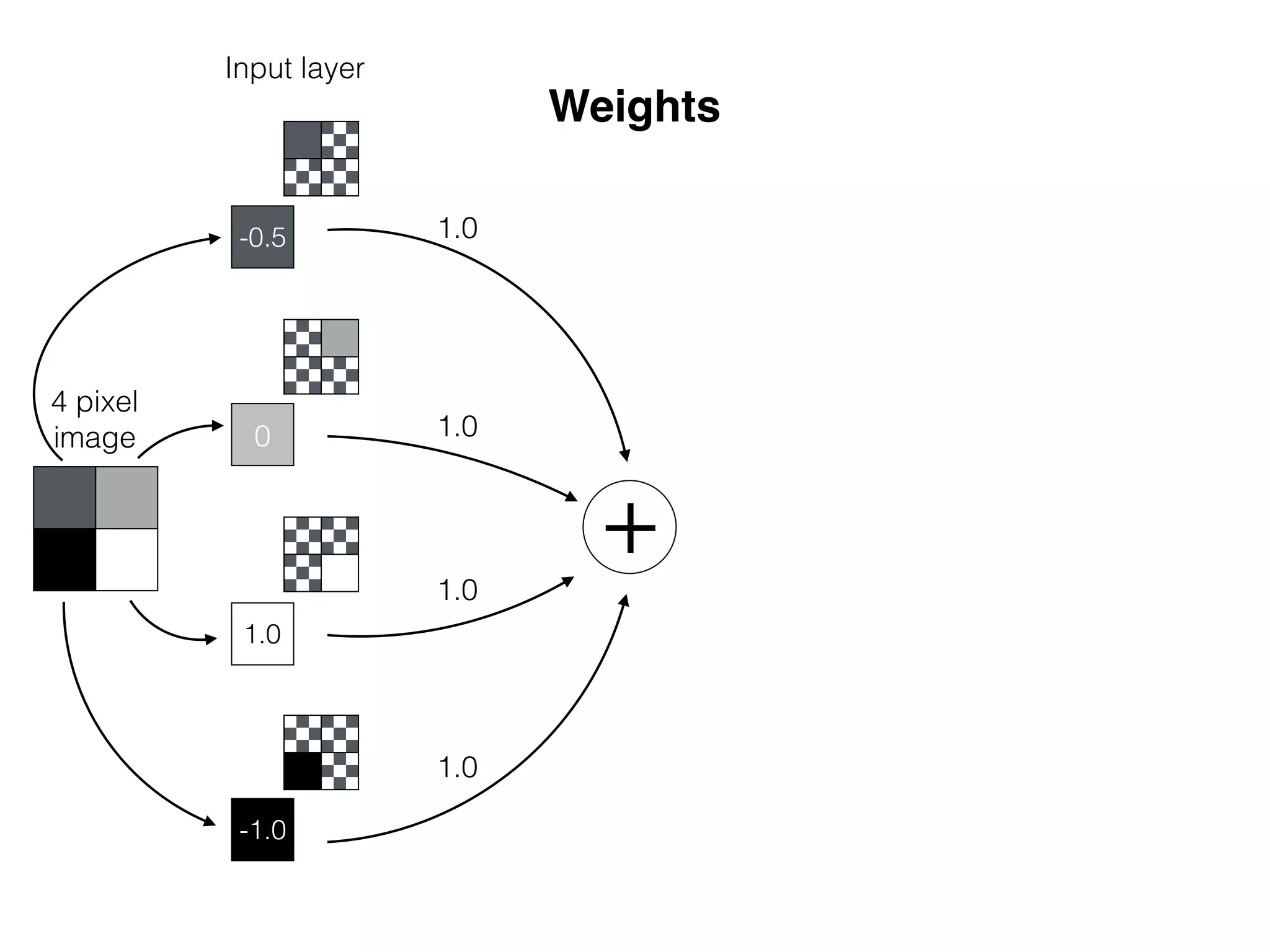
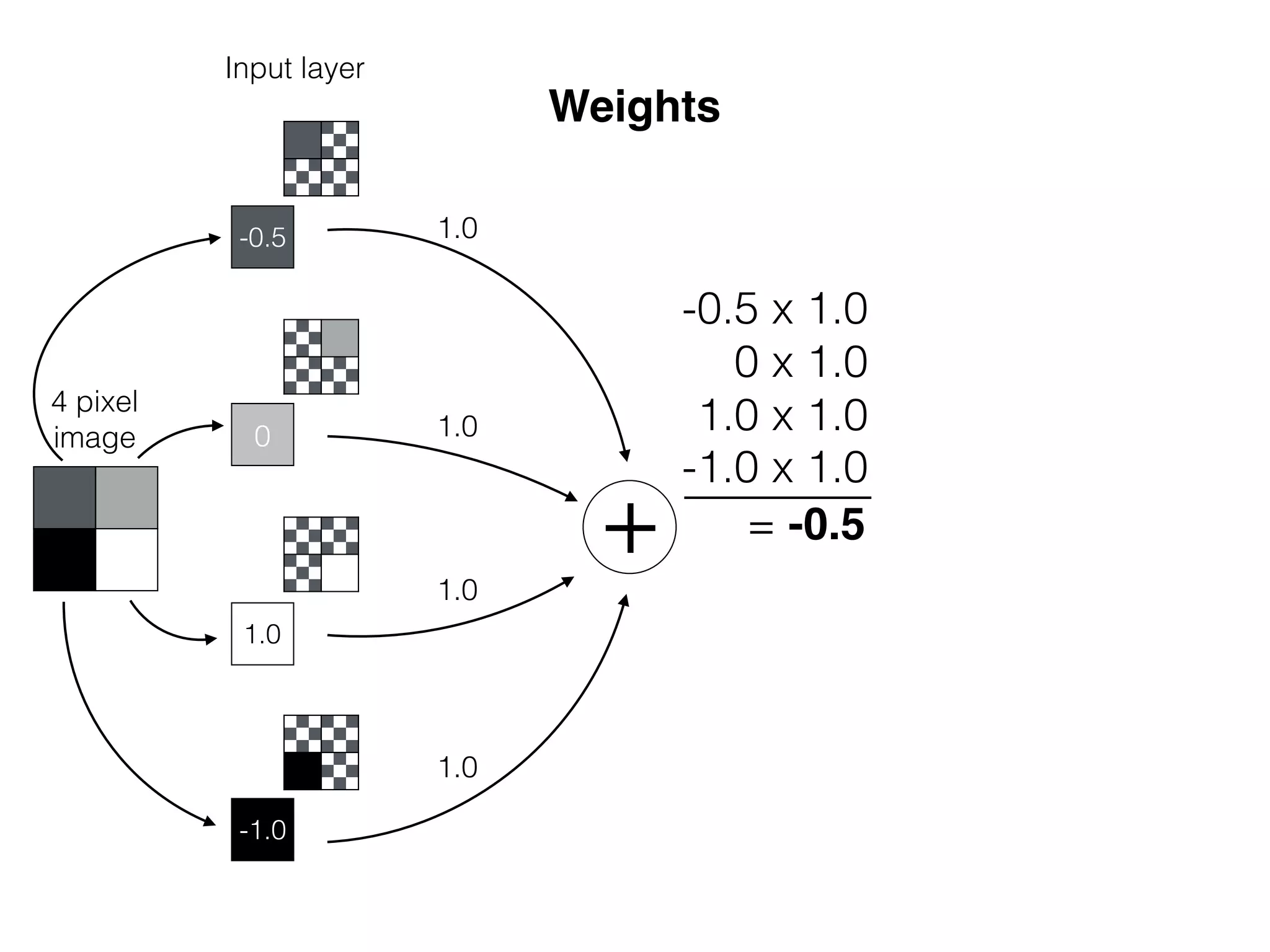
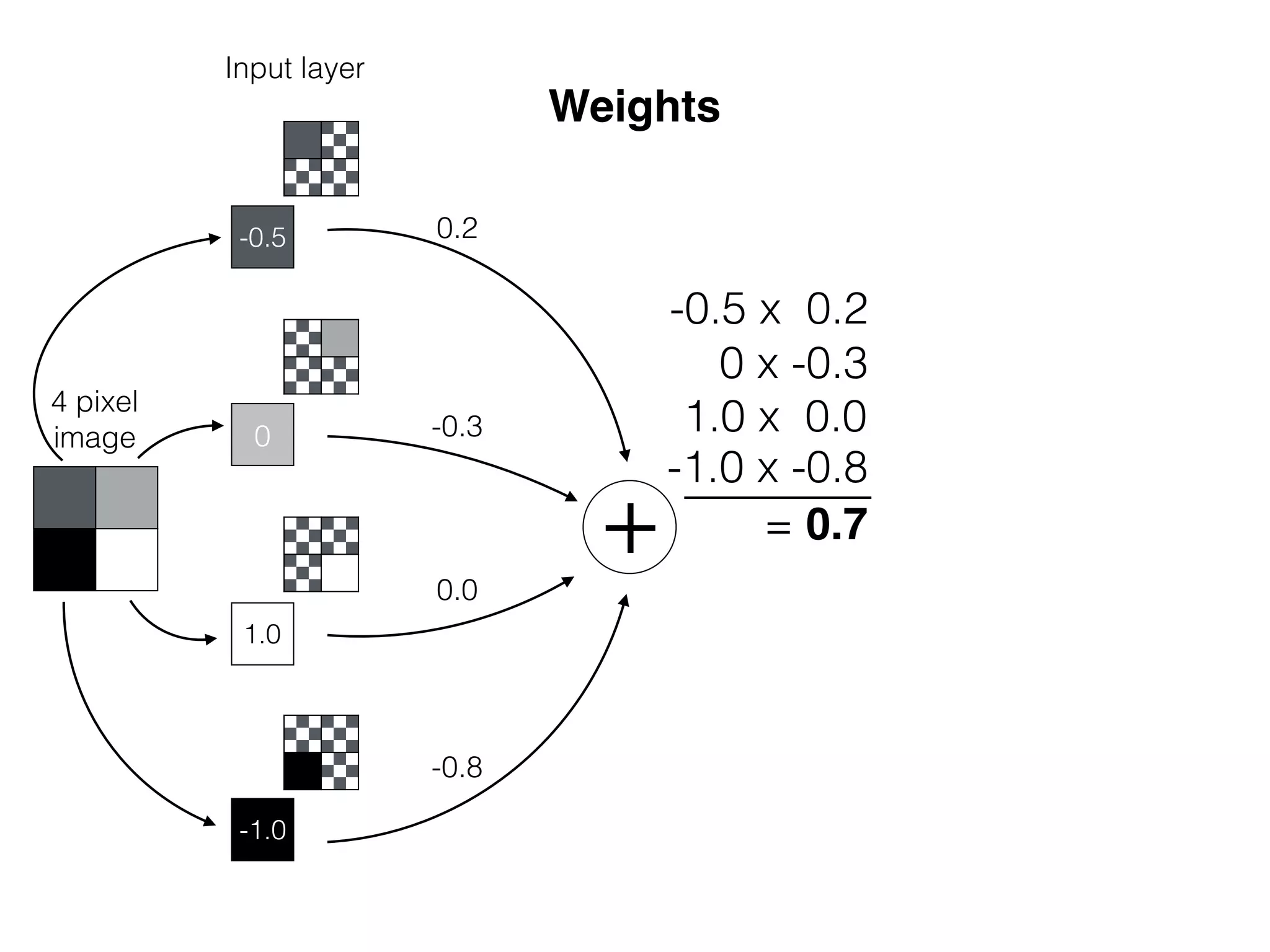
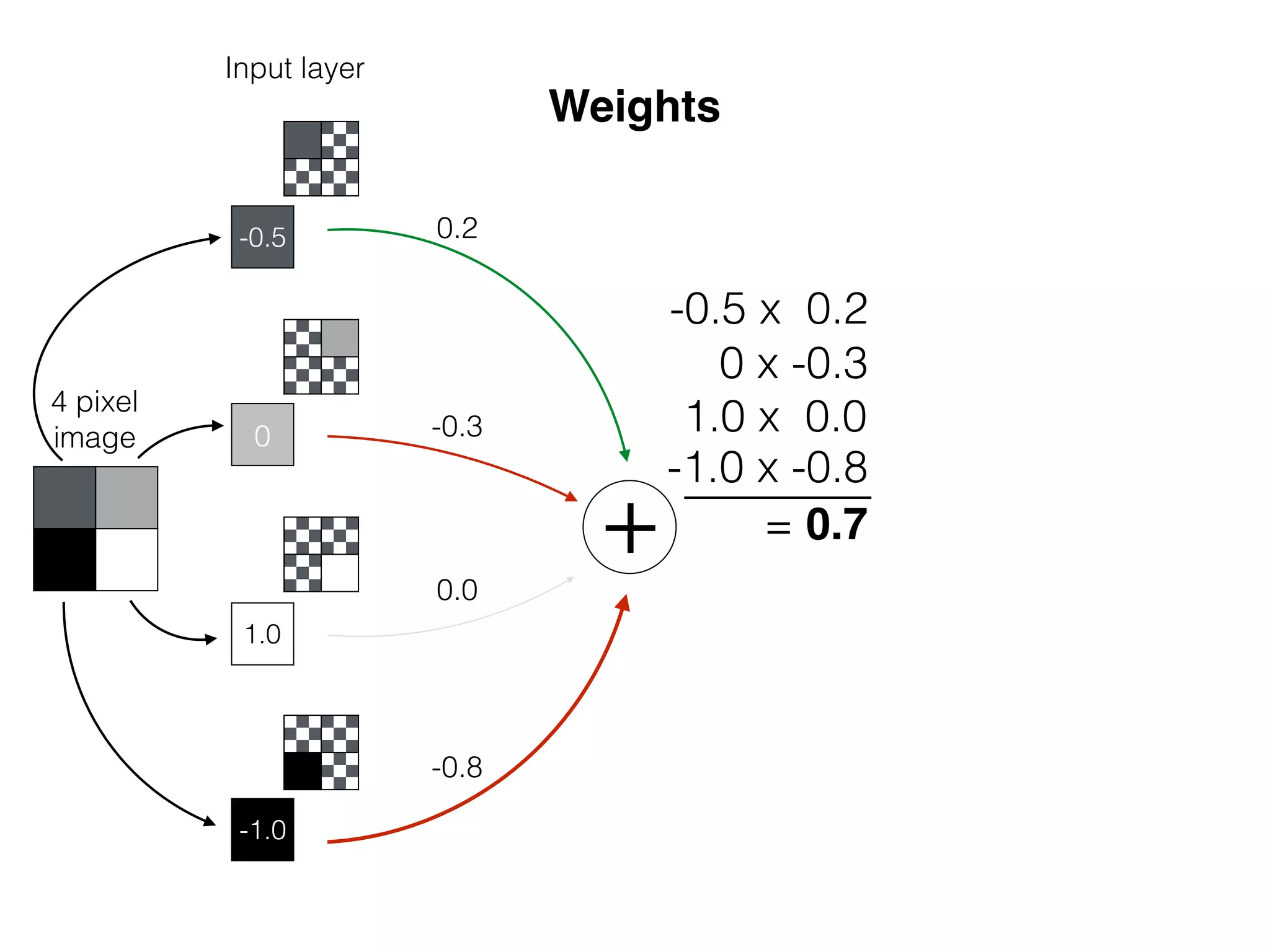
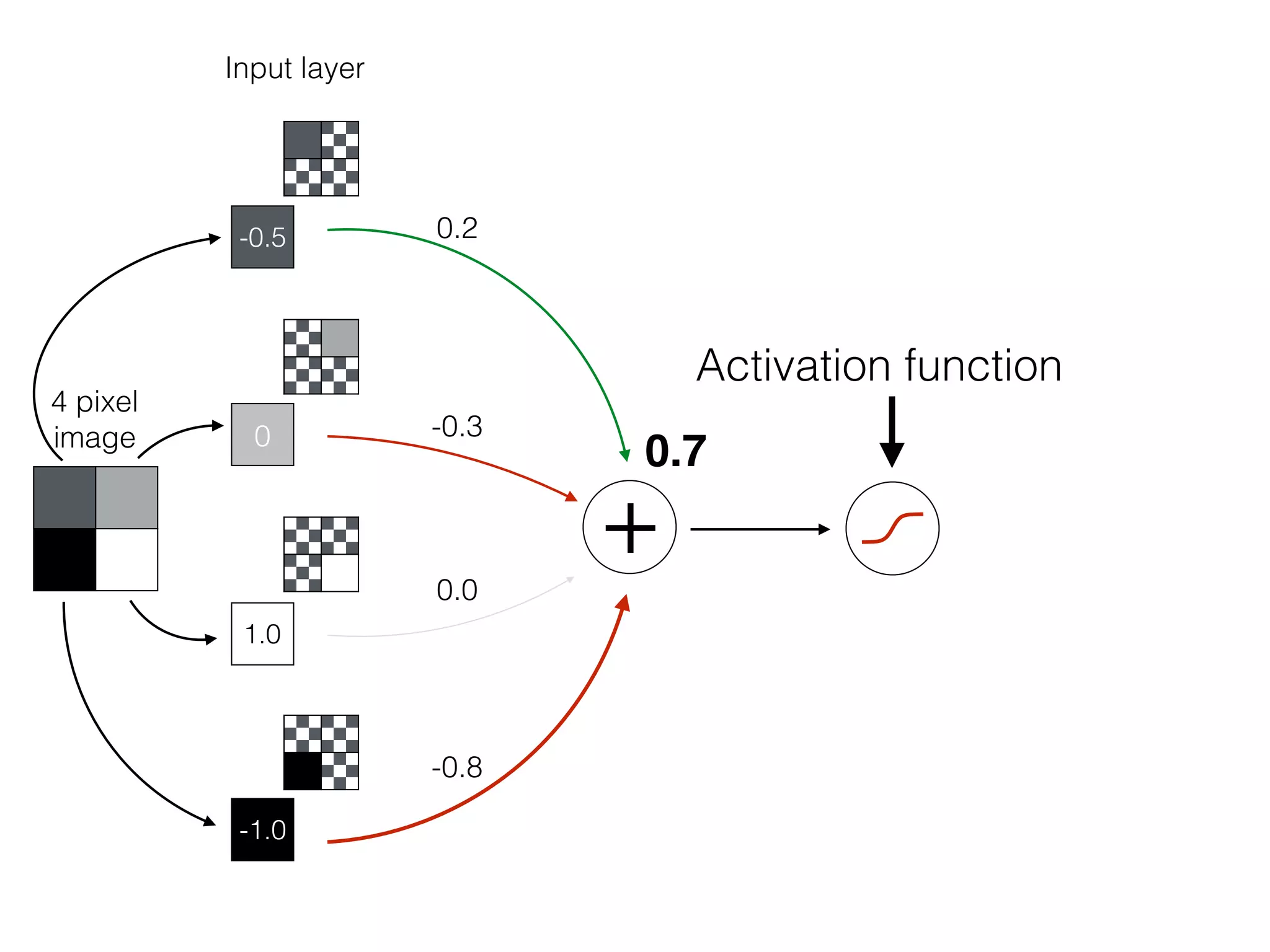
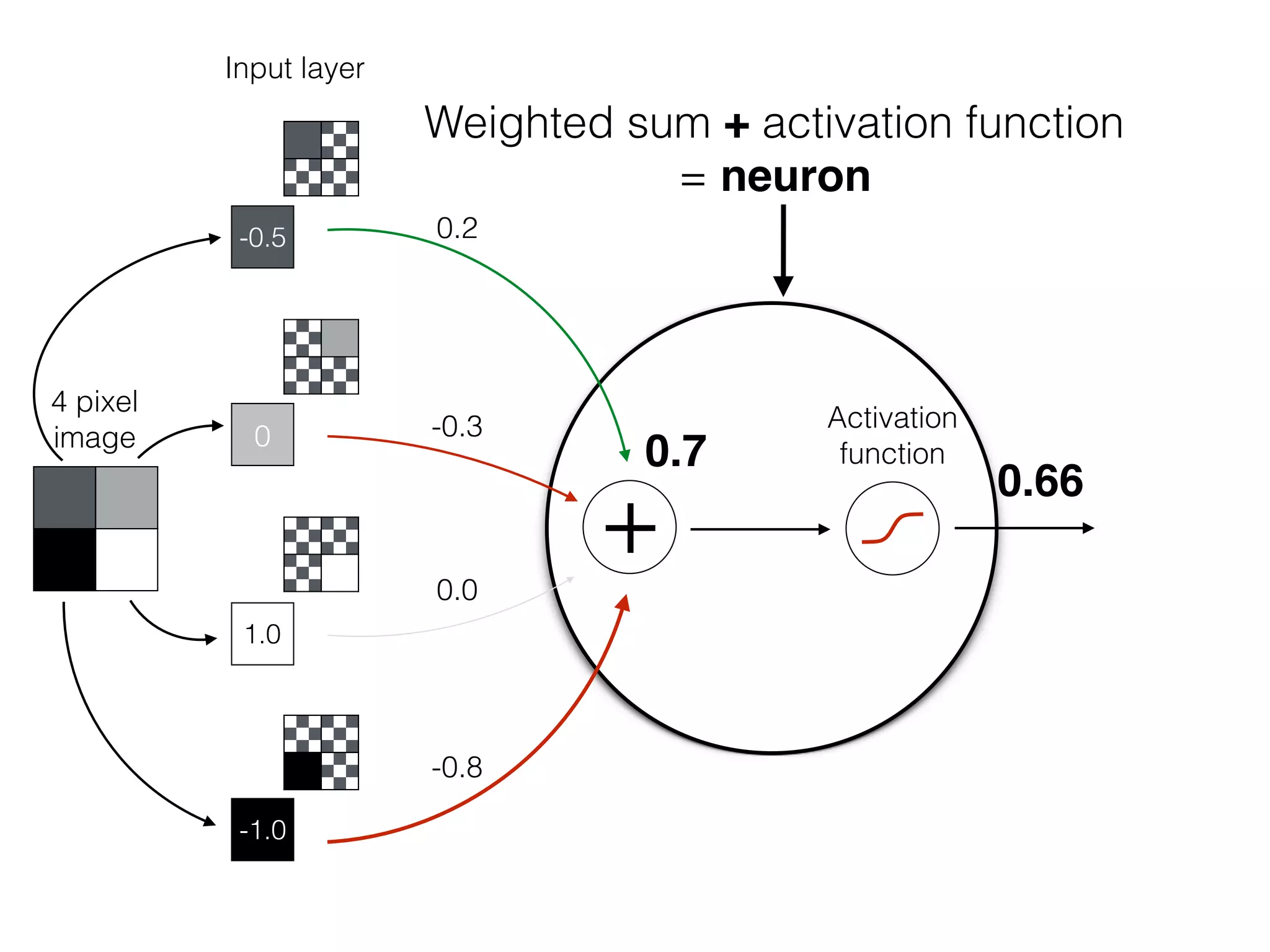
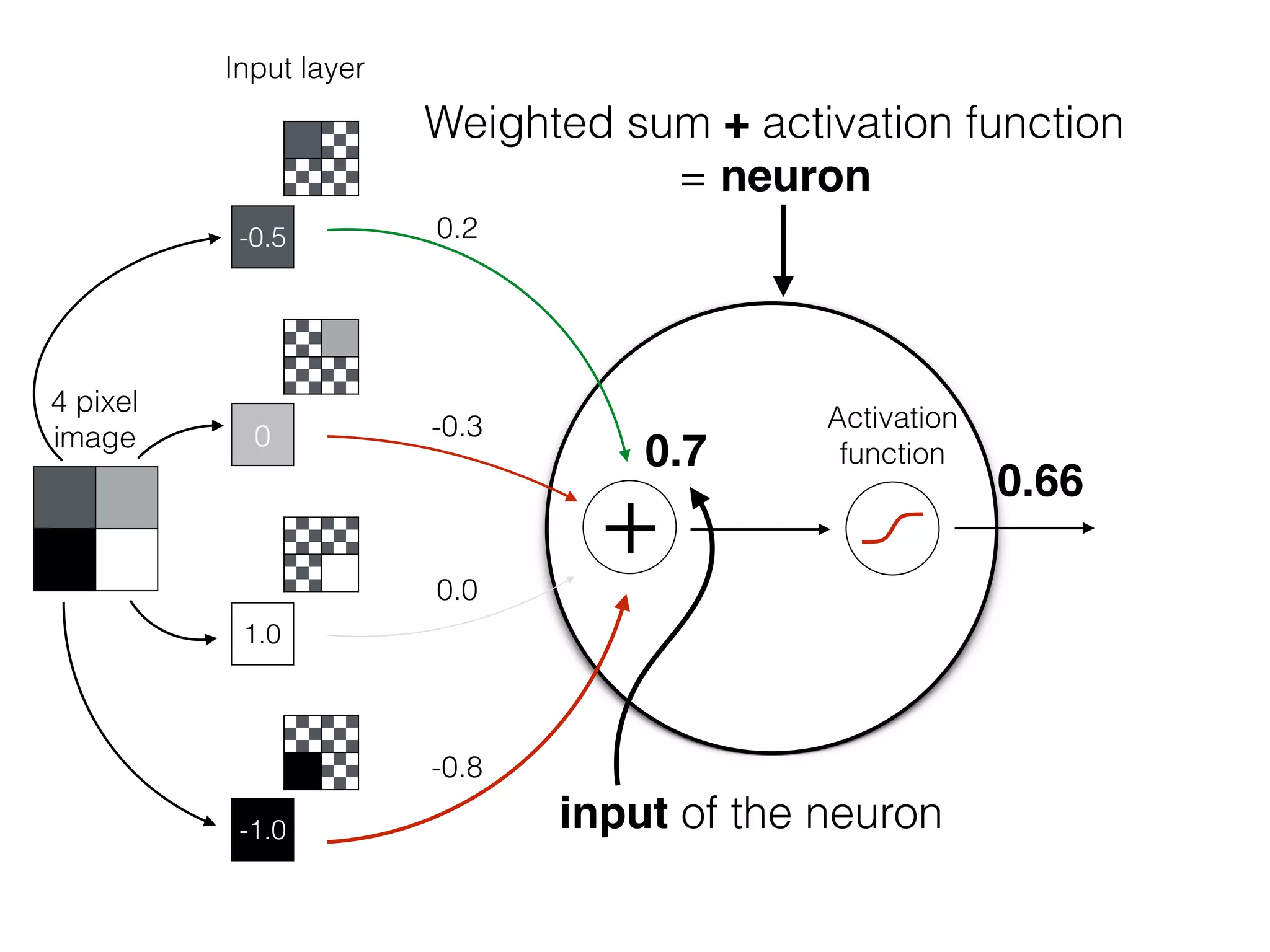
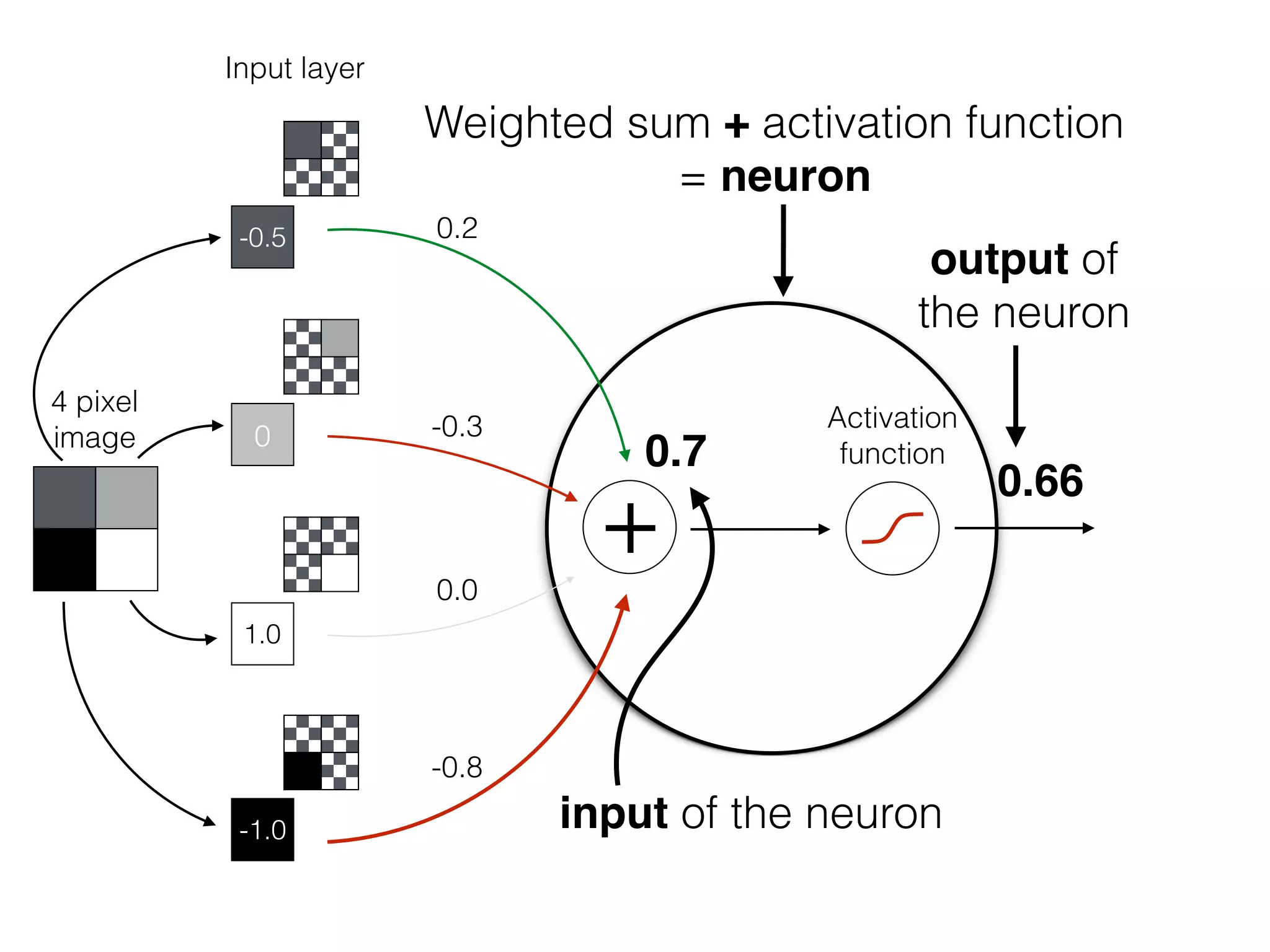
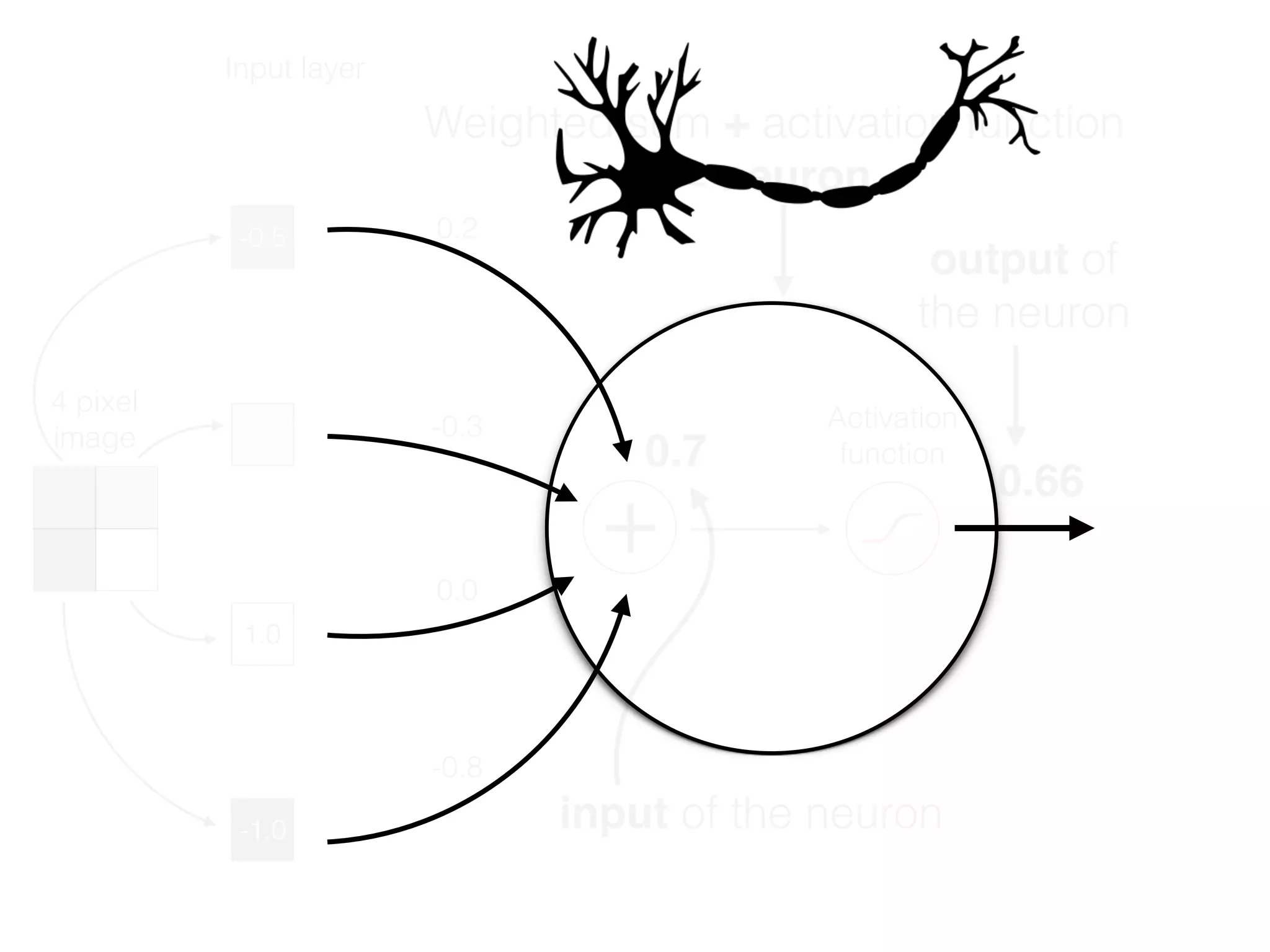
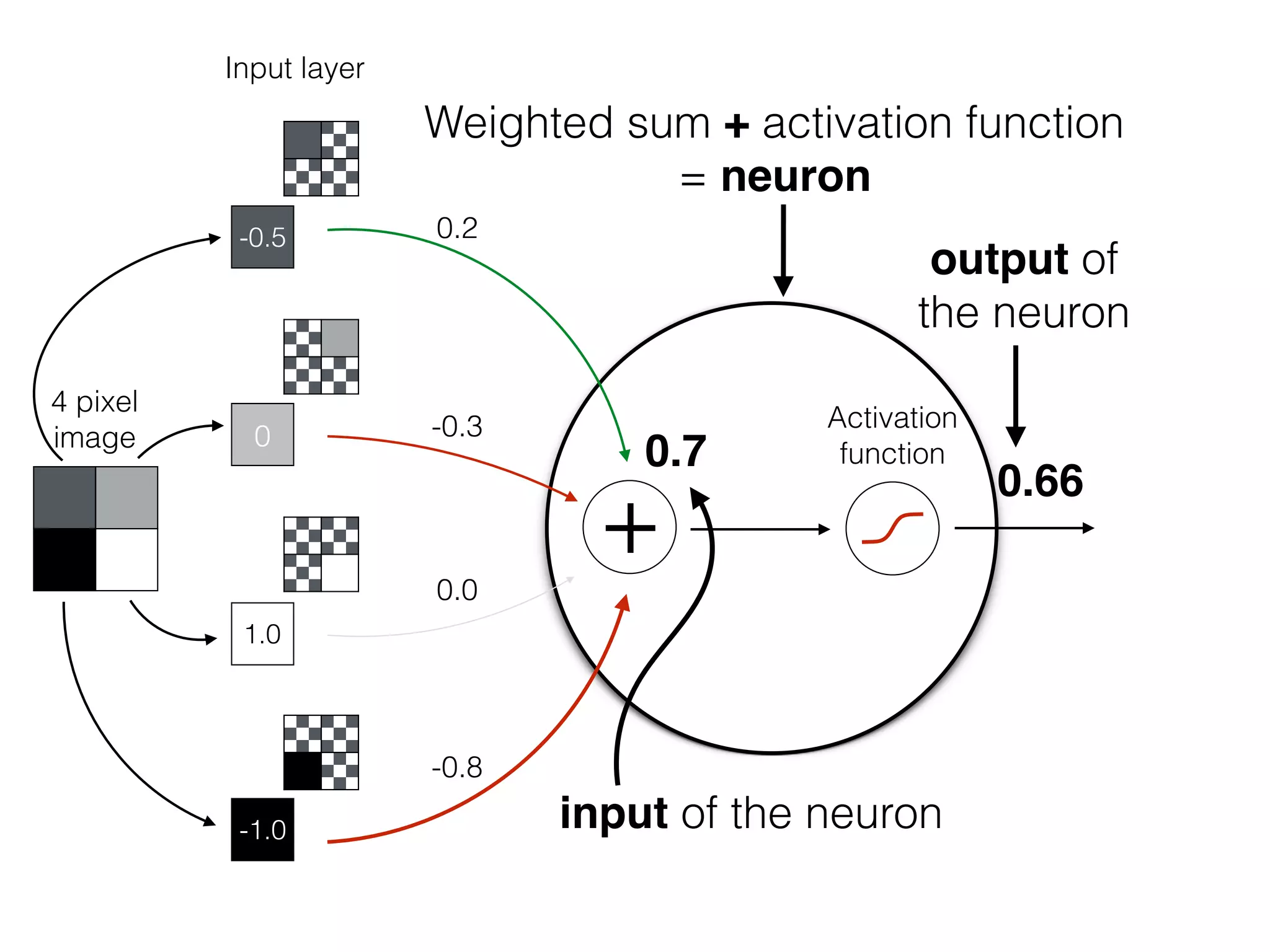
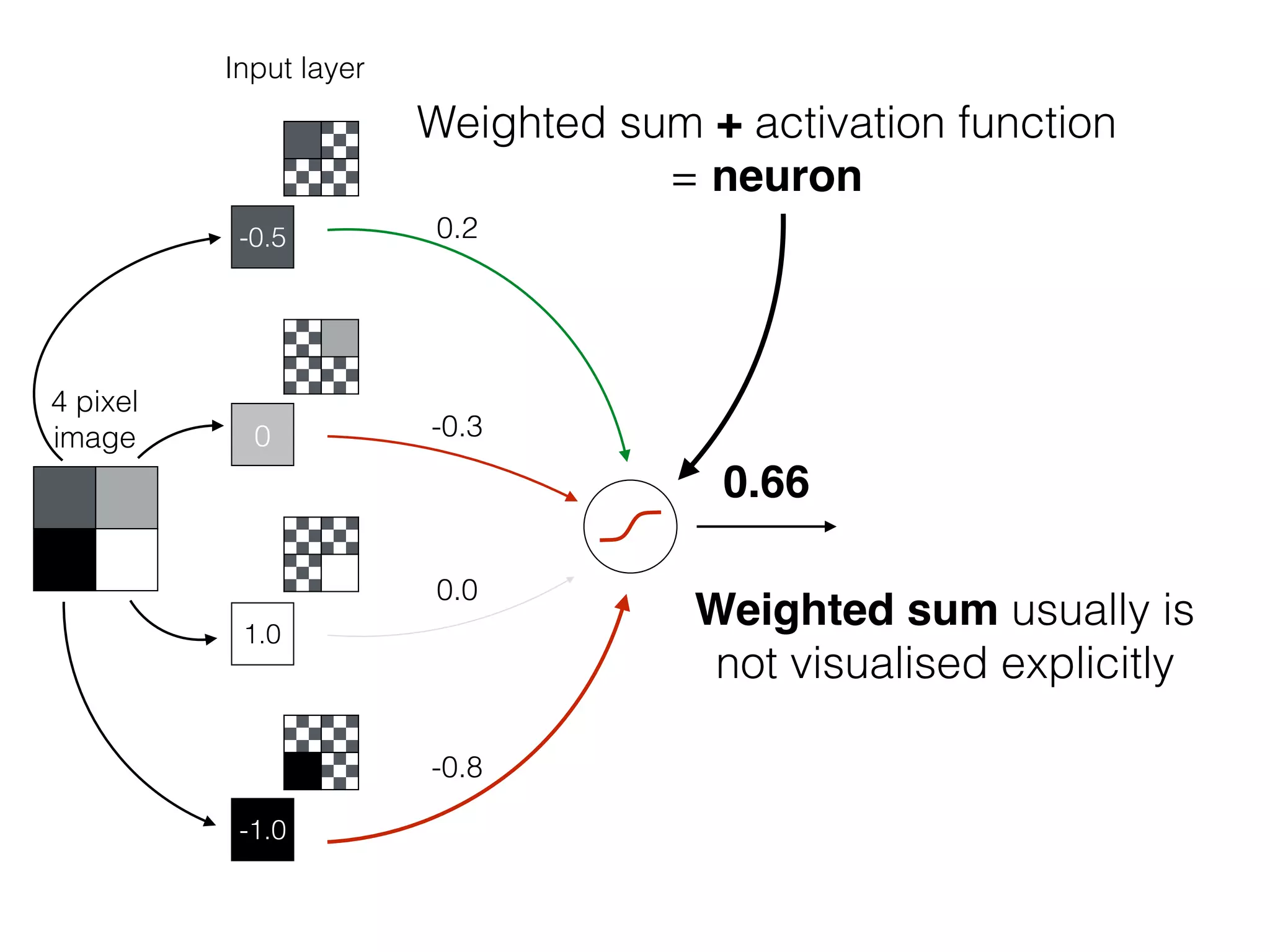
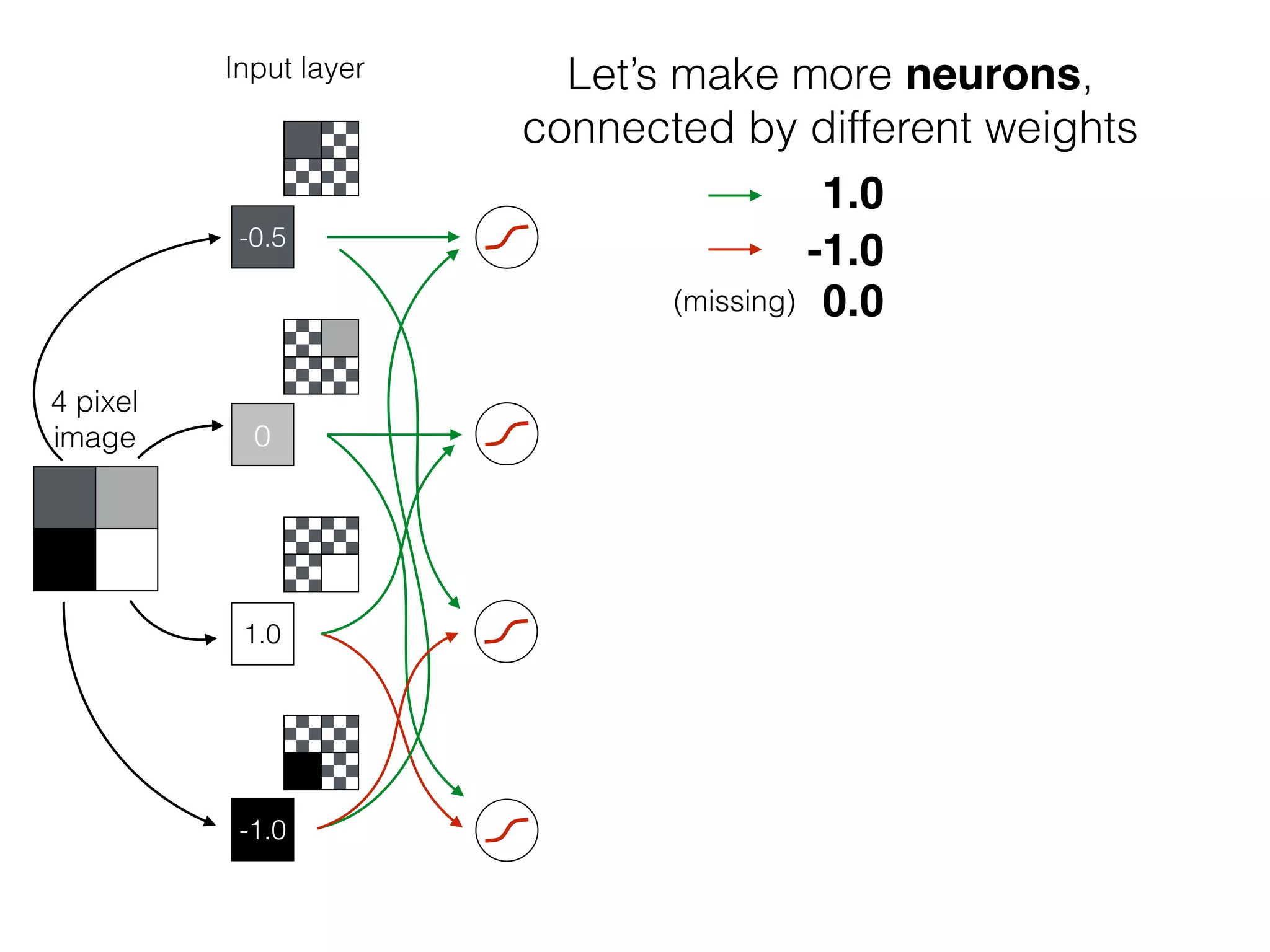
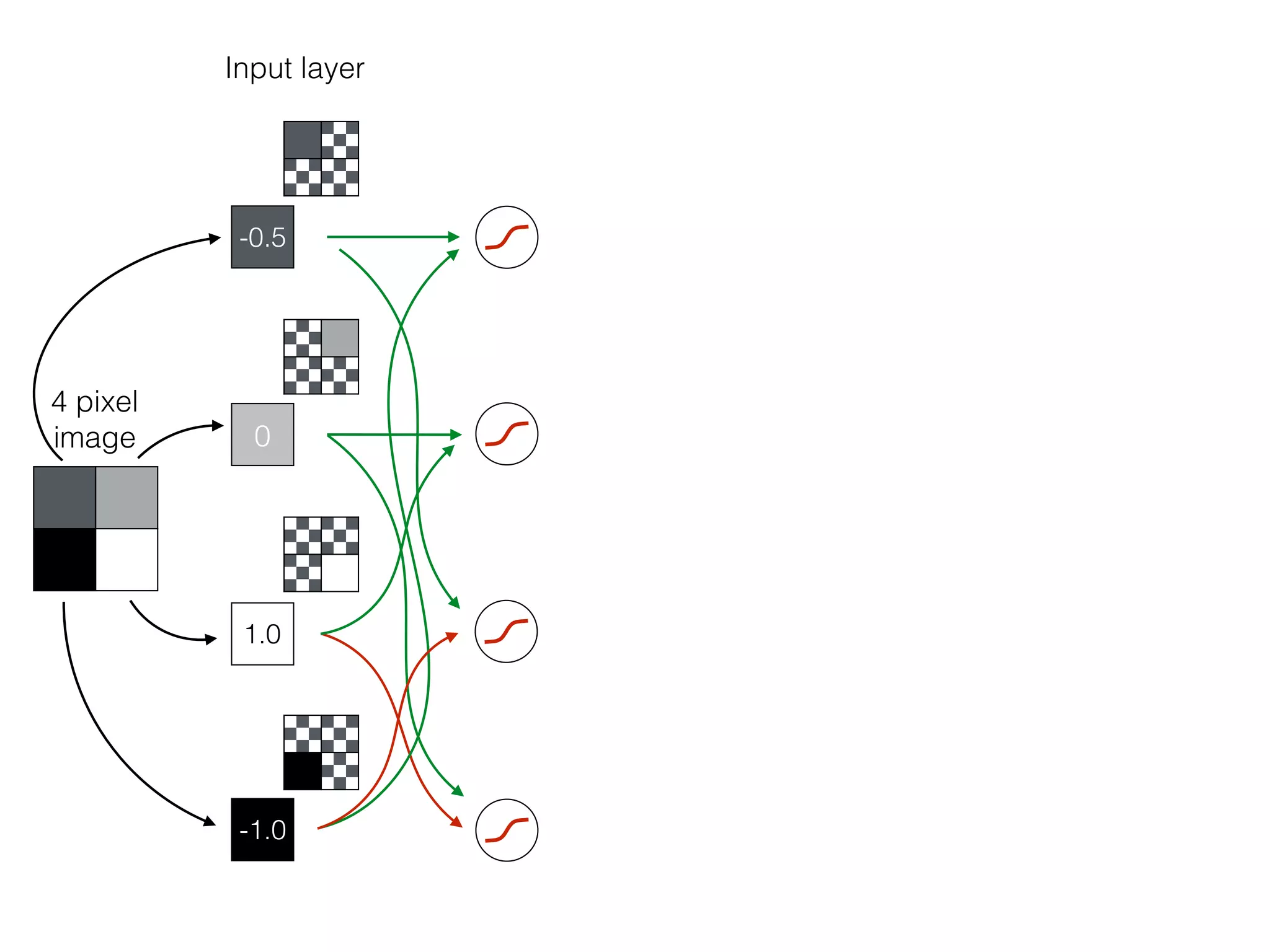
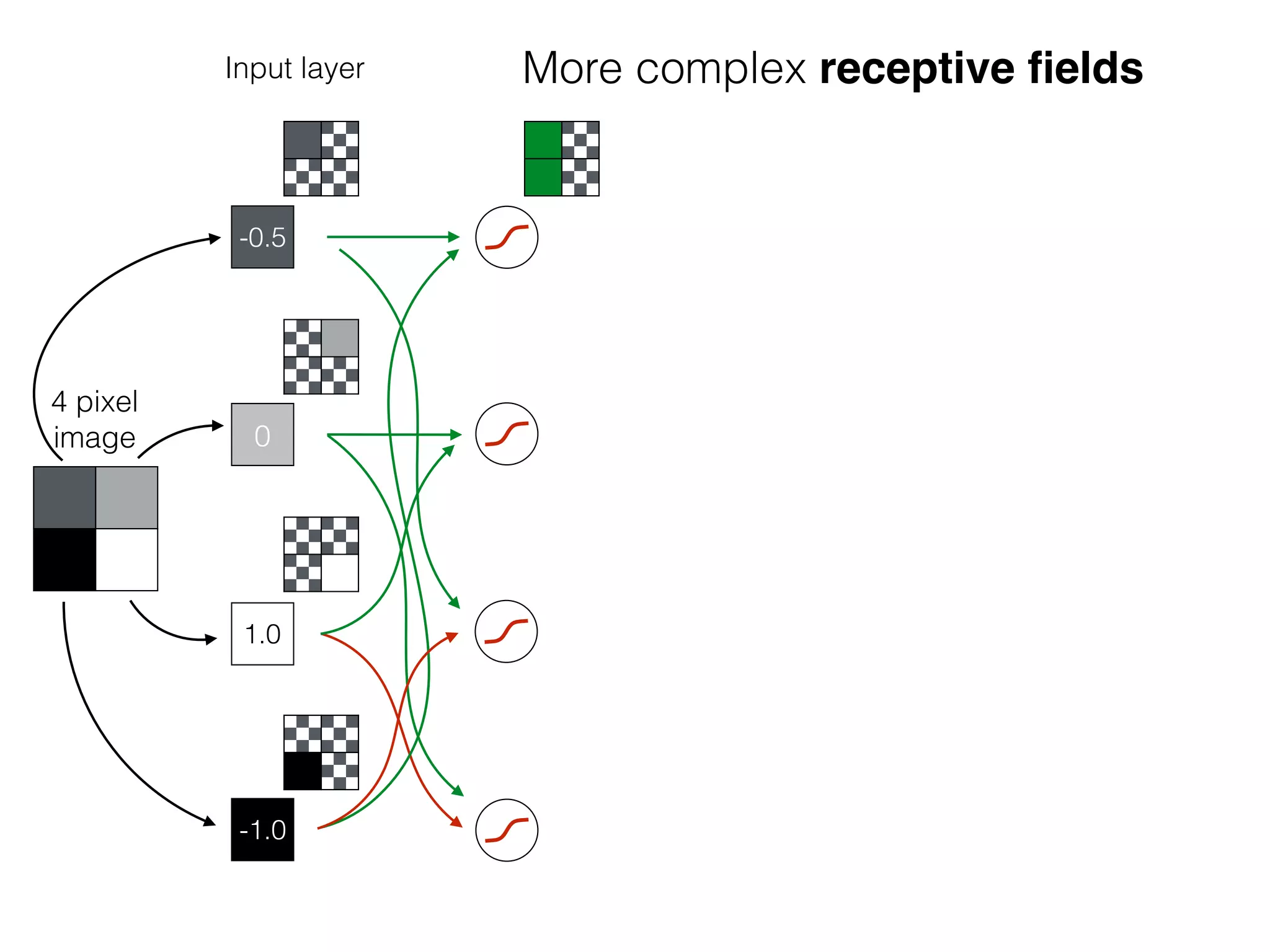
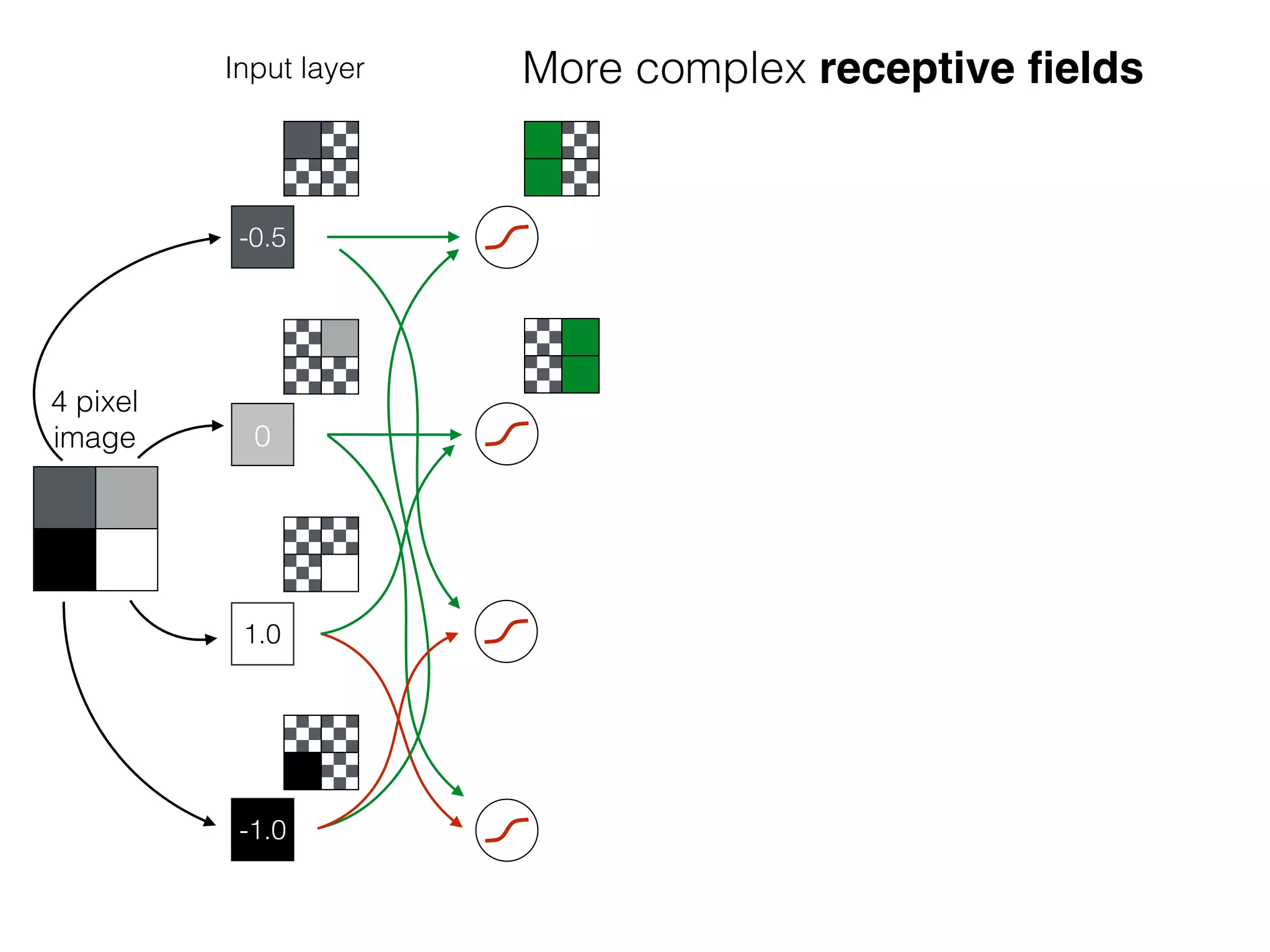
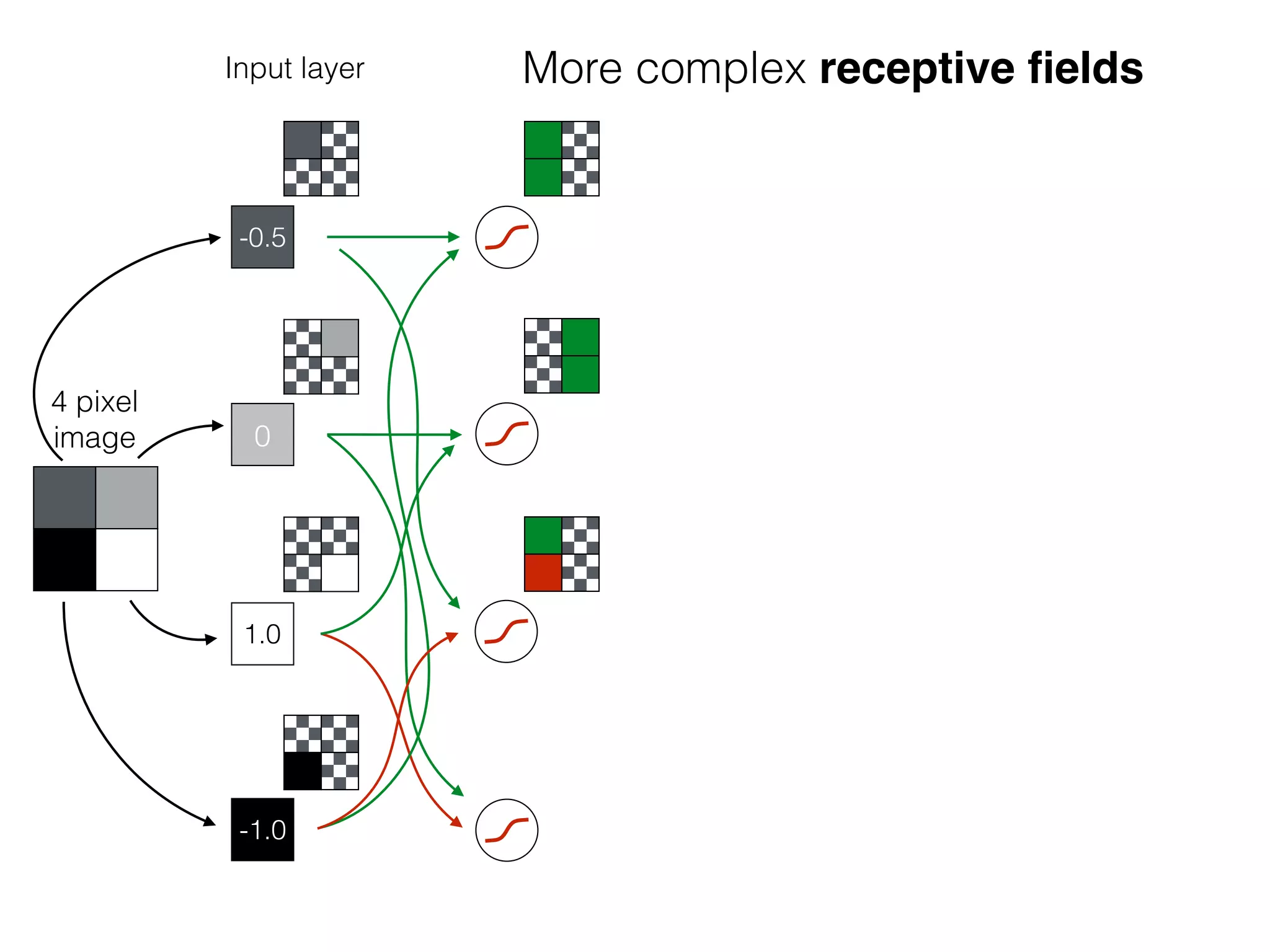
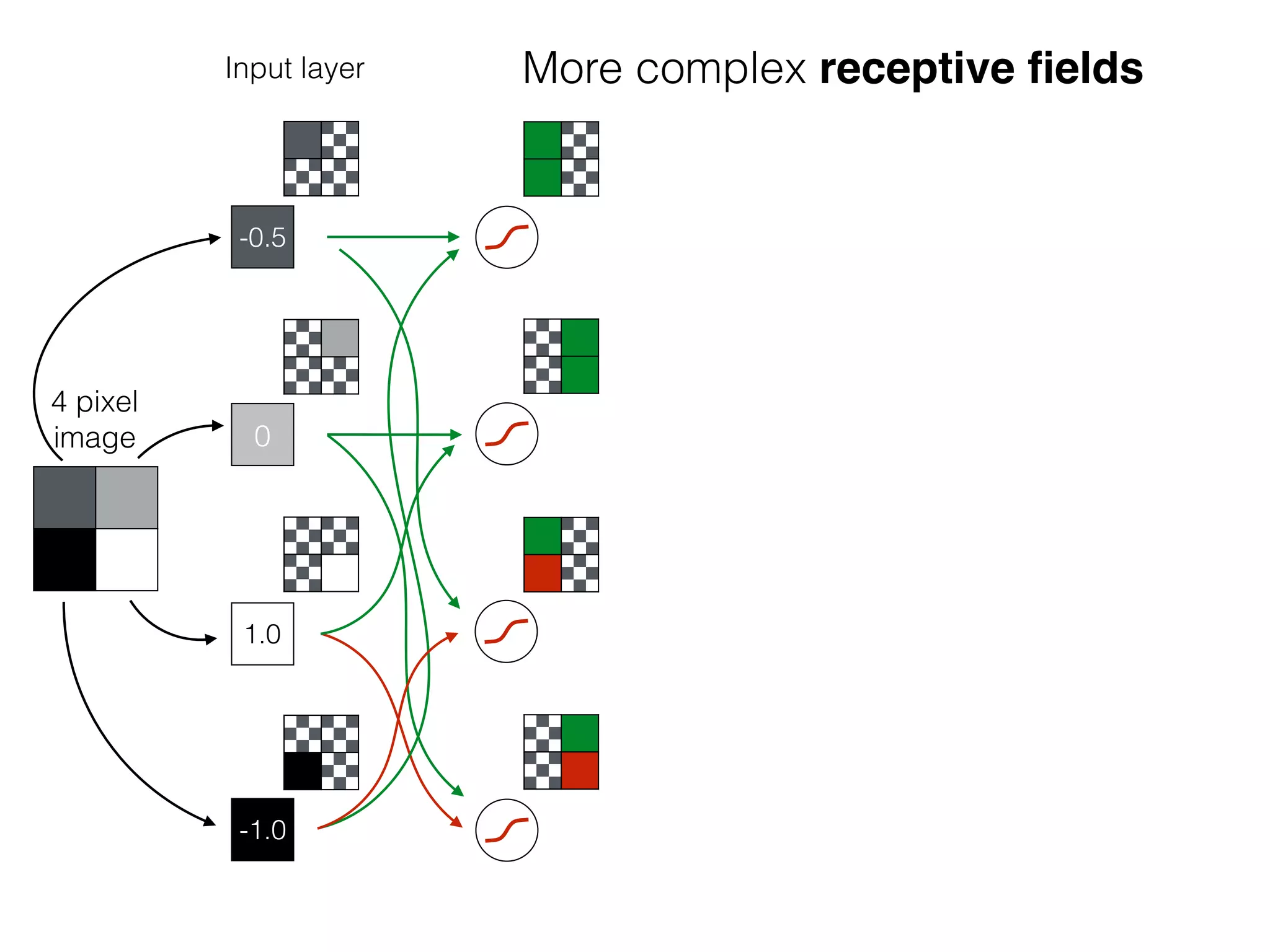
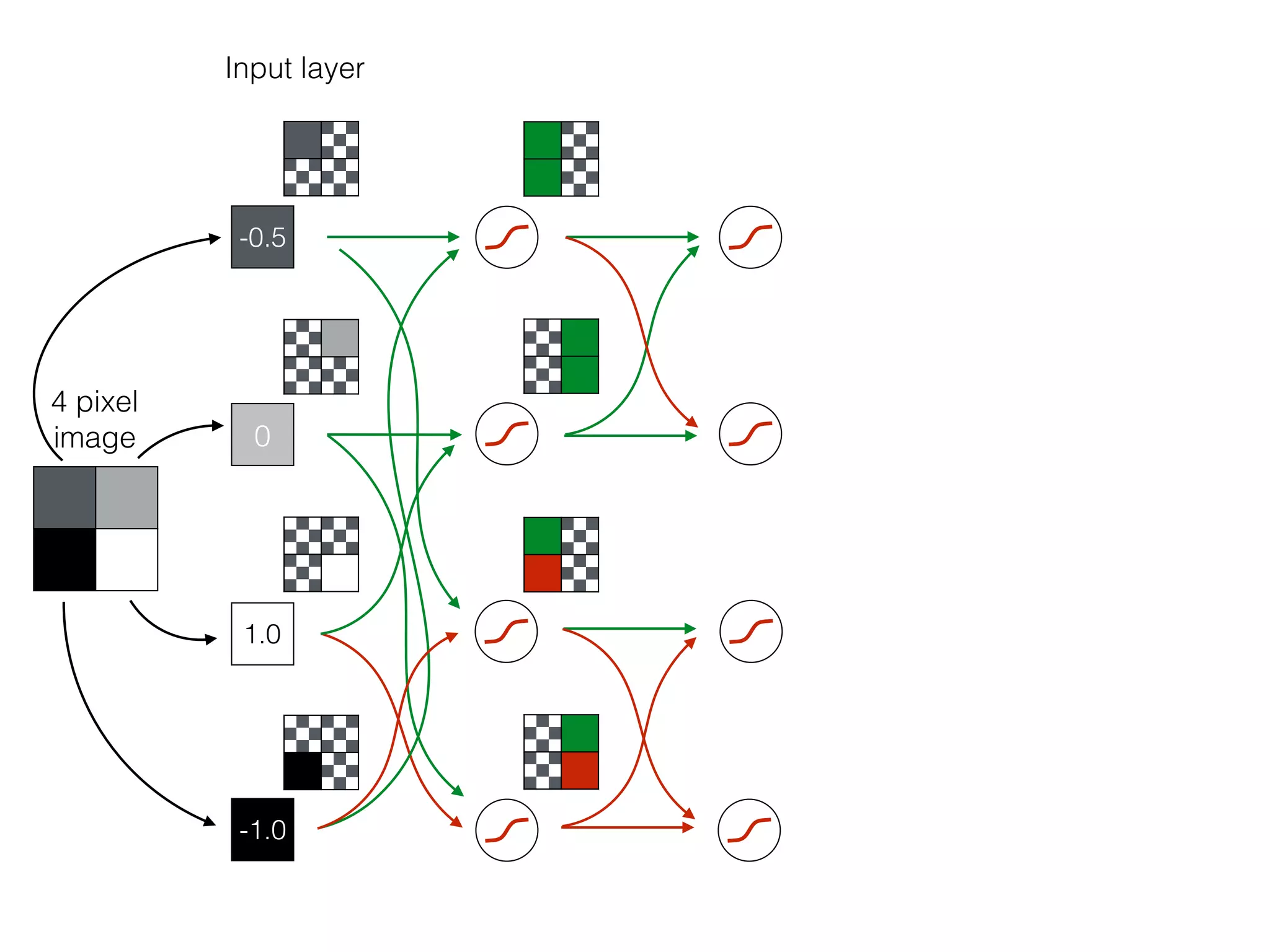
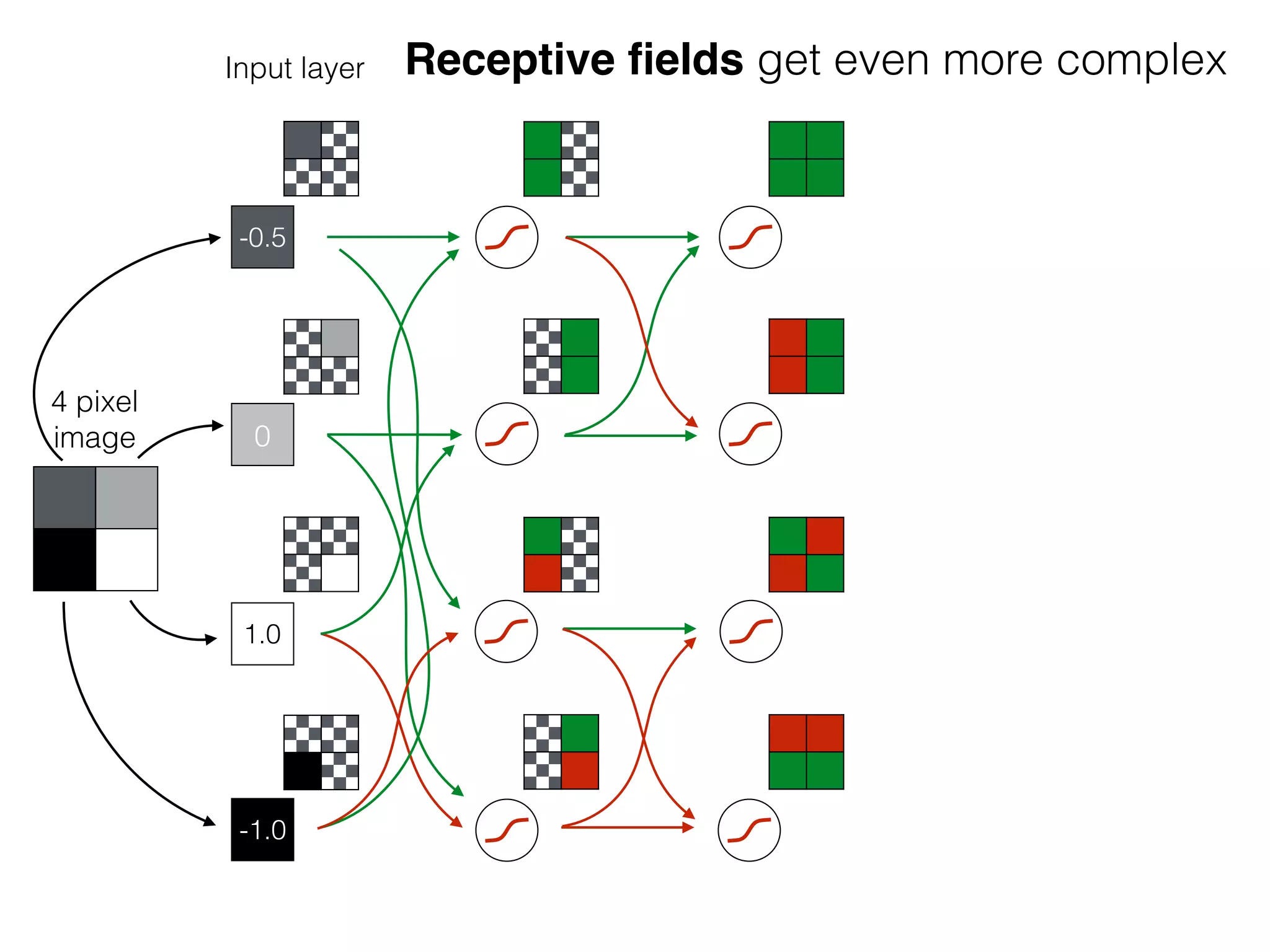
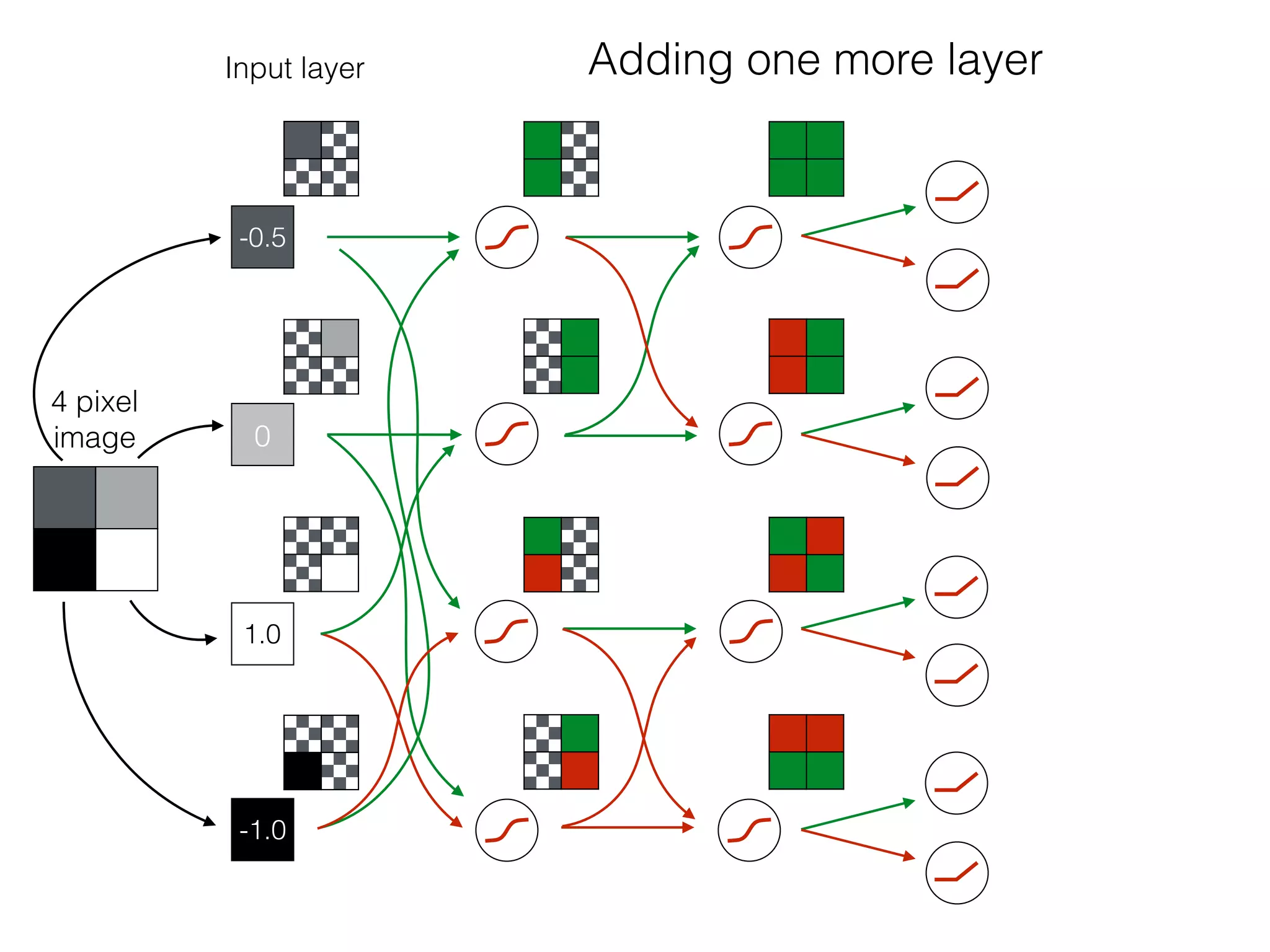
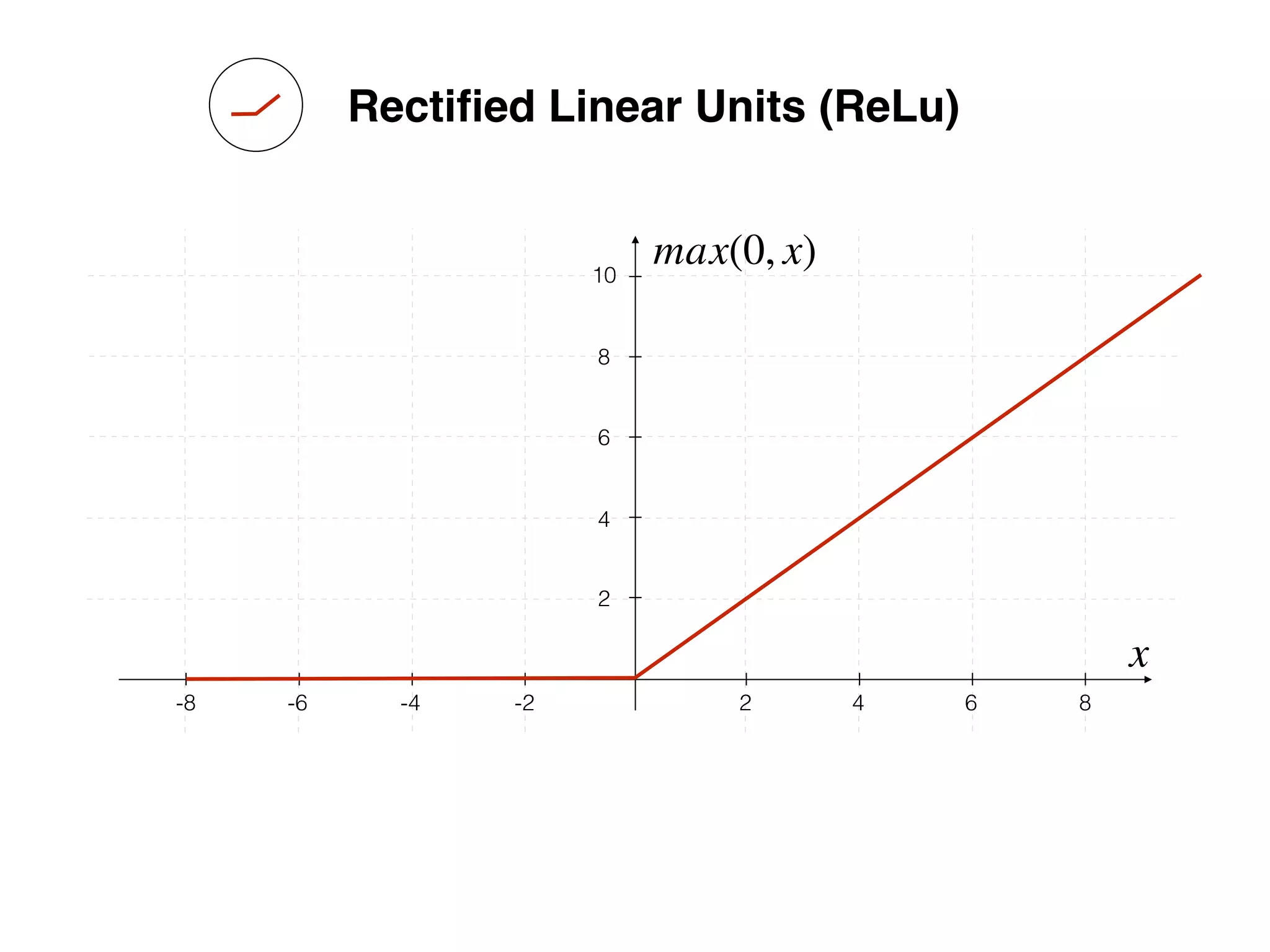
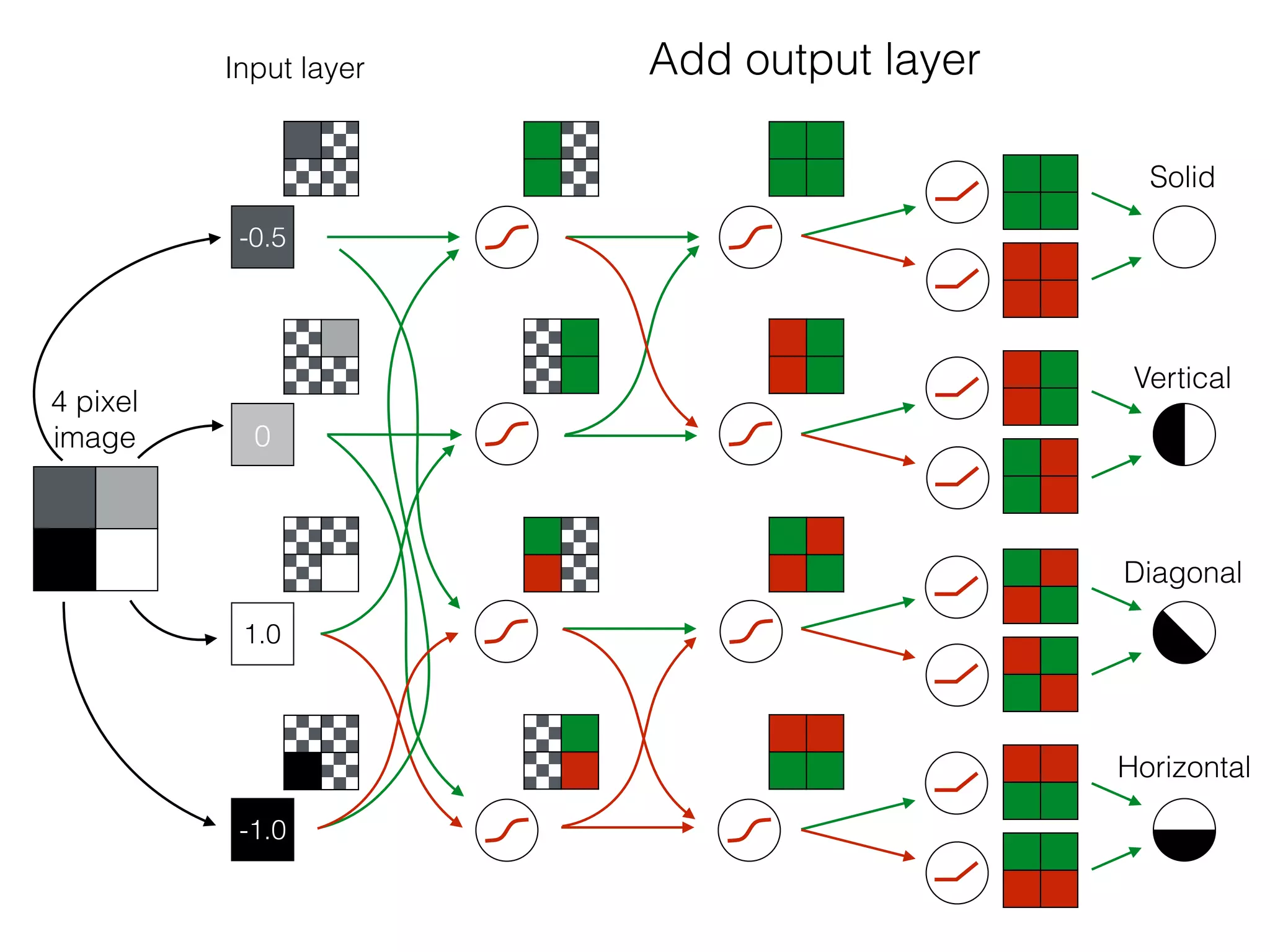
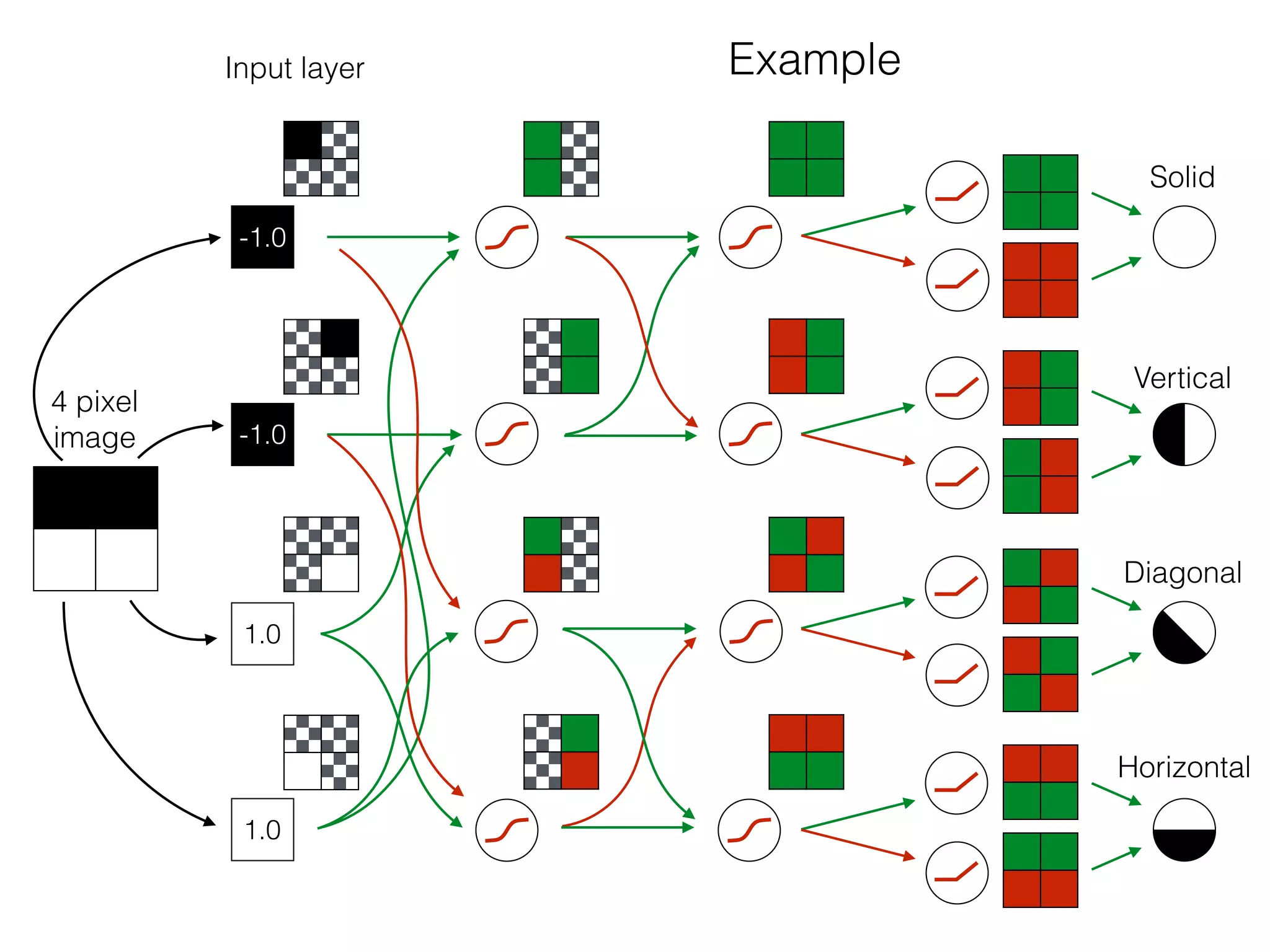
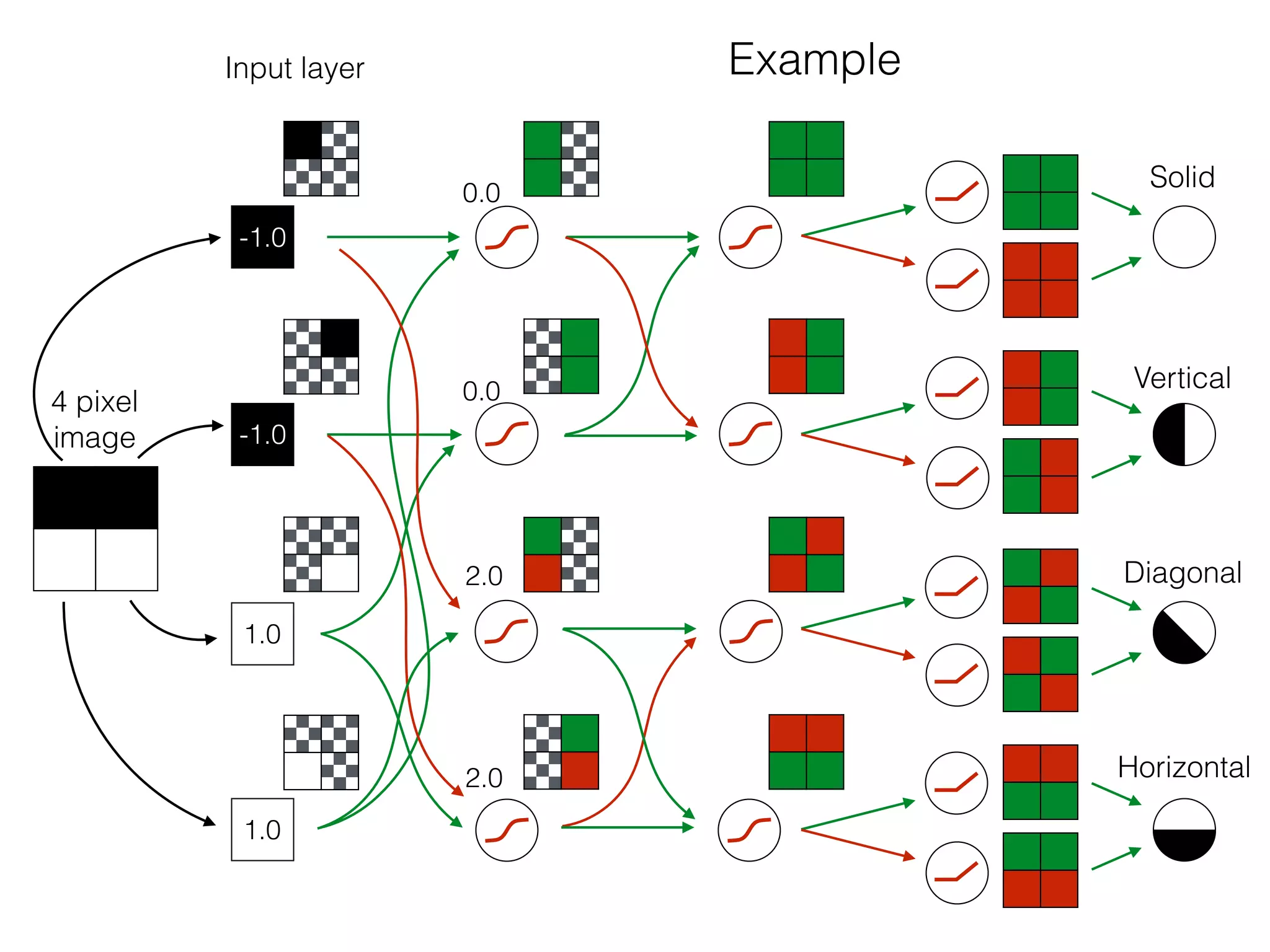
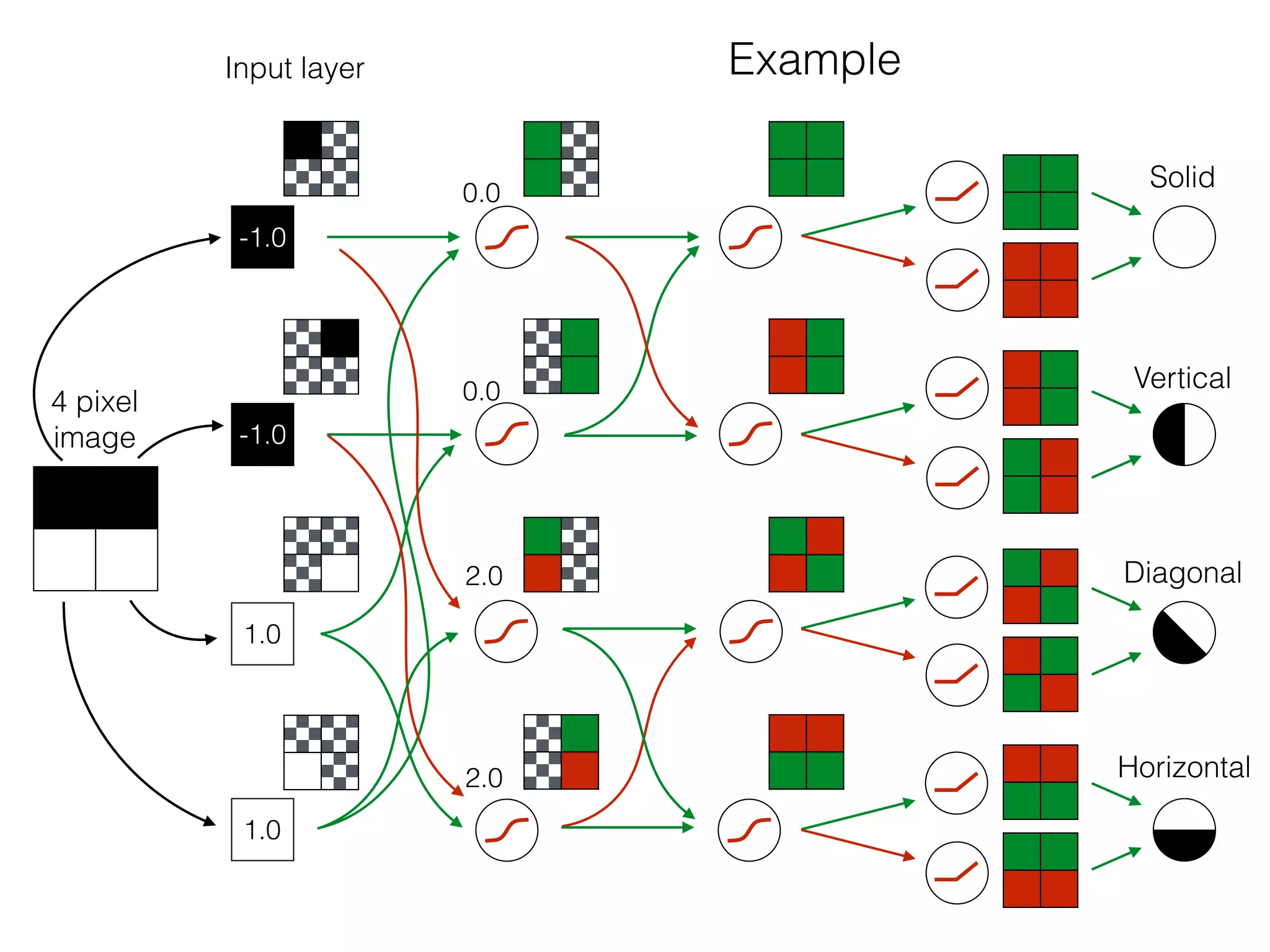
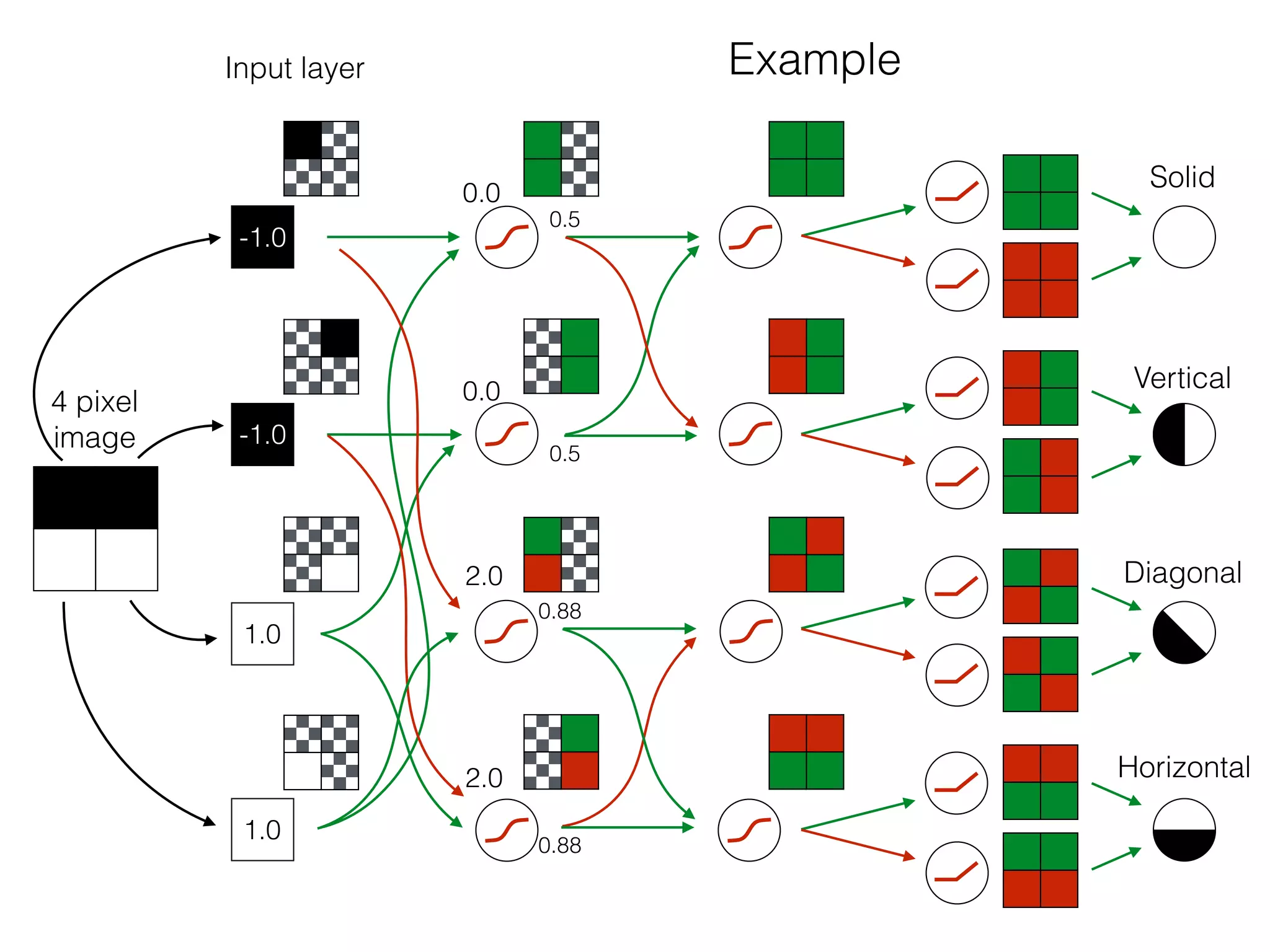
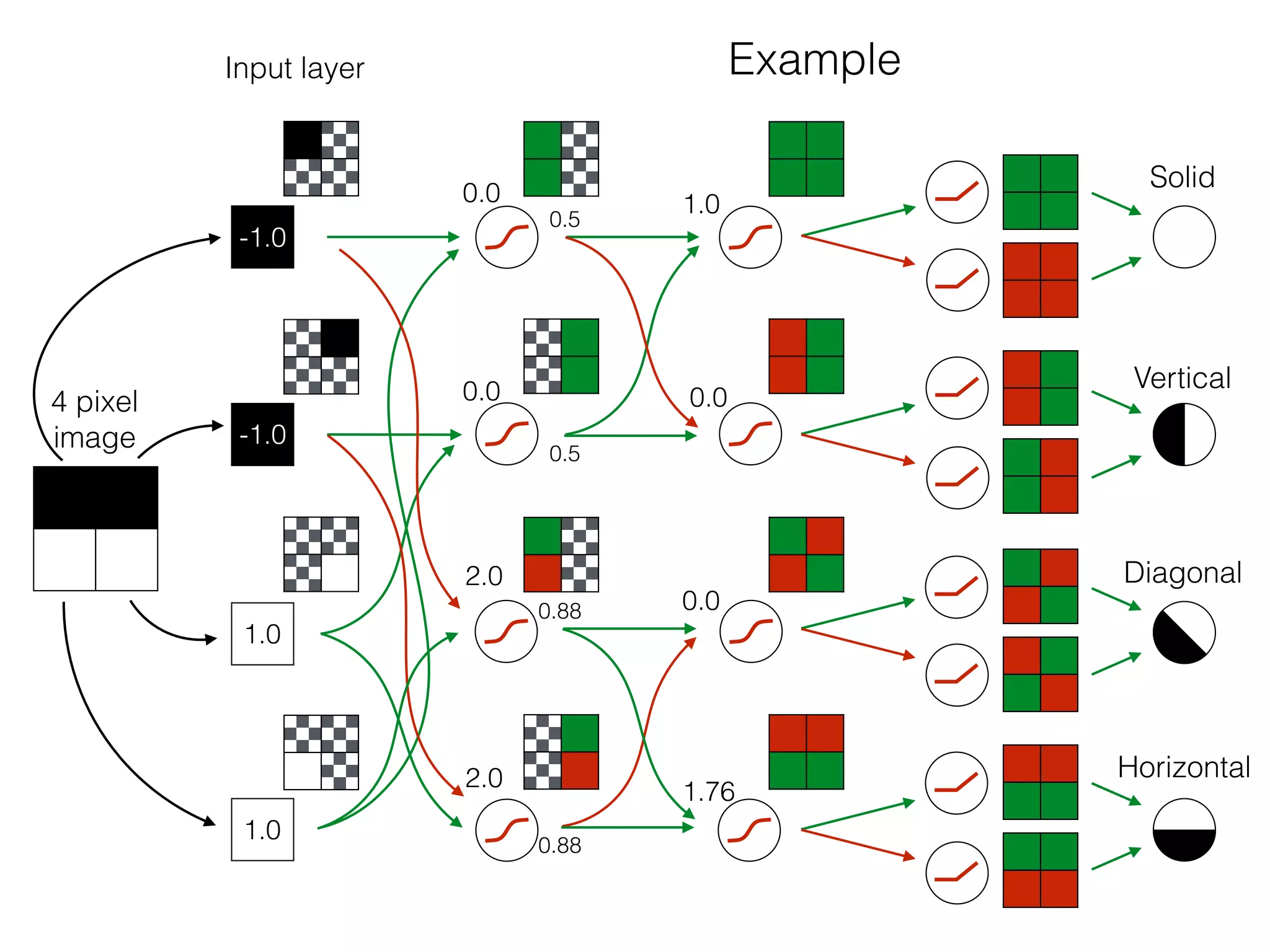
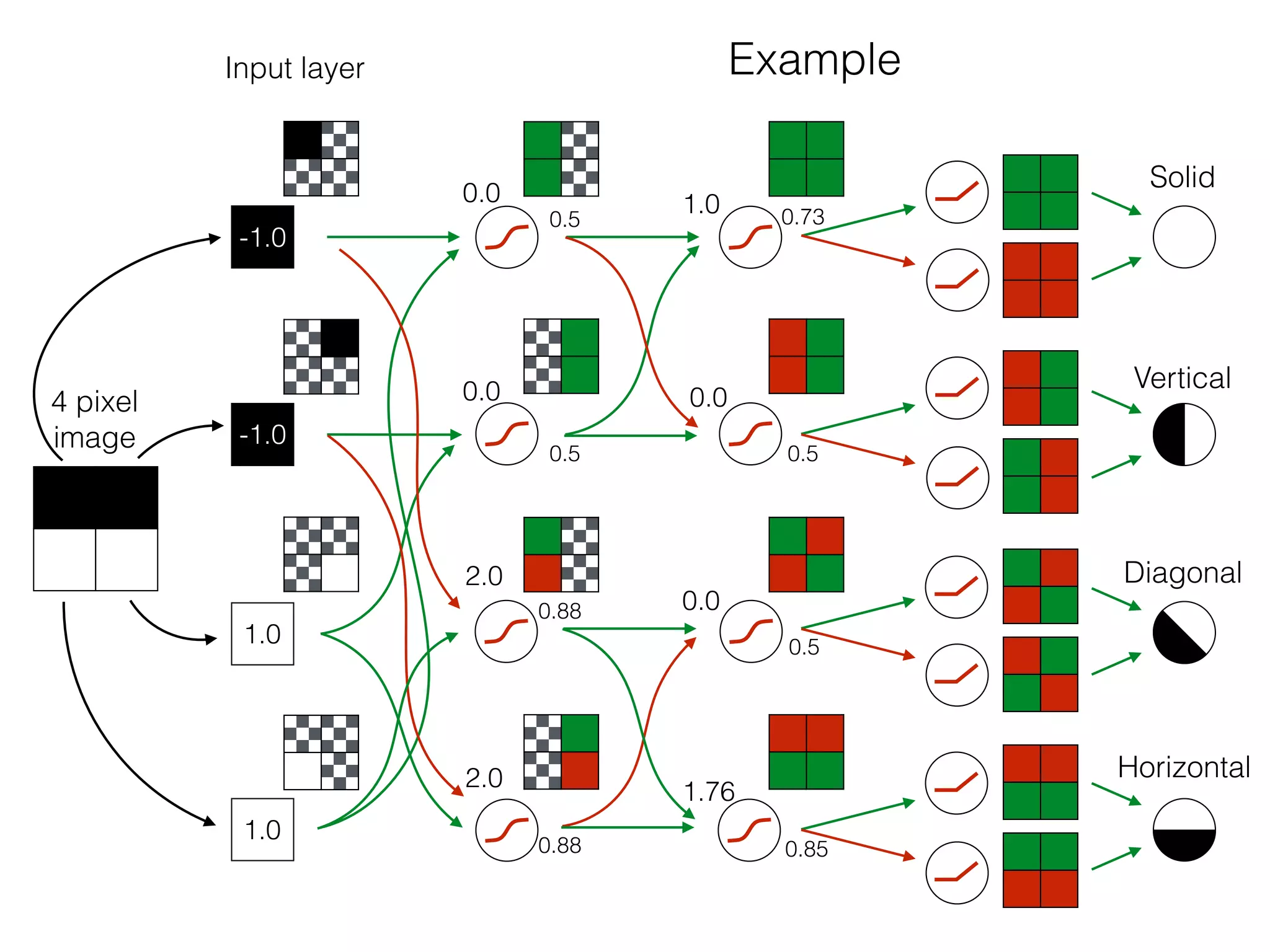
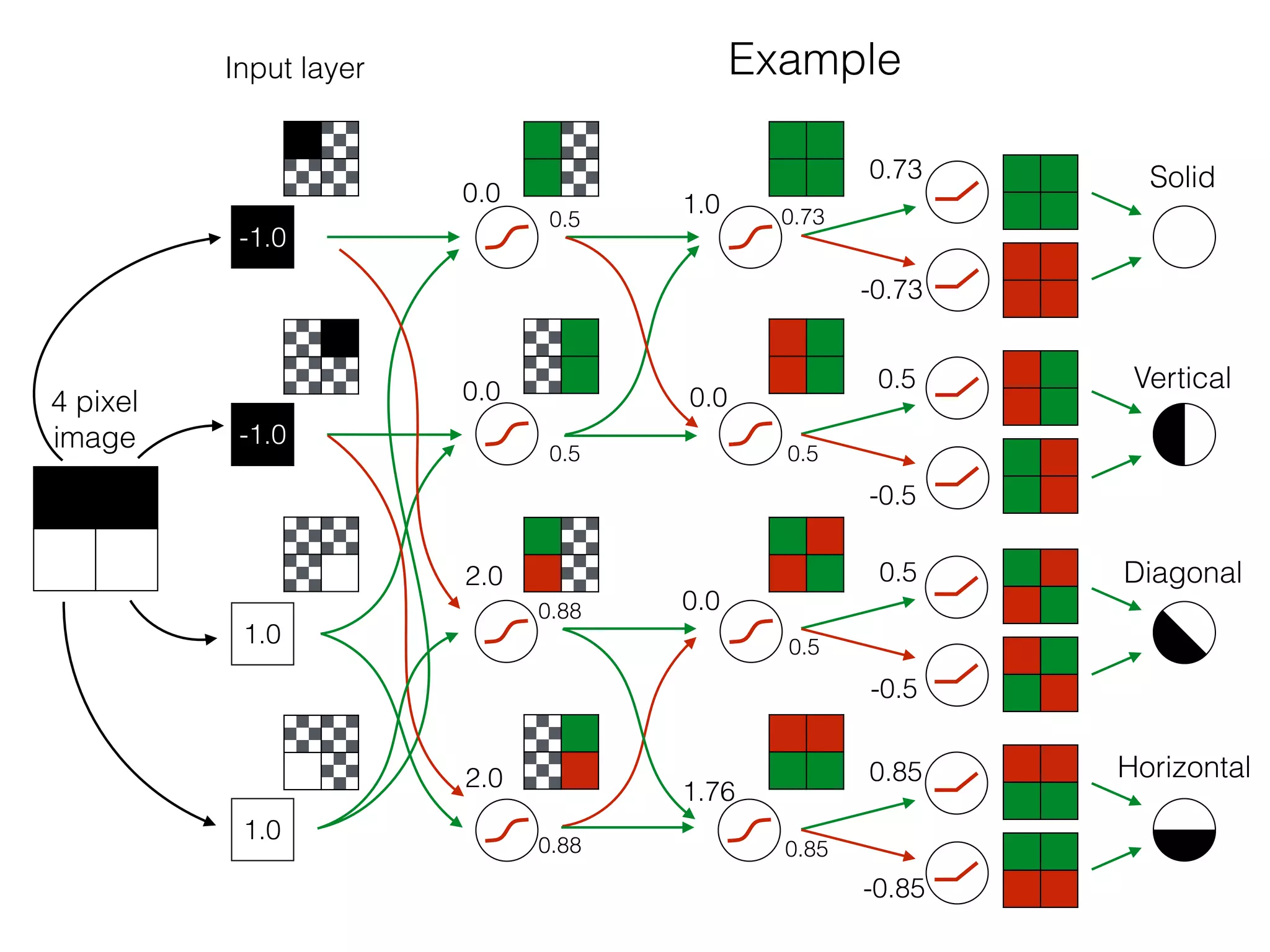
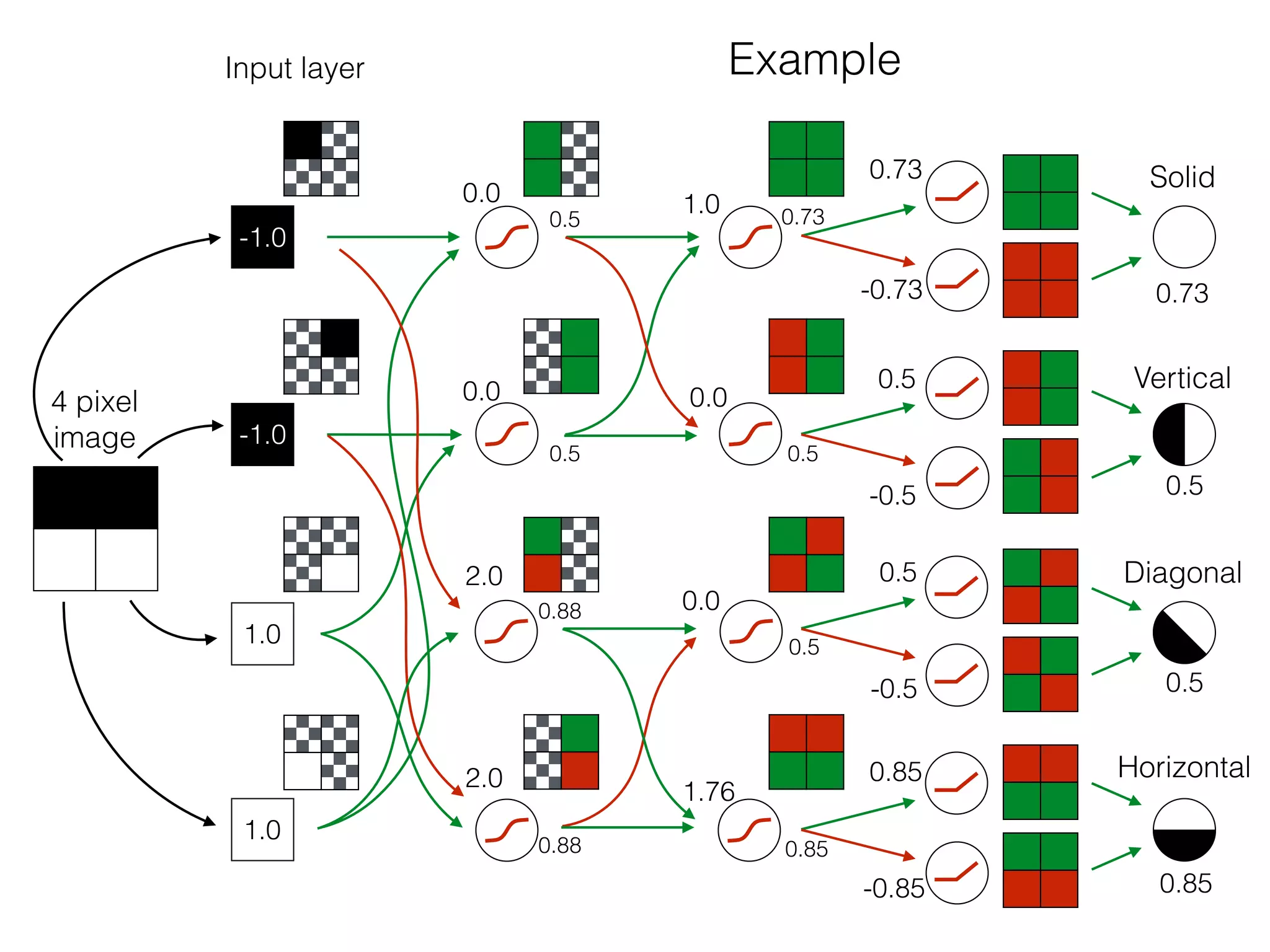
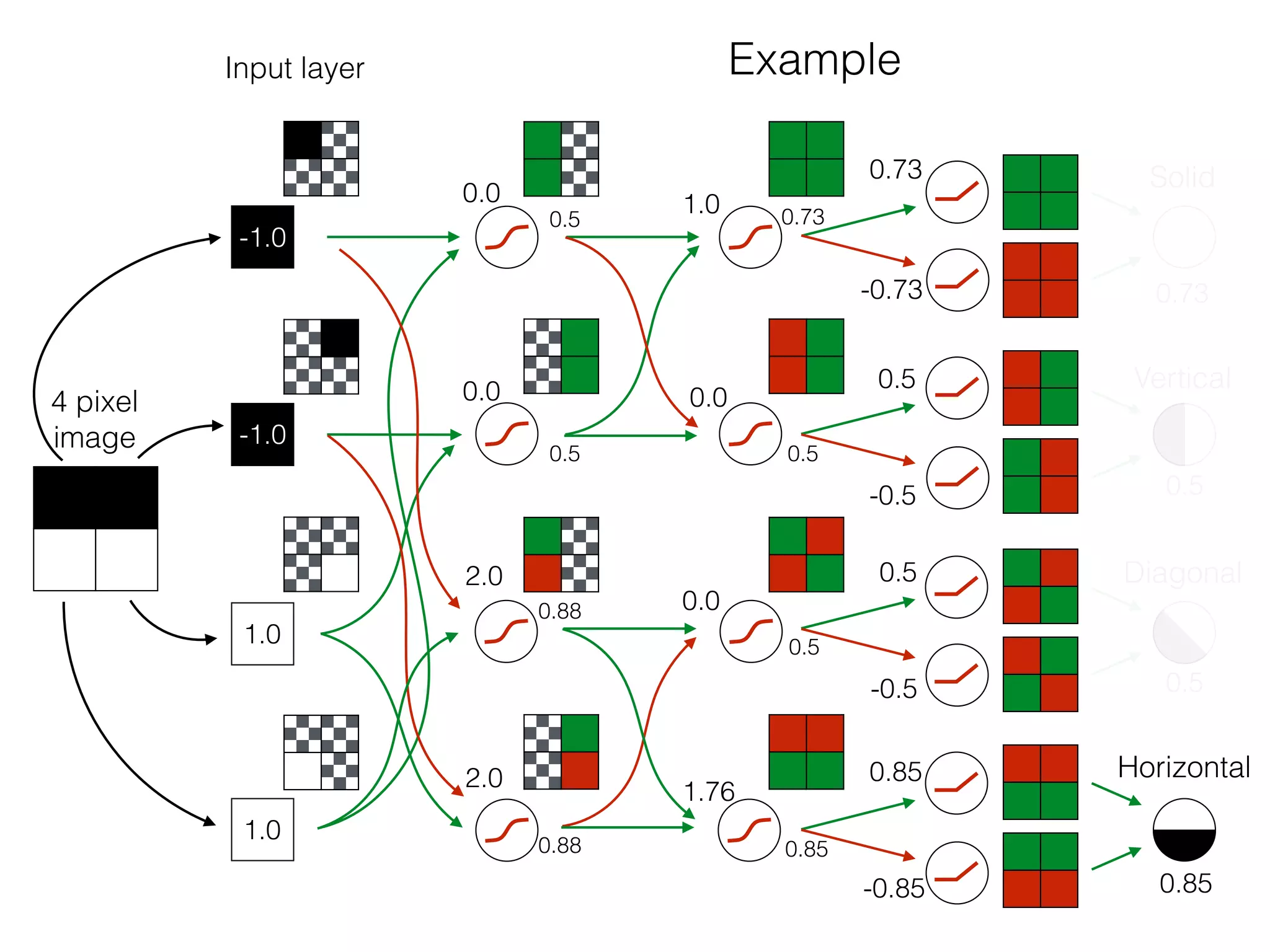
The document is an educational resource on deep learning, covering concepts such as artificial neural networks, supervised and unsupervised learning, and various activation functions like sigmoid and ReLU. It discusses the structure and functioning of neural networks, including input layers, hidden layers, and connections between neurons which contribute to decision-making in tasks such as image classification. The content emphasizes the complexity and adaptability of neural networks in processing various types of data.













![-8 -6 -4 -2 2 4 6 8
0.2
0.4
0.6
0.8
1.0
x
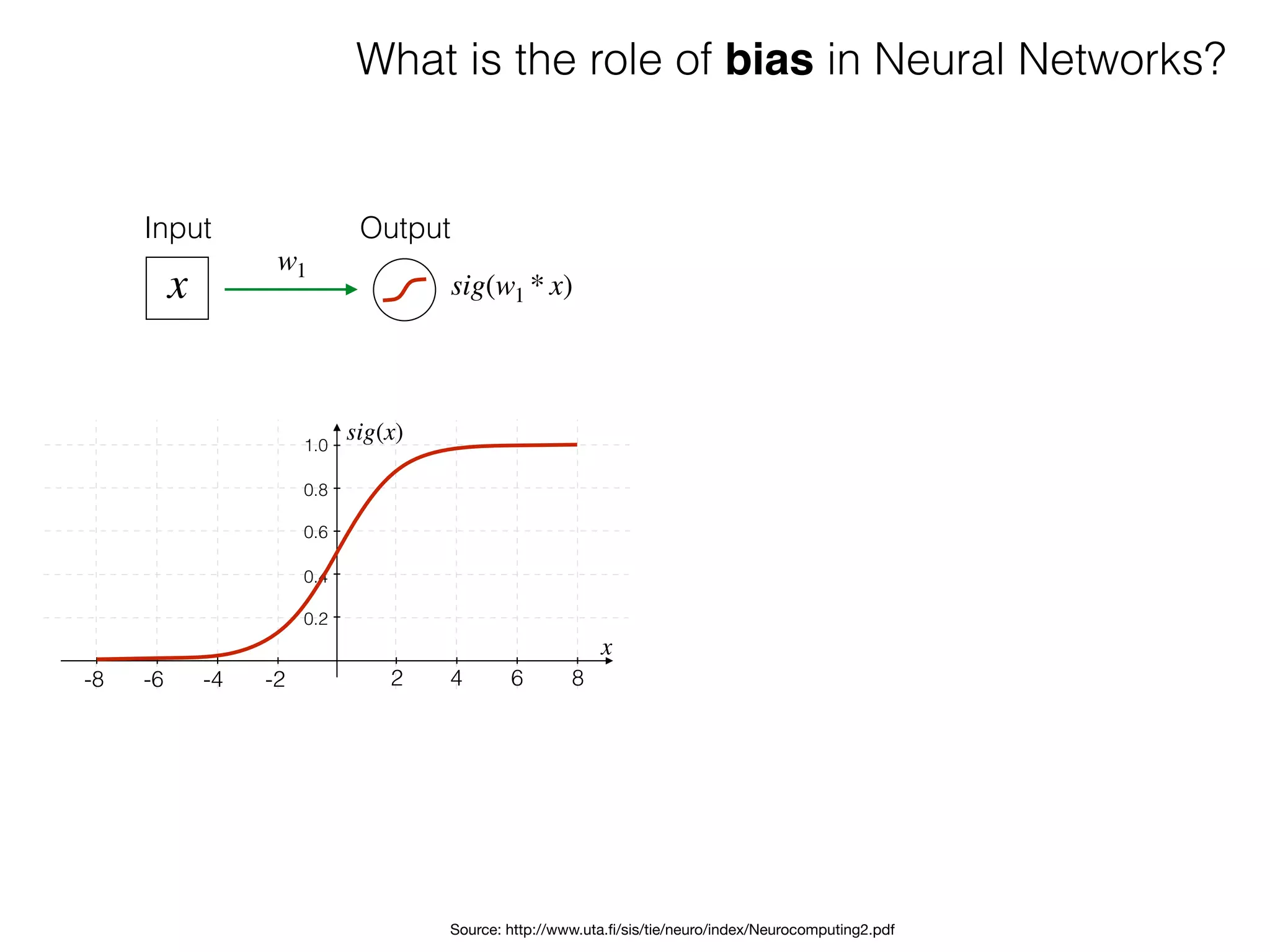
sig(w1 * x)
OutputInput
x
w1
sig(w1 * x)
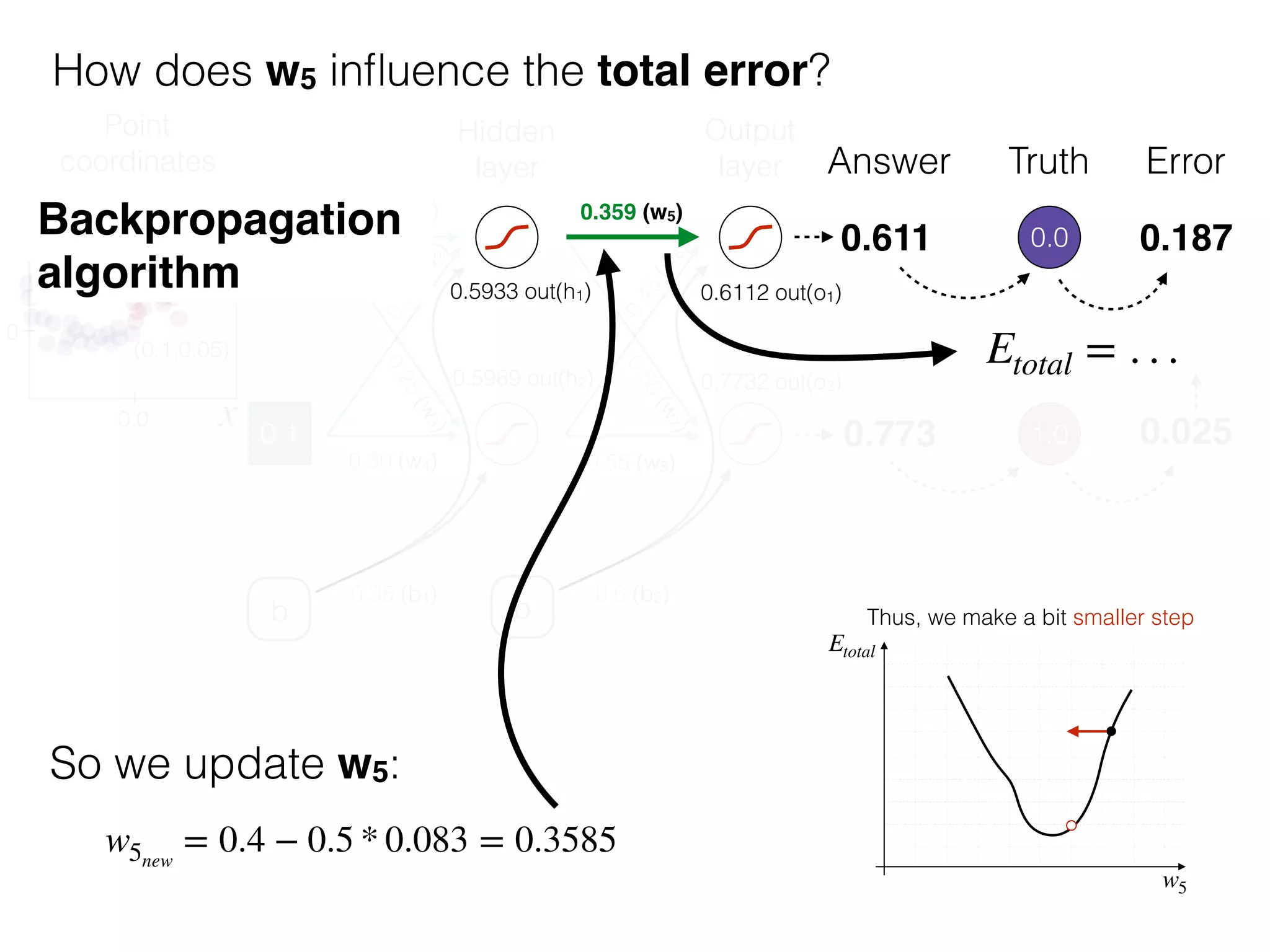
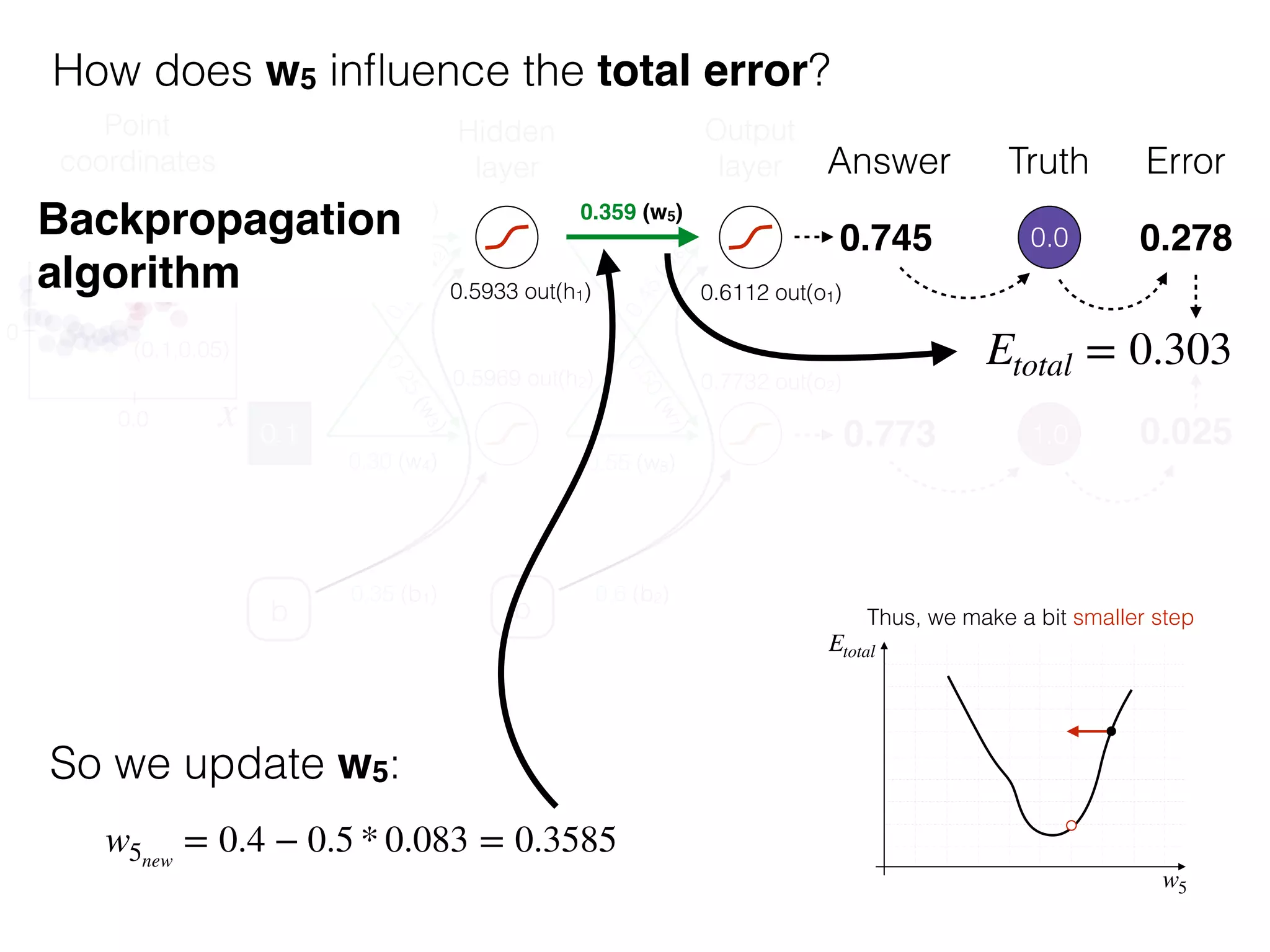
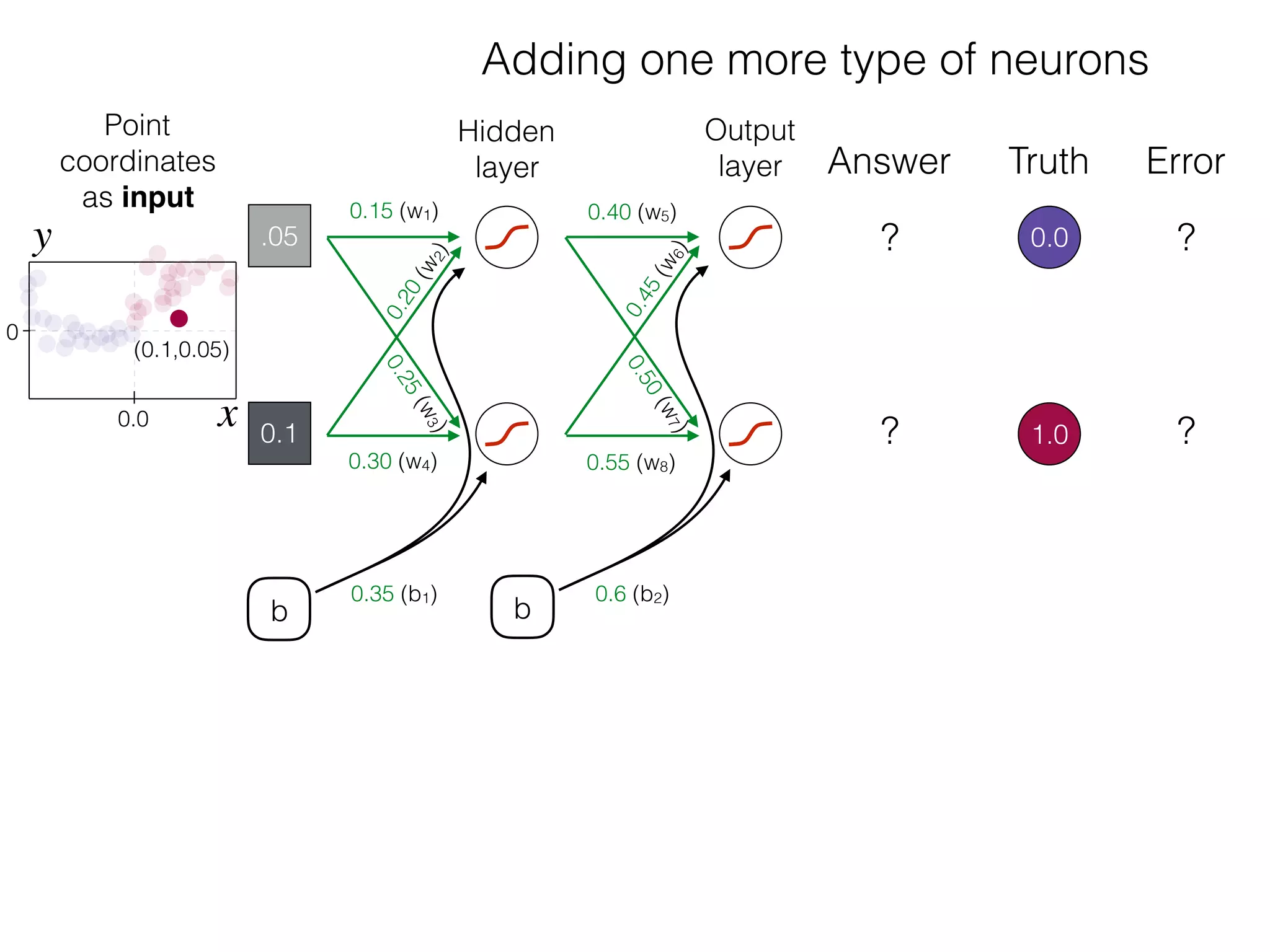
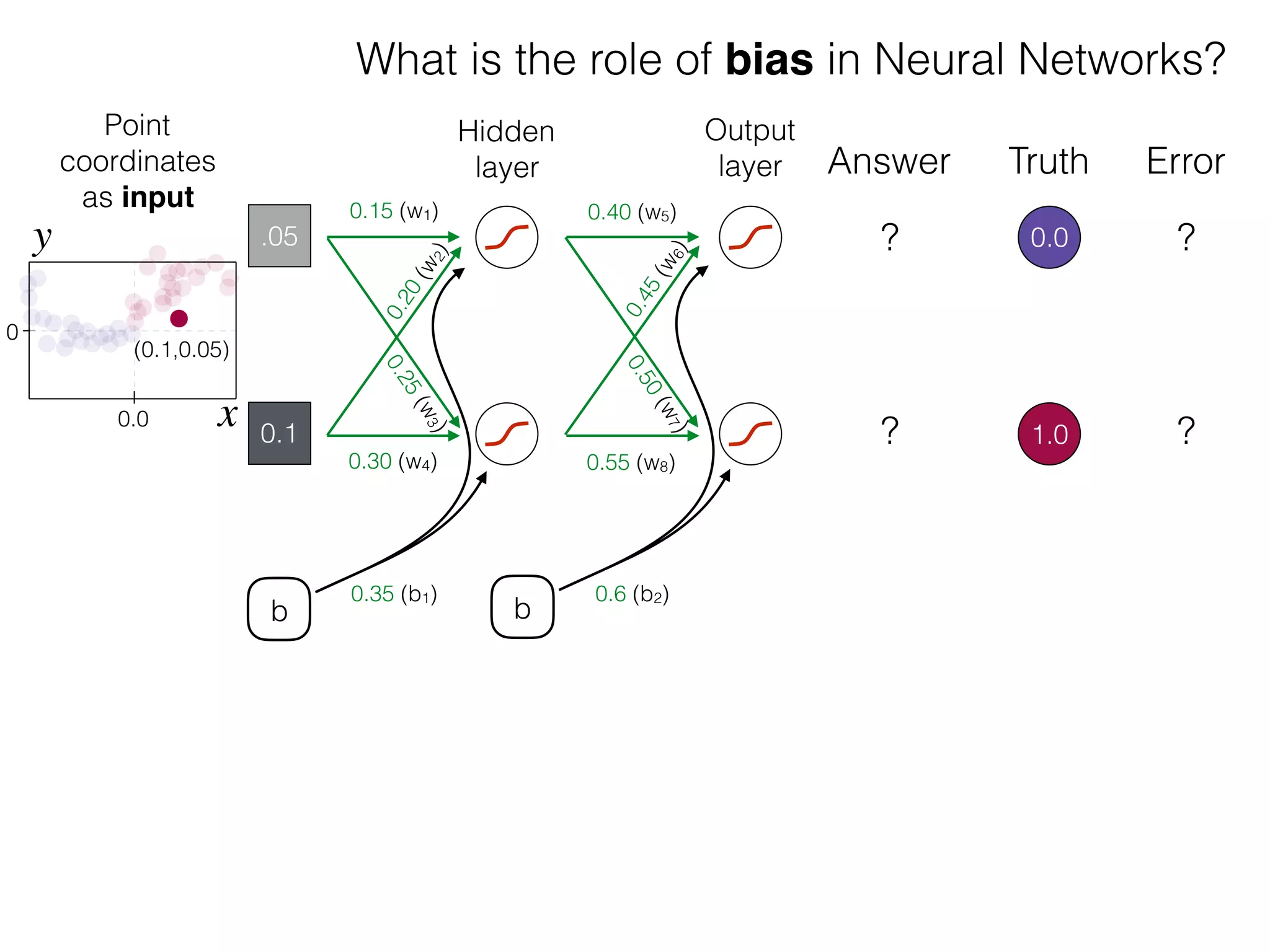
What is the role of bias in Neural Networks?
w1 =[0.5, 1.0, 2.0]
Source: http://www.uta.fi/sis/tie/neuro/index/Neurocomputing2.pdf](https://image.slidesharecdn.com/dllecturegeneral-190728122700/75/Introduction-to-Deep-Learning-95-2048.jpg)
![-8 -6 -4 -2 2 4 6 8
0.2
0.4
0.6
0.8
1.0
x
sig(w1 * x)
-8 -6 -4 -2 2 4 6 8
0.2
0.4
0.6
0.8
1.0
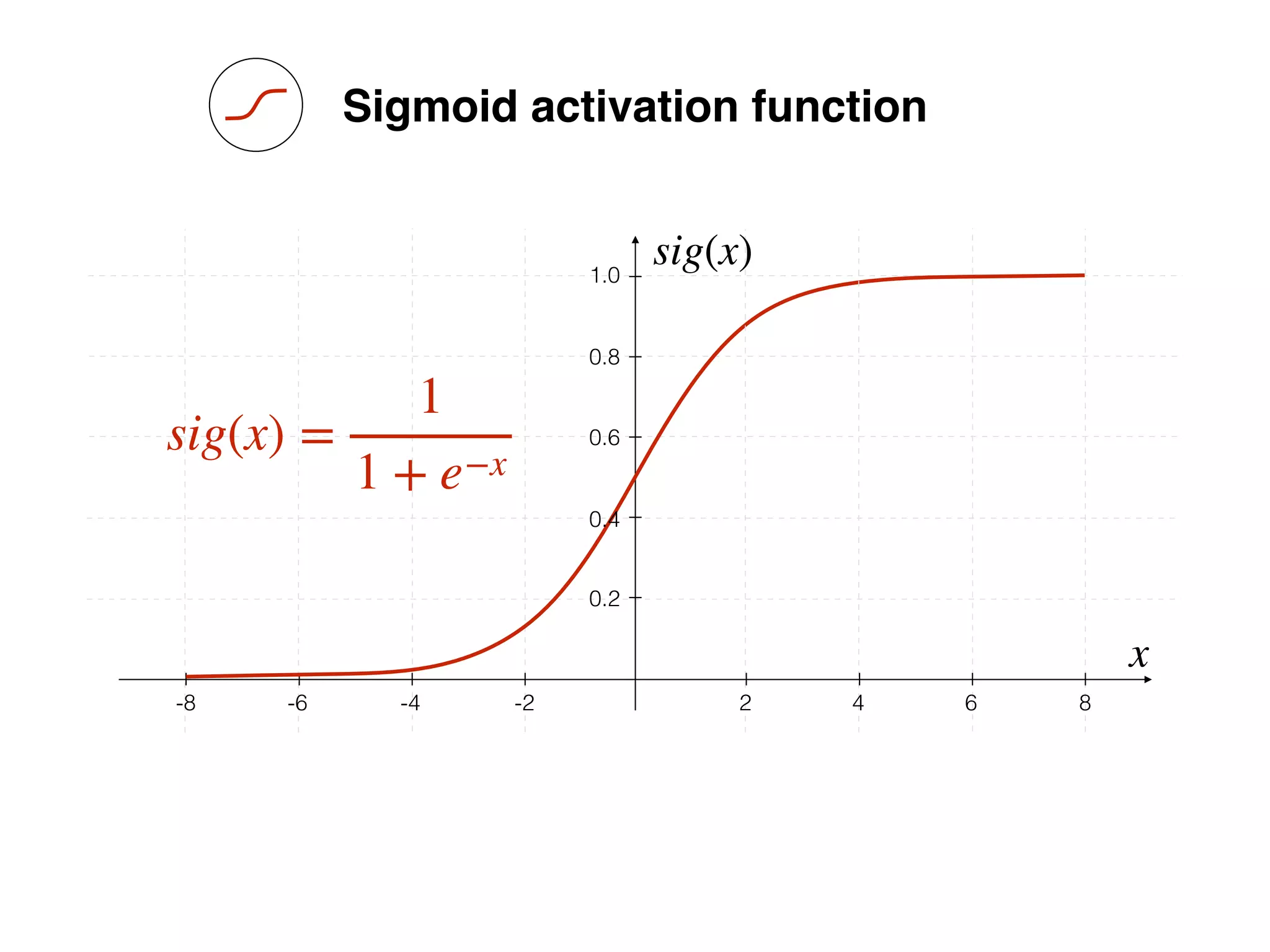
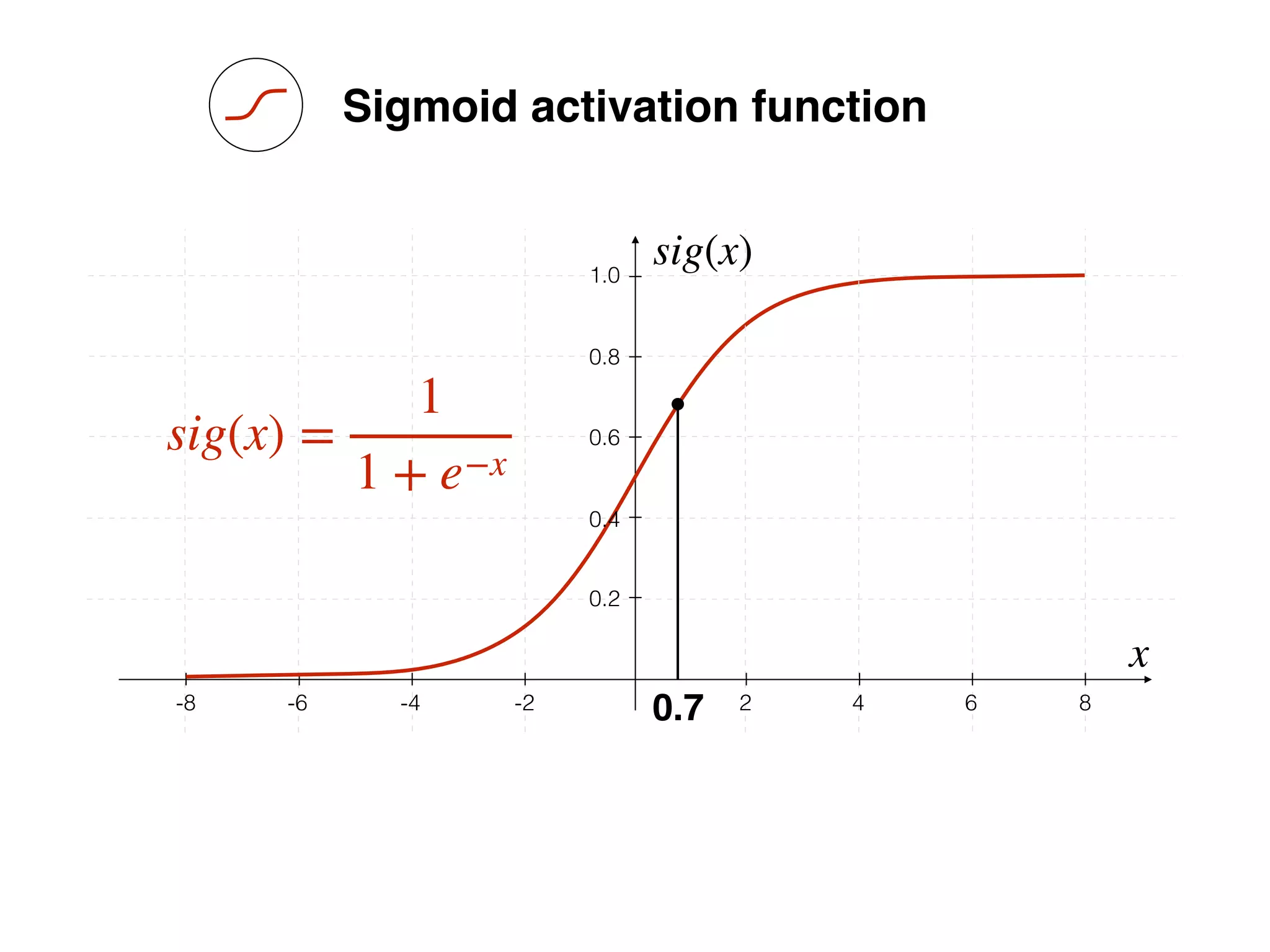
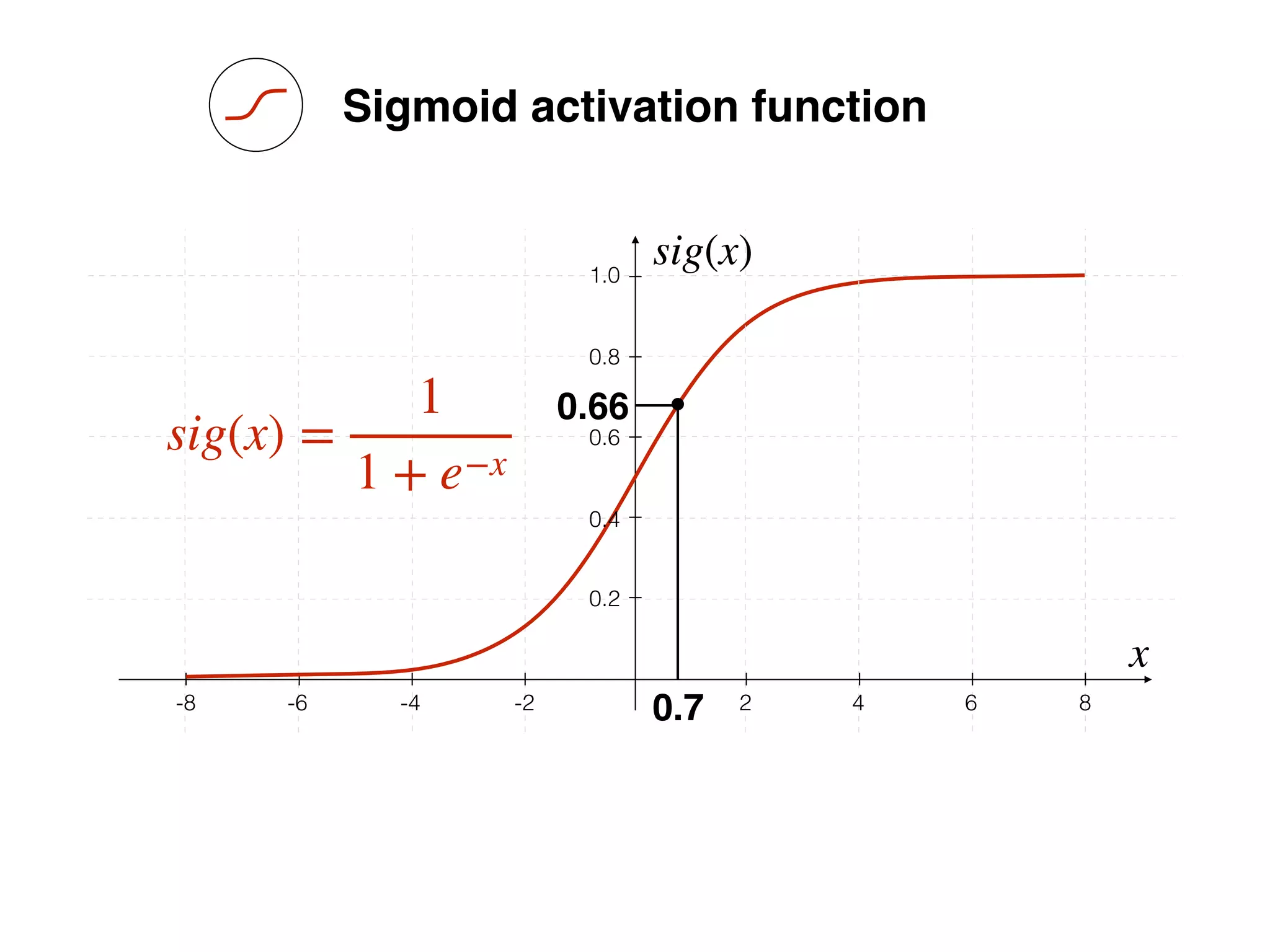
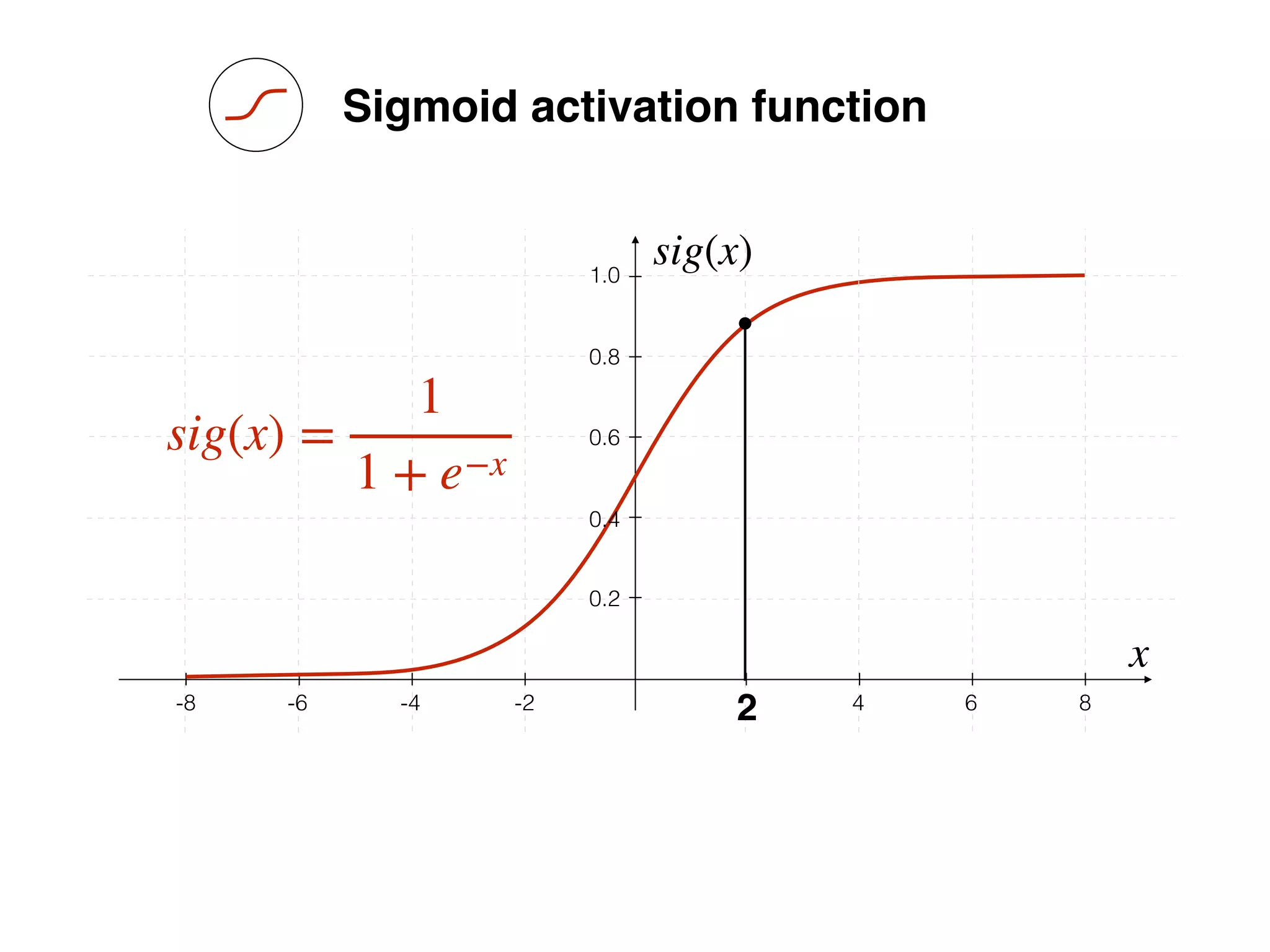
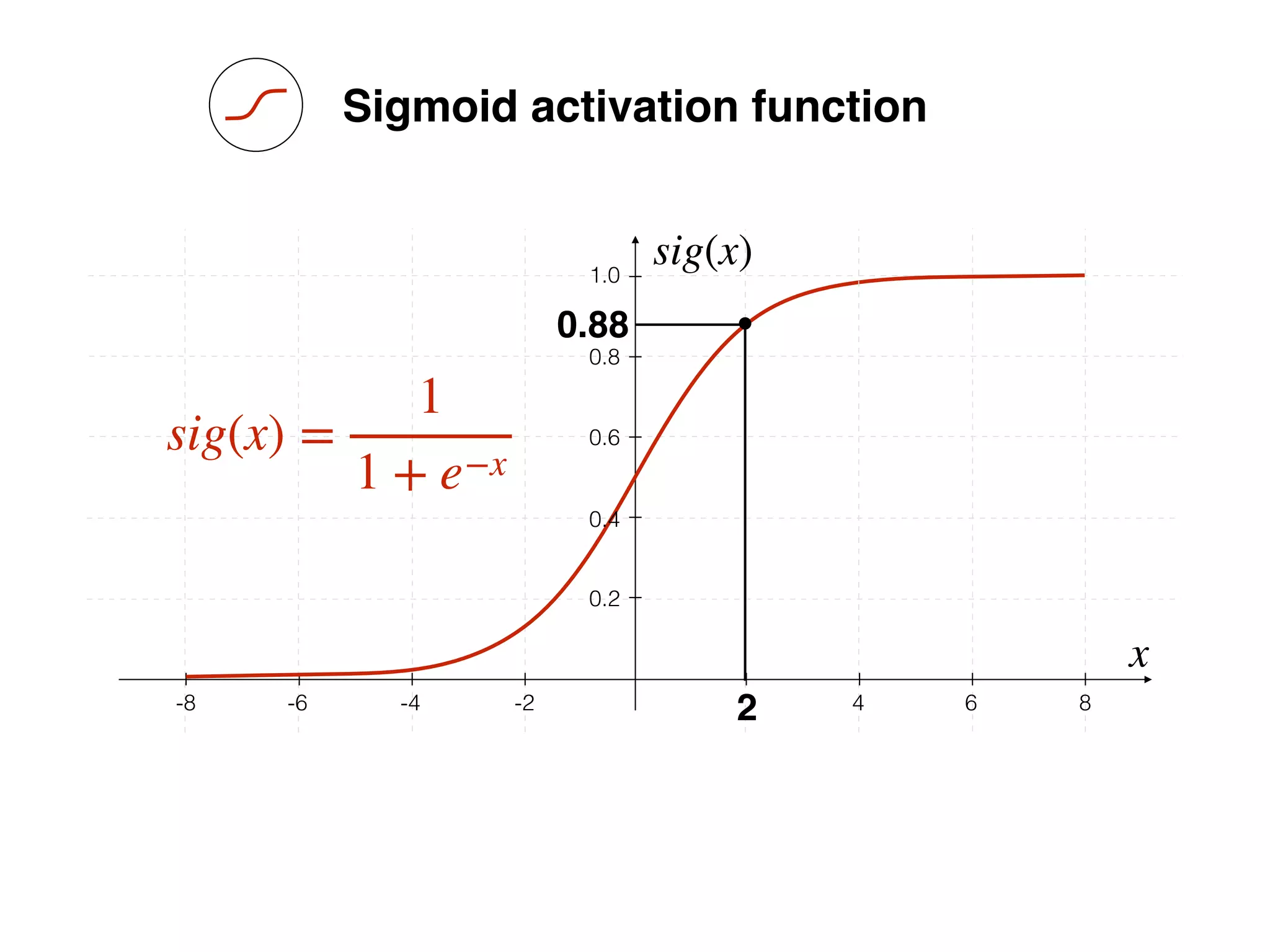
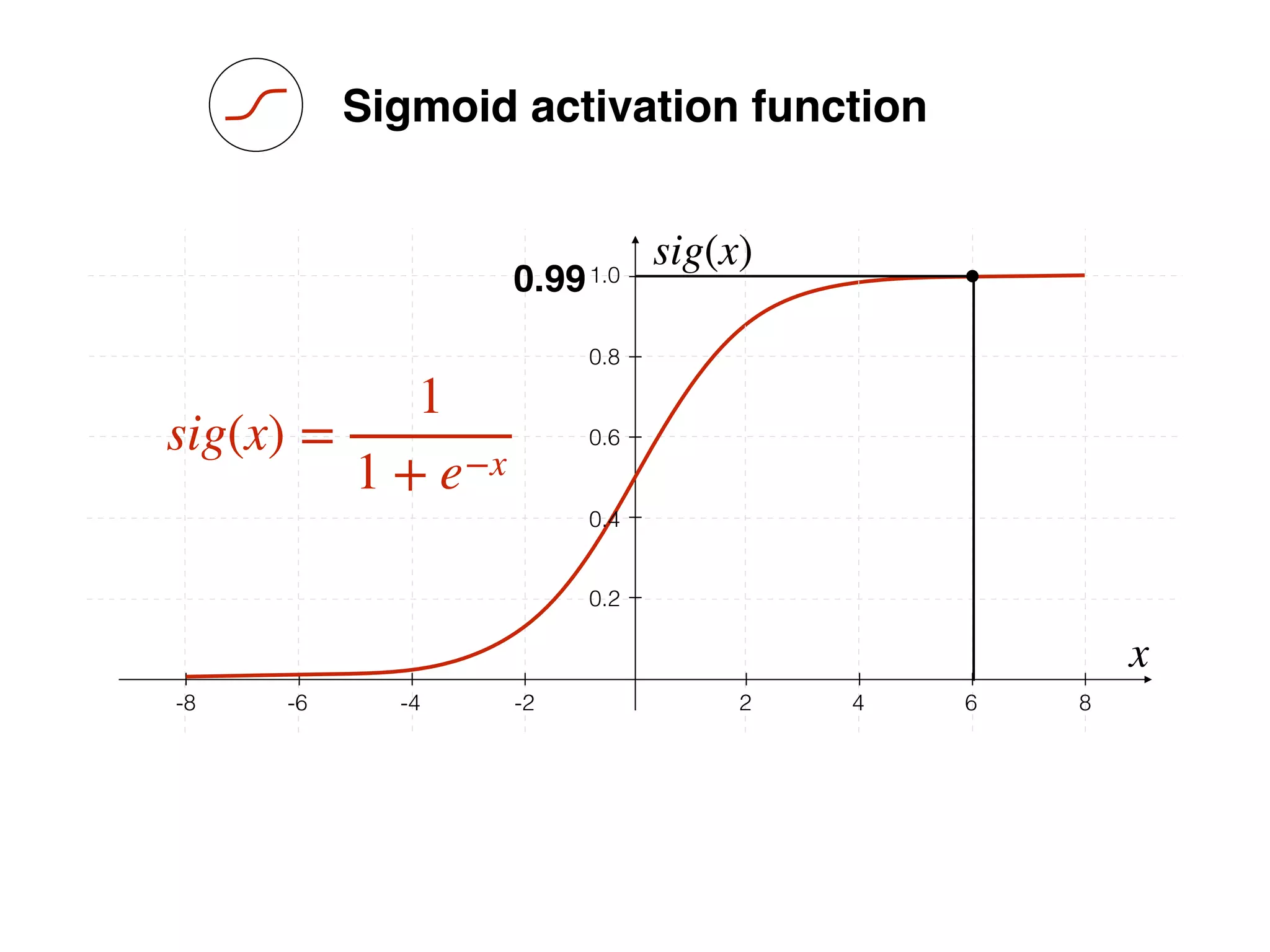
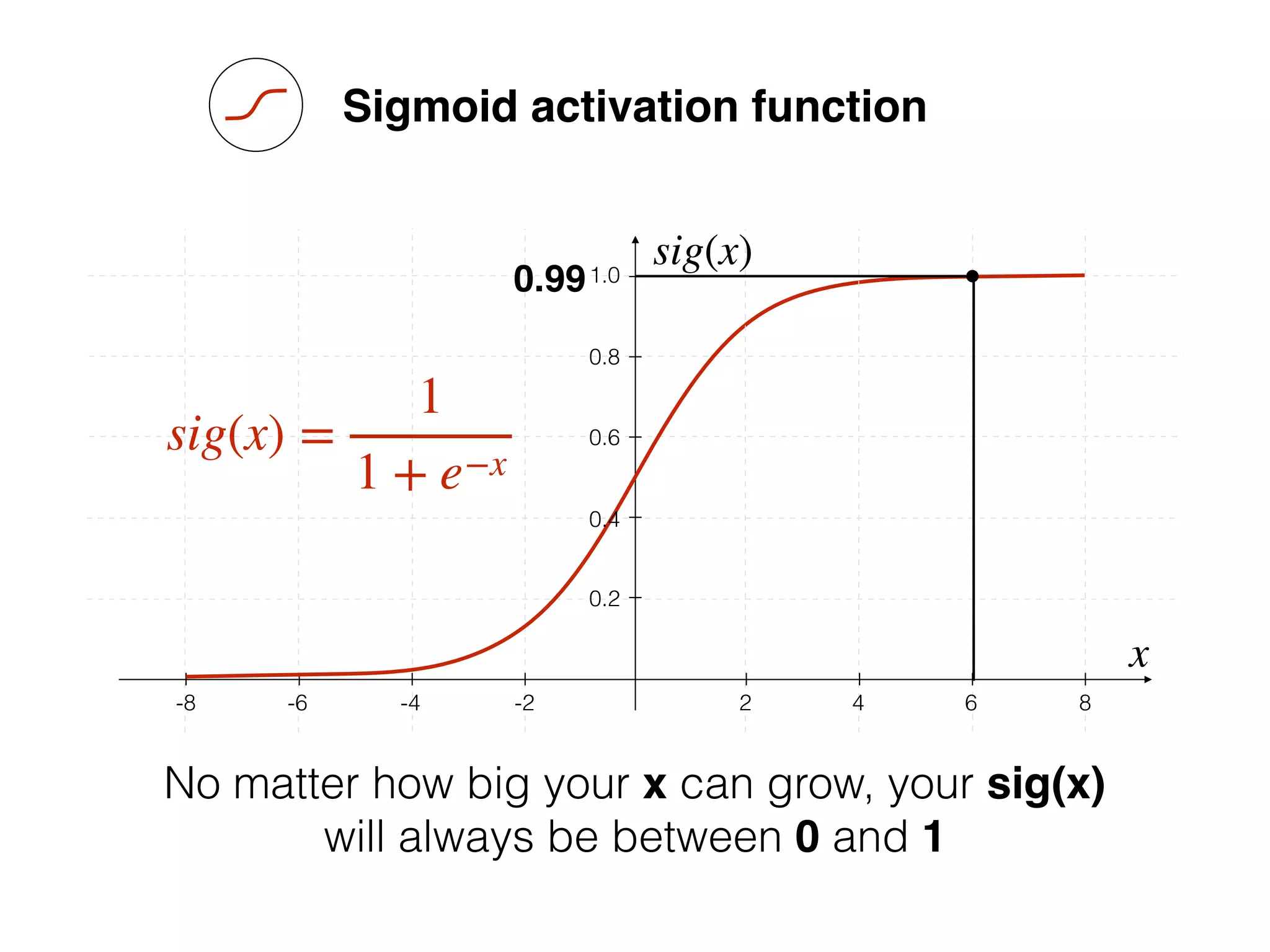
x
sig(x)
OutputInput
x
w1
sig(w1 * x)
What is the role of bias in Neural Networks?
w1 =[0.5, 1.0, 2.0]
OutputInput
x
w1
sig(w1 * x + b1)
b b1
Source: http://www.uta.fi/sis/tie/neuro/index/Neurocomputing2.pdf](https://image.slidesharecdn.com/dllecturegeneral-190728122700/75/Introduction-to-Deep-Learning-96-2048.jpg)
![OutputInput
x
w1
sig(w1 * x)
Bias helps to shift the resulting curve
w1 =[0.5, 1.0, 2.0]
OutputInput
x
w1
sig(w1 * x + b1)
b1
= [-4.0, 0.0, 4.0]
b b1
w1=[1.0]
-8 -6 -4 -2 2 4 6 8
0.2
0.4
0.6
0.8
1.0
x
sig(w1 * x + b1)
-8 -6 -4 -2 2 4 6 8
0.2
0.4
0.6
0.8
1.0
x
sig(w1 * x)
b1 b1
Source: http://www.uta.fi/sis/tie/neuro/index/Neurocomputing2.pdf](https://image.slidesharecdn.com/dllecturegeneral-190728122700/75/Introduction-to-Deep-Learning-97-2048.jpg)
![OutputInput
x
w1
sig(w1 * x)
Bias helps to shift the resulting curve
w1 =[0.5, 1.0, 2.0]
OutputInput
x
w1
sig(w1 * x + b1)
b1
= [-4.0, 0.0, 4.0]
b b1
w1=[1.0]
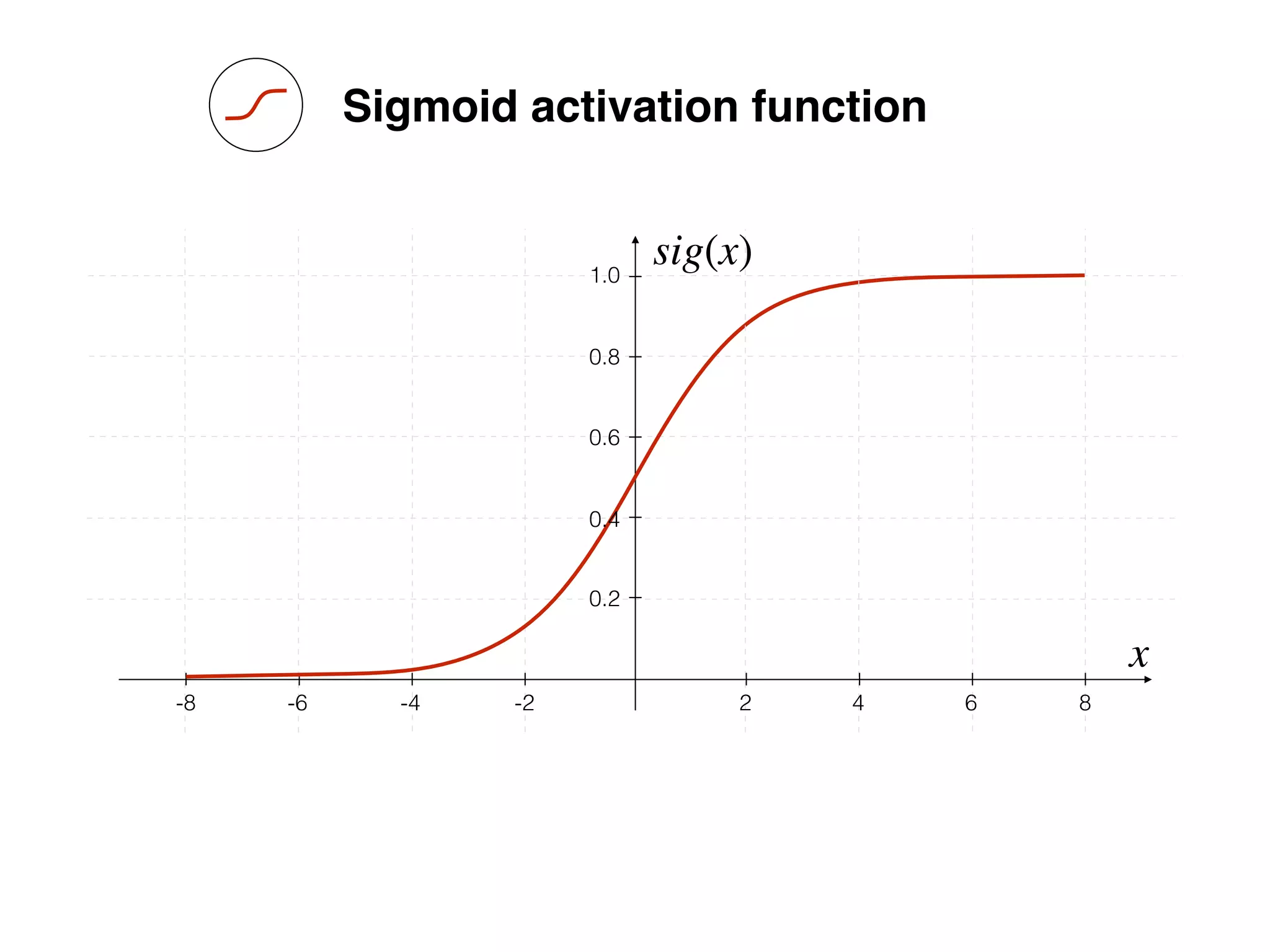
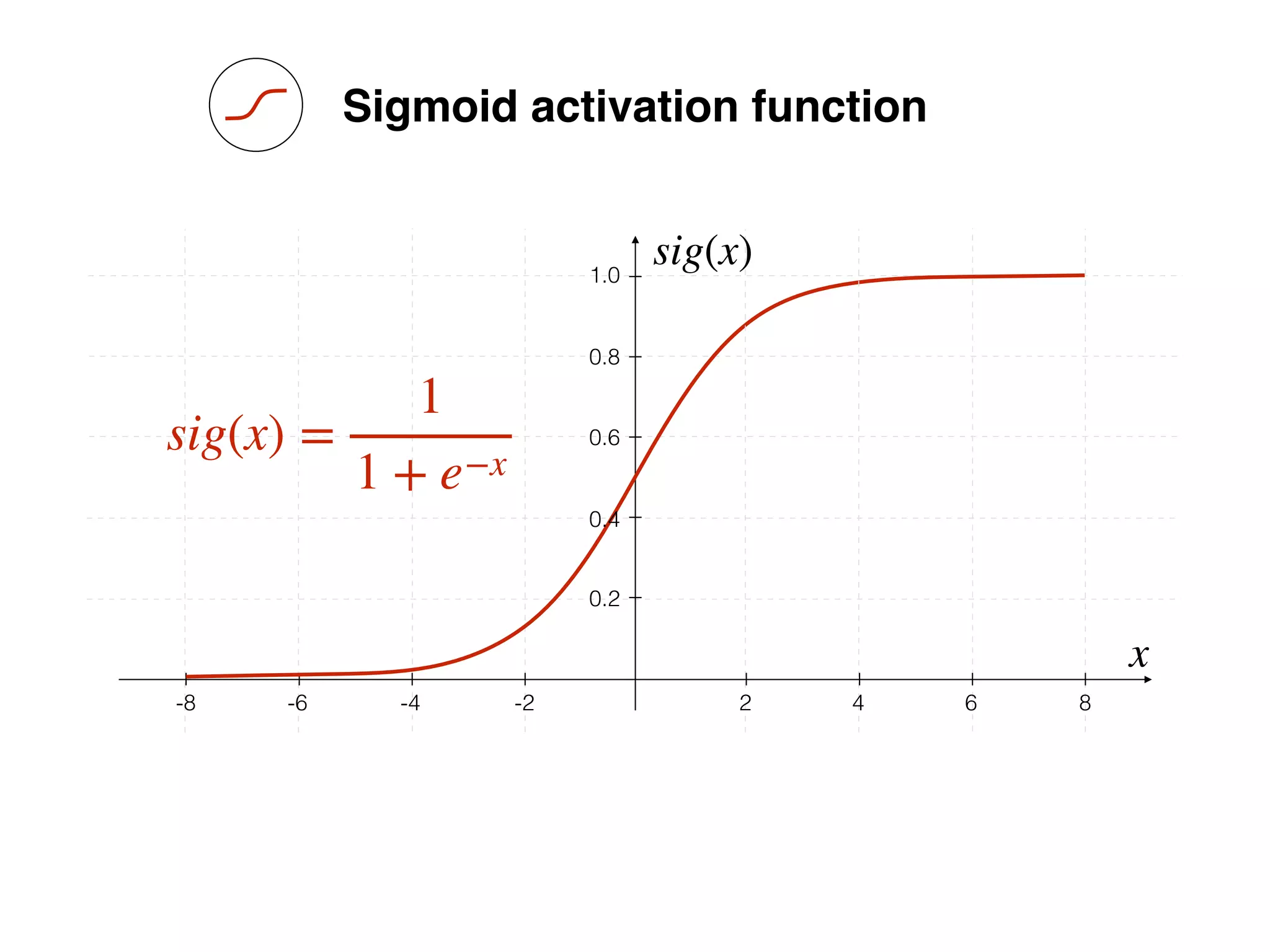
sig(x) =
1
1 + e−x
-8 -6 -4 -2 2 4 6 8
0.2
0.4
0.6
0.8
1.0
x
sig(w1 * x + b1)
-8 -6 -4 -2 2 4 6 8
0.2
0.4
0.6
0.8
1.0
x
sig(w1 * x)
b1 b1
Source: http://www.uta.fi/sis/tie/neuro/index/Neurocomputing2.pdf](https://image.slidesharecdn.com/dllecturegeneral-190728122700/75/Introduction-to-Deep-Learning-98-2048.jpg)
![OutputInput
x
w1
sig(w1 * x)
Bias helps to shift the resulting curve
w1 =[0.5, 1.0, 2.0]
OutputInput
x
w1
sig(w1 * x + b1)
b1
= [-4.0, 0.0, 4.0]
b b1
w1=[1.0]
sig(x) =
1
1 + e−(wx+b)
-8 -6 -4 -2 2 4 6 8
0.2
0.4
0.6
0.8
1.0
x
sig(w1 * x + b1)
-8 -6 -4 -2 2 4 6 8
0.2
0.4
0.6
0.8
1.0
x
sig(w1 * x)
b1 b1
Source: http://www.uta.fi/sis/tie/neuro/index/Neurocomputing2.pdf](https://image.slidesharecdn.com/dllecturegeneral-190728122700/75/Introduction-to-Deep-Learning-99-2048.jpg)