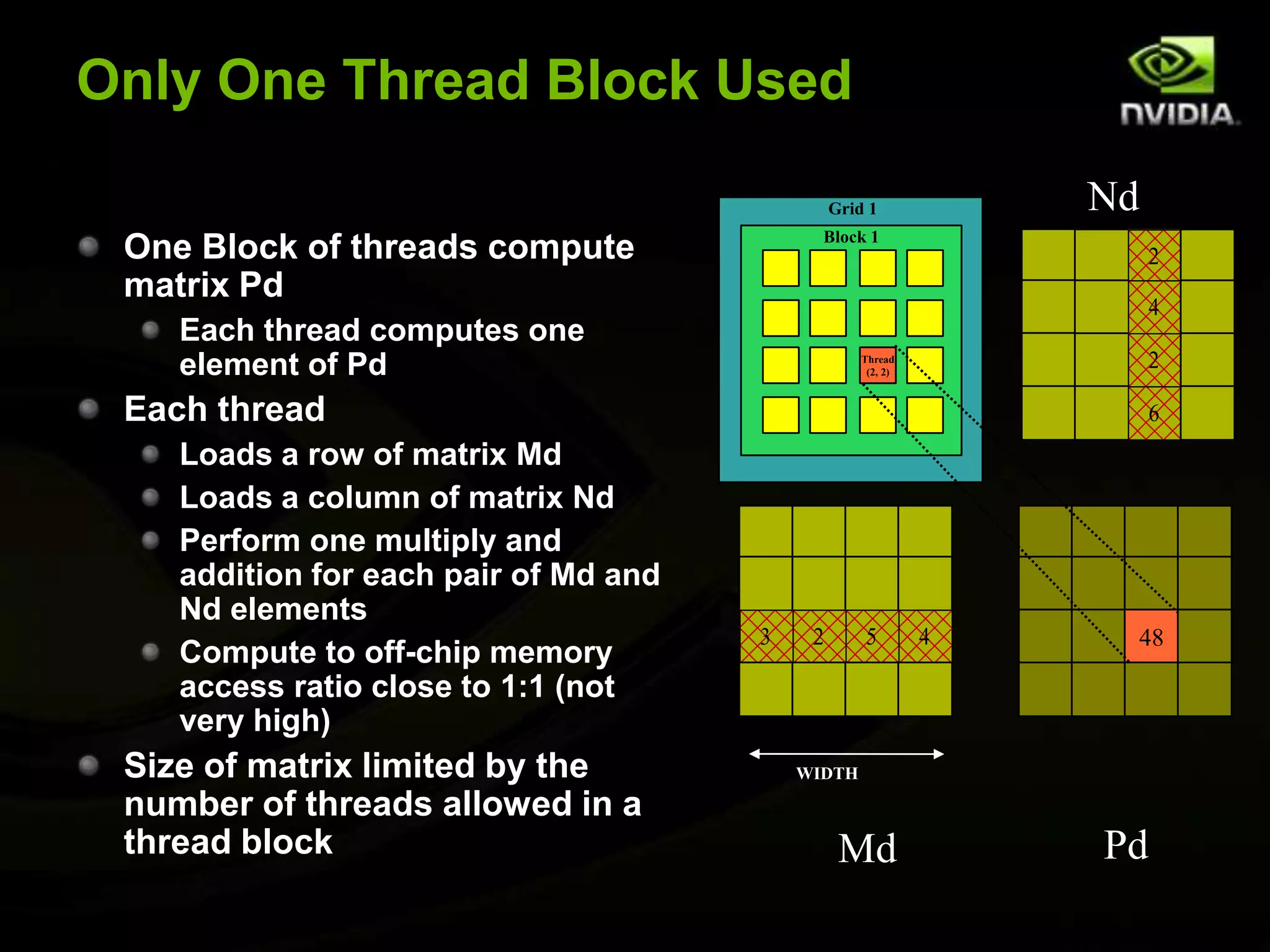
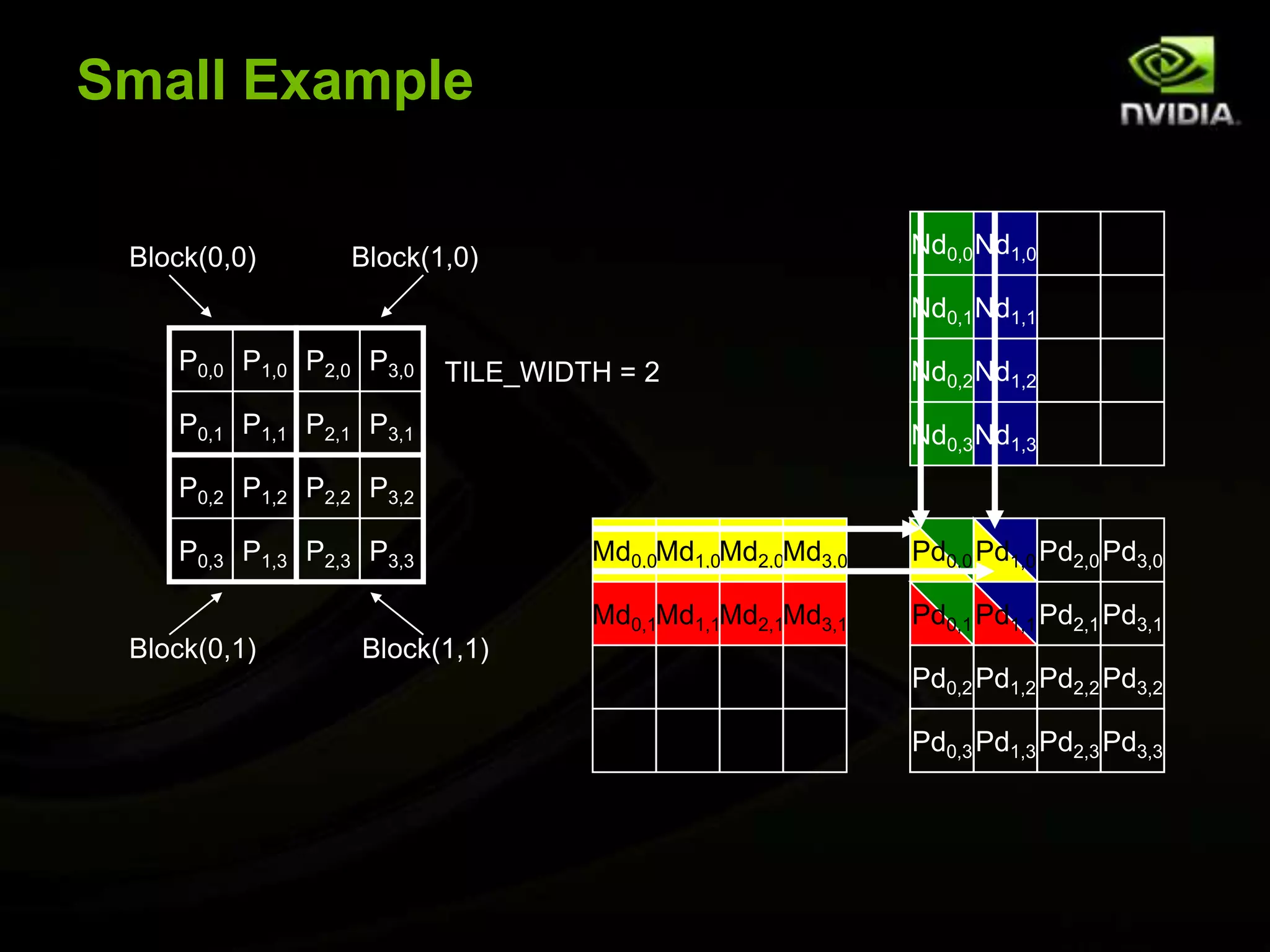
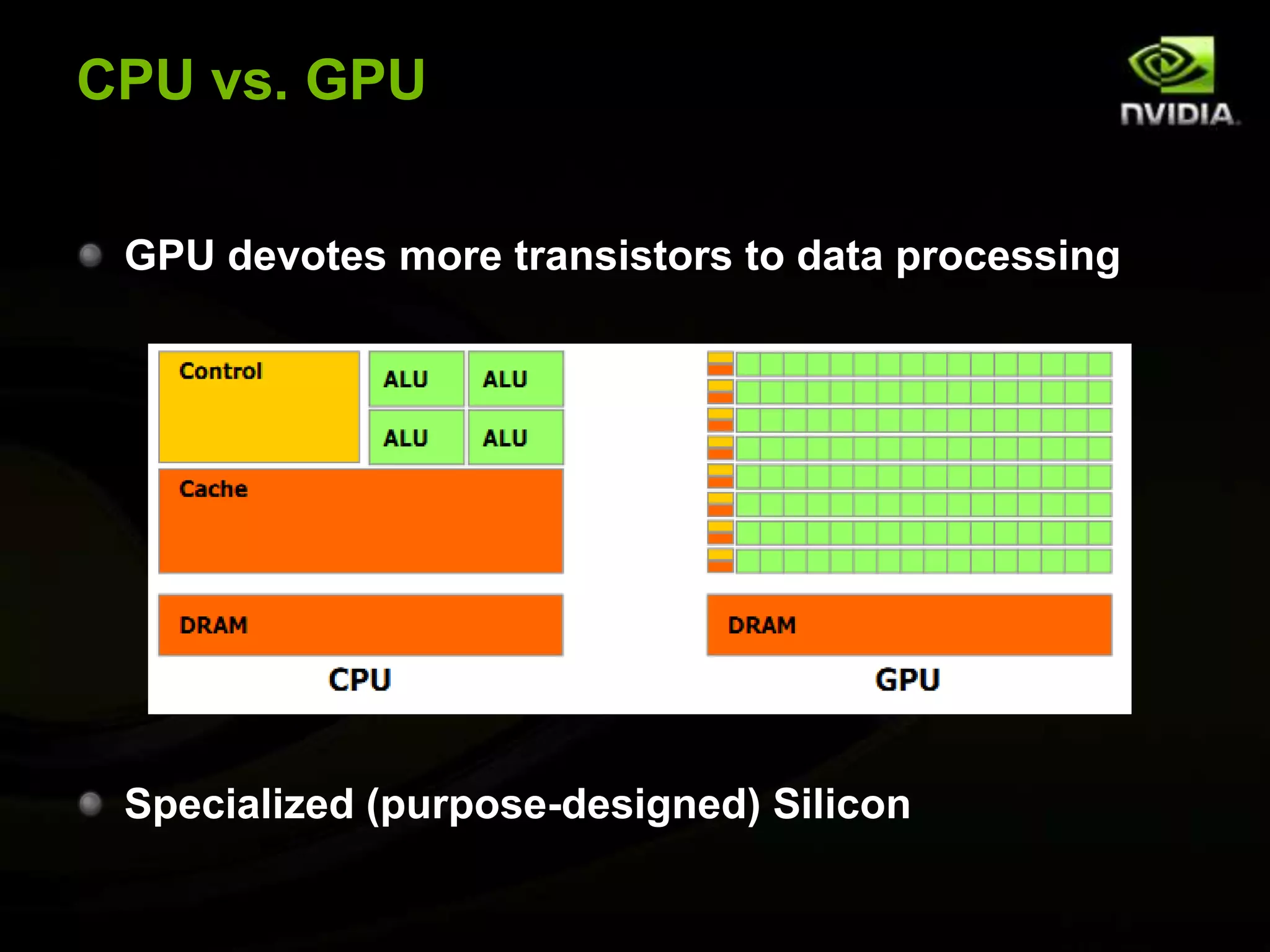
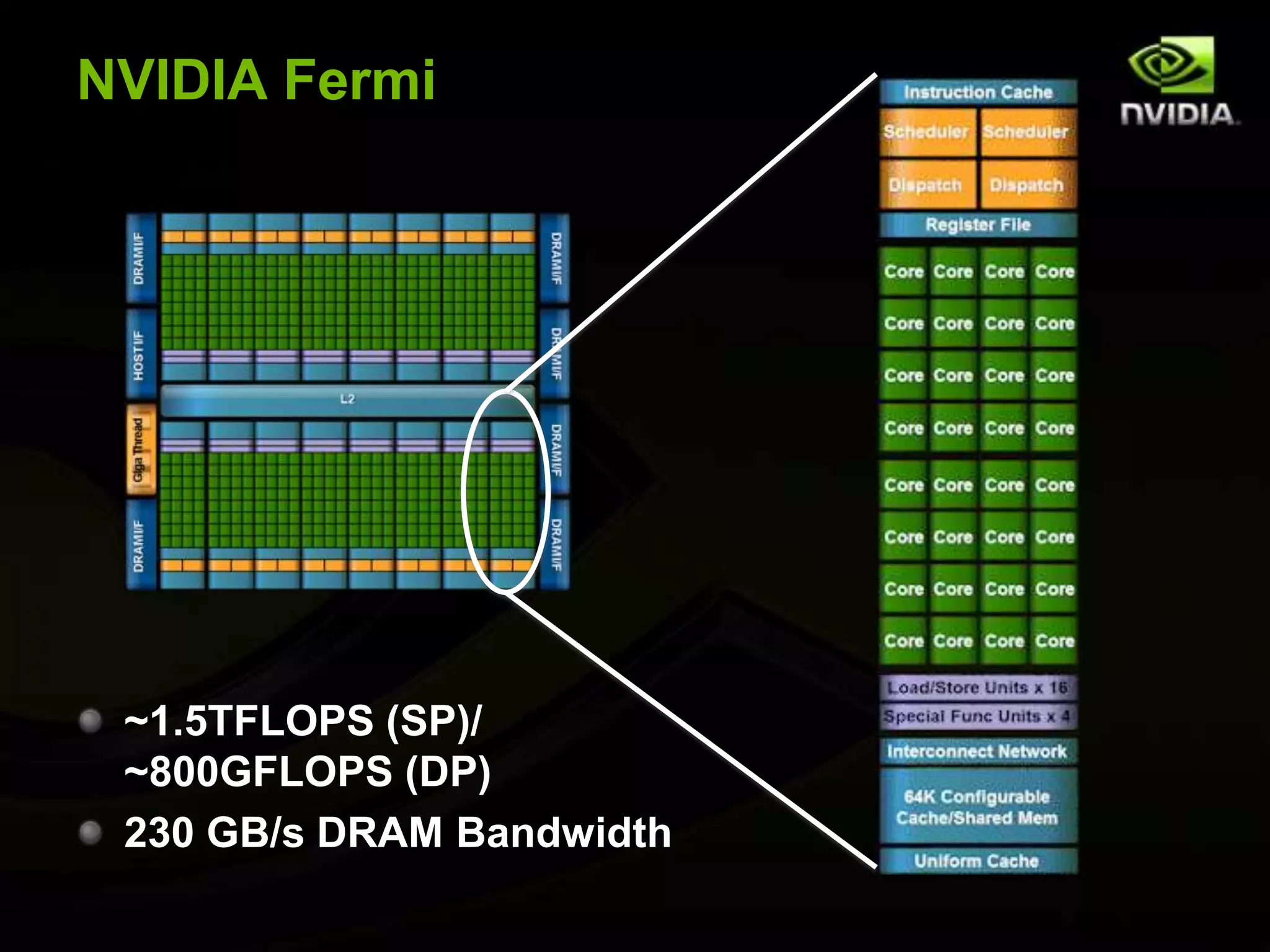
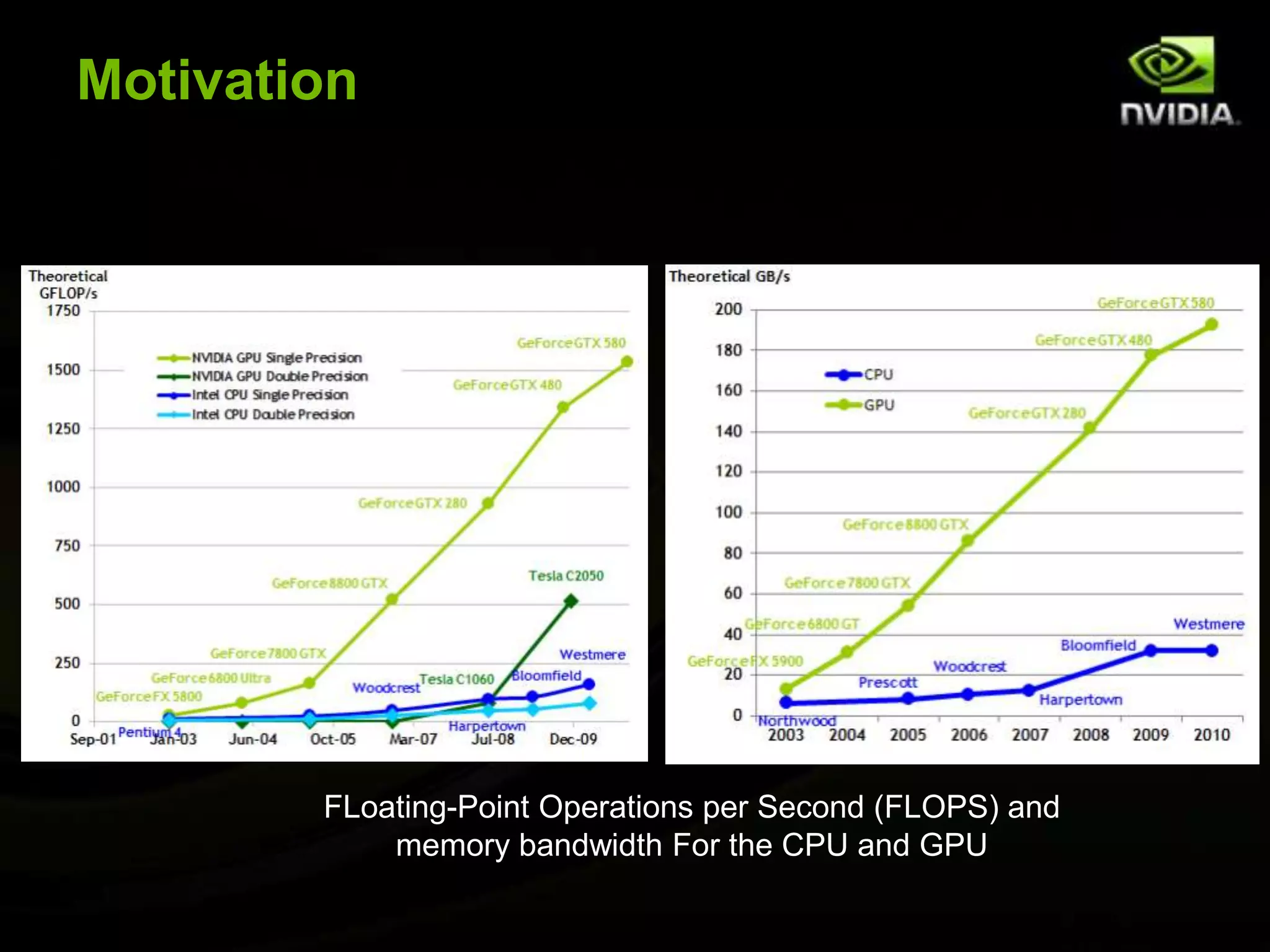
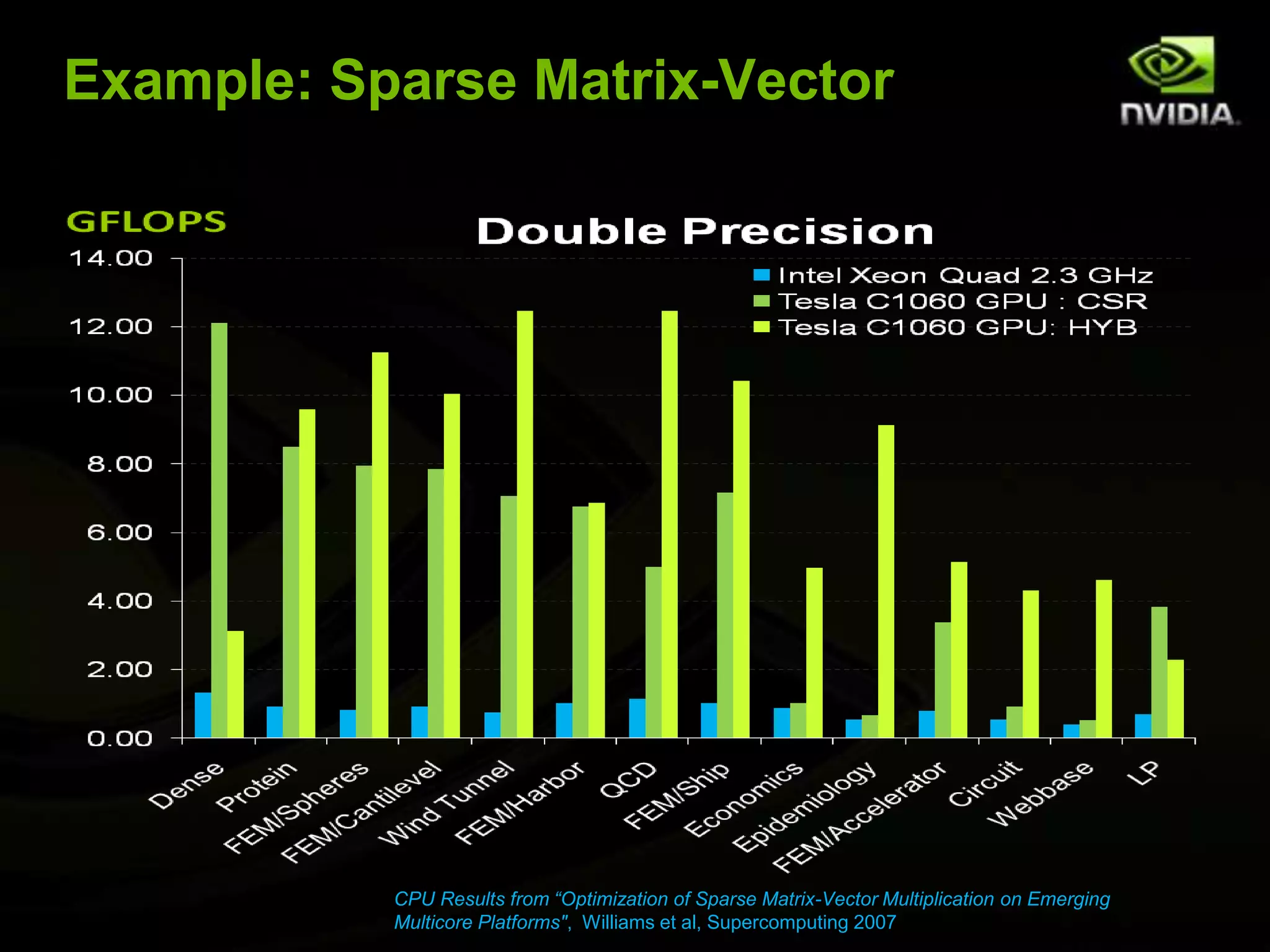
The document provides an overview of introductory GPGPU programming with CUDA. It discusses why GPUs are useful for parallel computing applications due to their high FLOPS and memory bandwidth capabilities. It then outlines the CUDA programming model, including launching kernels on the GPU with grids and blocks of threads, and memory management between CPU and GPU. As an example, it walks through a simple matrix multiplication problem implemented on the CPU and GPU to illustrate CUDA programming concepts.























![Kernel Variations and Output__global__ void kernel (int*a){intidx = blockIdx.x * blockDim.x + threadIdx.x; a[idx] = 7;} Output: 7777777777777777__global__ void kernel (int *a){intidx = blockIdx.x * blockDim.x + threadIdx.x; a[idx] = blockIdx.x;} Output: 000011112222333__global__ void kernel (int *a){intidx = blockIdx.x * blockDim.x + threadIdx.x; a[idx] = threadIdx.x;} Output: 0123012301230123](https://image.slidesharecdn.com/devlinkintrotogpgpuwithcuda-110905135246-phpapp01/75/Intro-to-GPGPU-with-CUDA-DevLink-33-2048.jpg)







![Simple Matrix Multiplication (CPU)void MatrixMulOnHost(float* M, float* N, float* P, int Width){ for (int i = 0; i < Width; ++i) { for (int j = 0; j < Width; ++j) { float sum = 0; for (int k = 0; k < Width; ++k) { float a = M[i * width + k];float b = N[k * width + j];sum += a * b;}P[i * Width + j] = sum; } }}NkjWIDTHMPiWIDTHk42WIDTHWIDTH](https://image.slidesharecdn.com/devlinkintrotogpgpuwithcuda-110905135246-phpapp01/75/Intro-to-GPGPU-with-CUDA-DevLink-42-2048.jpg)



![Kernel Function (contd.)for (int k = 0; k < Width; ++k) {float Melement = Md[threadIdx.y*Width+k];float Nelement = Nd[k*Width+threadIdx.x];Pvalue+= Melement * Nelement; }Pd[threadIdx.y*Width+threadIdx.x] = Pvalue;}NdkWIDTHtxMdPdtytyWIDTHtxk46WIDTHWIDTH](https://image.slidesharecdn.com/devlinkintrotogpgpuwithcuda-110905135246-phpapp01/75/Intro-to-GPGPU-with-CUDA-DevLink-46-2048.jpg)
![Kernel Function (full)// Matrix multiplication kernel – per thread code__global__ void MatrixMulKernel(float* Md, float* Nd, float* Pd, int Width){ // Pvalue is used to store the element of the matrix// that is computed by the threadfloat Pvalue = 0; for (int k = 0; k < Width; ++k) { float Melement = Md[threadIdx.y*Width+k]; float Nelement = Nd[k*Width+threadIdx.x];Pvalue += Melement * Nelement; }Pd[threadIdx.y*Width+threadIdx.x] = Pvalue;}](https://image.slidesharecdn.com/devlinkintrotogpgpuwithcuda-110905135246-phpapp01/75/Intro-to-GPGPU-with-CUDA-DevLink-47-2048.jpg)