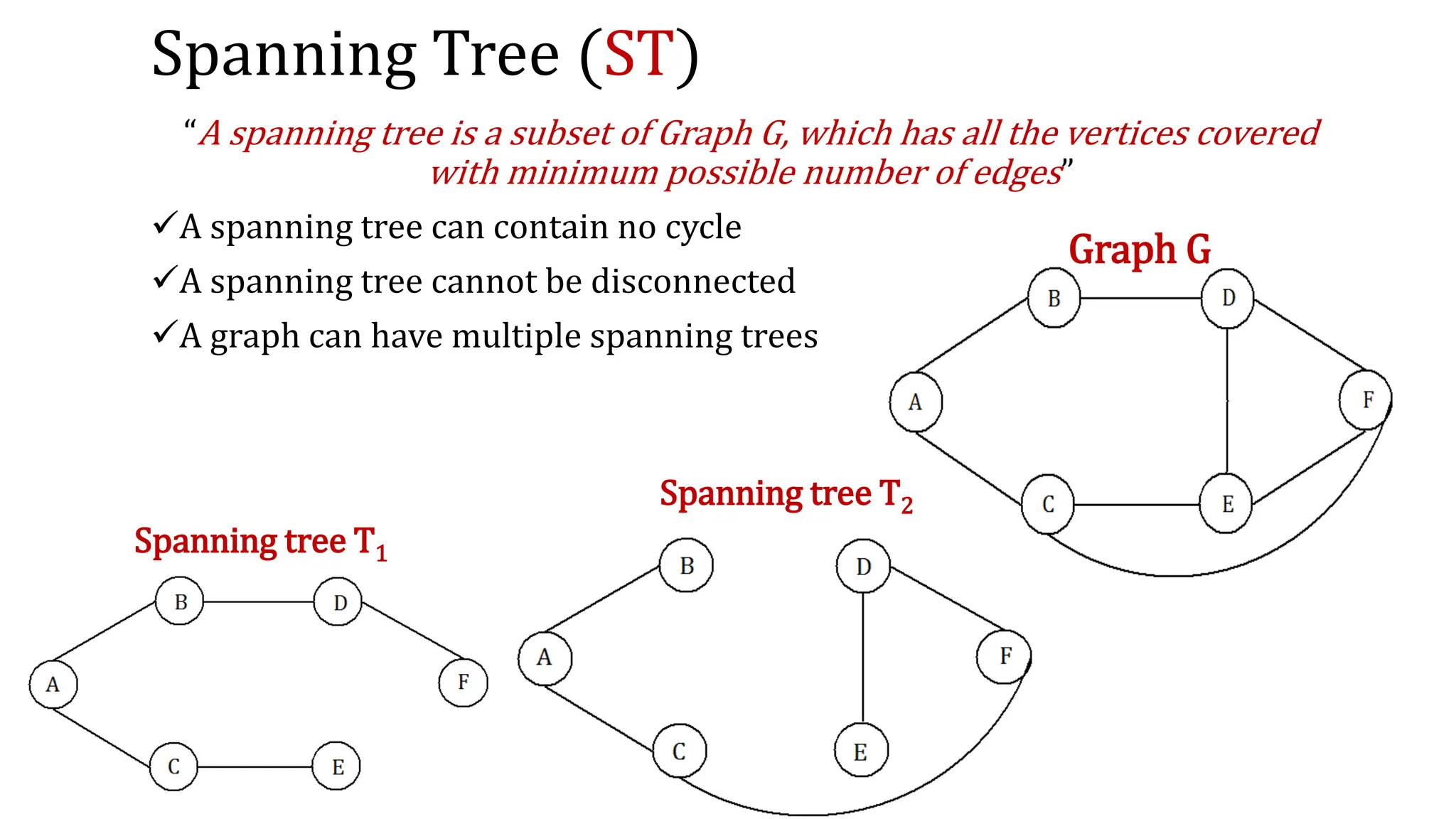
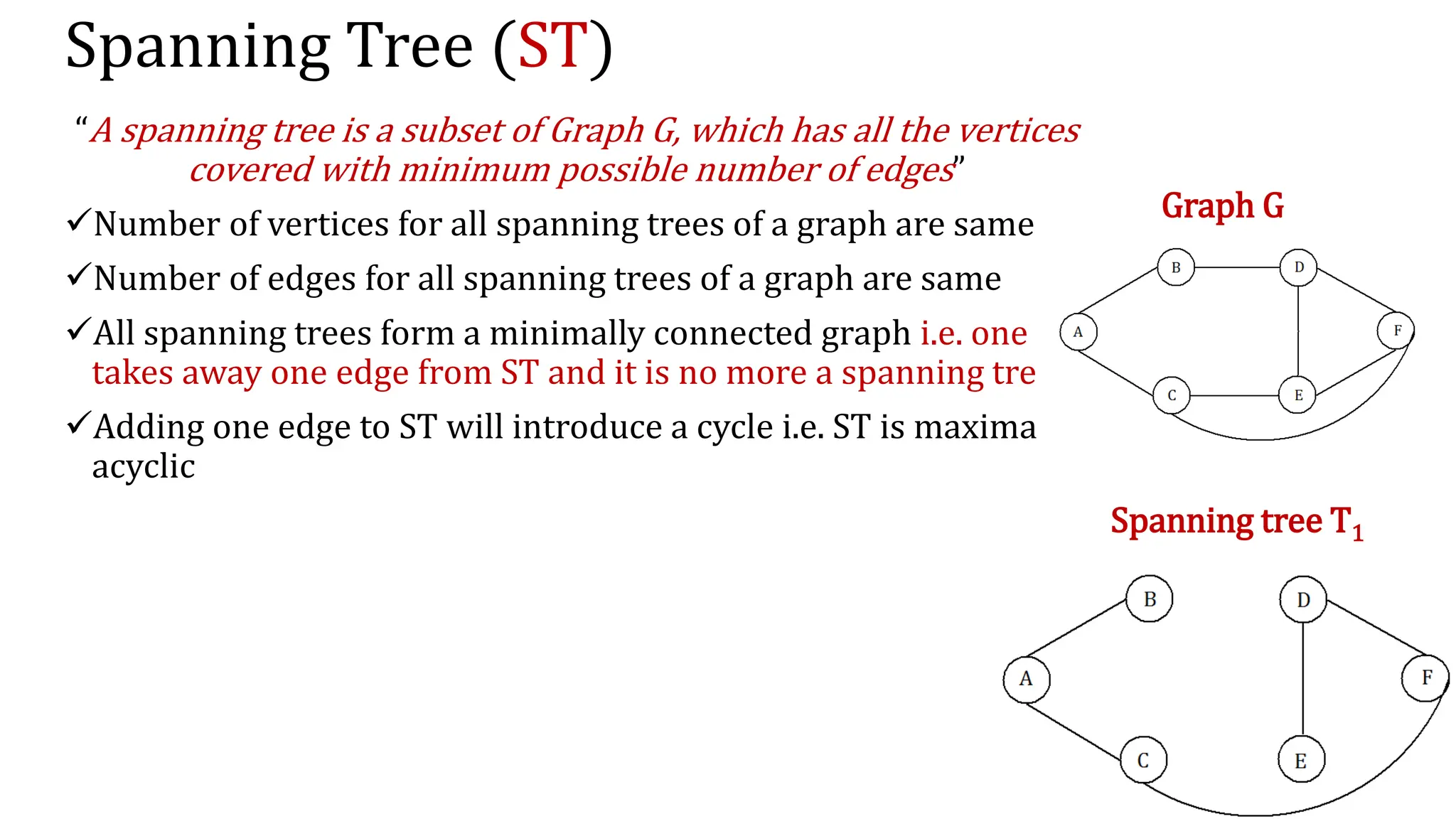
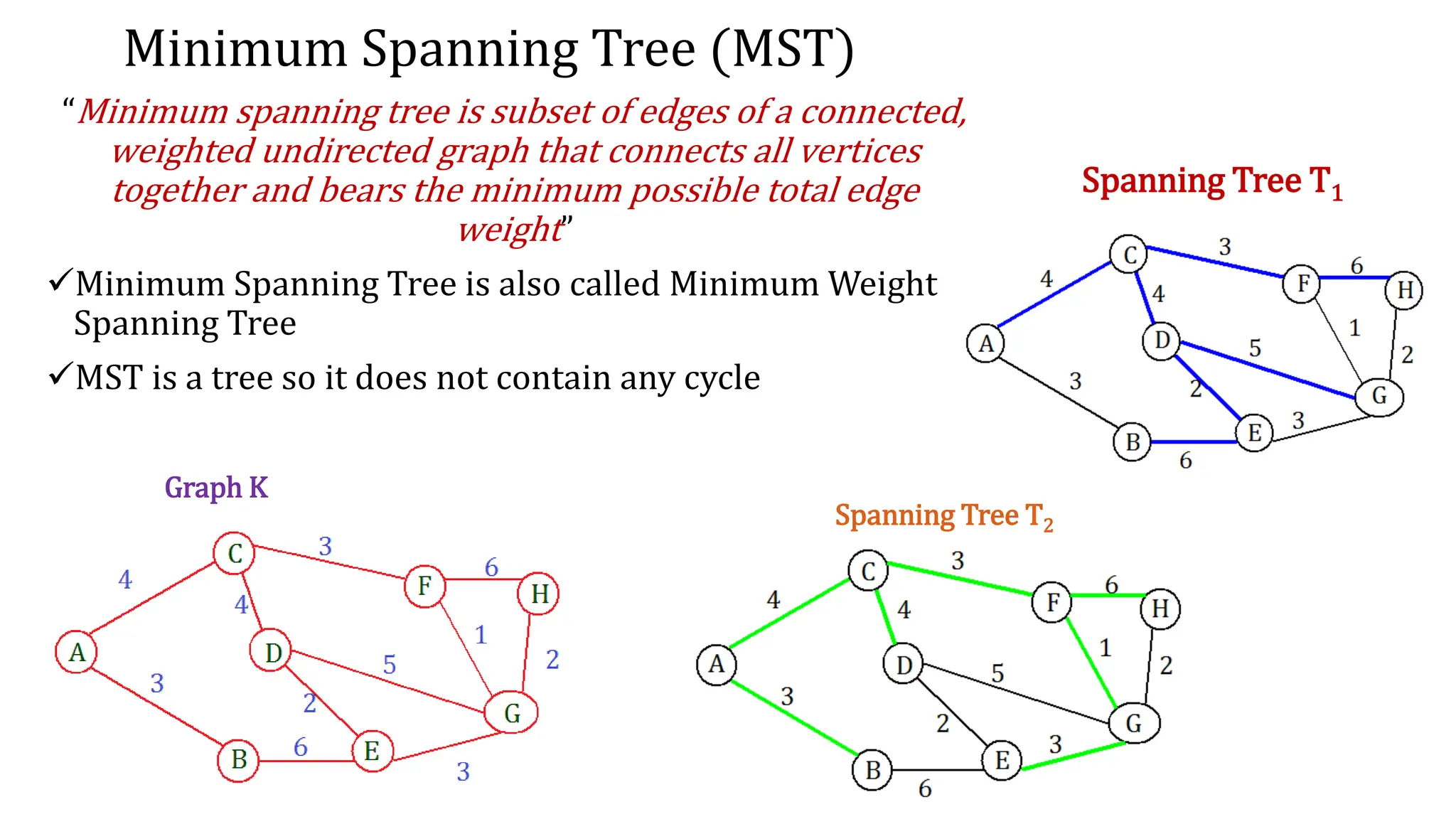
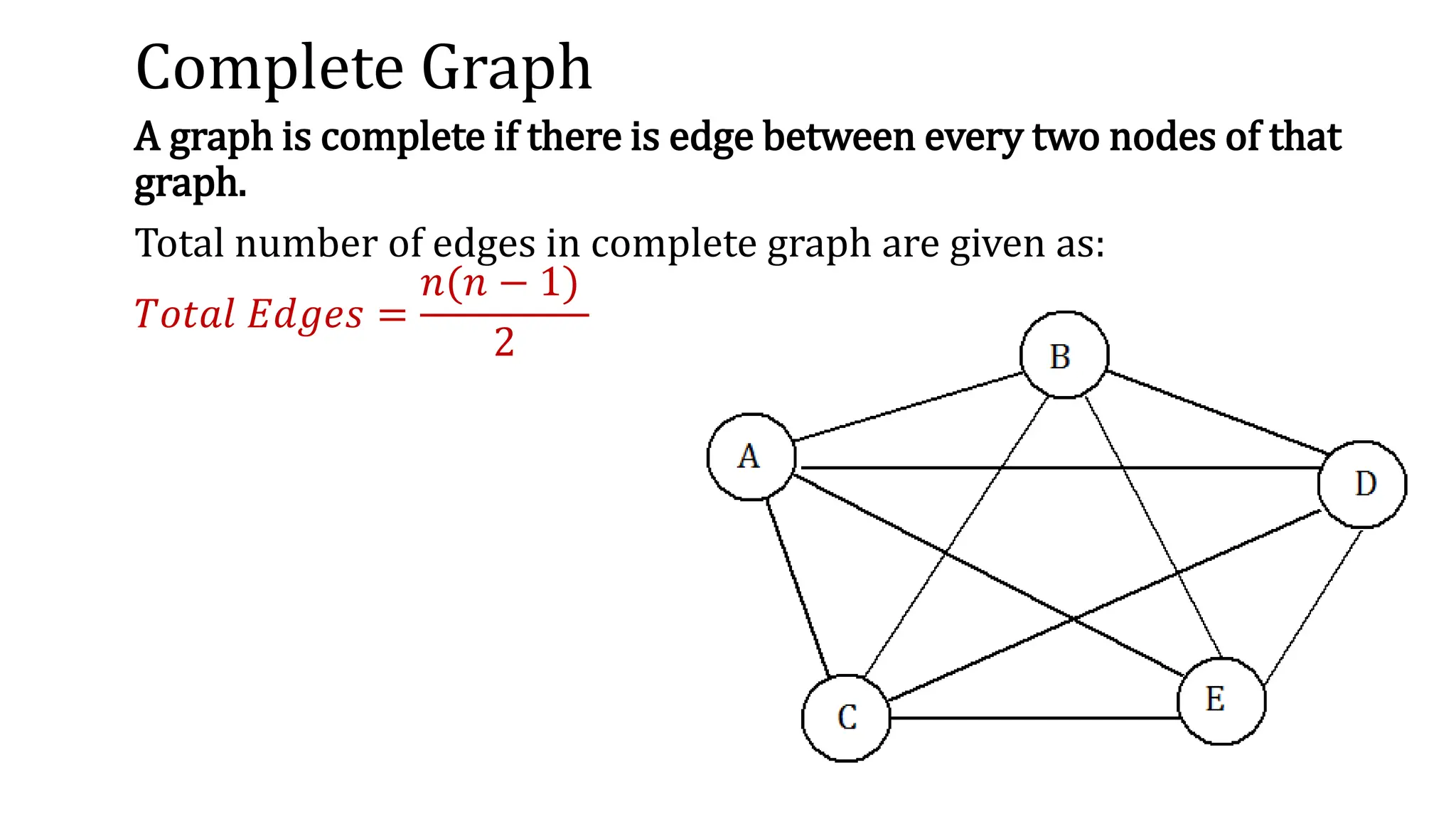
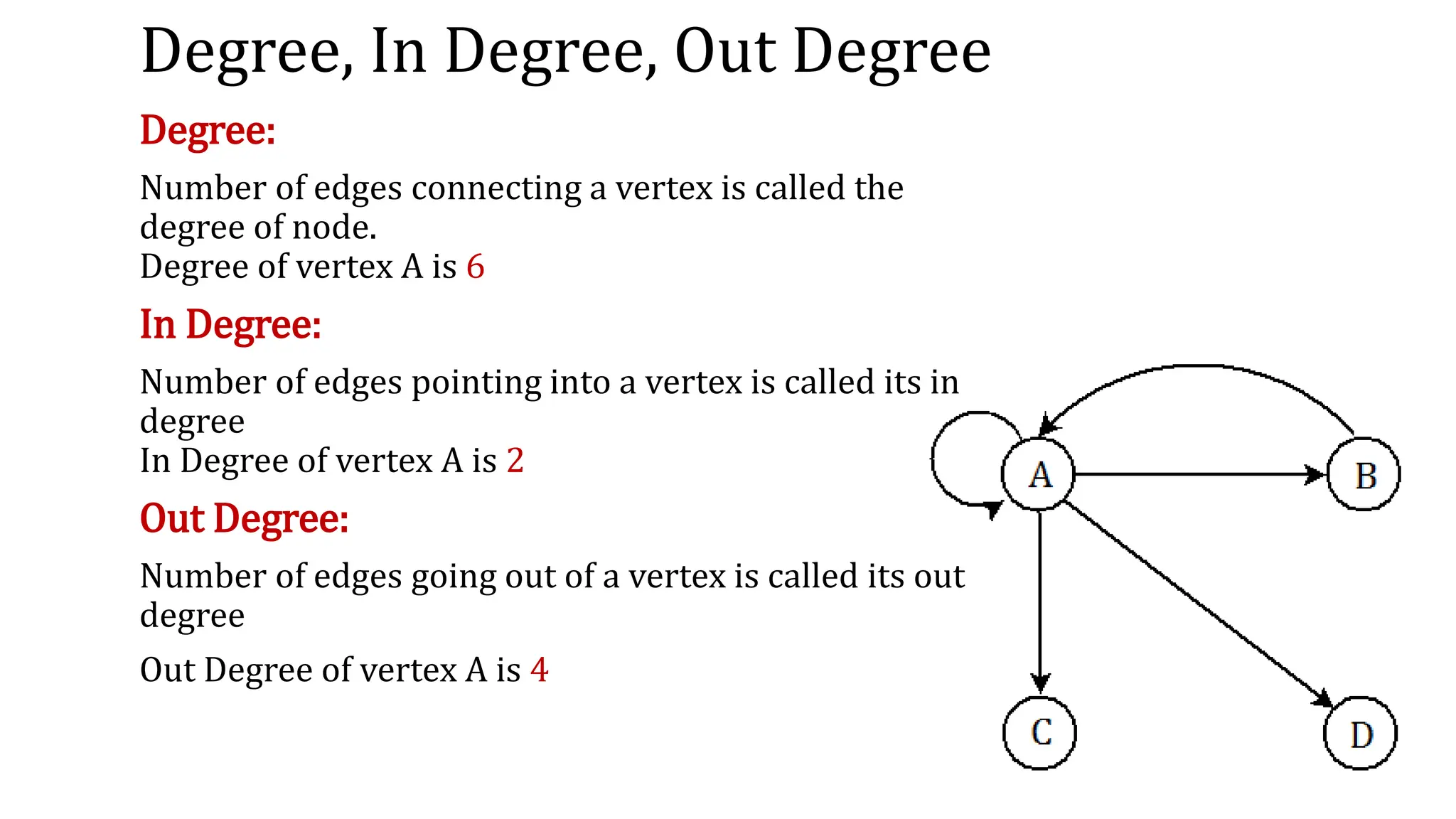
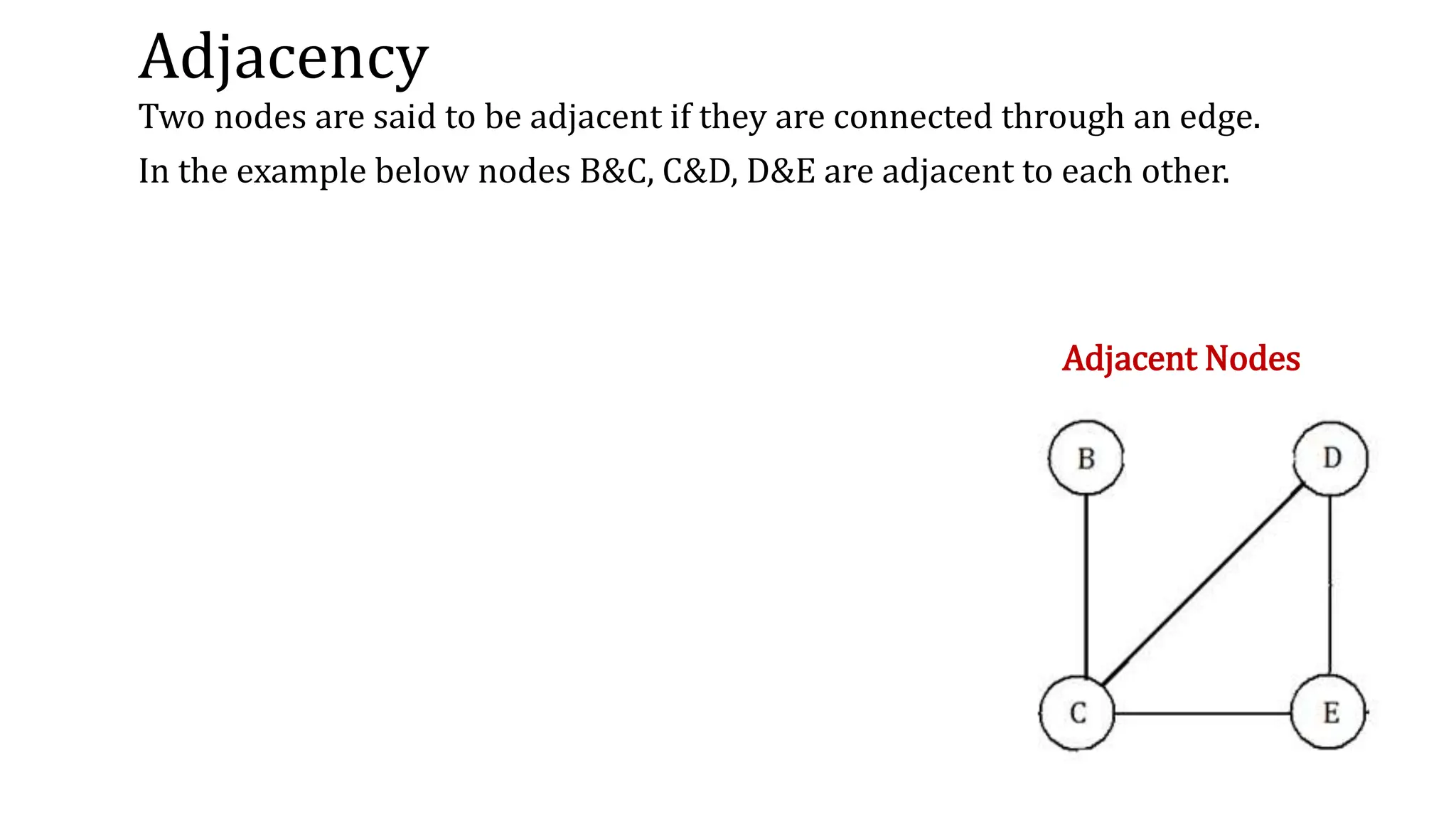
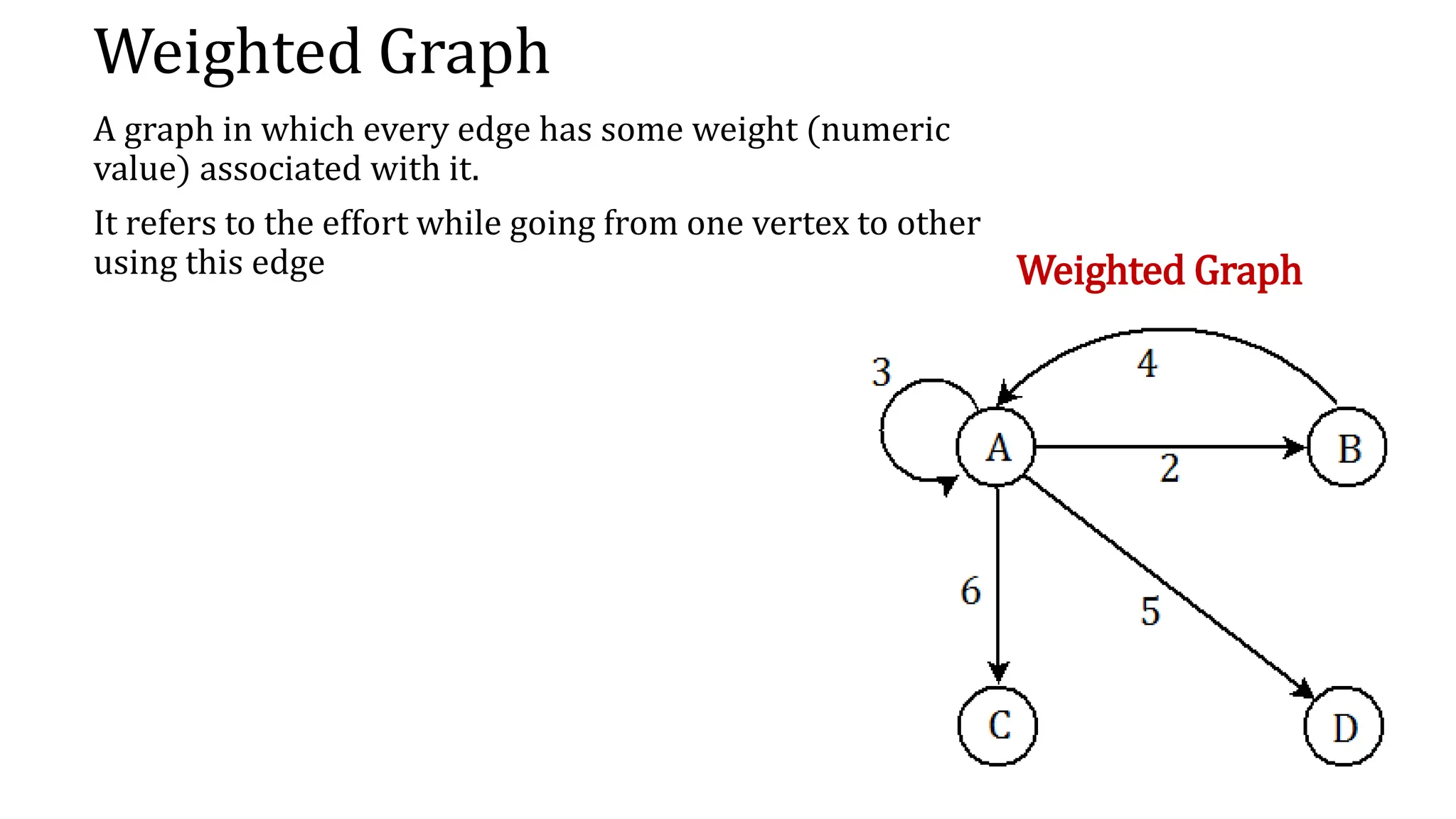
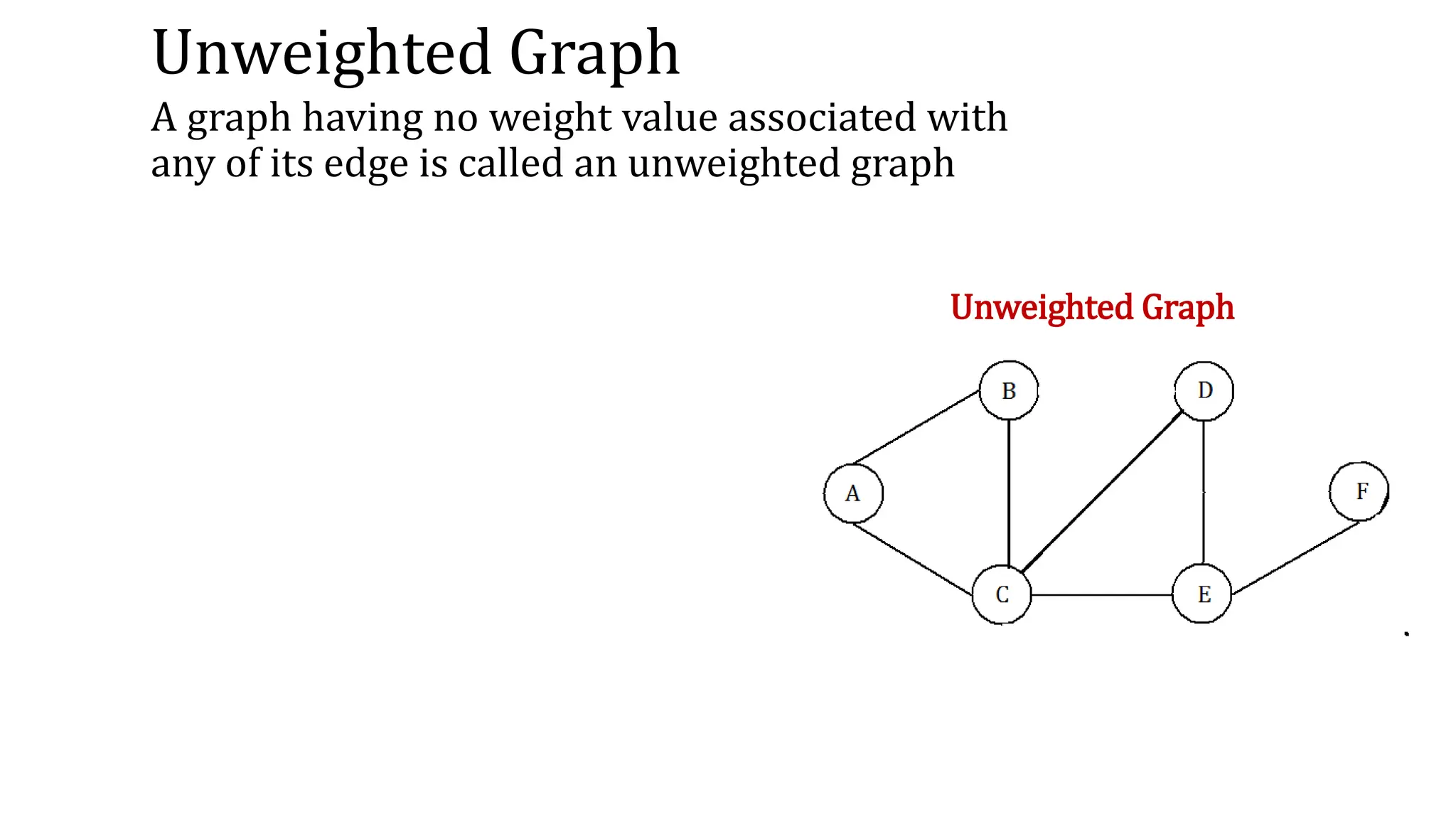
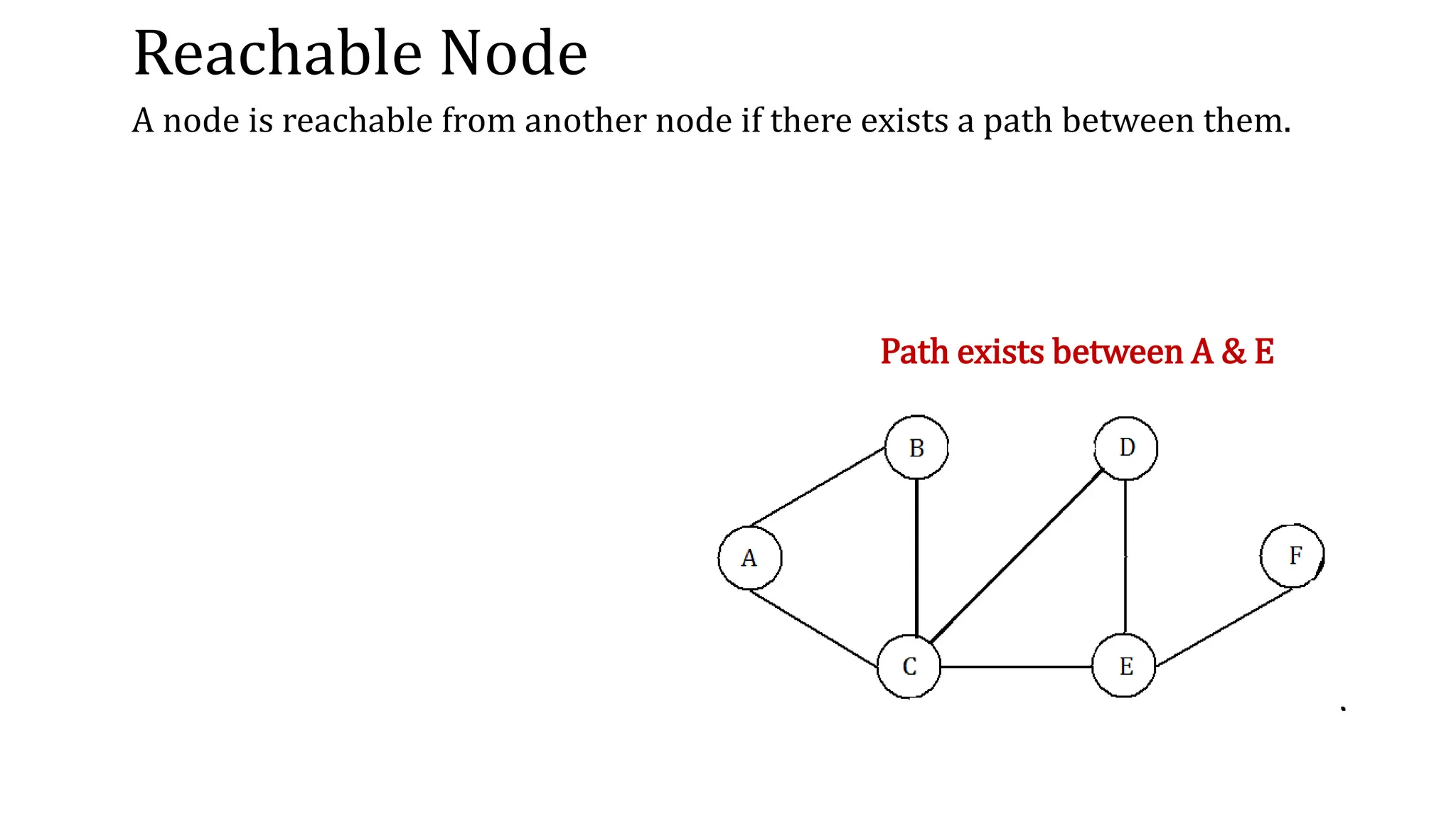
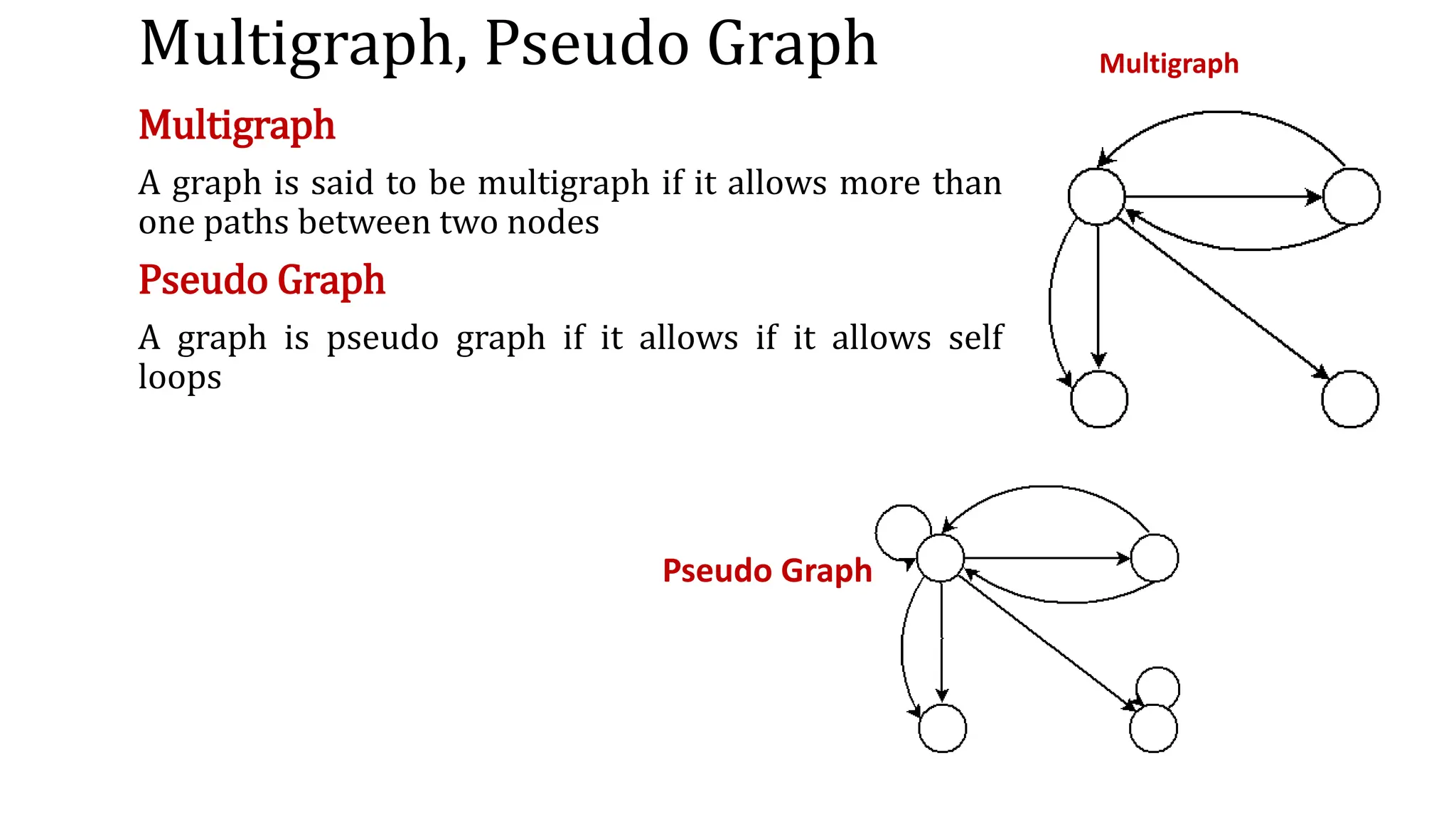
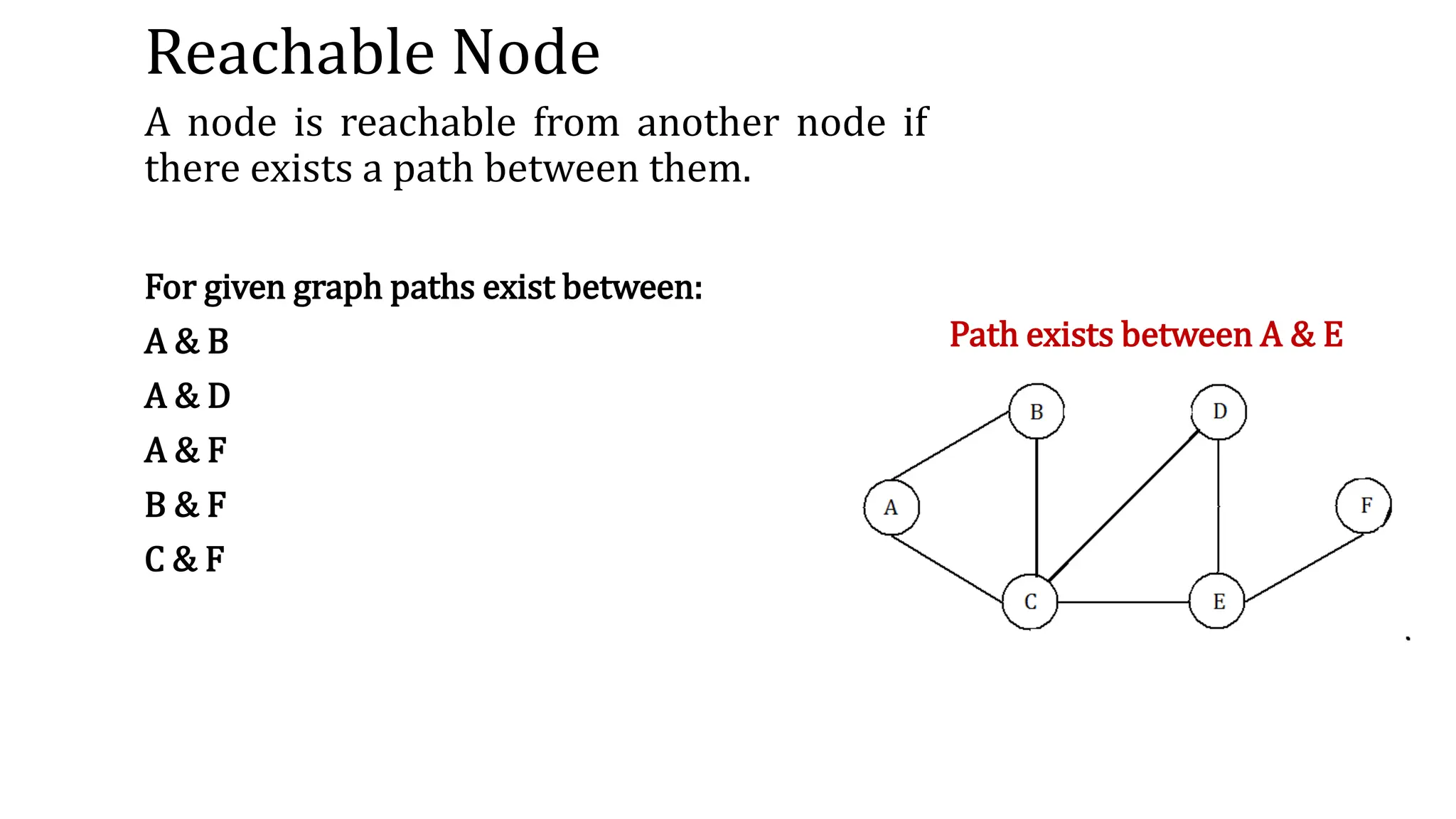
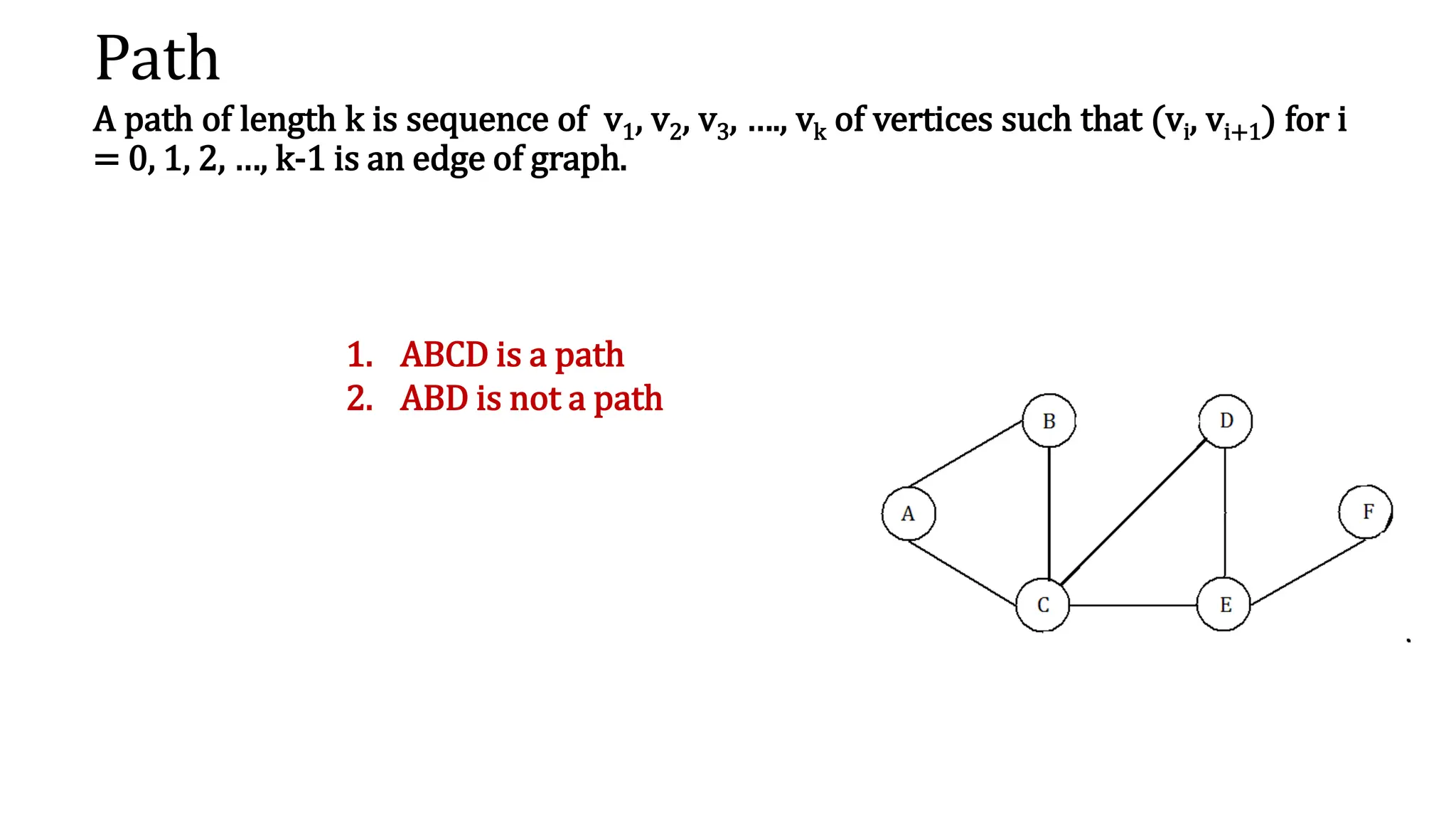
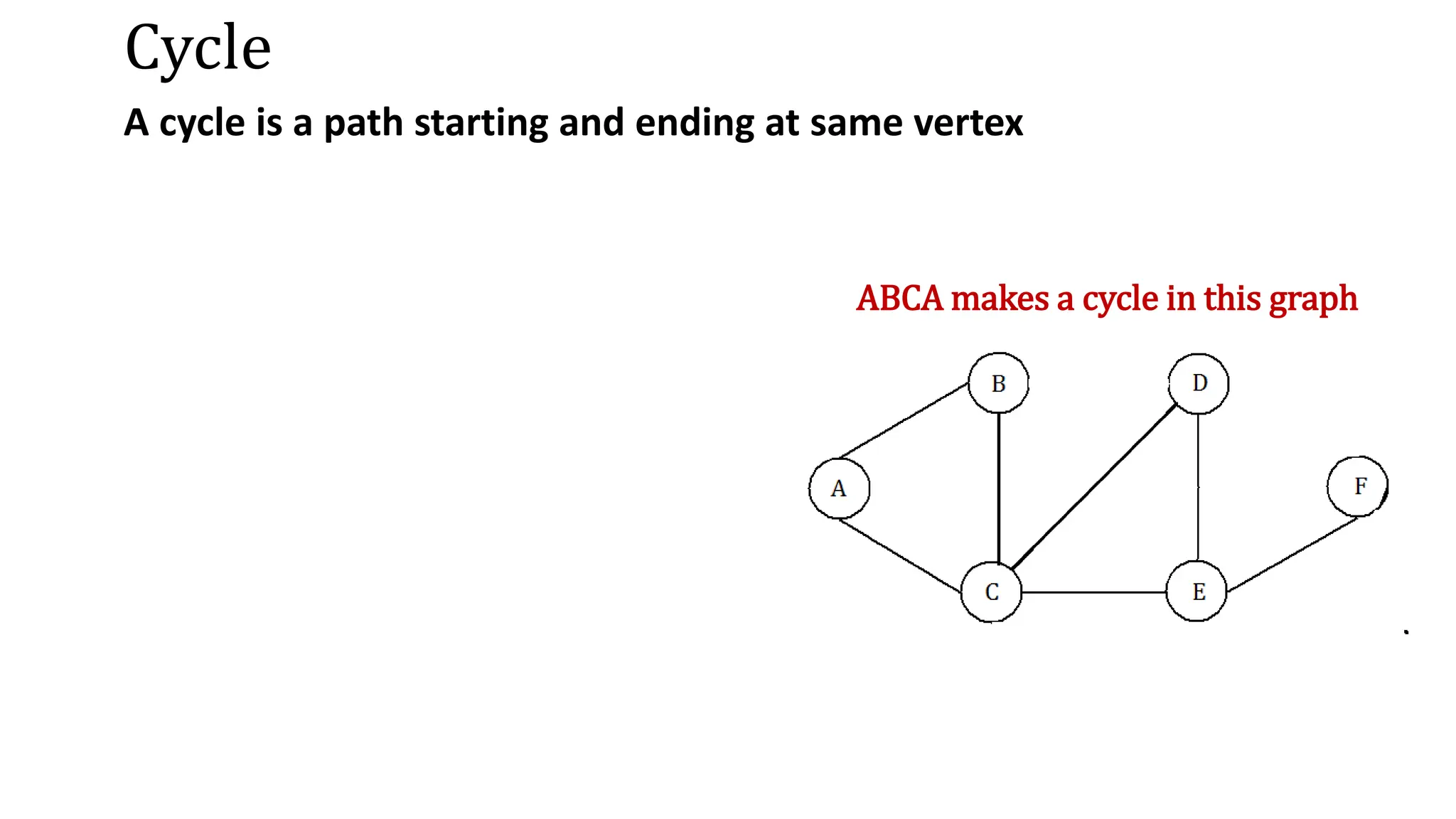
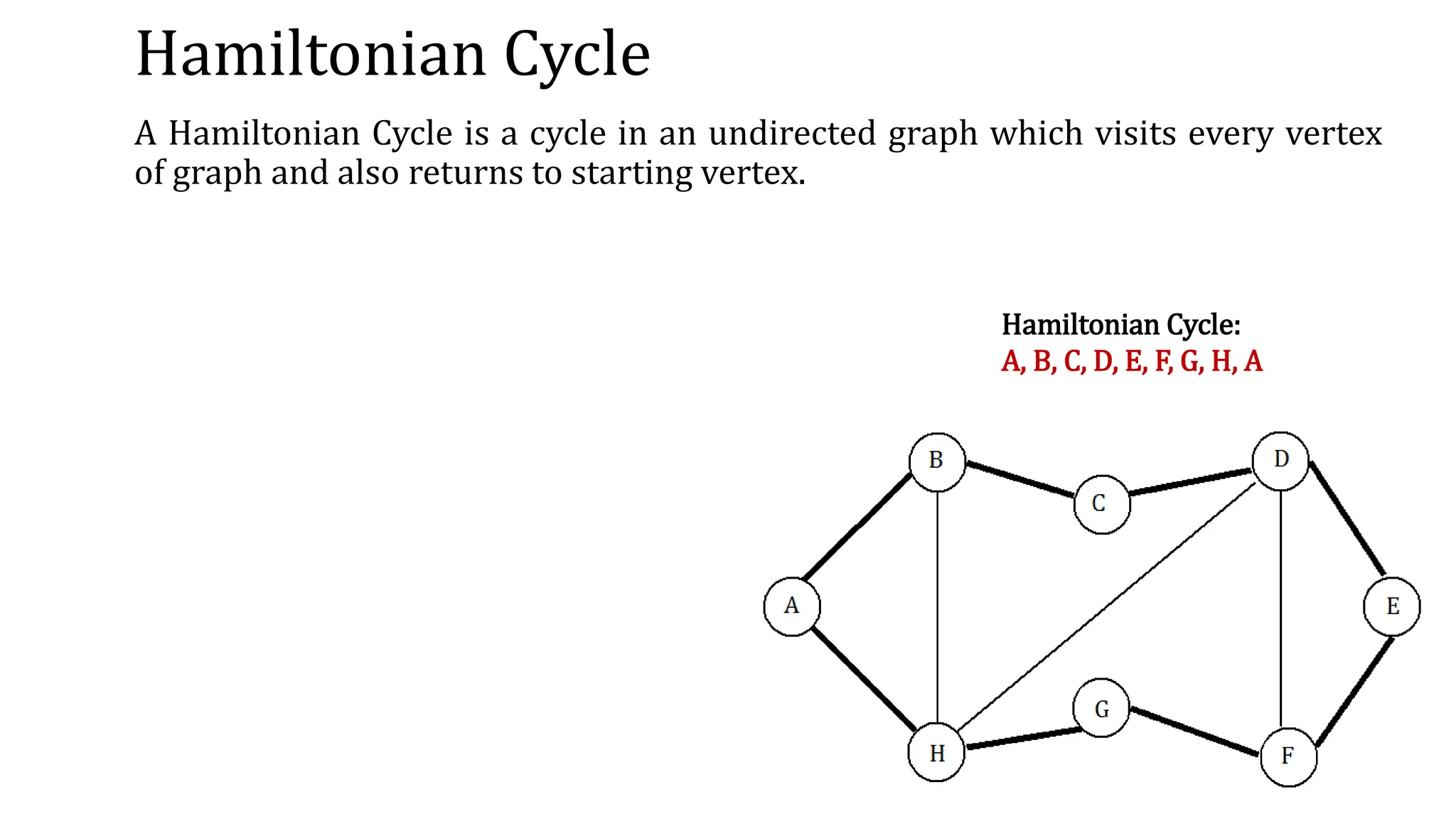
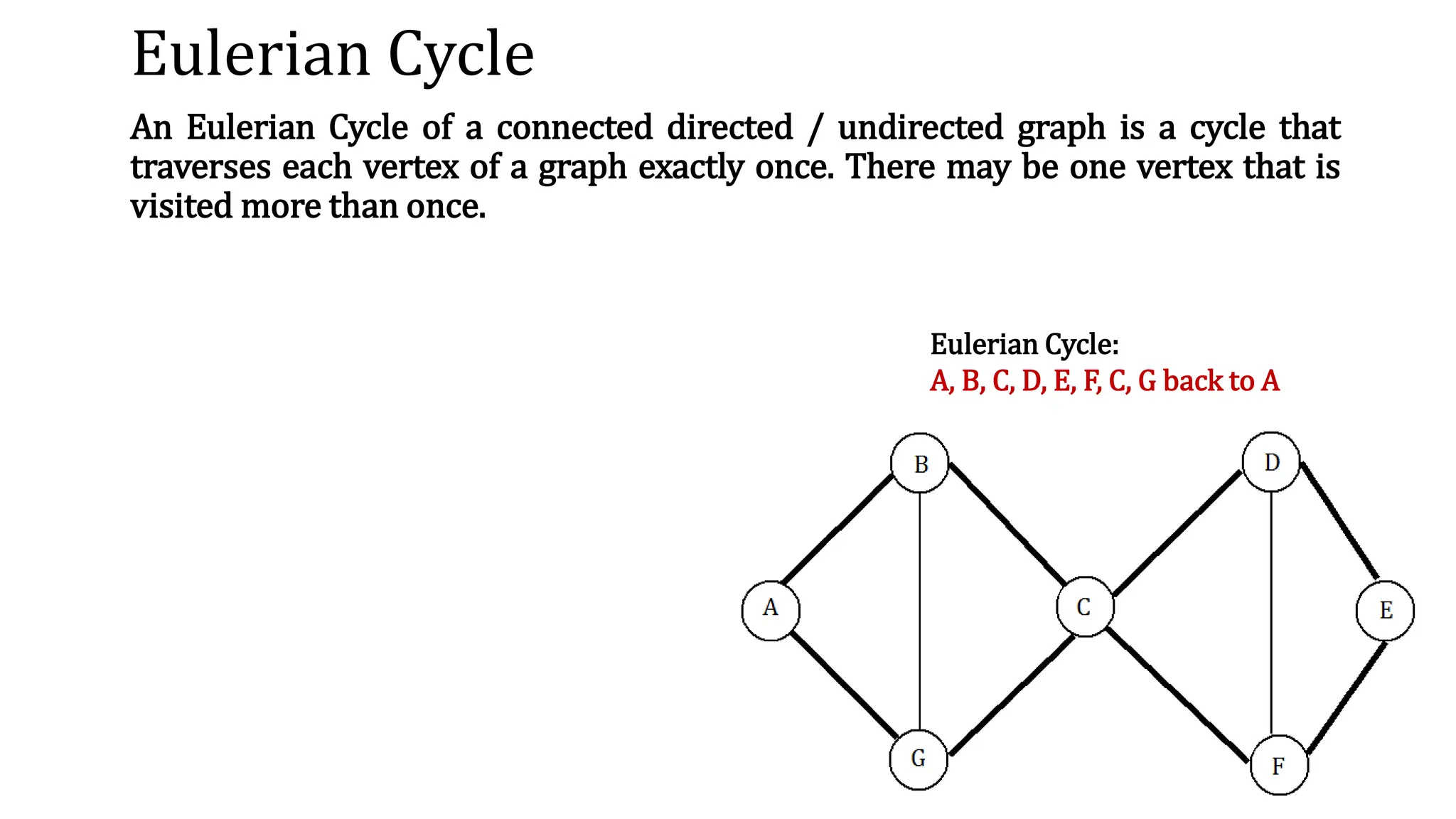
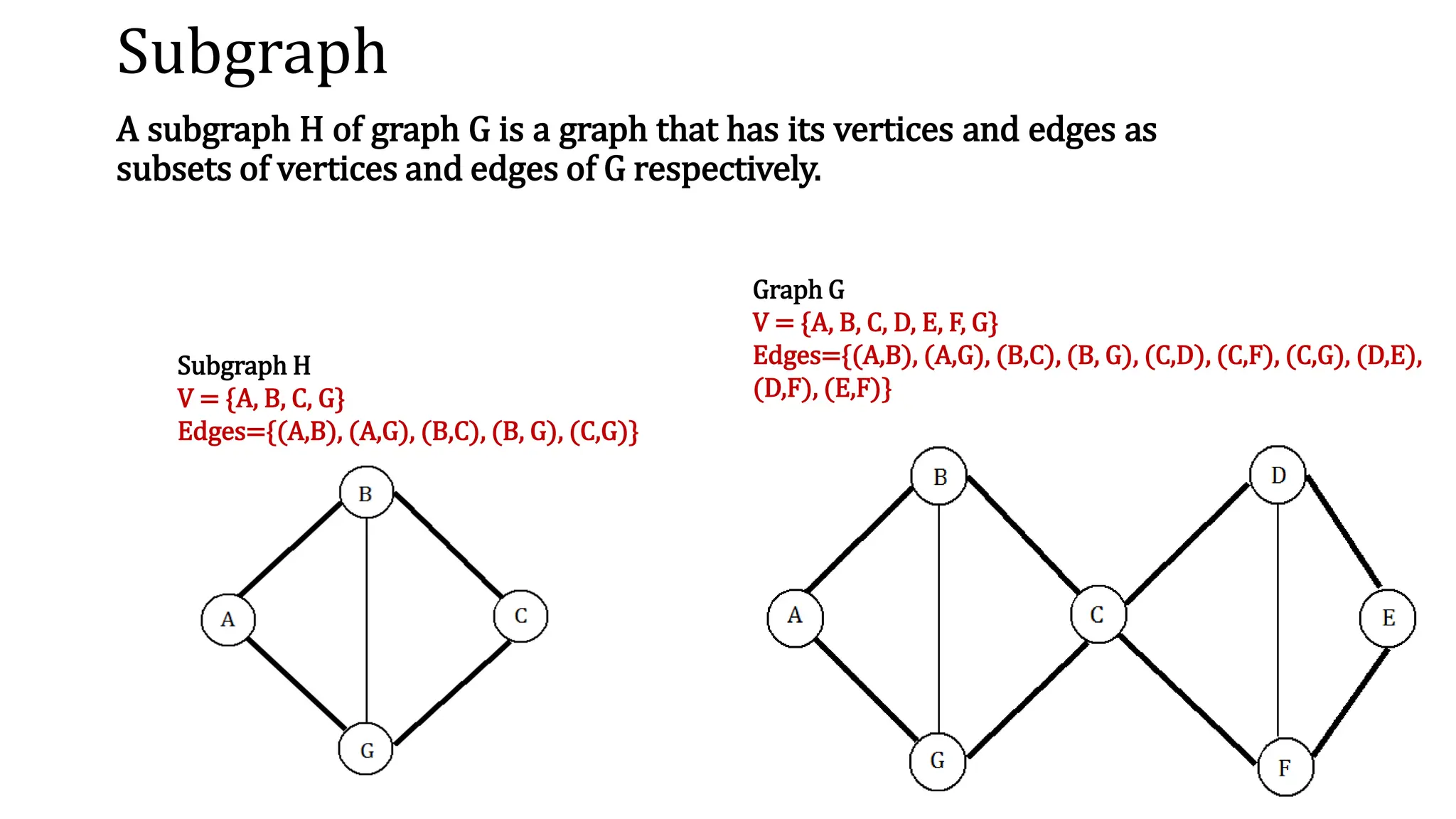
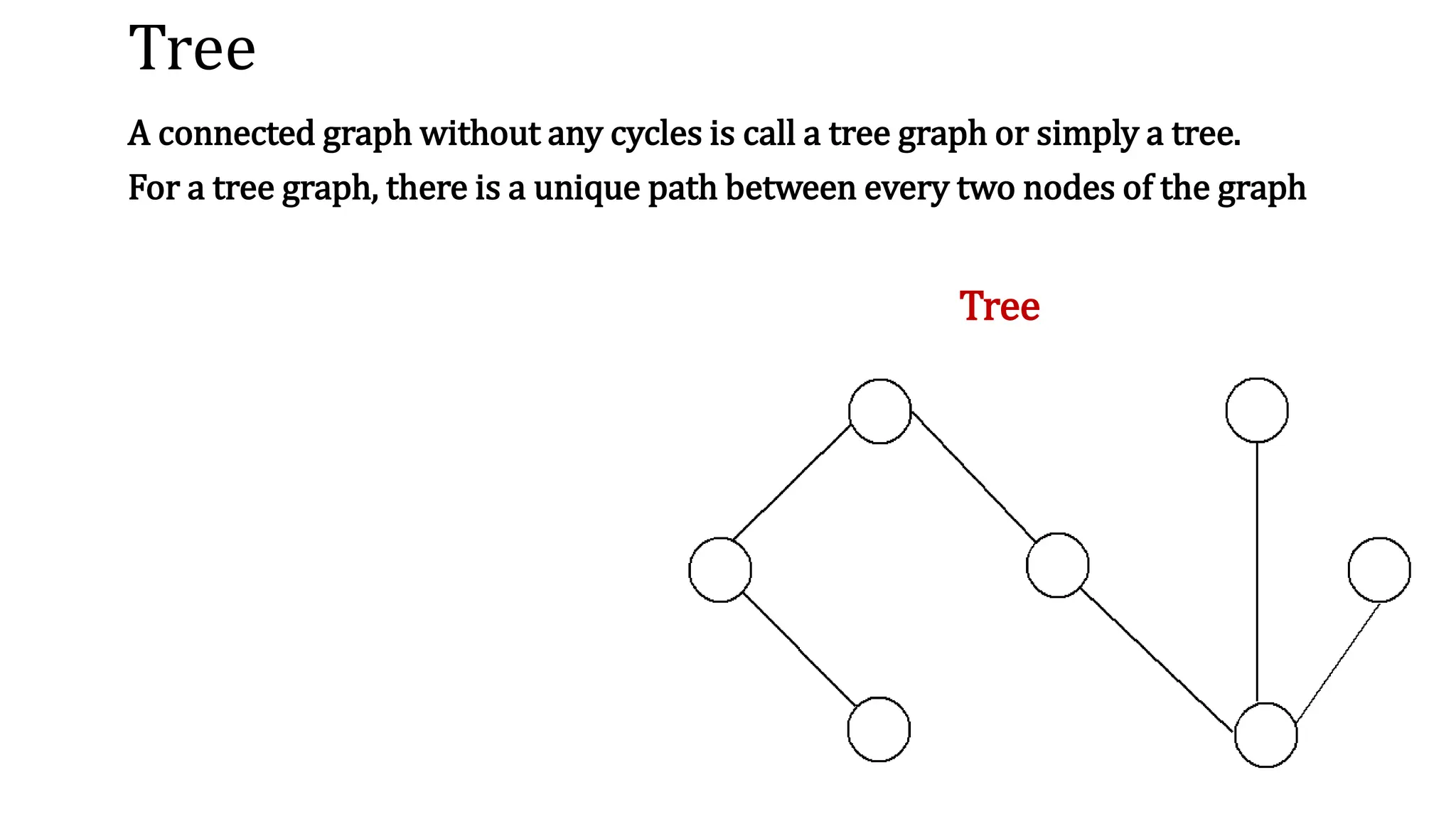
This document provides an overview of key concepts in graph theory including graph terminology, representations, traversals, spanning trees, minimum spanning trees, and shortest path algorithms. It defines graphs, directed vs undirected graphs, connectedness, degrees, adjacency, paths, cycles, trees, and graph representations using adjacency matrices and lists. It also describes breadth-first and depth-first traversals, spanning trees, minimum spanning trees, and algorithms for finding minimum spanning trees and shortest paths like Kruskal's, Prim's, Dijkstra's, Bellman-Ford and A* algorithms.



![Graph Adjacency Matrix Representation
Say a graph has V={1,2,3,…,n} vertices then graph is represented by a
NXN matrix A such that:
A[i, j] = 1 if there is edge between nodes i & j
= 0 otherwise
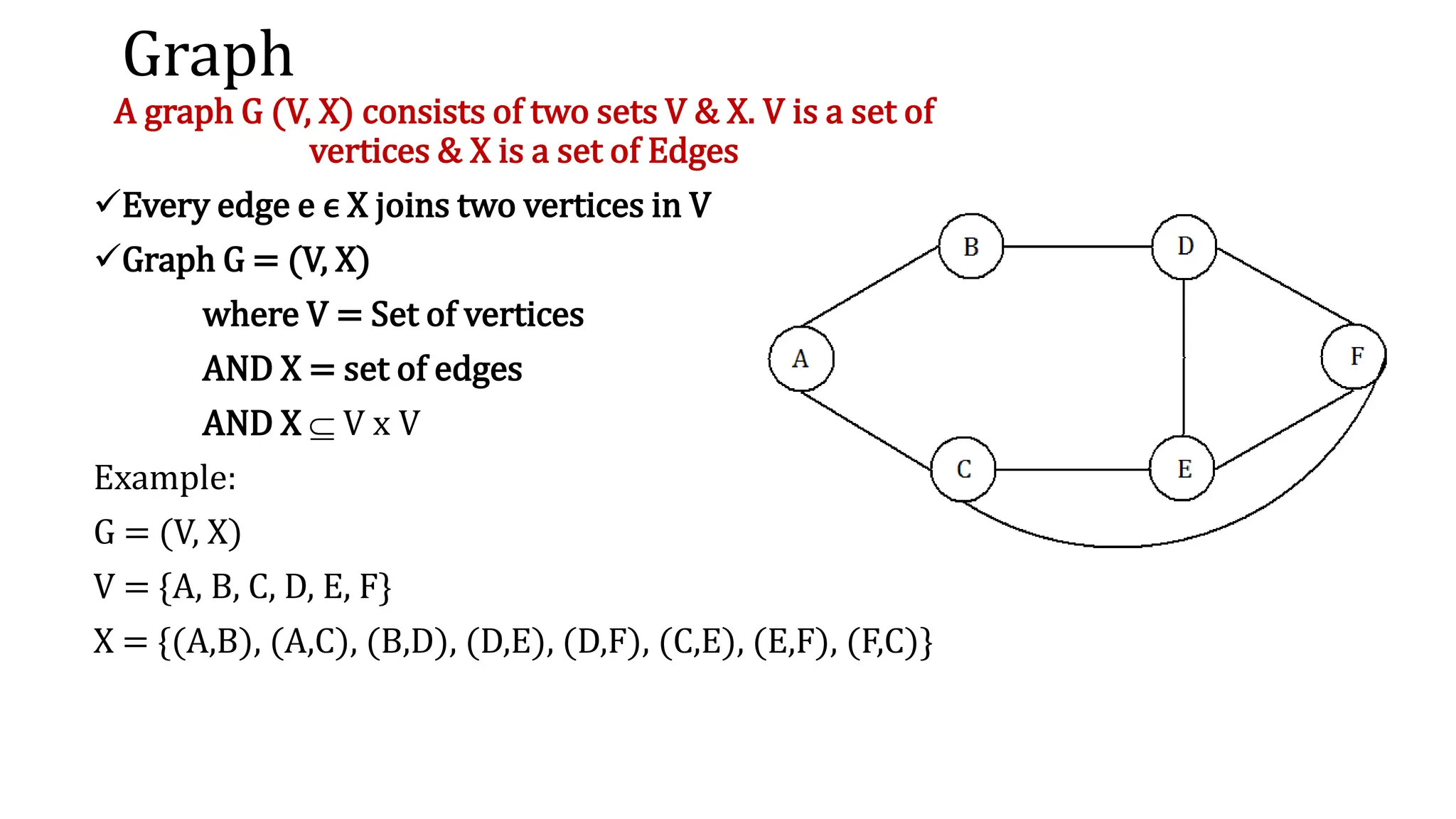
Graph G
Graph G 1 2 3 4
1 0 0 1 0
2 0 0 1 1
3 1 1 0 1
4 0 1 1 0
Space Complexity: ϴ|V2|](https://image.slidesharecdn.com/graphterminologyandalgos-240224171137-ebc280f7/75/Graph-terminology-and-algorithm-and-tree-pptx-22-2048.jpg)

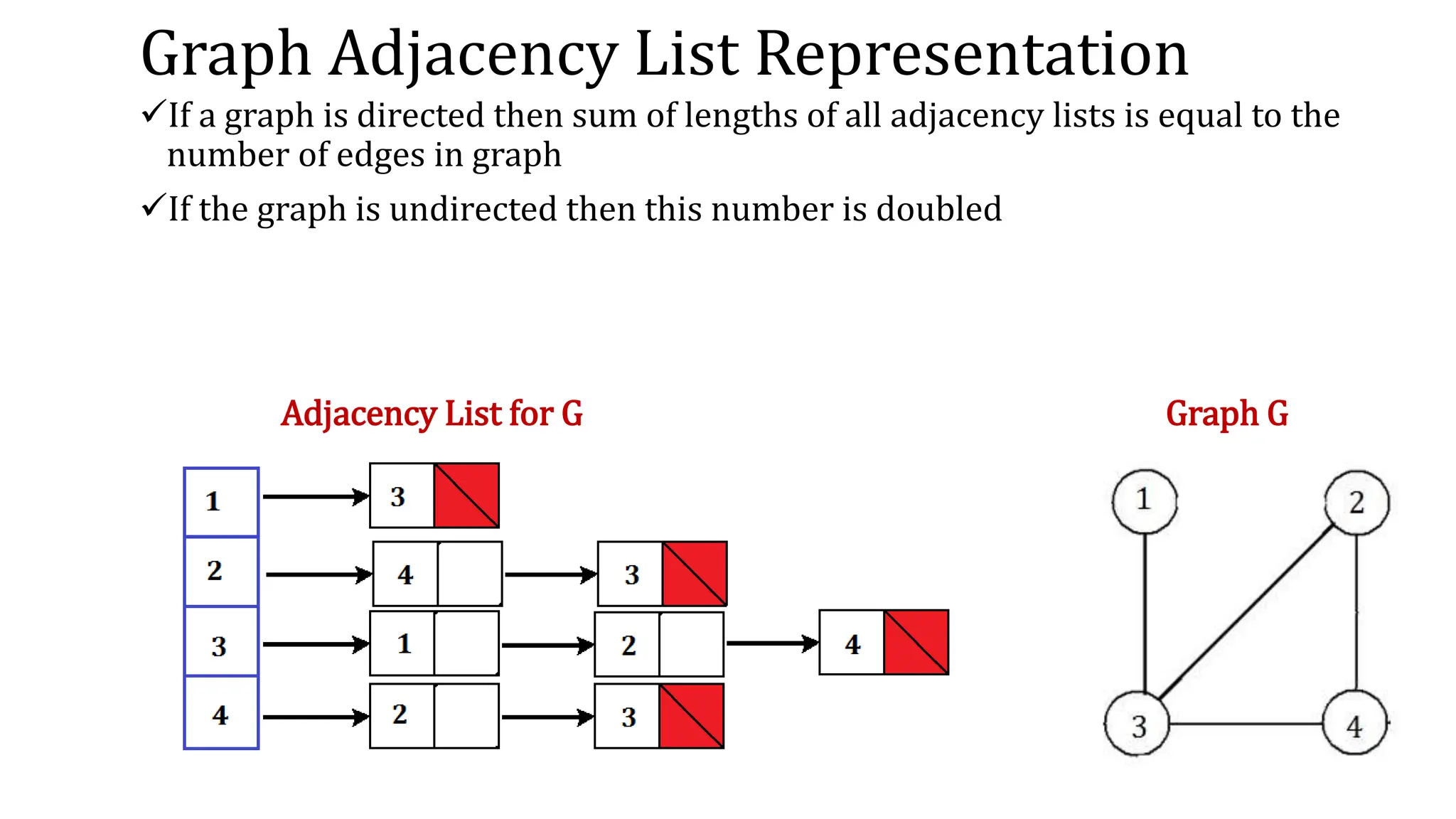
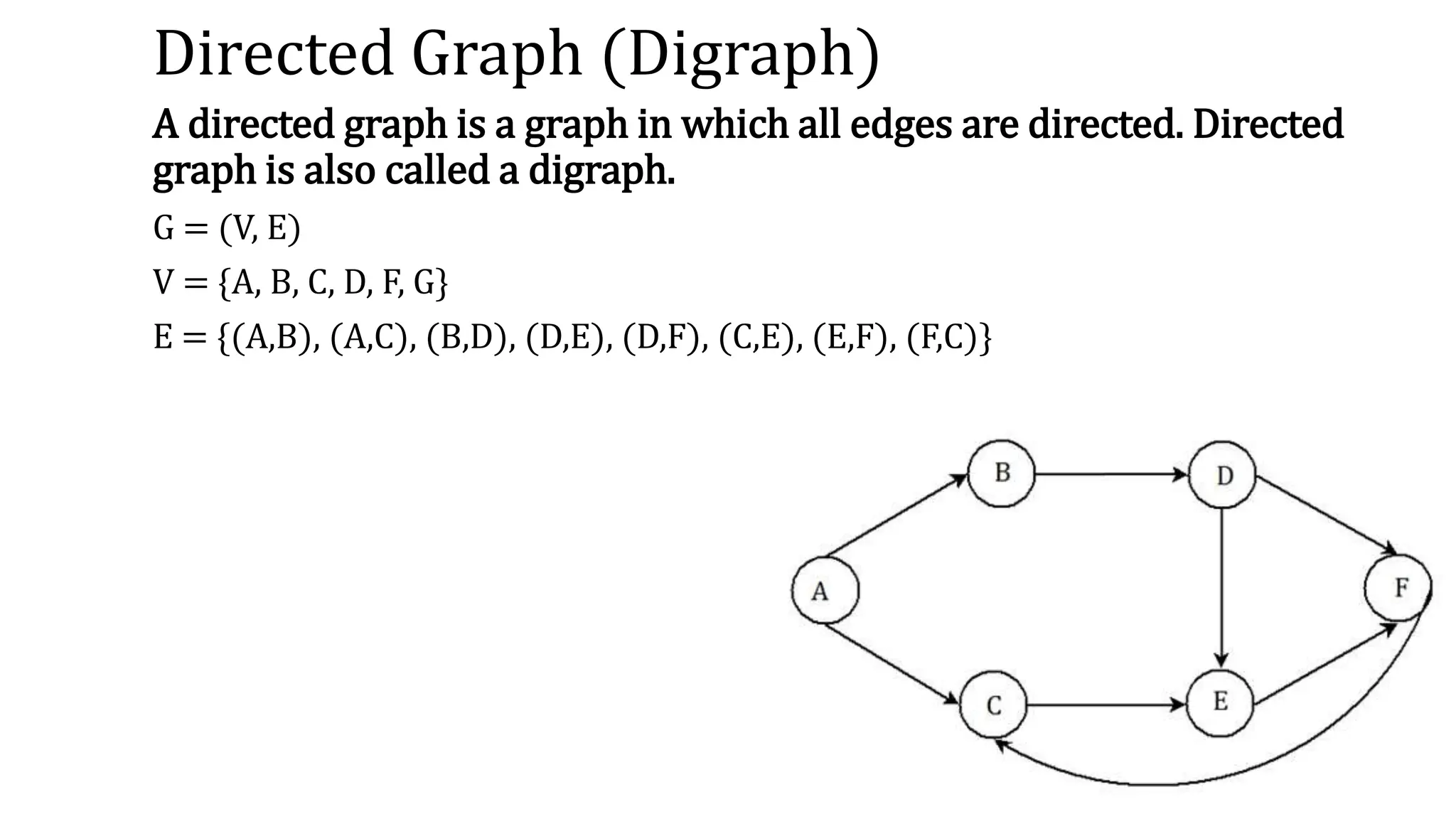
![Graph Adjacency List Representation
For each vertex, a list of adjacent vertices (neighbors) is
maintained
For the given graph:
Adj[1] = {3}
Adj[2]={3, 4}
Adj[3]={1, 2, 4}
Adj[4]={2, 3}
A possible variation can be to store the list of incoming edges
instead of outgoing edges
Graph G](https://image.slidesharecdn.com/graphterminologyandalgos-240224171137-ebc280f7/75/Graph-terminology-and-algorithm-and-tree-pptx-24-2048.jpg)