Download as PDF, PPTX
Uploaded byNicola Strisciuglio
Graph Based Pattern Recognition
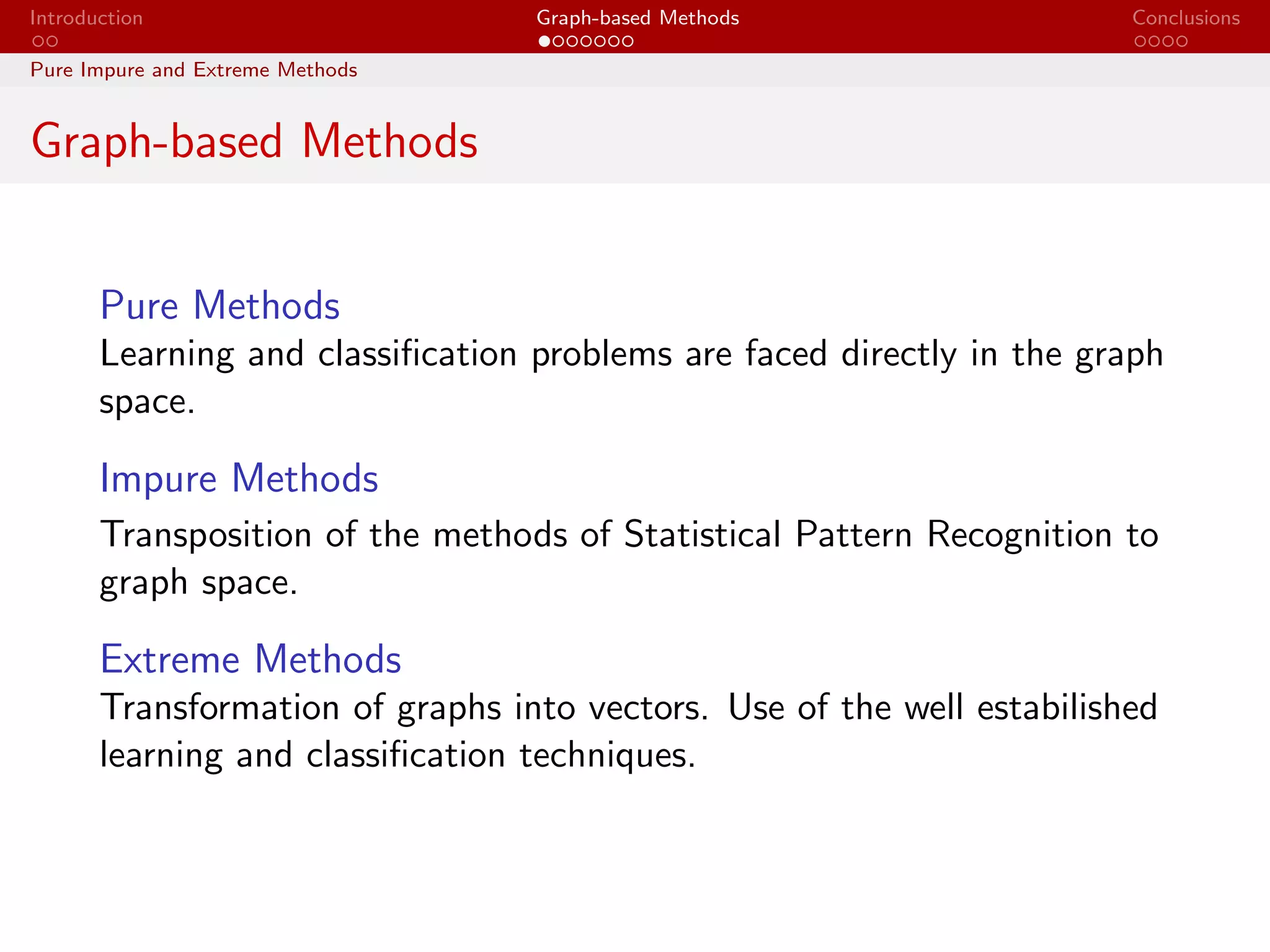
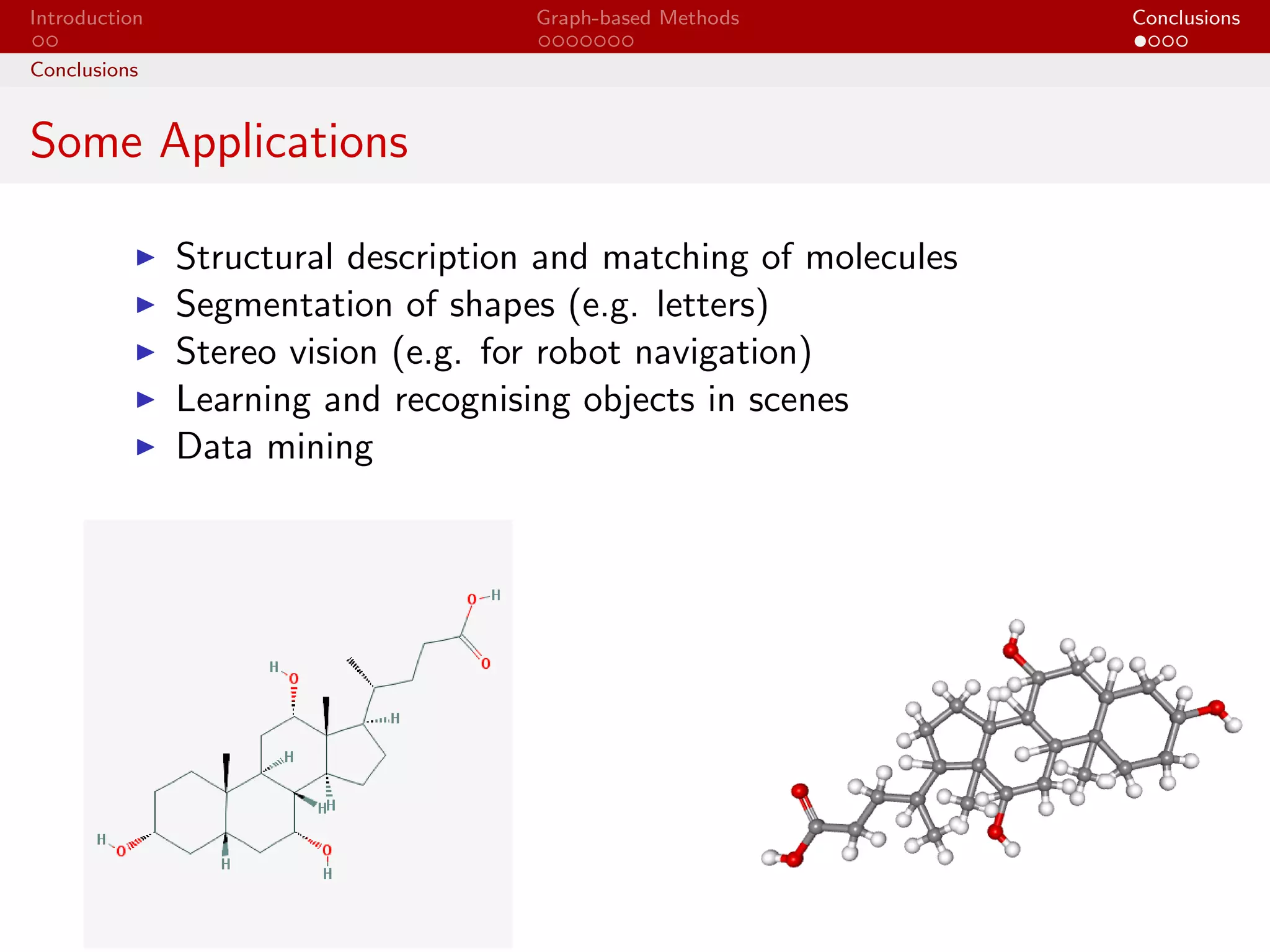
The document discusses graph-based methods in pattern recognition, comparing them to traditional statistical approaches. It classifies methods into pure, impure, and extreme categories, detailing techniques such as graph matching, k-means, and learning vector quantization. The applications of these methods include structural description of molecules and object recognition in scenes.
More Related Content
Similar to Graph Based Pattern Recognition
Graph Based Pattern Recognition
- 1. page.1 Introduction Graph-based Methods Graph-based PatternRecognition Nicola Strisciuglio University of Groningen n.strisciuglio@rug.nl 28/10/2013 Conclusions
- 2. page.2 Introduction Graph-based Methods Statistical vs.Graph-based PR Statistical vs. Graph-based Pattern Recognition Statistical PR I = x1 , x2 , . . . , xn Graph-based PR Conclusions
- 3. page.3 Introduction Graph-based Methods Statistical vs.Graph-based PR Statistical vs. Graph-based Pattern Recognition Statistical PR I = y1 , y2 , . . . , yn Graph-based PR Conclusions
- 4. page.4 Introduction Graph-based Methods Conclusions Pure Impureand Extreme Methods Graph-based Methods Pure Methods Learning and classification problems are faced directly in the graph space. Impure Methods Transposition of the methods of Statistical Pattern Recognition to graph space. Extreme Methods Transformation of graphs into vectors. Use of the well estabilished learning and classification techniques.
- 5. page.5 Introduction Graph-based Methods Pure Impureand Extreme Methods Pure Methods: Graph Matching Exact Matching: find an exact correspondence between graphs (or sub-graphs) Inexact Matching: deals with distortions in findinf a correspondence between graphs It needs a metric to define dissimilarities Conclusions
- 6. page.6 Introduction Graph-based Methods Conclusions Pure Impureand Extreme Methods Graph edit distance We need a distance metric between graphs: we have Graph edit distance. Cheapest sequence of operations to trasform one graph in another graph.
- 7. page.7 Introduction Graph-based Methods Conclusions Pure Impureand Extreme Methods Impure Methods: k-NN The reference set is made by a collection of graphs, instead of points in a m-dimensional space For a graph to classify, the graph edit distance is computed with respect to each of the graphs in the reference set The decision is taken as majority voting on the K nearest graphs Generally, the time needed for a classification is very high
- 8. page.8 Introduction Graph-based Methods Conclusions Pure Impureand Extreme Methods Impure Methods: k-Means For the classical k-Means algorithm a centroid is computed as the average of the vectors around it, while for the graph a median graph should be computed.
- 9. page.9 Introduction Graph-based Methods Conclusions Pure Impureand Extreme Methods Impure Methods: k-Means For the classical k-Means algorithm a centroid is computed as the average of the vectors around it, while for the graph a median graph should be computed. Median Graph ˆ S = arg min Gi ∈S Dg (Gi , Gj ) Gj ∈S
- 10. page.10 Introduction Graph-based Methods Conclusions Pure Impureand Extreme Methods Impure Methods: k-Means For the classical k-Means algorithm a centroid is computed as the average of the vectors around it, while for the graph a median graph should be computed. Median Graph ˆ S = arg min Gi ∈S Dg (Gi , Gj ) Gj ∈S Generalized Median Graph Dg (Gi , Gj ) S = arg min Gi ∈U Gj ∈S
- 11. page.11 Introduction Graph-based Methods Conclusions Pure Impureand Extreme Methods Impure Methods: LVQ Given a pattern x, the winner prototype Pk moves towards x by ∆ = α(x − Pk ) if the class of x is the same of Pk (by ∆ = −α(x − Pk ) otherwise) Updating a prototype requires its transformation in another graph more similar to the input pattern x by a fraction α of the distance
- 12. page.12 Introduction Graph-based Methods Conclusions Pure Impureand Extreme Methods Impure Methods: LVQ Given a pattern x, the winner prototype Pk moves towards x by ∆ = α(x − Pk ) if the class of x is the same of Pk (by ∆ = −α(x − Pk ) otherwise) Updating a prototype requires its transformation in another graph more similar to the input pattern x by a fraction α of the distance We need to compute a fraction of edit distance!!! Pk → Gx needs D = 7 operations on graph
- 13. page.13 Introduction Graph-based Methods Conclusions Pure Impureand Extreme Methods Impure Methods: LVQ Given a pattern x, the winner prototype Pk moves towards x by ∆ = α(x − Pk ) if the class of x is the same of Pk (by ∆ = −α(x − Pk ) otherwise) Updating a prototype requires its transformation in another graph more similar to the input pattern x by a fraction α of the distance We need to compute a fraction of edit distance!!! Pk → Gx needs D = 7 operations on graph If α = 0.3, we do D ∗ α = 2 operations to move Pk to an intermediate graph
- 14. page.14 Introduction Graph-based Methods Conclusions Pure Impureand Extreme Methods Extreme methods: Graph Embedding Represent a graph as a point in a suitable feature space Use of the classical statistical pattern recognition tools The similarity of graph in graph space should be preserved in the vector space The translation of a graph (including all the attributes and relations) into a fixed-lenght vector is difficult
- 15. page.15 Introduction Graph-based Methods Conclusions Some Applications Structuraldescription and matching of molecules Segmentation of shapes (e.g. letters) Stereo vision (e.g. for robot navigation) Learning and recognising objects in scenes Data mining Conclusions
- 16. page.16 Introduction Graph-based Methods Conclusions Some Applications Structuraldescription and matching of molecules Segmentation of shapes (e.g. letters) Stereo vision (e.g. for robot navigation) Learning and recognising objects in scenes Data mining Conclusions
- 17. page.17 Introduction Graph-based Methods Conclusions Conclusions Statistical vs.Graph-based Pattern Recognition Statistical PR Advantages Graph-based PR Advantages Theoretically estabilished Variable representation size Many powerful algorithms More description power (relationships) Disadvantages Size of the feature vector fixed Unary features: no relations Disadvantages Lack of algorithms Less mathematical foundations
- 18. page.18 Introduction Graph-based Methods Conclusions References Mario Vento(2013) A long trip in the charming world of graphs for Pattern Recognition Pattern Recognition Conclusions
- 19.