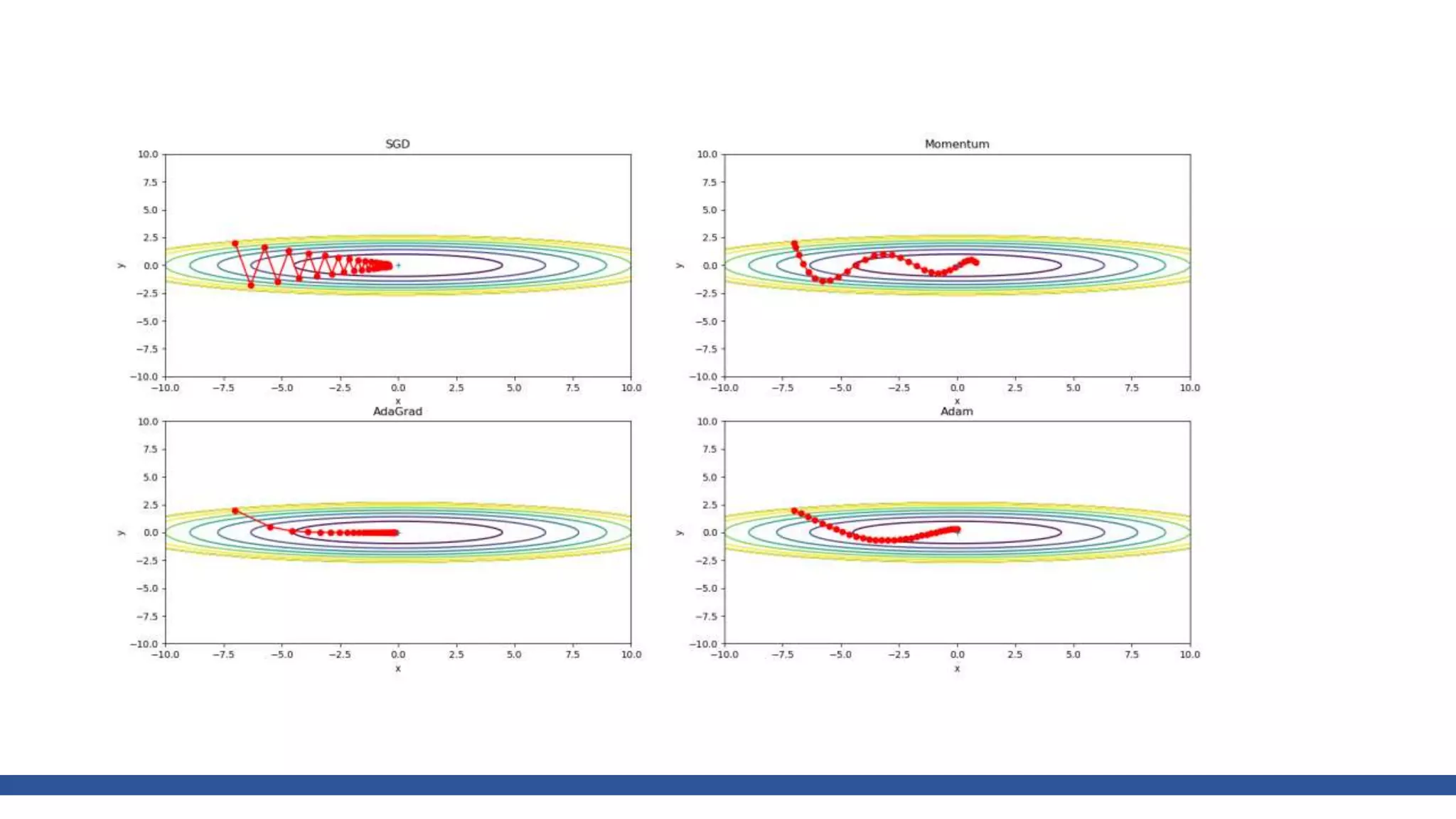
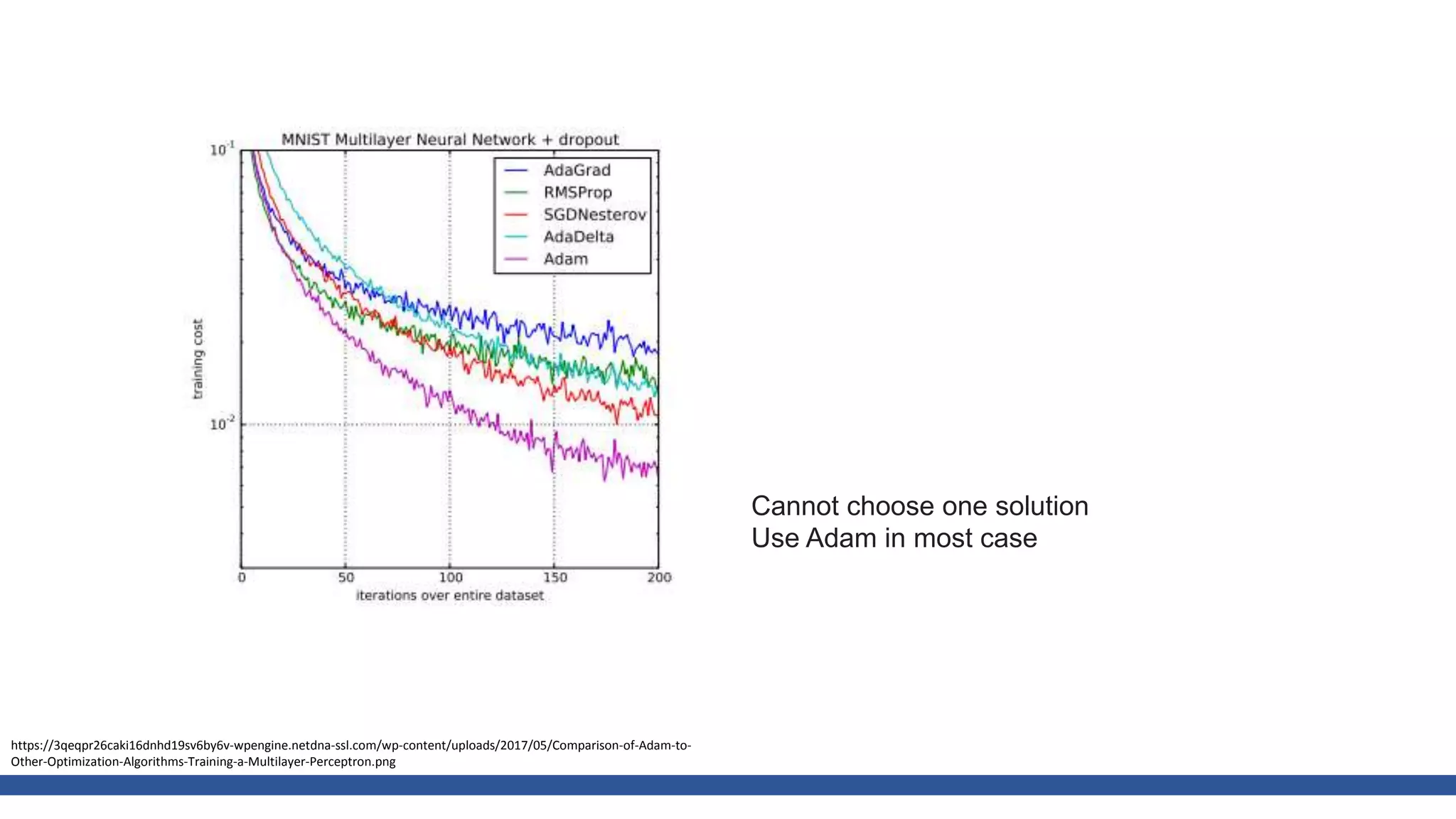
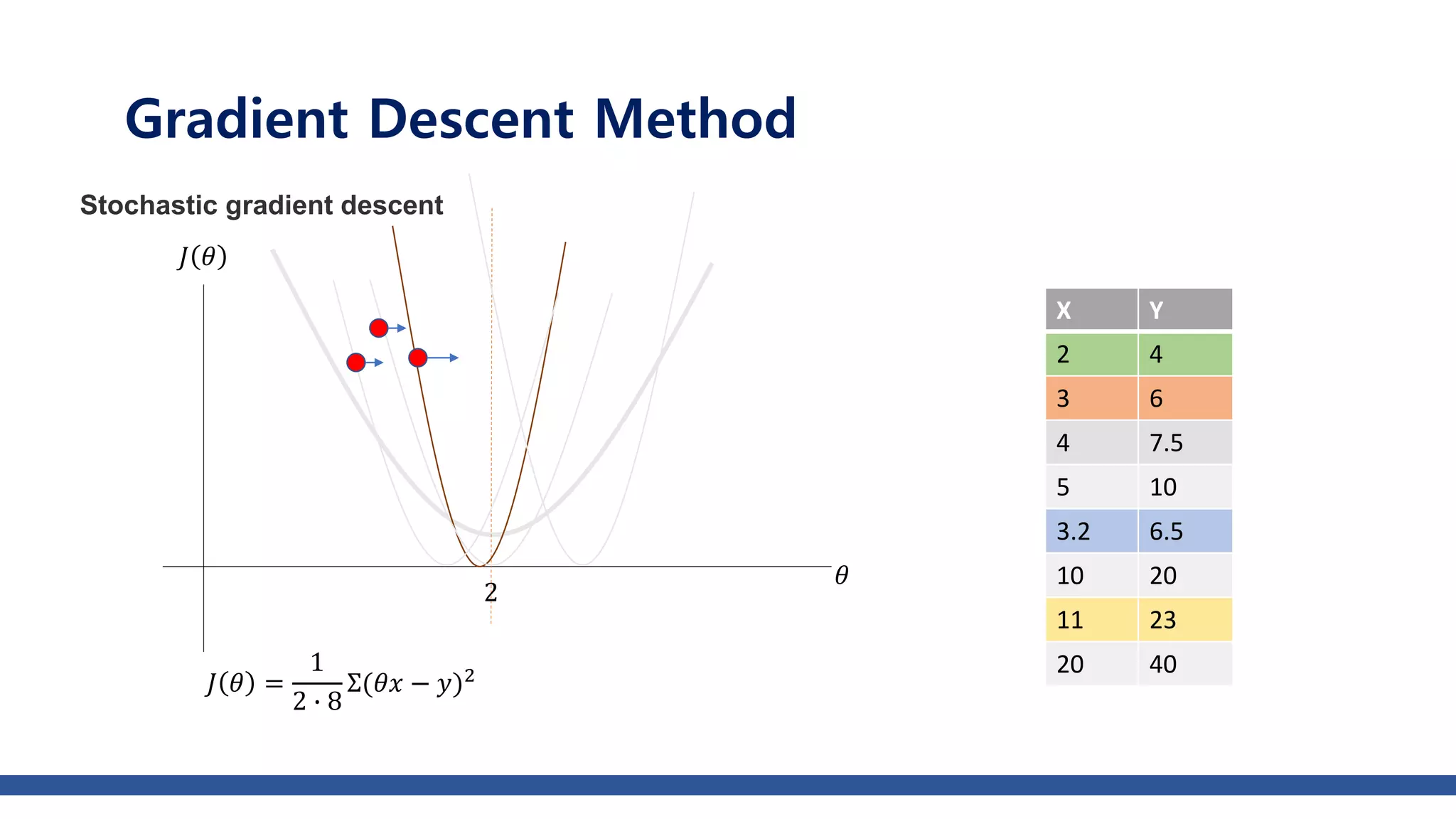
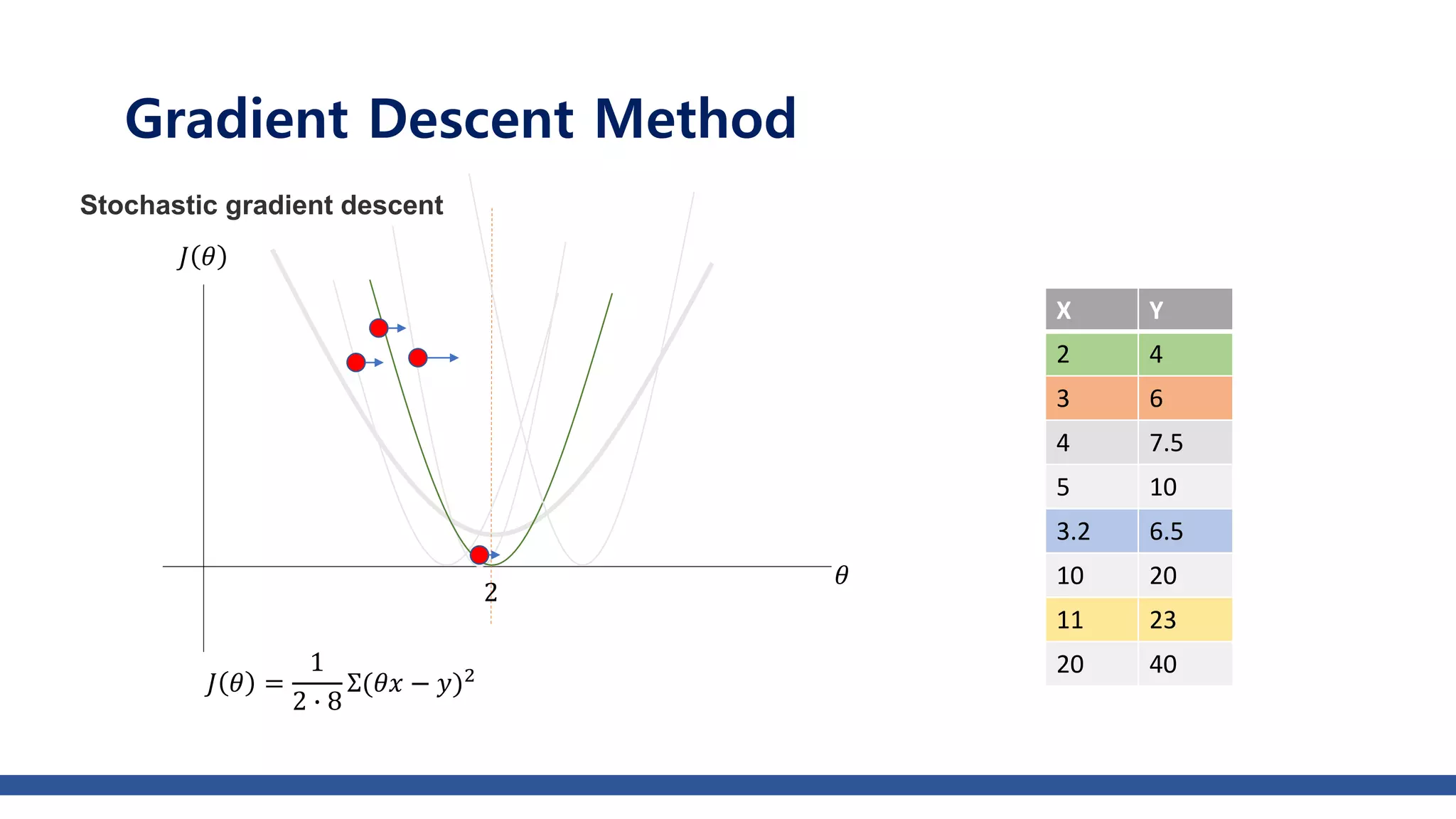
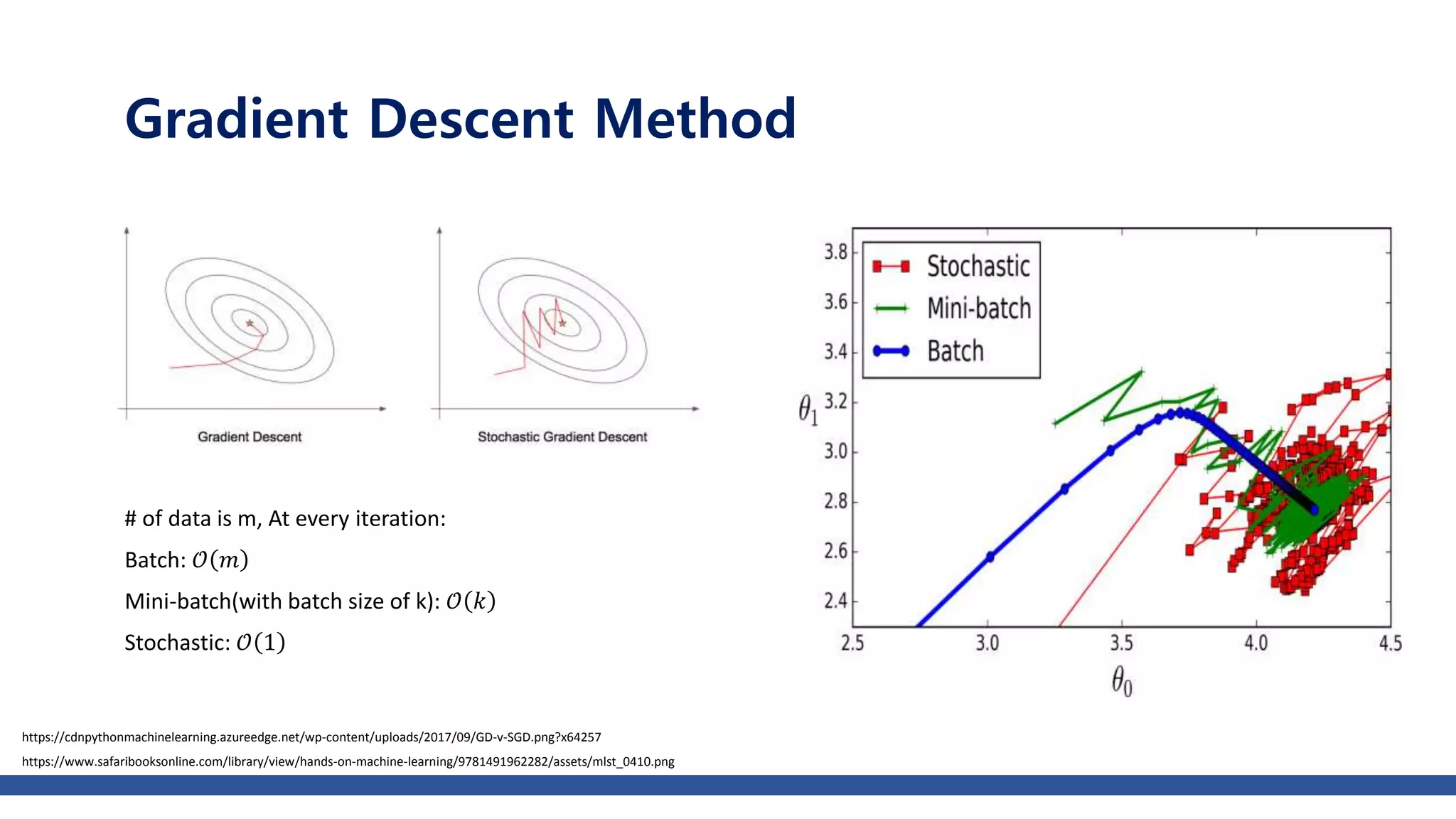
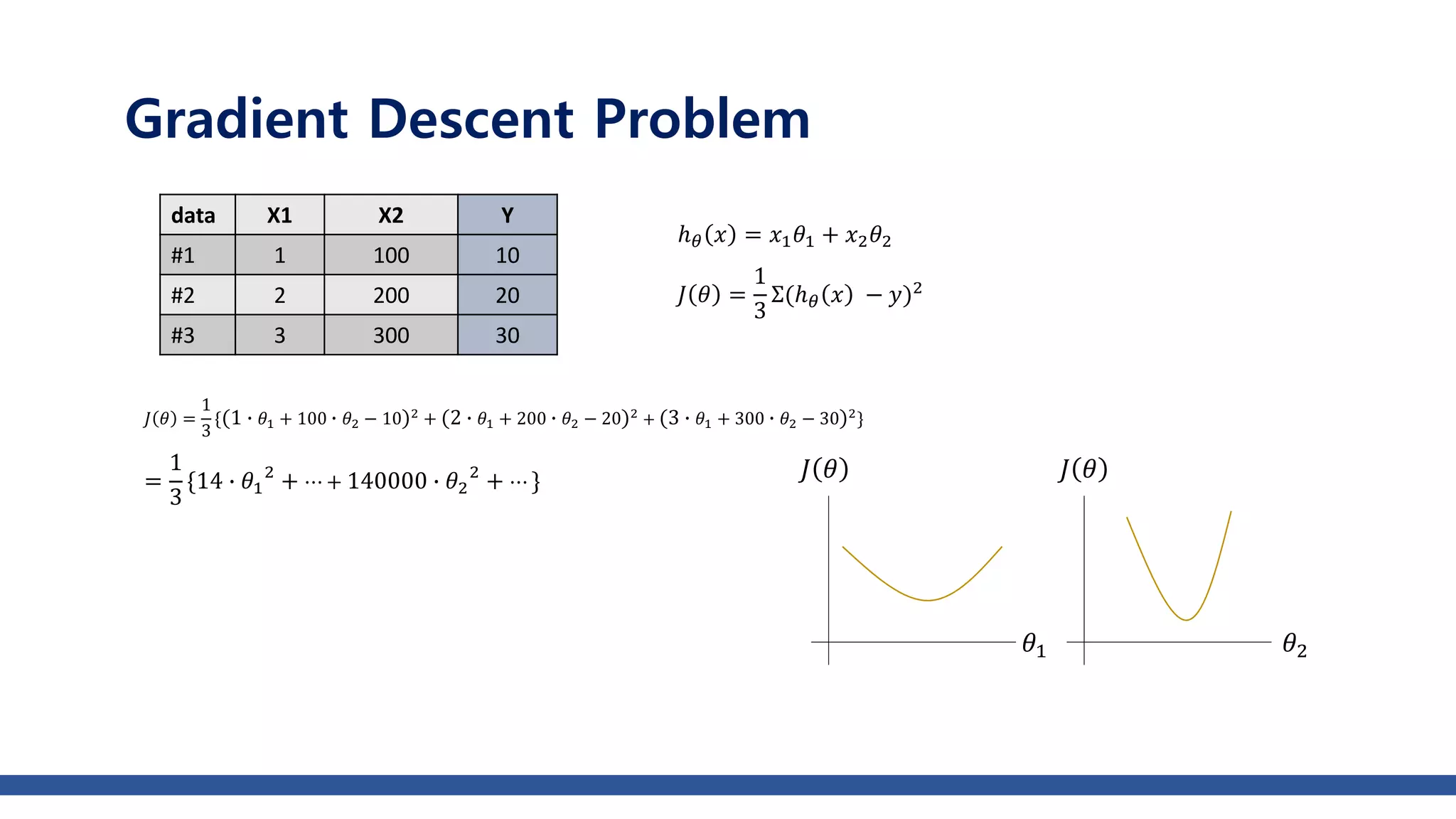
The document discusses various gradient descent optimization techniques used in machine learning, specifically batch, mini-batch, and stochastic gradient descent methods. It elaborates on advanced optimization algorithms like momentum, Adagrad, RMSProp, and Adam, explaining their mechanisms and applications. Each method aims to improve the convergence while minimizing a given loss function, with considerations for learning rate and gradients.






![class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]
Python
class
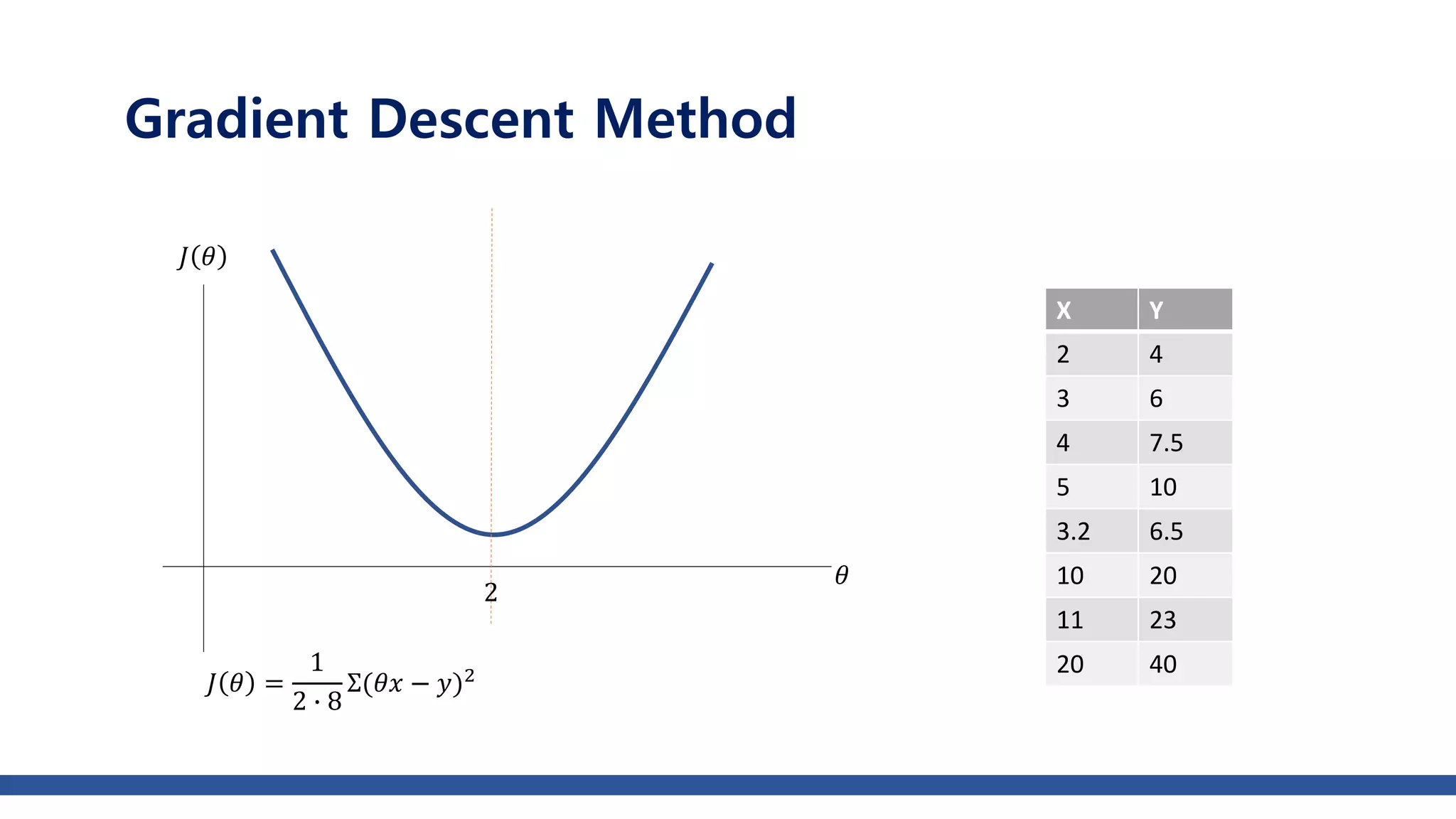
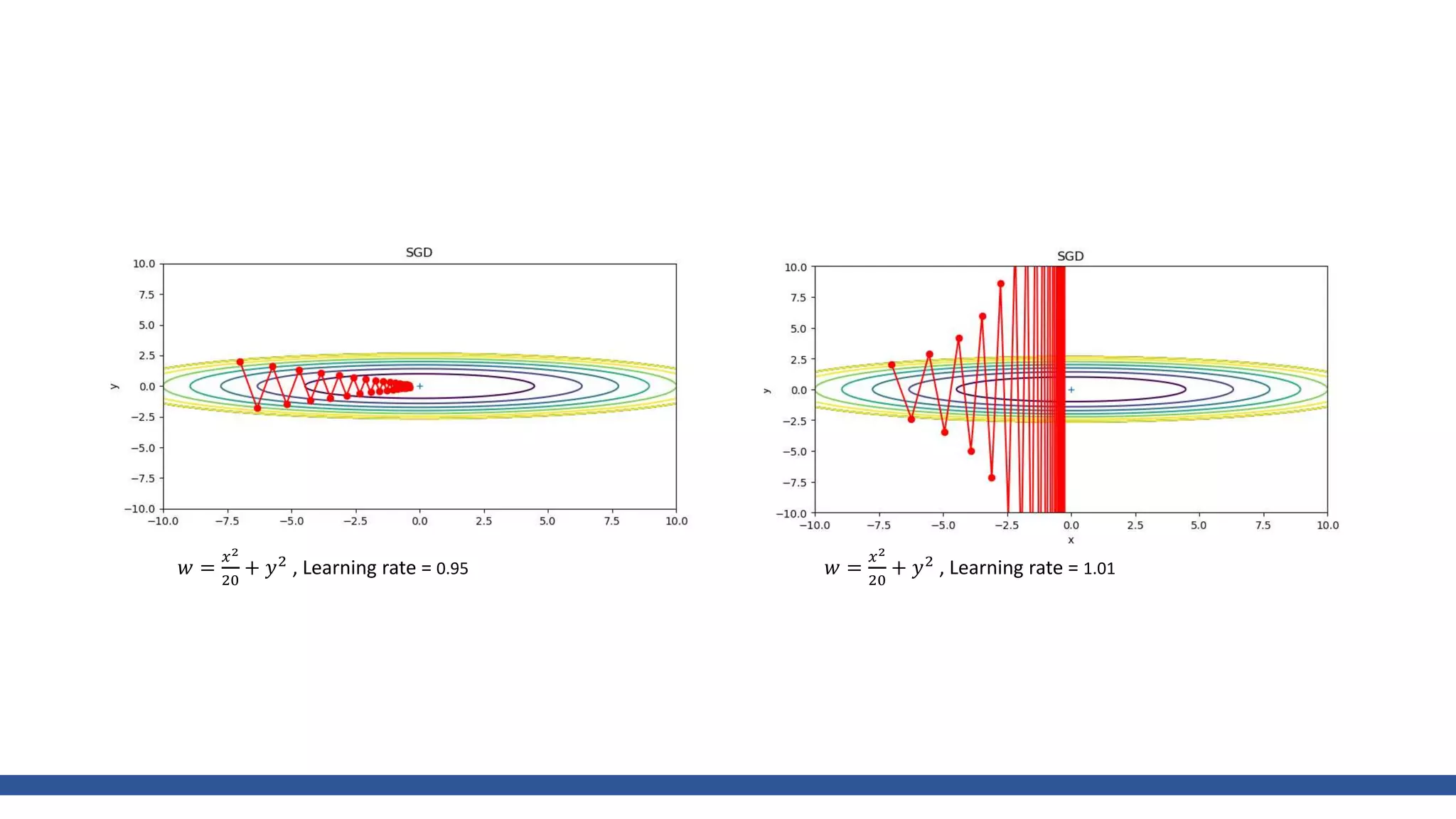
𝑤 =
𝑥2
20
+ 𝑦2
, Learning rate = 0.95, iter=30
https://github.com/WegraLee](https://image.slidesharecdn.com/gradientdescentoptimizer-180202151844/75/Gradient-descent-optimizer-16-2048.jpg)
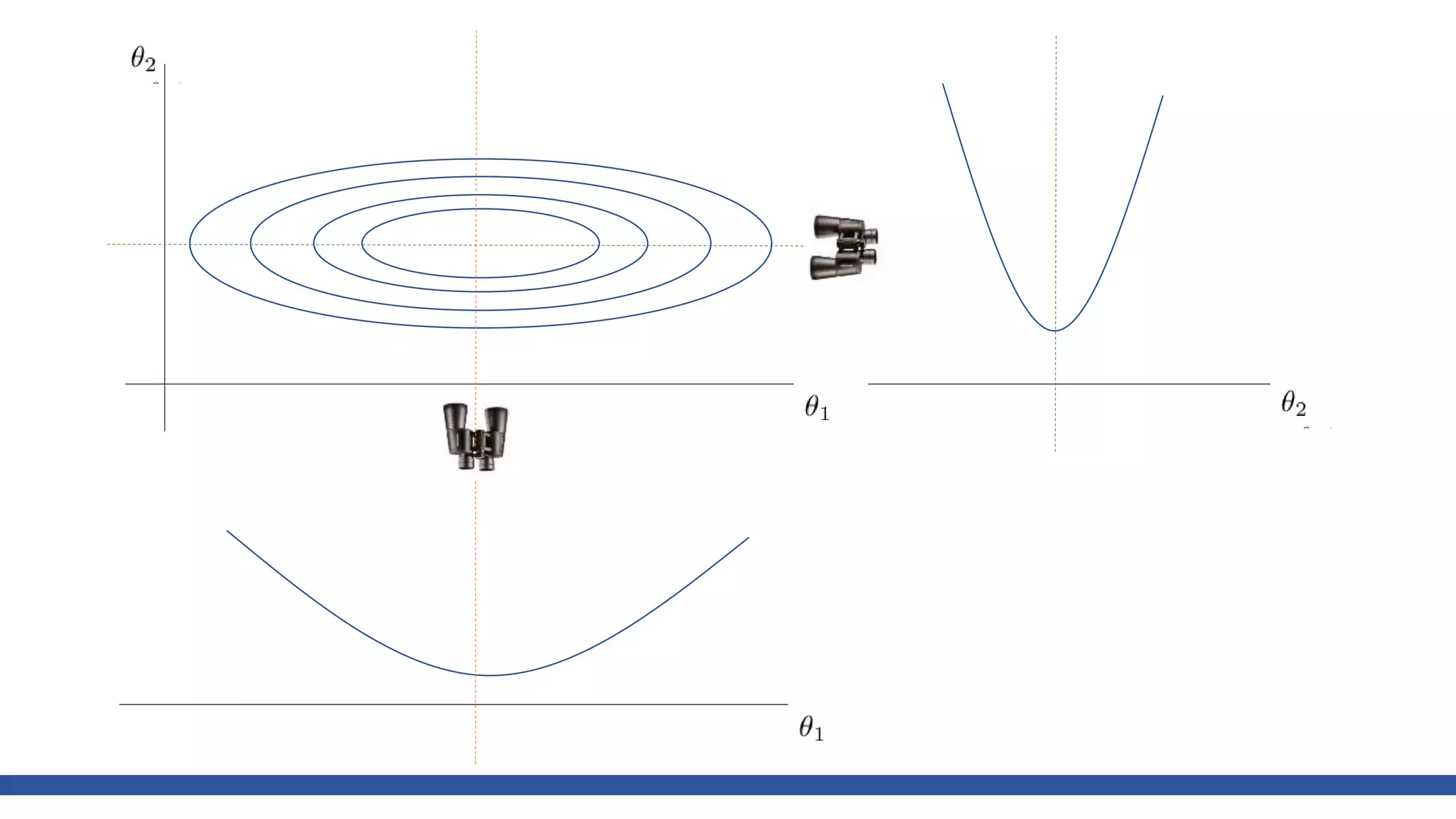
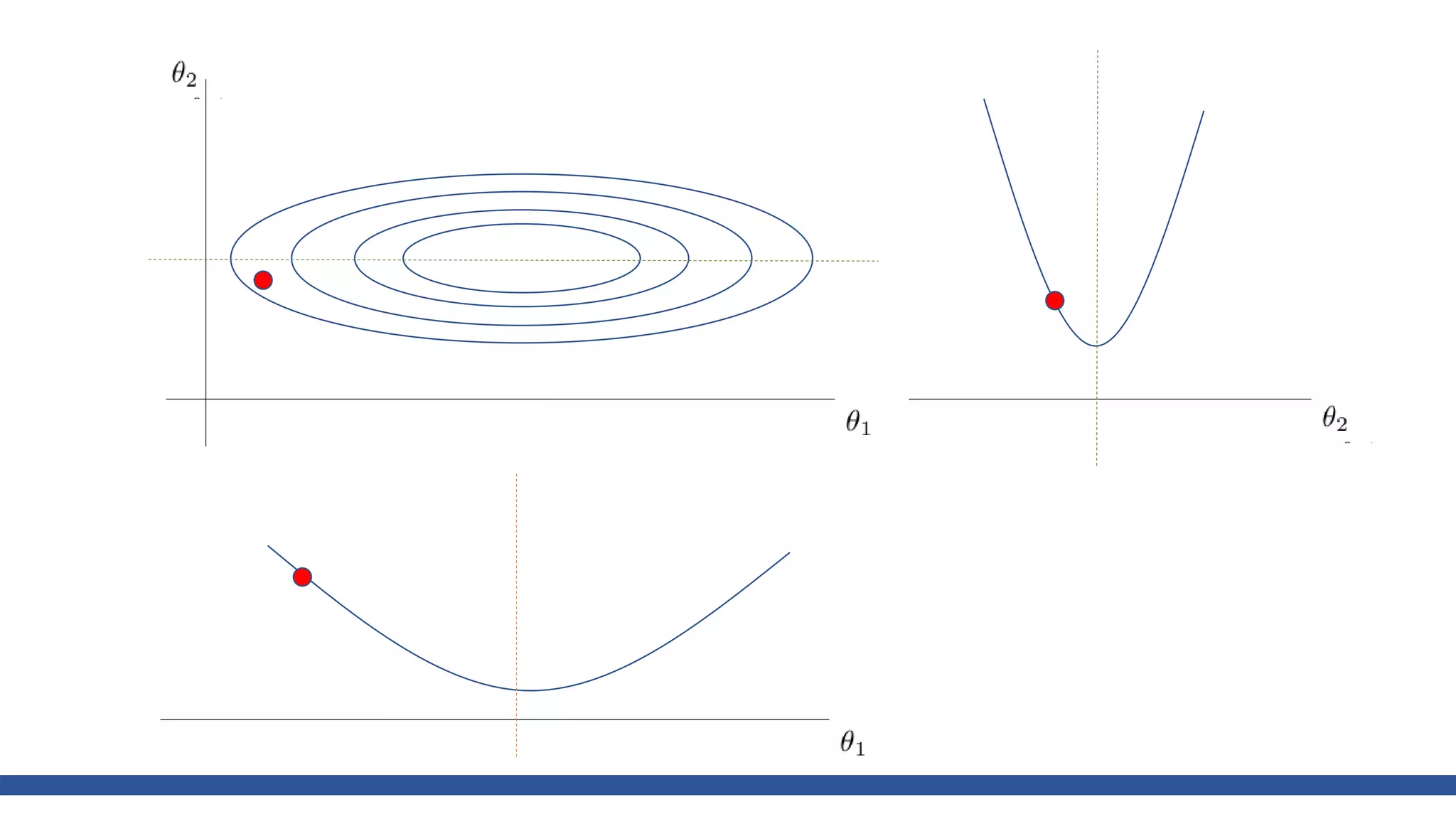
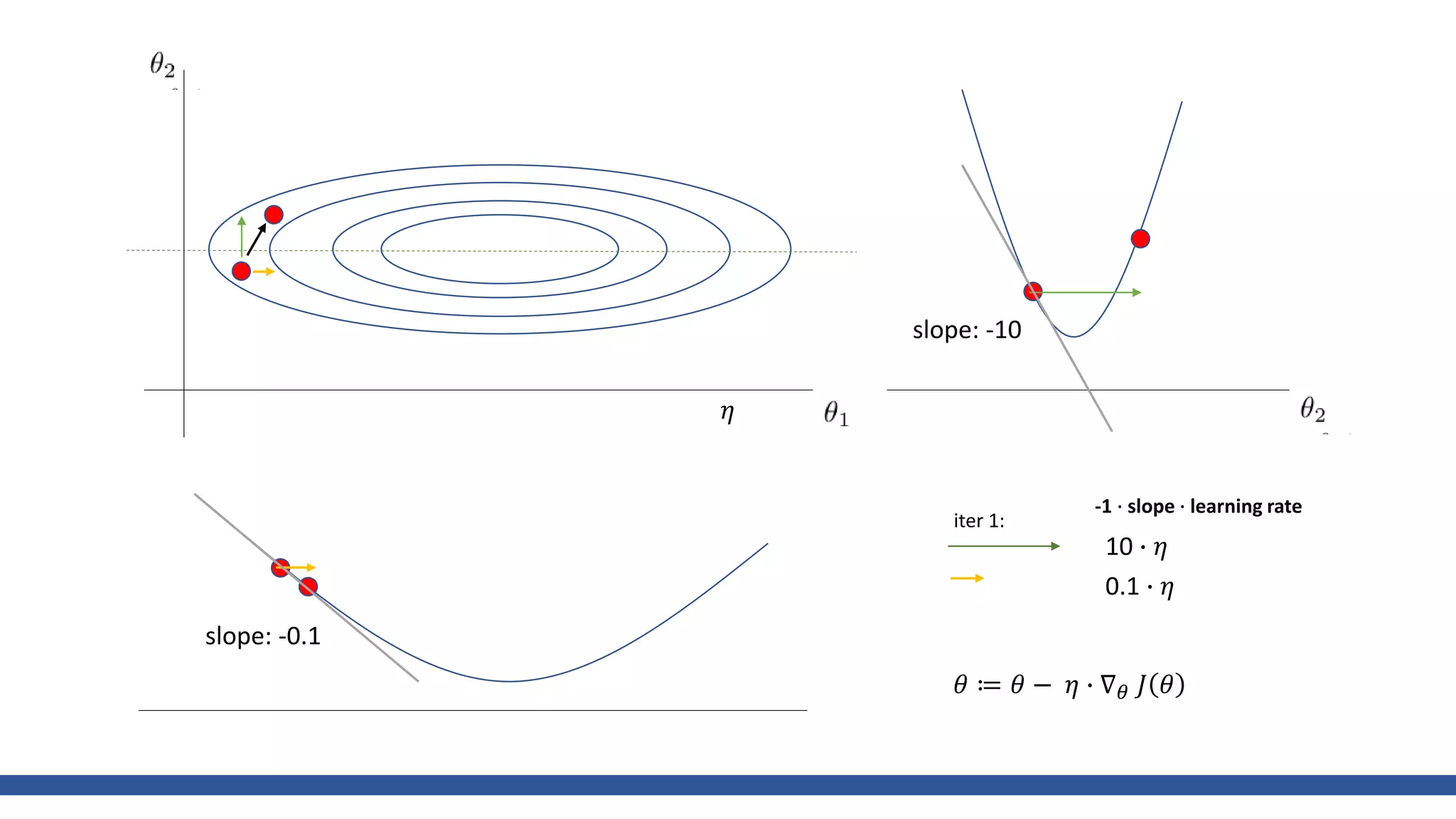
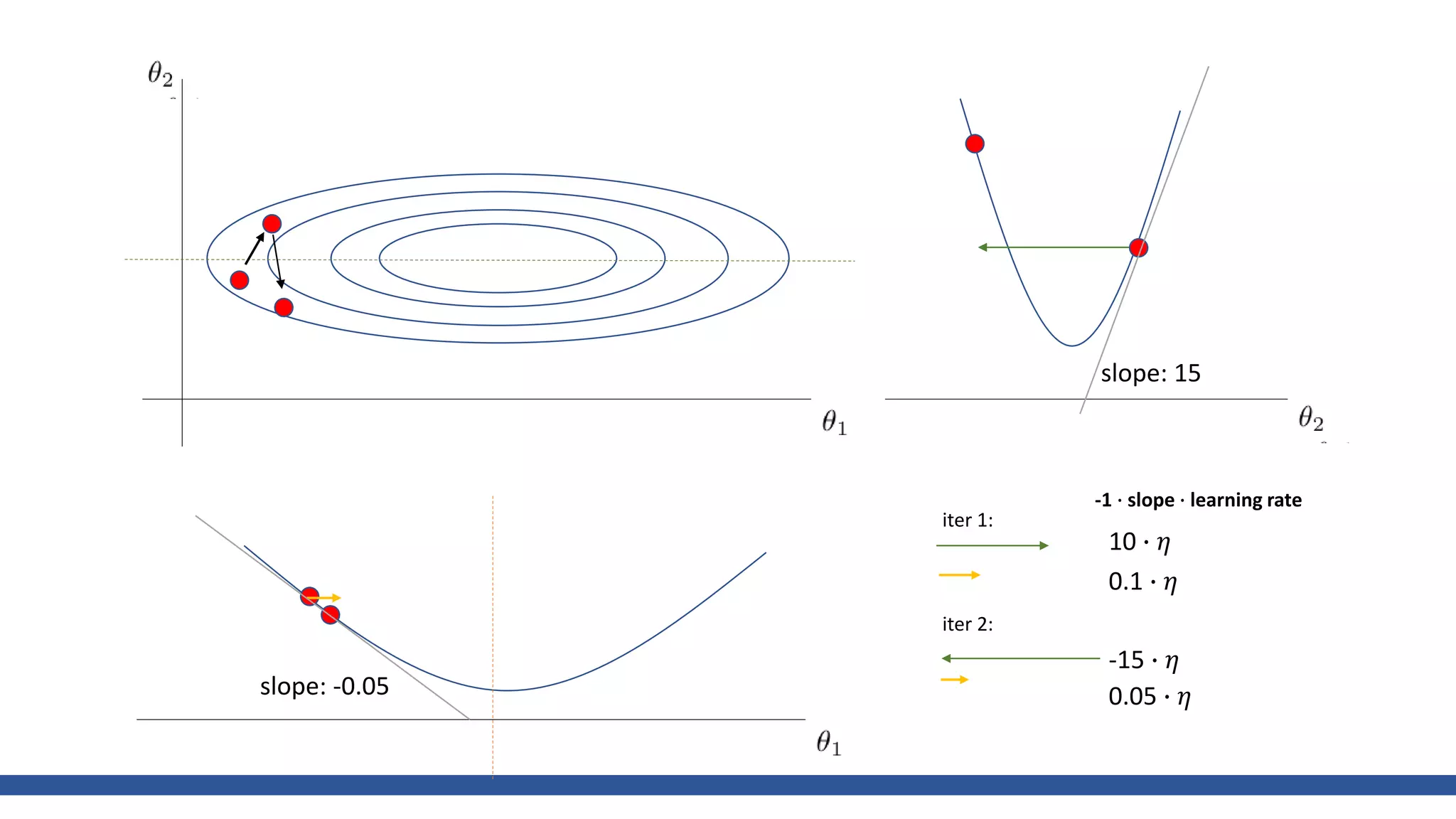
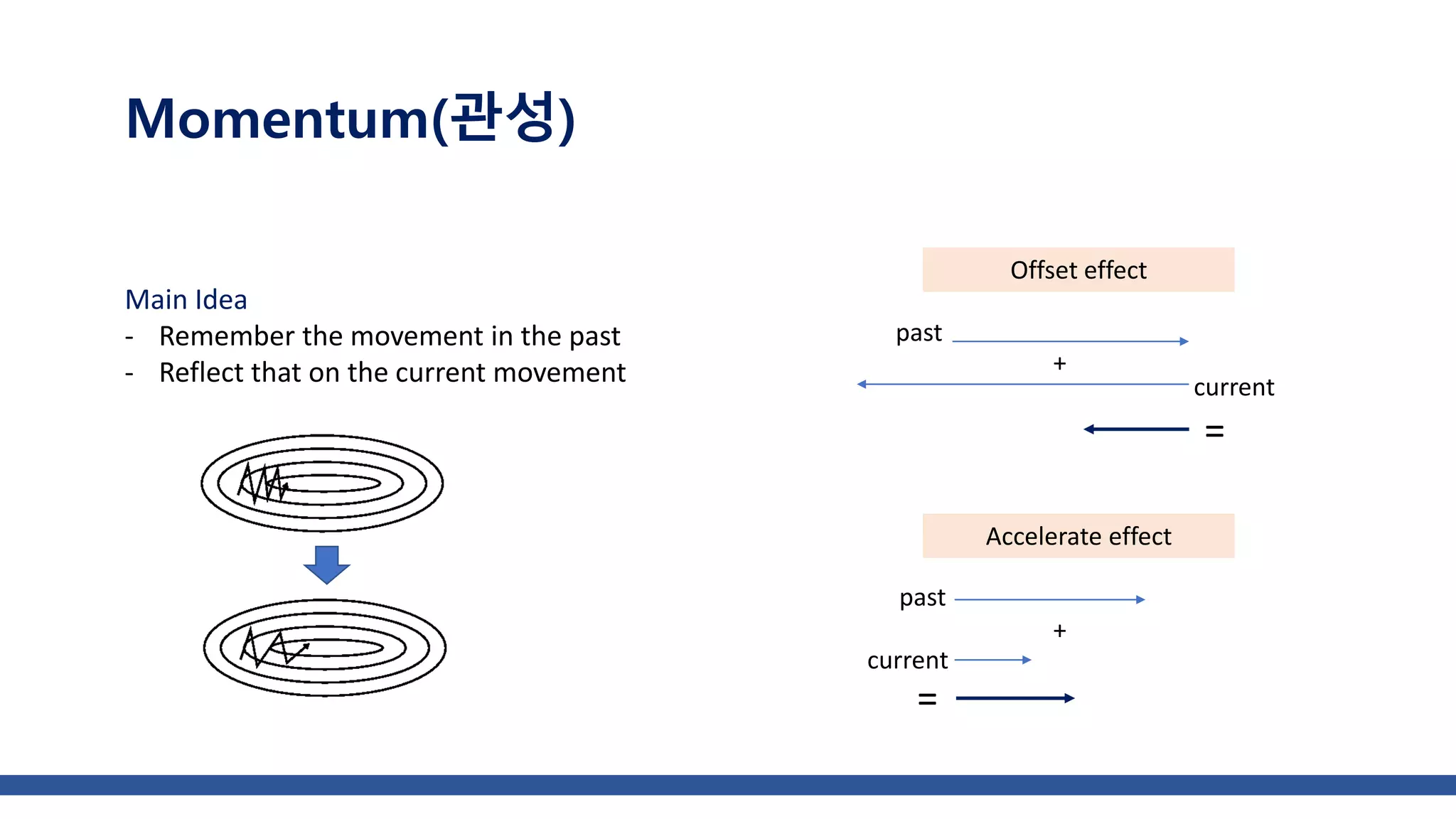
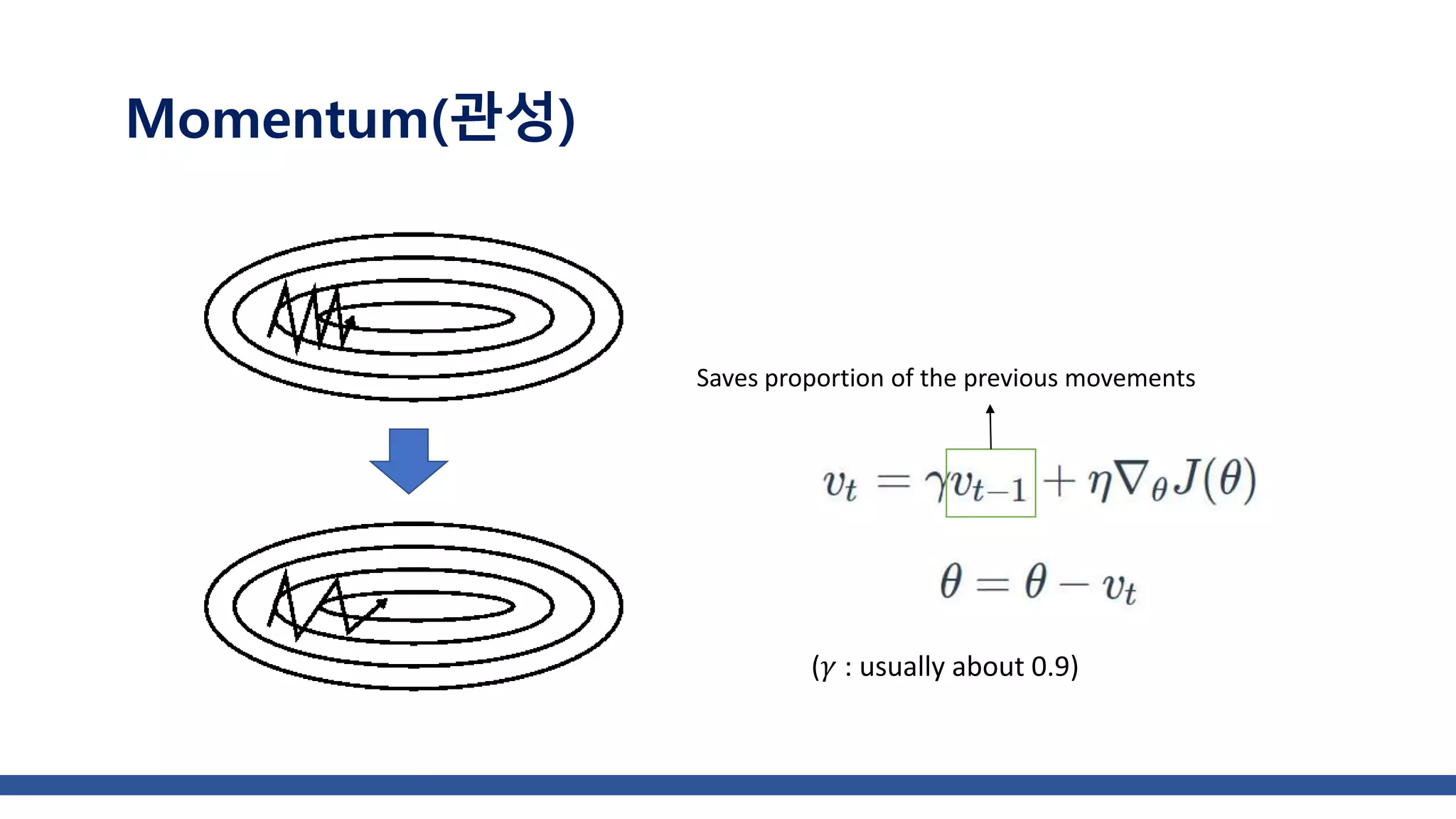
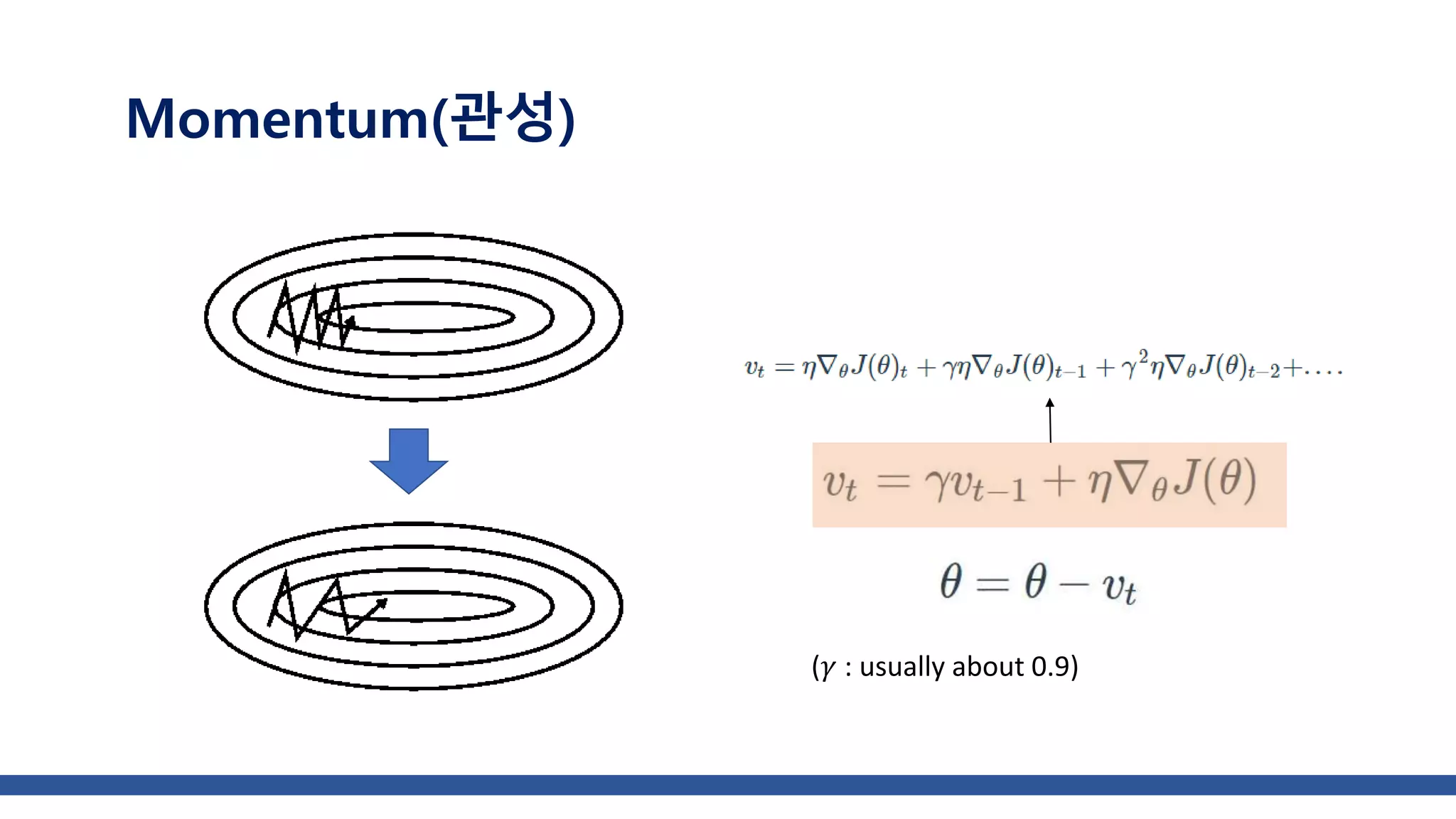
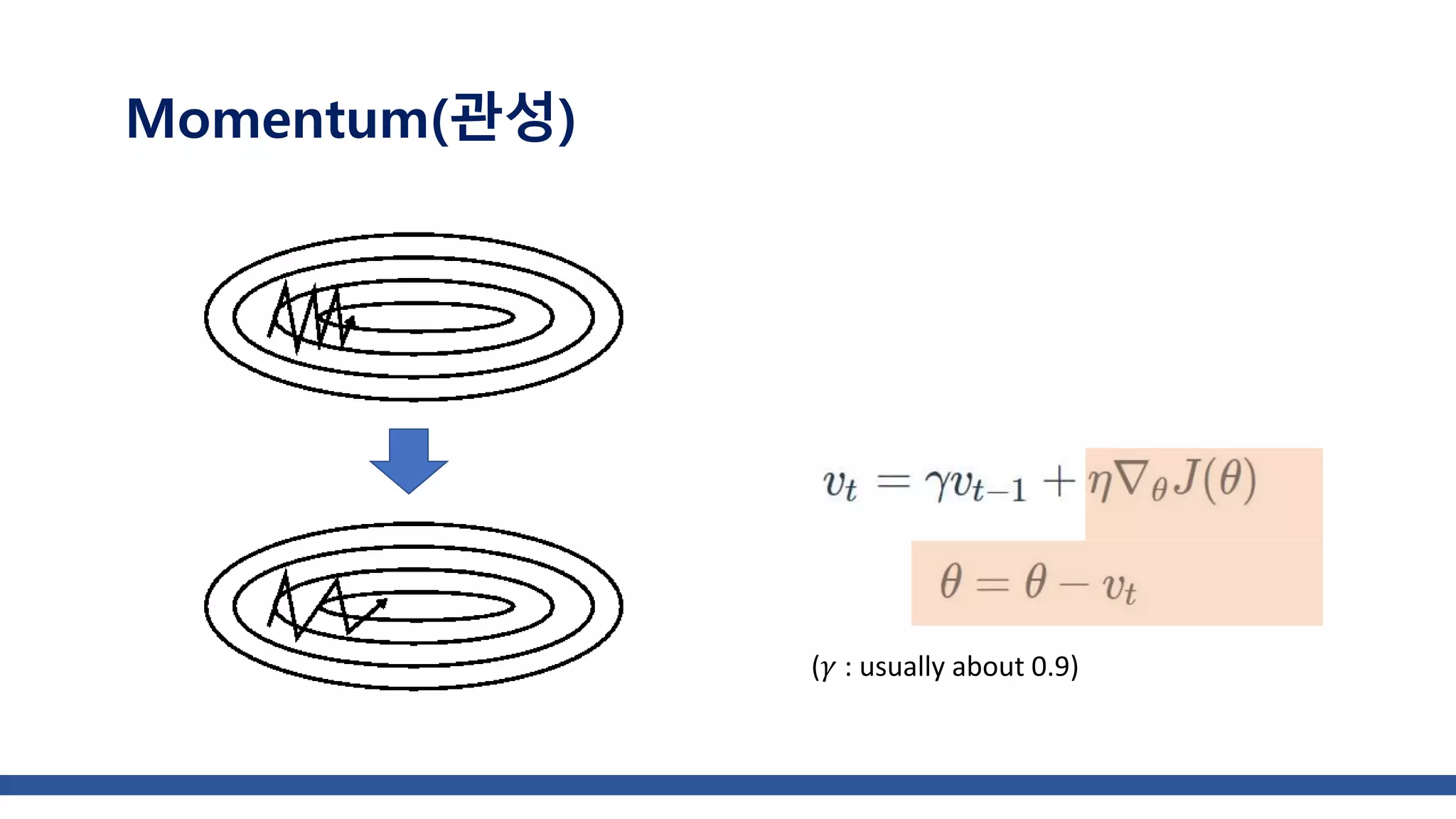
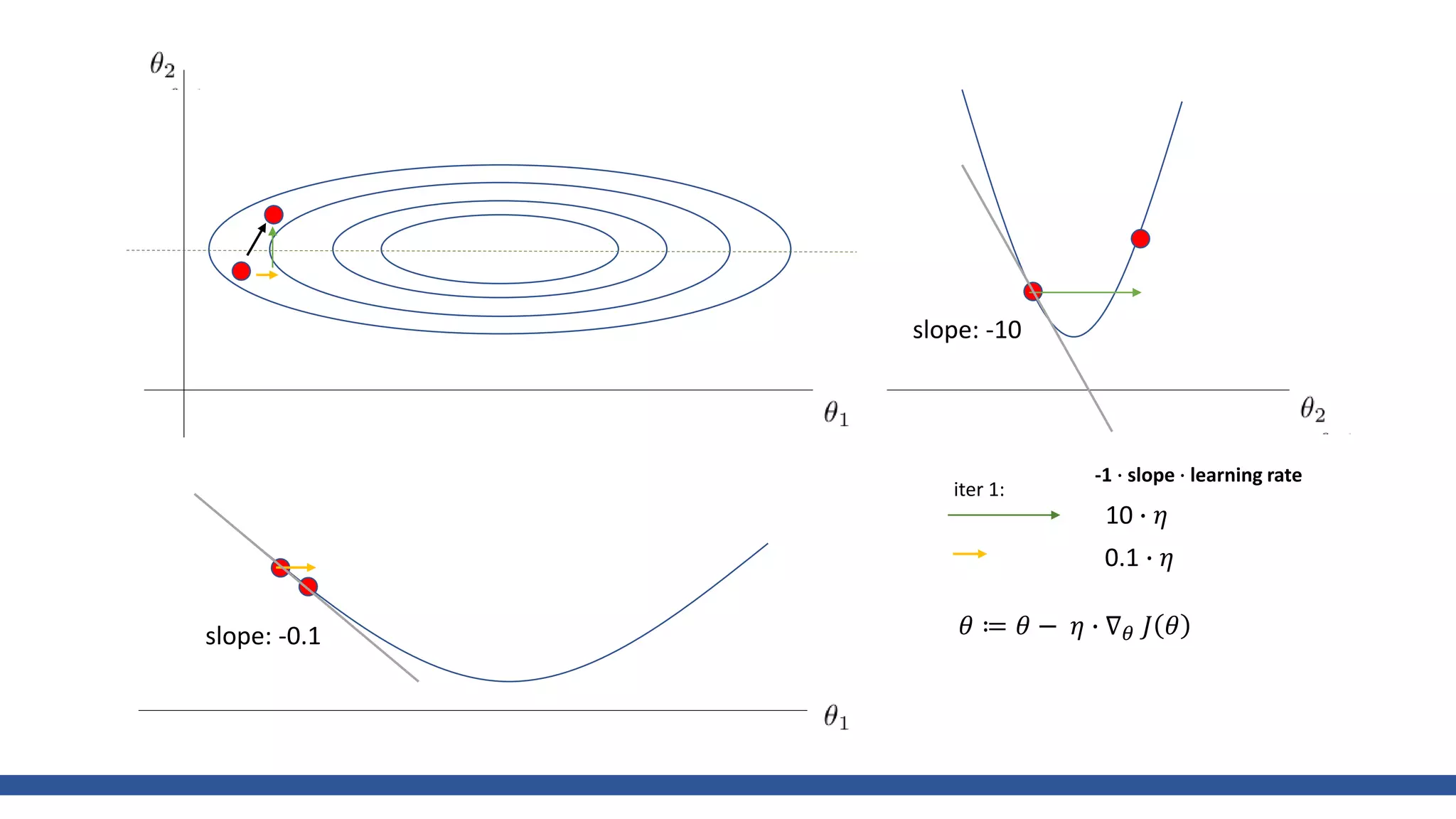
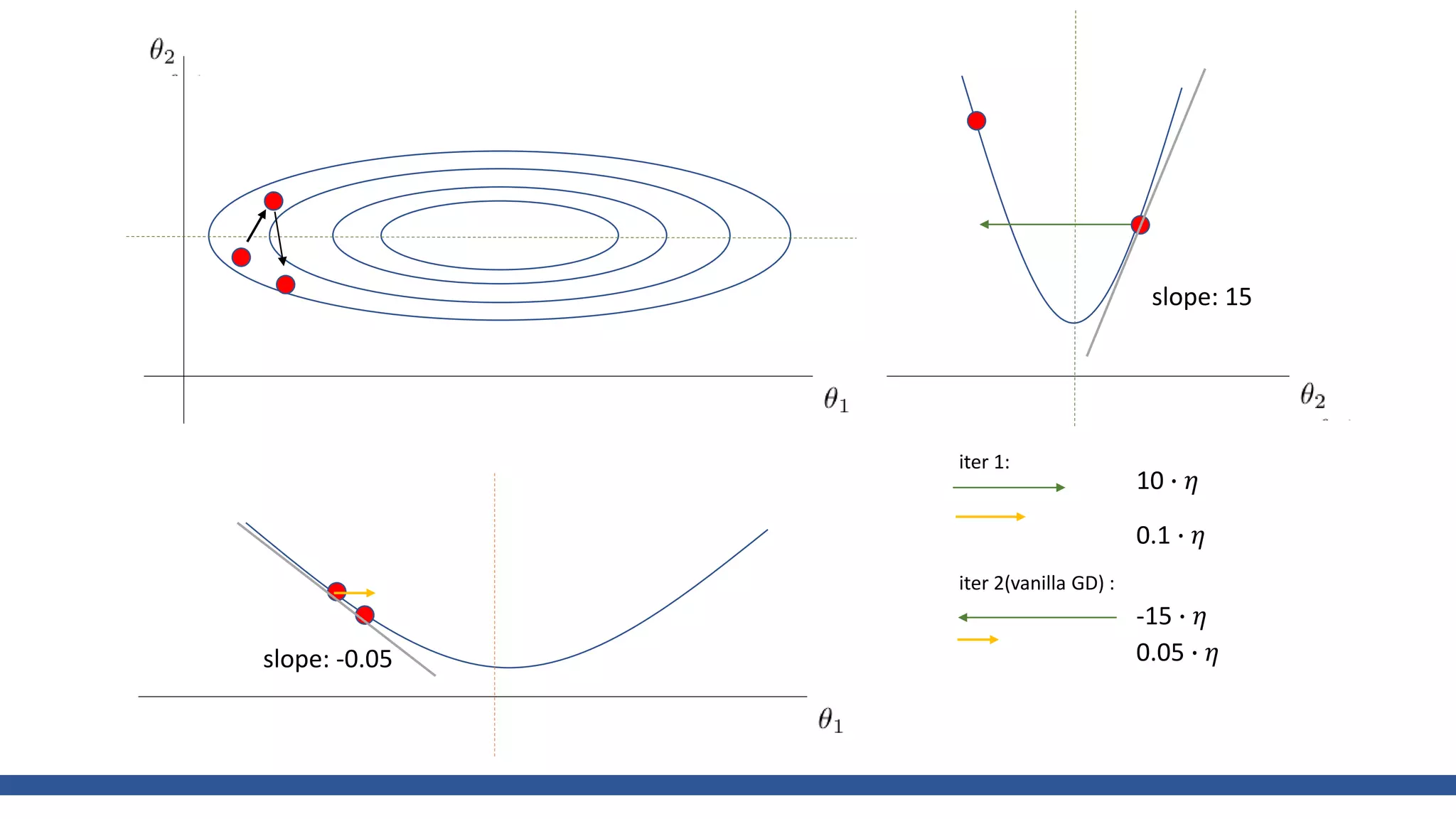
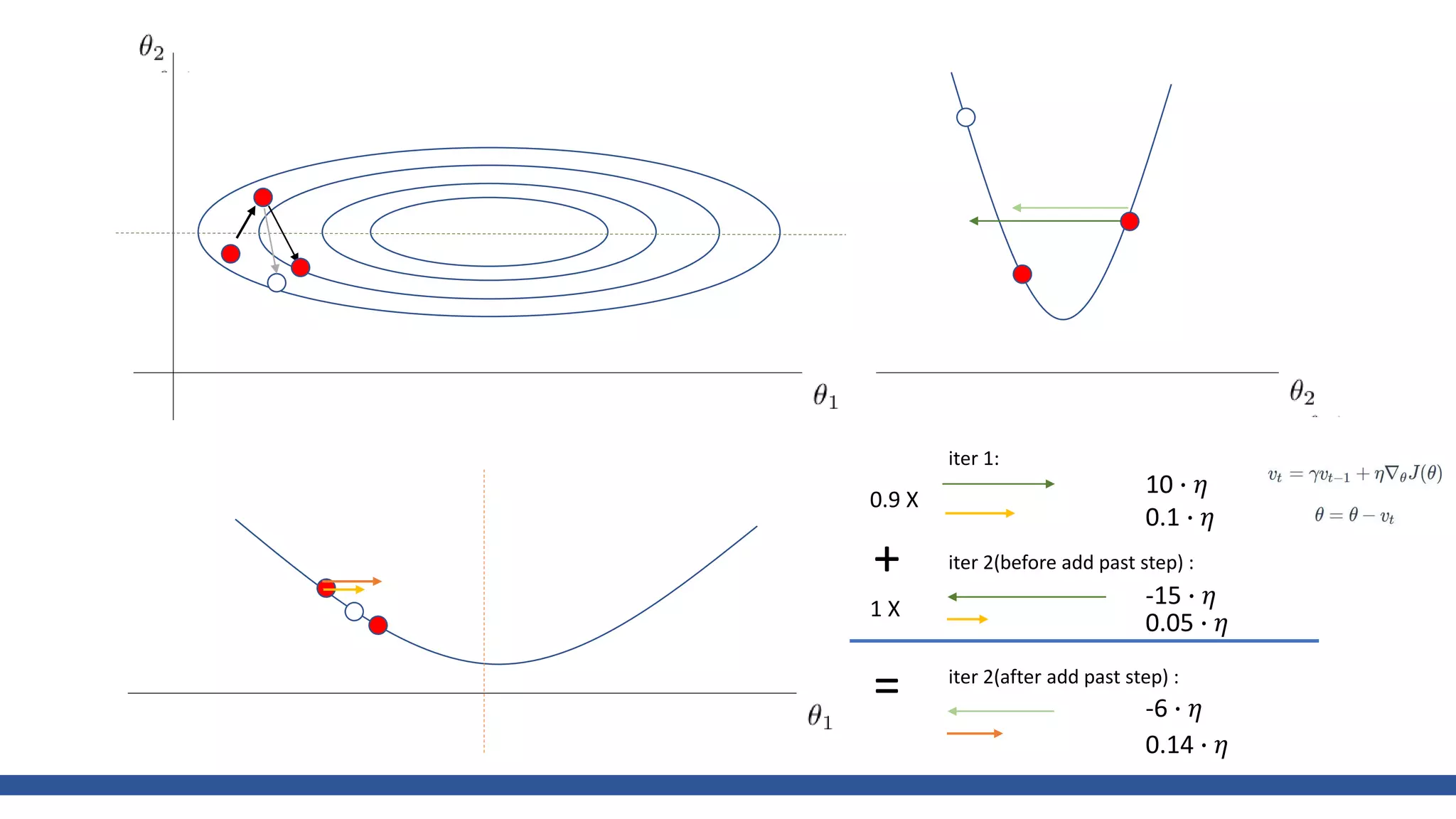
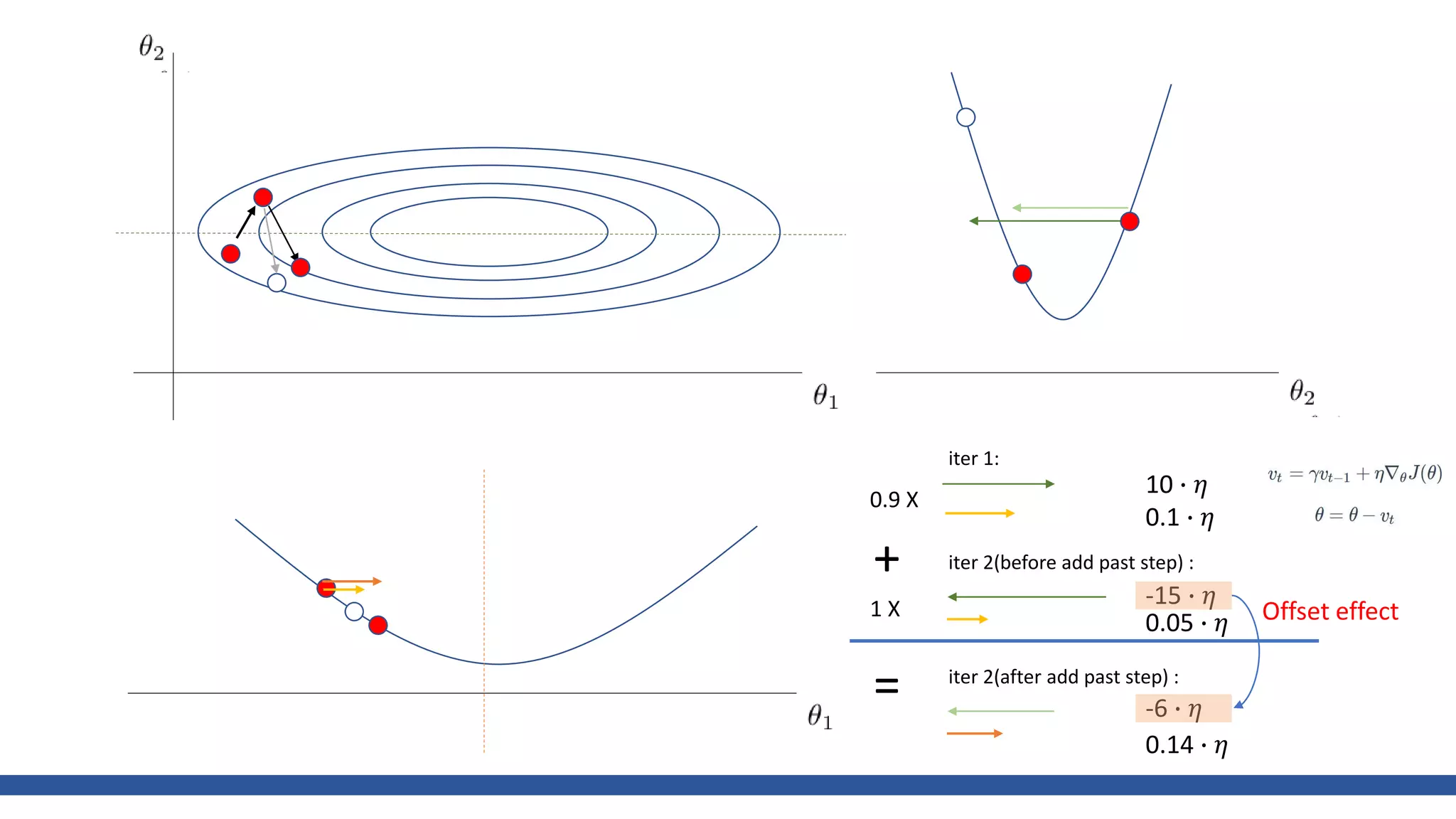
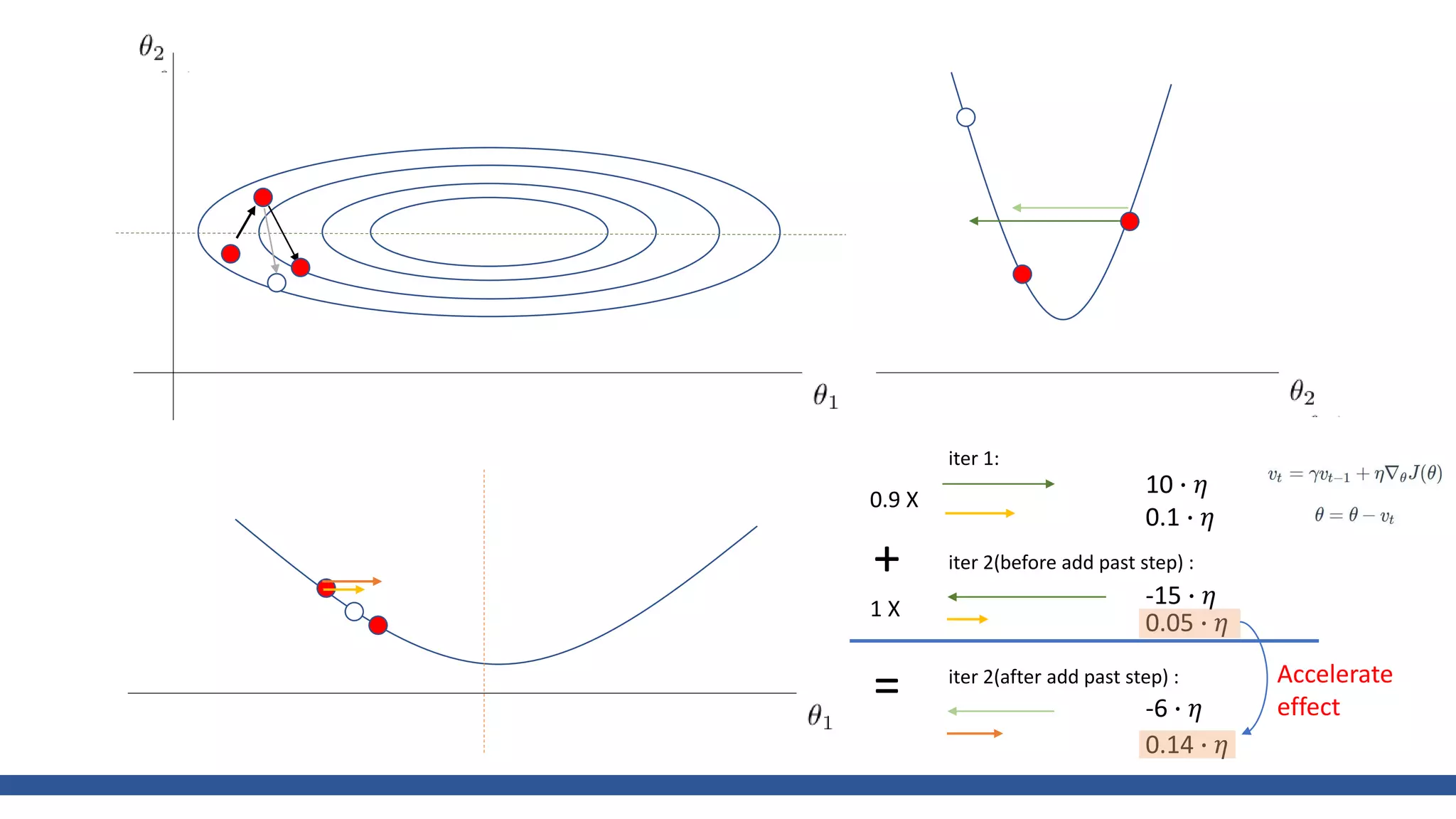
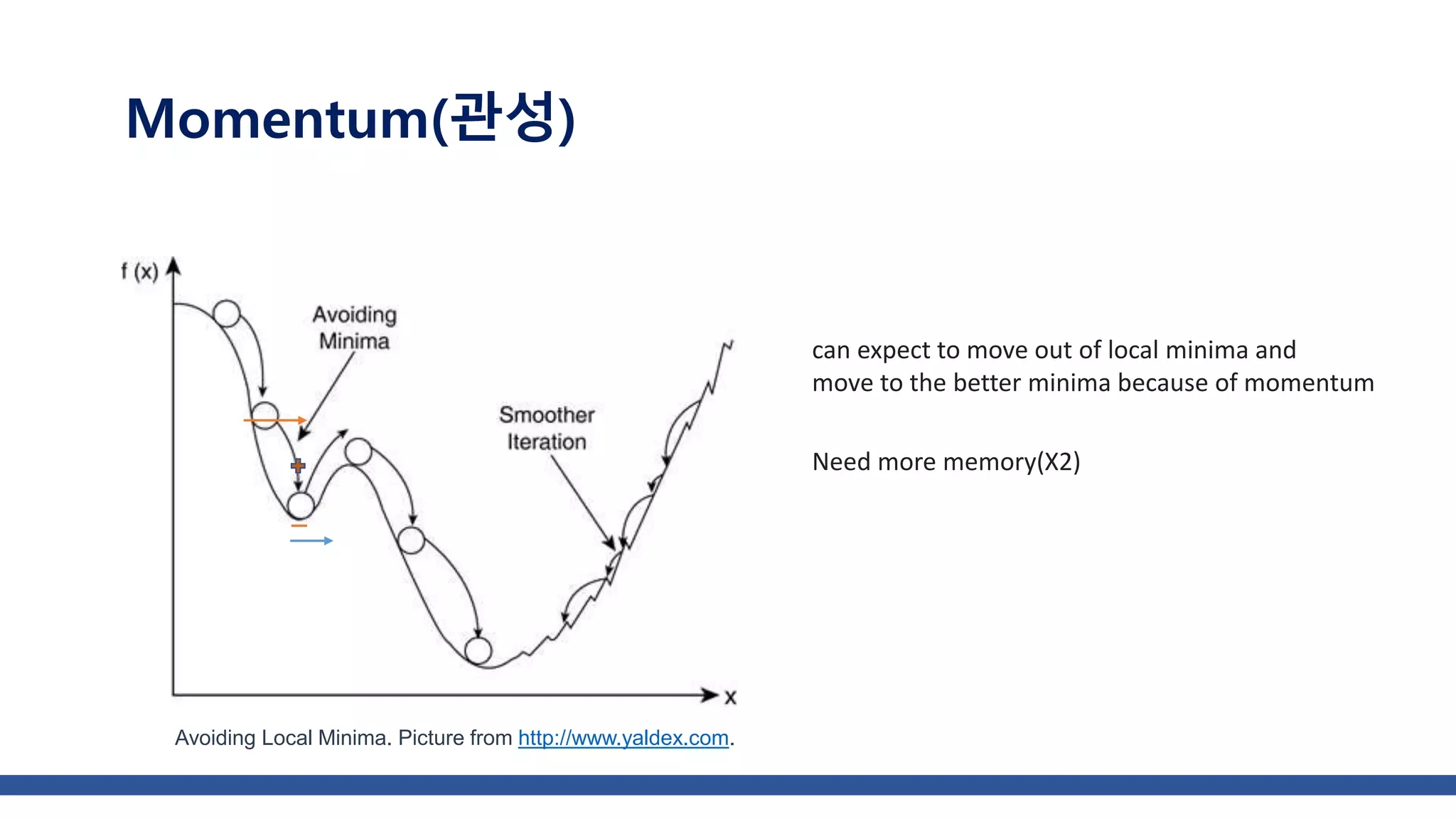
![class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]
Python
class
https://github.com/WegraLee](https://image.slidesharecdn.com/gradientdescentoptimizer-180202151844/75/Gradient-descent-optimizer-35-2048.jpg)
![W_decode = tf.Variable(tf.random_normal([n_hidden,n_input]))
b_decode = tf.Variable(tf.random_normal([n_input]))
decoder = tf.nn.sigmoid(tf.matmul(encoder,W_decode)+b_decode)
cost = tf.reduce_mean(tf.pow(X-decoder,2))
optimizer = tf.train.MomentumOptimizer(learning_rate, momentum).minimize(cost)
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
Tensor flow](https://image.slidesharecdn.com/gradientdescentoptimizer-180202151844/75/Gradient-descent-optimizer-36-2048.jpg)
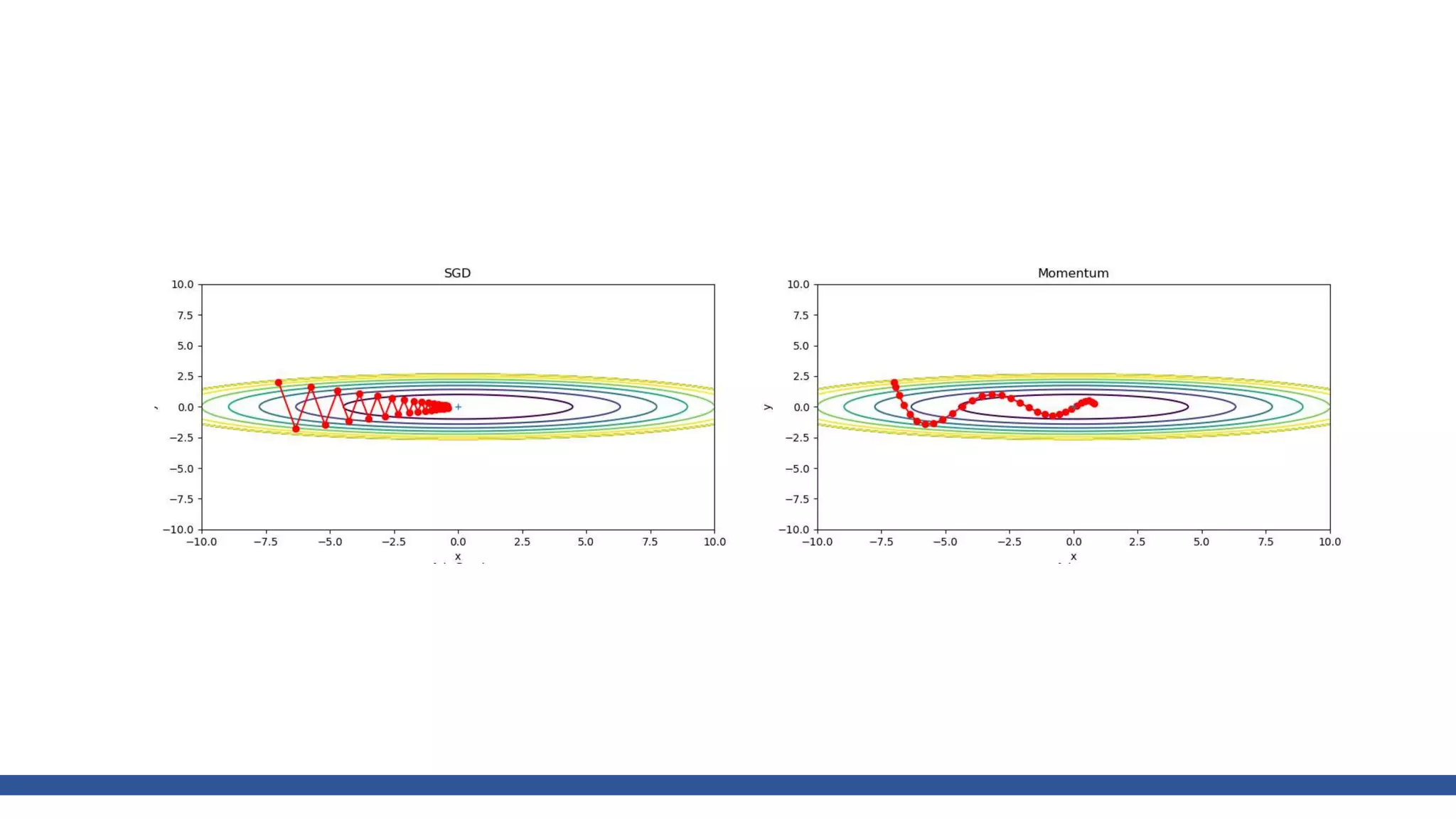
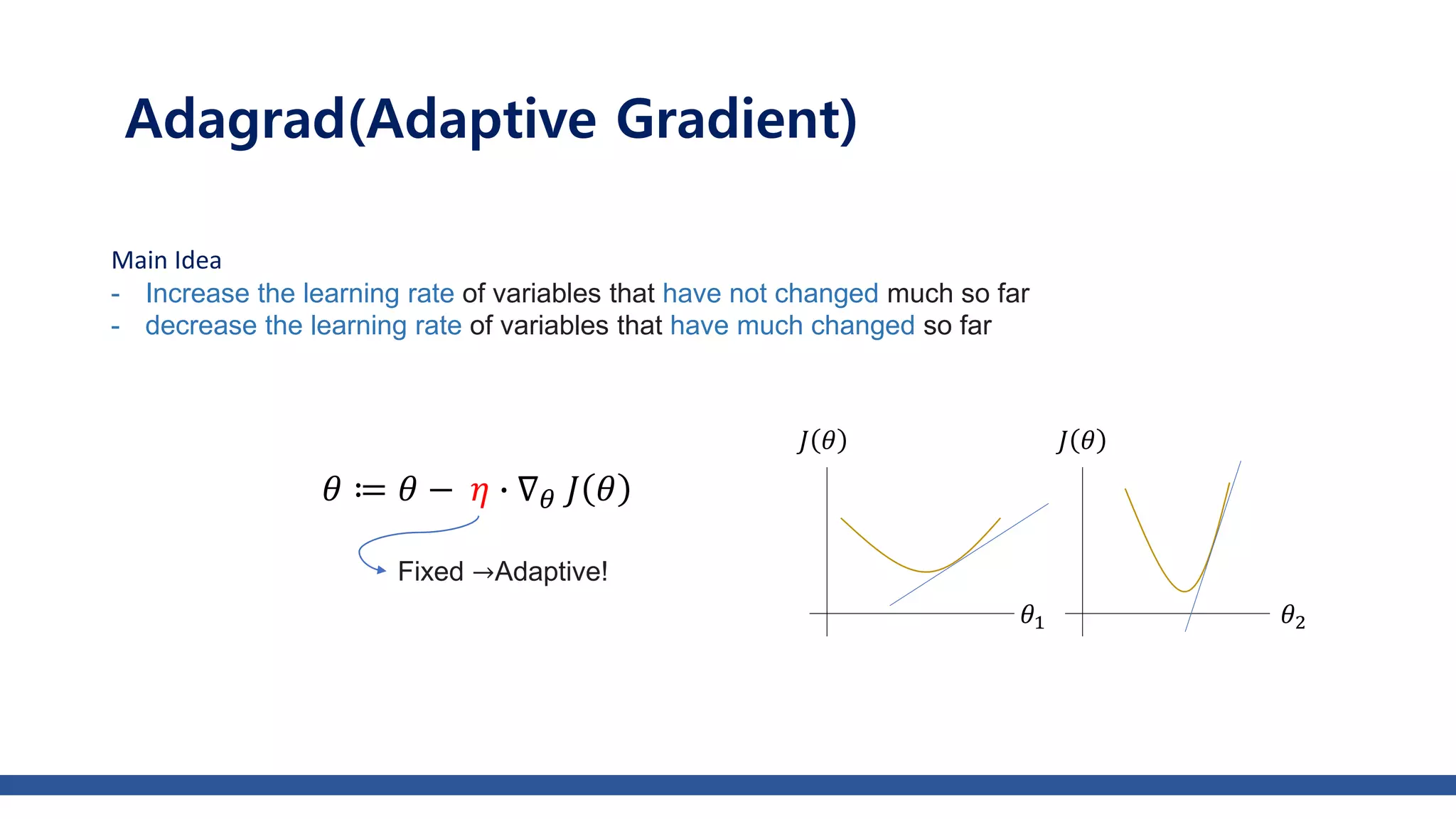

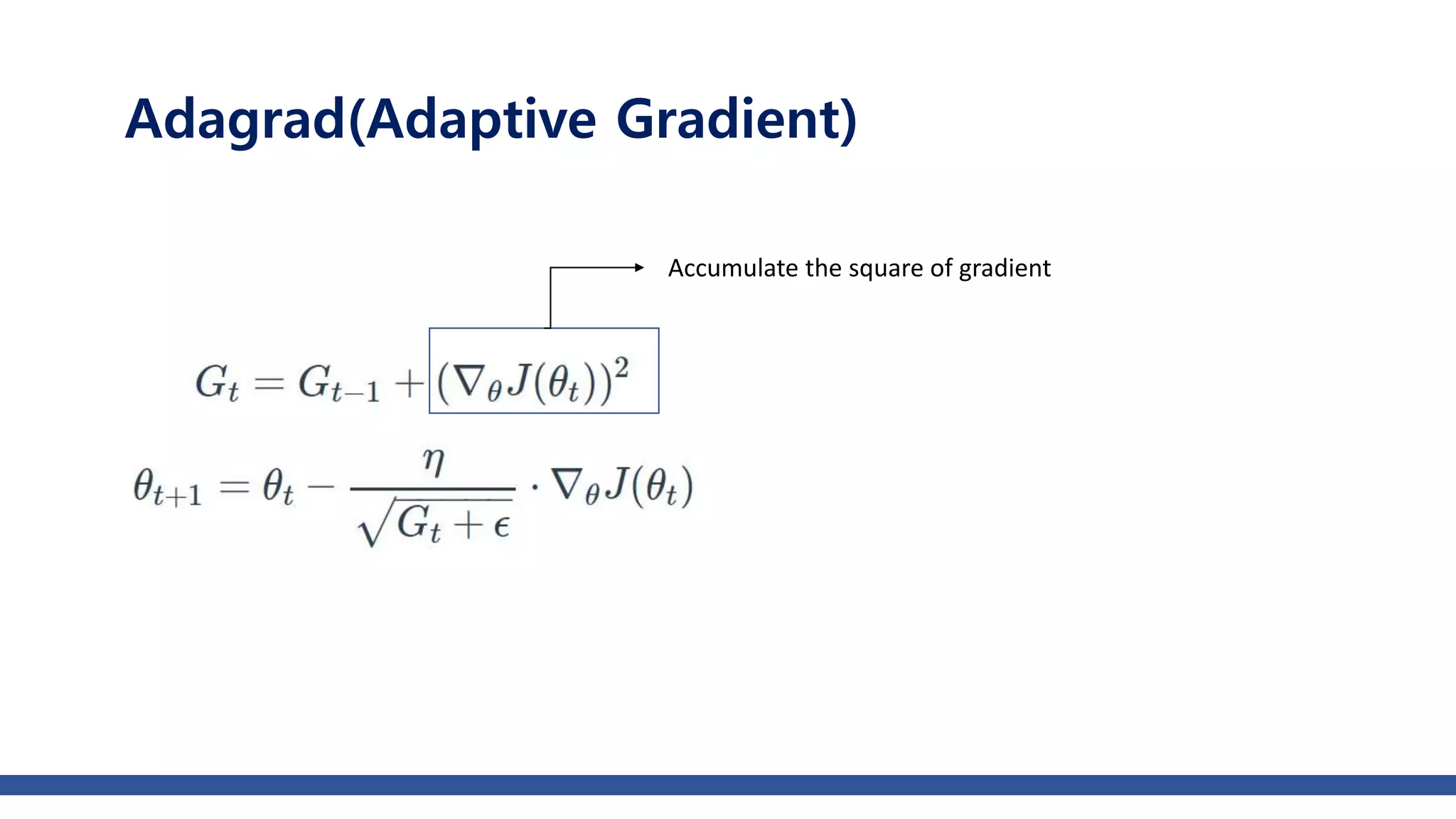
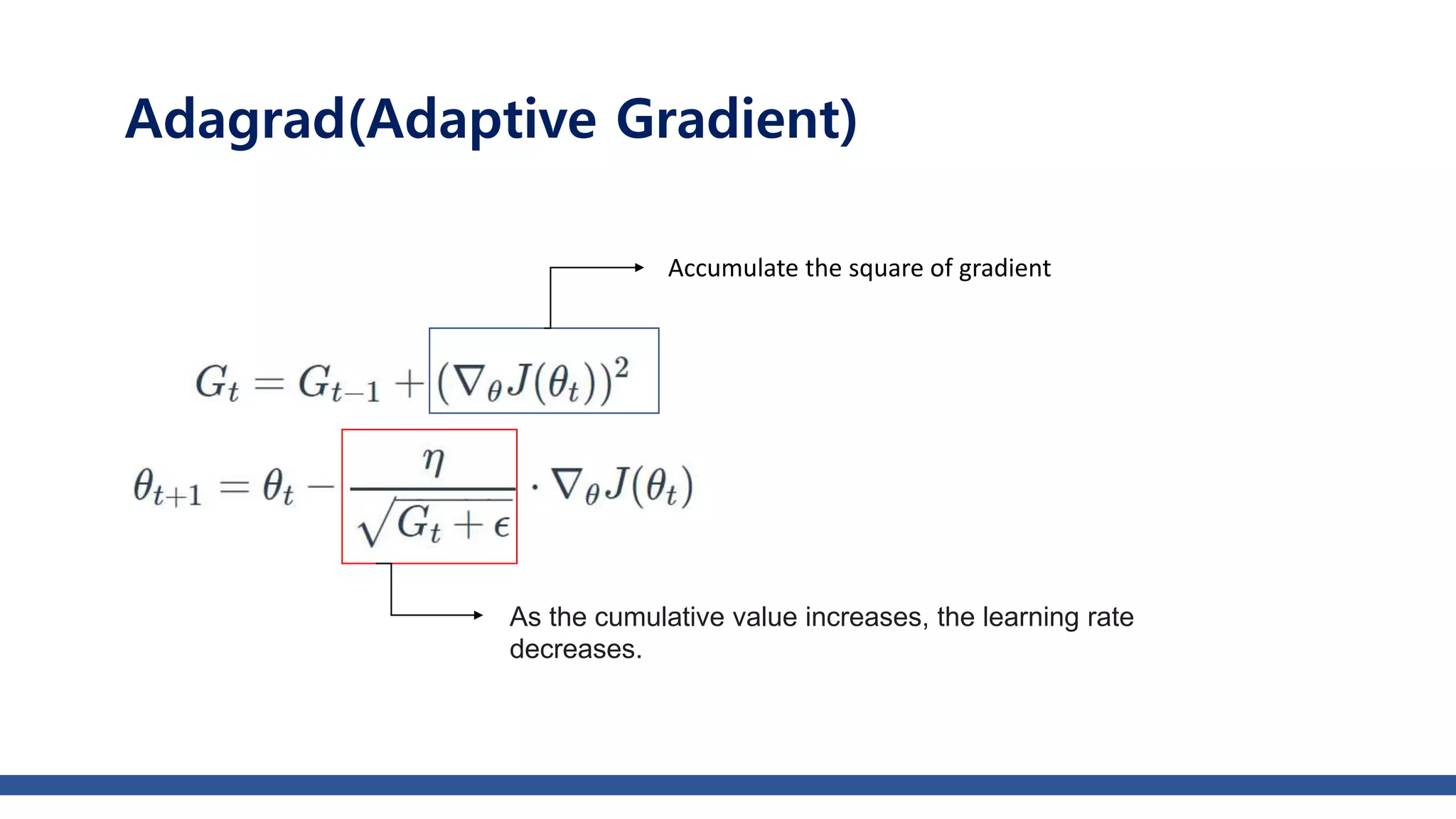
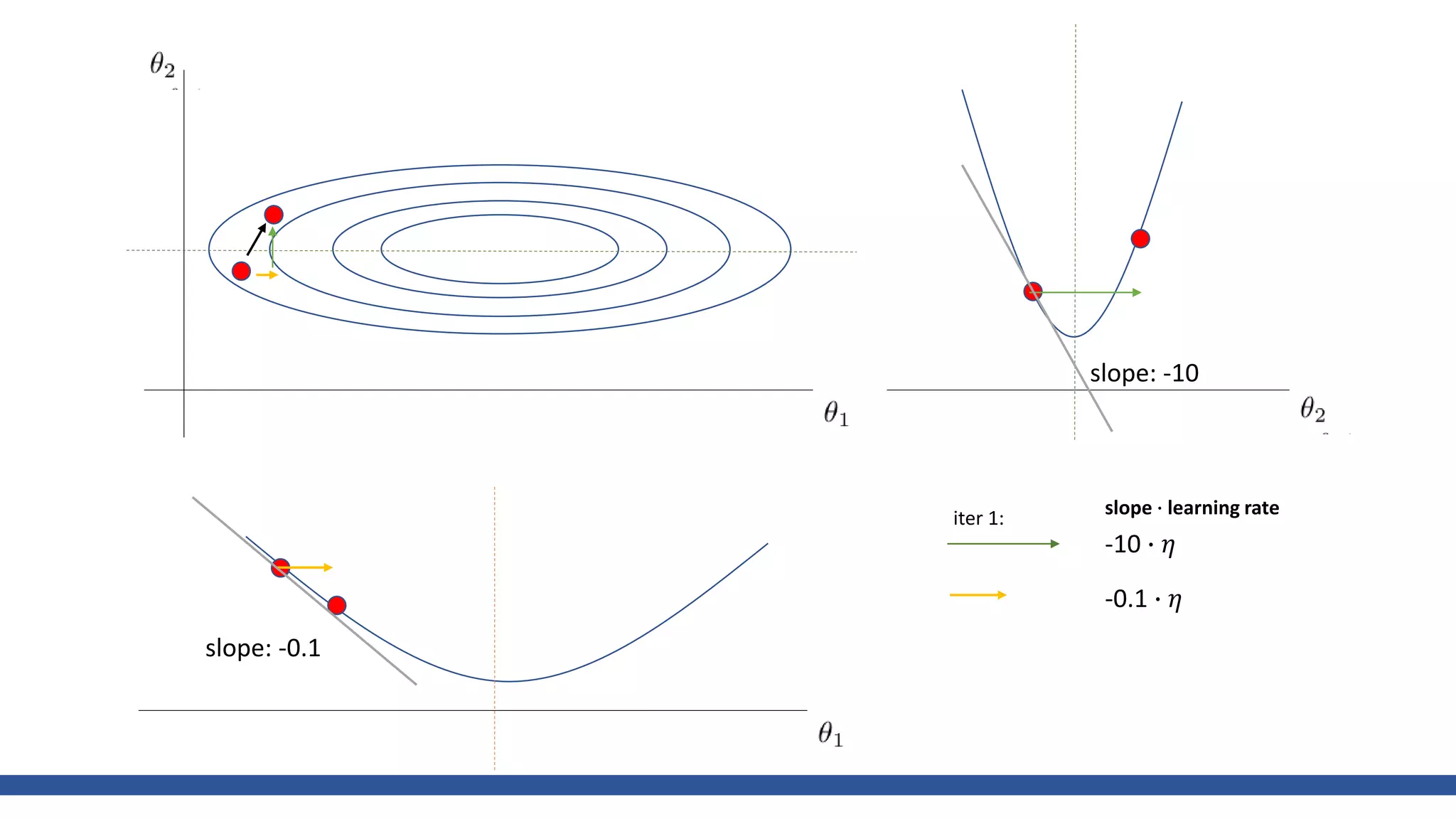
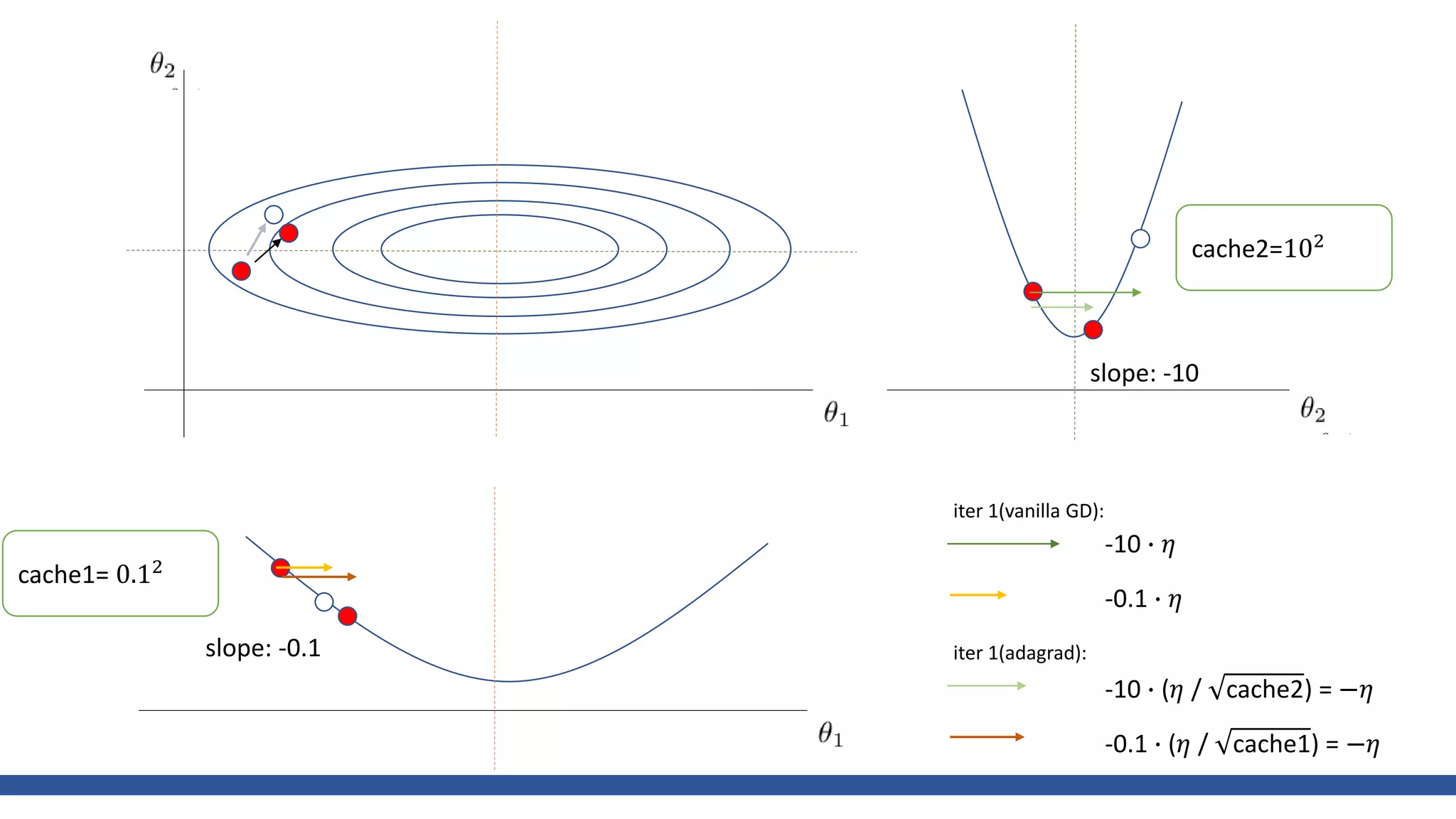
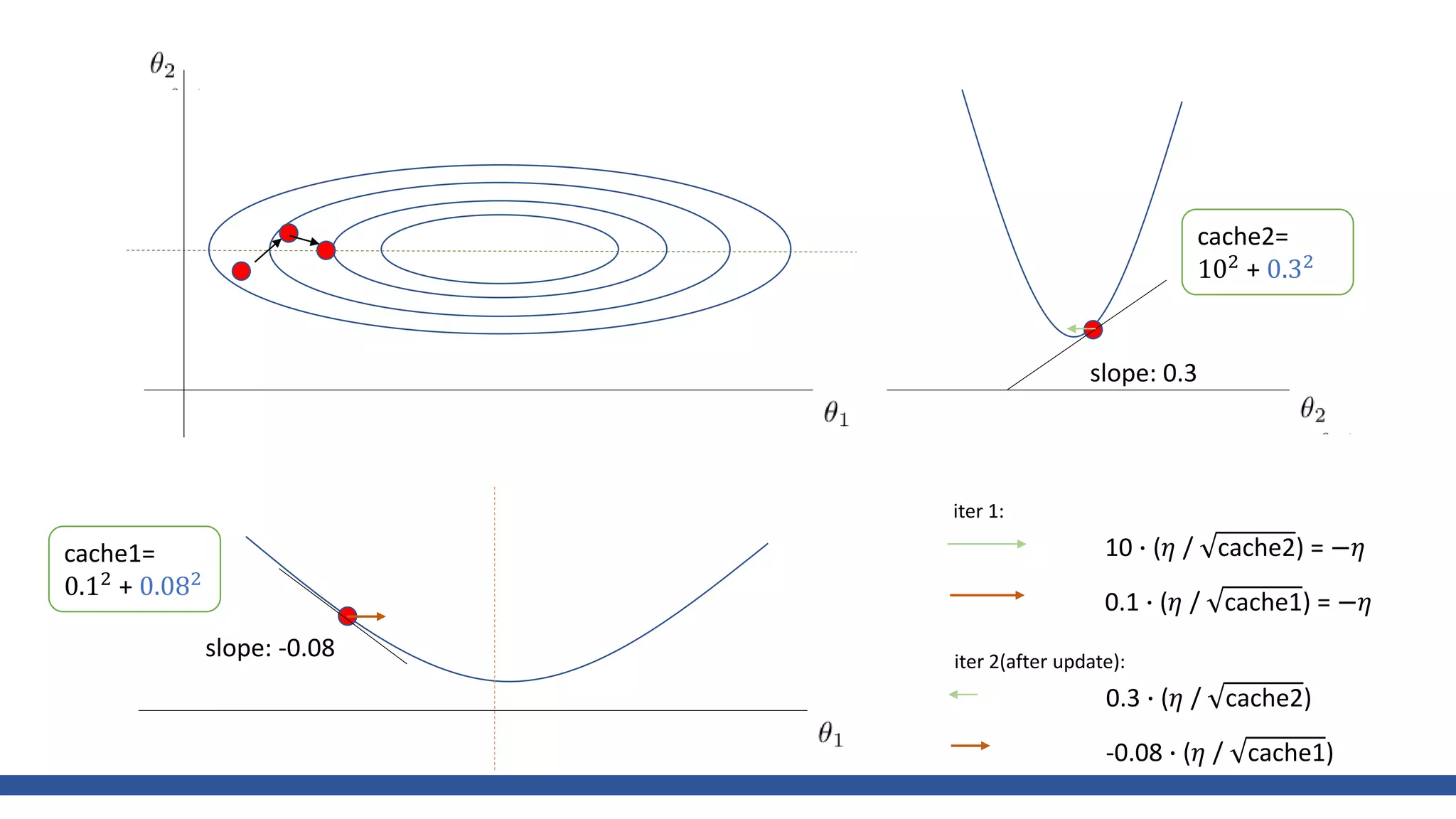
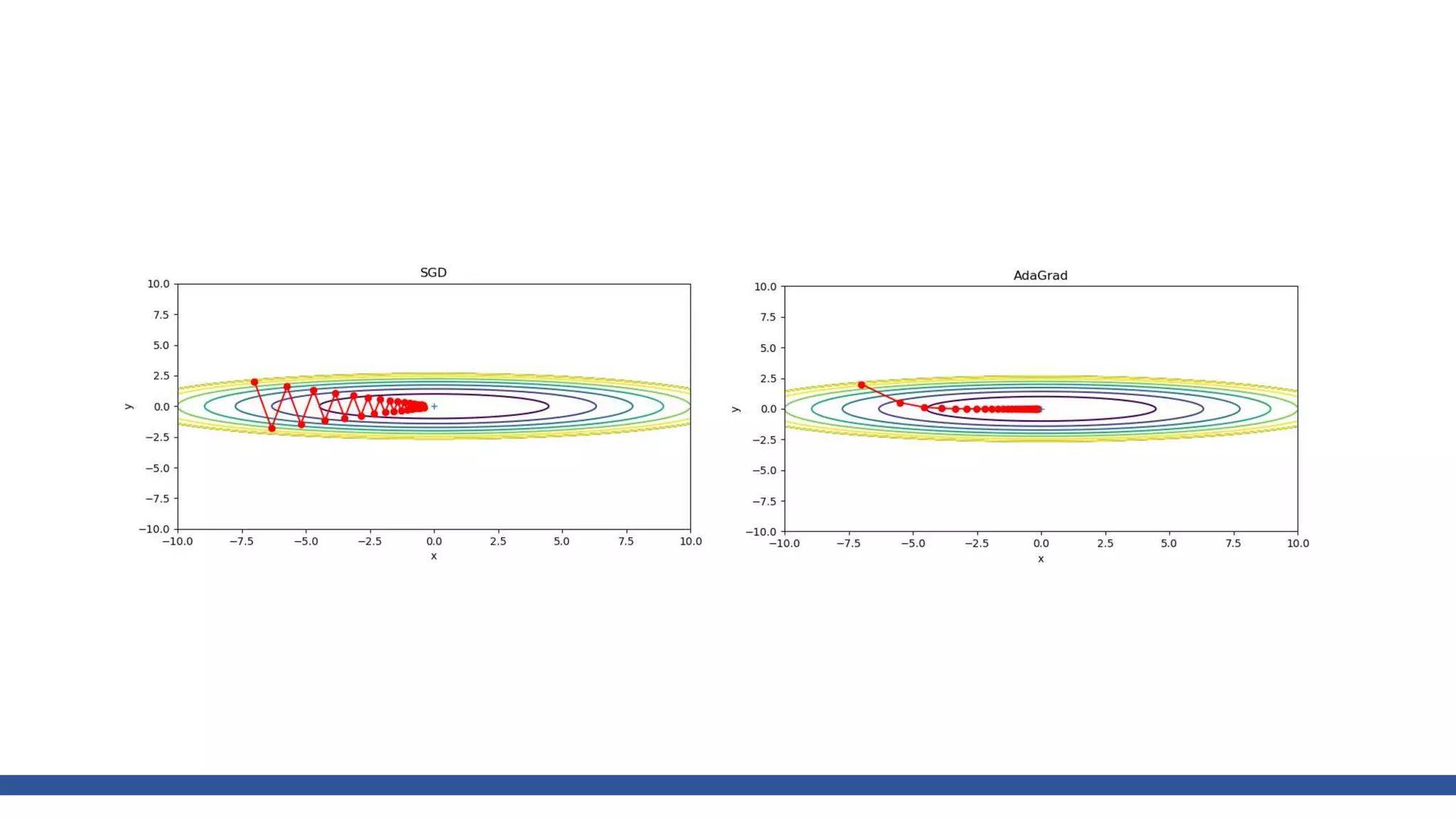
![class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
Python
class
https://github.com/WegraLee](https://image.slidesharecdn.com/gradientdescentoptimizer-180202151844/75/Gradient-descent-optimizer-45-2048.jpg)
![W_decode = tf.Variable(tf.random_normal([n_hidden,n_input]))
b_decode = tf.Variable(tf.random_normal([n_input]))
decoder = tf.nn.sigmoid(tf.matmul(encoder,W_decode)+b_decode)
cost = tf.reduce_mean(tf.pow(X-decoder,2))
optimizer = tf.train.AdagradOptimizer(learning_rate,initial_accumulator_value).minimize(cost)
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
Tensor flow](https://image.slidesharecdn.com/gradientdescentoptimizer-180202151844/75/Gradient-descent-optimizer-46-2048.jpg)





![W_decode = tf.Variable(tf.random_normal([n_hidden,n_input]))
b_decode = tf.Variable(tf.random_normal([n_input]))
decoder = tf.nn.sigmoid(tf.matmul(encoder,W_decode)+b_decode)
cost = tf.reduce_mean(tf.pow(X-decoder,2))
optimizer = tf.train.AdamOptimizer(learning_rate, beta1, beta2, epsilon).minimize(cost)
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
Tensor flow](https://image.slidesharecdn.com/gradientdescentoptimizer-180202151844/75/Gradient-descent-optimizer-53-2048.jpg)