Download to read offline
Uploaded byCoalesce
Generation and Storage Modeling Presentation
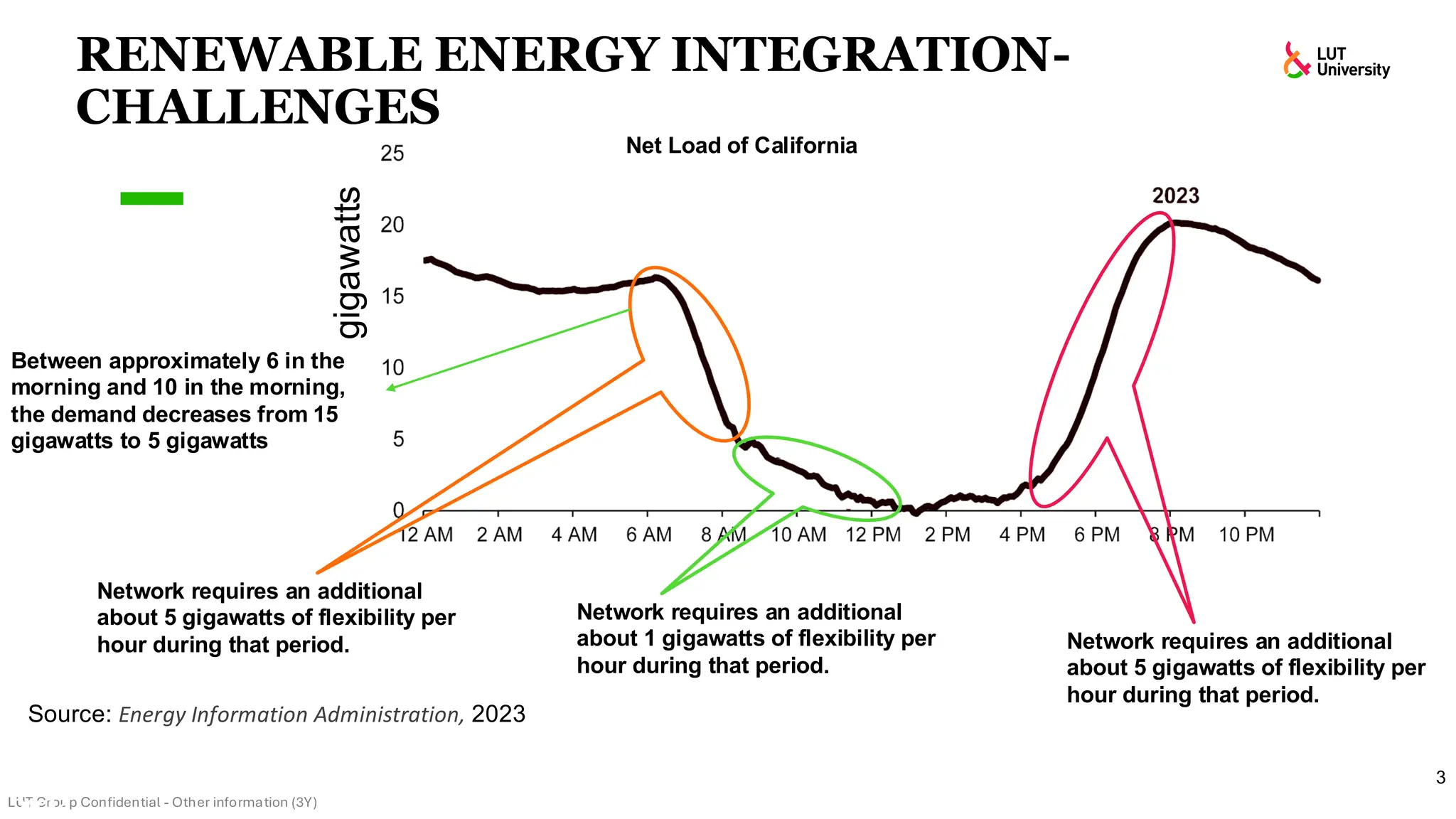
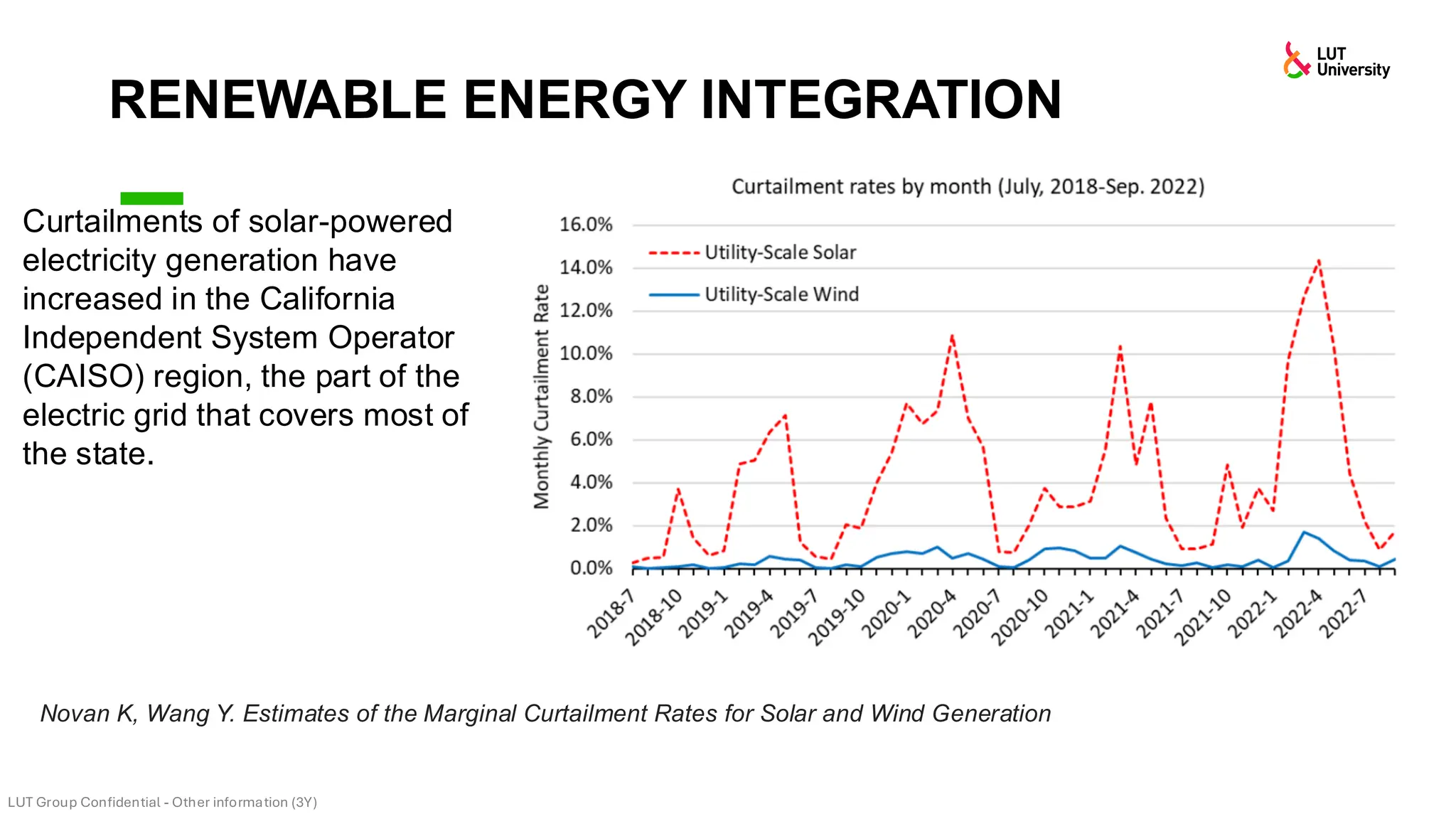
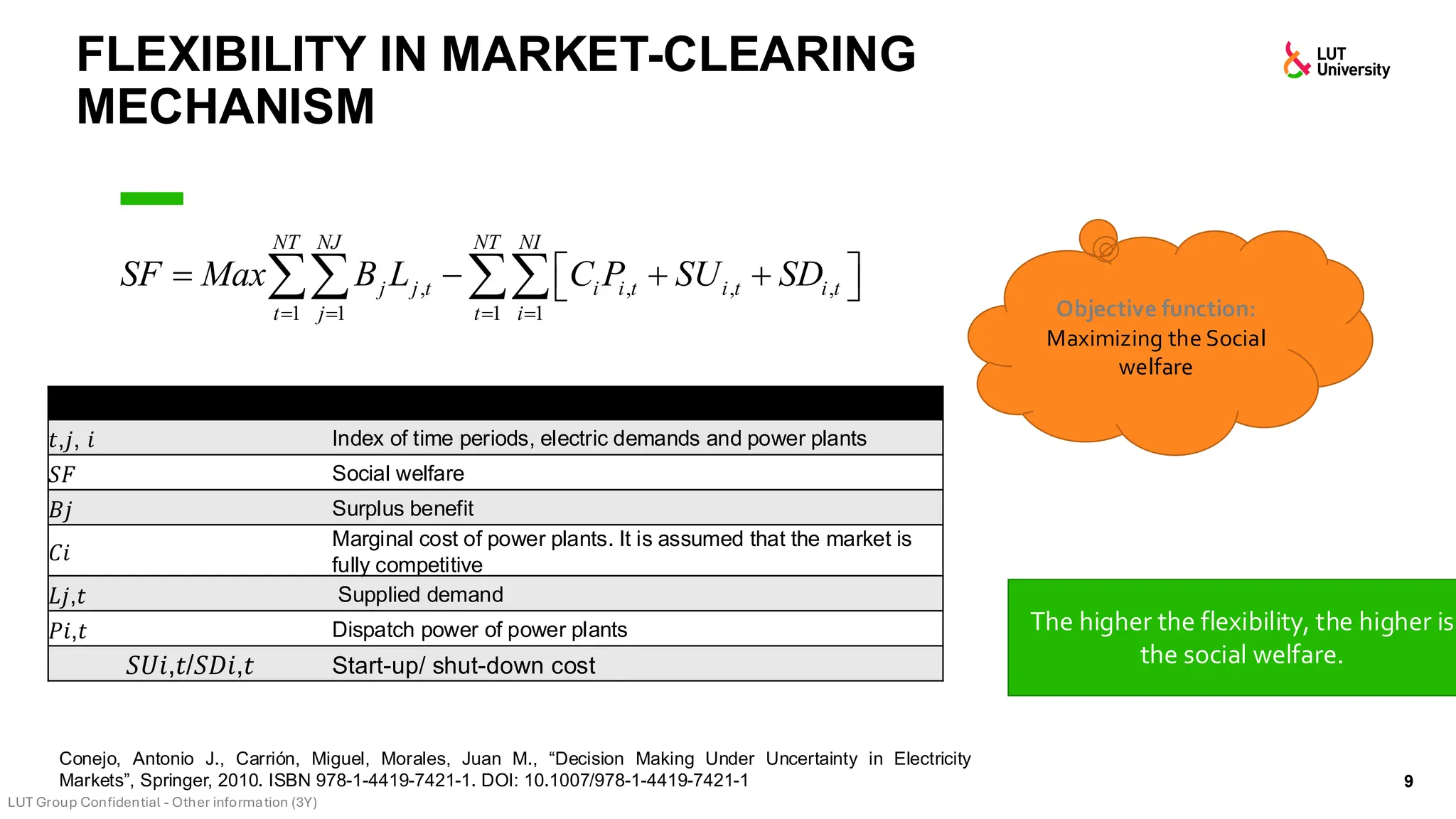
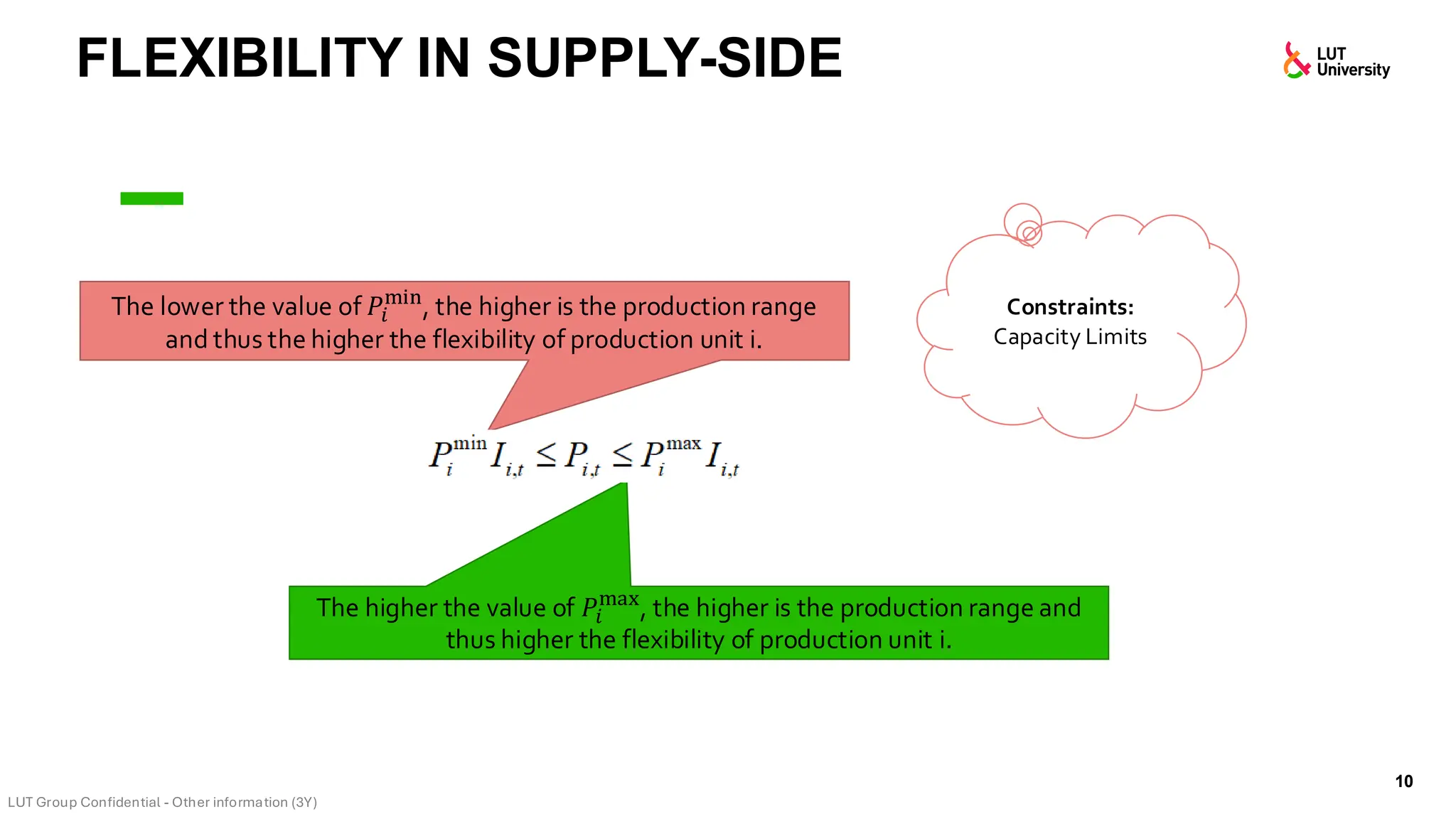
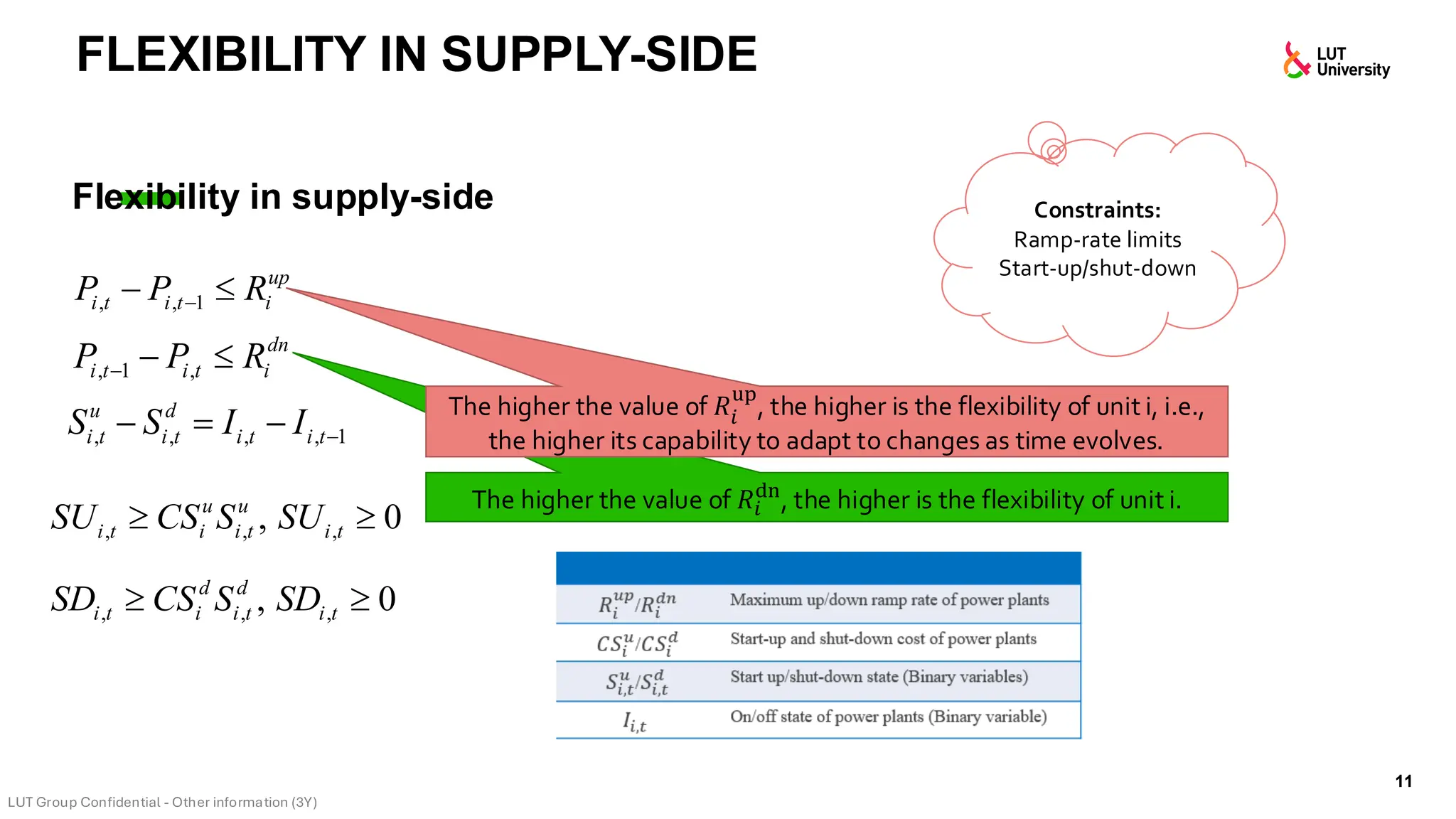
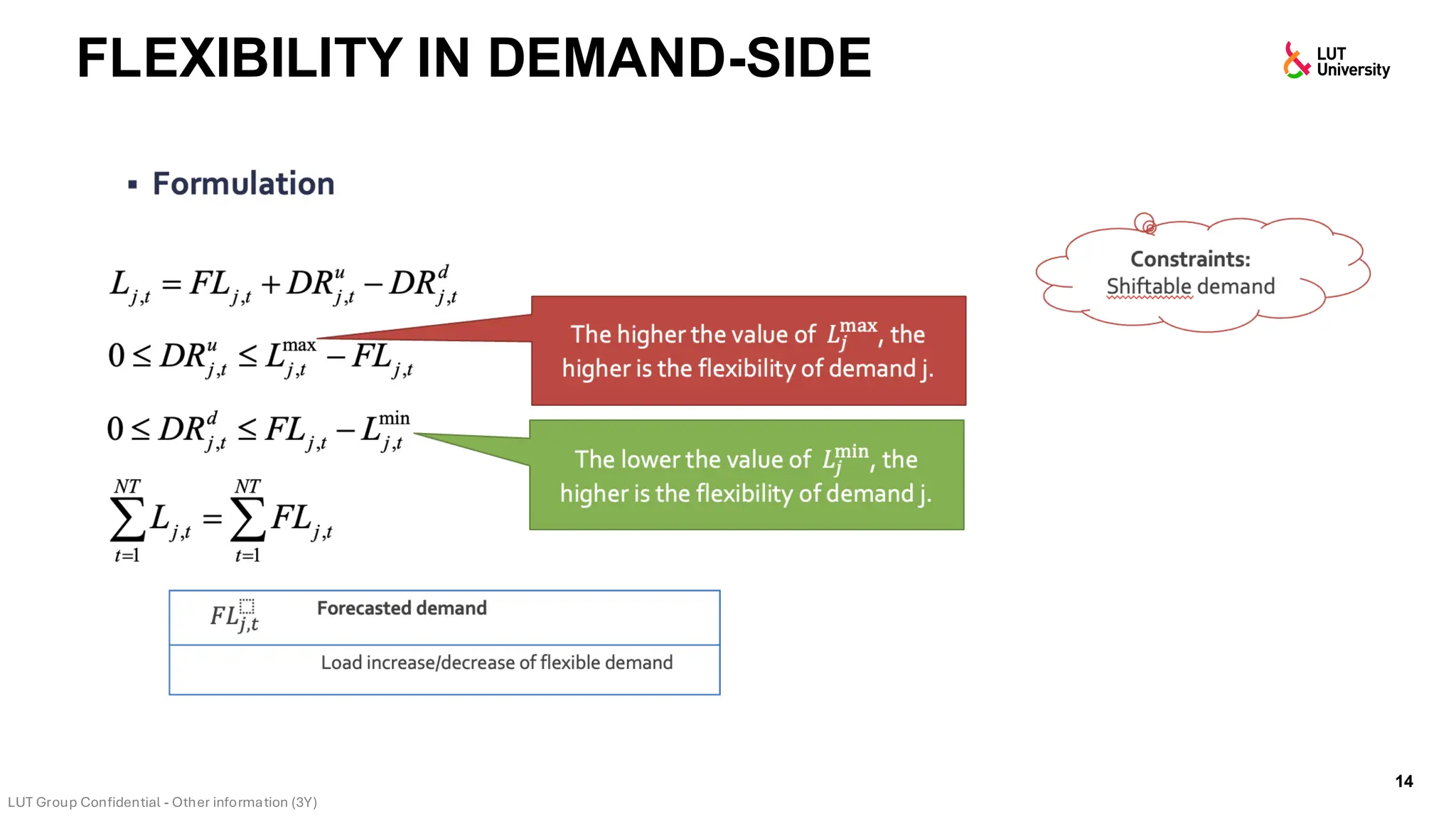
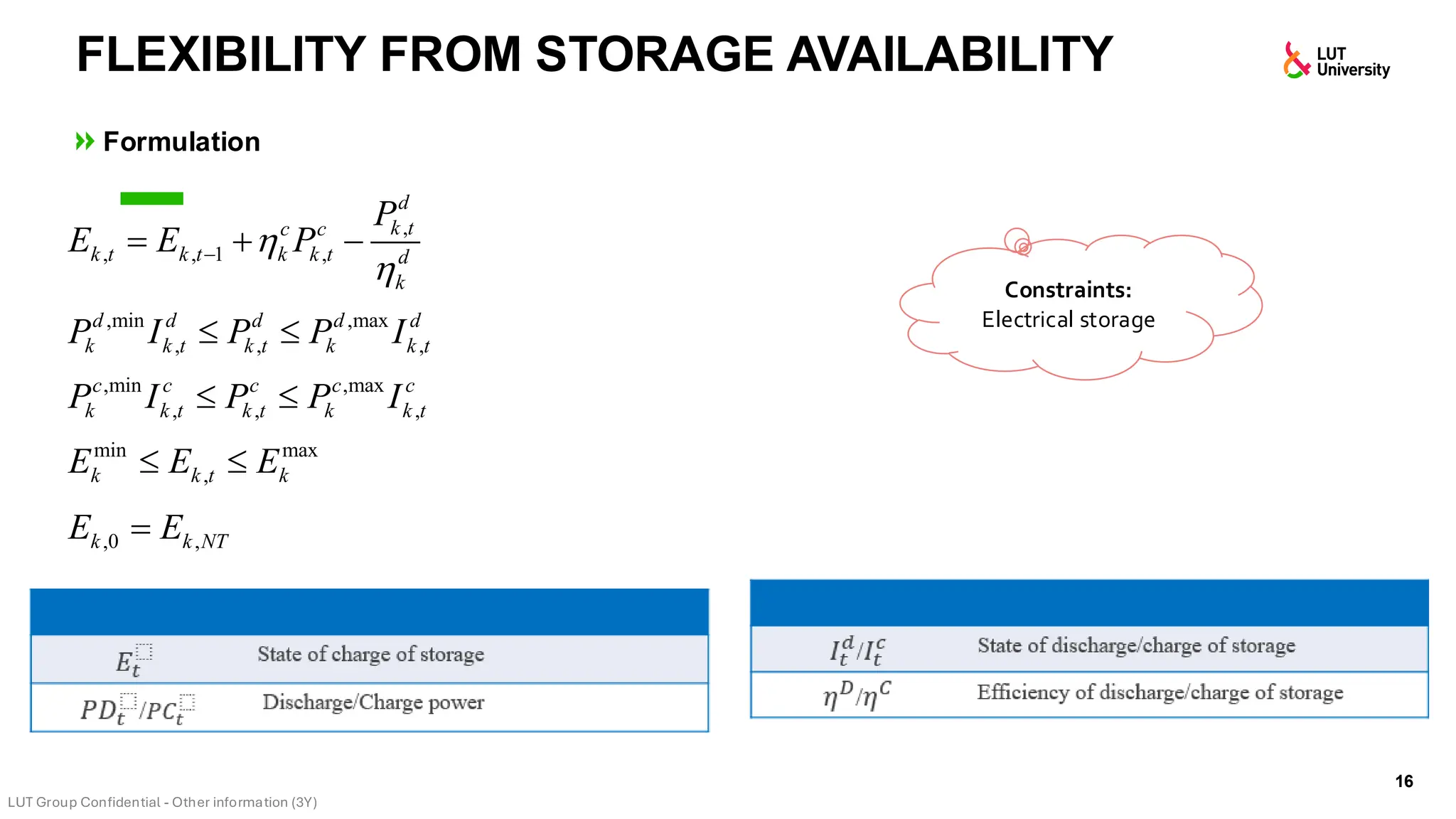
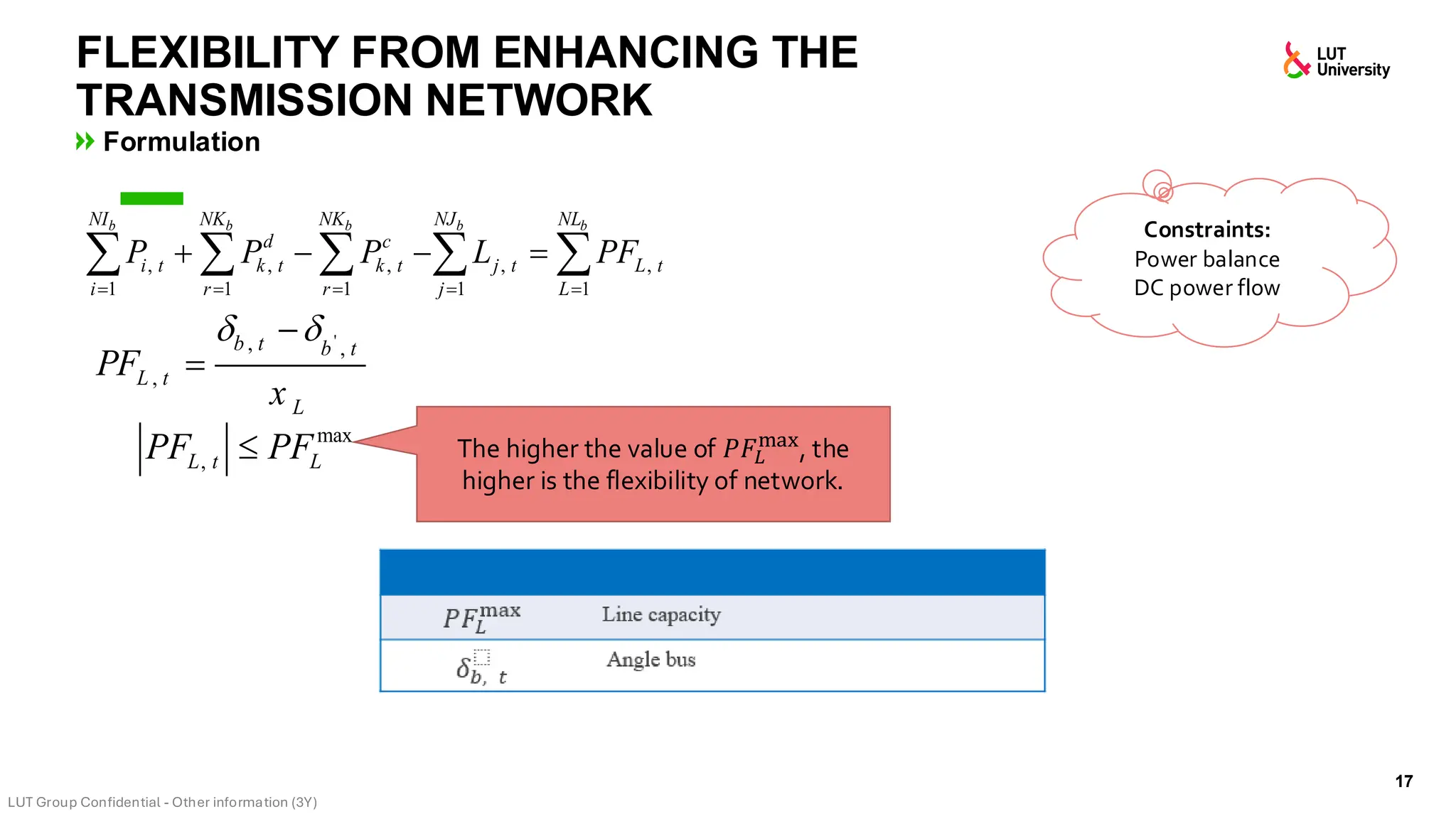
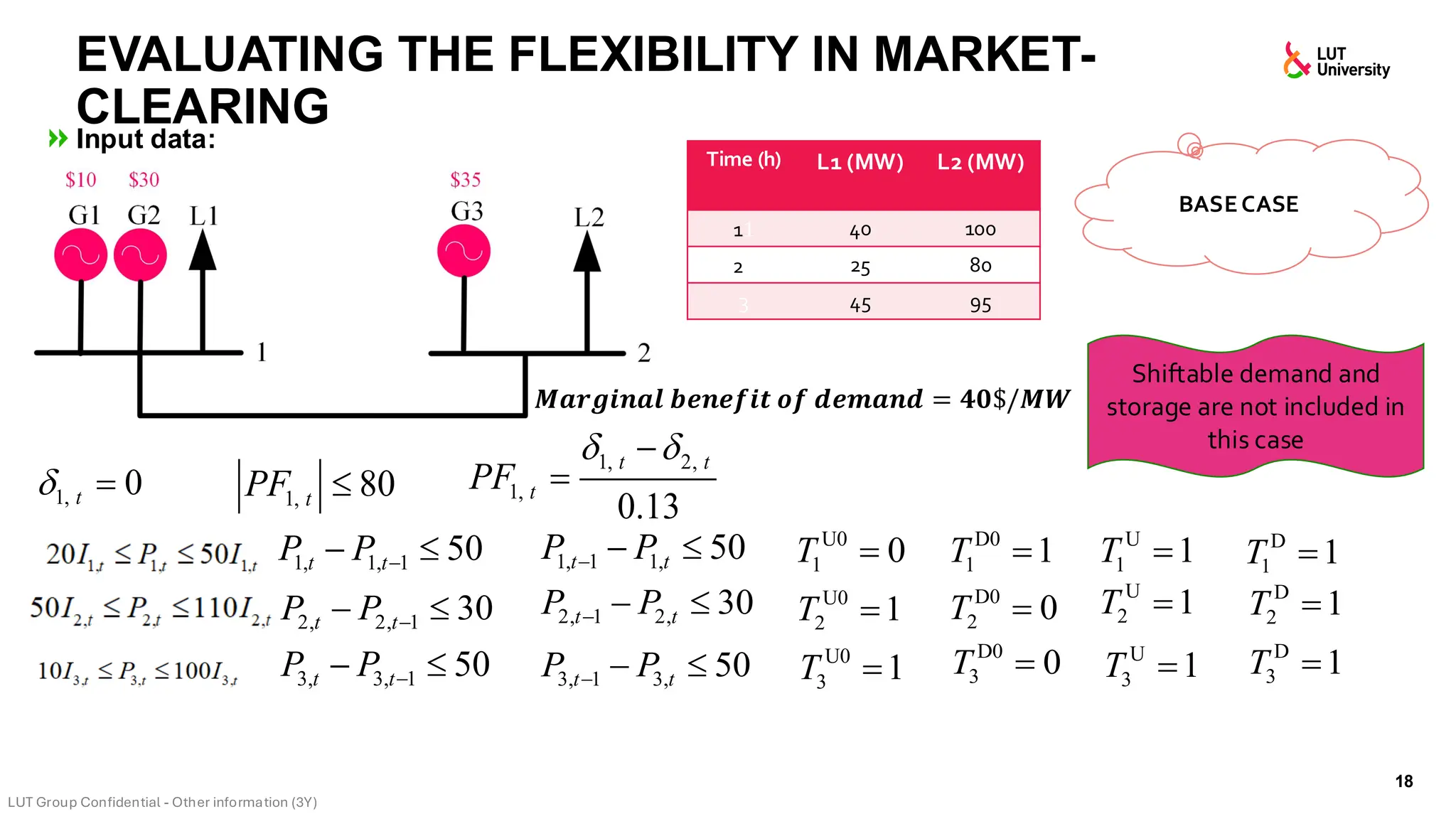
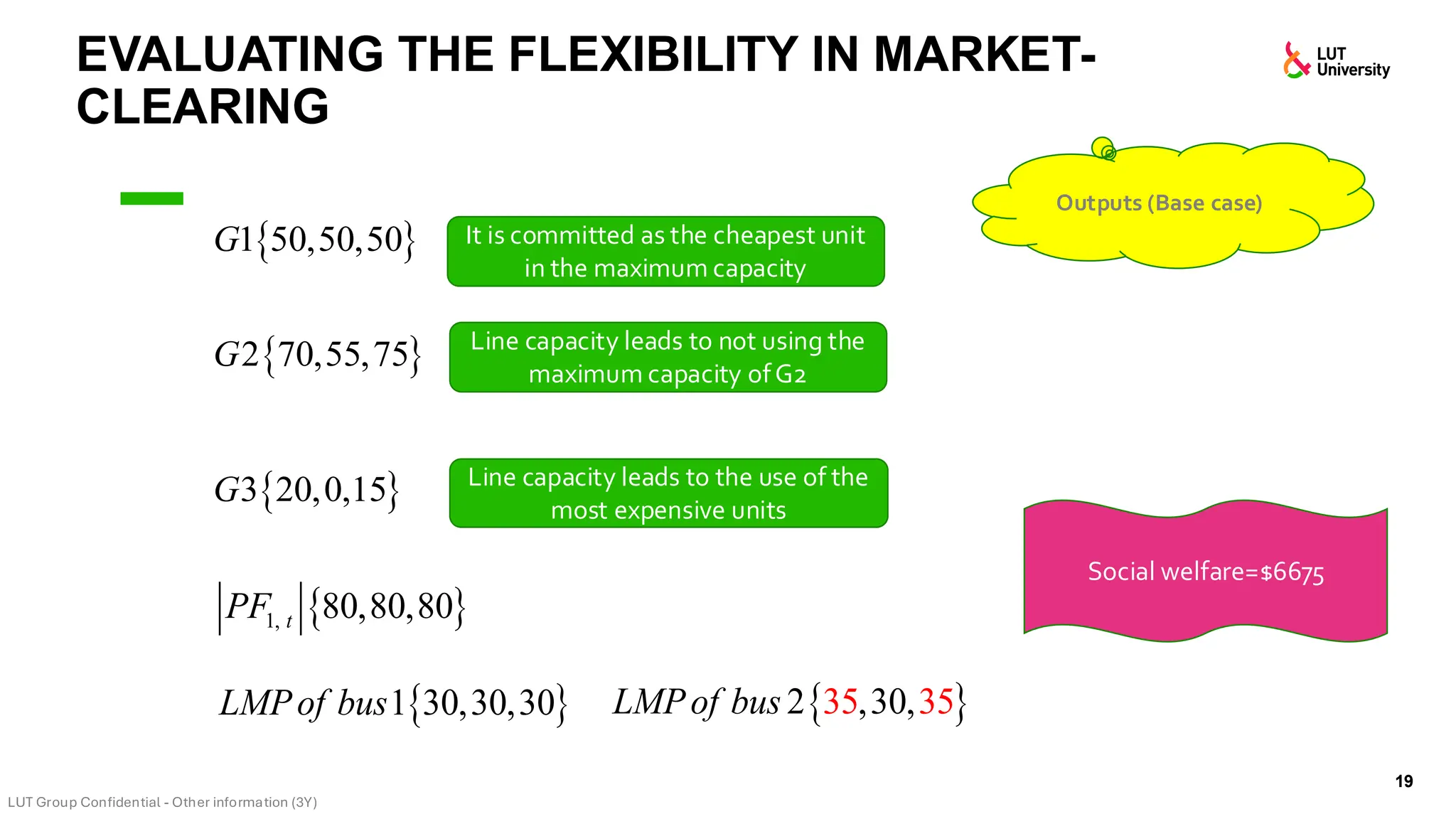
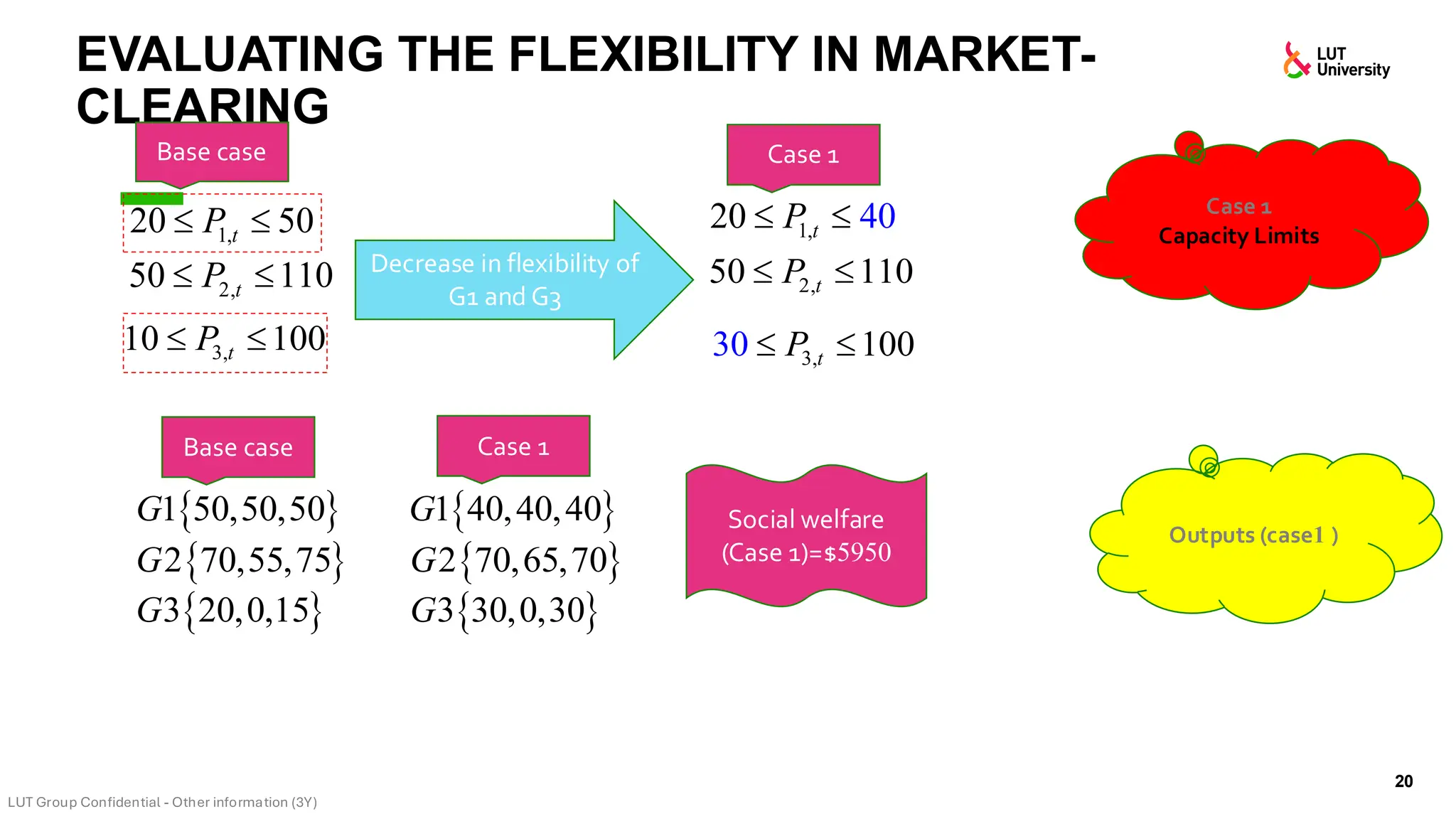
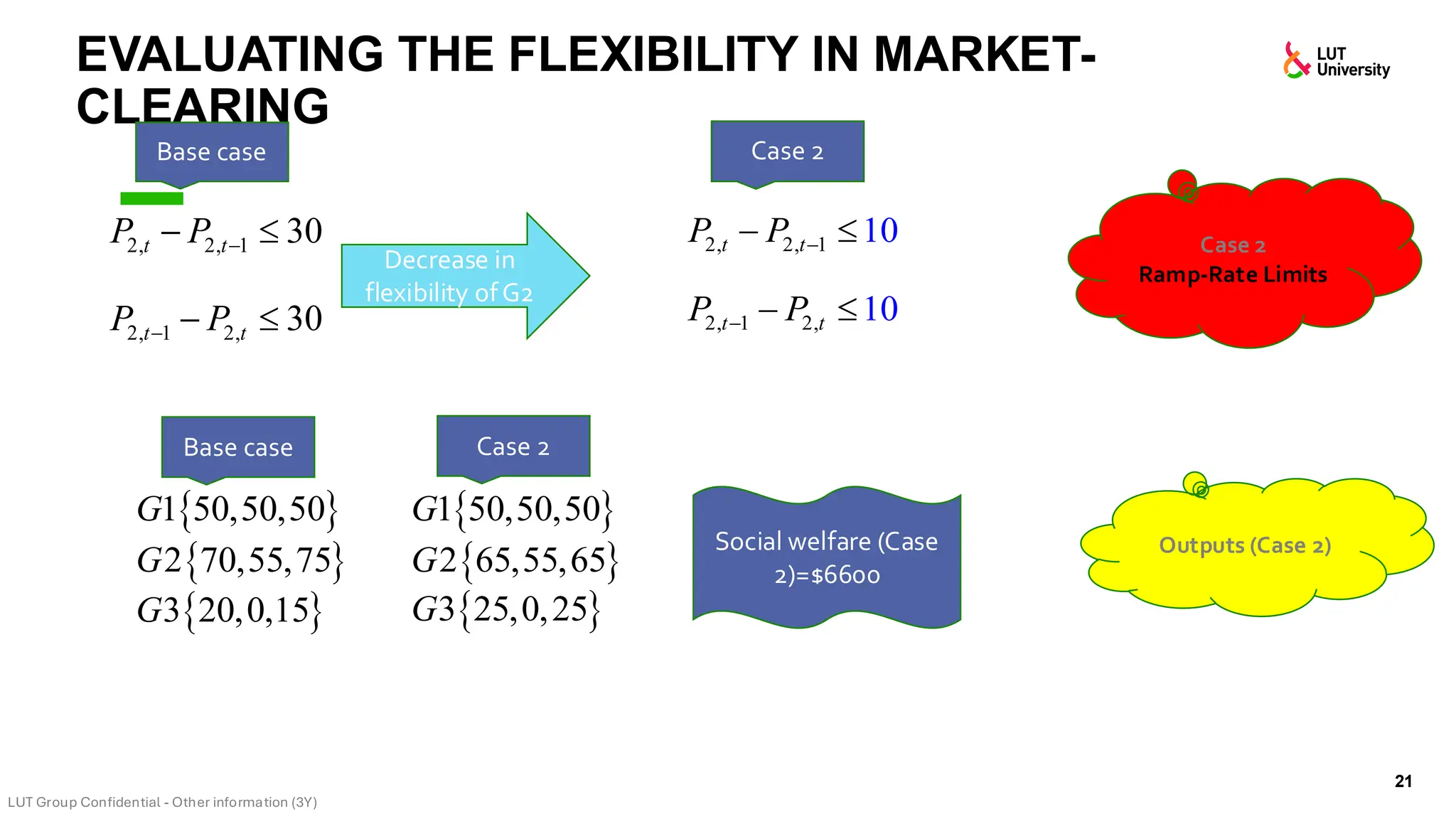
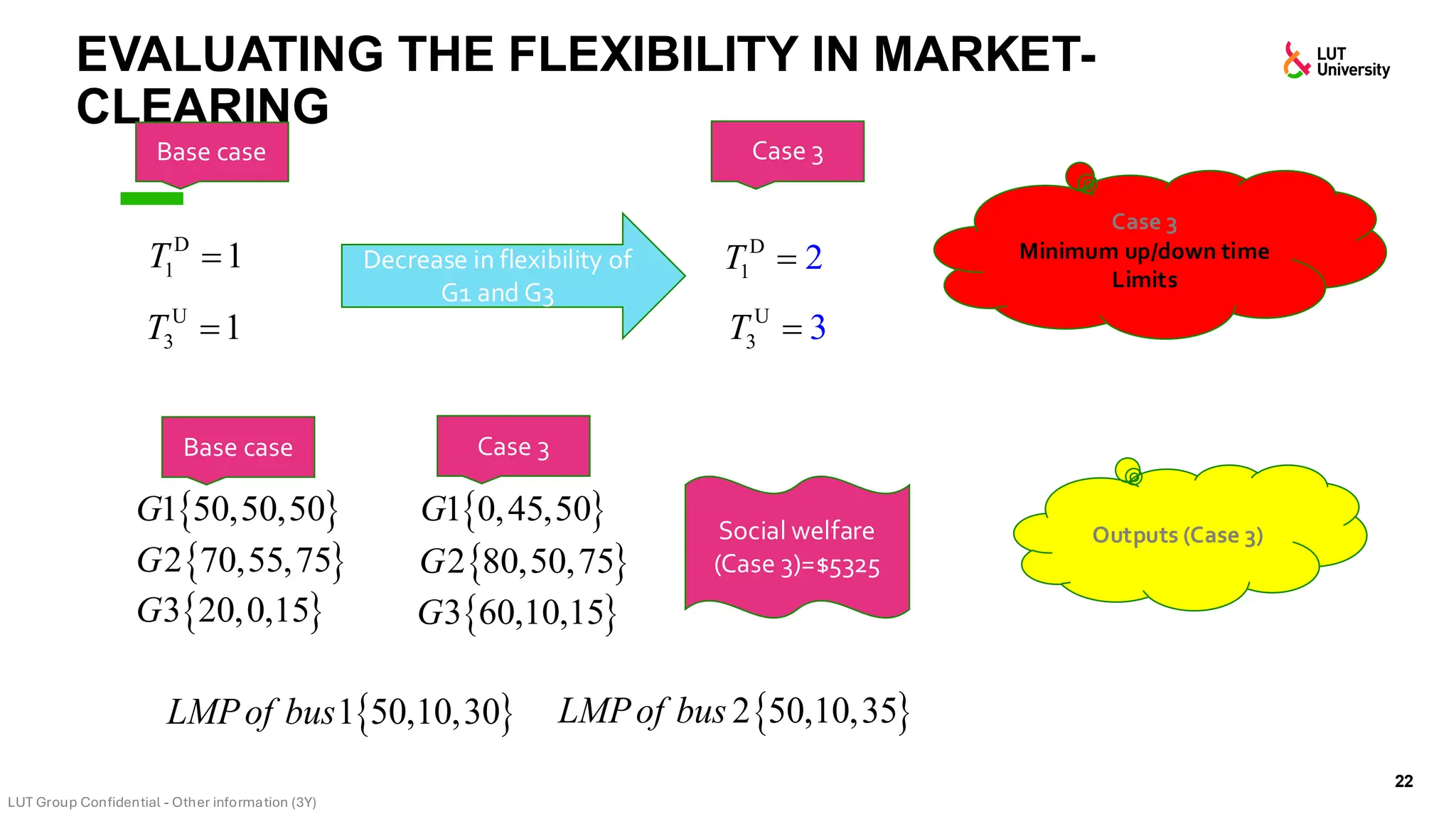
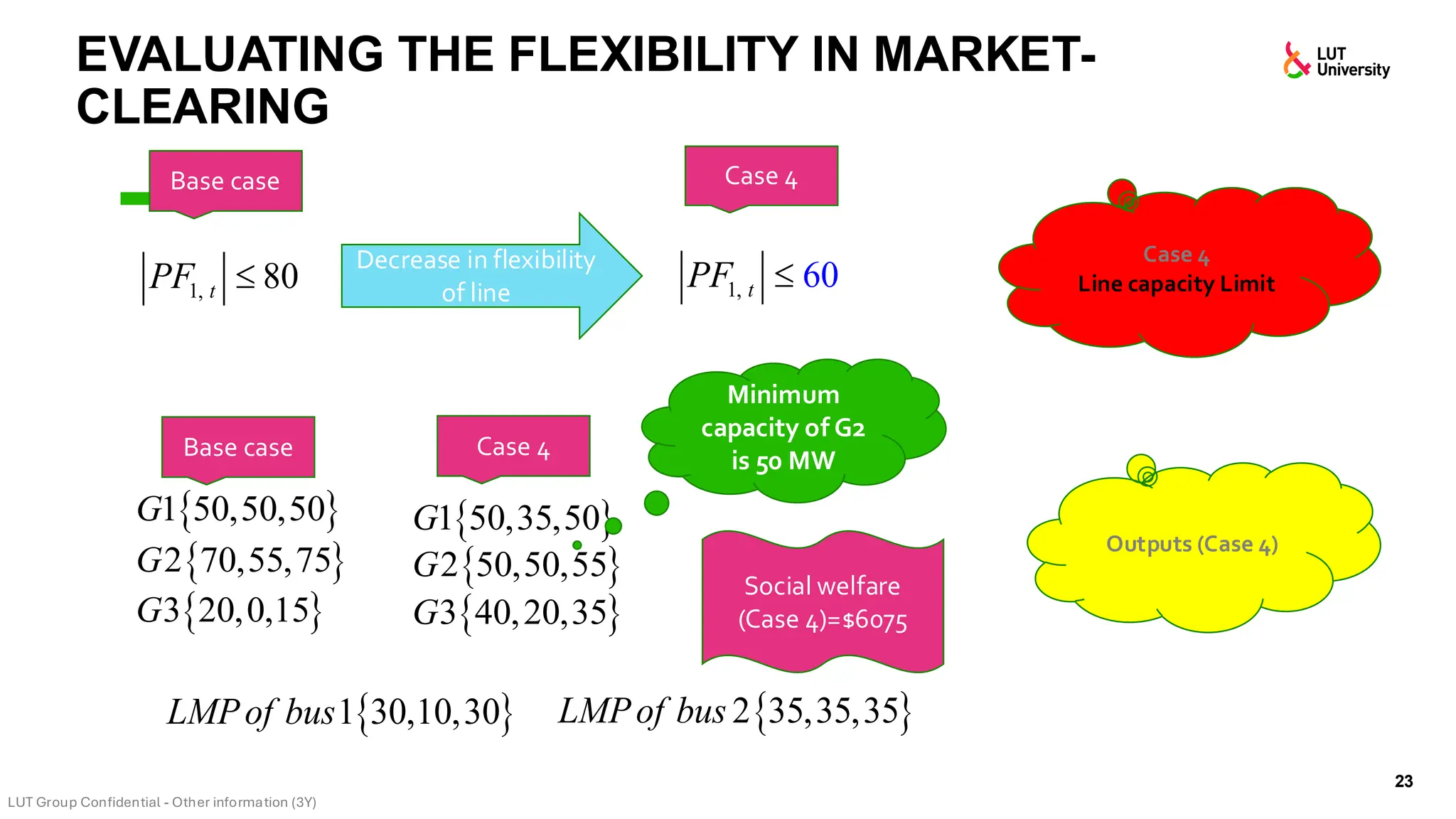
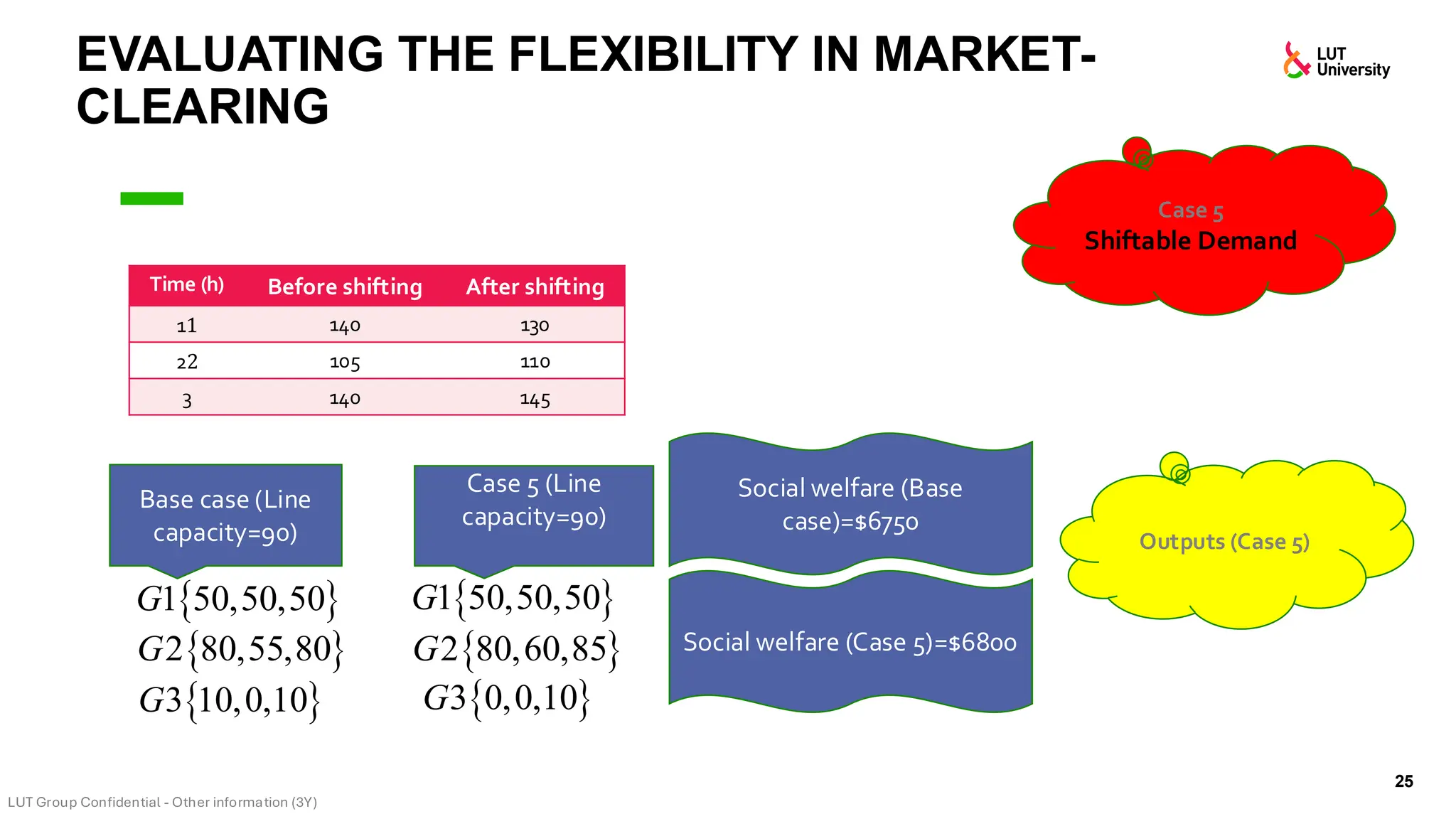
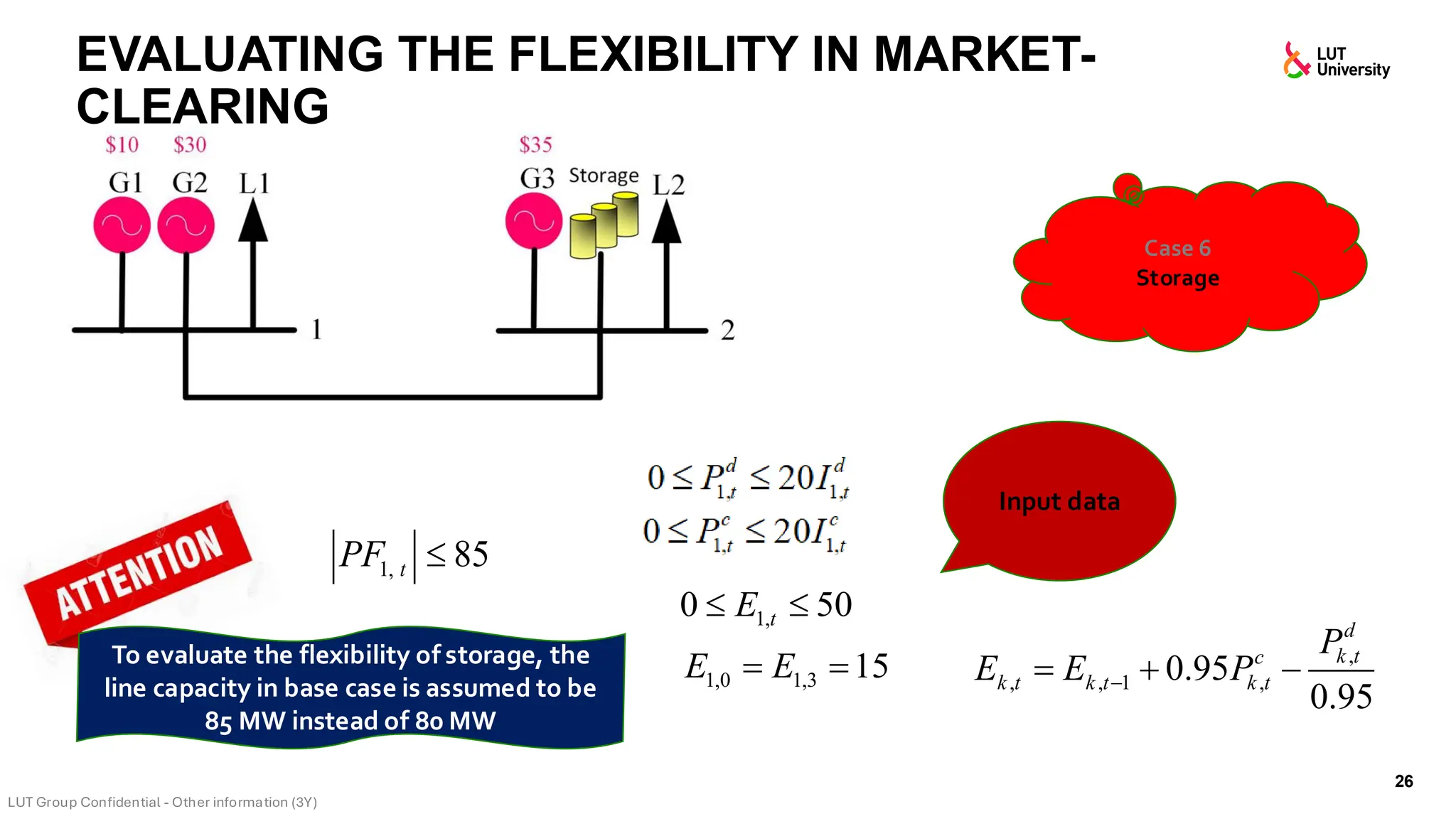
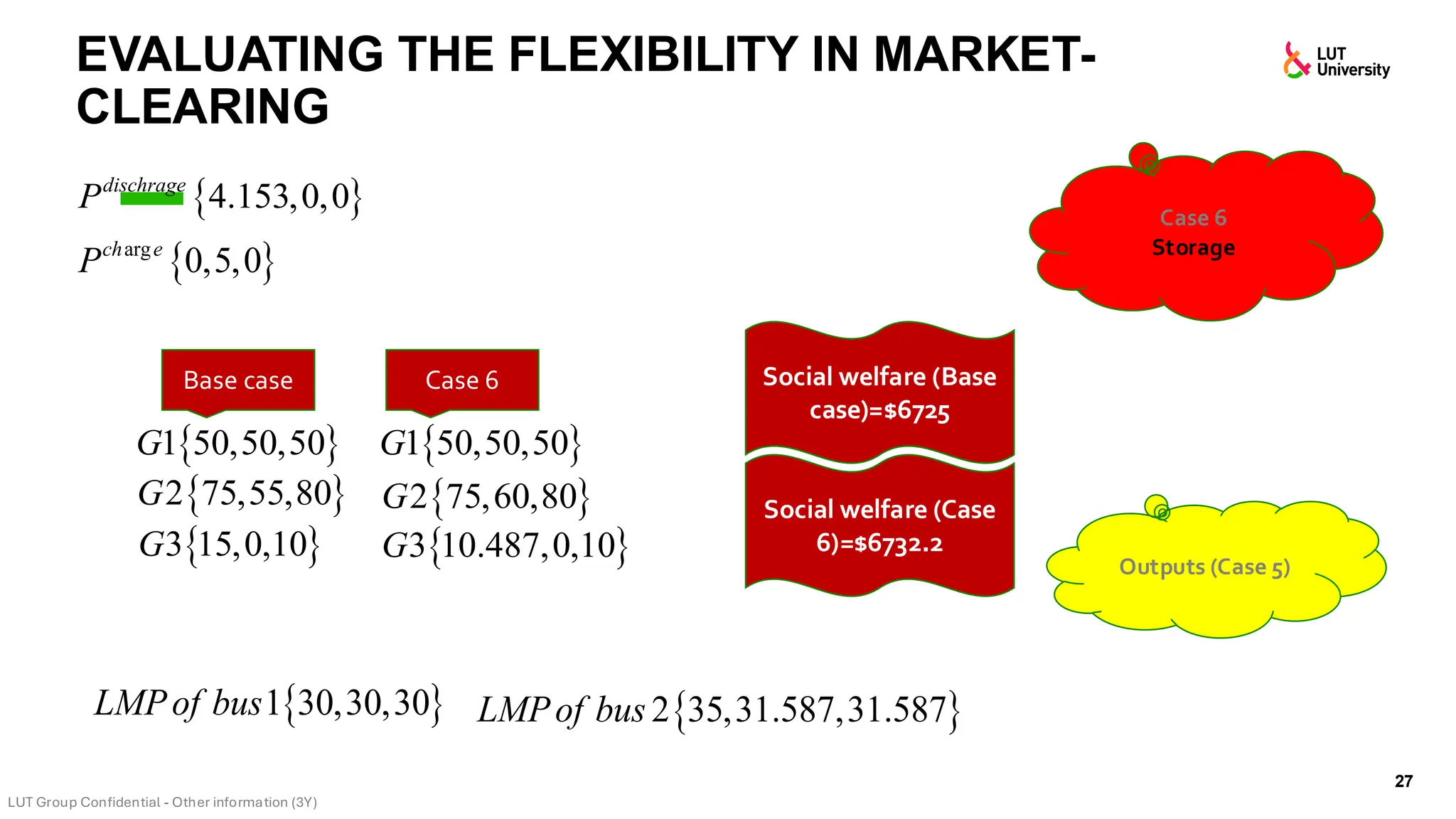
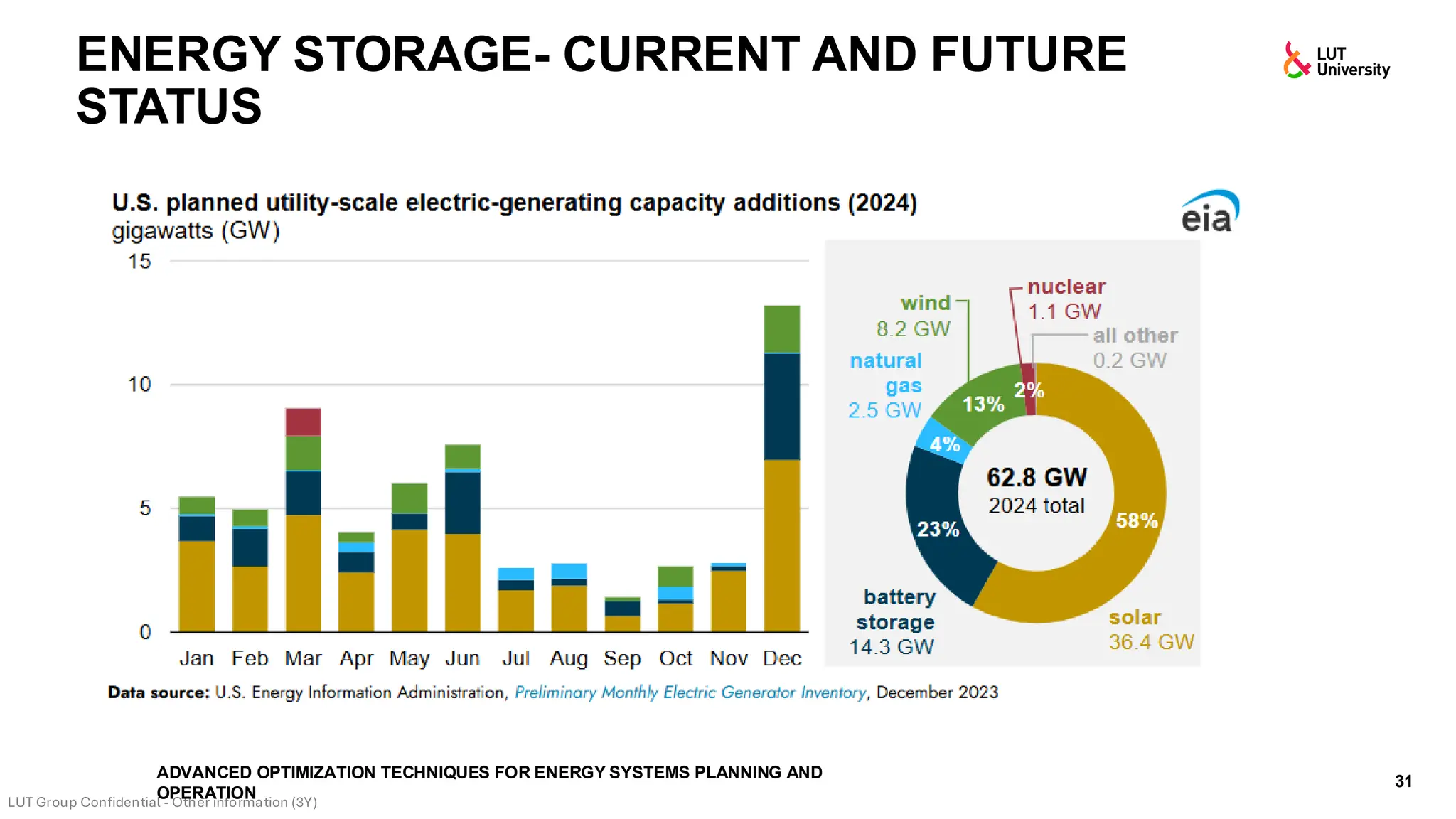
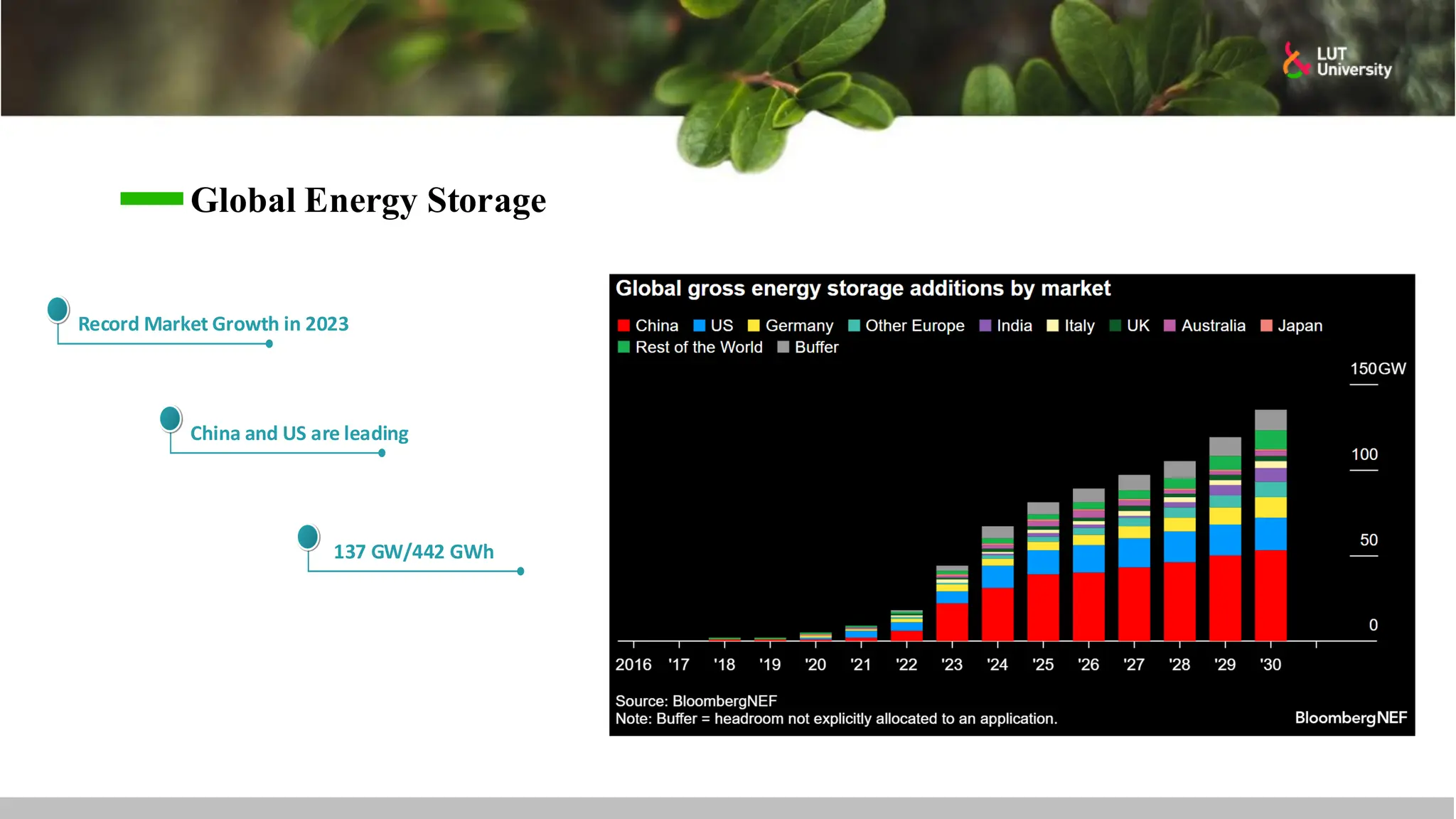
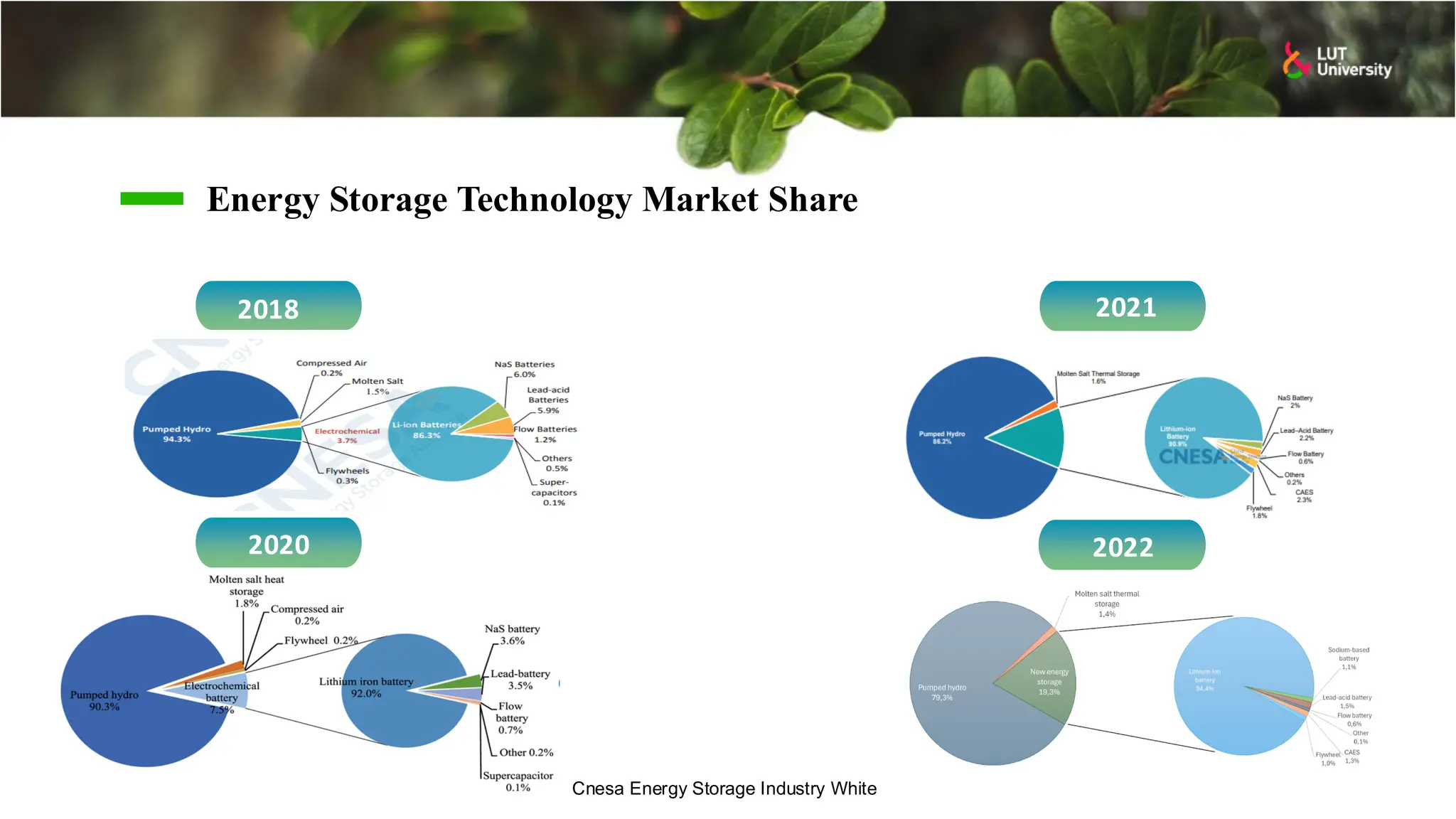
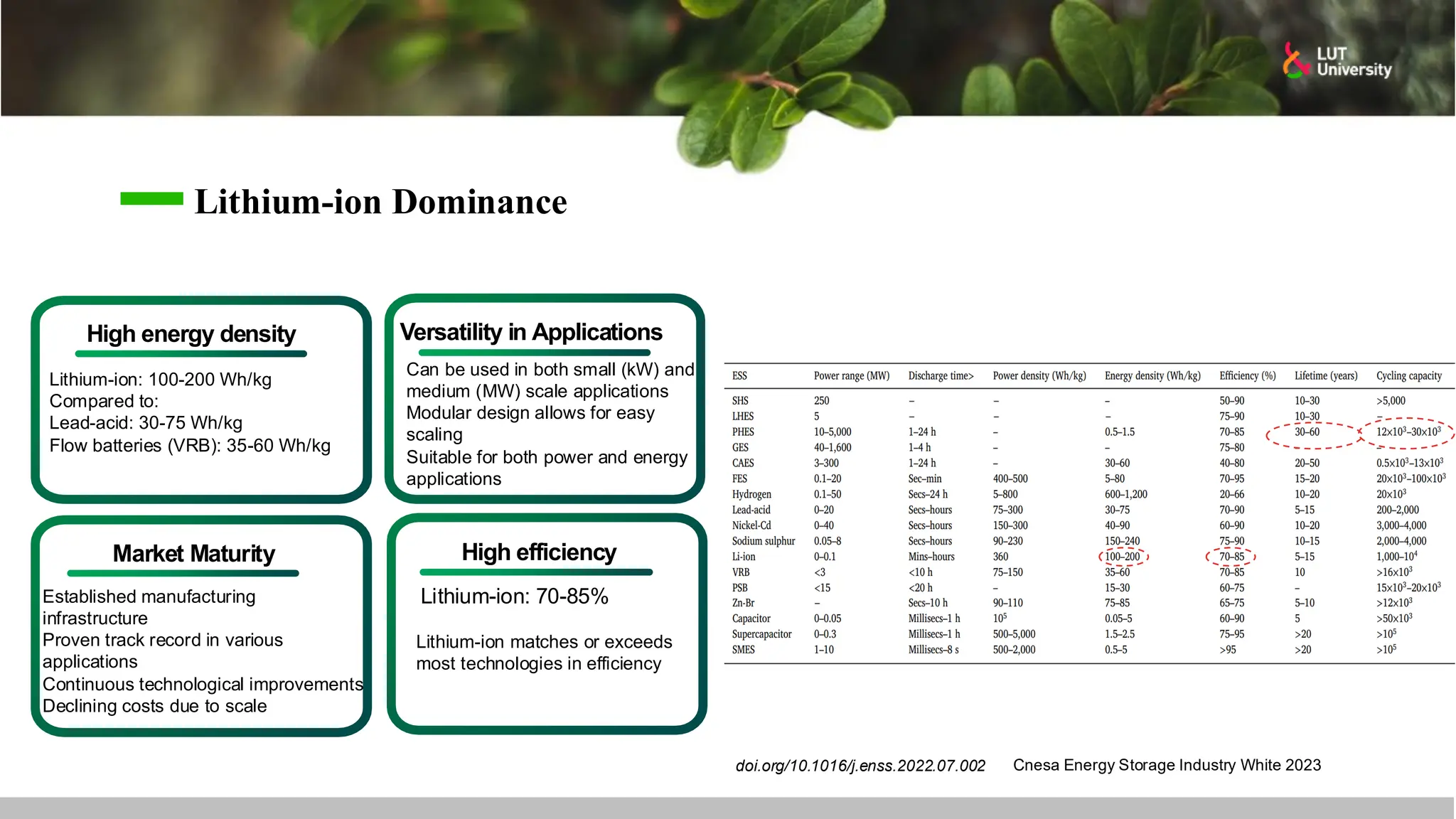
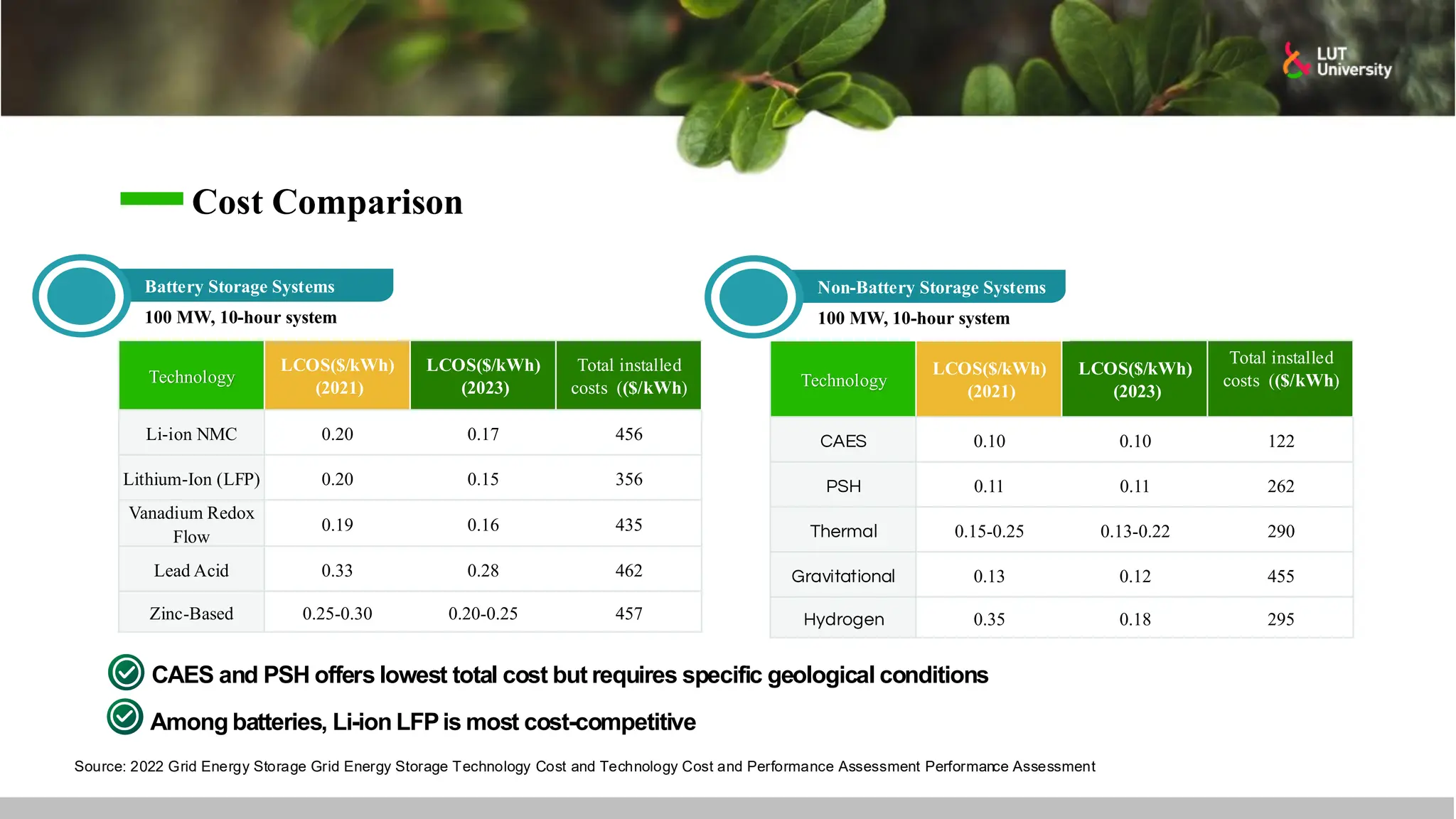
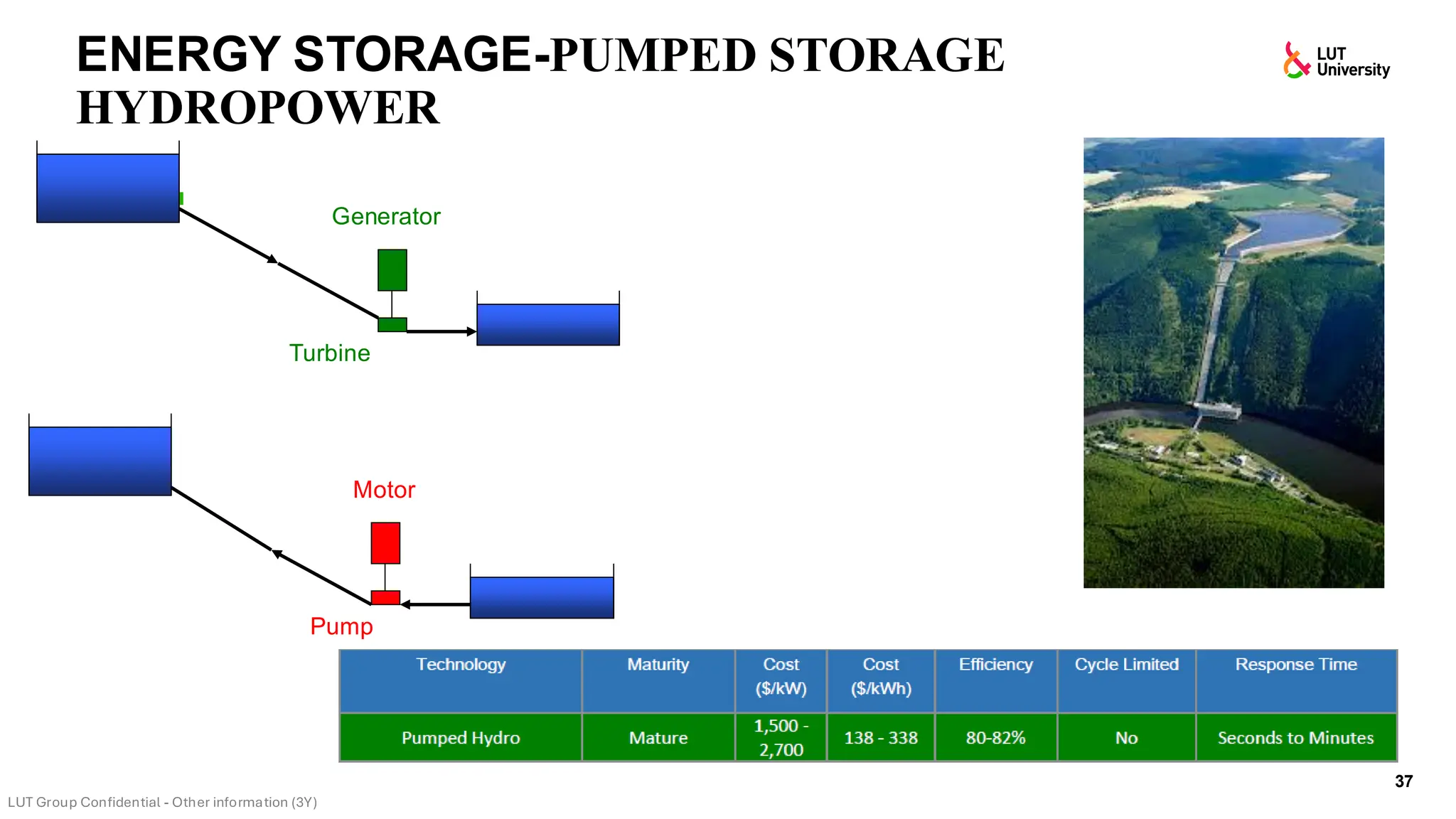
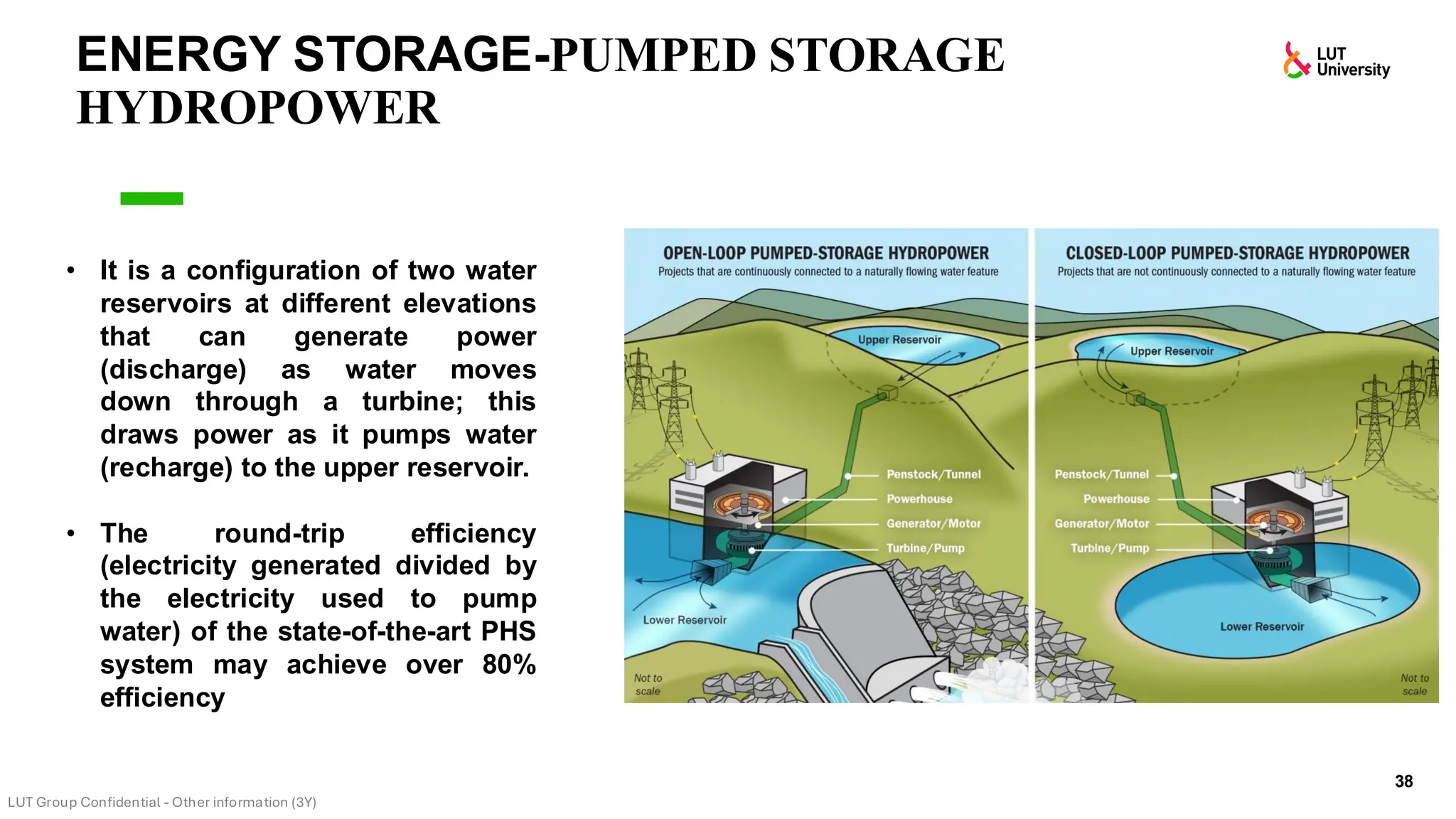
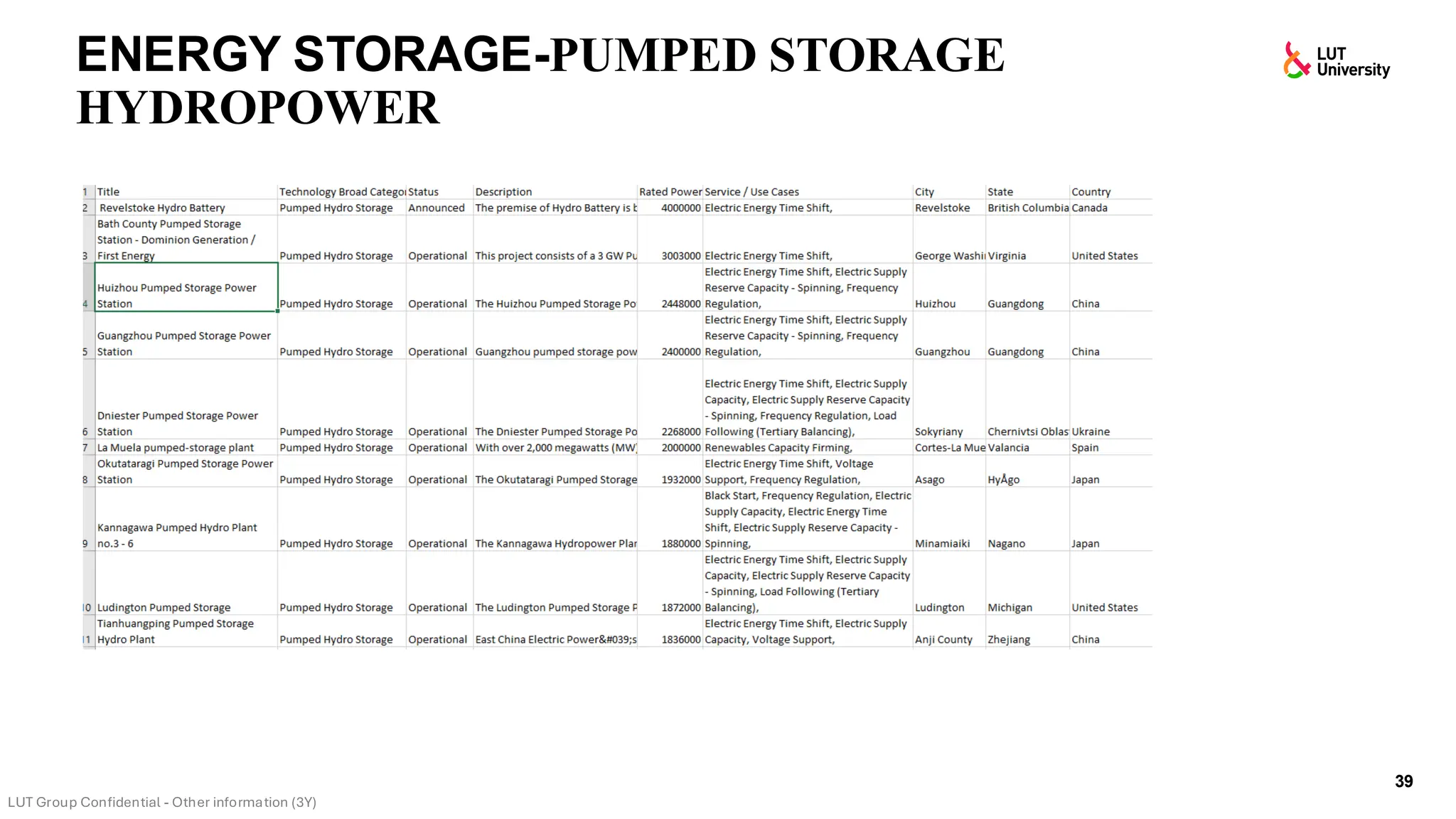
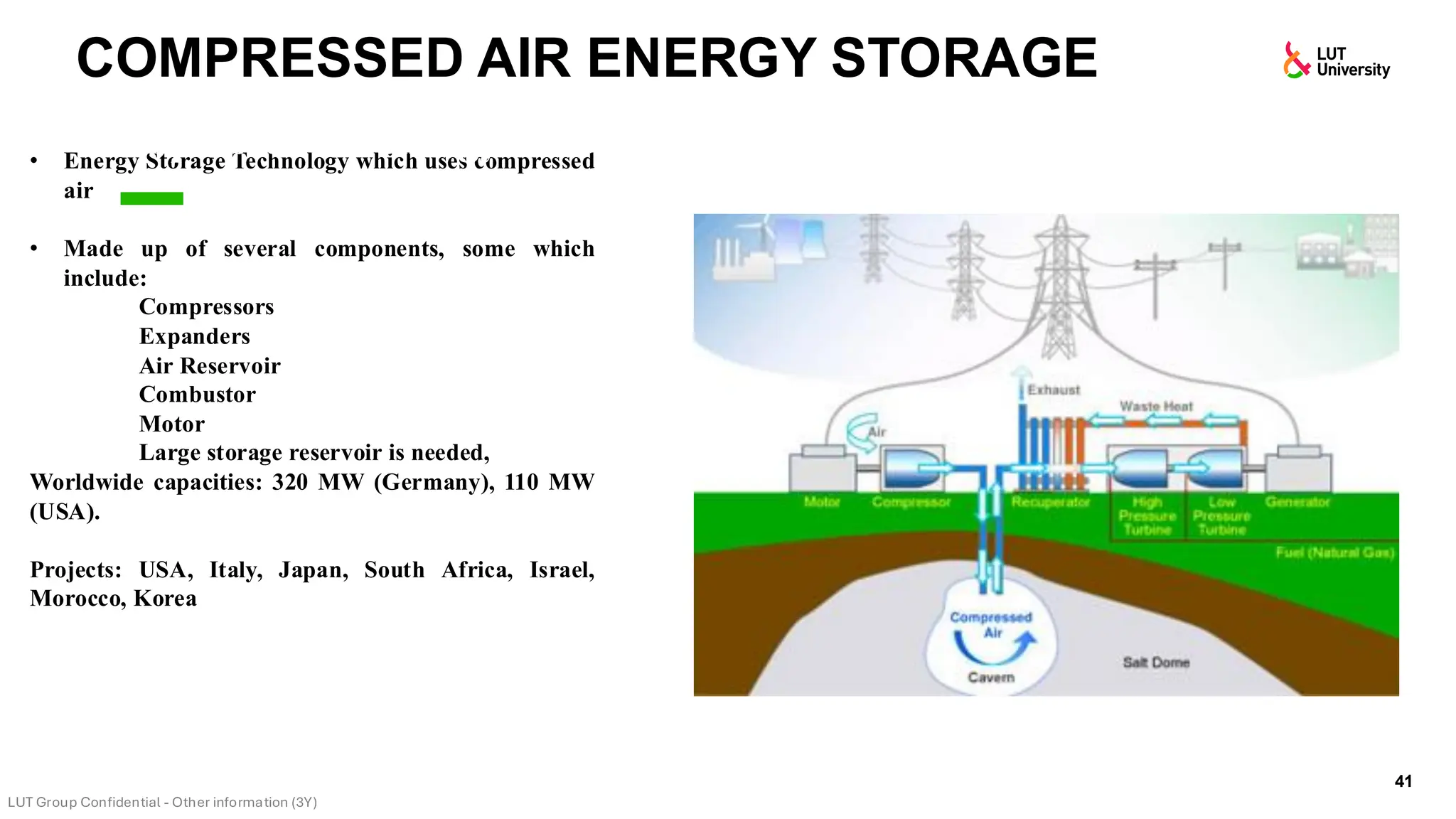
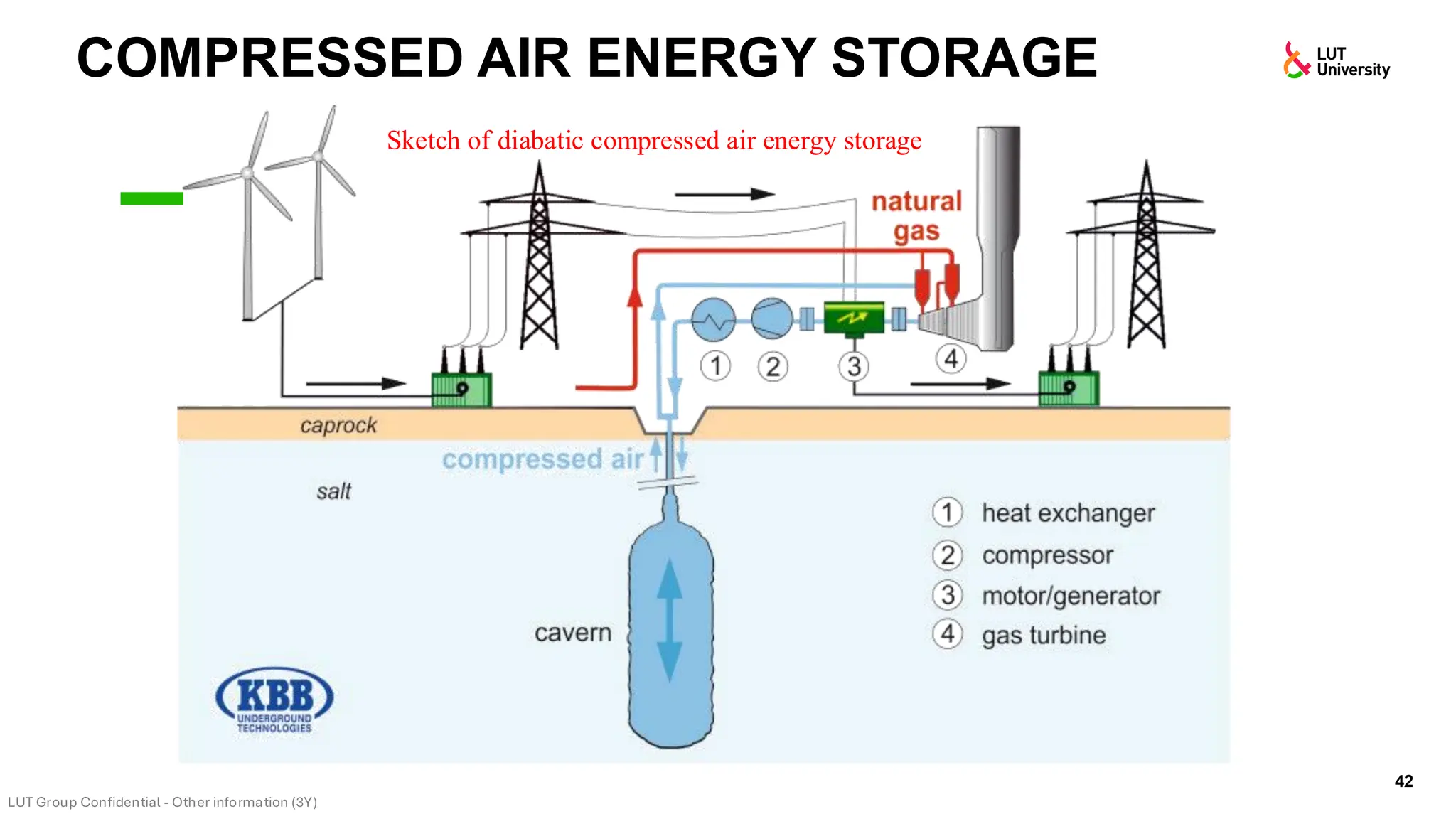
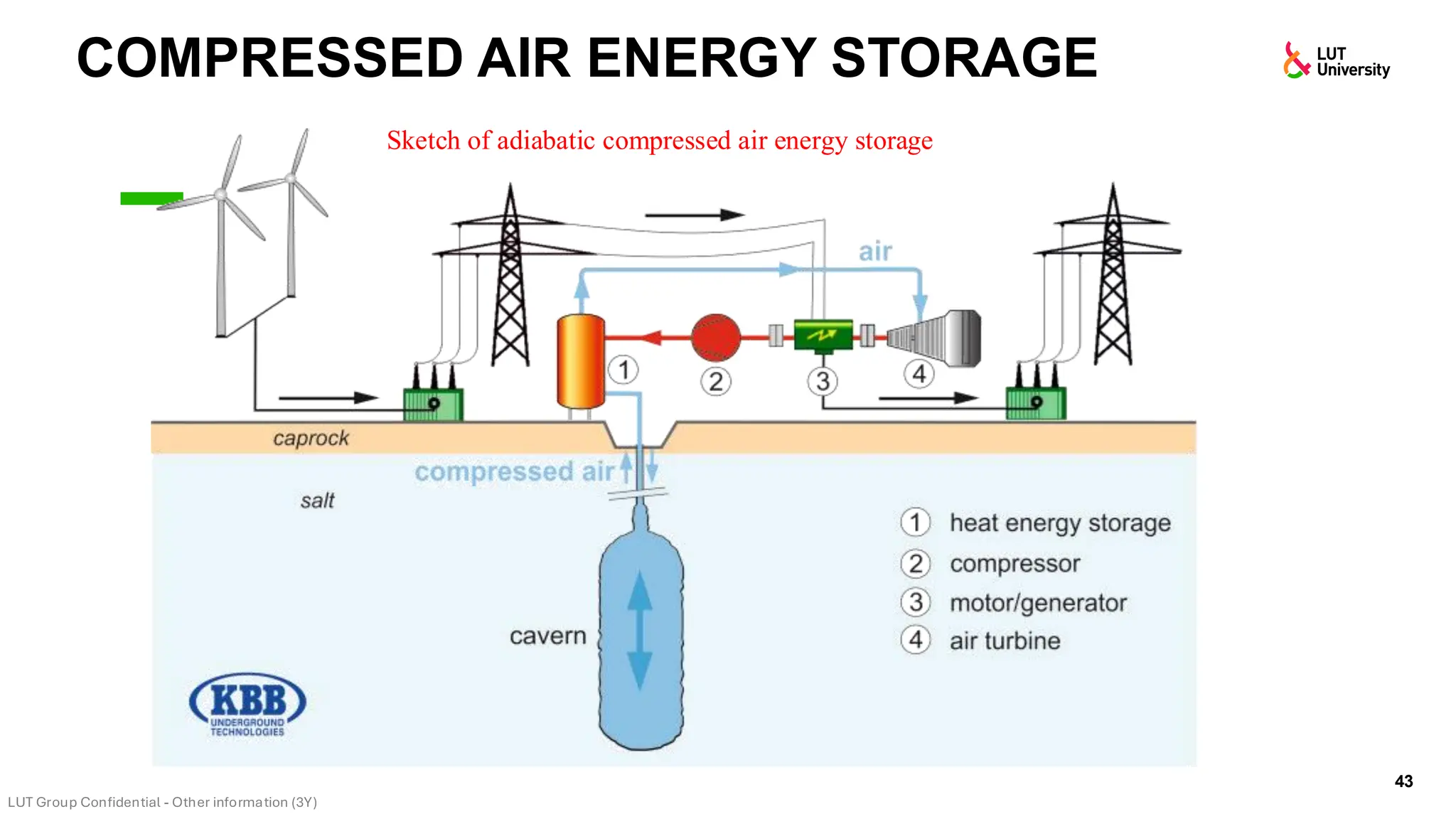
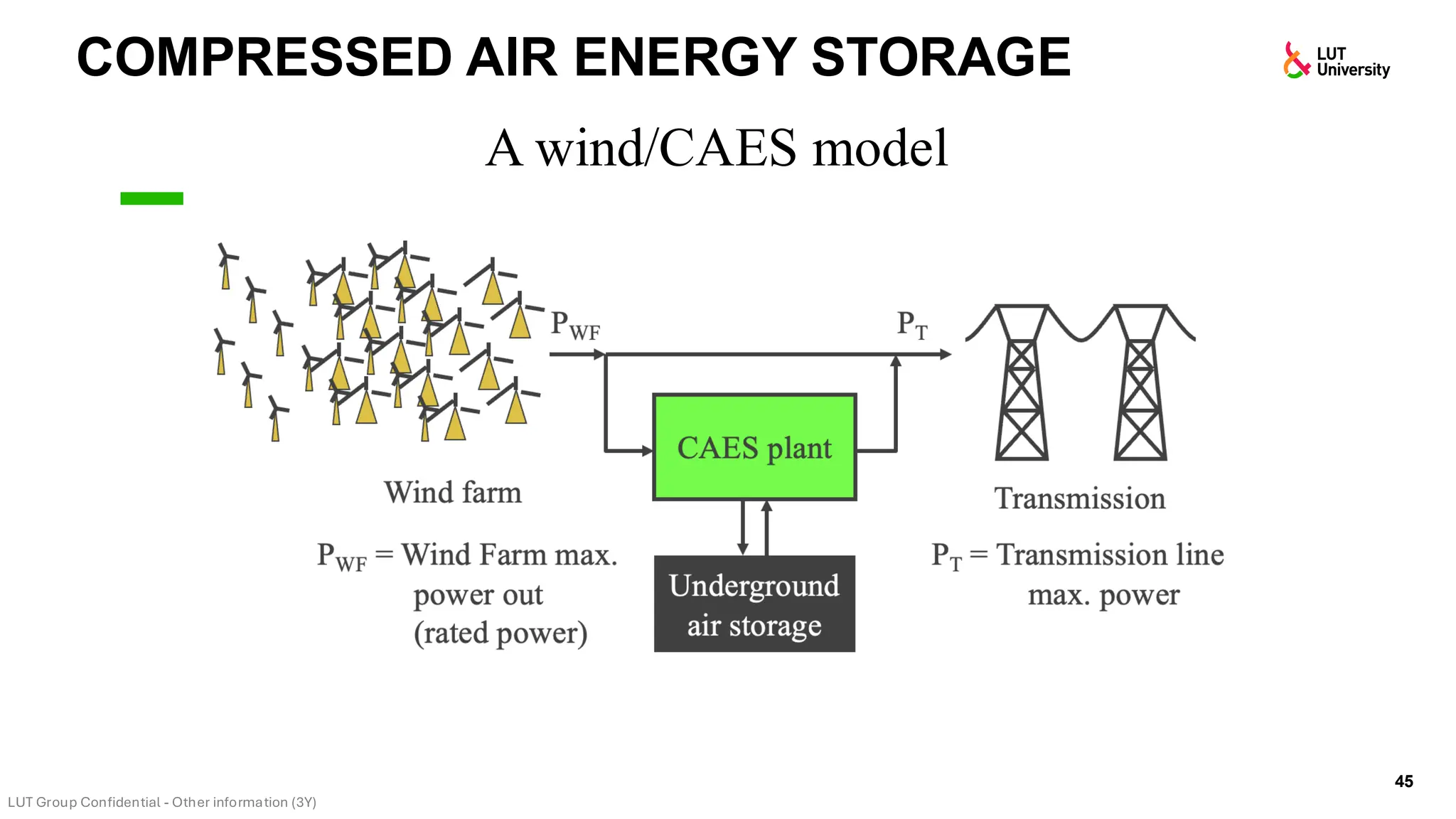
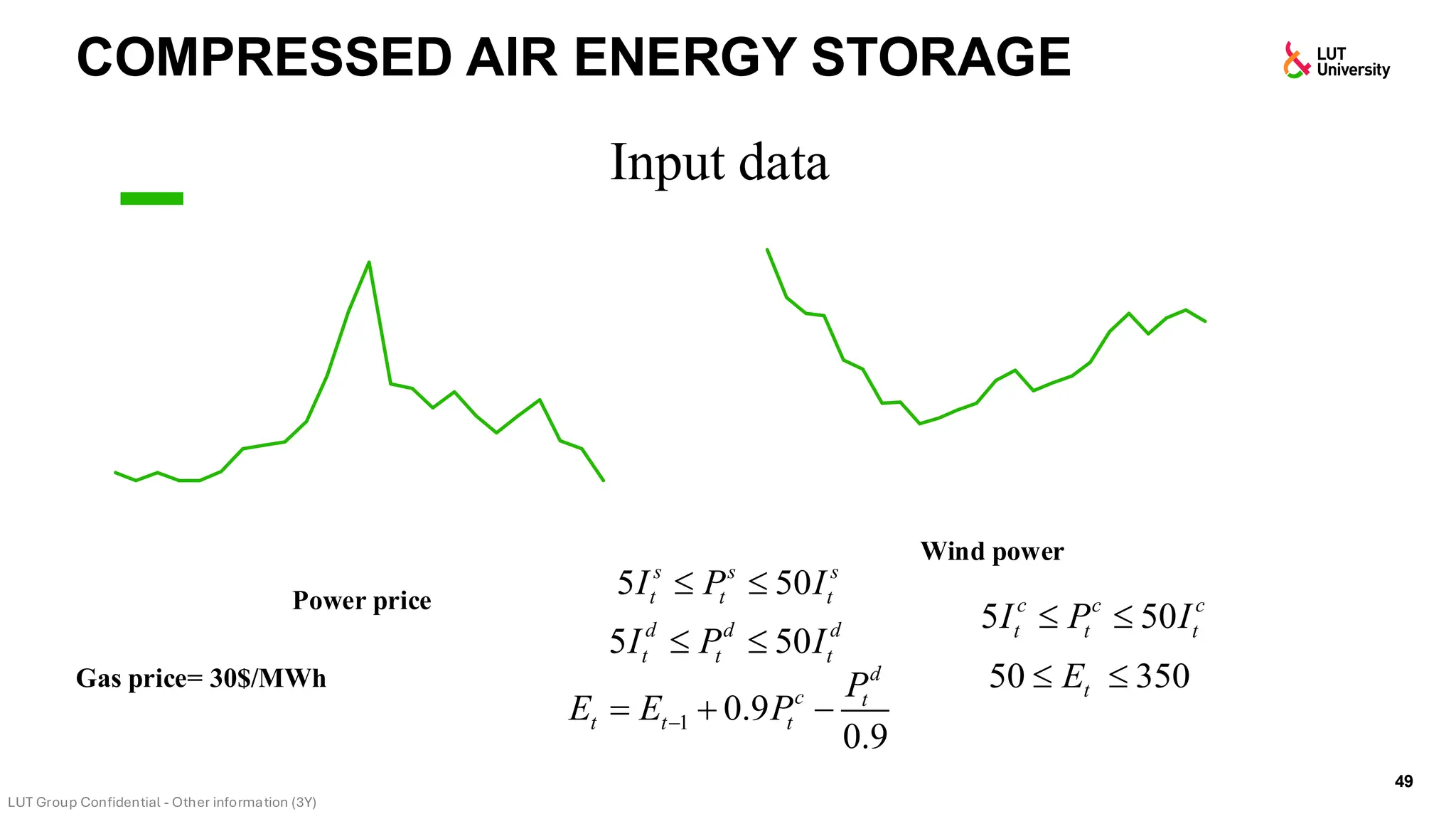
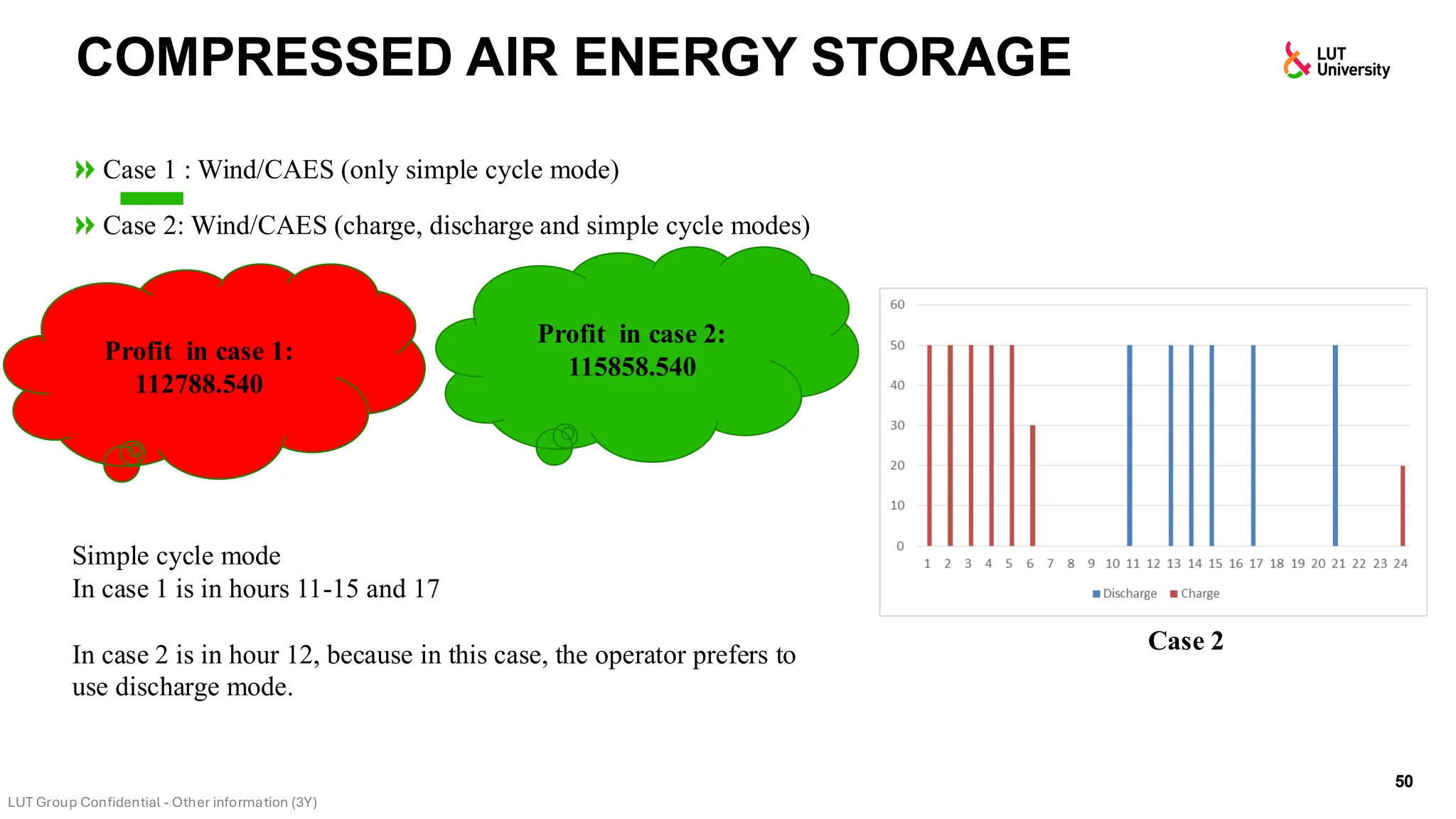
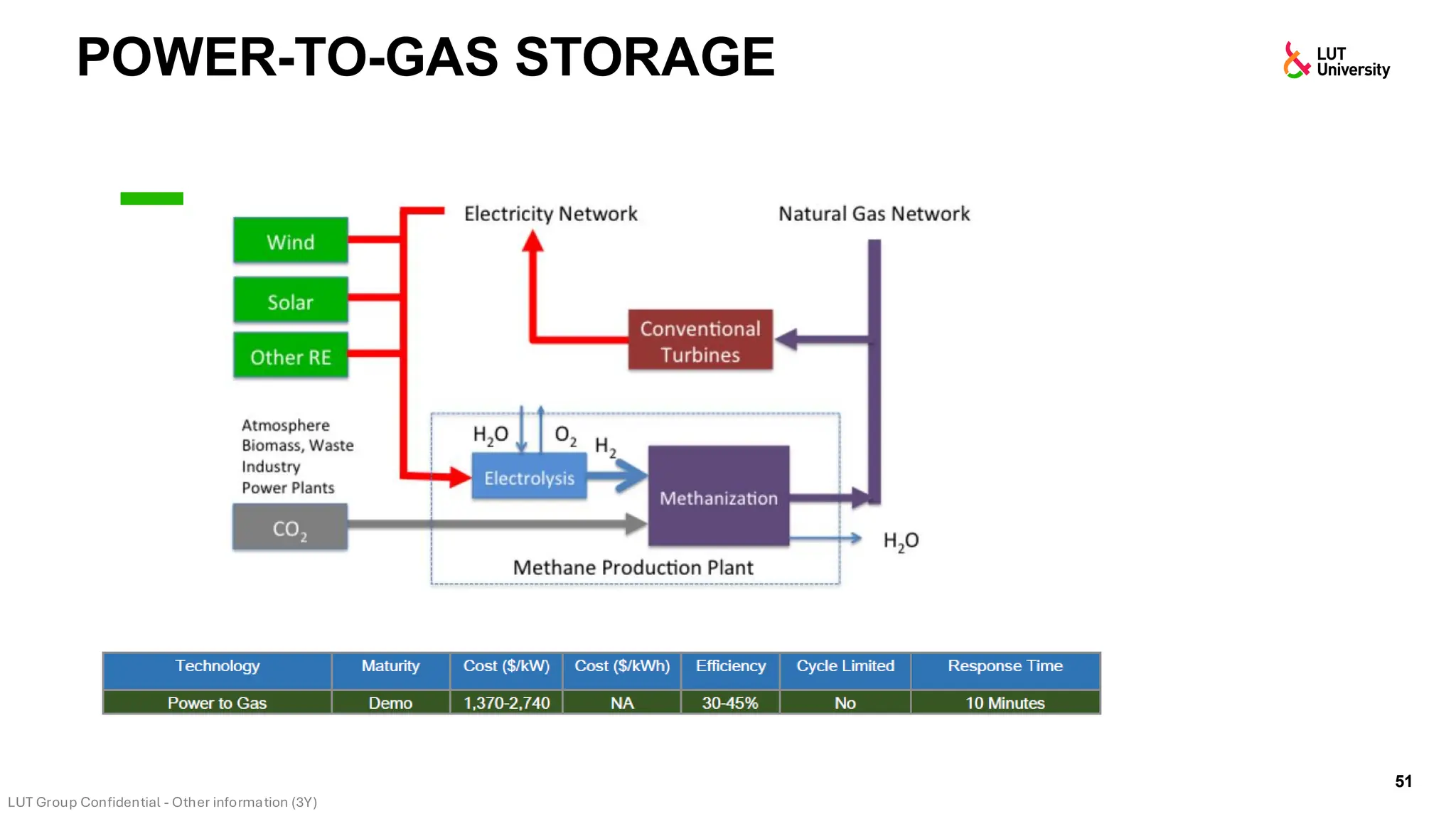
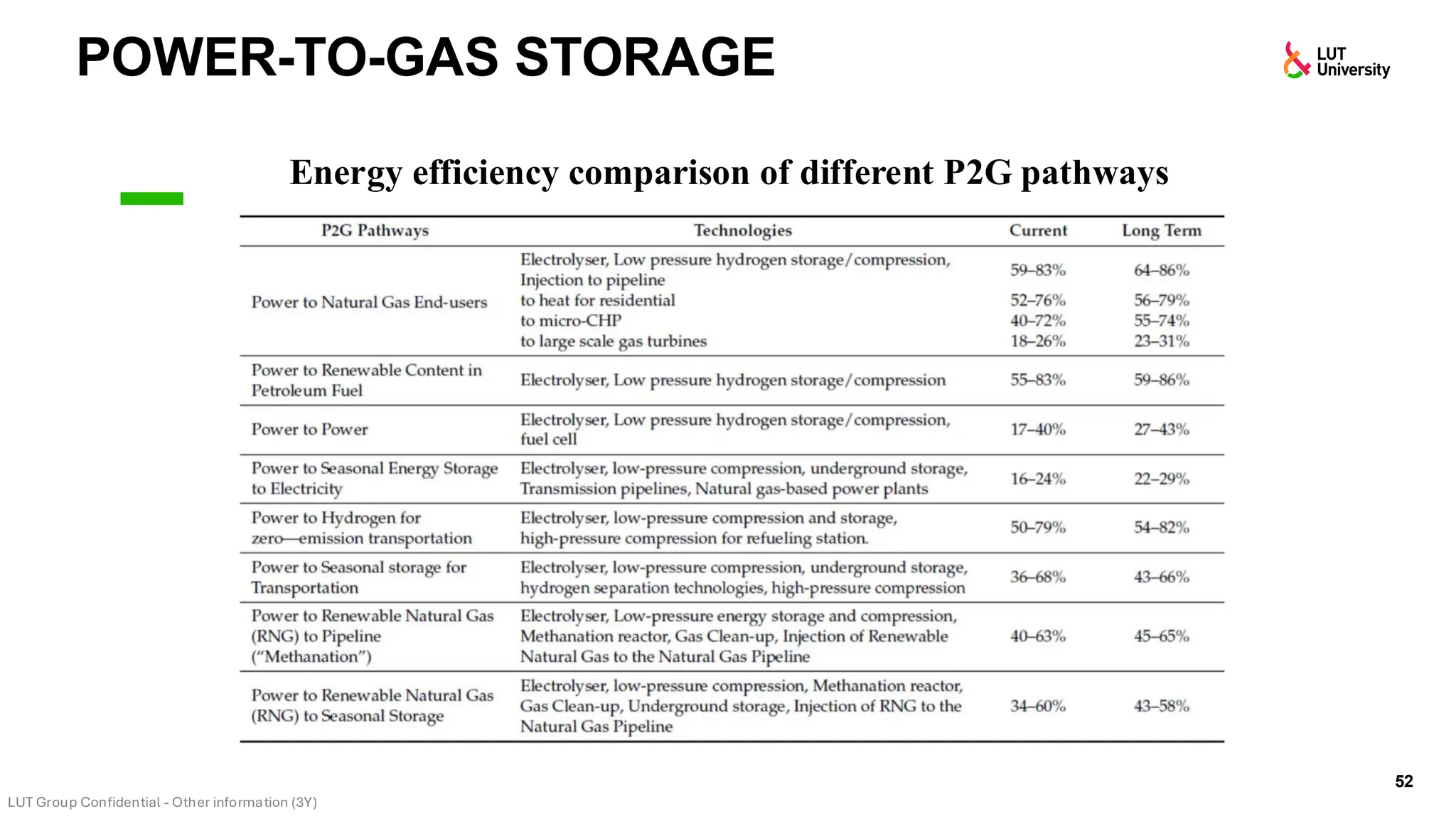
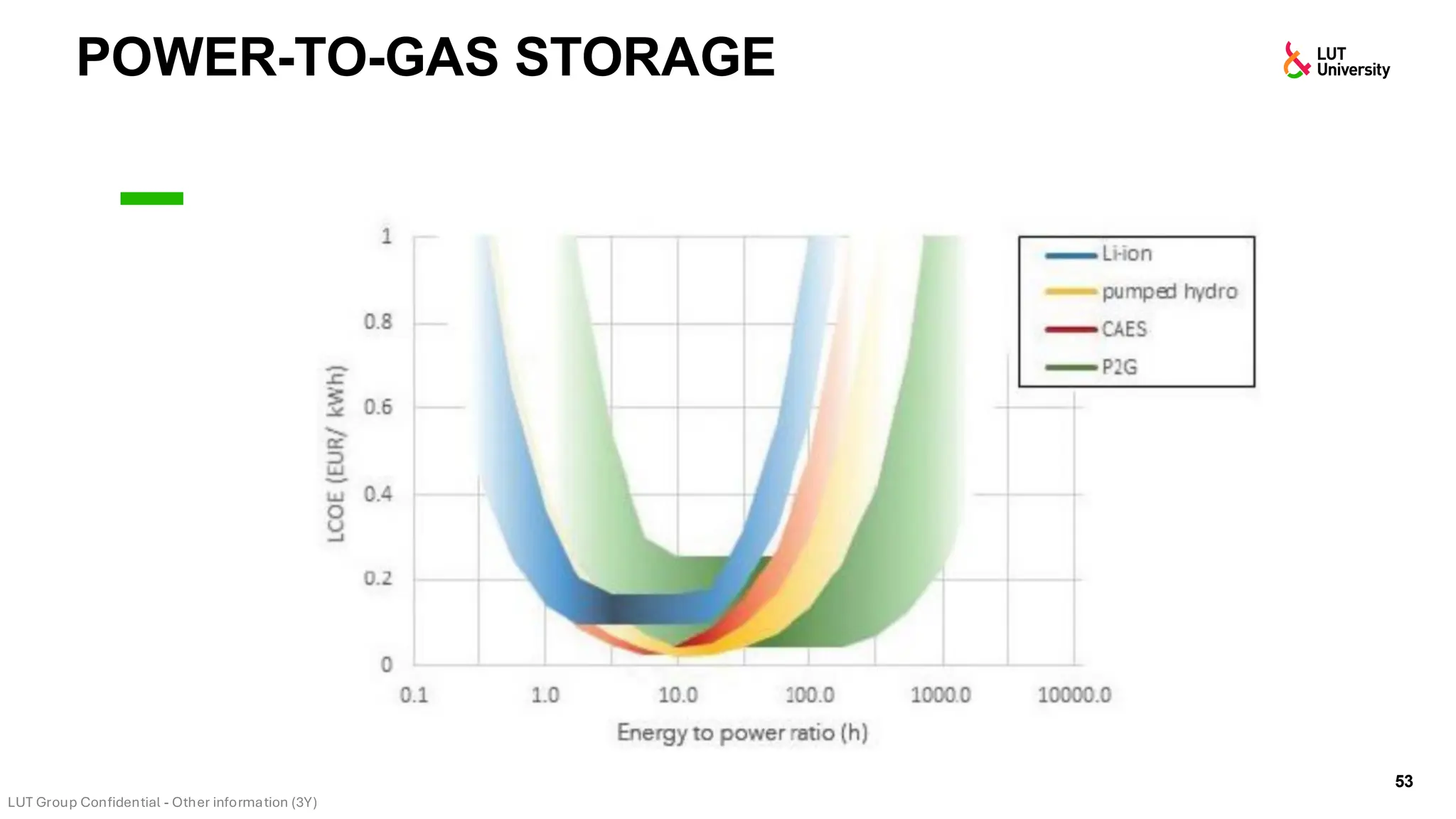
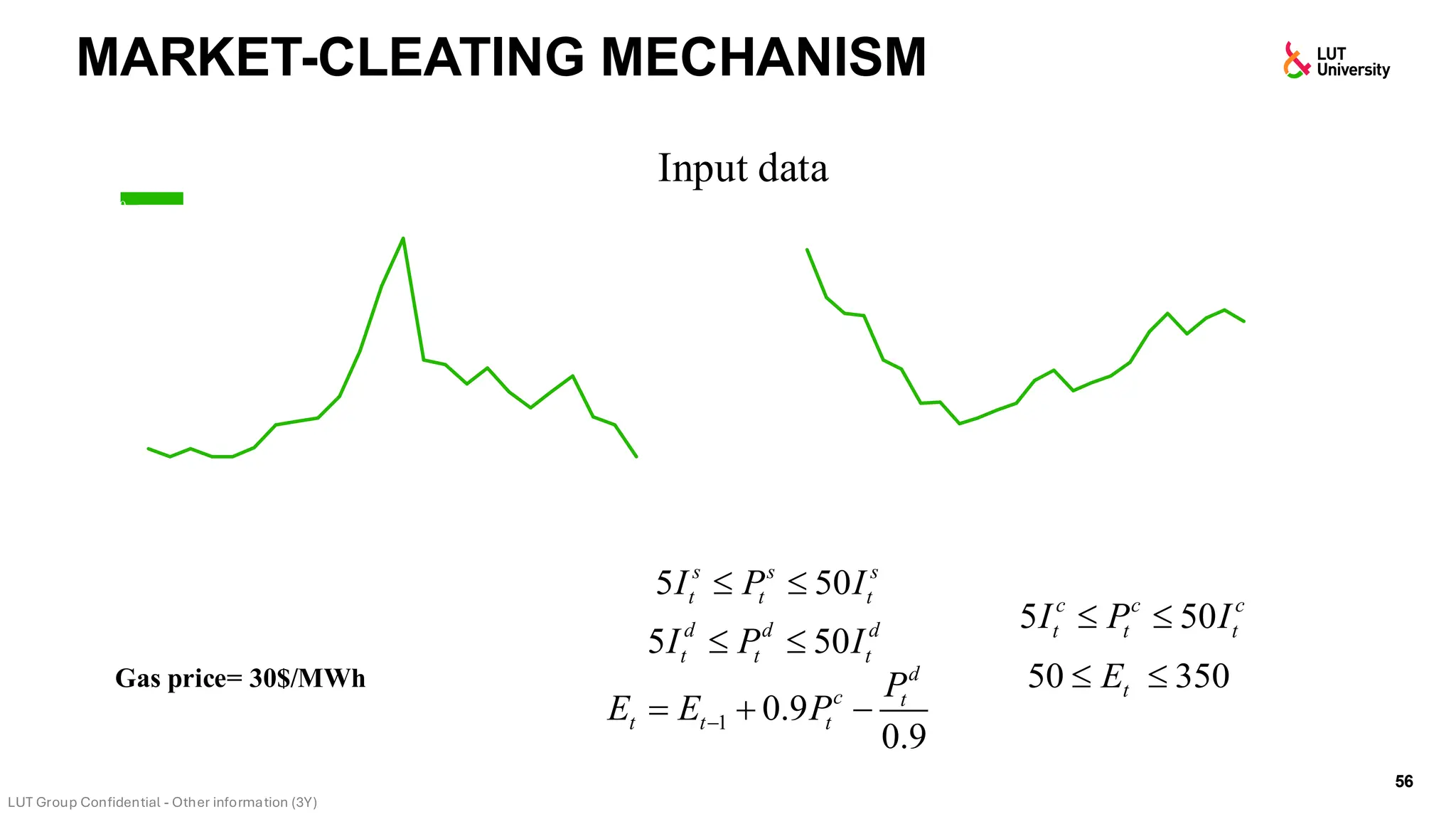
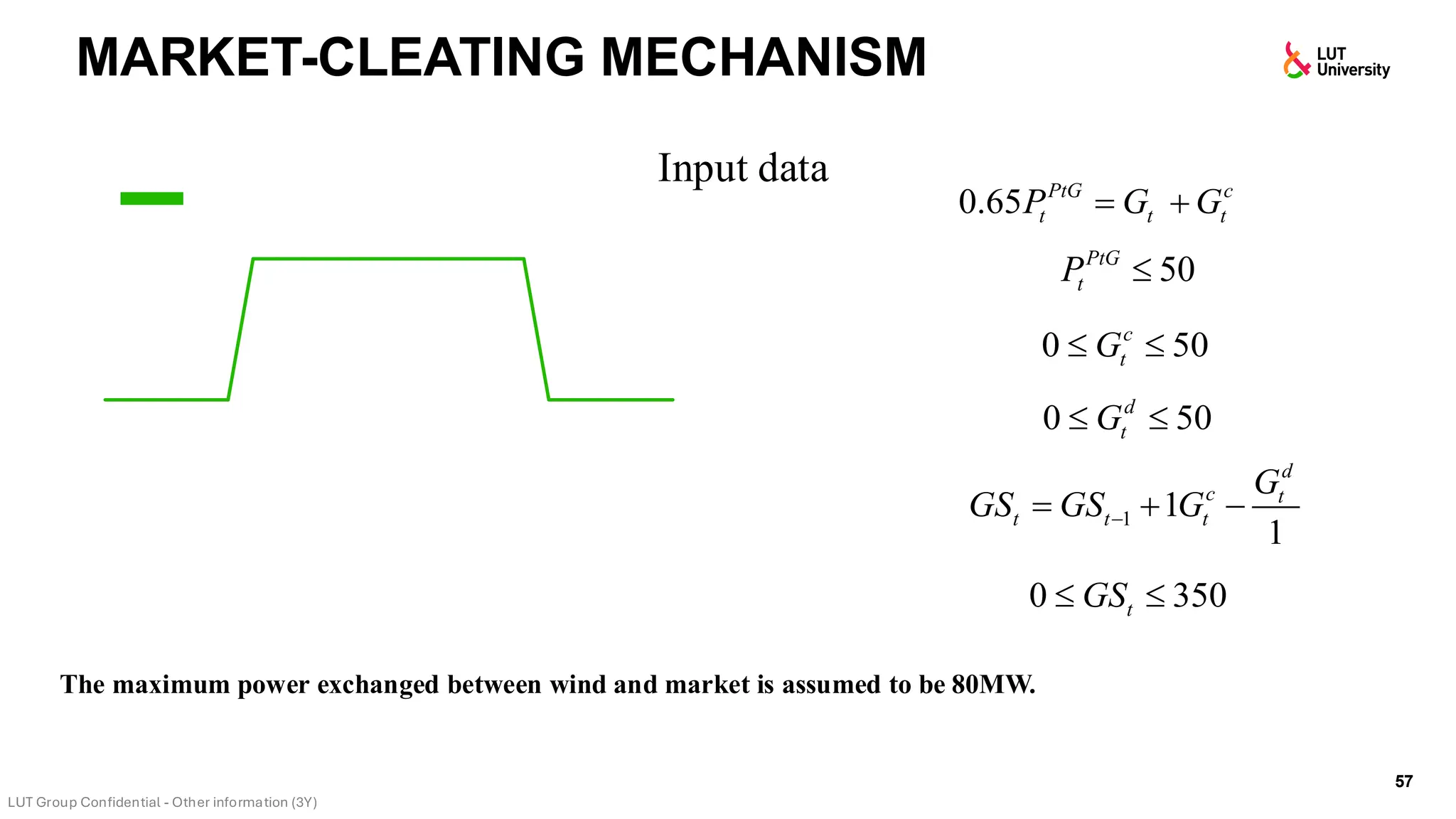
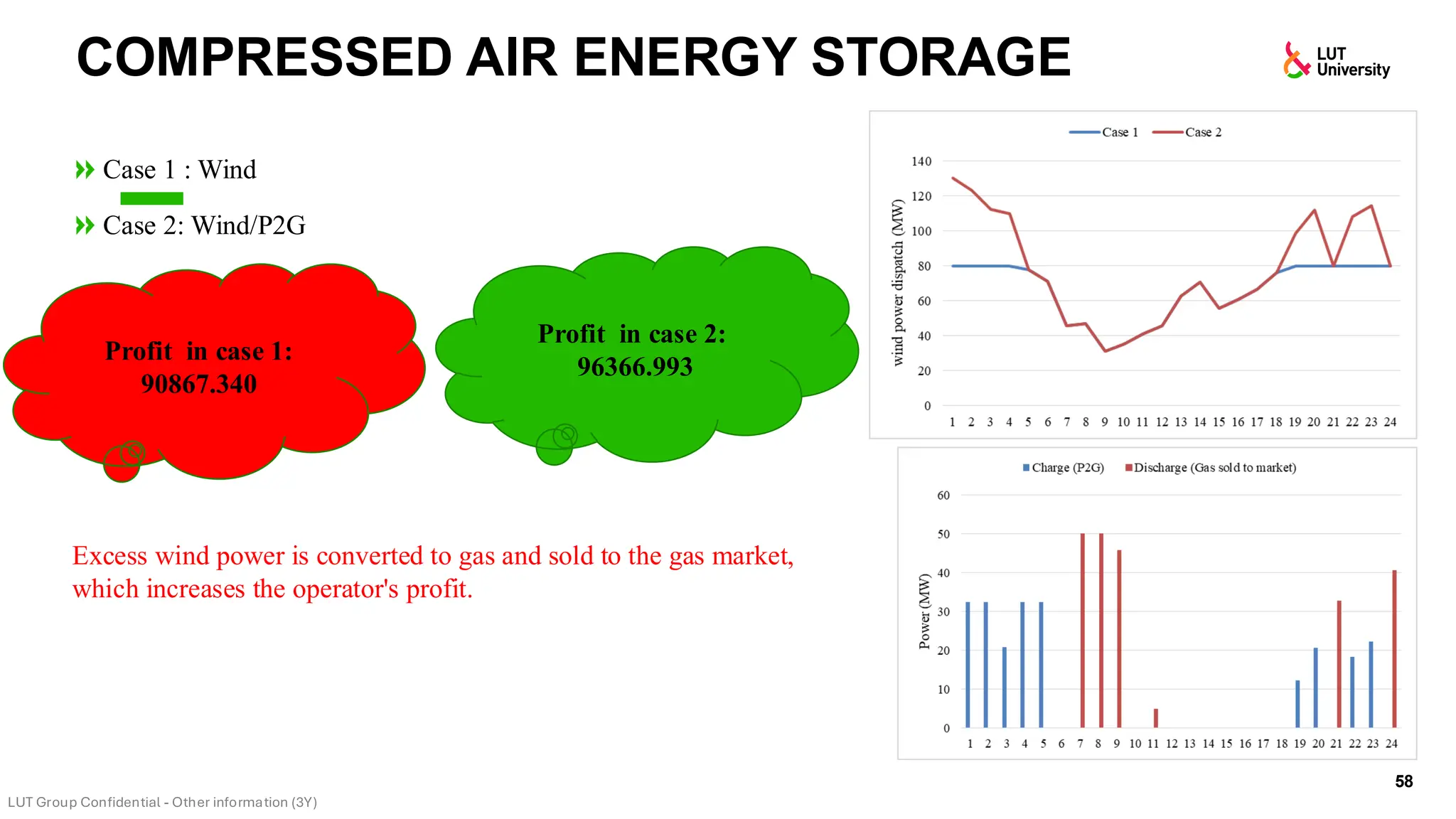
This slide-deck is a concise walkthrough of why high renewable penetration creates operational challenges (e.g., net-load “duck curve” flexibility needs and increasing curtailment), and how power systems respond through flexibility from the supply side, demand side, storage, and transmission. It introduces key operational optimization problems like (network-constrained) unit commitment, highlights the explosion of complexity with larger networks, and frames market-clearing as social welfare maximization with practical constraints (capacity, ramping, min up/down time, reserves, and power flow). The deck then uses step-by-step case studies to show how tightening/relaxing constraints (generator limits, ramps, min up/down time, line capacity) and adding shiftable demand or storage changes dispatch outcomes, prices, and welfare.
![[2020.2] PSOC - Unit_Commitment.pptx](https://cdn.slidesharecdn.com/ss_thumbnails/2020-230328034214-f9eb2e64-thumbnail.jpg?width=640&height=640&fit=bounds)
Generation and Storage Modeling Presentation
- 1. GENERATION AND STORAGEMODELING Prof. Behnam Mohammadi-Ivatloo LUT University
- 3. RENEWABLE ENERGY INTEGRATION- CHALLENGES 3 27November 2024 Source: Energy Information Administration, 2023 gigawatts Network requires an additional about 5 gigawatts of flexibility per hour during that period. Between approximately 6 in the morning and 10 in the morning, the demand decreases from 15 gigawatts to 5 gigawatts Network requires an additional about 1 gigawatts of flexibility per hour during that period. Network requires an additional about 5 gigawatts of flexibility per hour during that period. Net Load of California
- 4. RENEWABLE ENERGY INTEGRATION 4 27November 2024 Curtailments of solar-powered electricity generation have increased in the California Independent System Operator (CAISO) region, the part of the electric grid that covers most of the state. Novan K, Wang Y. Estimates of the Marginal Curtailment Rates for Solar and Wind Generation
- 5. ➢ Unit commitmentproblem is one of the key application in power system operation in a deregulated electricity market, UC is used by the independent system operator (ISO) for market clearing, reliability assessment and intra-day operations. ➢ Gencos are using PBUC to determine biding strategy. UC is applied for cost minimization in an integrated utility operation environment. ➢ The variables of UC is the commitment status and generation dispatch of various generating units satisfying system-wide considering load balance and specific unit constraints such as: Capacity and ramping limits Example of power system complexity: Network constrained Unit Commitment (NCUC)
- 6. 6 Objective function Minimizeoperation cost S.t: * Maximum/ Minimum power generation * Minimum up/ down time * Ramp rate in continuous times * Start up/ shut down state * AC power flow * Reserve requirements NCUC is an optimization problem as following: Example of power system complexity: Network constrained Unit Commitment (NCUC)
- 7. Solving the presentedproblem with a lot of variables is so difficult. Increasing the complexity of the problem with increasing network size. For example 24- hours scheduling for 6, 24 and 118-bus IEEE test system: 6-Bus 24-Bus 118-Bus 254 − 1 24 = 23 − 1 24 = 1.9115 × 1020 226 − 1 24 = 6.96 × 10187 Example of power system complexity: Network constrained Unit Commitment (NCUC)
- 8. GENERATION MODLEING 8 Flexibility inpower systems • According to the International Energy Agency, the flexibility of a power system refers to "the extent to which a power system can modify electricity production or consumption in response to variability, expected or otherwise". • Flexibility from the Supply Side • Flexibility from the Demand Side • Flexibility from Storage Availability • Flexibility from Enhancing the Transmission Network
- 9. FLEXIBILITY IN MARKET-CLEARING MECHANISM 9 Objectivefunction: Maximizing the Social welfare , , , , 1 1 1 1 NT NJ NT NI j j t i i t i t i t t j t i SF Max B L C P SU SD = = = = = − + + The higher the flexibility, the higher is the social welfare. 𝑡,𝑗, 𝑖 Index of time periods, electric demands and power plants 𝑆𝐹 Social welfare 𝐵𝑗 Surplus benefit 𝐶𝑖 Marginal cost of power plants. It is assumed that the market is fully competitive 𝐿𝑗,𝑡 Supplied demand 𝑃𝑖,𝑡 Dispatch power of power plants 𝑆𝑈𝑖,𝑡/𝑆𝐷𝑖,𝑡 Start-up/ shut-down cost Conejo, Antonio J., Carrión, Miguel, Morales, Juan M., “Decision Making Under Uncertainty in Electricity Markets”, Springer, 2010. ISBN 978-1-4419-7421-1. DOI: 10.1007/978-1-4419-7421-1
- 10. FLEXIBILITY IN SUPPLY-SIDE 10 Constraints: CapacityLimits P_i^min/P_i^ma x𝑃𝑖 max Min/max power generation of power plants The higher the value of 𝑃𝑖 max , the higher is the production range and thus higher the flexibility of production unit i. The lower the value of 𝑃𝑖 min , the higher is the production range and thus the higher the flexibility of production unit i.
- 11. FLEXIBILITY IN SUPPLY-SIDE 11 Flexibilityin supply-side Constraints: Ramp-rate limits Start-up/shut-down , , 1 up i t i t i P P R − − , 1 , dn i t i t i P P R − − , , , , 0 u u i t i i t i t SU CS S SU , , , , 0 d d i t i i t i t SD CS S SD , , , , 1 u d i t i t i t i t S S I I − − = − The higher the value of 𝑅𝑖 dn , the higher is the flexibility of unit i. The higher the value of 𝑅𝑖 up , the higher is the flexibility of unit i, i.e., the higher its capability to adapt to changes as time evolves.
- 12. FLEXIBILITY IN SUPPLY-SIDE 12 Constraints: Minimumup time Minimum down time , 1 Ue i T Ue i t i t I T = = 1 , , 1,...., 1 U i t T U u Ue U i k i i t i i k t I T S t T NT T + − = = + − + , , 0 2,...., NT u U i k i t i k t I S t NT T NT = − = − + , 1 0 De i T i t t I = = 1 , , 1 1,...., 1 D i t T D d De D i k i i t i i k t I T S t T NT T + − = − = + − + , , 1 0 2,...., NT d D i k i t i k t I S t NT T NT = − − = − + U0 min , Ue i i T NT T = D0 min , De i i T NT T = The lower the value of both 𝑇𝑖 U and 𝑇𝑖 D , the higher is the flexibility of unit i. ADVANCED OPTIMIZATION TECHNIQUES FOR ENERGY SYSTEMS PLANNING AND OPERATION
- 13. Demands can contributeto system flexibility through a number of actions: 1. By lowering the rate of increase at periods of high demand increase. 2. By lowering the rate of decrease at periods of high demand decrease. 3. By lowering the peak demand. 4. By increasing the valley demand. 5. By shifting energy from high demand to low demand periods. FLEXIBILITY IN DEMAND-SIDE 13 For example, during the early morning (say around 7 a.m.), when wind power production is typically decreasing and solar power production has not picked up yet, a lower demand-increase rate helps the operation of the system, as the requirement to increase power imposed on regulating flexible units (e.g., CCGTs) decreases.
- 14.
- 15. FLEXIBILITY FROM STORAGEAVAILABILITY 15 • Storage plants allow shifting in time the demand by consuming electricity at low demand (low-price) periods and producing it during high-demand (high-price) periods. • This demand shifting is not free, involving generally an overall efficiency ranging between 75 and 80 %. • Increasing consumption at low-demand periods allows inflexible production units with limited capability of reducing their power outputs to maintain their production levels throughout these low demand periods. • Producing from storage units at high demand periods reduce the need of reserve and the use of costly peakers. ADVANCED OPTIMIZATION TECHNIQUES FOR ENERGY SYSTEMS PLANNING AND OPERATION
- 16. Formulation FLEXIBILITY FROM STORAGEAVAILABILITY 16 , , , 1 , d k t c c k t k t k k t d k P E E P − = + − ,min ,max , , , d d d d d k k t k t k k t P I P P I ,min ,max , , , c c c c c k k t k t k k t P I P P I Constraints: Electrical storage 𝐸𝑡 State of charge of storage 𝑃𝐷𝑡 /𝑃𝐶𝑡 Discharge/Charge power 𝐼𝑡 𝑑 /𝐼𝑡 𝑐 State of discharge/charge of storage 𝜂𝐷/𝜂𝐶 Efficiency of discharge/charge of storage min max , k k t k E E E ,0 , k k NT E E =
- 17. Formulation FLEXIBILITY FROM ENHANCINGTHE TRANSMISSION NETWORK 17 Constraints: Power balance DC power flow 𝑃𝐹𝐿 max Line capacity 𝛿𝑏, 𝑡 Angle bus , , , , , 1 1 1 1 1 b b b b b NI NK NK NJ NL d c i t k t k t j t L t i r r j L P P P L PF = = = = = + − − = max , L t L PF PF ' , , , b t b t L t L PF x − = The higher the value of 𝑃𝐹𝐿 max , the higher is the flexibility of network.
- 18. Input data: EVALUATING THEFLEXIBILITY IN MARKET- CLEARING 18 Time (h) L1 (MW) L2 (MW) 11 40 100 22 25 80 3 45 95 1, 1, 1 50 t t P P − − 1, 1 1, 50 t t P P − − 2, 2, 1 30 t t P P − − 2, 1 2, 30 t t P P − − 3, 3, 1 50 t t P P − − 3, 1 3, 50 t t P P − − U0 2 1 T = U0 1 0 T = U0 3 1 T = D0 2 0 T = D0 1 1 T = D0 3 0 T = U 2 1 T = U 1 1 T = U 3 1 T = D 2 1 T = D 1 1 T = D 3 1 T = 1, 80 t PF BASECASE 1, 2, 1, 0.13 t t t PF − = Shiftable demand and storage are not included in this case 1, 0 t = 𝑴𝒂𝒓𝒈𝒊𝒏𝒂𝒍 𝒃𝒆𝒏𝒆𝒇𝒊𝒕 𝒐𝒇 𝒅𝒆𝒎𝒂𝒏𝒅 = 𝟒𝟎$/𝑴𝑾
- 19. EVALUATING THE FLEXIBILITYIN MARKET- CLEARING 19 1 50,50,50 G 1, 80,80,80 t PF Outputs (Base case) Social welfare=$6675 2 70,55,75 G 3 20,0,15 G It is committed as the cheapest unit in the maximum capacity Line capacity leads to not using the maximum capacity ofG2 Line capacity leads to the use of the most expensive units 1 30,30,30 LMPof bus 5 2 3 3 ,30, 5 LMPof bus
- 20. EVALUATING THE FLEXIBILITYIN MARKET- CLEARING 20 Case 1 Capacity Limits 1, 20 50 t P 2, 50 110 t P 3, 10 100 t P Base case Decrease in flexibility of G1 and G3 1, 40 20 t P 2, 50 110 t P 3, 100 30 t P Case 1 Outputs (case1 ) 1 50,50,50 G 2 70,55,75 G 3 20,0,15 G 1 40,40,40 G 2 70,65,70 G 3 30,0,30 G Case 1 Base case Social welfare (Case 1)=$5950
- 21. EVALUATING THE FLEXIBILITYIN MARKET- CLEARING 21 Case 2 Ramp-Rate Limits Base case Decrease in flexibility ofG2 Case 2 Outputs (Case 2) 1 50,50,50 G 2 70,55,75 G 3 20,0,15 G 1 50,50,50 G 2 65,55,65 G 3 25,0,25 G Case 2 Base case Social welfare (Case 2)=$6600 2, 2, 1 30 t t P P − − 2, 1 2, 30 t t P P − − 2, 2, 1 10 t t P P − − 2, 1 2, 10 t t P P − −
- 22. EVALUATING THE FLEXIBILITYIN MARKET- CLEARING 22 Case 3 Minimum up/down time Limits Base case Decrease in flexibility of G1 and G3 Case 3 Outputs (Case 3) 1 50,50,50 G 2 70,55,75 G 3 20,0,15 G 1 0,45,50 G 2 80,50,75 G 3 60,10,15 G Case 3 Base case Social welfare (Case 3)=$5325 U 3 3 T = D 1 2 T = U 3 1 T = D 1 1 T = 1 50,10,30 LMPof bus 2 50,10,35 LMPof bus
- 23. EVALUATING THE FLEXIBILITYIN MARKET- CLEARING 23 Case 4 Line capacity Limit Base case Decrease in flexibility of line Case 4 Outputs (Case 4) 1 50,50,50 G 2 70,55,75 G 3 20,0,15 G 1 50,35,50 G 2 50,50,55 G 3 40,20,35 G Case 4 Base case Social welfare (Case 4)=$6075 1 30,10,30 LMPof bus 2 35,35,35 LMPof bus 1, 80 t PF 1, 60 t PF Minimum capacity of G2 is 50 MW
- 24. EVALUATING THE FLEXIBILITYIN MARKET- CLEARING 24 Case 5 Shiftable Demand Input data for shiftable load Time (h) 𝐿𝟏,𝑡 max (MW) 𝐿𝟐,𝑡 max (MW) 𝐿𝟏,𝑡 𝐦𝐢𝐧 (MW) 𝐿𝟐,𝑡 𝐦𝐢𝐧 (MW) 11 44 110 36 90 22 27.5 88 22.5 72 3 49.5 104.5 40.5 85.5 To evaluate the flexibility in demand side, the line capacity in base case is assumed to be 90 MW instead of 80 MW
- 25. EVALUATING THE FLEXIBILITYIN MARKET- CLEARING 25 Case 5 Shiftable Demand Outputs (Case 5) Base case (Line capacity=90) 1 50,50,50 G 2 80,55,80 G 3 10,0,10 G 1 50,50,50 G 2 80,60,85 G 3 0,0,10 G Case 5 (Line capacity=90) Social welfare (Case 5)=$6800 Social welfare (Base case)=$6750 Time (h) Before shifting After shifting 11 140 130 22 105 110 3 140 145 Supplied demand
- 26. EVALUATING THE FLEXIBILITYIN MARKET- CLEARING 26 Case 6 Storage 1, 0 50 t E 1,0 1,3 15 E E = = Input data To evaluate the flexibility of storage, the line capacity in base case is assumed to be 85 MW instead of 80 MW 1, 85 t PF , , , 1 , 0.95 0.95 d k t c k t k t k t P E E P − = + −
- 27. EVALUATING THE FLEXIBILITYIN MARKET- CLEARING 27 Case 6 Storage Outputs (Case 5) Social welfare (Case 6)=$6732.2 Social welfare (Base case)=$6725 Base case 1 50,50,50 G 2 75,55,80 G 3 15,0,10 G Case 6 1 50,50,50 G 2 75,60,80 G 3 10.487,0,10 G 1 30,30,30 LMPof bus 2 35,31.587,31.587 LMPof bus 4.153,0,0 dischrage P arg 0,5,0 ch e P
- 28. RES integration Pricearbitrage Peak shaving Ancillary services Flexibility Electricity price Why Energy Storage?
- 29. WHAT WILL THEFUTURE ENERGY SYSTEM LOOK LIKE? ARUP. Energy systems: A view from 2035. What will a future energy market look like? Future Energy Decentralized Disaggregated Multi-vector Storage & Flexibility Solutions Balances supply and demand across all sectors Enables high renewable energy integration Provides grid stability and reliability Supports sector coupling between electricity, gas, heat, and transport Facilitates decentralized energy management
- 30. ENERGY STORAGE APPLICATIONS ADVANCEDOPTIMIZATION TECHNIQUES FOR ENERGY SYSTEMS PLANNING AND OPERATION 30 https://www.worldenergy.org/assets/downloads/ESM_Final_Report_05-Nov-2019.pdf
- 31. ENERGY STORAGE- CURRENTAND FUTURE STATUS ADVANCED OPTIMIZATION TECHNIQUES FOR ENERGY SYSTEMS PLANNING AND OPERATION 31
- 32. Various Types ofESS Batteries • Lithium-ion • Sodium-Based • Flow Batteries • Lead Acid Pumped hydro storage 01 04 Compressed Air Energy Storage 02 Thermal storage 05 Flywheels and Supercapacitors 03
- 33. Global Energy Storage FirstStage Record Market Growth in 2023 First Stage China and US are leading First Stage 137 GW/442 GWh
- 34. Energy Storage TechnologyMarket Share 2022 2021 2018 2020 Cnesa Energy Storage Industry White
- 35. Lithium-ion Dominance Cnesa EnergyStorage Industry White 2023 doi.org/10.1016/j.enss.2022.07.002 High energy density Versatility in Applications Market Maturity High efficiency Lithium-ion: 100-200 Wh/kg Compared to: Lead-acid: 30-75 Wh/kg Flow batteries (VRB): 35-60 Wh/kg Lithium-ion: 70-85% Lithium-ion matches or exceeds most technologies in efficiency Can be used in both small (kW) and medium (MW) scale applications Modular design allows for easy scaling Suitable for both power and energy applications Established manufacturing infrastructure Proven track record in various applications Continuous technological improvements Declining costs due to scale
- 36. Cost Comparison Technology LCOS($/kWh) (2021) LCOS($/kWh) (2023) Total installed costs(($/kWh) Li-ion NMC 0.20 0.17 456 Lithium-Ion (LFP) 0.20 0.15 356 Vanadium Redox Flow 0.19 0.16 435 Lead Acid 0.33 0.28 462 Zinc-Based 0.25-0.30 0.20-0.25 457 Technology LCOS($/kWh) (2021) LCOS($/kWh) (2023) Total installed costs (($/kWh) CAES 0.10 0.10 122 PSH 0.11 0.11 262 Thermal 0.15-0.25 0.13-0.22 290 Gravitational 0.13 0.12 455 Hydrogen 0.35 0.18 295 Battery Storage Systems 100 MW, 10-hour system Non-Battery Storage Systems 100 MW, 10-hour system CAES and PSH offers lowest total cost but requires specific geological conditions Among batteries, Li-ion LFPis most cost-competitive Source: 2022 Grid Energy Storage Grid Energy Storage Technology Cost and Technology Cost and Performance Assessment Performance Assessment
- 37.
- 38. ENERGY STORAGE-PUMPED STORAGE HYDROPOWER 38 •It is a configuration of two water reservoirs at different elevations that can generate power (discharge) as water moves down through a turbine; this draws power as it pumps water (recharge) to the upper reservoir. • The round-trip efficiency (electricity generated divided by the electricity used to pump water) of the state-of-the-art PHS system may achieve over 80% efficiency
- 39.
- 40. BATTERY STORAGE-NAS BATTERIES 40 https://www.nrel.gov/docs/fy19osti/73222.pdf NaSbattery technology has been demonstrated at over 190 sites in Japan. Location Rokkasho, Aomori, Japan Project Status : Commissioned 2008 Rated Capacity: Total 85MW Wind 51 MW Battery Storage 34 MW ES Cycle Efficiency 89% to 92% Owner Japan Wind Development Company, Ltd. Construction EPC: Kandenko Company, Ltd. Generation Offtaker Tohoku Electric Power Company…LT PPA Wind 34 nos. of GE 1.5 MW WTs Battery Storage 17 X 2 MW NGK Insulators’ NaS batteries Grid monitoring & Control Yokogawa Electric Corporation systems More than 270 MW of power (generated from stored energy) suitable for 6 hours of daily peak shaving have been installed.
- 41. COMPRESSED AIR ENERGYSTORAGE 41 • Energy Storage Technology which uses compressed air • Made up of several components, some which include: Compressors Expanders Air Reservoir Combustor Motor Large storage reservoir is needed, Worldwide capacities: 320 MW (Germany), 110 MW (USA). Projects: USA, Italy, Japan, South Africa, Israel, Morocco, Korea Compressed air energy storage
- 42. COMPRESSED AIR ENERGYSTORAGE 42 Sketch of diabatic compressed air energy storage
- 43. COMPRESSED AIR ENERGYSTORAGE 43 Sketch of adiabatic compressed air energy storage
- 44. COMPRESSED AIR ENERGYSTORAGE 44 Conventional Gas Turbine The air that drives the turbine is compressed and heated using natural gas. Nearly two-thirds of the natural gas is consumed by a typical natural gas turbine because the gas is used to drive the machine compressor. Both compression ad generation are on a single shaft and must work in unison. CAES Needs lees gas to produce power during periods of peak demand because it uses air that has already been compressed and stored underground. Uses low-cost heated compressed air to power the turbines and create off-peak electricity, conserving some natural gas. Compression and generation units are completely separated.
- 45. COMPRESSED AIR ENERGYSTORAGE 45 A wind/CAES model
- 46. COMPRESSED AIR ENERGYSTORAGE 46 Mathematical model of wind/CAES In each hour, CAES facility could be only utilized in one particular mode (charge, discharge and simple cycle) which forced by The charging and discharging power and energy limits of the CAES are specified by ,min ,max d d d d d t t t P I P P I ,min ,max c c c c c t t t P I P P I 1 d c s t t t I I I + + ,min ,max s s s s s t t t P I P P I 𝐸𝑡 State of charge of storage 𝑃𝑡 𝑑 /𝑃𝑡 𝑐 /𝑃𝑡 𝑠 Discharge/Charge/simple cycle power 𝐼𝑡 𝑑 /𝐼𝑡 𝑐 /𝐼𝑡 𝑠 State of discharge/charge /simple cycle 𝜂𝐷/𝜂𝐶 Efficiency of discharge/charge of storage
- 47. COMPRESSED AIR ENERGYSTORAGE 47 Mathematical model of wind/CAES The level of stored energy in the CAES in each hour is fulfilled by the upper and lower bound of the stored energy in storage is defined as The initial (t=0) and final (t=24) values of the stored power in storage system are the same which is defined by 1 d c c t t t t d P E E P − = + − min max t E E E 0 NT E E =
- 48. COMPRESSED AIR ENERGYSTORAGE 48 Mathematical model of wind/CAES w d s market c t t t t t P P P P P + + = + 1 1 max ( ) NT NT el market gas d d s s t t t t t t t obj P HR P HR P = = = − + Objective function: Maximizing profit by selling power to the market. 𝐻𝑅𝑑 /𝐻𝑅𝑠 Heat rate of discharge and simple cycle modes 𝜆𝑡 𝑔𝑎𝑠 /𝜆𝑡 𝑒𝑙 Gas and power prices
- 49. COMPRESSED AIR ENERGYSTORAGE 49 Input data 0 20 40 60 80 100 120 140 160 180 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Power price ($/MWh) Time (h) 0 20 40 60 80 100 120 140 160 180 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Forecasted wind power (MW) Time (h) Power price Wind power Gas price= 30$/MWh 5 50 d d d t t t I P I 5 50 c c c t t t I P I 5 50 s s s t t t I P I 50 350 t E 1 0.9 0.9 d c t t t t P E E P − = + −
- 50. Case 1 :Wind/CAES (only simple cycle mode) Case 2: Wind/CAES (charge, discharge and simple cycle modes) COMPRESSED AIR ENERGY STORAGE 50 Profit in case 1: 112788.540 Profit in case 2: 115858.540 Case 2 Simple cycle mode In case 1 is in hours 11-15 and 17 In case 2 is in hour 12, because in this case, the operator prefers to use discharge mode.
- 51.
- 52. POWER-TO-GAS STORAGE 52 Energy efficiencycomparison of different P2G pathways
- 53. POWER-TO-GAS STORAGE 53 Comparison ofstorage LCoE for Li-ion batteries, CAES, pumped hydro and P2G
- 54. POWER-TO-GAS 54 Mathematical model ofwind/P2G Converted natural gas by P2G storage can be injected into the upstream gas network or stored in the gas storage: The limit on electricity power consumed by the P2G storage: PtG c PtG t t t P G G = + ,max 0 c c t t G G ,max PtG PtG t t P P ,max 0 d d t t G G 1 d c t t t c t d G GS GS G − = + − max 0 t t GS GS The maximum gas stored or released in gas storage: Gas available in gas storage per hour: Capacity limitation of gas storage:
- 55. POWER-TO-GAS 55 Mathematical model ofwind/P2G 1 1 max ( ) NT NT el market gas d t t t t t t t obj P G G = = = + + Objective function: Maximizing profit by selling power and gas to the market. w PtG market t t t P P P − =
- 56. MARKET-CLEATING MECHANISM 56 0 20 40 60 80 100 120 140 160 180 1 23 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Power price ($/MWh) Time (h) 0 20 40 60 80 100 120 140 160 180 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Forecasted wind power (MW) Time (h) Gas price= 30$/MWh 5 50 d d d t t t I P I 5 50 c c c t t t I P I 5 50 s s s t t t I P I 50 350 t E 1 0.9 0.9 d c t t t t P E E P − = + − Input data
- 57. MARKET-CLEATING MECHANISM 57 Input data 0 5 10 15 20 25 30 35 40 45 12 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 Gas price ($/MWh) 0.65 PtG c t t t P G G = + 0 50 c t G 50 PtG t P 0 50 d t G 1 1 1 d c t t t t G GS GS G − = + − 0 350 t GS The maximum power exchanged between wind and market is assumed to be 80MW.
- 58. Case 1 :Wind Case 2: Wind/P2G COMPRESSED AIR ENERGY STORAGE 58 Profit in case 1: 90867.340 Profit in case 2: 96366.993 Excess wind power is converted to gas and sold to the gas market, which increases the operator's profit.
- 59.
- 60. 60 REFERENCES CONEJO,ANTONIOJ.,CARRIÓN,MIGUEL,MORALES,JUANM.,“DECISION MAKING UNDERUNCERTAINTY IN ELECTRICITY MARKETS”,SPRINGER,2010.ISBN978-1-4419-7421-1.DOI:10.1007/978-1-4419-7421-1 SHAHIDEHPOUR, MOHAMMAD, HATIM YAMIN, AND ZUYI LI. MARKET OPERATIONS IN ELECTRIC POWER SYSTEMS: FORECASTING, SCHEDULING, AND RISK MANAGEMENT. JOHN WILEY & SONS, 2003.