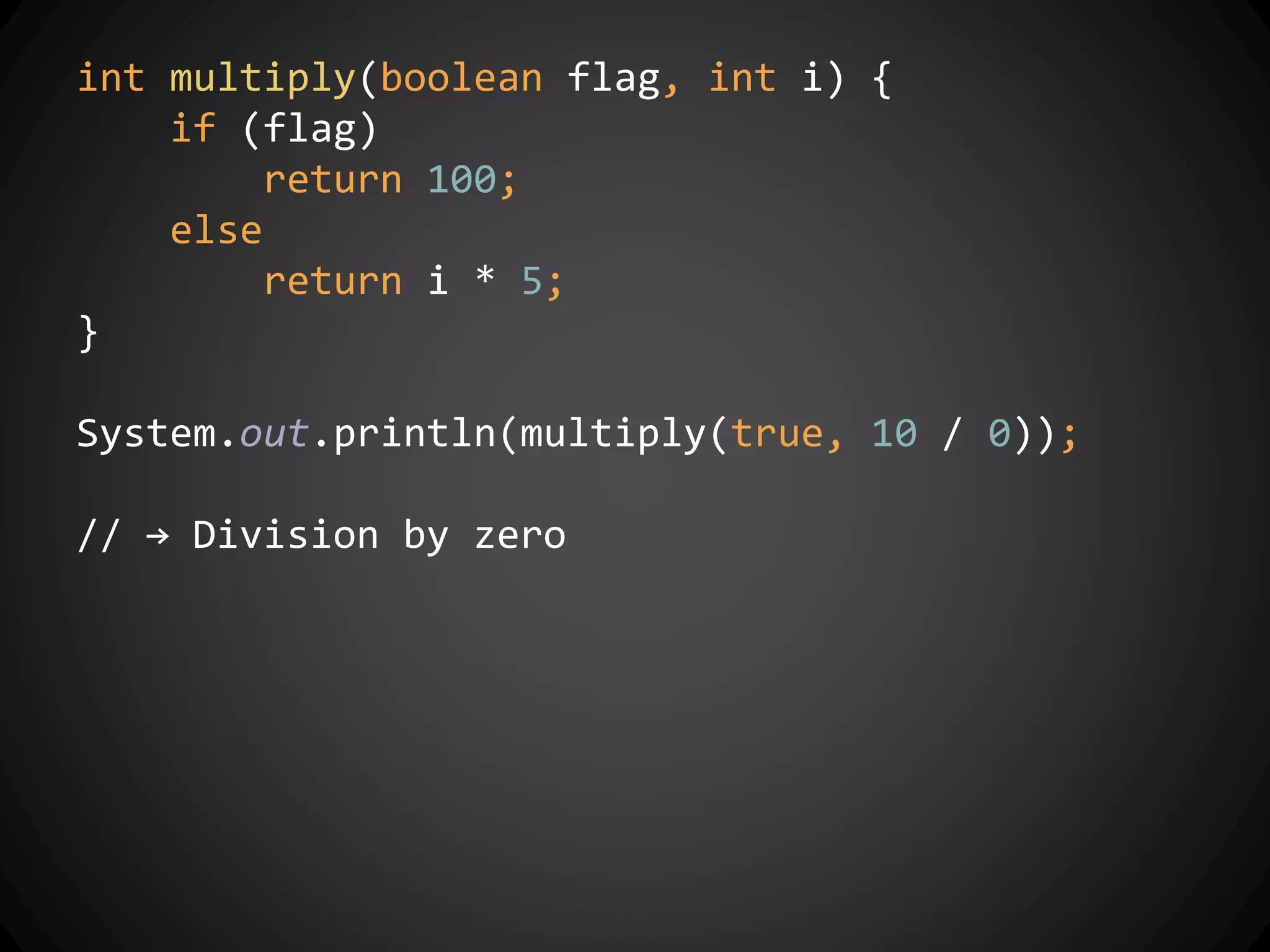
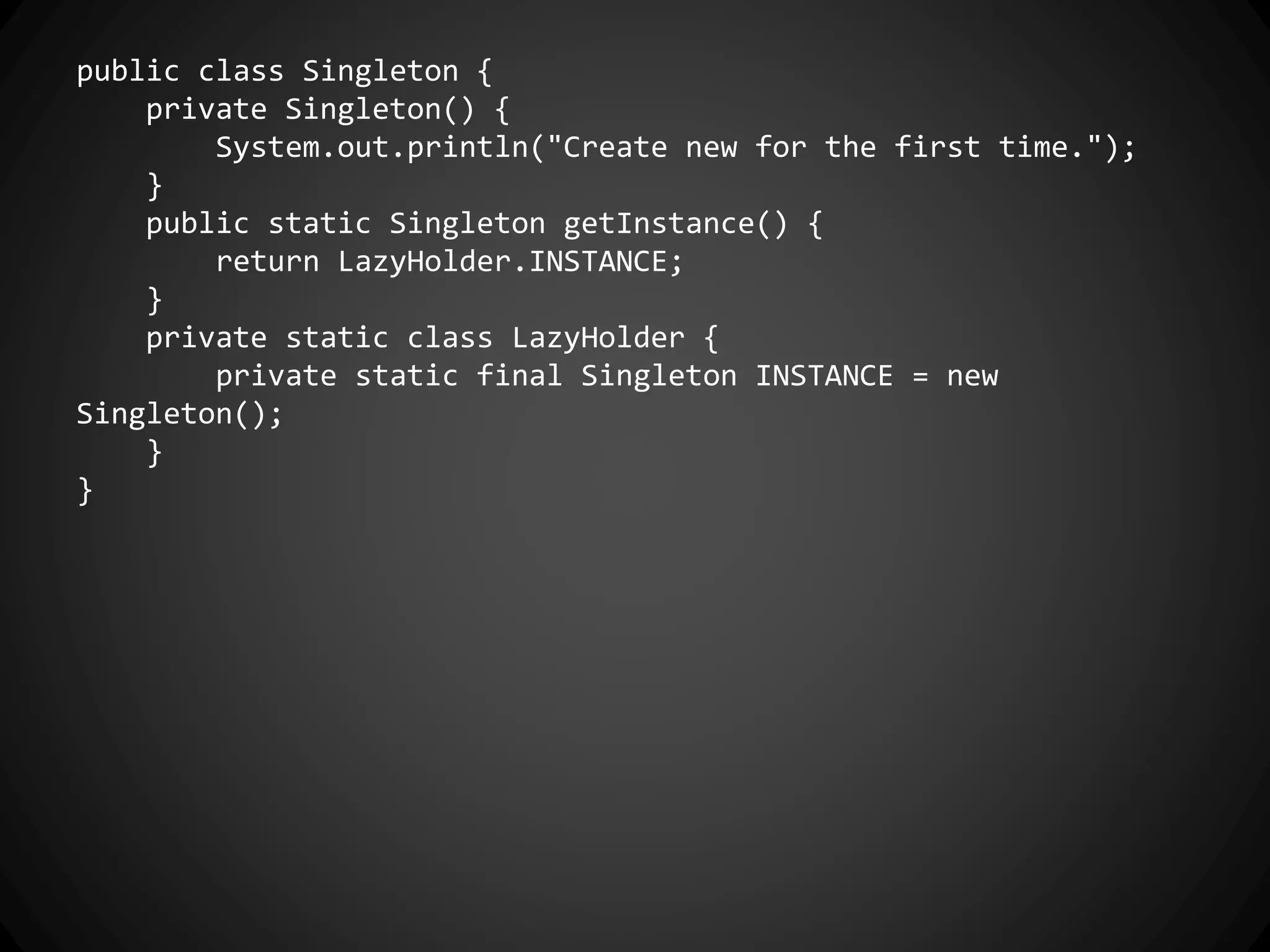
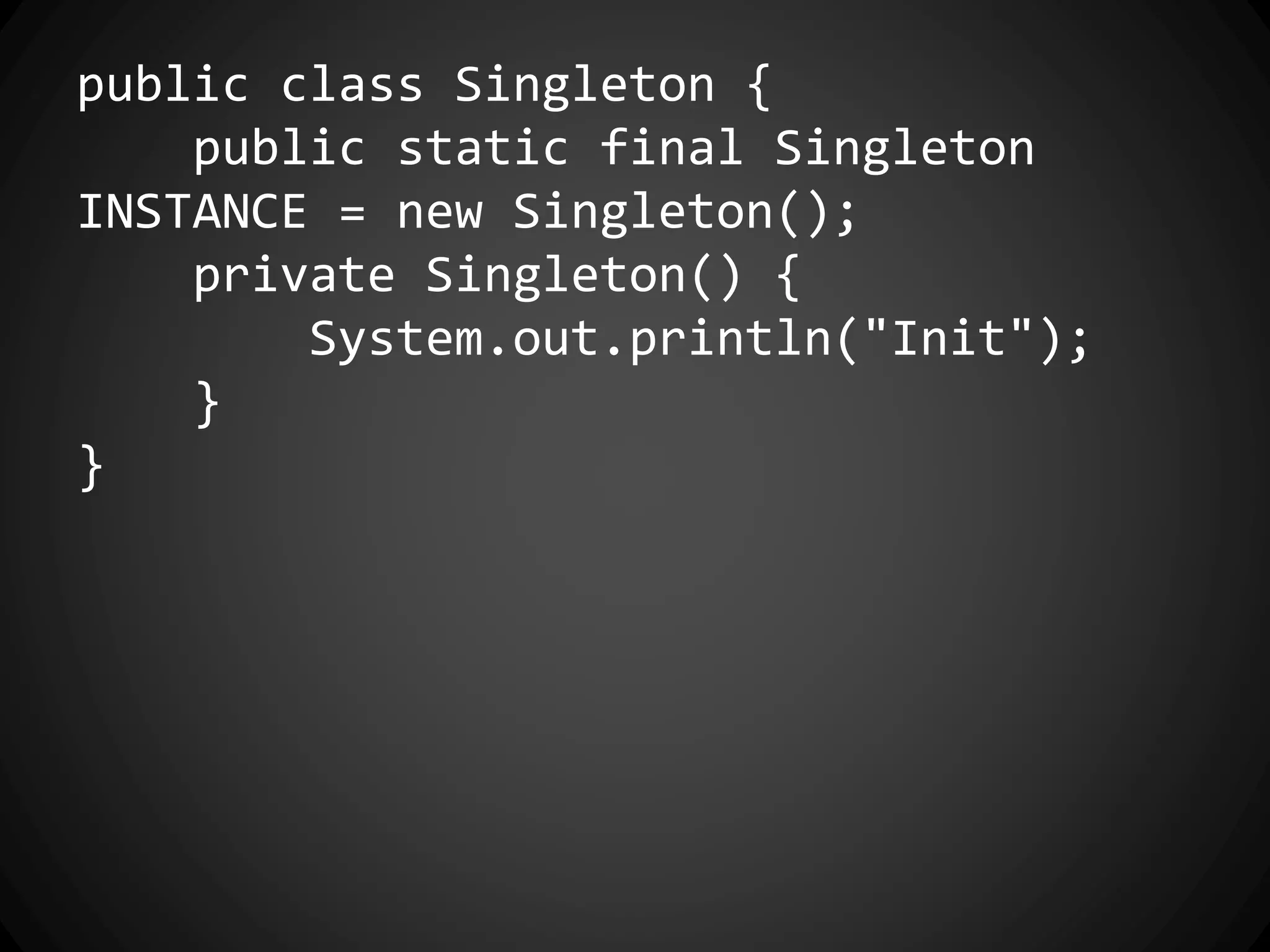
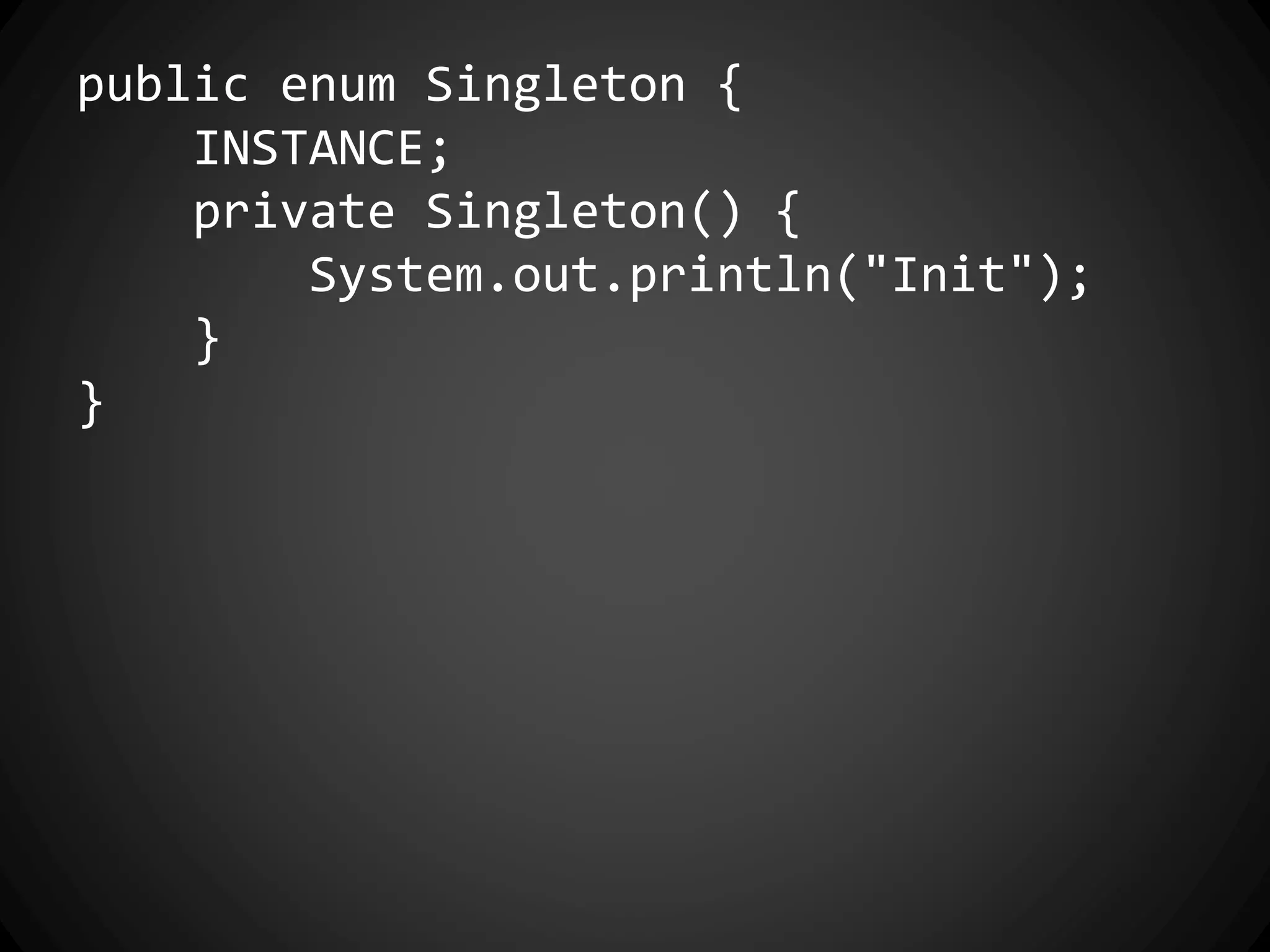
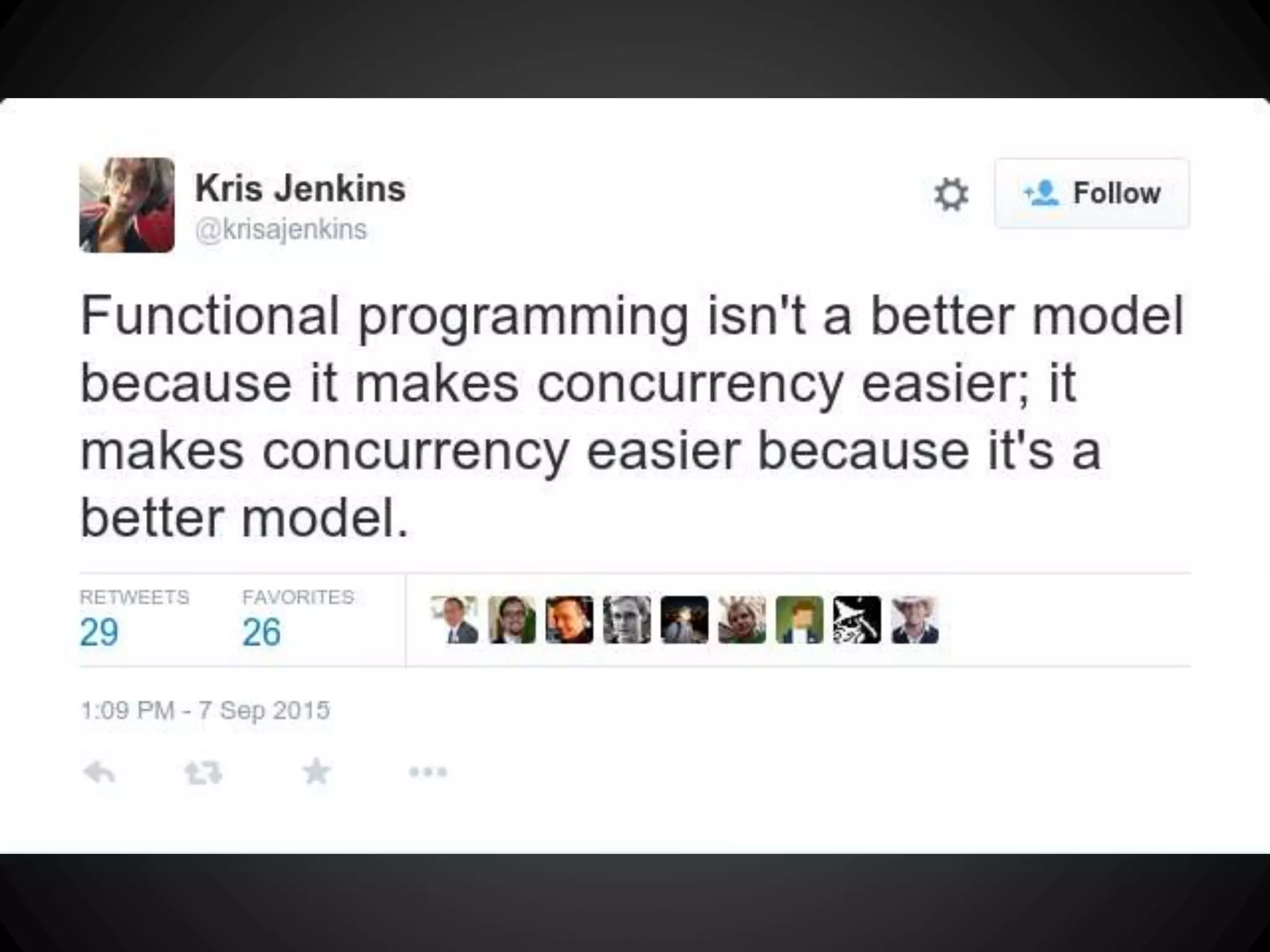
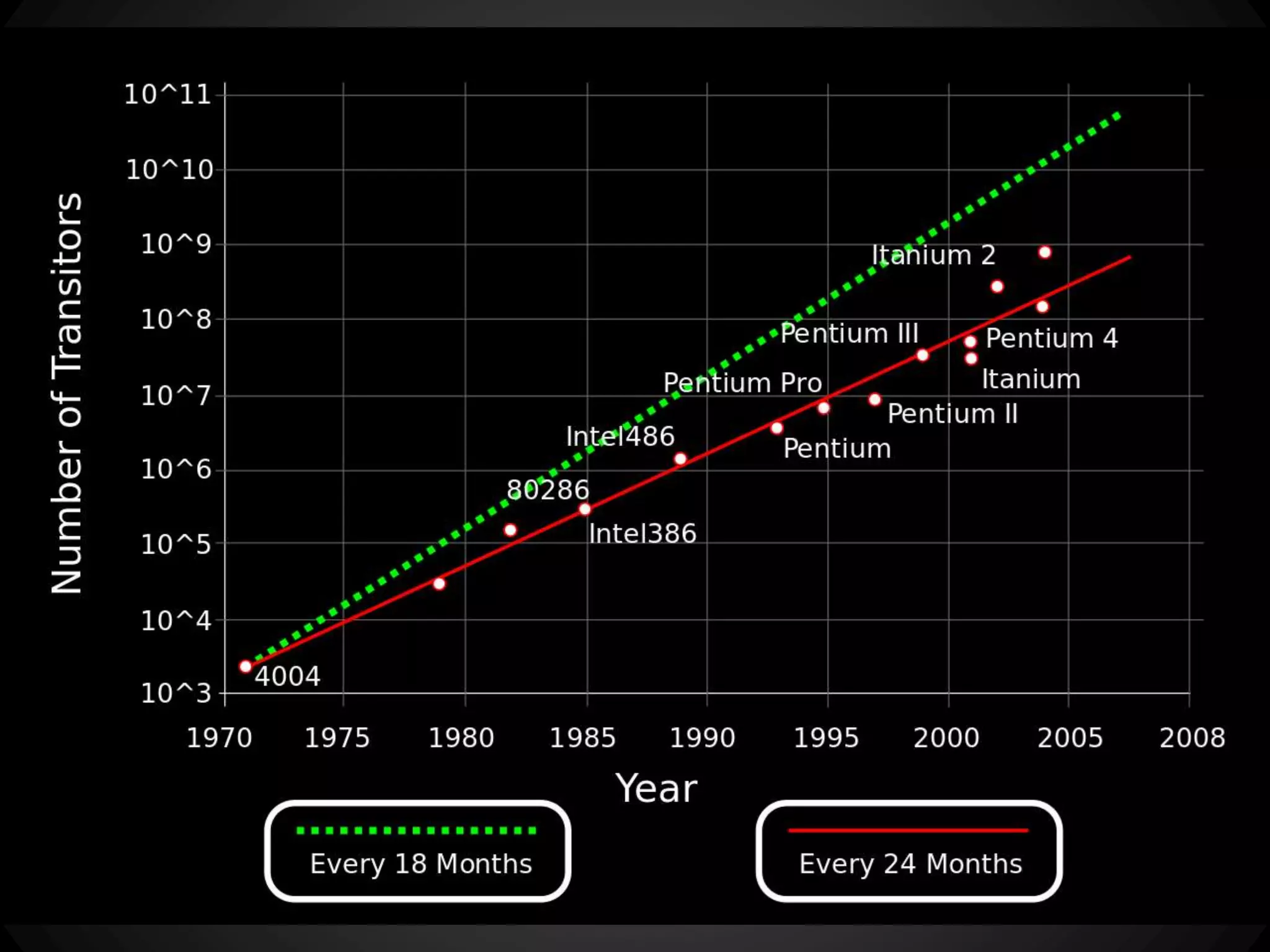
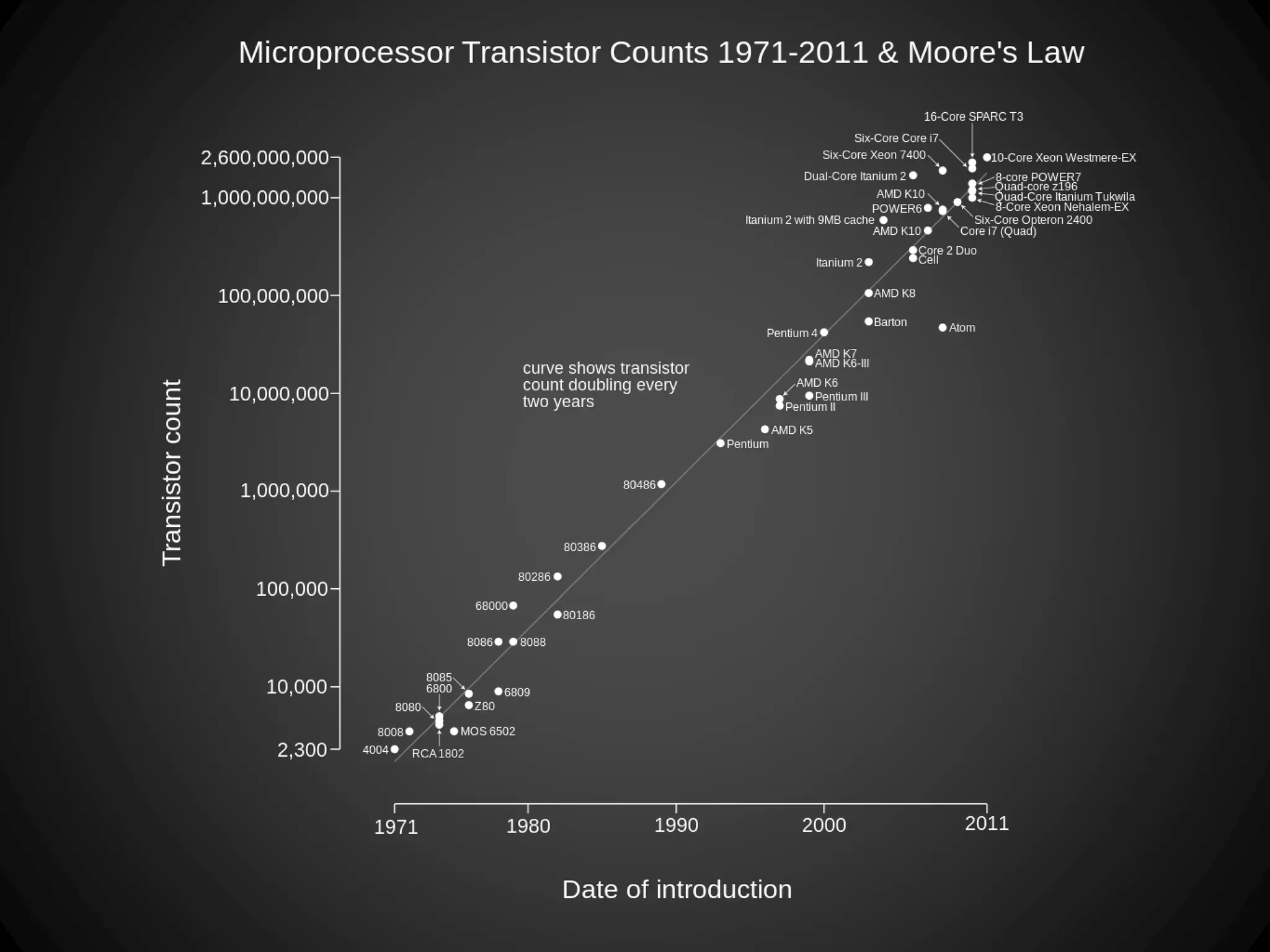
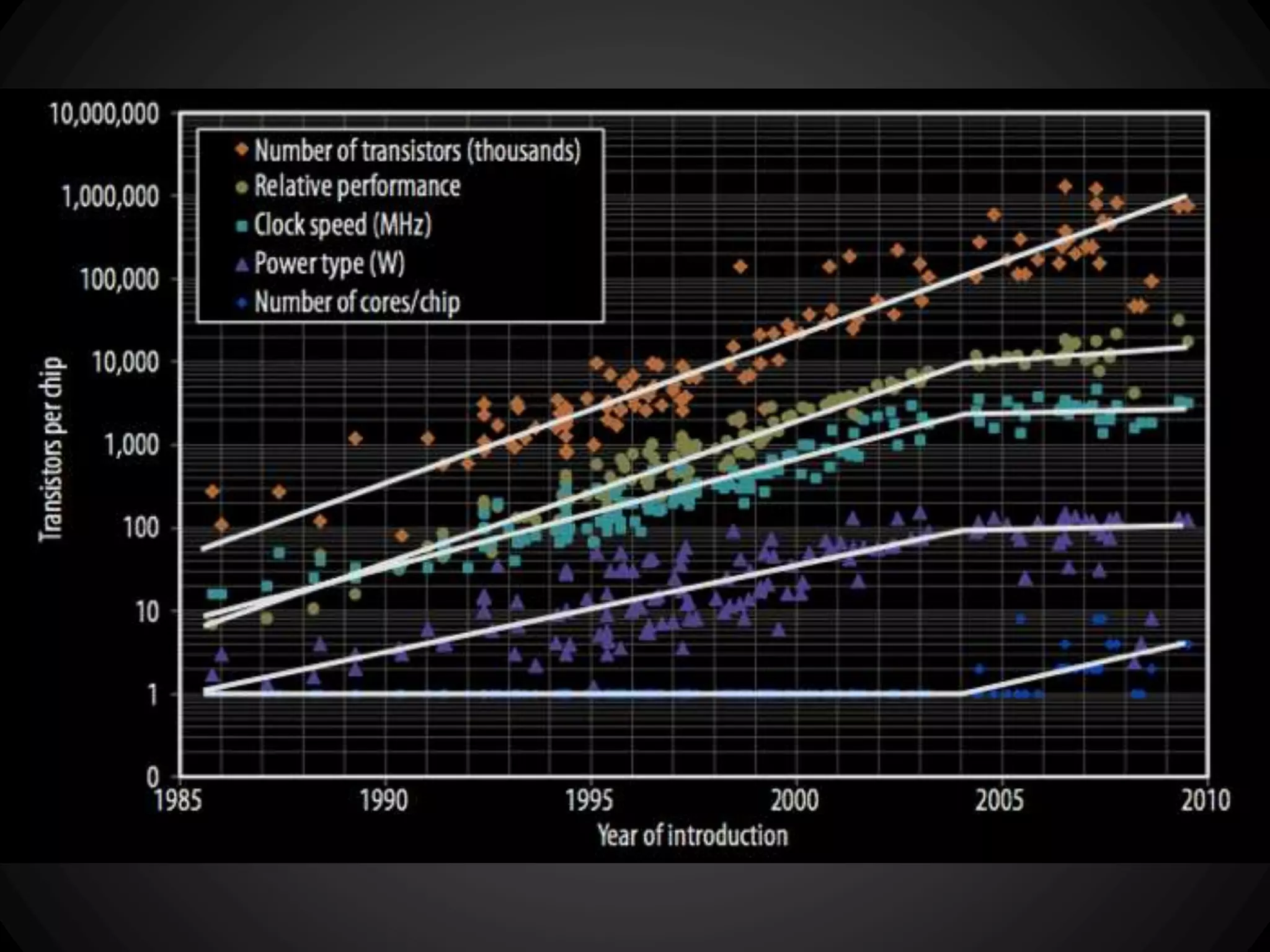
The document discusses the history of functional programming from 1903 to the present. It covers early developments like the lambda calculus in the 1930s and languages like Lisp in 1958. It also discusses key people who advanced functional programming like Alonzo Church, John McCarthy, and John Backus. The document then covers important milestones in functional programming languages between 1936 and 2013. It discusses concepts like purity, higher-order functions, and how functional programming relates to object-oriented programming.

















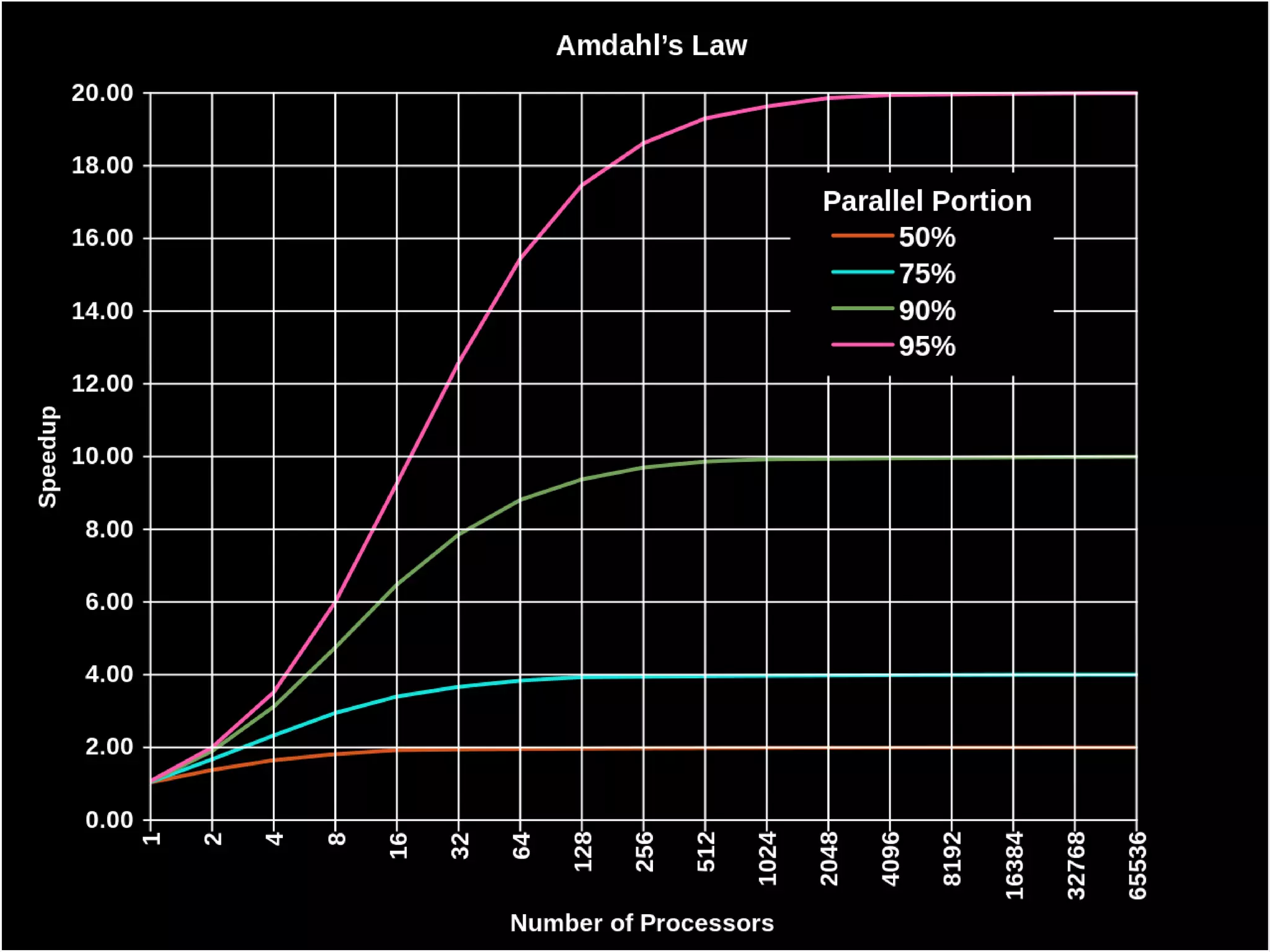
![Amdahl’s Law
Given
●𝑛 ∊ ℕ, the number of threads of execution
●B ∊ [0, 1], strictly serial fraction of algorithm
Time T(𝑛) it takes to finish with n threads is
T(𝑛) = T(1)(B + 1/𝑛 (1 − B))
Therefore, the theoretical speedup S(𝑛) is
S(𝑛) = T(1) / T(𝑛) = 1 / (B + 1/𝑛 (1 - B))](https://image.slidesharecdn.com/3ofzgd4scm0phnsdo7ha-signature-c42cd288f9f5fa19cb66a0002488f3771119bbe3db2edf123c6c85ff47b7d3f3-poli-150912132756-lva1-app6892/75/Functional-programming-22-2048.jpg)






























![Find Even Numbers
Double it
Sum it up
public int calculate() {
int[] numbers = {1, 5, 10, 9, 12};
List<Integer> doubledEvenNumbers = new ArrayList<>();
for (int number : numbers)
if (number % 2 == 0)
doubleEvenNumbers.add(num * 2);
int total = 0;
for (int even : doubleEvenNumbers)
total = total + even;
return total;
}
Imperative Style](https://image.slidesharecdn.com/3ofzgd4scm0phnsdo7ha-signature-c42cd288f9f5fa19cb66a0002488f3771119bbe3db2edf123c6c85ff47b7d3f3-poli-150912132756-lva1-app6892/75/Functional-programming-61-2048.jpg)











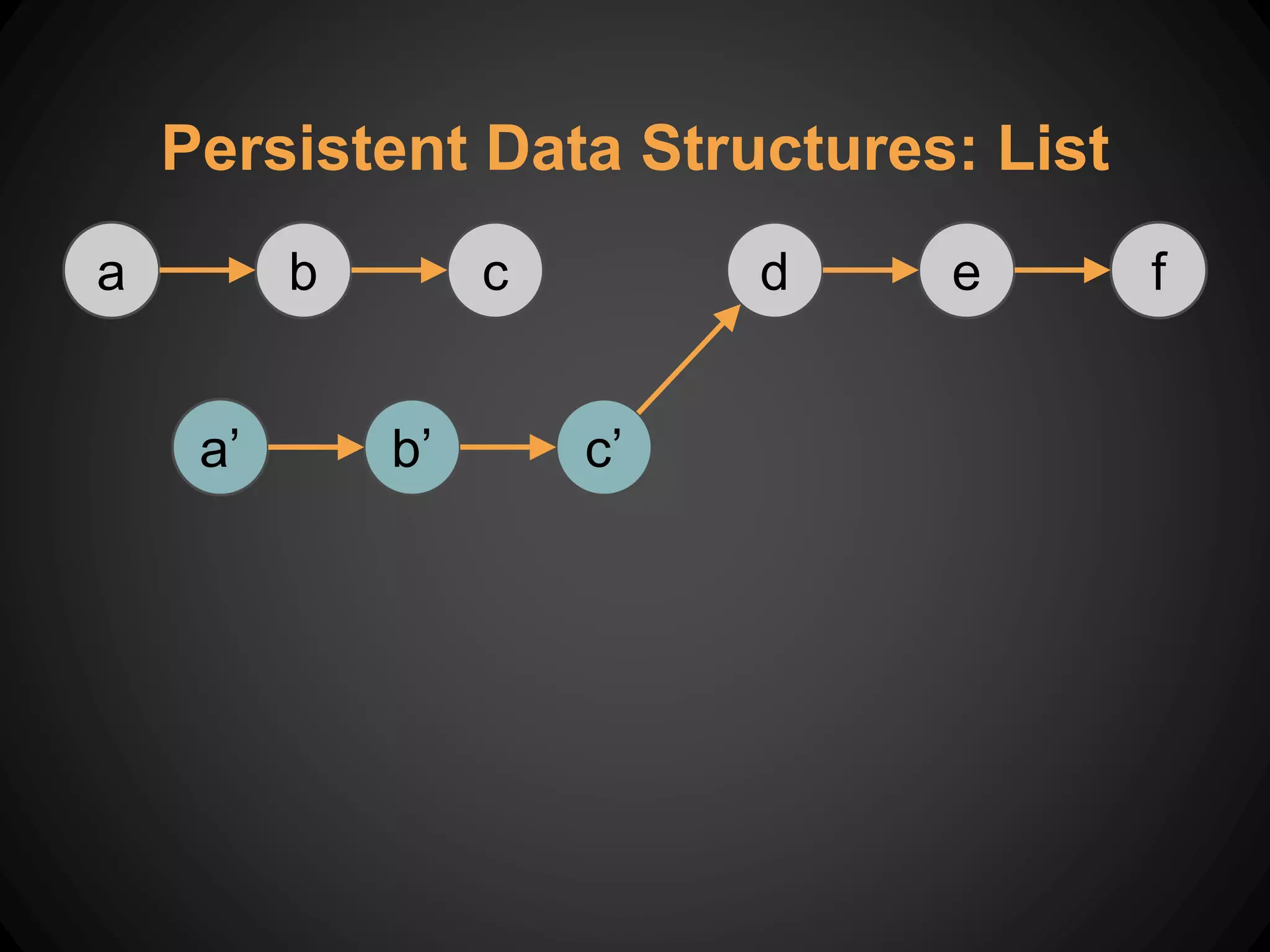










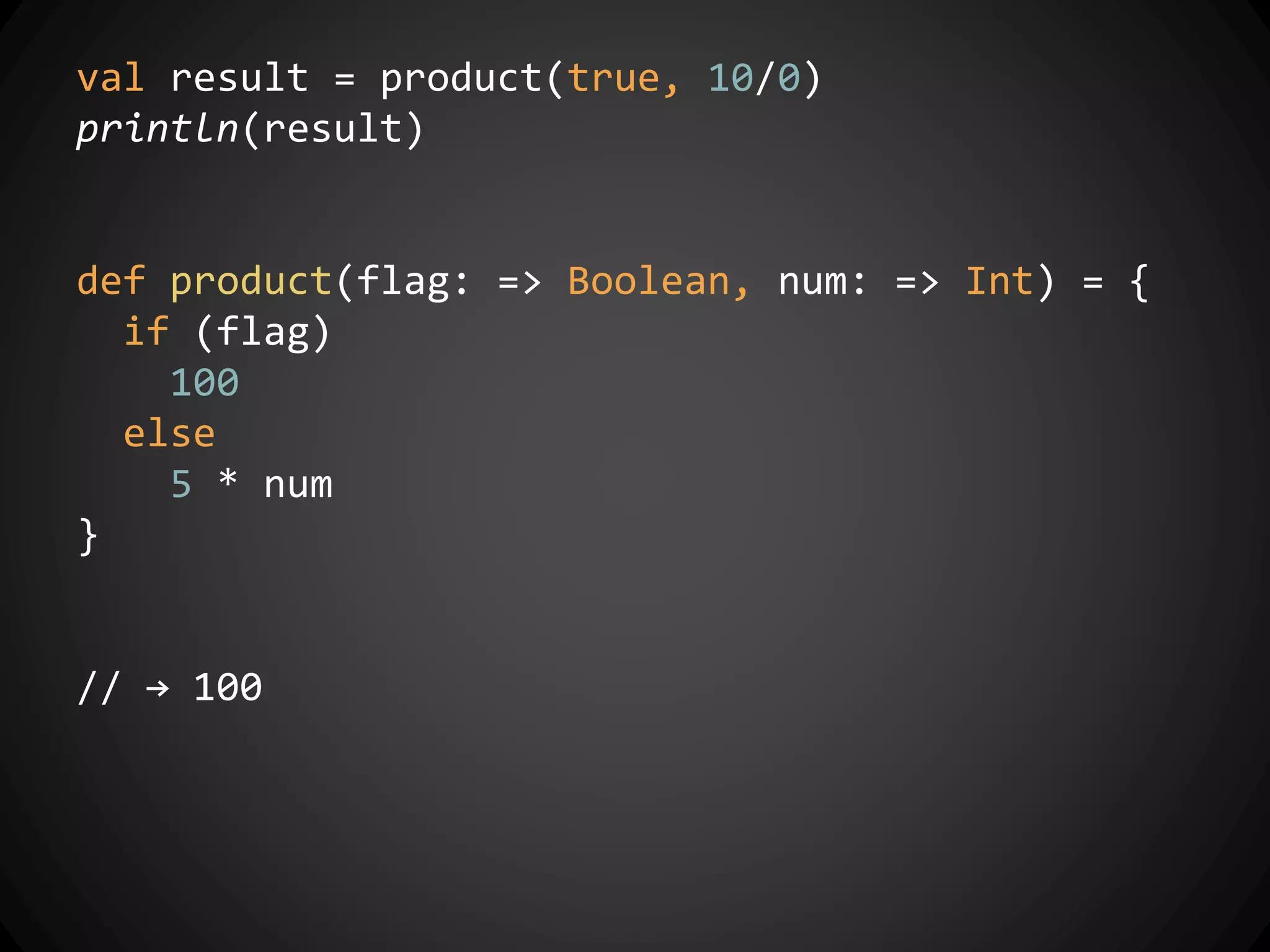

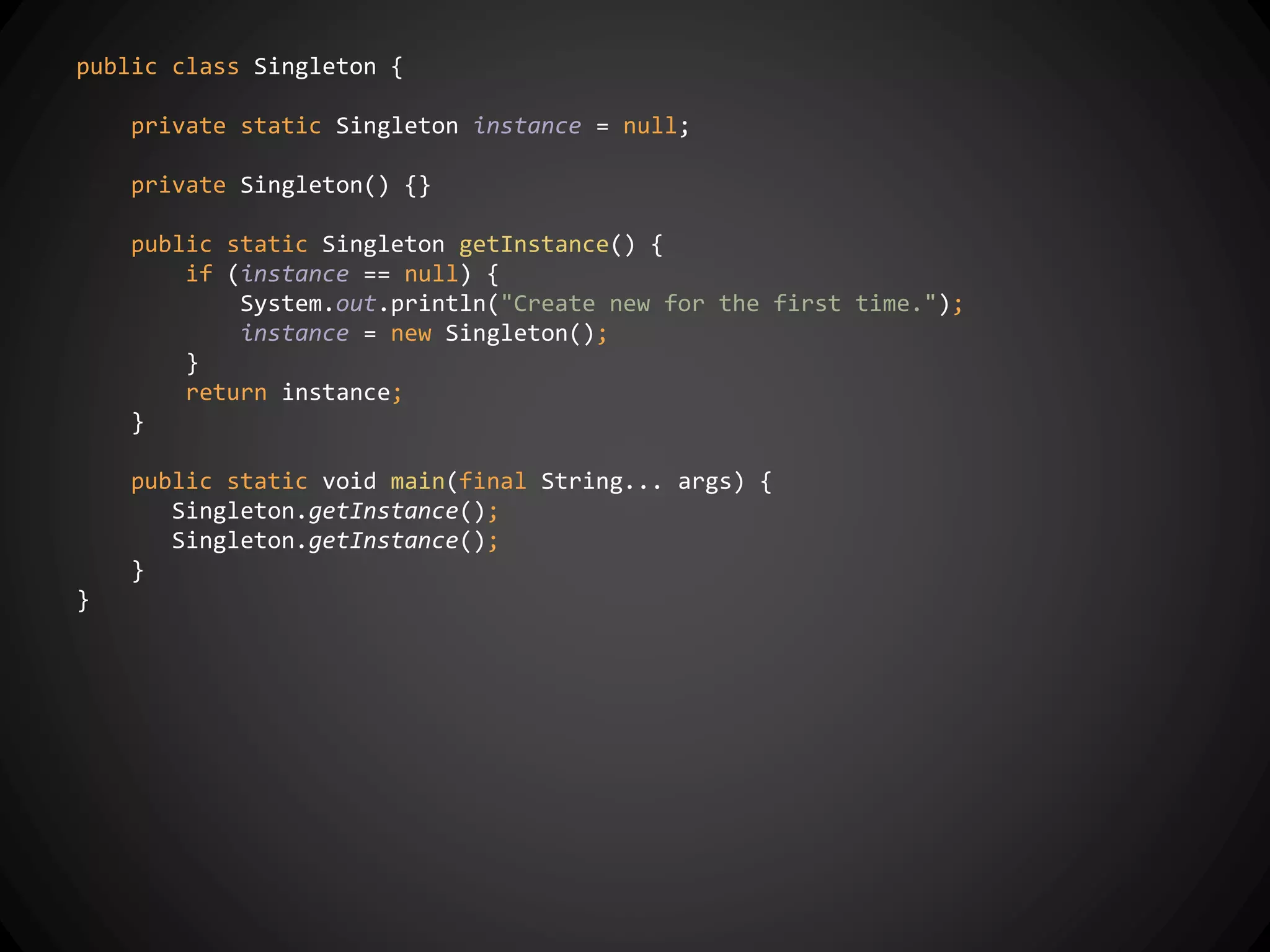
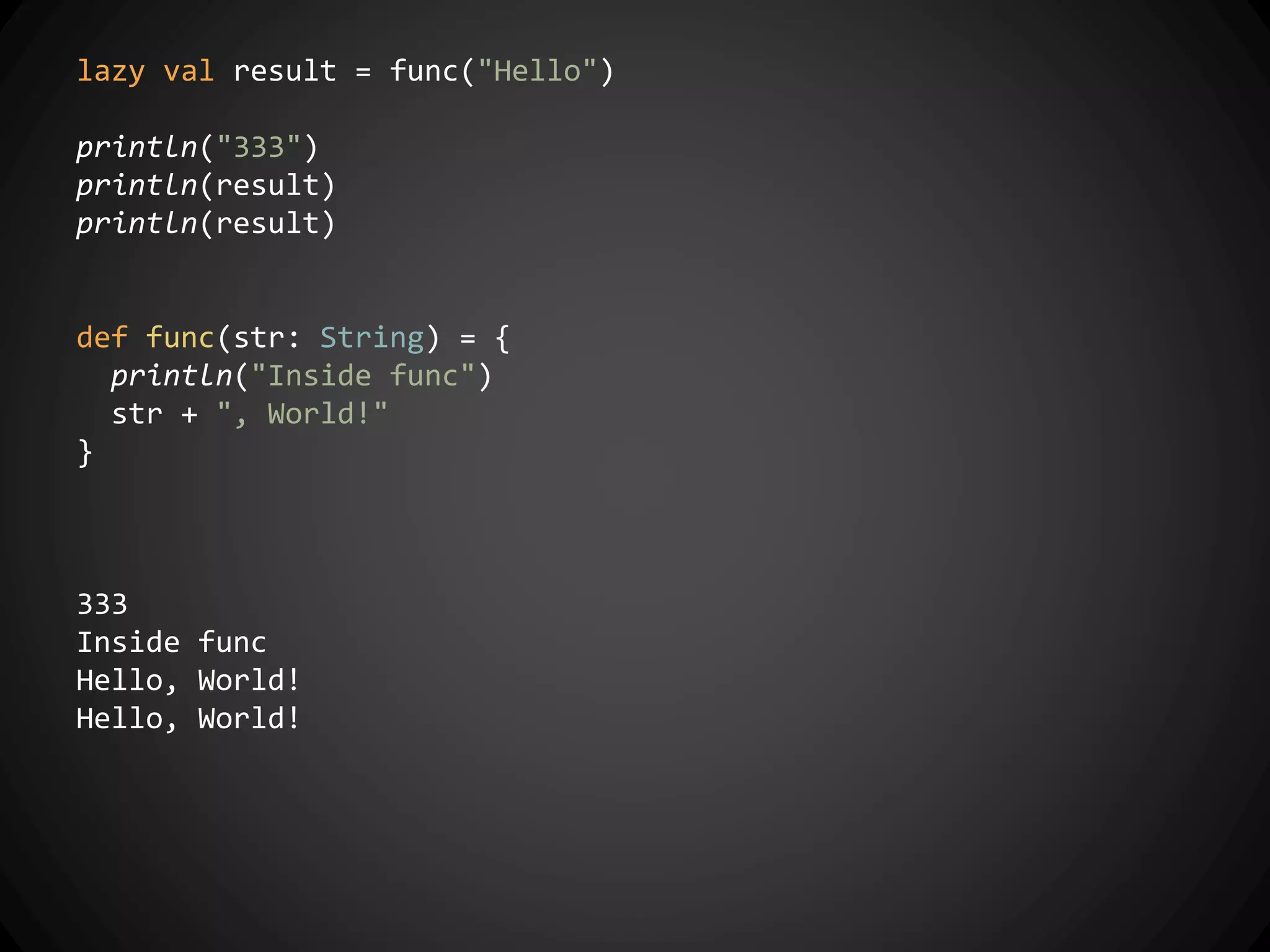







![Partial Functions in Scala
val isEven: PartialFunction[Int, String] = {
case x if x % 2 == 0 => x + "is even"
}
val isOdd: PartialFunction[Int, String] = {
case x if x % 2 == 1 => x + "is odd"
}
val sample = 1 to 10
val evenNumbers = sample collect isEven
val numbers = sample map (isEven orElse isOdd)](https://image.slidesharecdn.com/3ofzgd4scm0phnsdo7ha-signature-c42cd288f9f5fa19cb66a0002488f3771119bbe3db2edf123c6c85ff47b7d3f3-poli-150912132756-lva1-app6892/75/Functional-programming-95-2048.jpg)


















![main(Argv) :- echo(Argv).
echo([]) :- nl.
echo([Last]) :- write(Last), echo([]).
echo([H|T]) :- write(H), write(' '), echo(T).
Echo in Prolog](https://image.slidesharecdn.com/3ofzgd4scm0phnsdo7ha-signature-c42cd288f9f5fa19cb66a0002488f3771119bbe3db2edf123c6c85ff47b7d3f3-poli-150912132756-lva1-app6892/75/Functional-programming-114-2048.jpg)
![qsort :: (Ord a) => [a] -> [a]
qsort [] = []
qsort (x:xs) =
let left = qsort [a | a <- xs, a <= x]
right = qsort [a | a <- xs, a > x]
in left ++ [x] ++ right
--or even shorter
qsort (x:xs) =
qsort [a | a <- xs, a <= x]
++ [x] ++
qsort [a | a <- xs, a > x]
Quicksort in Haskell](https://image.slidesharecdn.com/3ofzgd4scm0phnsdo7ha-signature-c42cd288f9f5fa19cb66a0002488f3771119bbe3db2edf123c6c85ff47b7d3f3-poli-150912132756-lva1-app6892/75/Functional-programming-115-2048.jpg)

(implicit ev1: T =>
Ordered[T]): List[T] = list match {
case Nil => Nil
case p :: xs =>
val (lesser, greater) = xs partition (_ <=
p)
qsort(lesser) ++ List(p) ++ qsort(greater)
}](https://image.slidesharecdn.com/3ofzgd4scm0phnsdo7ha-signature-c42cd288f9f5fa19cb66a0002488f3771119bbe3db2edf123c6c85ff47b7d3f3-poli-150912132756-lva1-app6892/75/Functional-programming-117-2048.jpg)

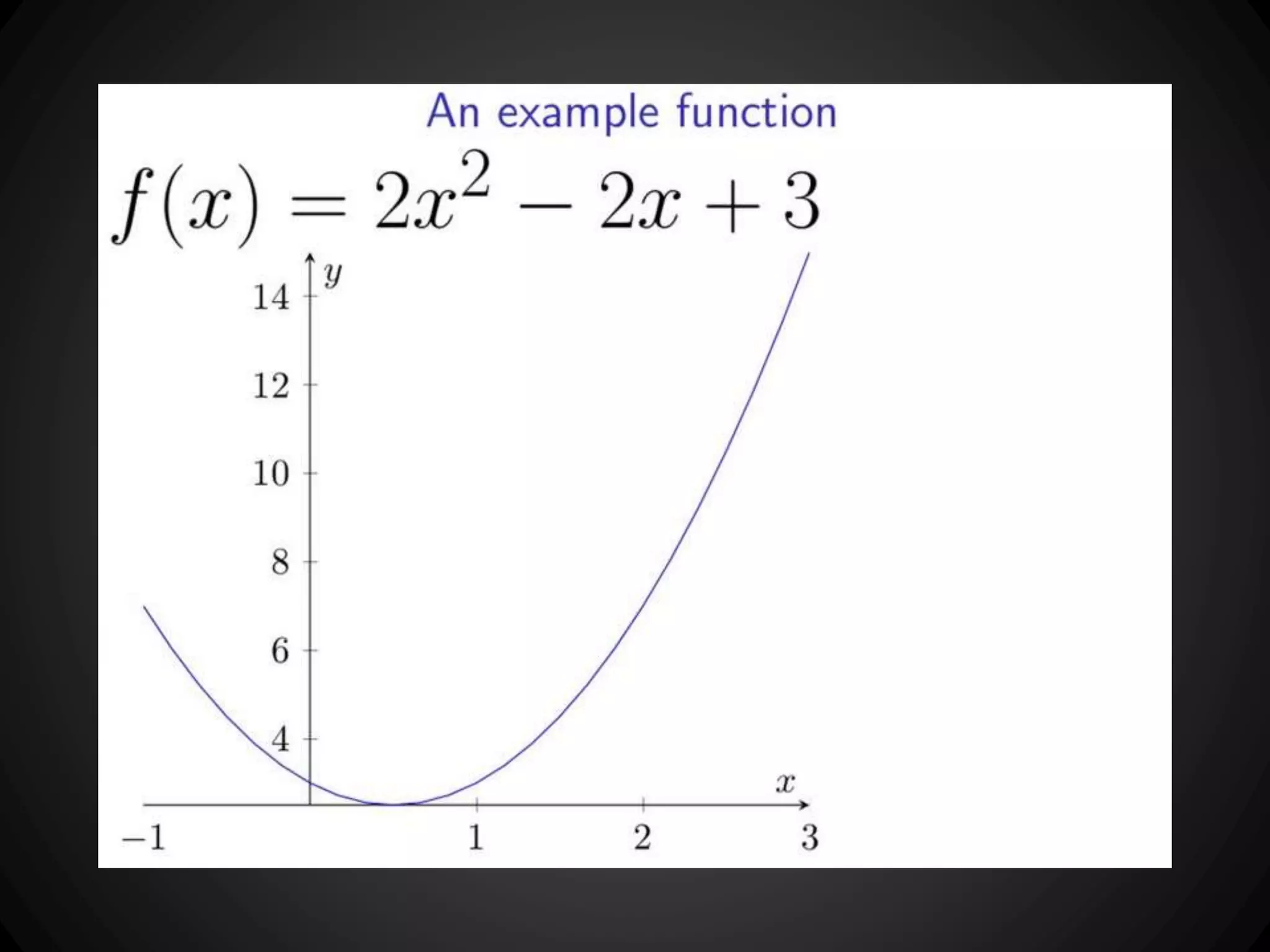
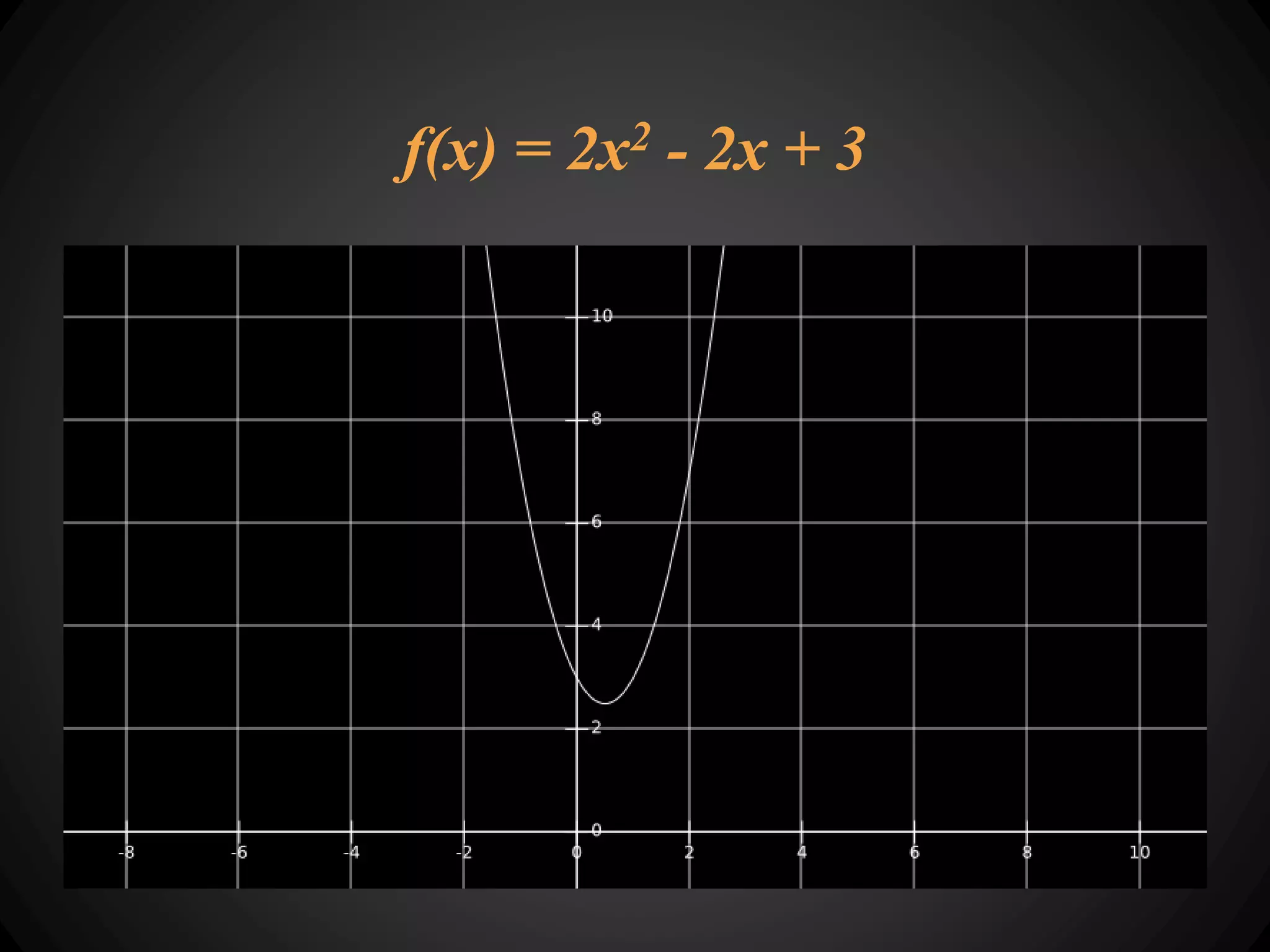

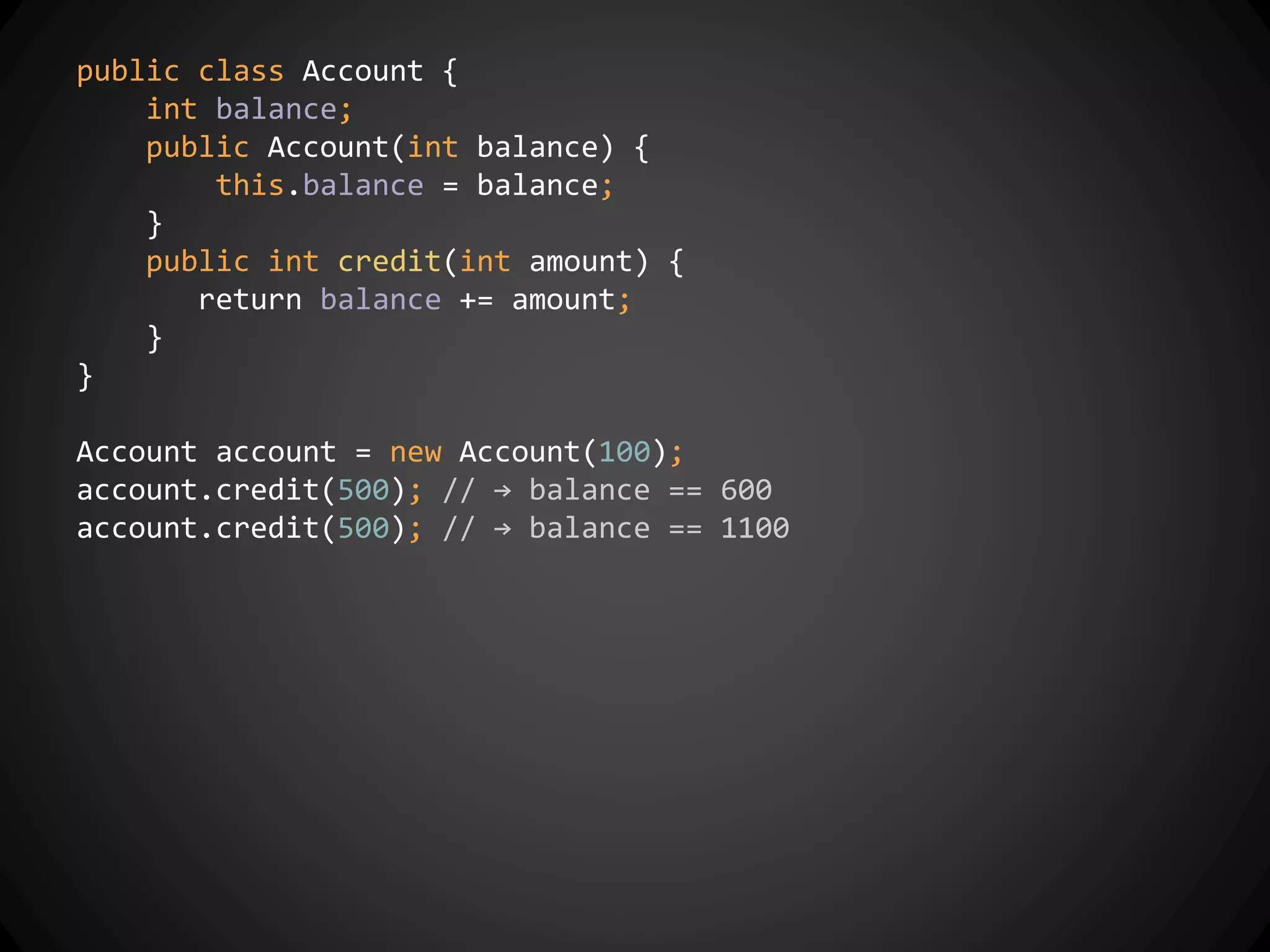
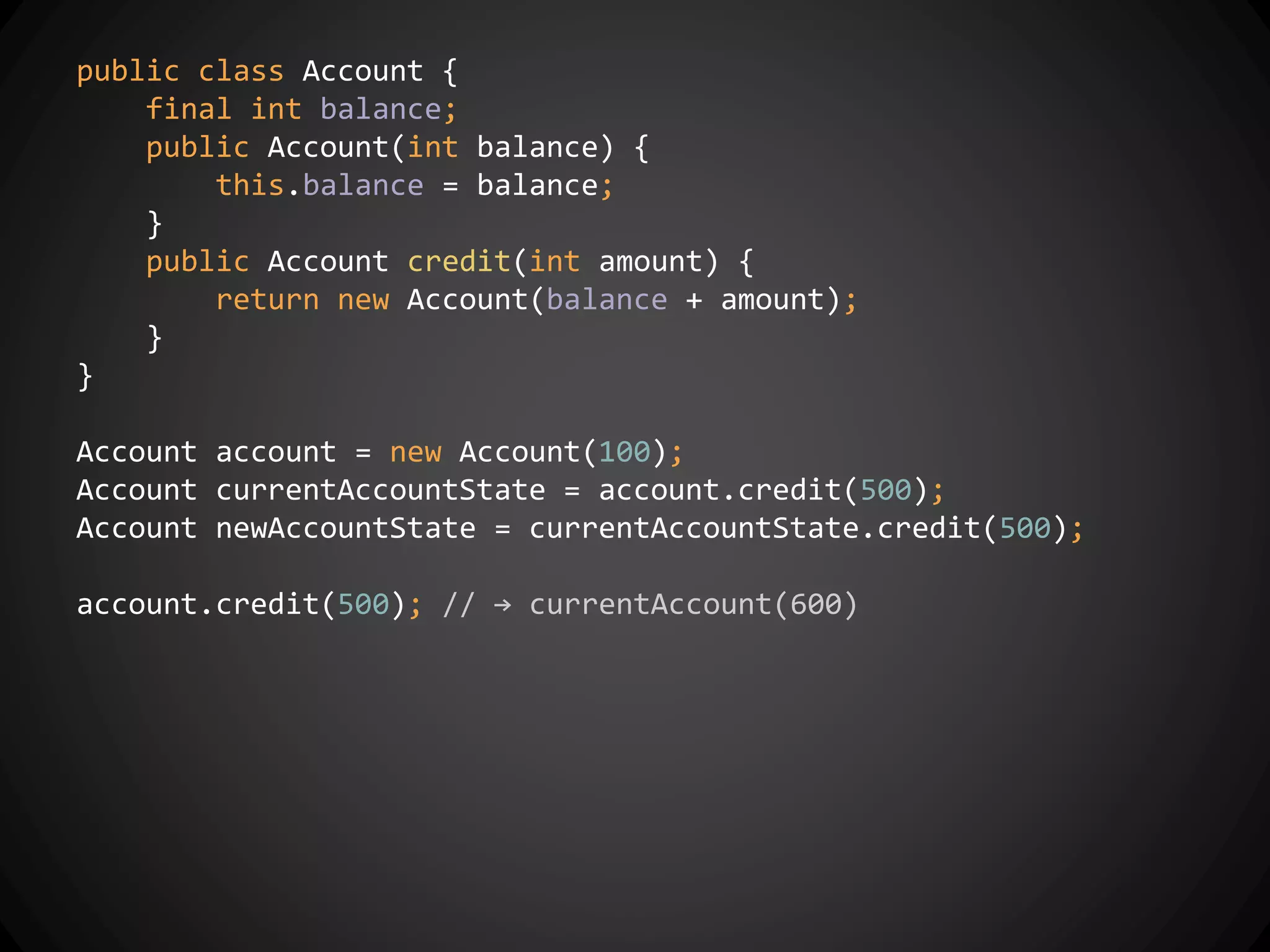


![public int calculate() {
int[] numbers = {1, 5, 10, 9, 12};
List<Integer> doubledEvenNumbers = new ArrayList<>();
int total = c;
for (int number : numbers)
if (number % 2 == 0)
total += num * 2;
return total;
}
Imperative Style](https://image.slidesharecdn.com/3ofzgd4scm0phnsdo7ha-signature-c42cd288f9f5fa19cb66a0002488f3771119bbe3db2edf123c6c85ff47b7d3f3-poli-150912132756-lva1-app6892/75/Functional-programming-126-2048.jpg)