Data structures in scala

Data structures in scala

• 1.
  Data Structures InScala Meetu Maltiar Principal Consultant Knoldus
• 2.
  Agenda Queue Binary Tree Binary TreeTraversals
• 3.
  Functional Queue Functional Queueis a data structure that has three operations: head: returns first element of the Queue tail: returns a Queue without its Head enqueue: returns a new Queue with given element at Head Has therefore First In First Out (FIFO) property
• 4.
  Functional Queue Continued scala>val q = scala.collection.immutable.Queue(1, 2, 3) q: scala.collection.immutable.Queue[Int] = Queue(1, 2, 3) scala> val q1 = q enqueue 4 q1: scala.collection.immutable.Queue[Int] = Queue(1, 2, 3, 4) scala> q res3: scala.collection.immutable.Queue[Int] = Queue(1, 2, 3) scala> q1 res4: scala.collection.immutable.Queue[Int] = Queue(1, 2, 3, 4)
• 5.
  Simple Queue Implementation classSlowAppendQueue[T](elems: List[T]) { def head = elems.head def tail = new SlowAppendQueue(elems.tail) def enqueue(x: T) = new SlowAppendQueue(elems ::: List(x)) } Head and tail operations are fast. Enqueue operation is slow as its performance is directly proportional to number of elements.
• 6.
  Queue Optimizing Enqueue classSlowHeadQueue[T](smele: List[T]) { // smele is elems reversed def head = smele.last // Not efficient def tail = new SlowHeadQueue(smele.init) // Not efficient def enqueue(x: T) = new SlowHeadQueue(x :: smele) } smele is elems reversed. Head operation is not efficient. Neither is tail operation. As both last and init performance is directly proportional to number of elements in Queue
• 7.
  Functional Queue class Queue[T](privateval leading: List[T], private val trailing: List[T]) { private def mirror = if (leading.isEmpty) new Queue(trailing.reverse, Nil) else this def head = mirror.leading.head def tail = { val q = mirror new Queue(q.leading.tail, q.trailing) } def enqueue(x: T) = new Queue(leading, x :: trailing) }
• 8.
  Binary Search Tree BSTis organized tree. BST has nodes one of them is specified as Root node. Each node in BST has not more than two Children. Each Child is also a Sub-BST. Child is a leaf if it just has a root.
• 9.
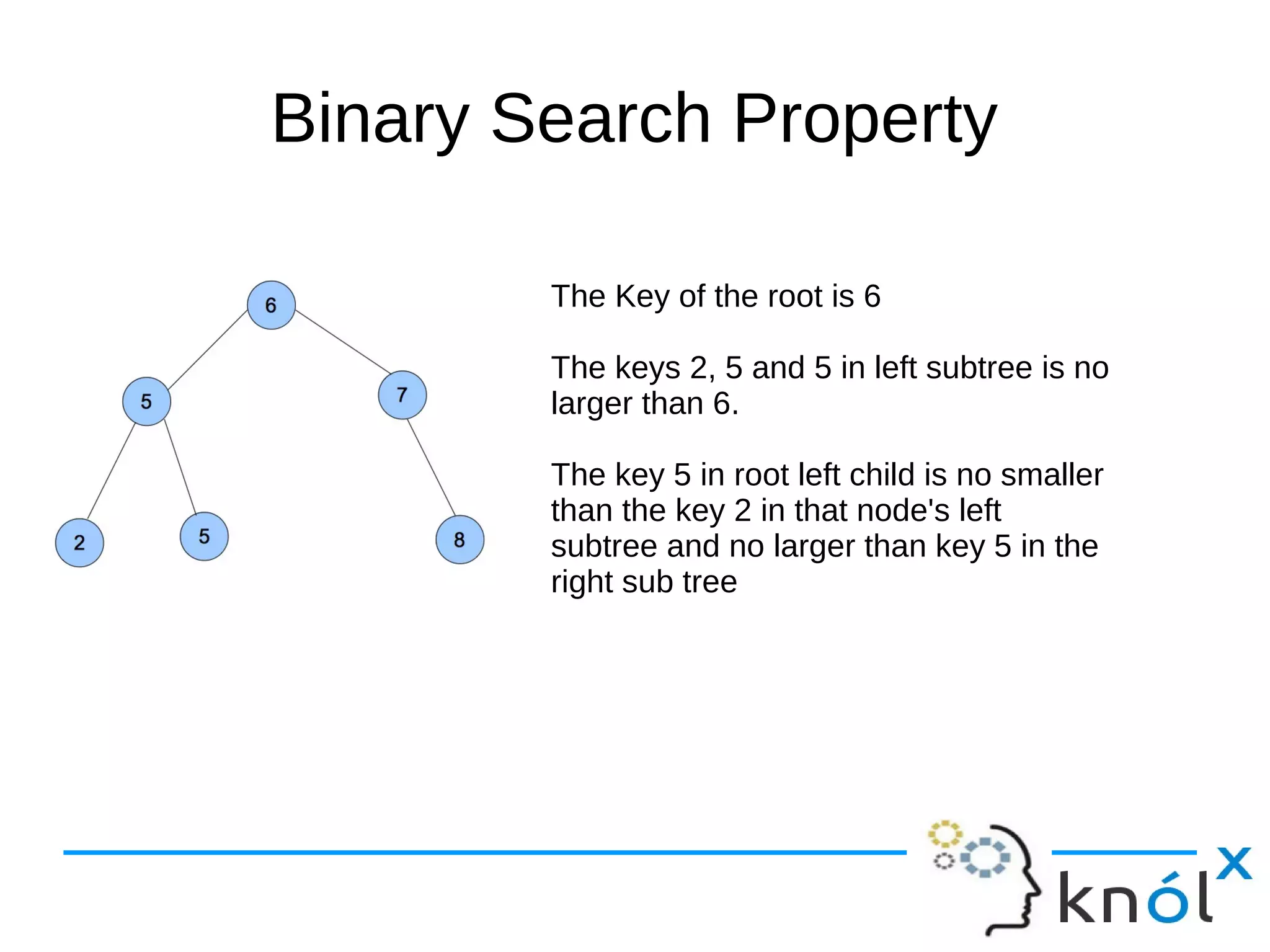
  Binary Search Property Thekeys in Binary Search Tree is stored to satisfy following property: Let x be a node in BST. If y is a node in left subtree of x Then Key[y] less than equal key[x] If y is a node in right subtree of x Then key[x] less than equal key[y]
• 10.
  Binary Search Property The Key of the root is 6 The keys 2, 5 and 5 in left subtree is no larger than 6. The key 5 in root left child is no smaller than the key 2 in that node's left subtree and no larger than key 5 in the right sub tree
• 11.
  Tree Scala Representation caseclass Tree[+T](value: T, left: Option[Tree[T]], right: Option[Tree[T]]) This Tree representation is a recursive definition and has type parameterization and is covariant due to is [+T] signature This Tree class definition has following properties: 1. Tree has value of the given node 2. Tree has left sub-tree and it may have or do not contain value 3. Tree has right sub-tree and it may have or do not contain value It is covariant to allow subtypes to be contained in the Tree
• 12.
  Tree In-order Traversal BSTproperty enables us to print out all the Keys in a sorted order using simple recursive In-order traversal. It is called In-Order because it prints key of the root of a sub-tree between printing of the values in its left sub- tree and printing those in its right sub- tree
• 13.
  Tree In-order Algorithm INORDER-TREE-WALK(x) 1.if x != Nil 2. INORDER-TREE-WALK(x.left) 3. println x.key 4. INORDER-TREE-WALK(x.right) For our BST in example before the output expected will be: 255678
• 14.
  Tree In-order Scala def inOrder[A](t: Option[Tree[A]], f: Tree[A] => Unit): Unit = t match { case None => case Some(x) => if (x.left != None) inOrder(x.left, f) f(x) if (x.right != None) inOrder(x.right, f) }
• 15.
  Tree Pre-order Algorithm PREORDER-TREE-WALK(x) 1.if x != Nil 2. println x.key 3. PREORDER-TREE-WALK(x.left) 4. PREORDER-TREE-WALK(x.right) For our BST in example before the output expected will be: 652578
• 16.
  Tree Pre-order Scala defpreOrder[A](t: Option[Tree[A]], f: Tree[A] => Unit): Unit = t match { case None => case Some(x) => f(x) if (x.left != None) inOrder(x.left, f) if (x.right != None) inOrder(x.right, f) } Pre-Order traversal is good for creating a copy of the Tree
• 17.
  Tree Post-Order Algorithm POSTORDER-TREE-WALK(x) 1.if x != Nil 2. POSTORDER-TREE-WALK(x.left) 3. POSTORDER-TREE-WALK(x.right) 4. println x.key For our BST in example before the output expected will be: 255876 Useful in deleting a tree. In order to free up resources a node in the tree can only be deleted if all the children (left and right) are also deleted Post-Order does exactly that. It processes left and right sub-trees before processing current node
• 18.
  Tree Post-order Scala defpostOrder[A](t: Option[Tree[A]], f: Tree[A] => Unit): Unit = t match { case None => case Some(x) => if (x.left != None) postOrder(x.left, f) if (x.right != None) postOrder(x.right, f) f(x) }
• 19.
  References 1. Cormen Introductionto Algorithms 2. Binary Search Trees Wikipedia 3. Martin Odersky “Programming In Scala” 4. Daniel spiewak talk “Extreme Cleverness: Functional Data Structures In Scala”
• 20.
  Thank You!!