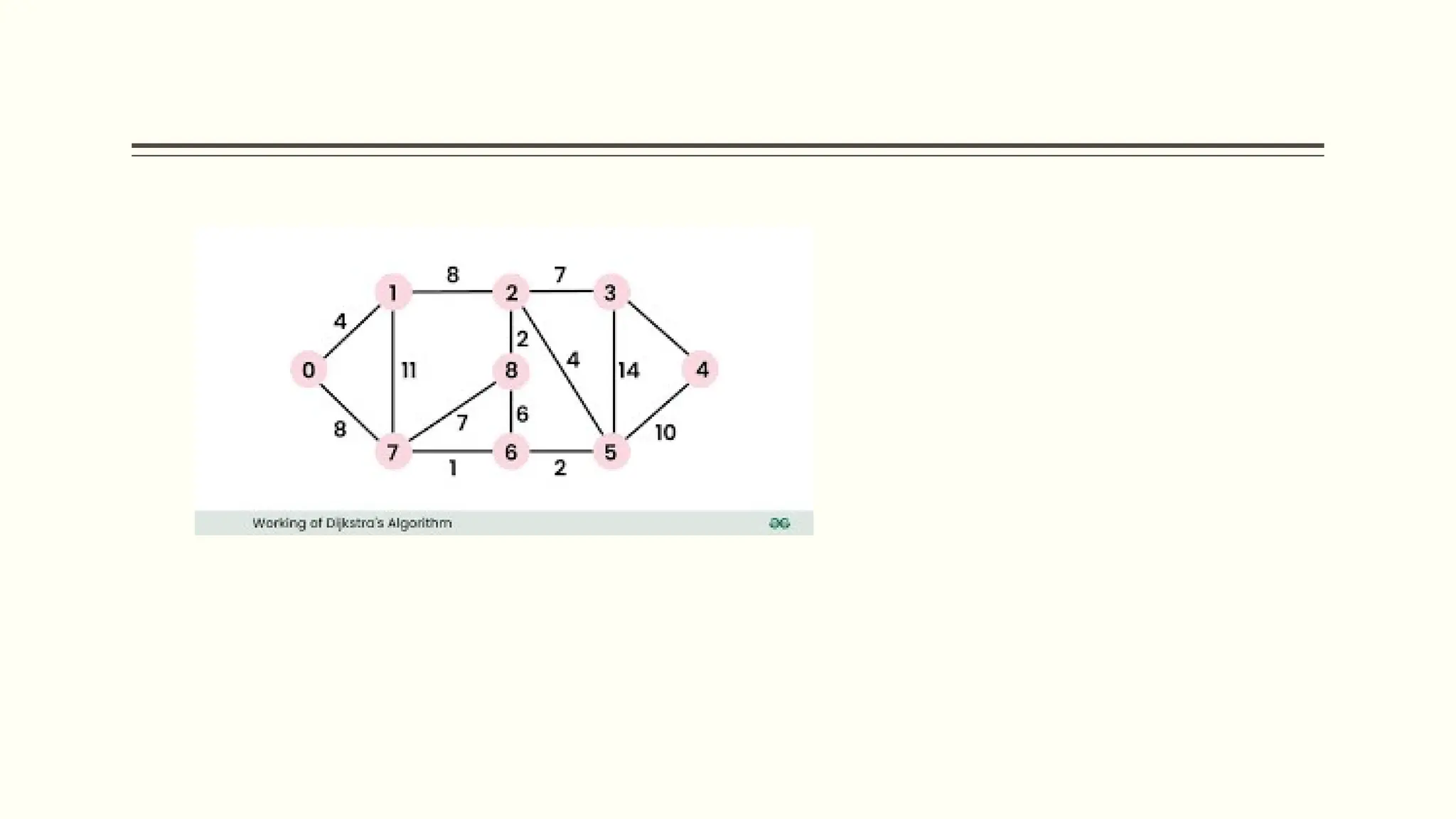
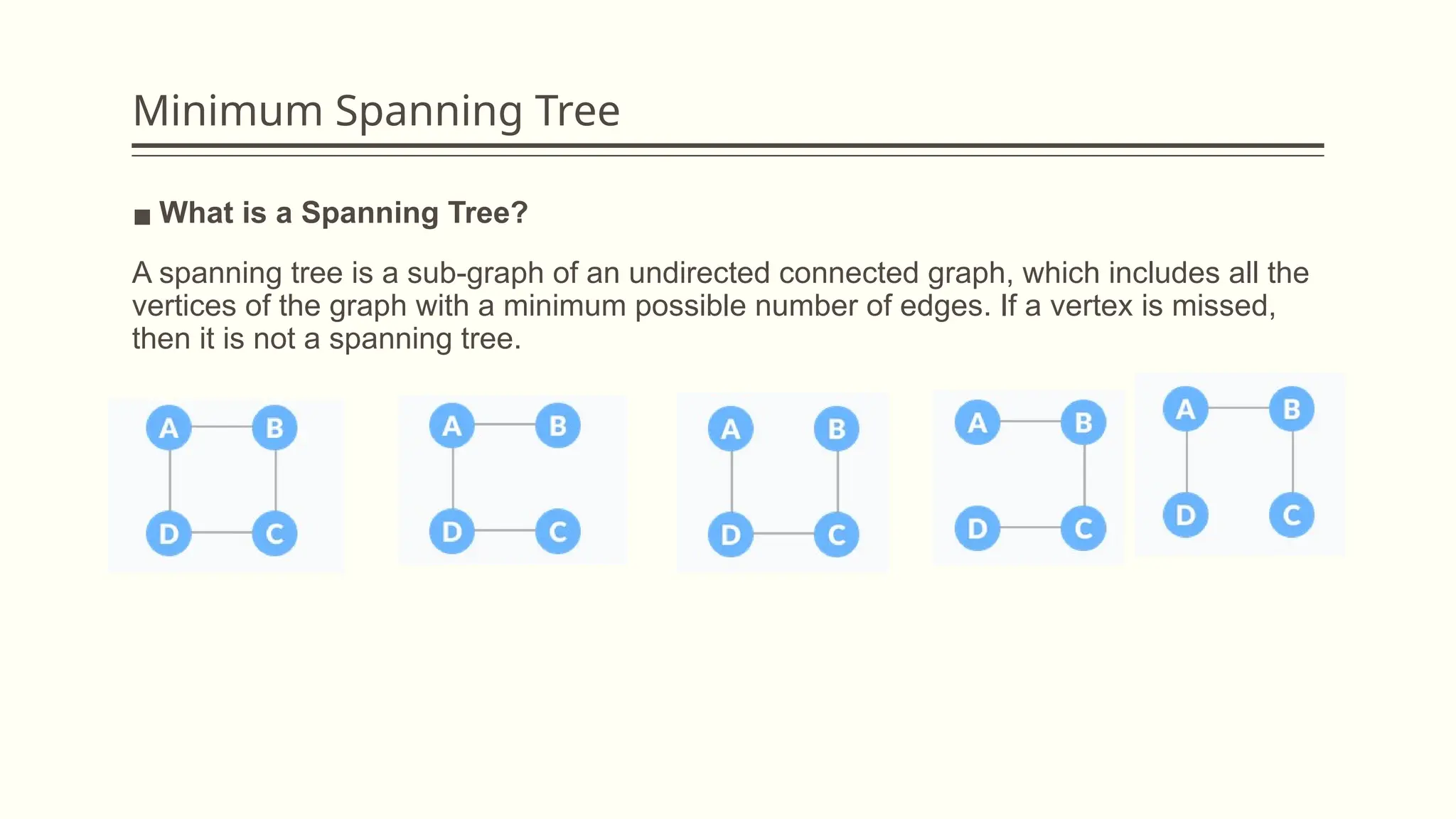
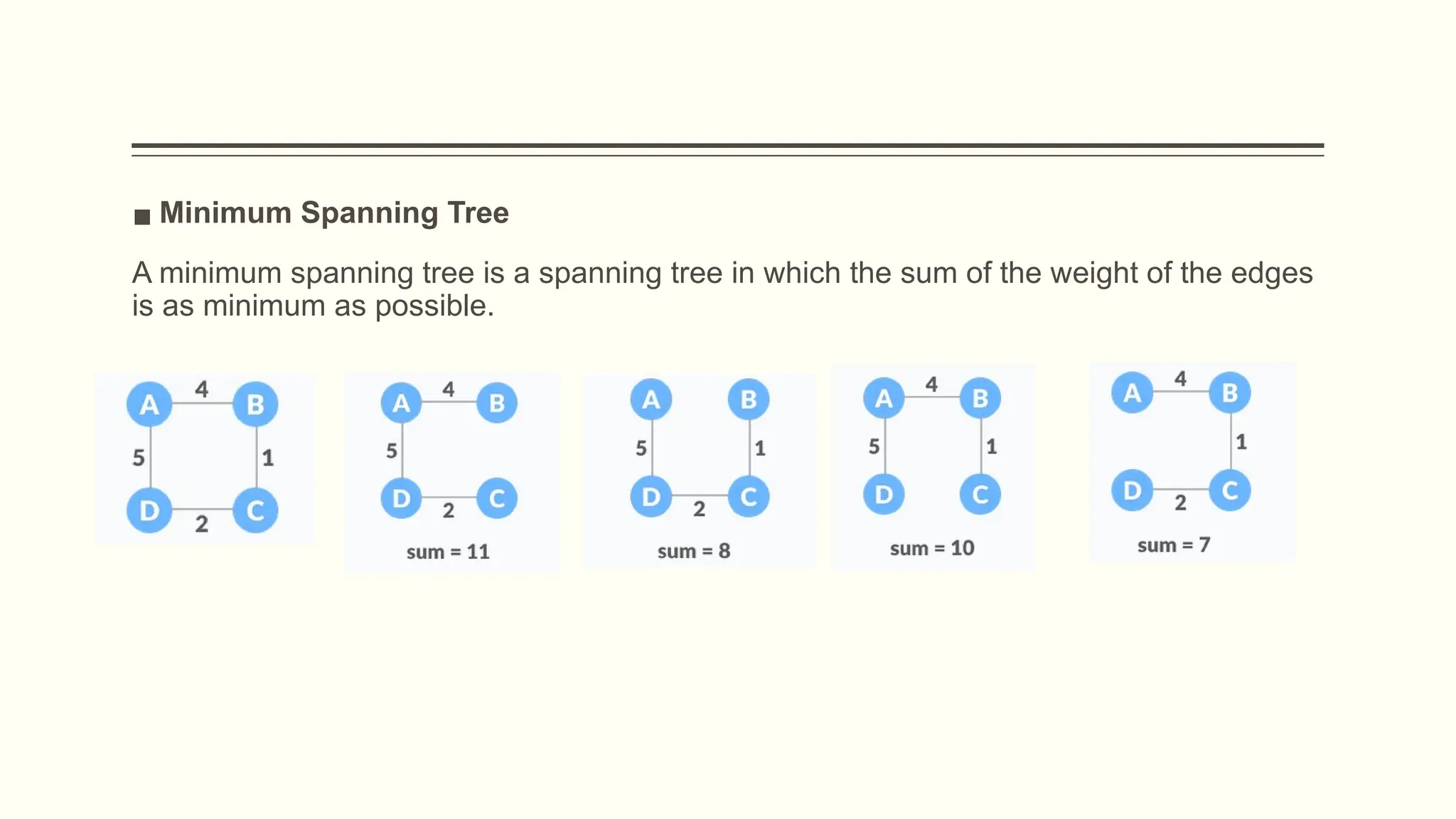
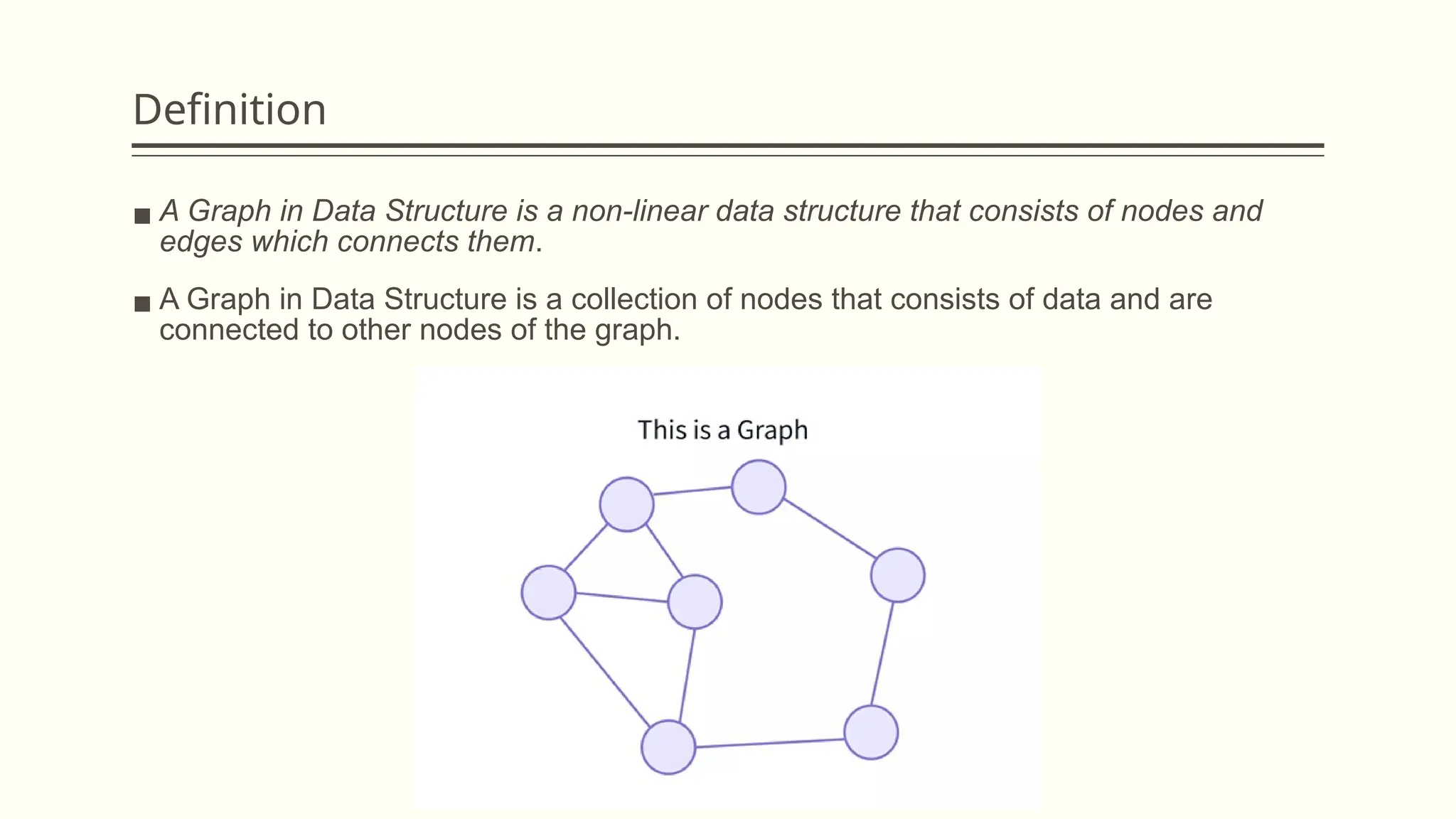
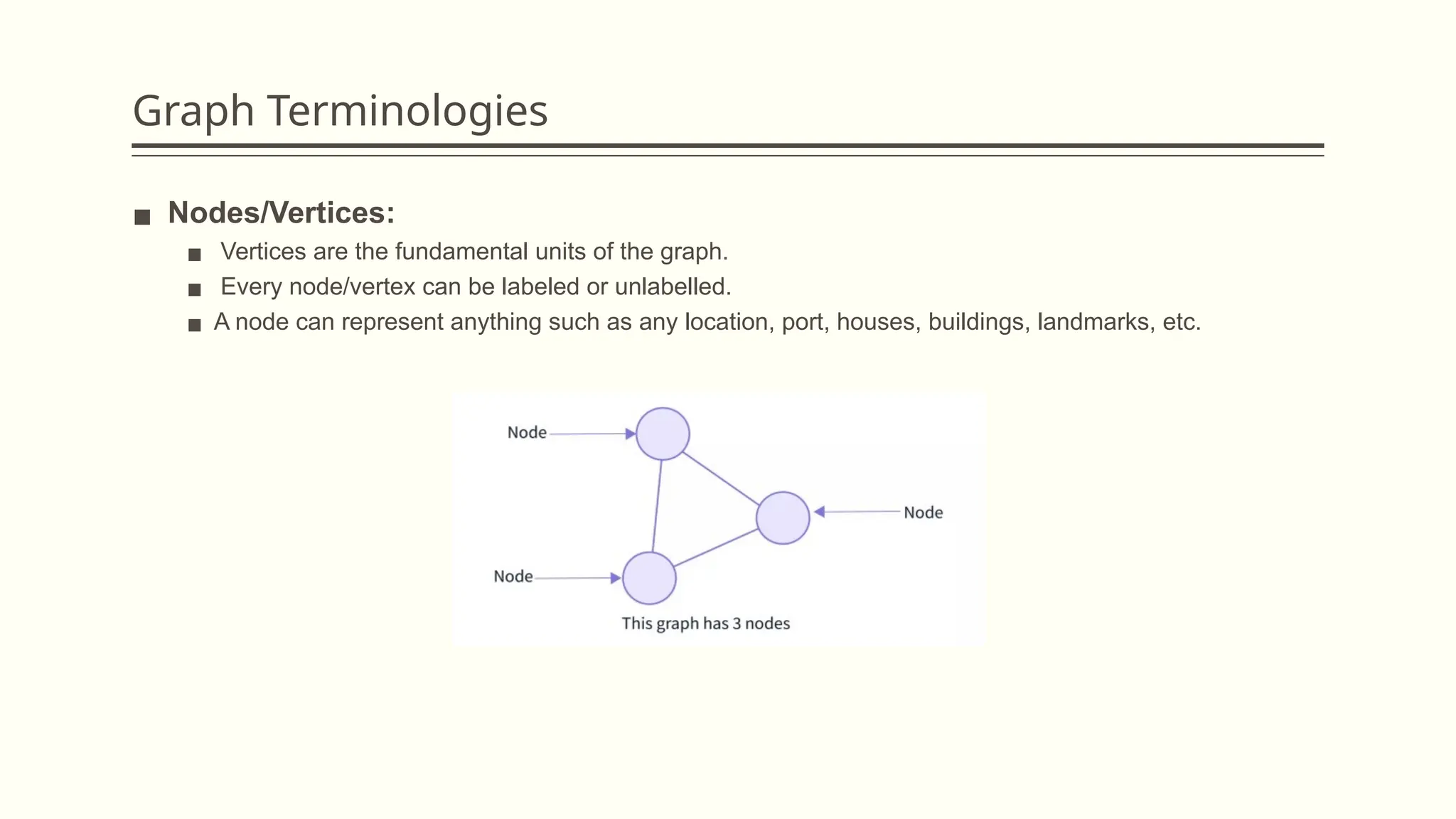
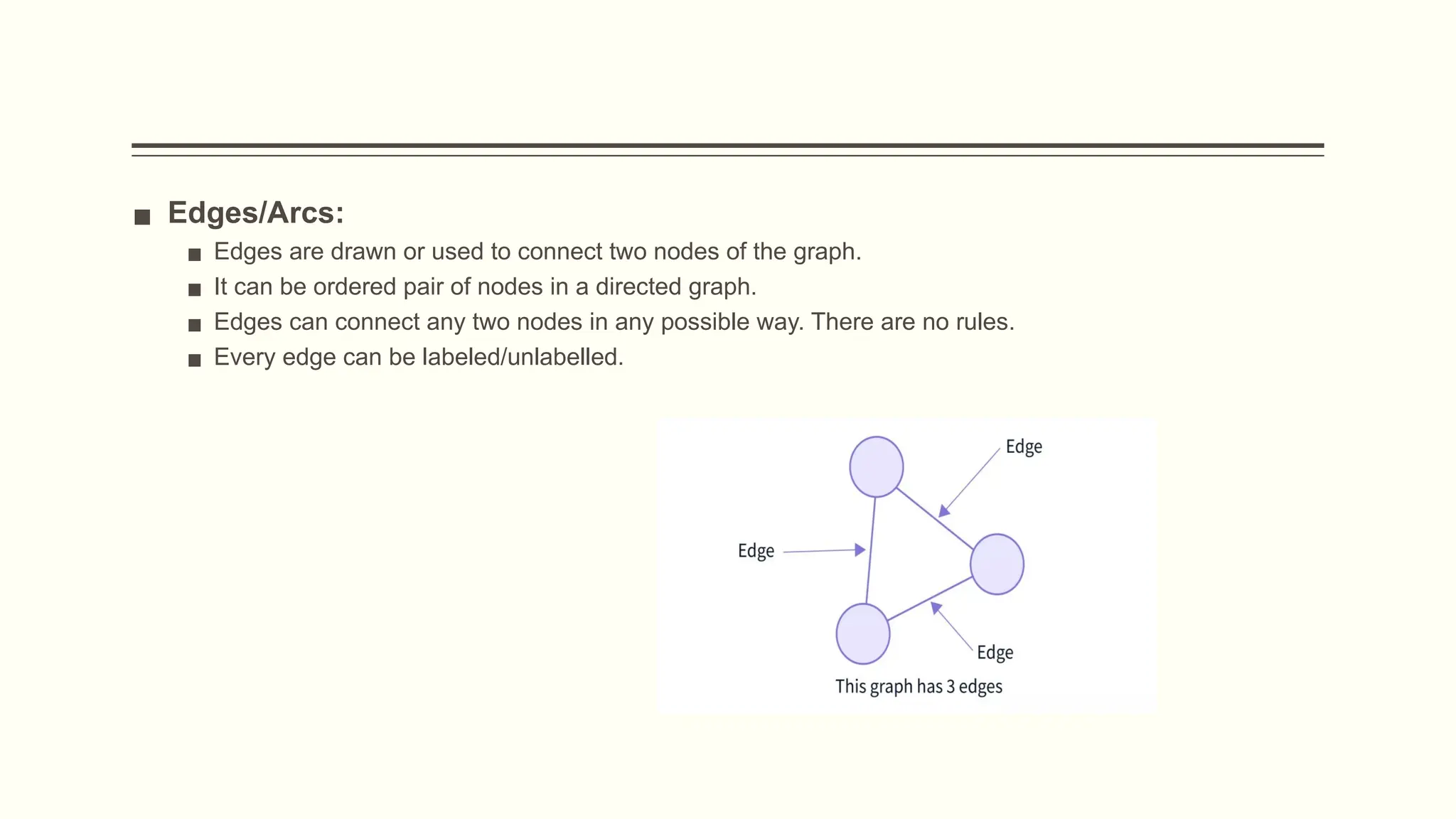
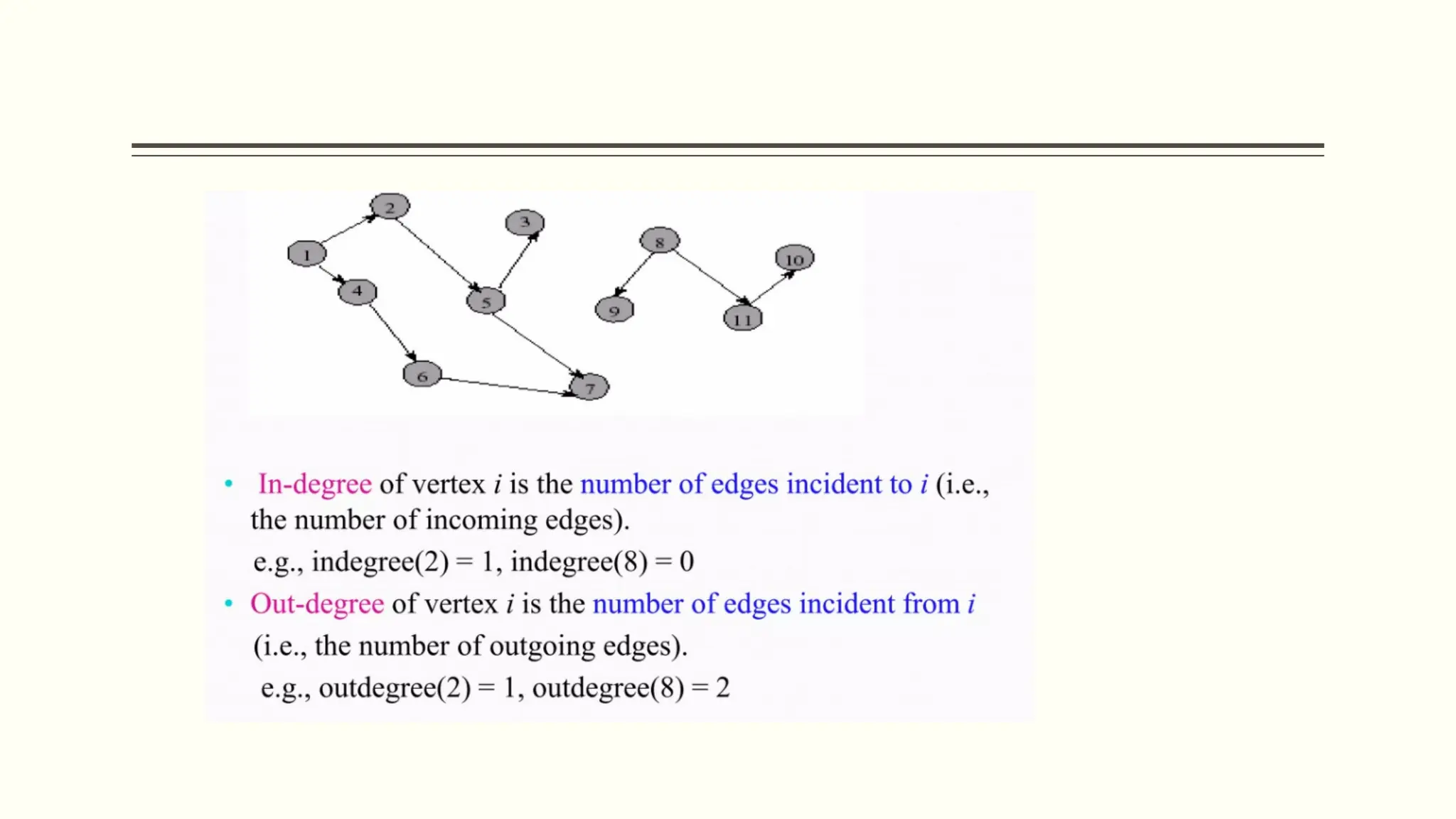
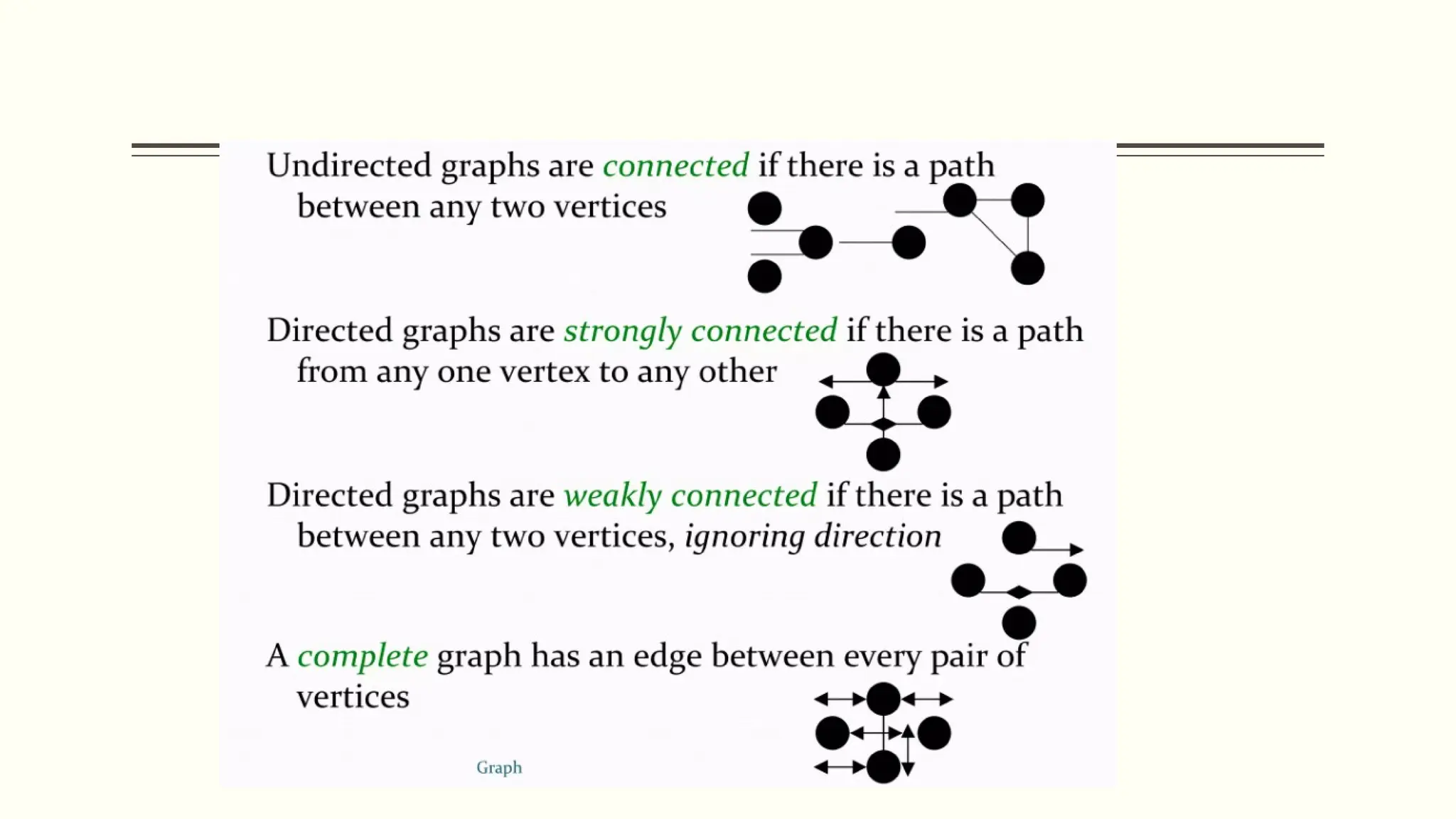
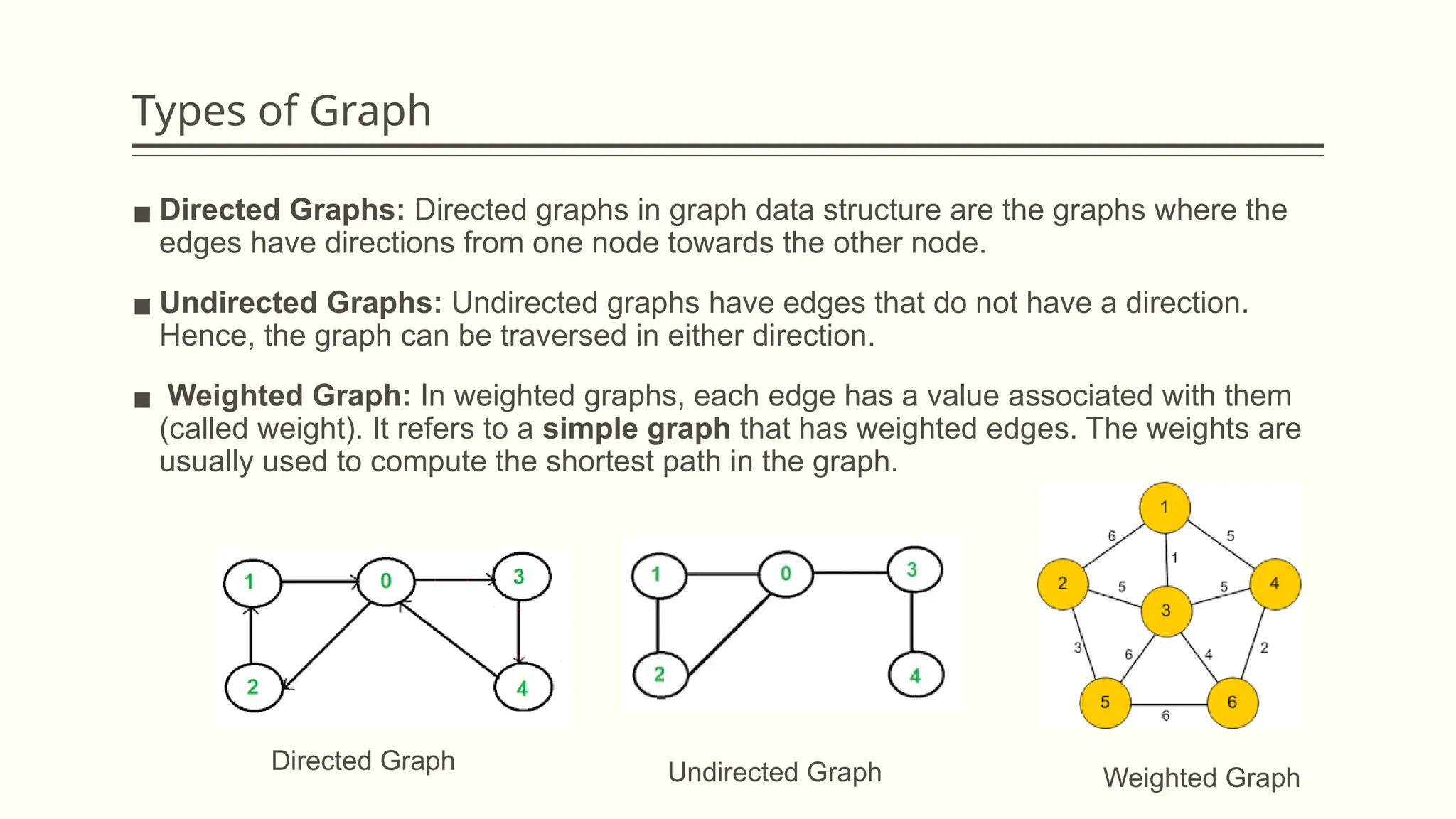
The document provides a comprehensive overview of graph data structures, explaining key concepts such as nodes, edges, graph types, and terminologies like cycles and paths. It introduces various graph representations like adjacency matrices and lists, as well as traversal techniques such as Depth First Search (DFS) and Breadth First Search (BFS). Additionally, it discusses applications of graphs in fields like computer science, social networks, and GPS systems, highlighting algorithms for finding shortest paths and constructing minimum spanning trees.



![Degree of a Node
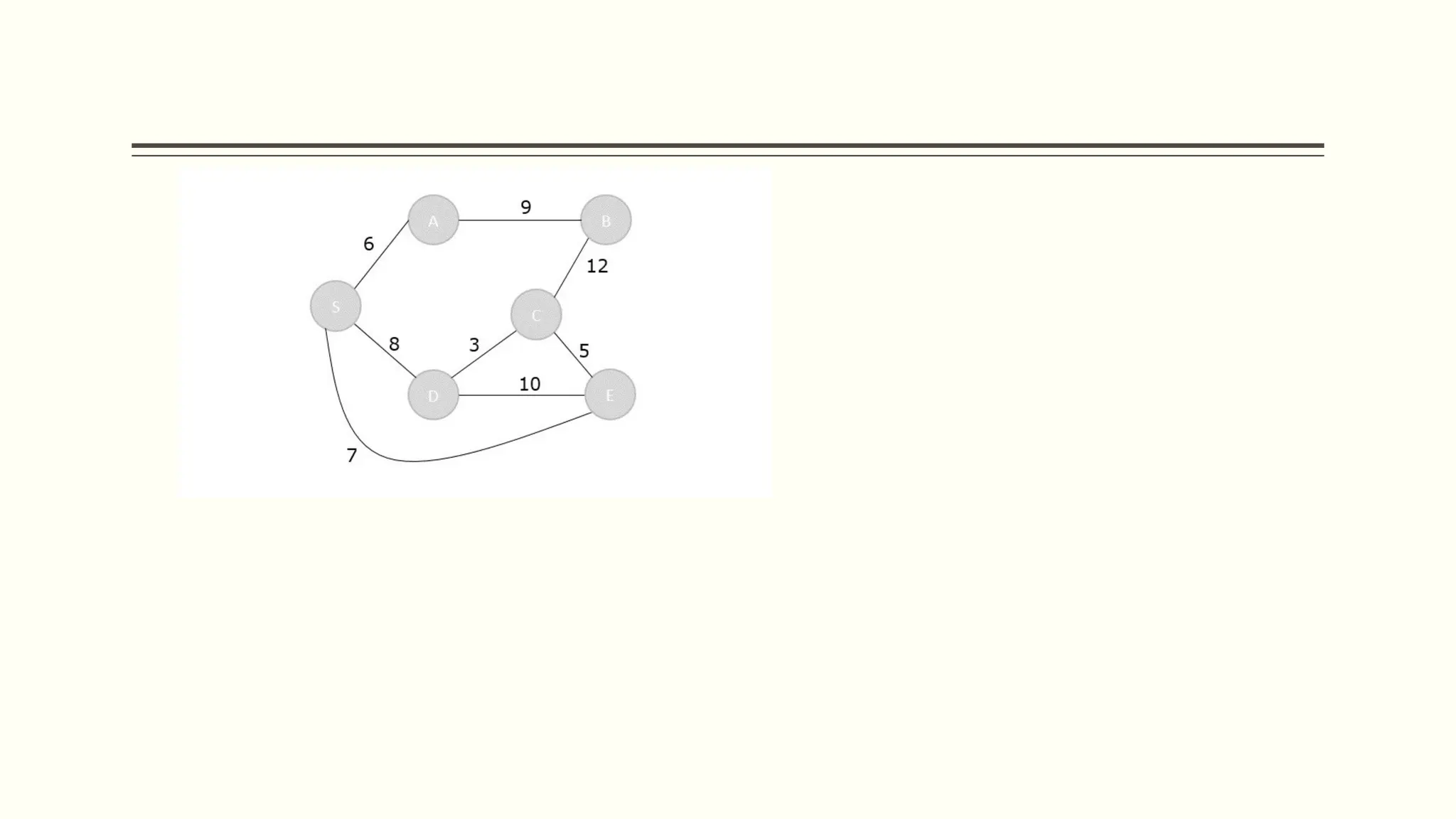
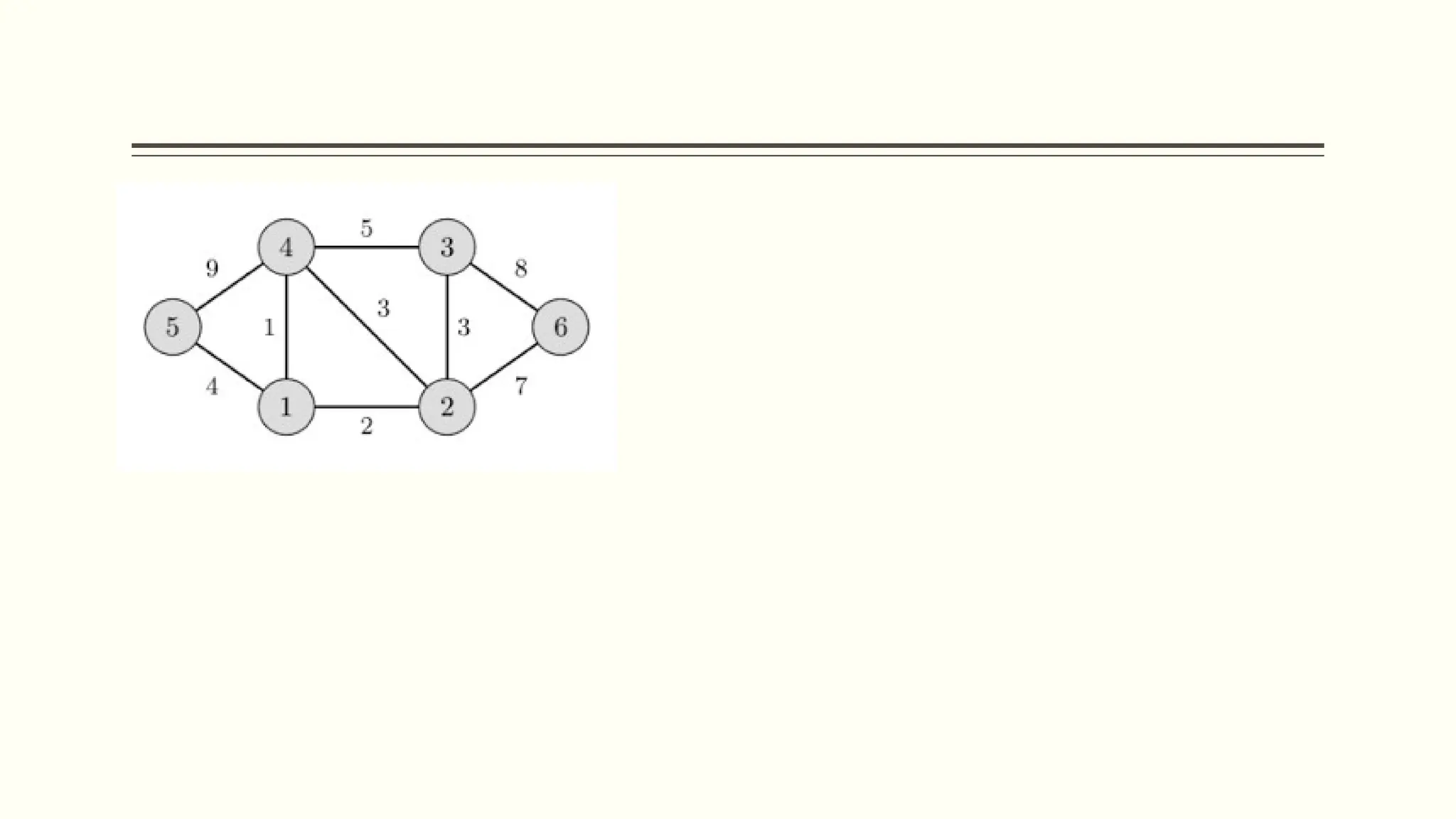
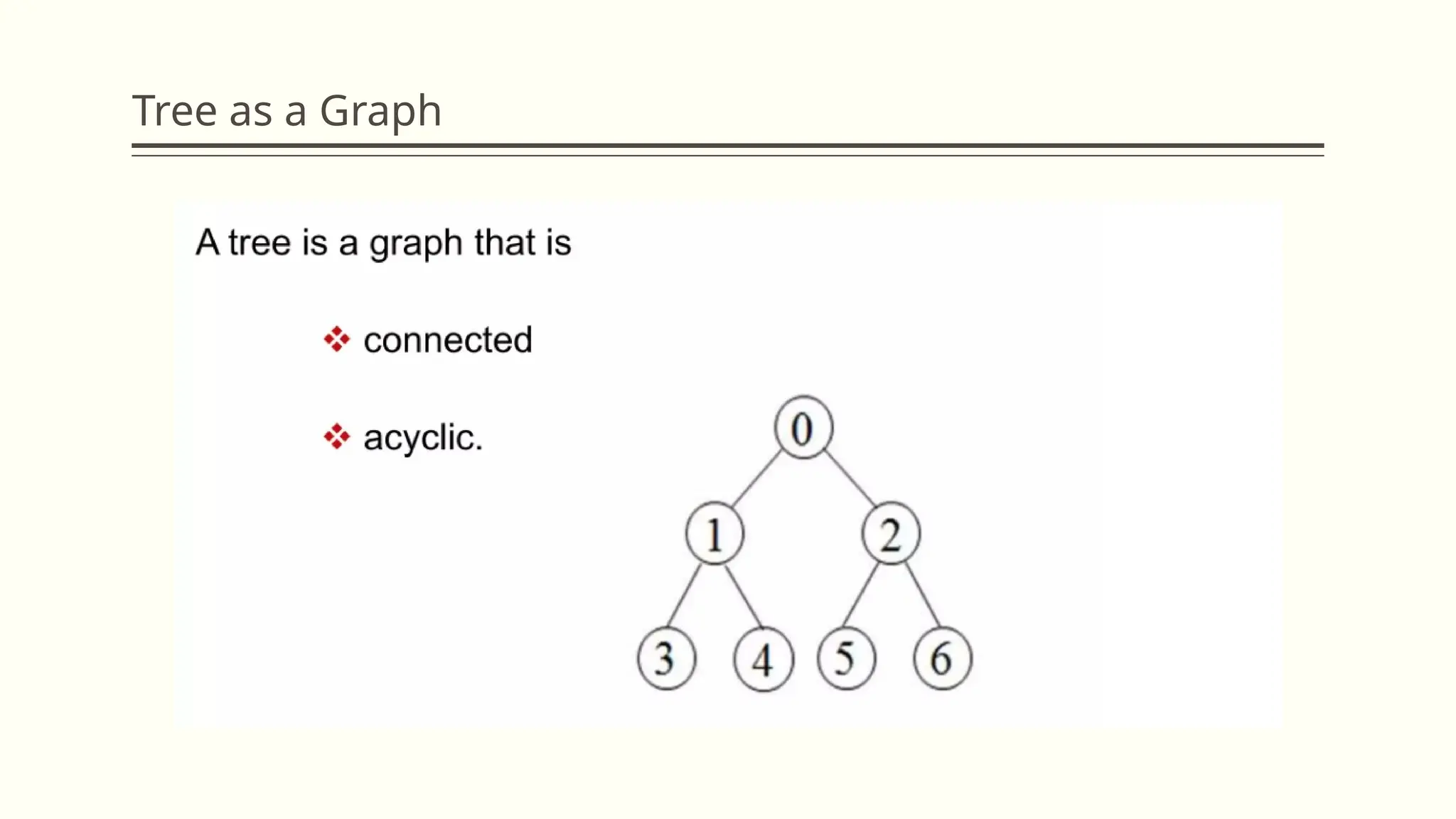
▪ Cycle: a path that starts and ends on the same vertex
▪ Simple path: a path that does not cross itself
▪ That is, no vertex is repeated (except first and last)
▪ Simple paths cannot contain cycles
A sequence of vertices: (A, B, C, D) [Is this path, simple
path, cycle?]
(A, B, D, A, C) [path, simple path, cycle?]
(A, B, D, A, C) [path, simple path, cycle?]
Cycle: ?](https://image.slidesharecdn.com/graph1-241206032209-2f480573/75/Data-Structure-and-algorithms-Graph1-pptx-8-2048.jpg)

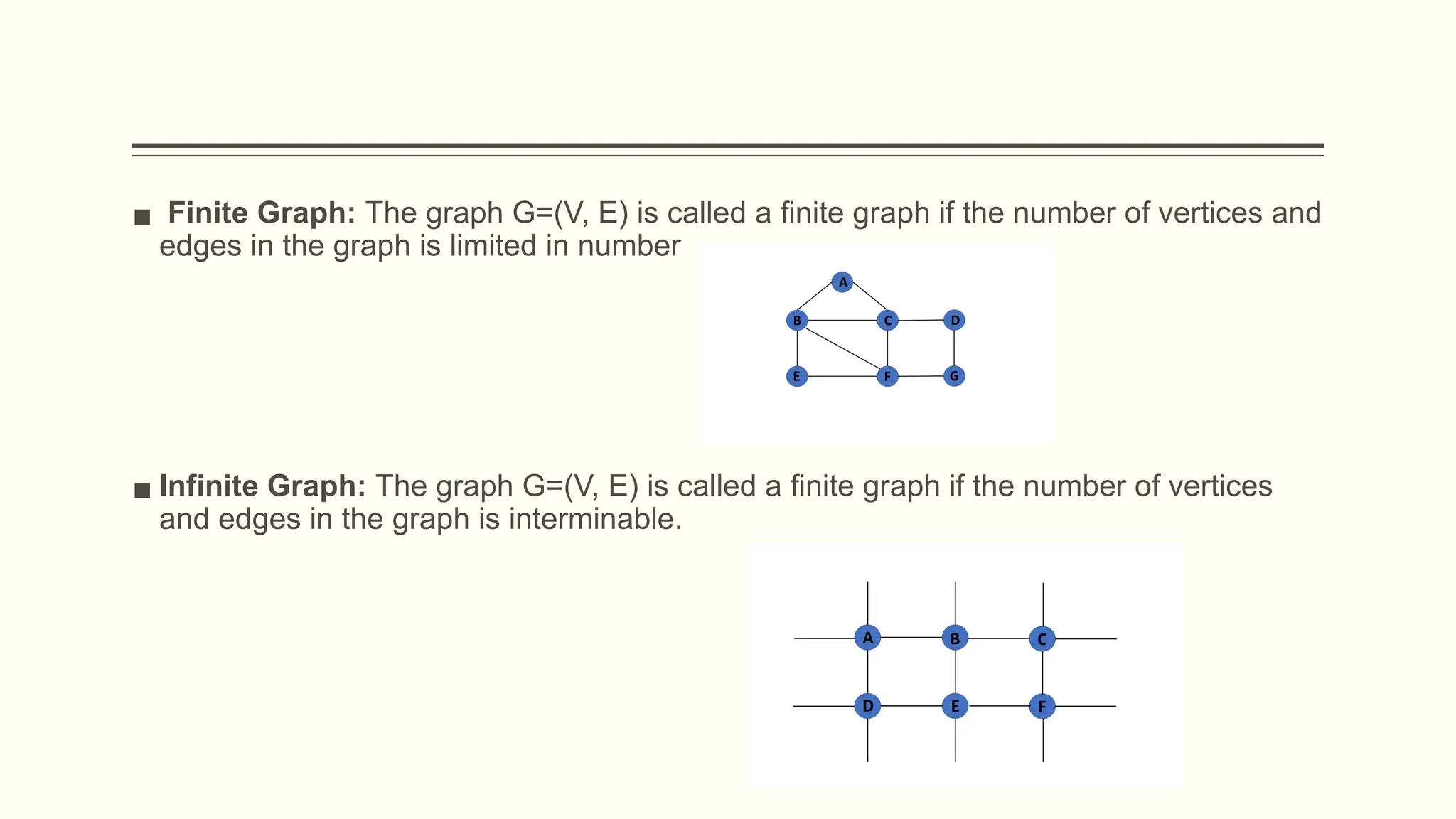
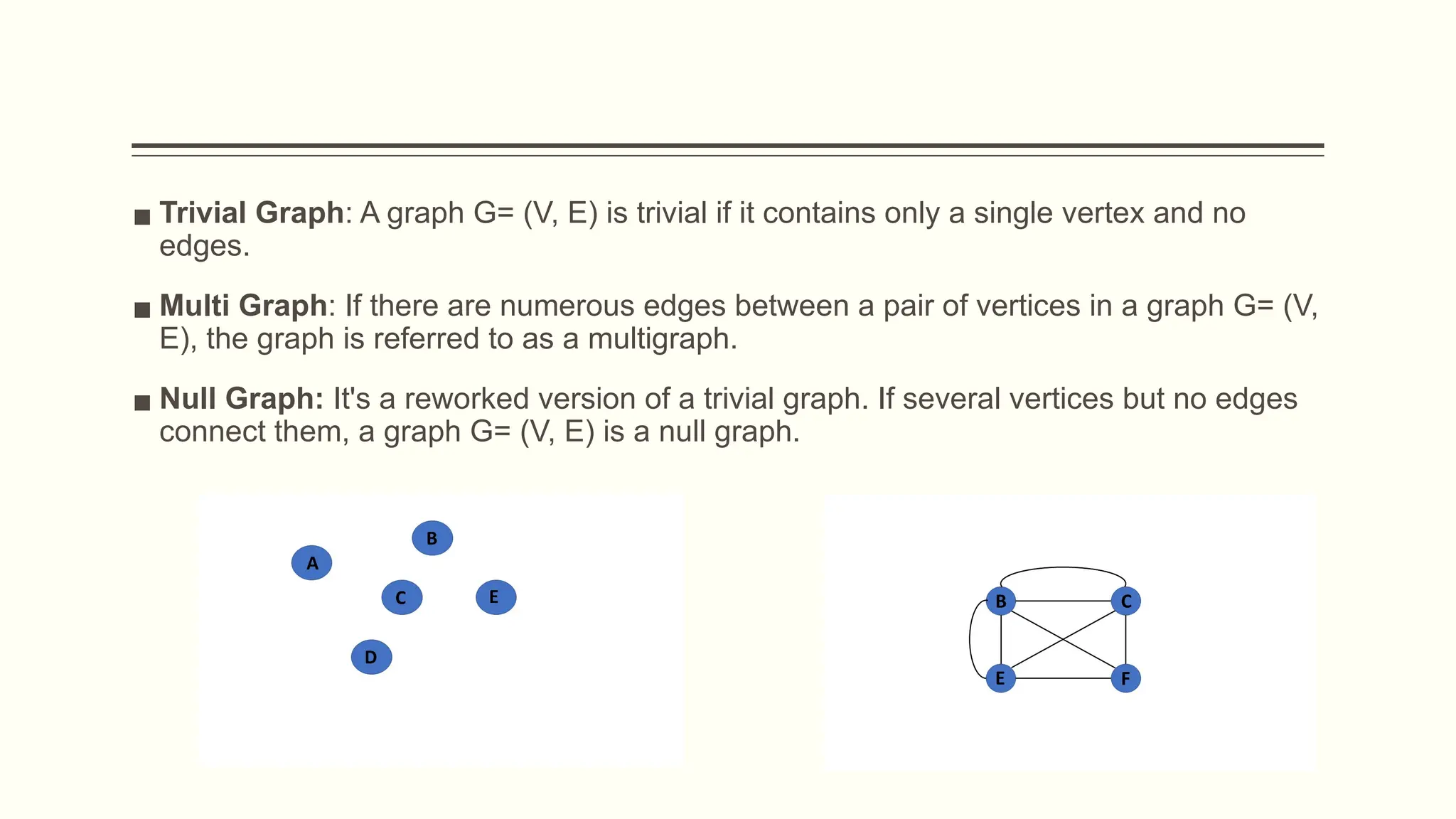
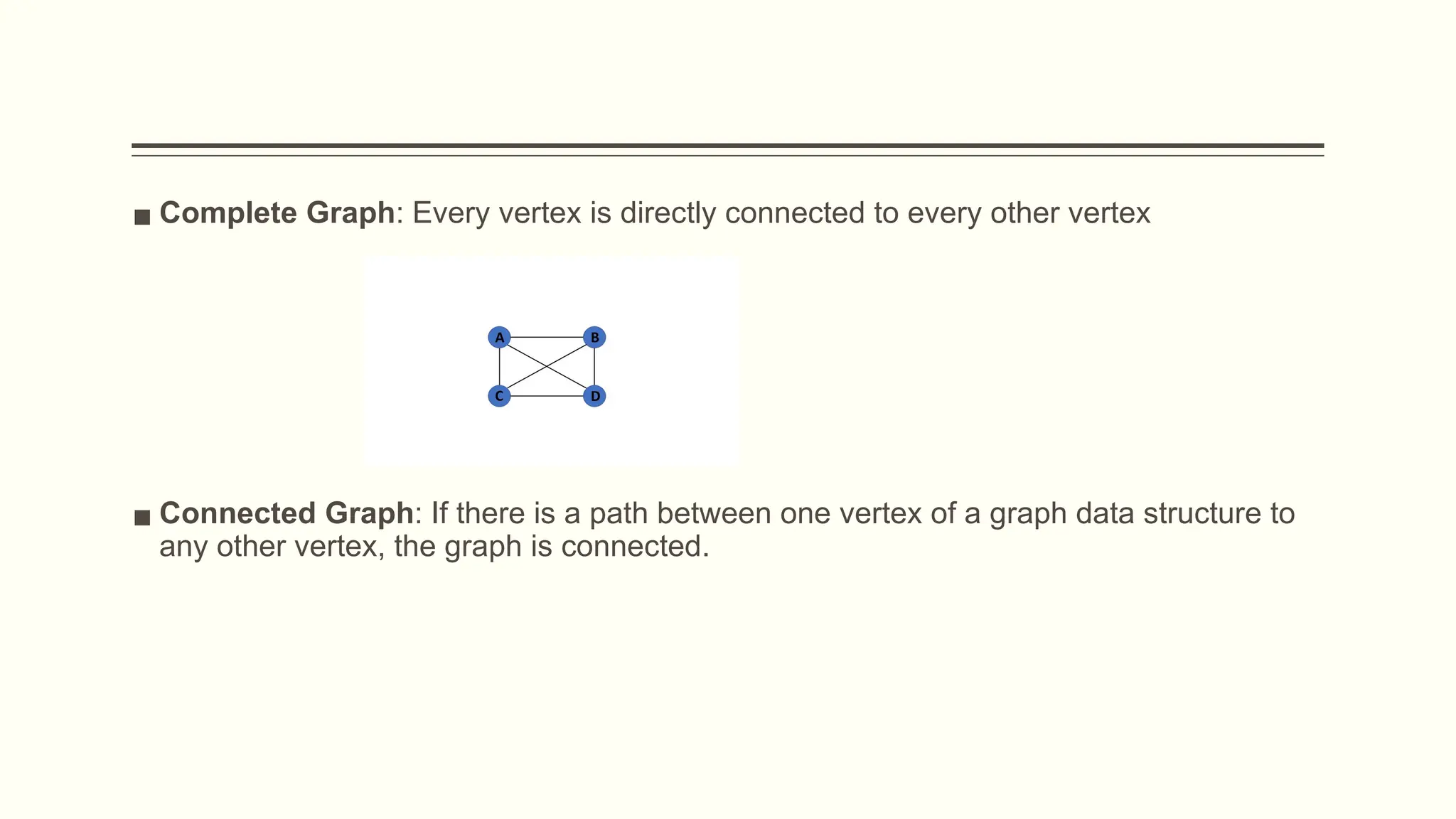
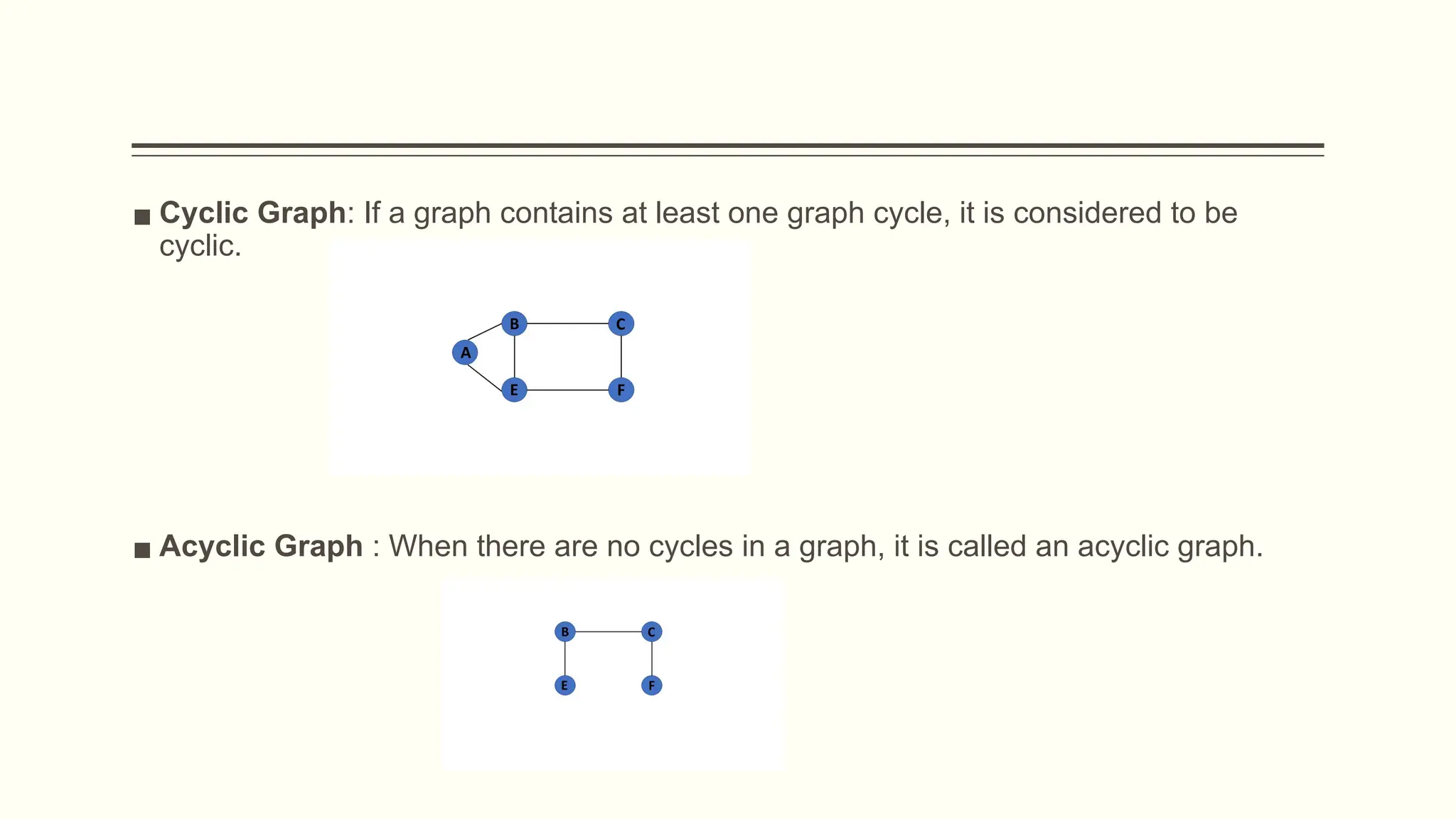







![DFS Traversal
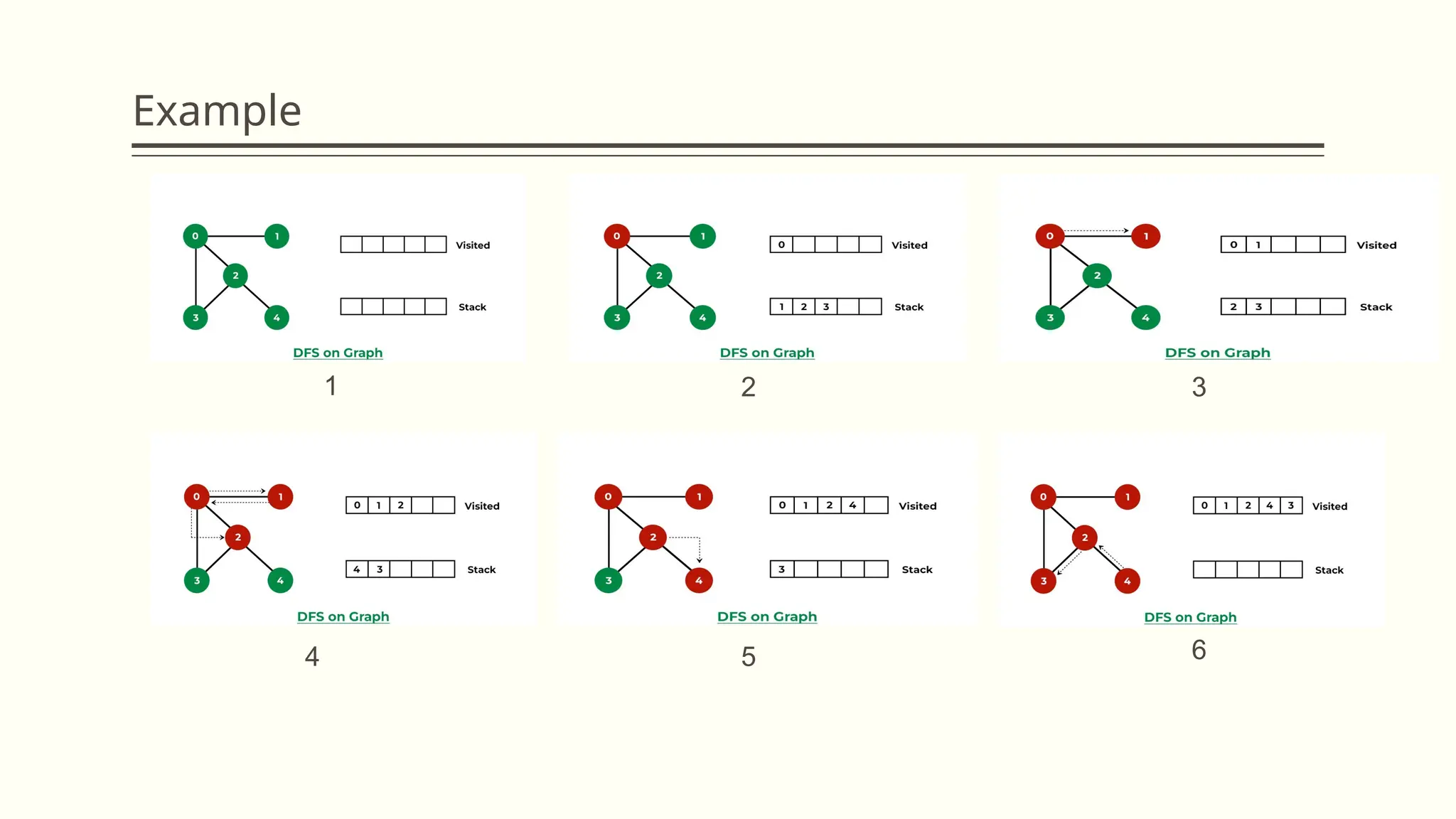
▪ Step 1: SET STATUS = 1 (ready state) for each node in G
▪ Step 2: Push the starting node A on the stack and set its STATUS = 2 (waiting state)
▪ Step 3: Repeat Steps 4 and 5 until STACK is empty
▪ Step 4: Pop the top node N. Process it and set its STATUS = 3 (processed state)
▪ Step 5: Push on the stack all the neighbors of N that are in the ready state (whose STATUS = 1) and
set their STATUS = 2 (waiting state)
▪ [END OF LOOP]
▪ Step 6: EXIT](https://image.slidesharecdn.com/graph1-241206032209-2f480573/75/Data-Structure-and-algorithms-Graph1-pptx-30-2048.jpg)
![Pseudocode
DFS(G,v) ( v is the vertex where the search starts )
Stack S := {}; ( start with an empty stack )
for each vertex u, set visited[u] := false;
push S, v;
while (S is not empty) do
u := pop S;
if (not visited[u]) then
visited[u] := true;
for each unvisited neighbor w of u
push S, w;
end if
end while
END DFS()](https://image.slidesharecdn.com/graph1-241206032209-2f480573/75/Data-Structure-and-algorithms-Graph1-pptx-31-2048.jpg)

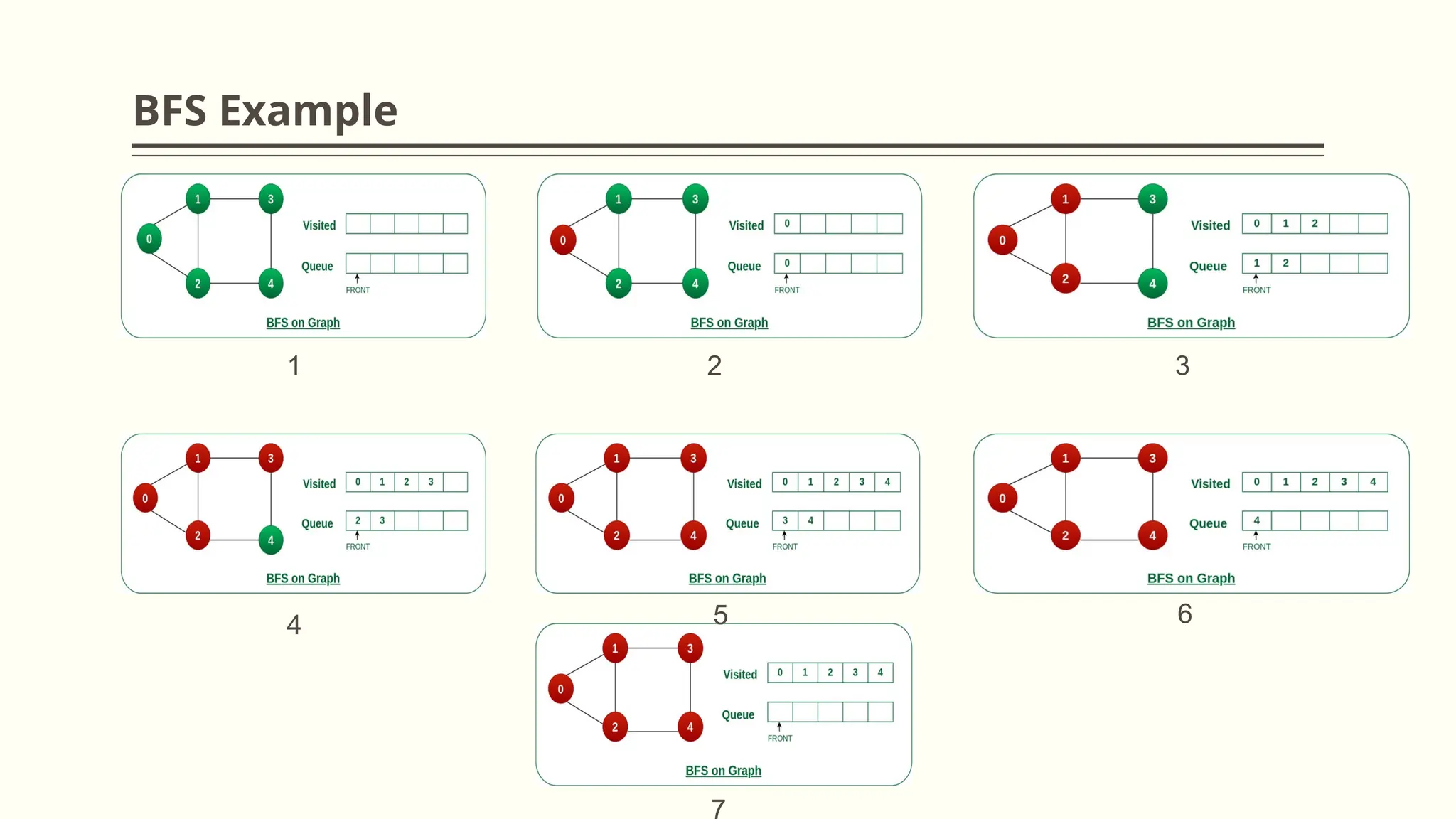
![BFS Traversal
▪ Step 1: SET STATUS = not visited (ready state) for each node in G
▪ Step 2: Enqueue the starting node A and set its STATUS = Waiting
▪ Step 3: Repeat Steps 4 and 5 until QUEUE is empty
▪ Step 4: Dequeue a node N. Process it and set its STATUS =3 (Visited/Processed)
▪ Step 5: Enqueue all the neighbors of N that are in the ready state (whose STATUS = 1) and set their
STATUS = 2 (waiting state)
[END OF LOOP]
Step 6: EXIT](https://image.slidesharecdn.com/graph1-241206032209-2f480573/75/Data-Structure-and-algorithms-Graph1-pptx-35-2048.jpg)
![Pseudocode
BFS(G,v) ( v is the vertex where the search starts )
Queue Q := {}; ( start with an empty queue )
for each vertex u, set visited[u] := false;
enque Q, v;
while (Q is not empty) do
u := Deque Q;
if (not visited[u]) then
visited[u] := true;
for each unvisited neighbour w of u
enque Q, w;
end if
end while
END BFS()](https://image.slidesharecdn.com/graph1-241206032209-2f480573/75/Data-Structure-and-algorithms-Graph1-pptx-36-2048.jpg)