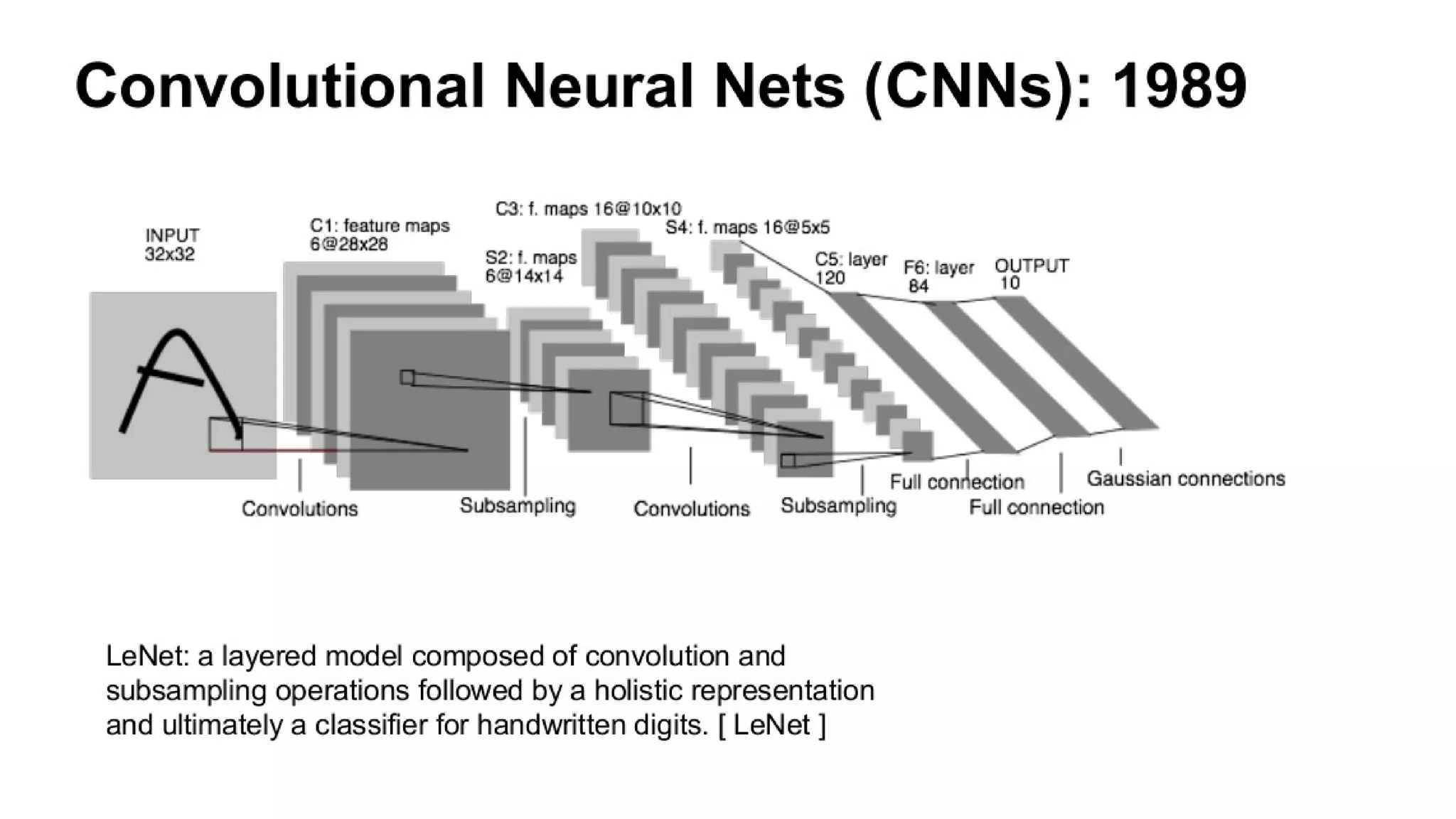
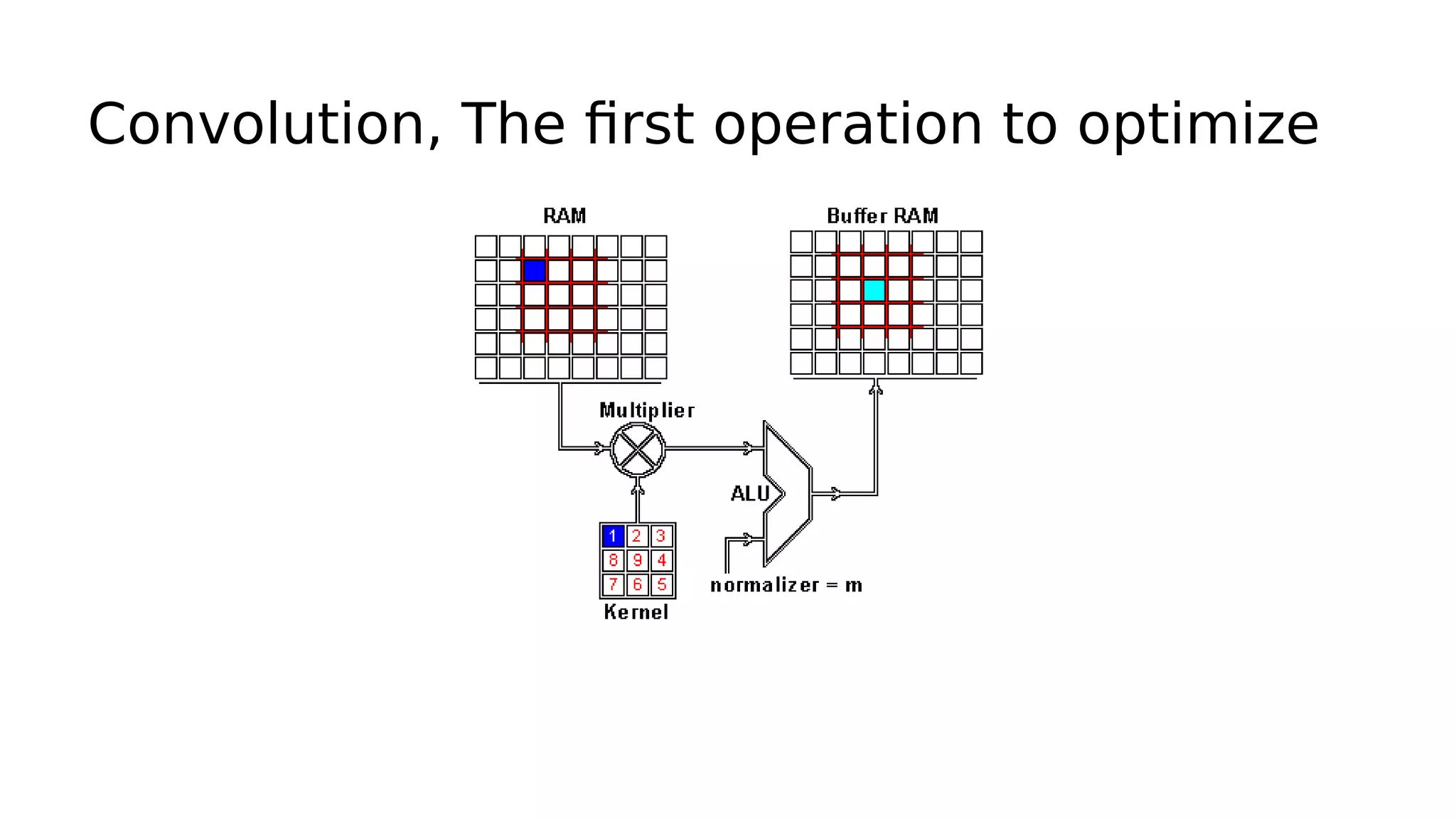
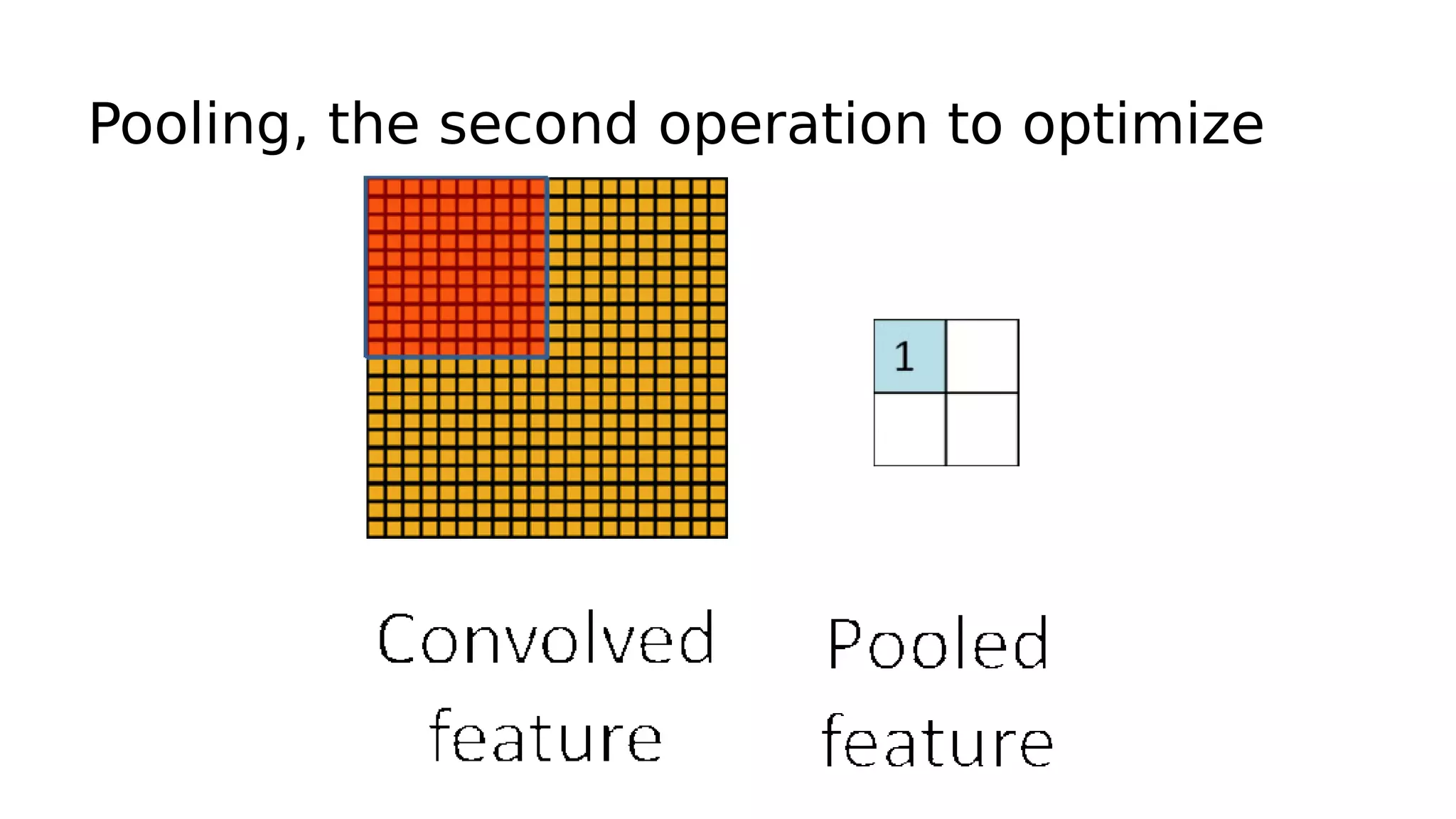
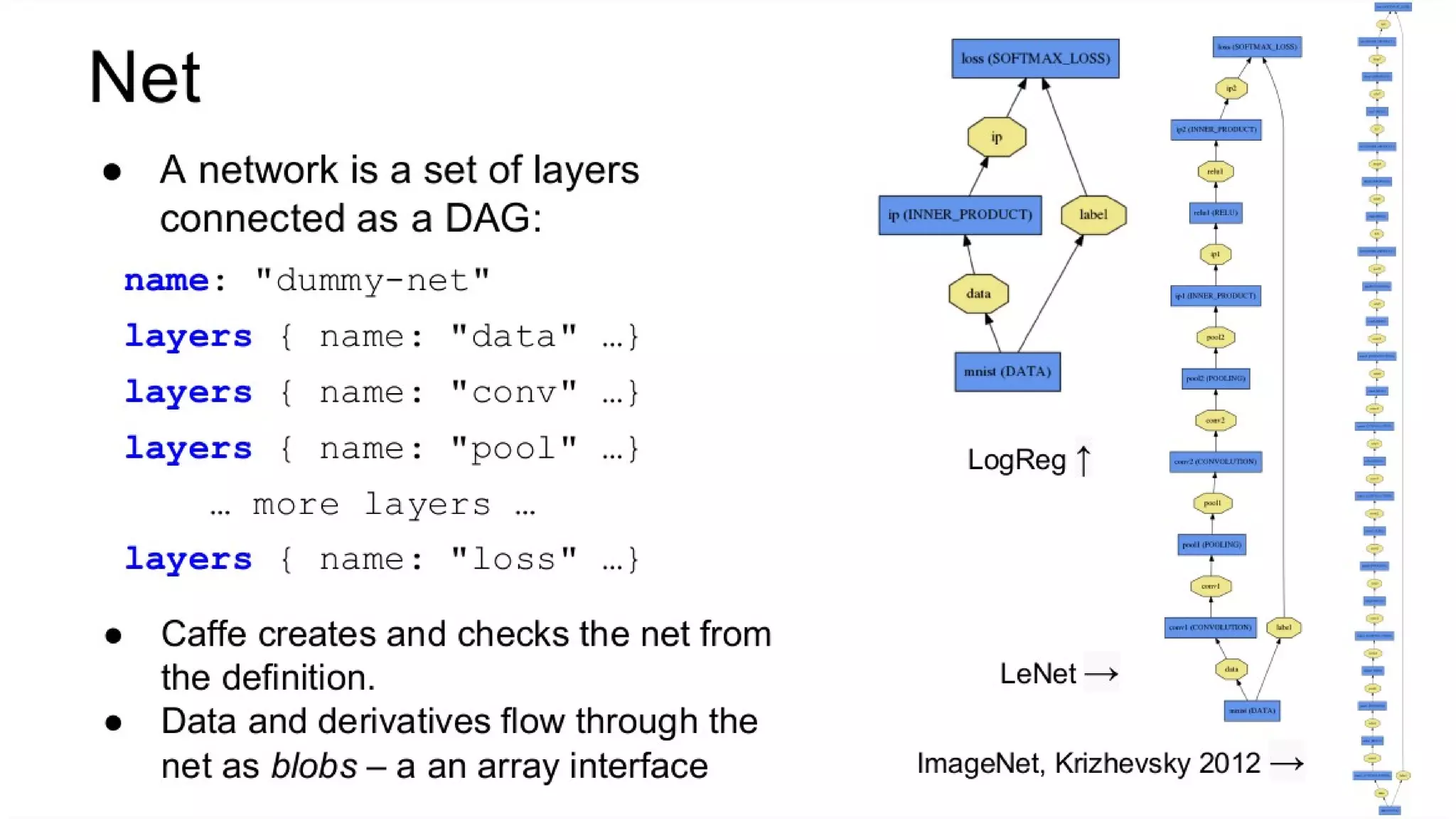
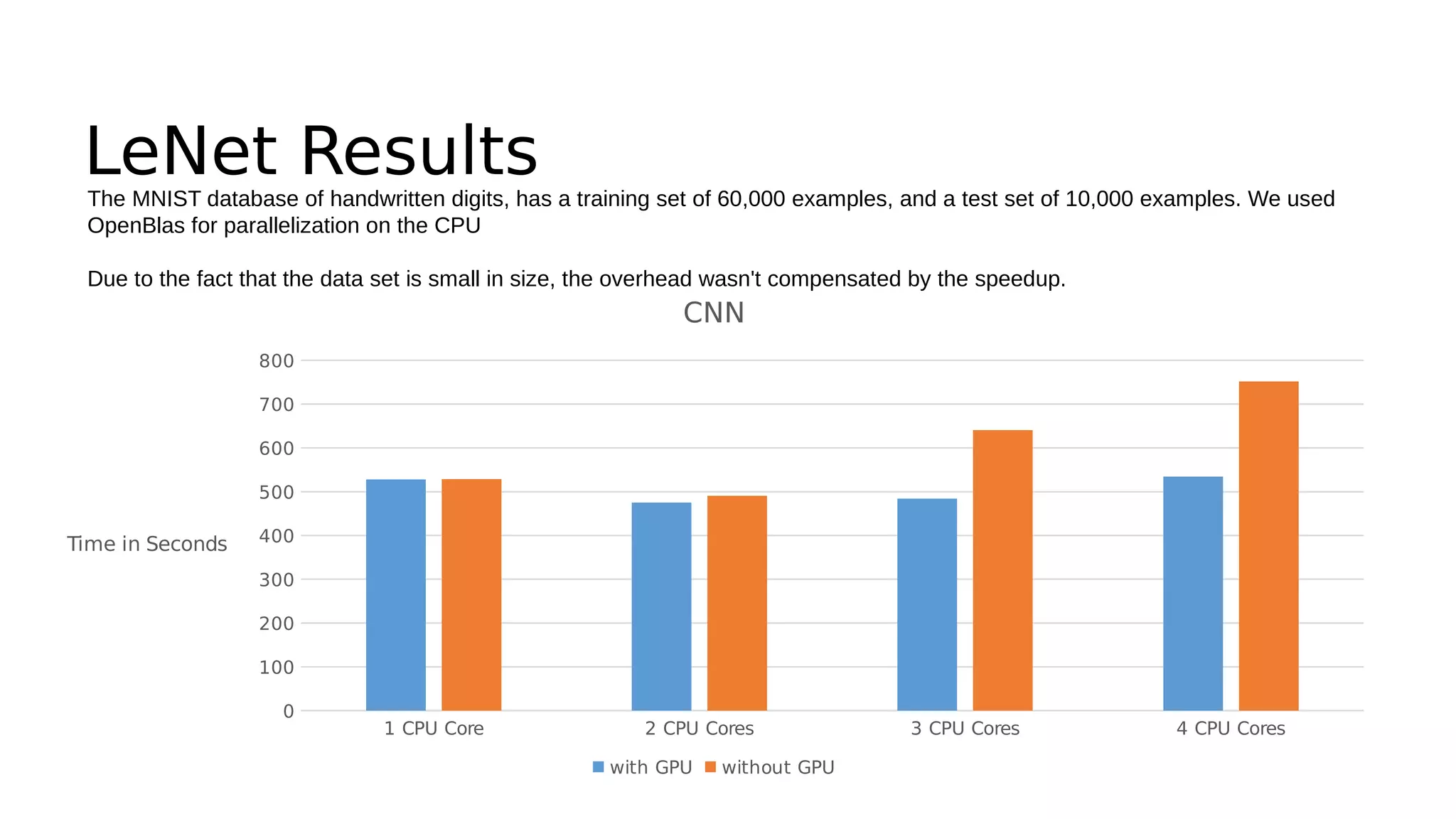
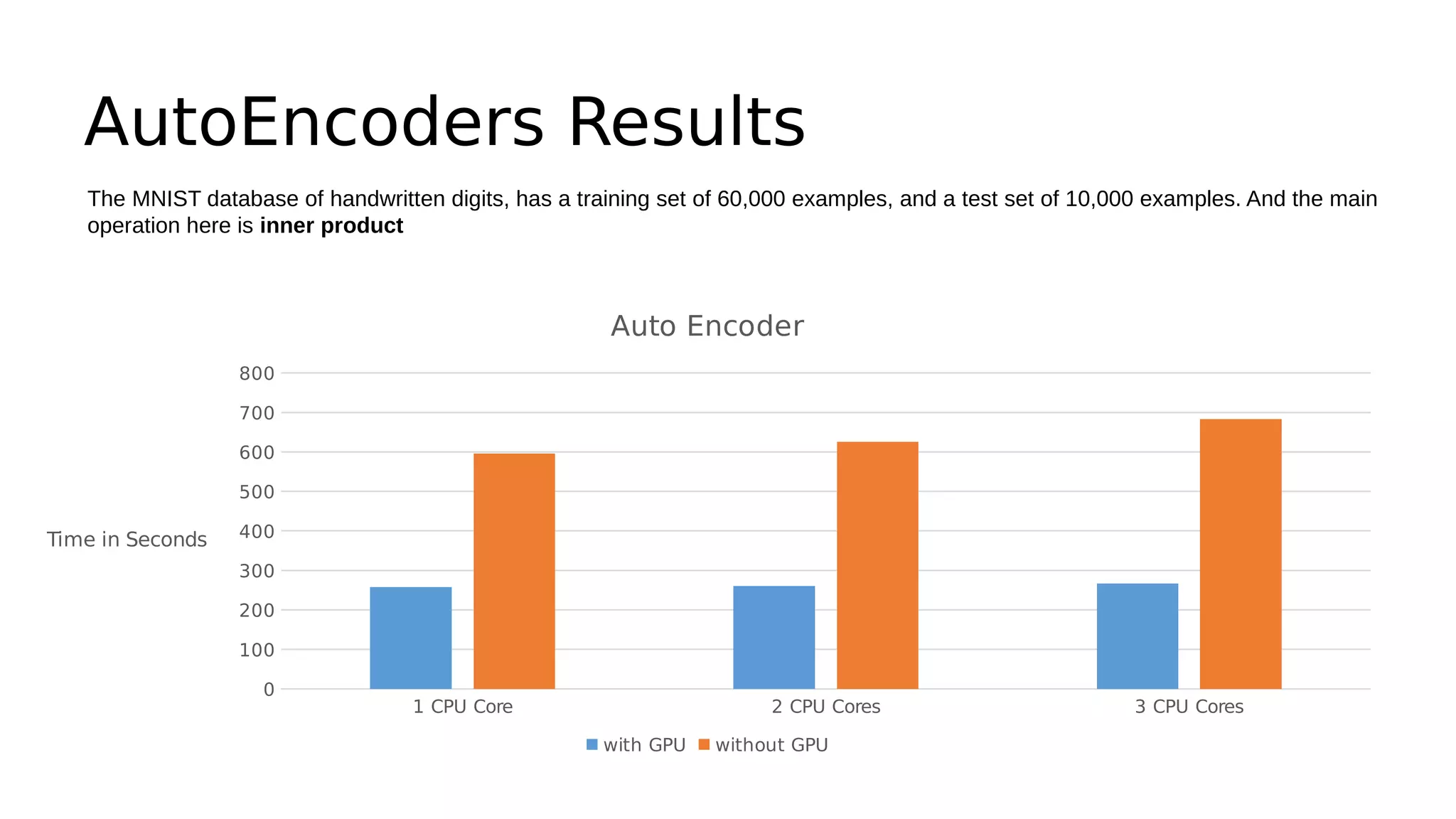
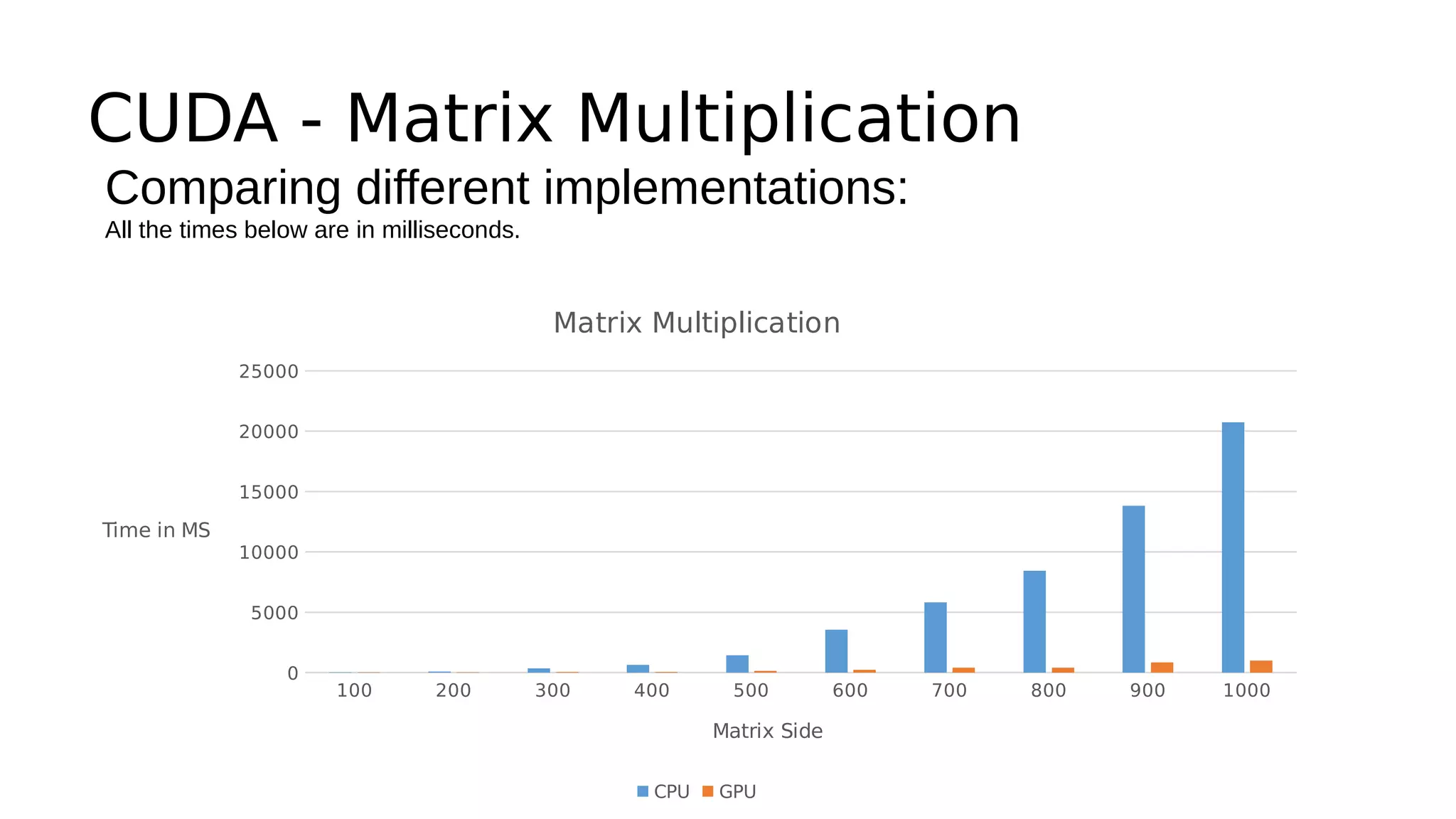
This document discusses GPU computing and CUDA programming. It begins with an introduction to GPU computing and CUDA. CUDA (Compute Unified Device Architecture) allows programming of Nvidia GPUs for parallel computing. The document then provides examples of optimizing matrix multiplication and closest pair problems using CUDA. It also discusses implementing and optimizing convolutional neural networks (CNNs) and autoencoders for GPUs using CUDA. Performance results show speedups for these deep learning algorithms when using GPUs versus CPU-only implementations.




![[Bryan Catanzaro]](https://image.slidesharecdn.com/cudaandcaffe-141214063345-conversion-gate02/75/CUDA-and-Caffe-for-deep-learning-5-2048.jpg)




![CUDA - Closest Pair in 2D (cont.)
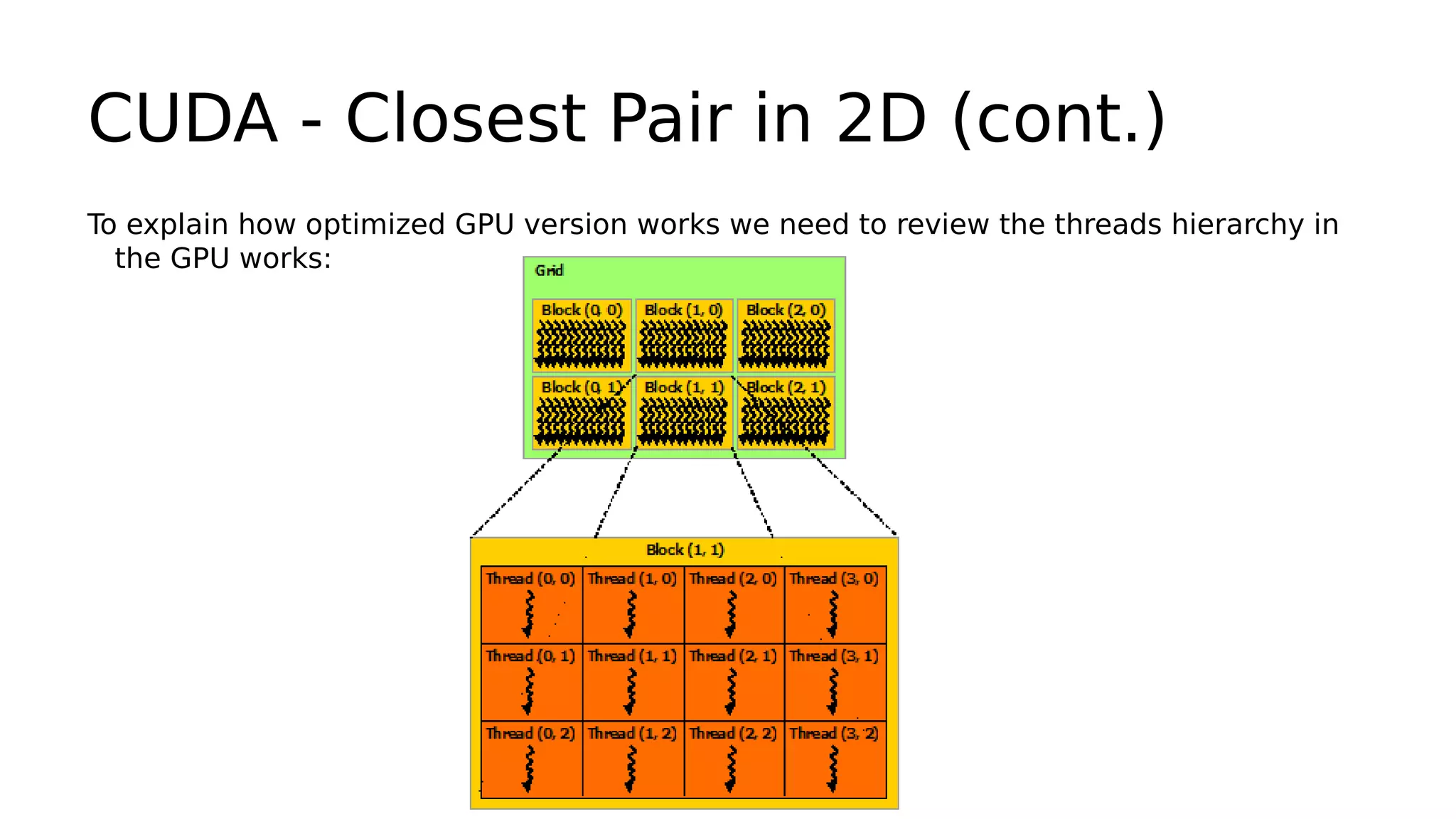
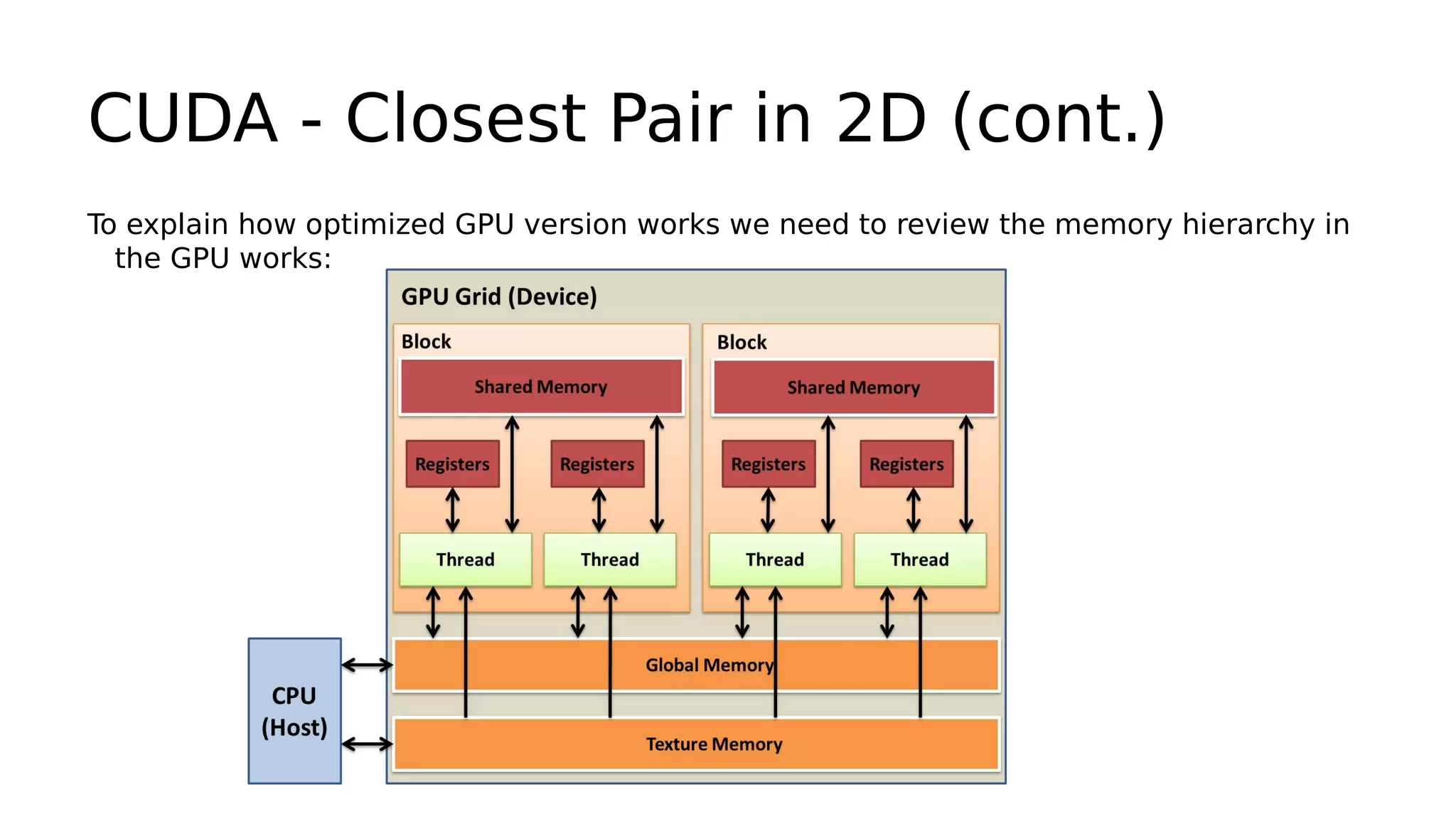
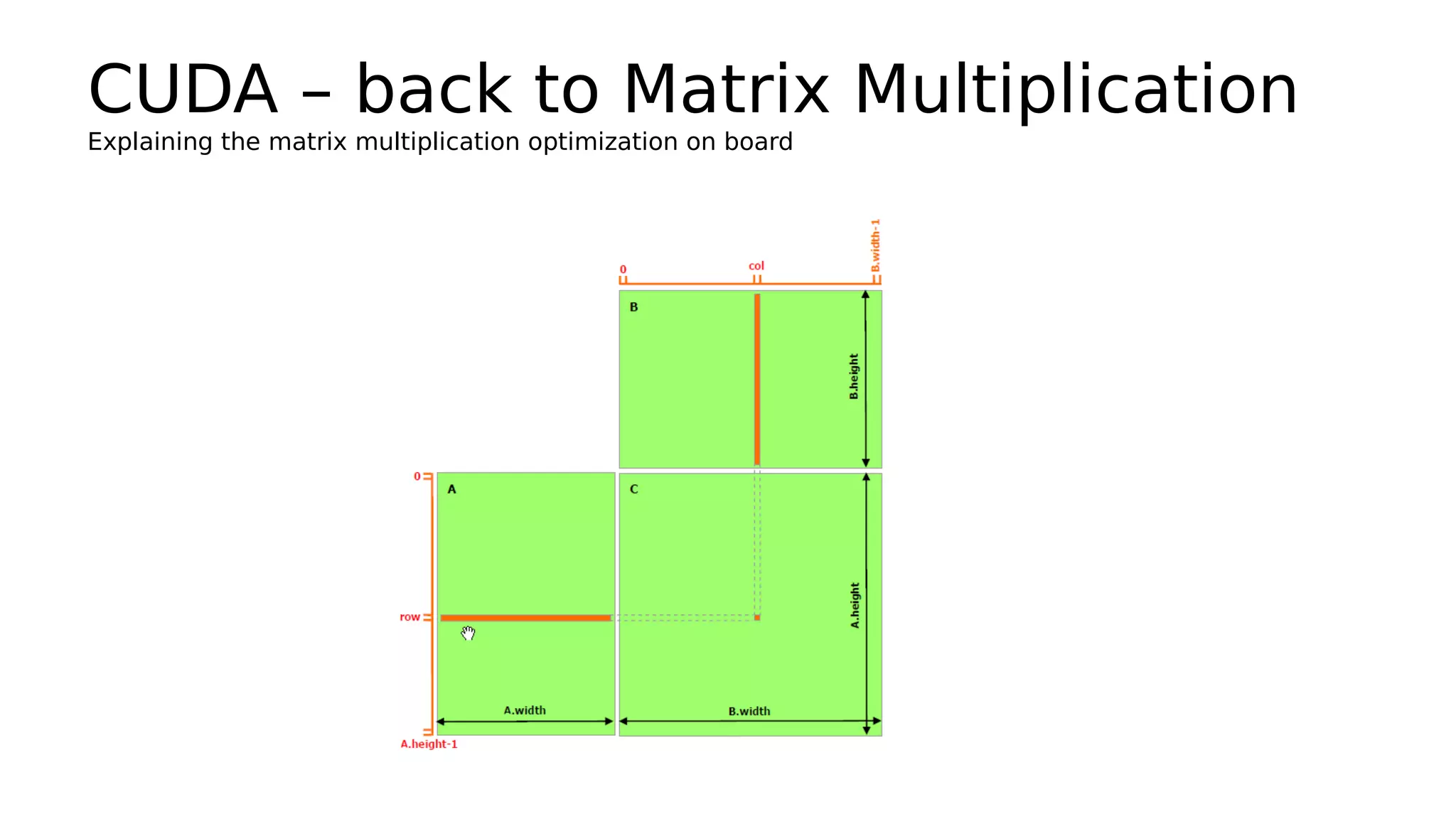
Explaining the optimized code on board
__global__ void FindClosestGPU2(float2* points, float* vals, int count)
{
__shared__ float2 sharedPoints[blockSize];
if(count <= 1) return;
int idx = threadIdx.x + blockIdx.x * blockDim.x;
float2 thisPoint;
float distanceToClosest = FLT_MAX;
if(idx < count) thisPoint = points[idx];
for(int currentBlockOfPoints = 0; currentBlockOfPoints < gridDim.x; currentBlockOfPoints++) {
if(threadIdx.x + currentBlockOfPoints * blockSize < count)
sharedPoints[threadIdx.x] = points[threadIdx.x + currentBlockOfPoints * blockSize];
else
sharedPoints[threadIdx.x].x = reasonableINF, sharedPoints[threadIdx.x].y = reasonableINF;
__syncthreads();
if(idx < count) {
float *ptr = &sharedPoints[0].x;
for(int i = 0; i < blockSize; i++) {
float dist = (thisPoint.x - ptr[0]) * (thisPoint.x - ptr[0]) +
(thisPoint.y - ptr[1]) * (thisPoint.y - ptr[1]);
ptr += 2;
if(dist < distanceToClosest && (i + currentBlockOfPoints * blockSize < count)
&& (i + currentBlockOfPoints * blockSize != idx))
distanceToClosest = dist;
}
}_
_syncthreads();
}i
f(idx < count)
vals[idx] = distanceToClosest;
}](https://image.slidesharecdn.com/cudaandcaffe-141214063345-conversion-gate02/75/CUDA-and-Caffe-for-deep-learning-16-2048.jpg)