Download as PDF, PPTX
Uploaded byAmol Gaikwad
Computer Graphics - Cartesian Coordinate System.pdf
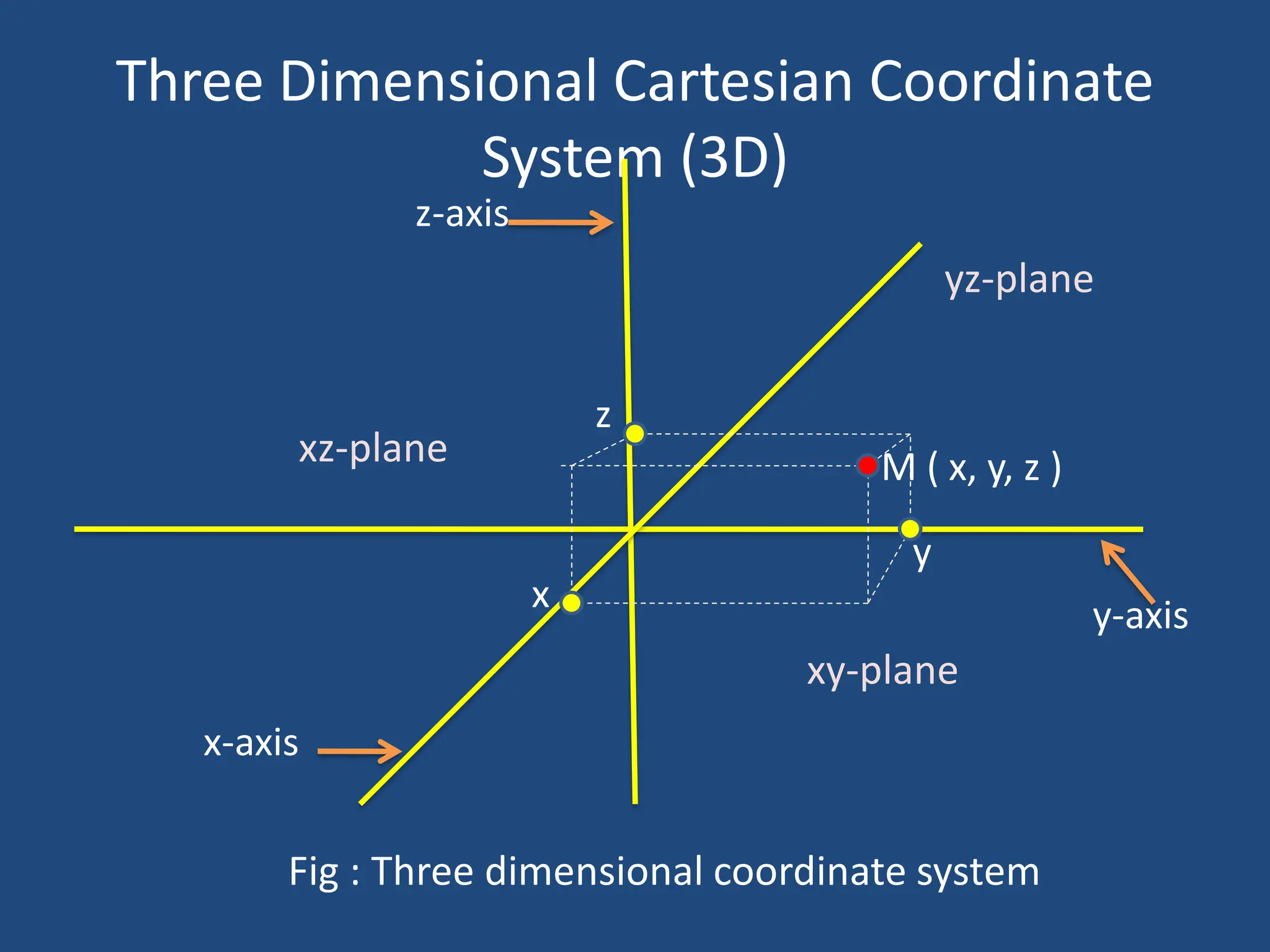
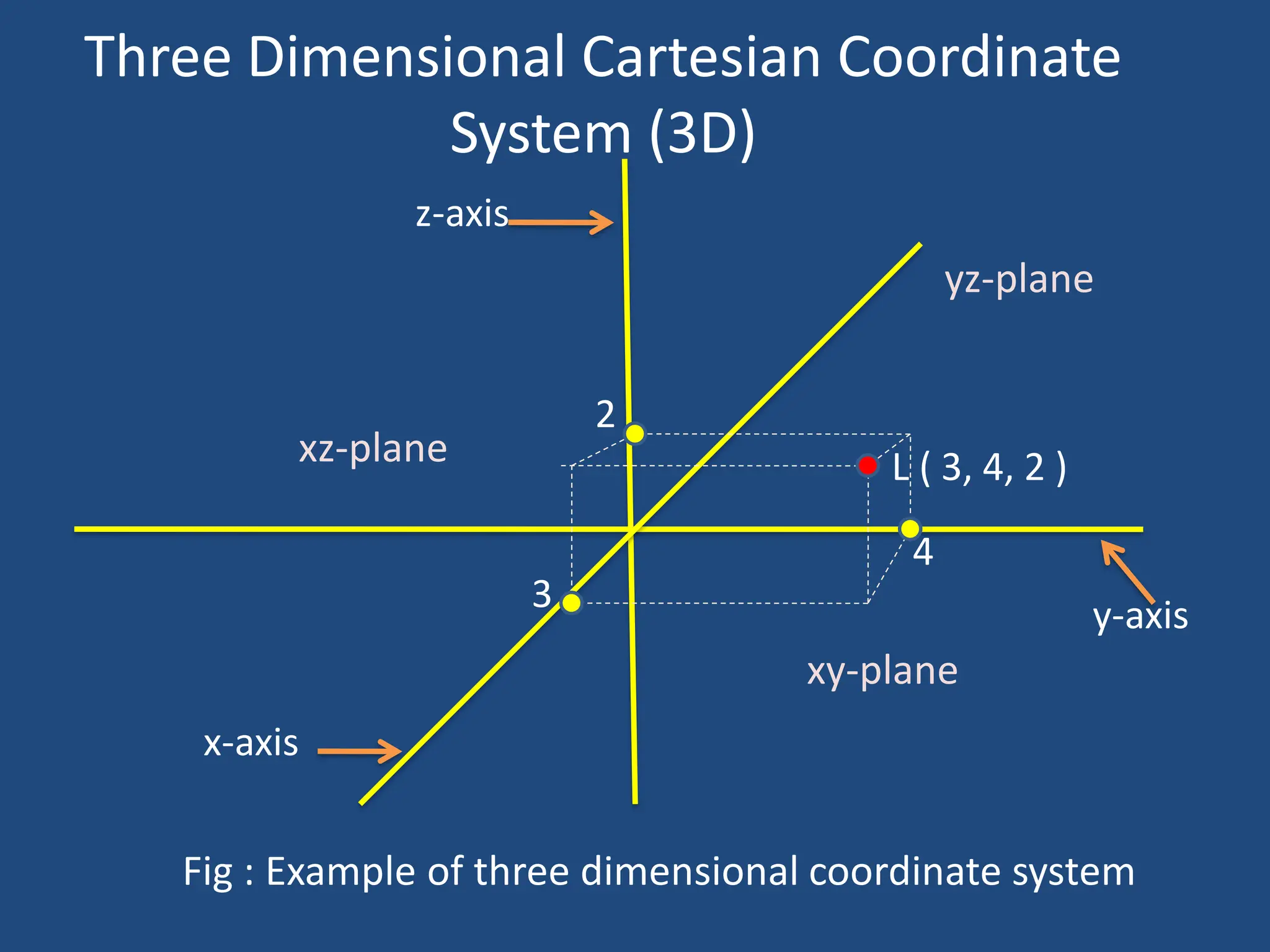
The document explains the Cartesian coordinate system, which is used to determine the position of points in two-dimensional (2D) and three-dimensional (3D) space through perpendicular lines drawn to axes. It outlines the structure of one-dimensional, two-dimensional, and three-dimensional systems, describing how coordinates are identified and how planes and quadrants are utilized for their representation. Additionally, it highlights applications of the Cartesian coordinate system in fields such as computer graphics and design.
More Related Content
Similar to Computer Graphics - Cartesian Coordinate System.pdf
Computer Graphics - Cartesian Coordinate System.pdf
- 1. Computer Graphics Cartesian CoordinateSystem -Amol S. Gaikwad Lecturer, Government Polytechnic Gadchiroli
- 2. Learning Outcomes • Describecoordinate system. • Find the position of a given point in two dimensional and three dimensional coordinate system.
- 3. Cartesian Coordinate System •Cartesian coordinate system is method to show the position of a point in space. • It is used to show the location of a point in a plane (two dimensional) and three-dimensional space. • The position of point is decided by drawing a perpendicular line (90 degree line) from the point to the axis. • Cartesian coordinate system can be divided into three types – One dimensional, two-dimensional system (2D) and three-dimensional system (3D). • Cartesian coordinate system is also called as rectangular coordinate system.
- 4. One Dimensional Cartesian CoordinateSystem • A one dimensional coordinate system consist of a single straight line. • The straight line contains origin (0 value), positive and negative values. • The straight line can be horizontal or vertical. • If the straight line is horizontal then right side of the origin(0) have positive values and left side of the origin have negative values. • If the straight line is vertical then upper side of the origin(0) have positive values and below side of origin(0) have negative values .
- 5. One Dimensional CartesianCoordinate System Fig : One dimensional coordinate system (horizontal) 0 1 2 3 -1 -2 -3 -3 0 2 1 3 -1 -2 Fig : One dimensional coordinate system (vertical) origin Left (negative) Right (positive) Upper (Positive) below (negative)
- 6. Two Dimensional CartesianCoordinate System (2D) • In two dimensional coordinate system two axes are used to decide the location of point one is x- axis and other is y-axis. • These axes are also called as Cartesian axes. • To identify the position of point in two dimension two numbers are required. • These numbers are written as pair (x,y) • Number ‘x’ is called as x-coordinate and number ‘y’ is called as y-coordinate, x-coordinate is written first and then y-coordinate.
- 7. Two Dimensional CartesianCoordinate System (2D) • The point where x-axis and y-axis intersect each other is called as origin. • The coordinates of origin are (0,0). • The distance on x-axis and y-axis are calculated from origin. • x-coordinate is also called as ‘abscissa’ and y- coordinate is called as ‘ordinate’.
- 8. Two Dimensional CartesianCoordinate System (2D) 1 2 3 4 5 -5 -4 -3 -2 -1 1 2 3 4 5 -5 -4 -3 -2 -1 0 x-axis y-axis P ( x, y ) R ( x’, y’ ) First Quadrant Second Quadrant Third Quadrant Fourth Quadrant Fig : Two dimensional coordinate system
- 9. Two Dimensional CartesianCoordinate System (2D) • In the above diagram to find the x-coordinate of point ‘P’ we drawn a straight perpendicular line from point ‘P’ to x-axis there we got value 2 on x-axis. Hence value of x-coordinate for point ‘P’ is 2. • Similarly to find the y-coordinate of point ‘P’ we drawn a straight perpendicular line from point ‘P’ to y-axis, there we got intersection point 3 on y-axis. Hence the value of y-coordinate for point ‘P’ is 3. • So the final position of point ‘P’ in two dimensional coordinate system is (2,3). • In this way find the position of any point in two dimensional coordinate system.
- 10. Two Dimensional CartesianCoordinate System (2D) • Similarly to find the position of point ‘R’ we have also drawn straight perpendicular lines from point ‘R’ to x-axis and y-axis there we get intersection point -3 on x-axis and point 2 on y-axis. • So the final position of point ‘R’ is (-3,2)
- 11. xy-plane and Quadrants •xy-plane :- In the above diagram we have drawn x-axis and y-axis and quadrants on a plane surface. This plane surface is called as xy-plane or Cartesian plane. • Quadrant :- x-axis and y-axis divide the xy-plane into four parts these parts are called as quadrants. • First Quadrant :-This quadrant contains positive values of both x-axis and y-axis.It is also written as Quadrant-I. • Second Quadrant :- This quadrant contains negative values of x-axis and positive values of y-axis. It is also written as Quadrant-II.
- 12.
- 13. xy-plane and Quadrants •Third Quadrant :- It contains negative values of both x-axis and y-axis. It is also written as quadrant-III. • Fourth Quadrant :- It contains positive values of x-axis and negative values of y-axis. It is also written as quadrant-IV. • Quadrants are numbered from I to IV in anti- clockwise direction.
- 14. Three Dimensional Cartesian CoordinateSystem (3D) • In three dimensional coordinate system to find the location of a point in space three axes are used they are – x-axis, y-axis, z-axis. • The location of point is represented by three numbers and written as (x, y, z) where x is called as x-coordinate, y is called as y- coordinate and z is called as z-coordinate. • z-coordinate is also called as ‘applicate’. • To identify the position of a point in three dimensional system we have to draw a straight perpendicular line from the point to xy- plane, xz-plane and yz-plane. • Then again straight perpendicular lines are drawn from these planes to x, y and z-axis as shown in figure. • The intersection points with these three axes is the consider as the final position of a point.
- 15. Three Dimensional CartesianCoordinate System (3D) xz-plane x-axis y-axis z-axis M ( x, y, z ) x z y xy-plane yz-plane Fig : Three dimensional coordinate system
- 16. Three Dimensional CartesianCoordinate System (3D) xz-plane x-axis y-axis z-axis L ( 3, 4, 2 ) 3 2 4 xy-plane yz-plane Fig : Example of three dimensional coordinate system
- 17. Three Dimensional Cartesian CoordinateSystem (3D) • In the above example we can see that to find the position of point ‘L’ we have drawn straight line from point ‘L’ to xy, xz and yz plane and from these planes we have drawn a straight perpendicular lines to x, y and z axis. This creates a box like figure. • The intersection point with x axis is 3, y axis is 4 and z axis is 2 which is written as (3,4,2), this is consider as a position of point L in the space.
- 18. Applications of CartesianCoordinate System • Computer Graphics • Computer aided design • Geometry related data processing
- 19.