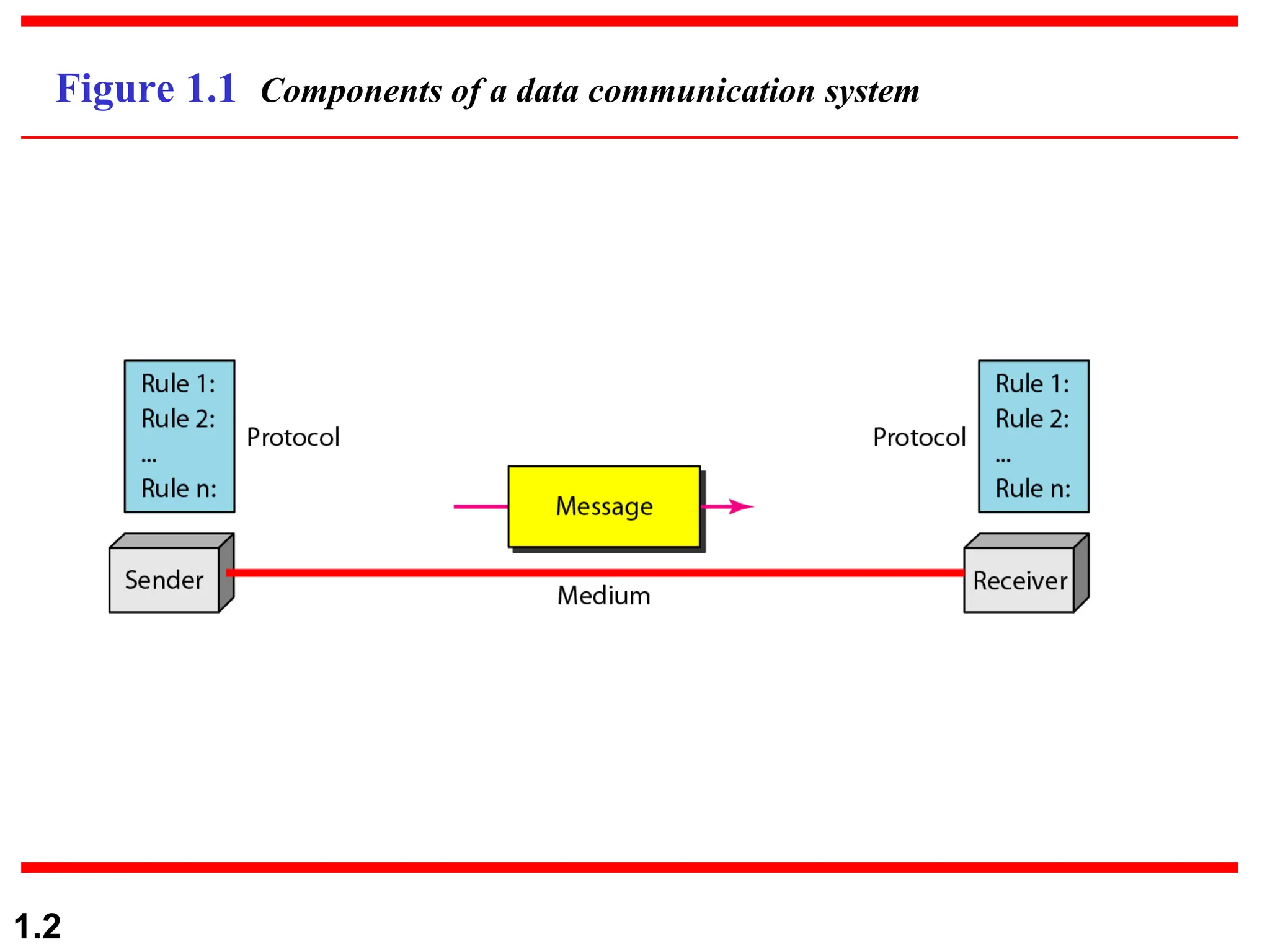
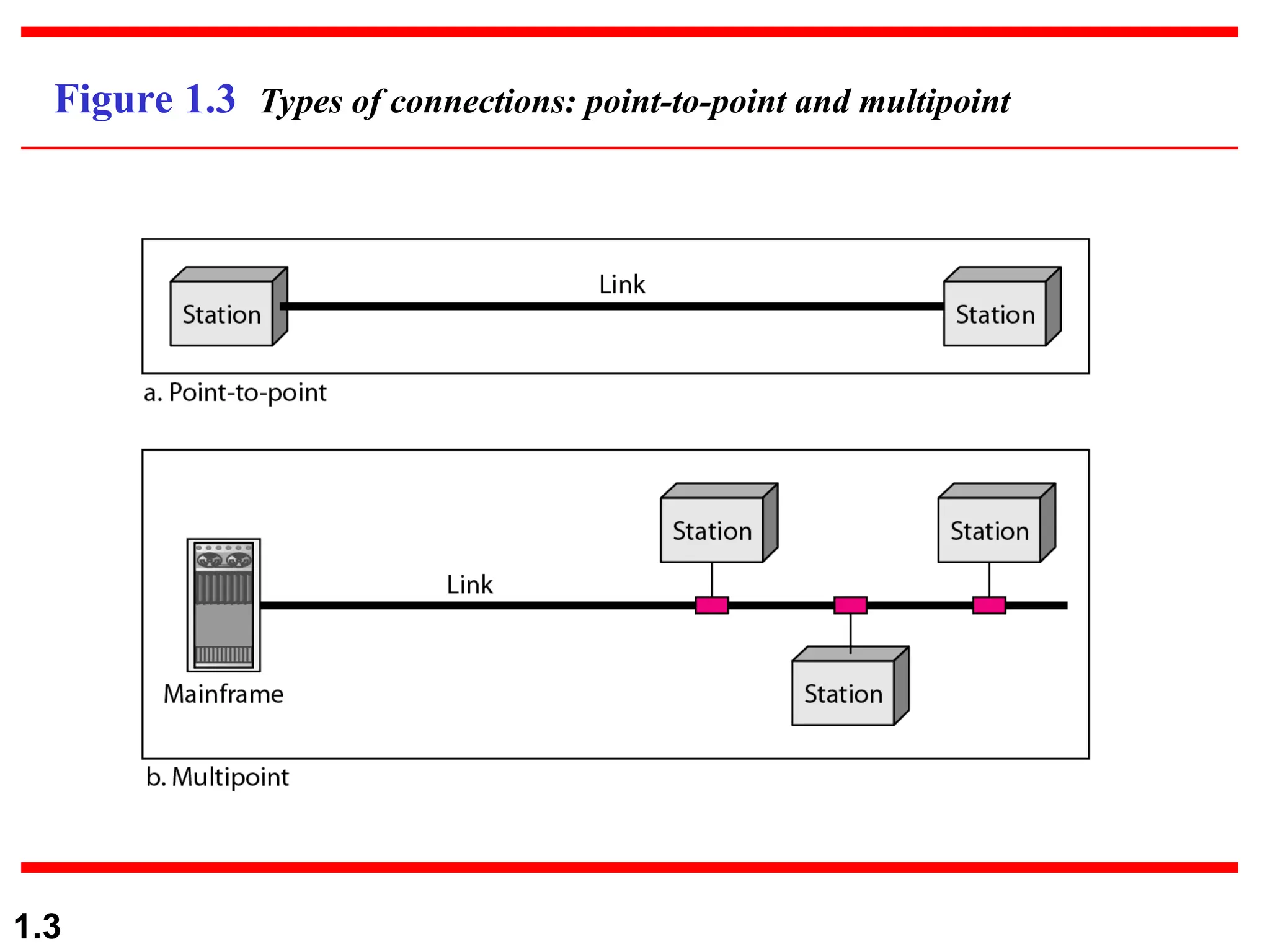
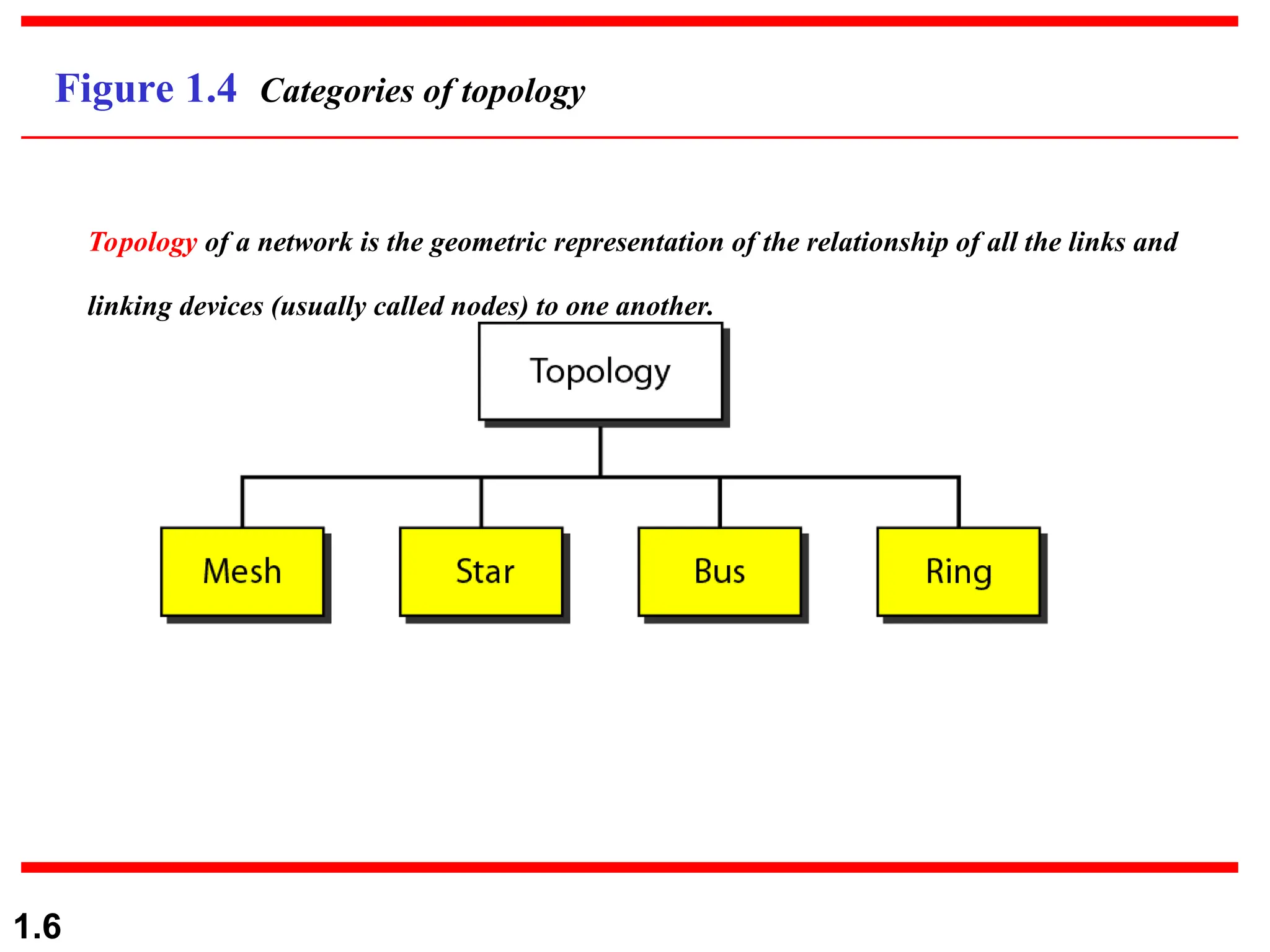
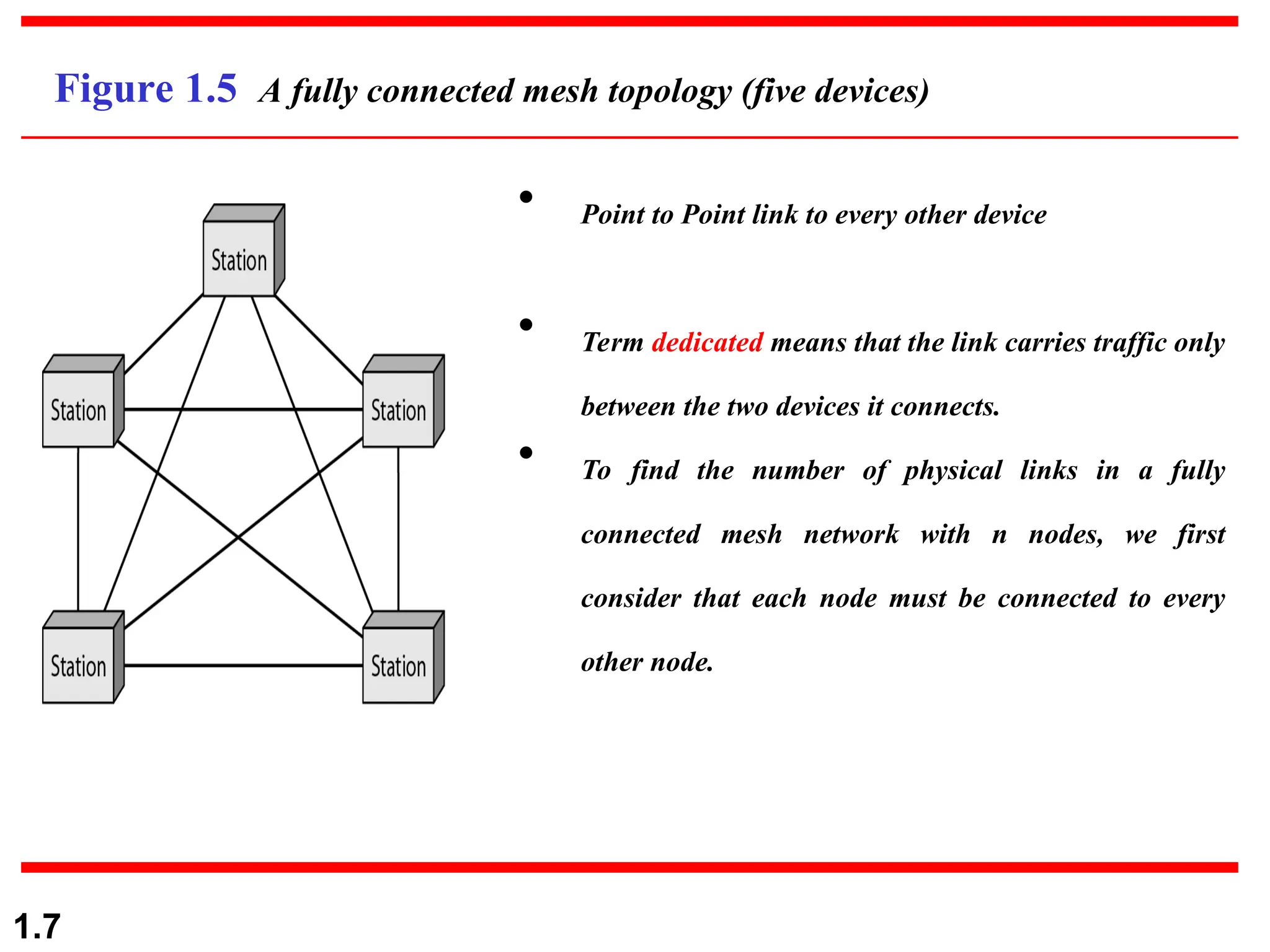
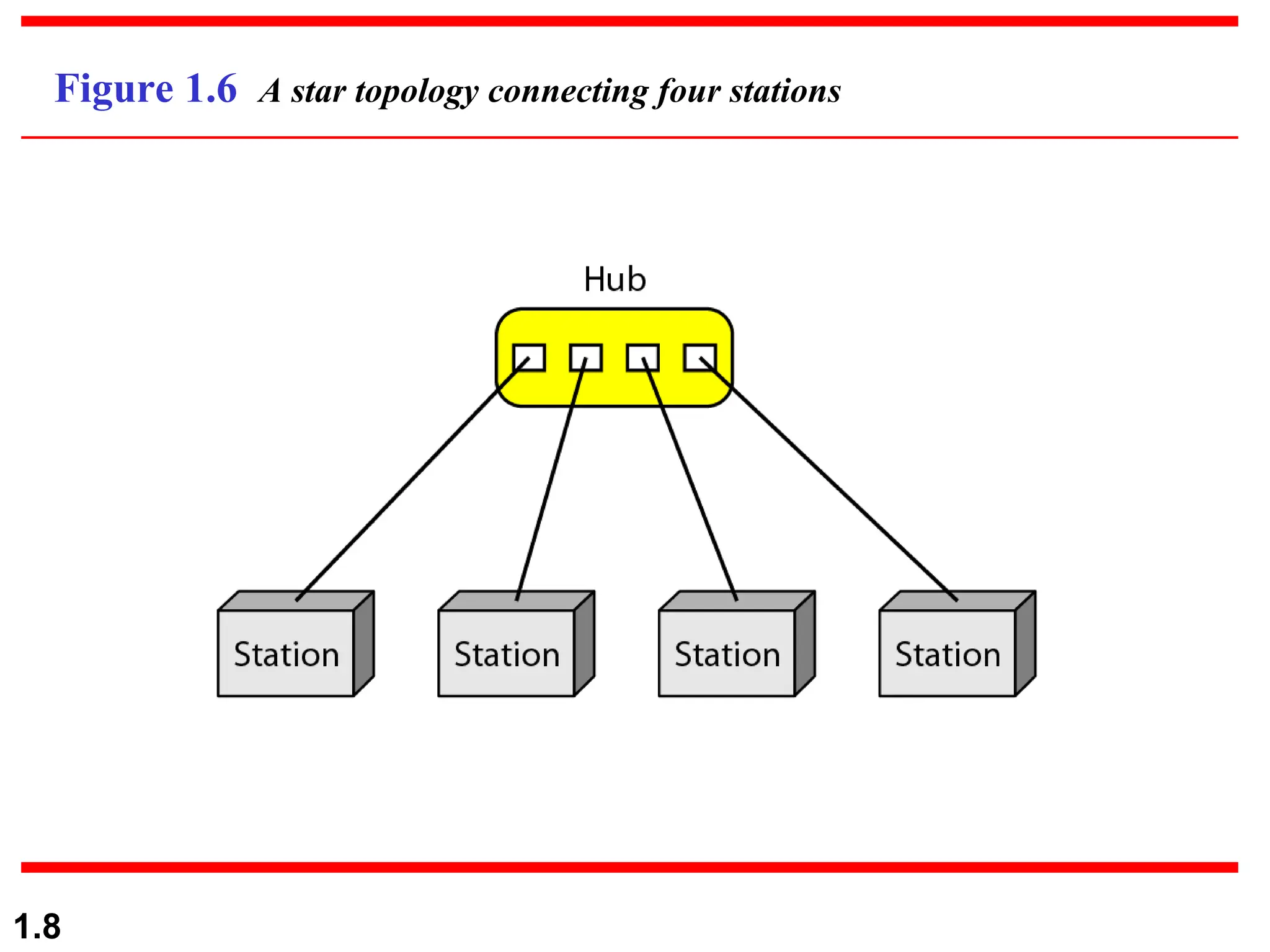
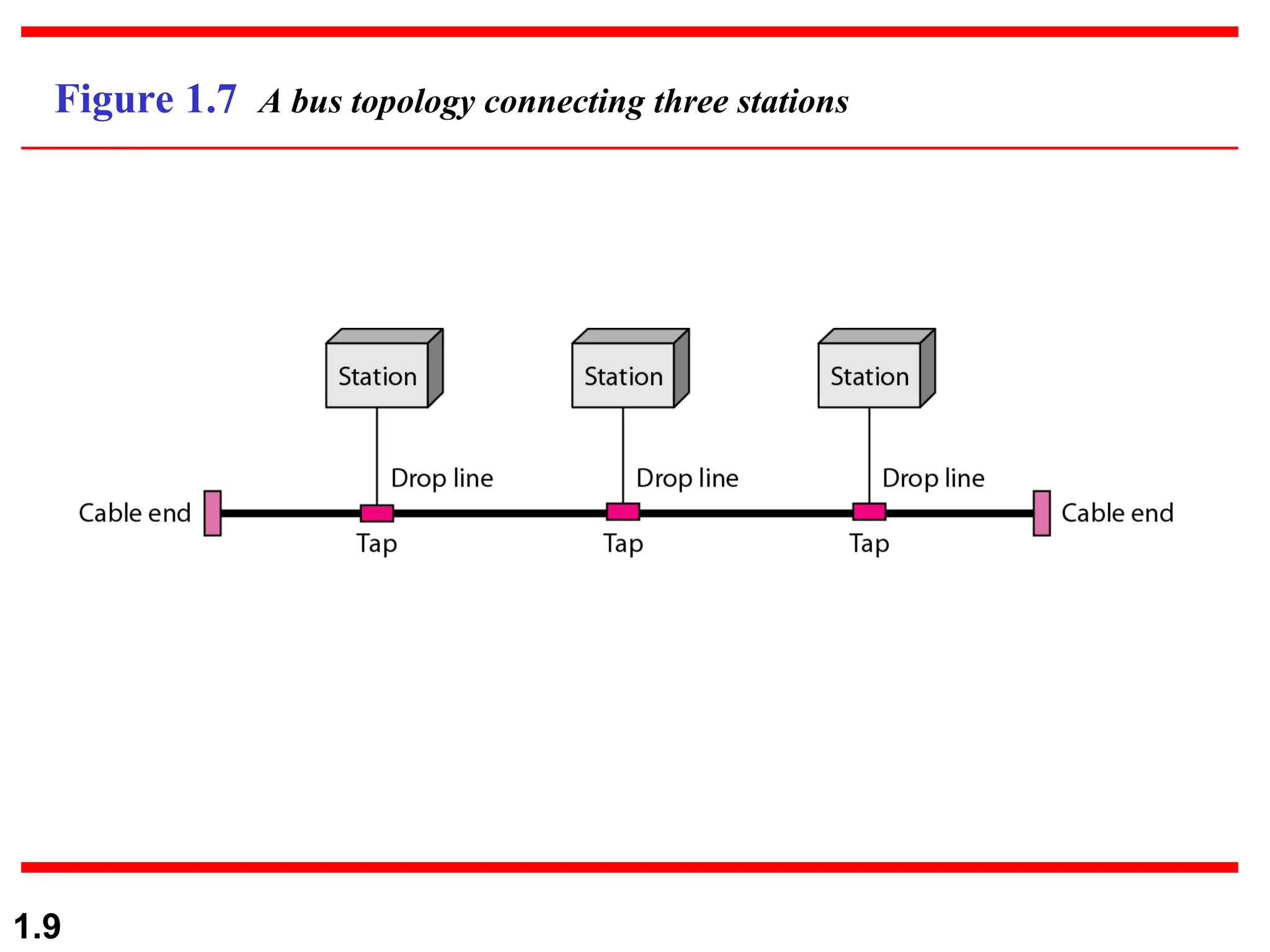
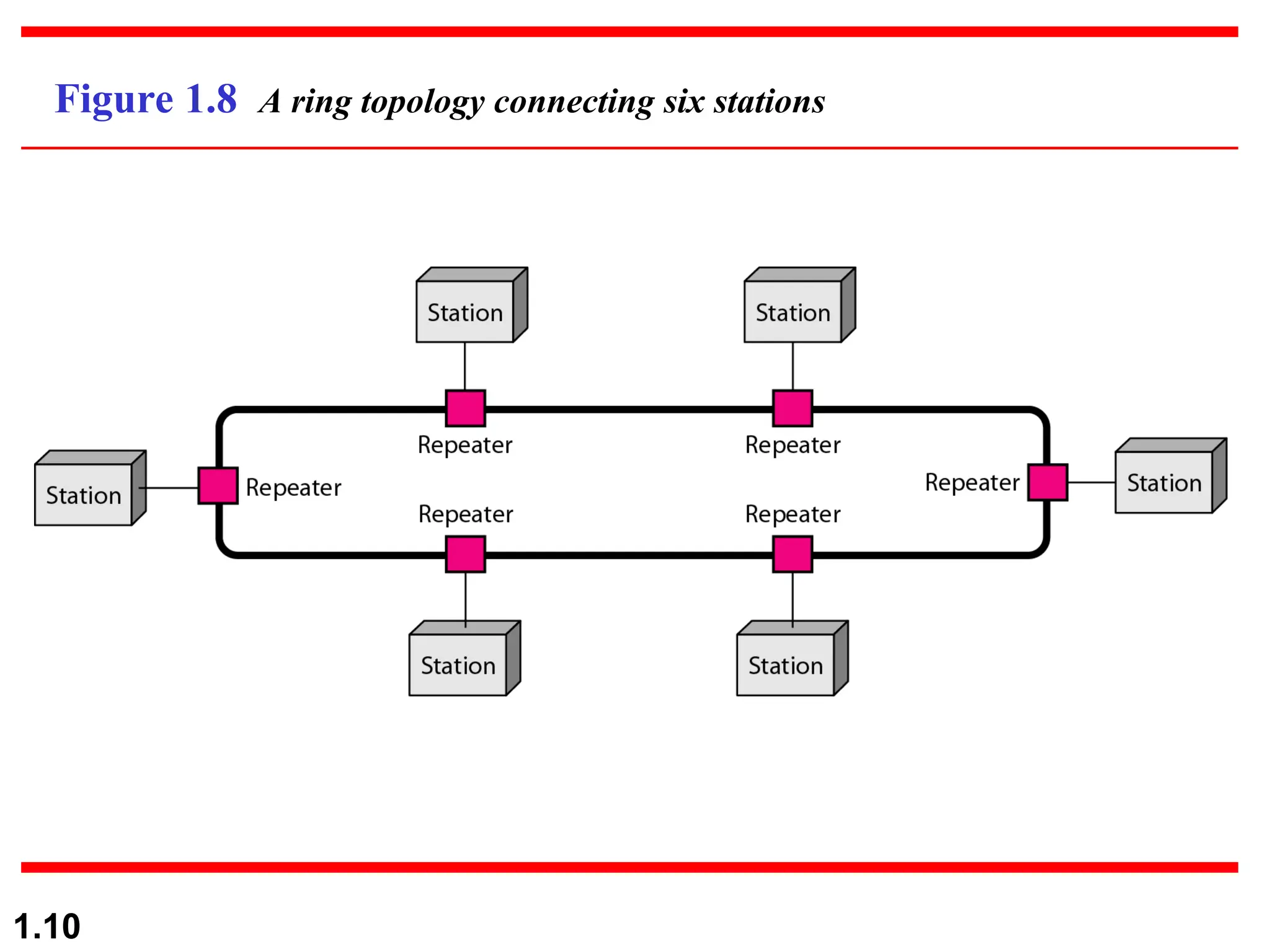
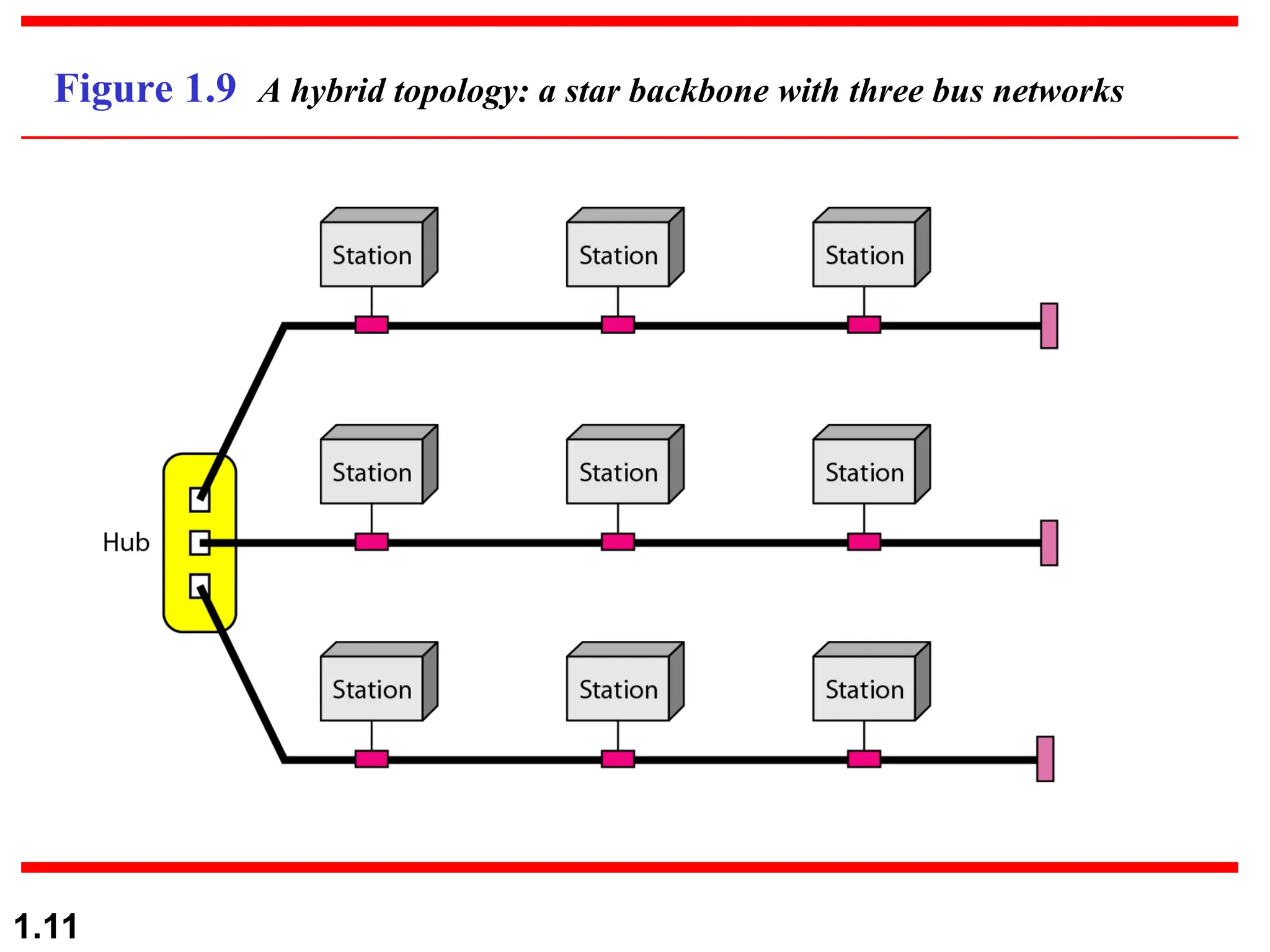
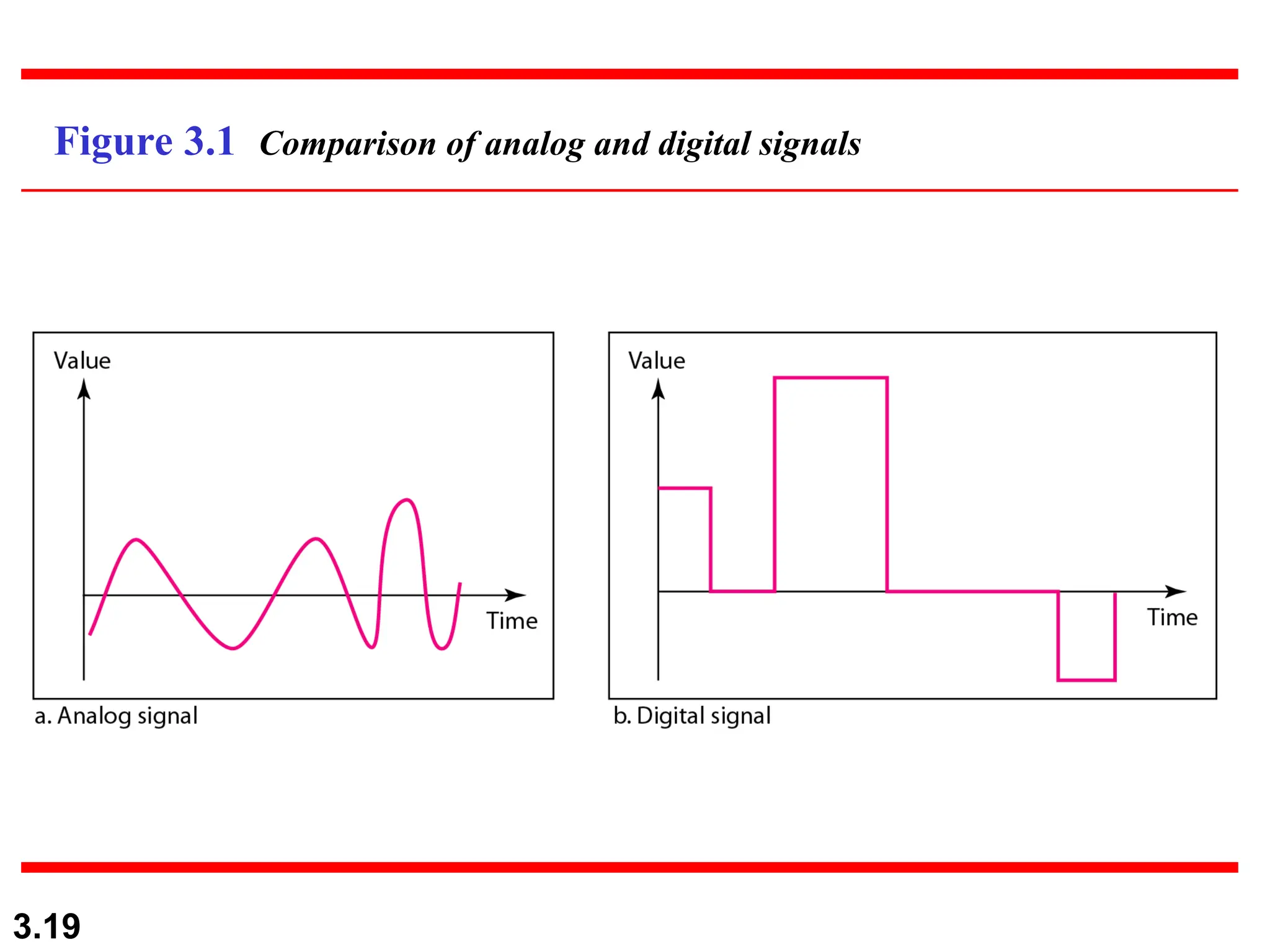
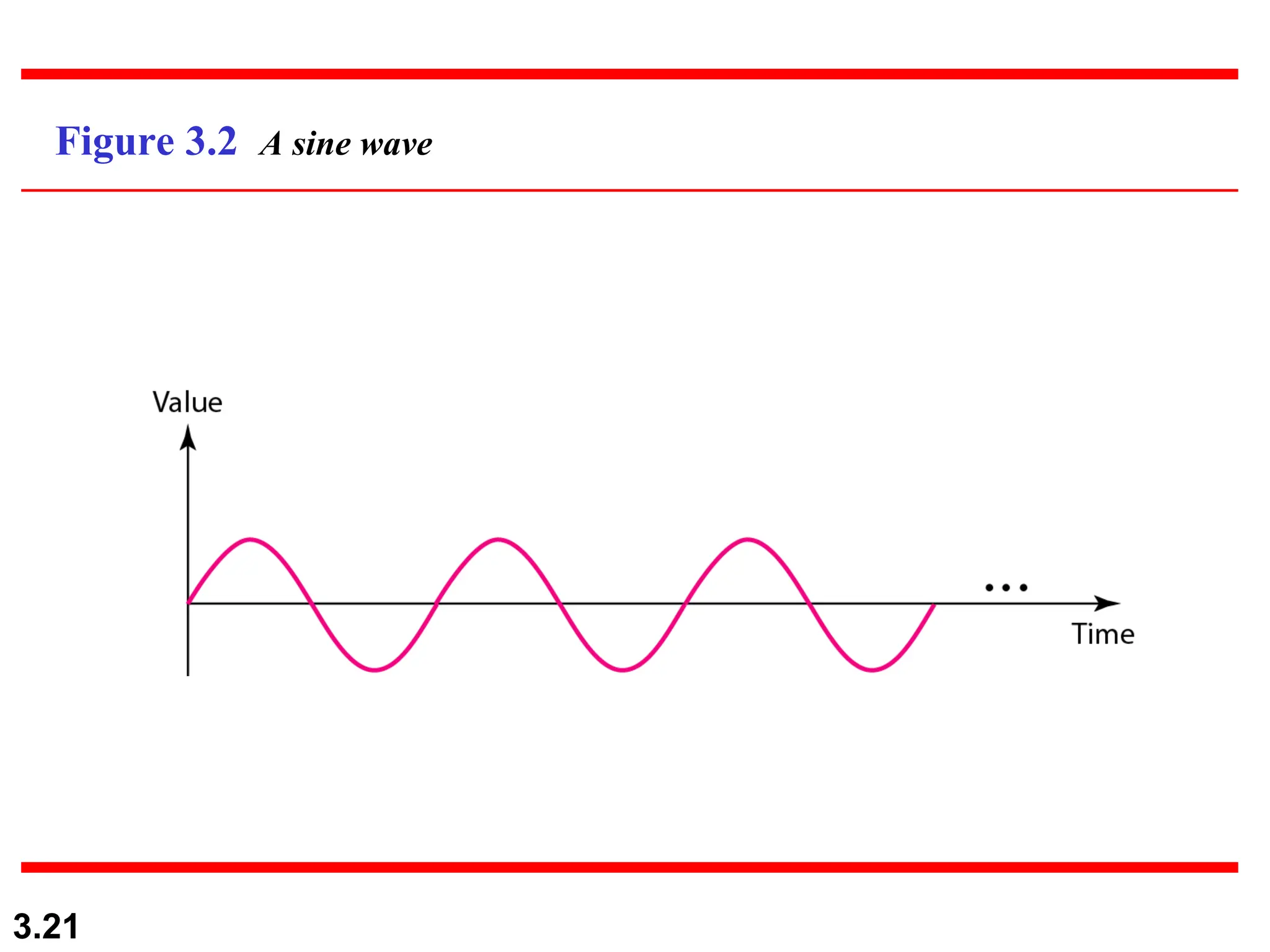
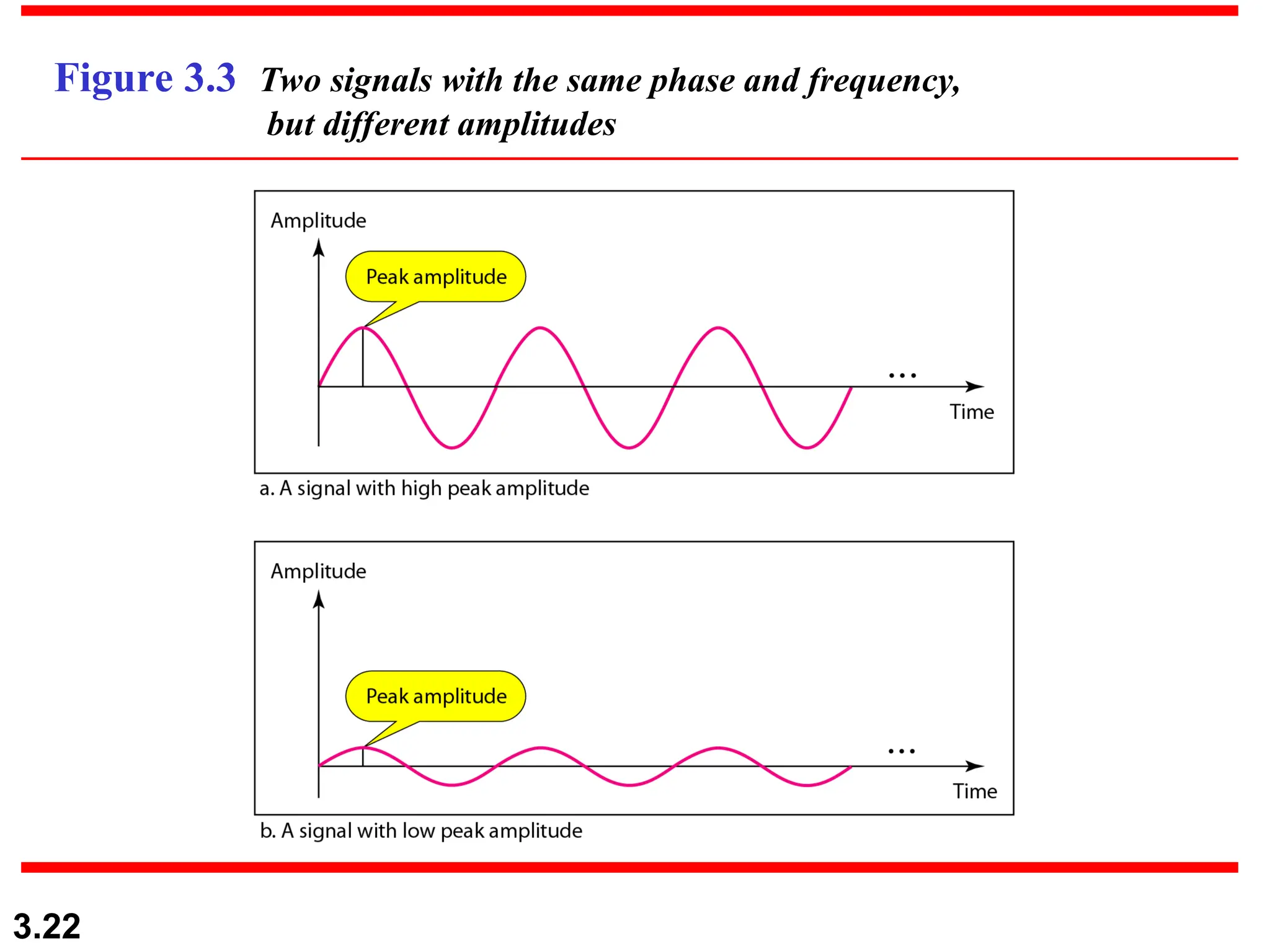
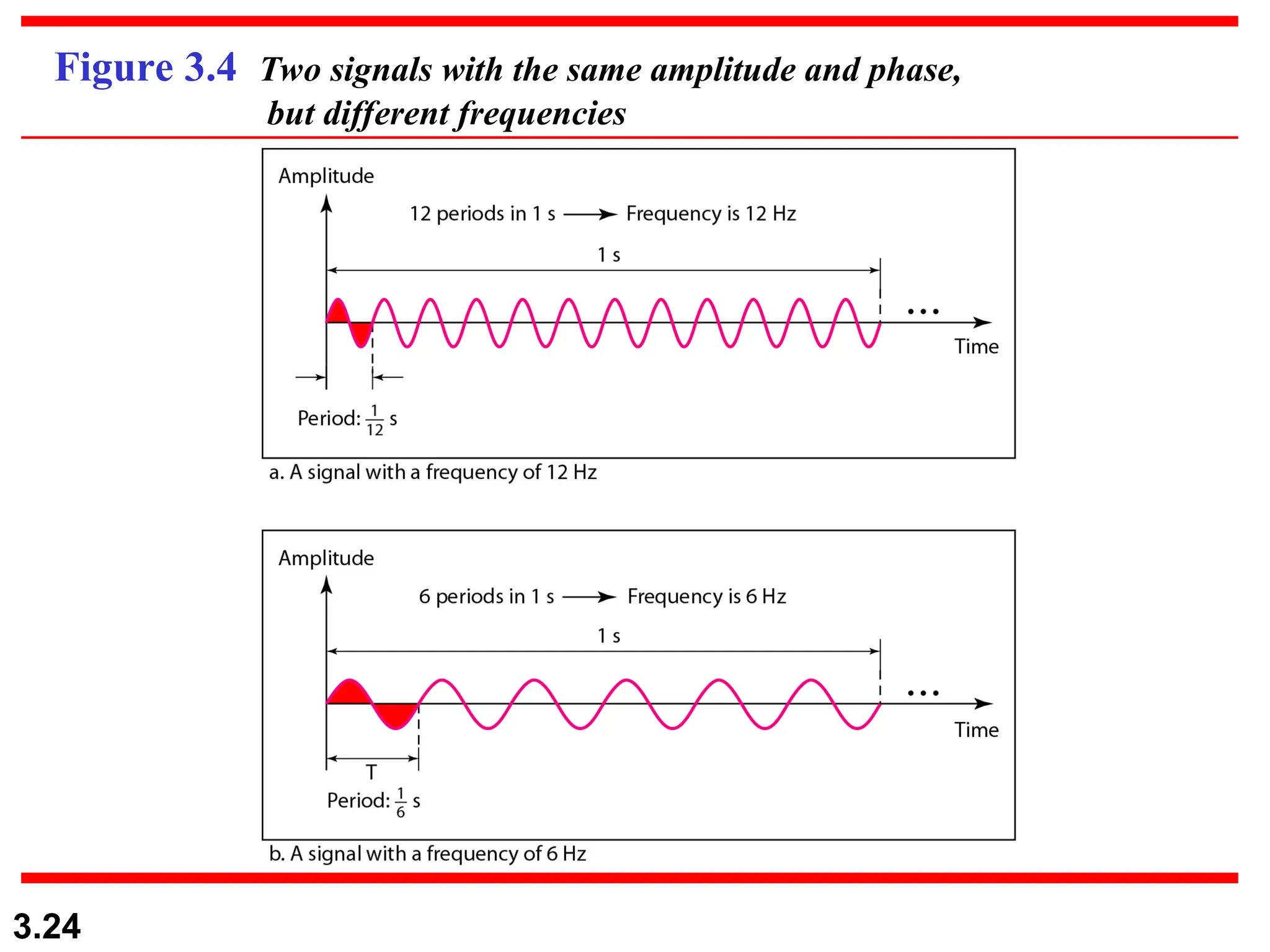
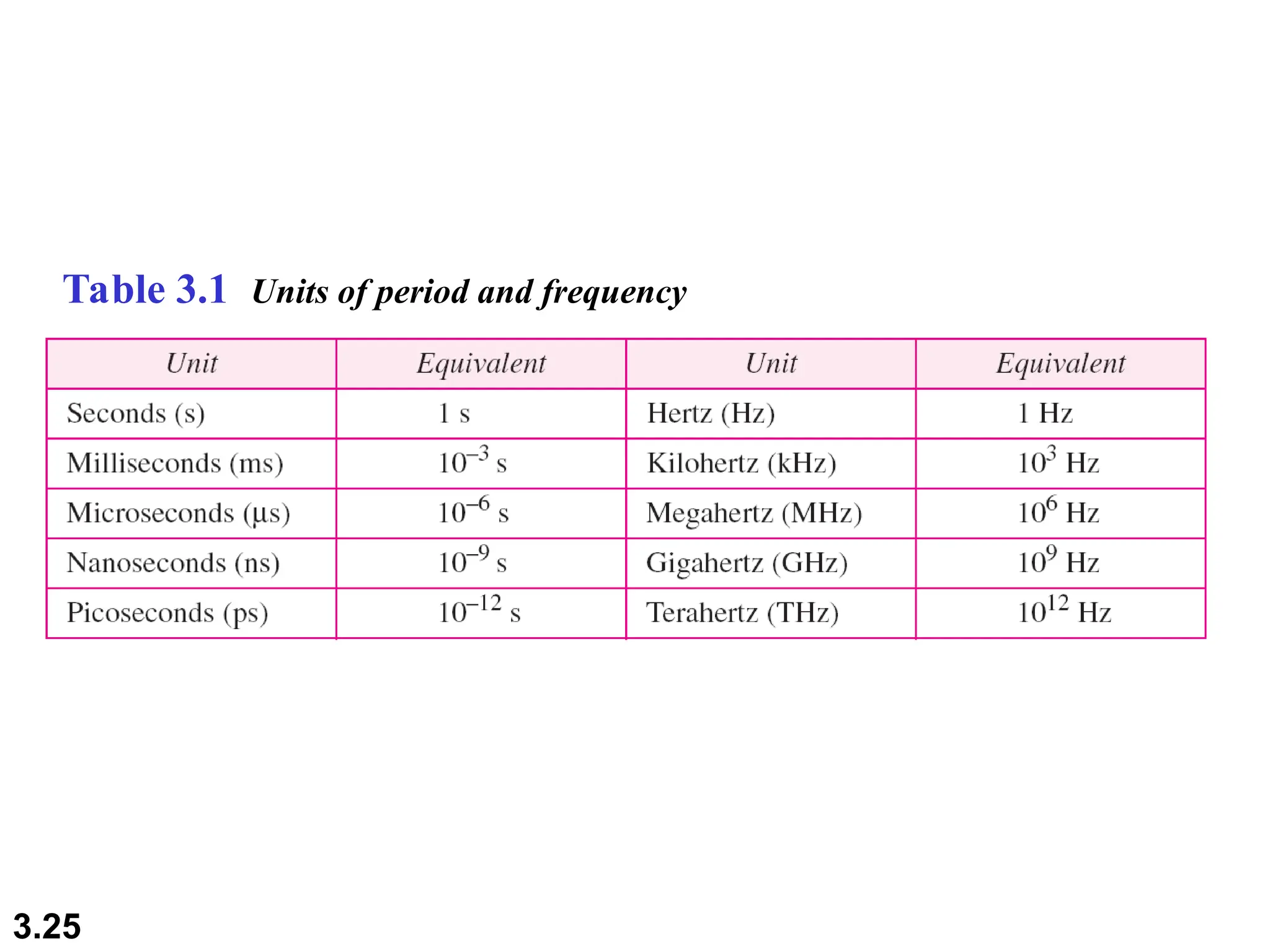
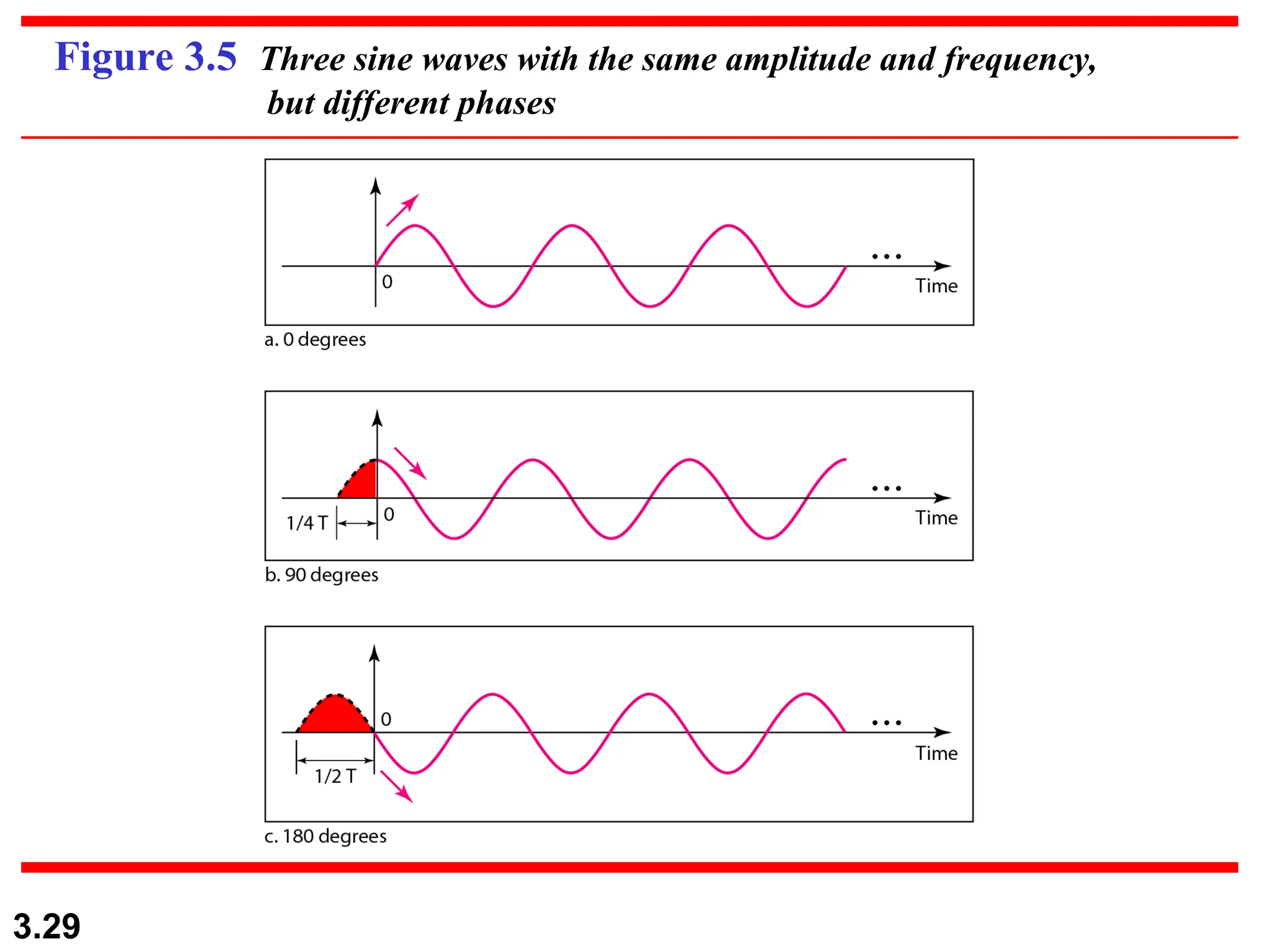
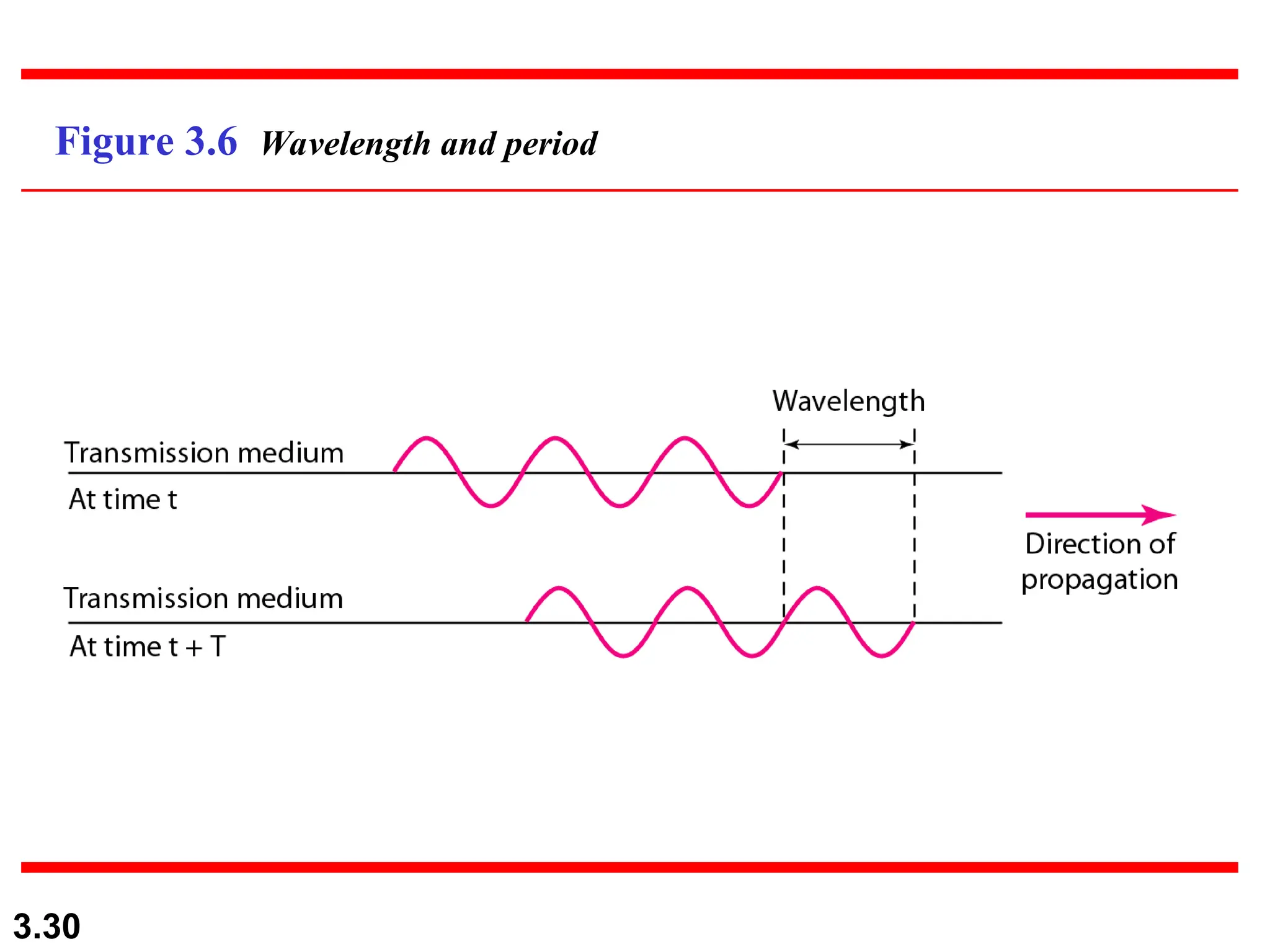
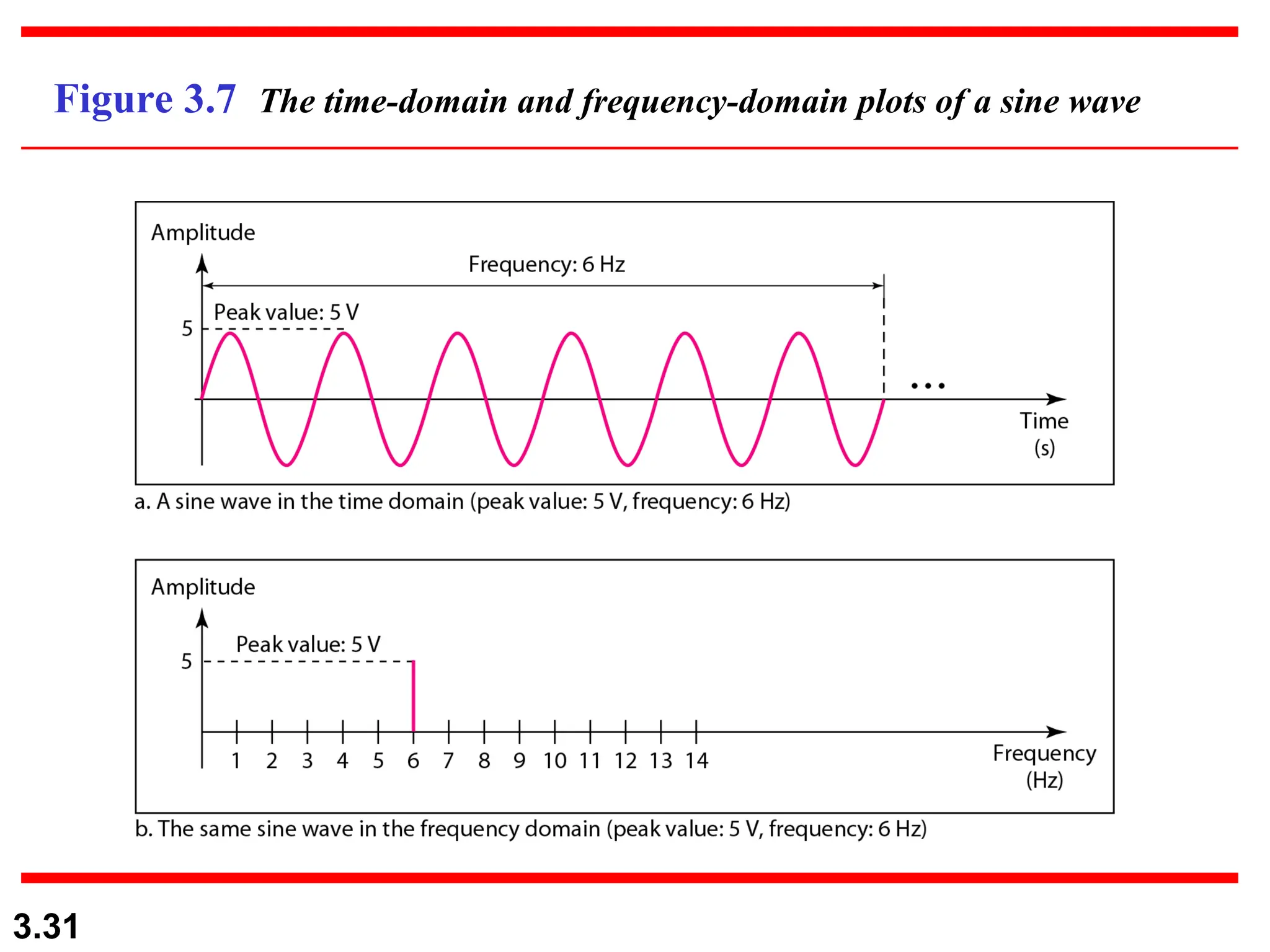
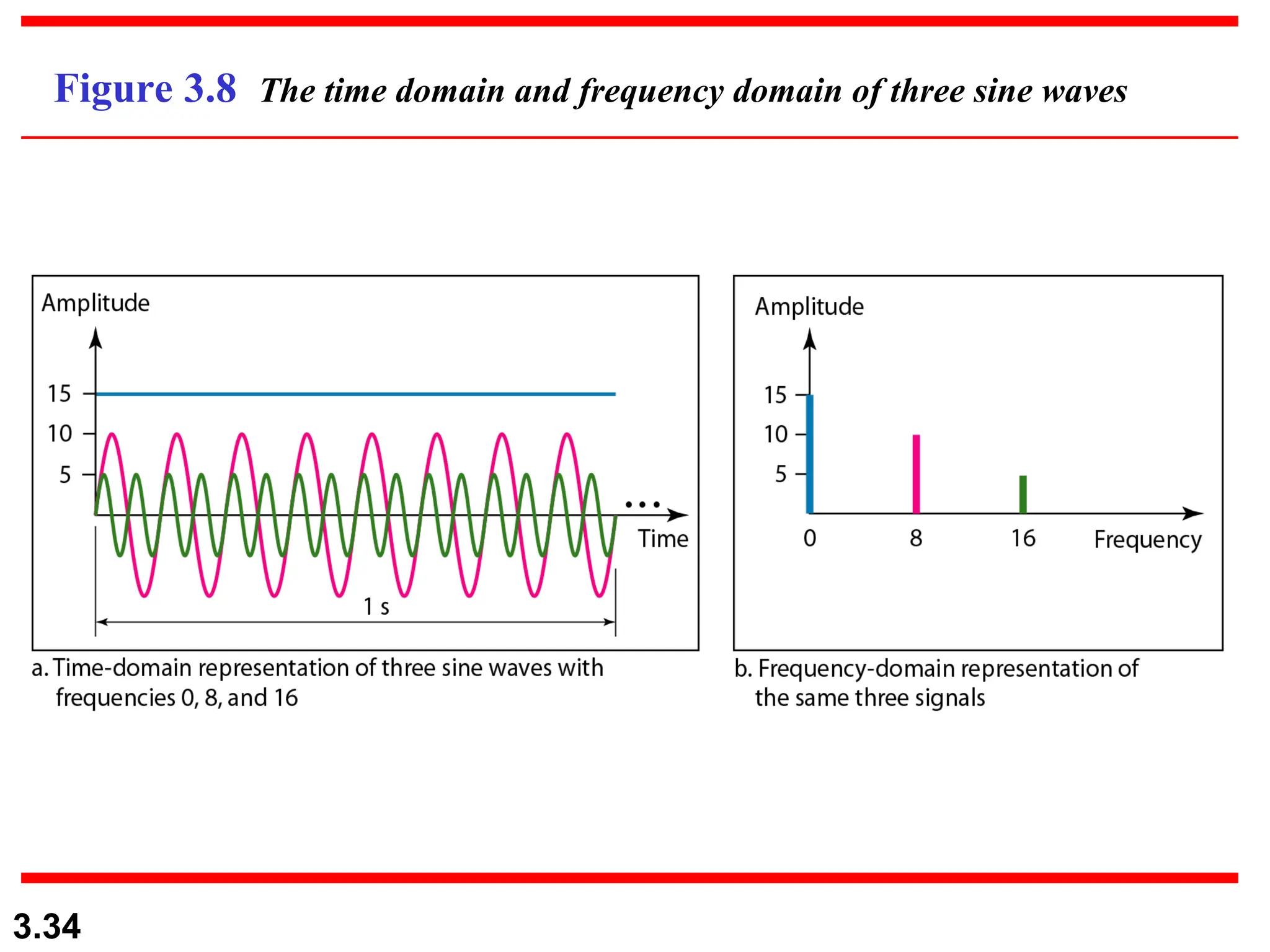
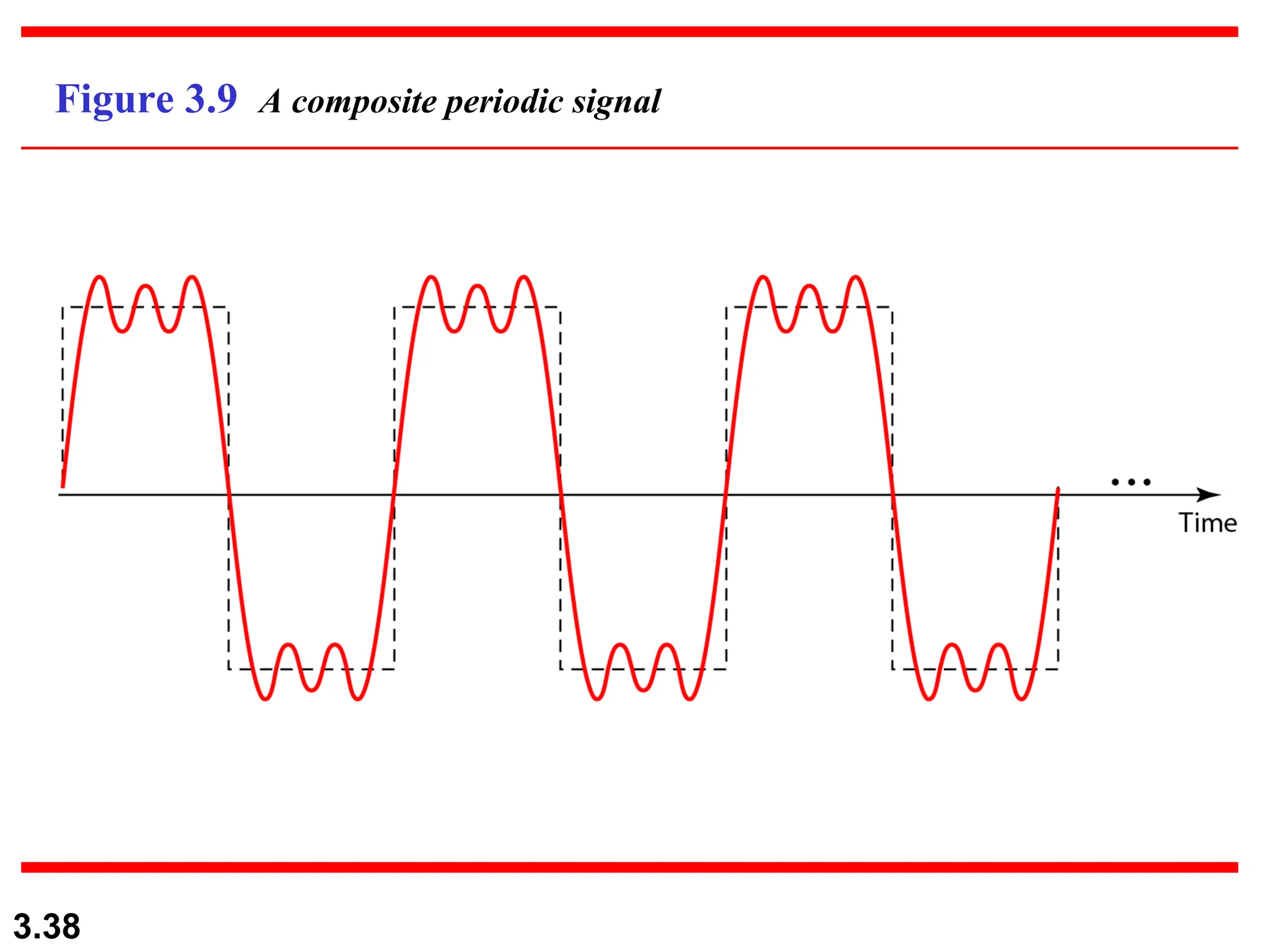
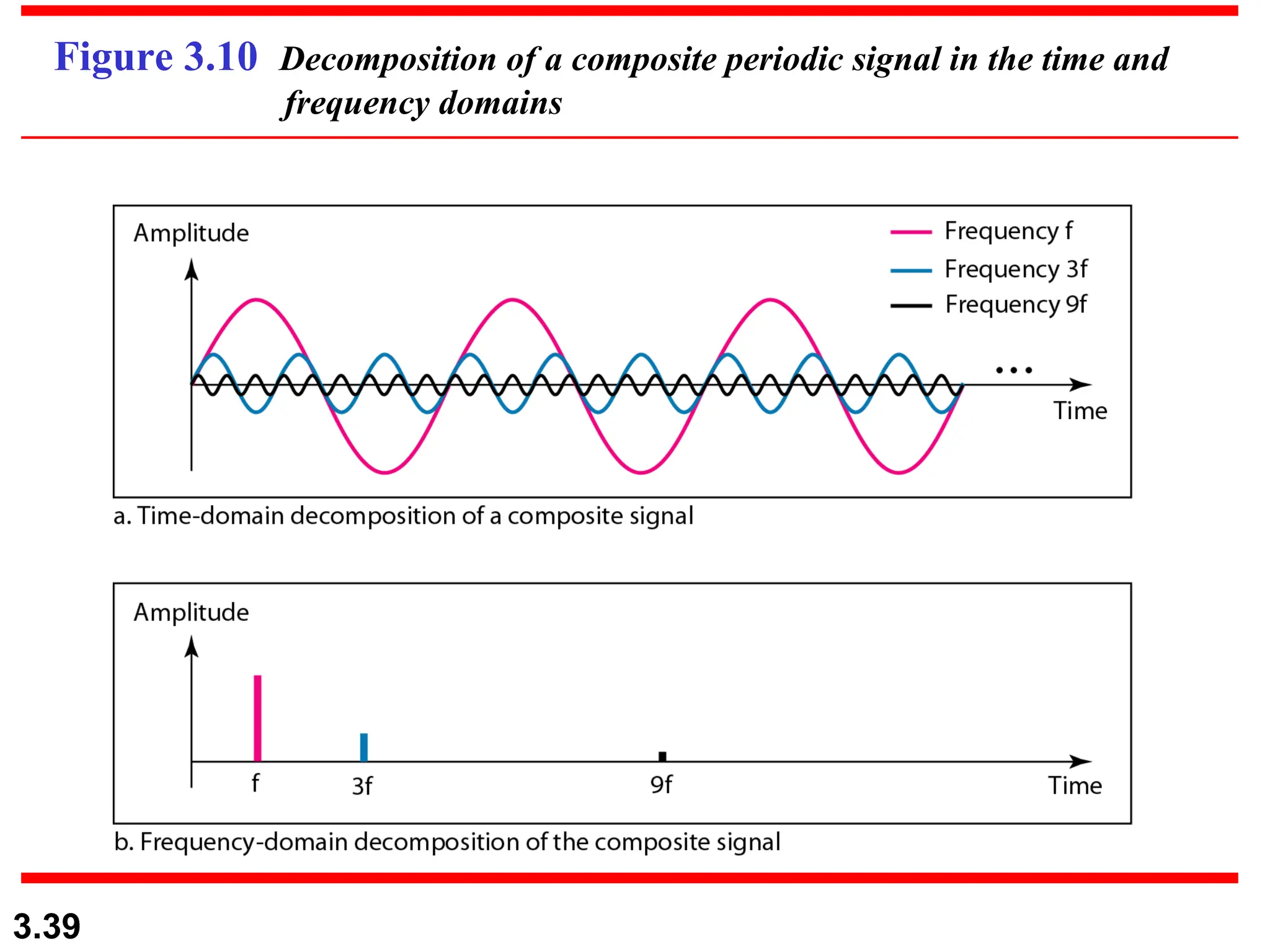
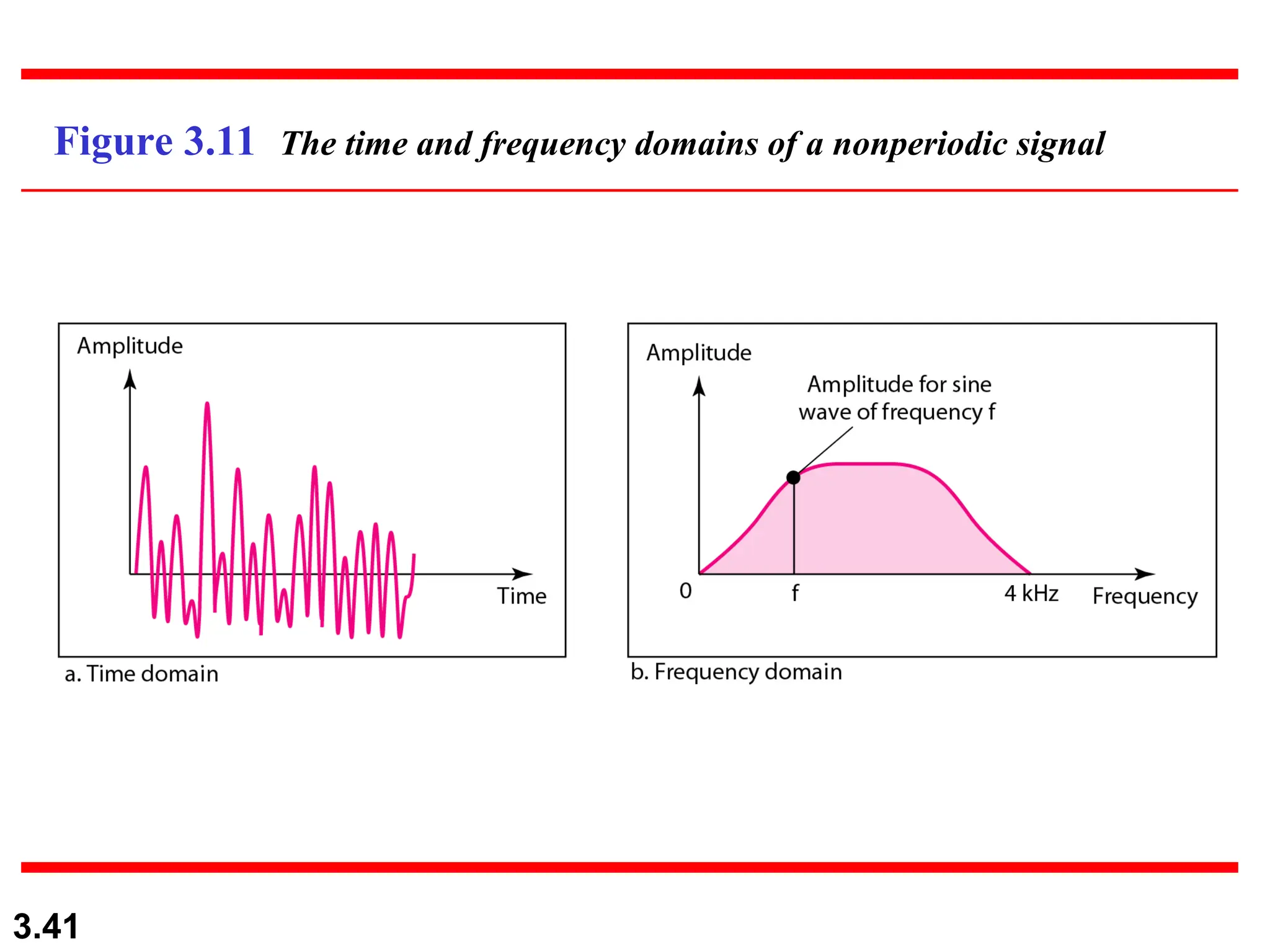
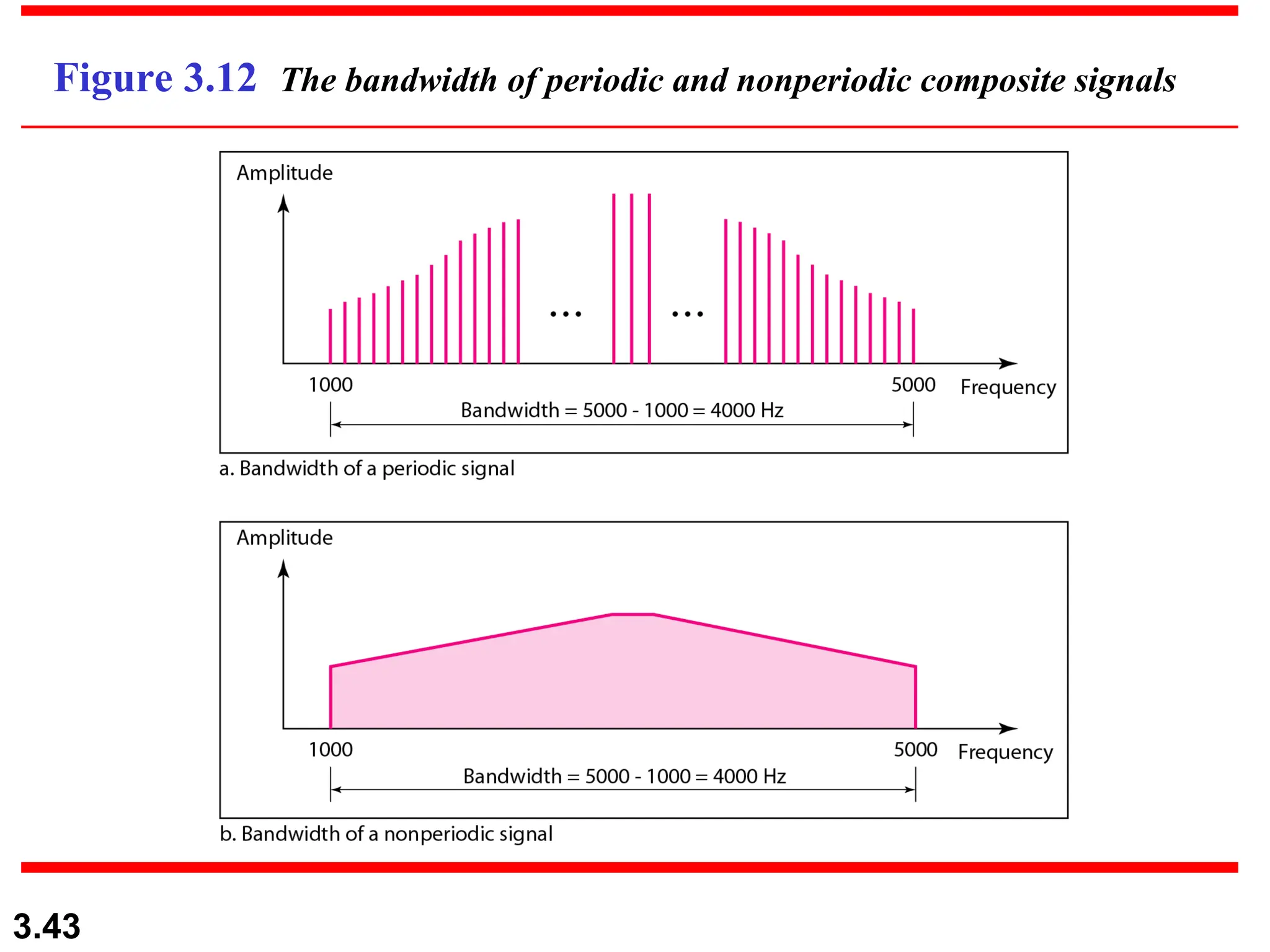
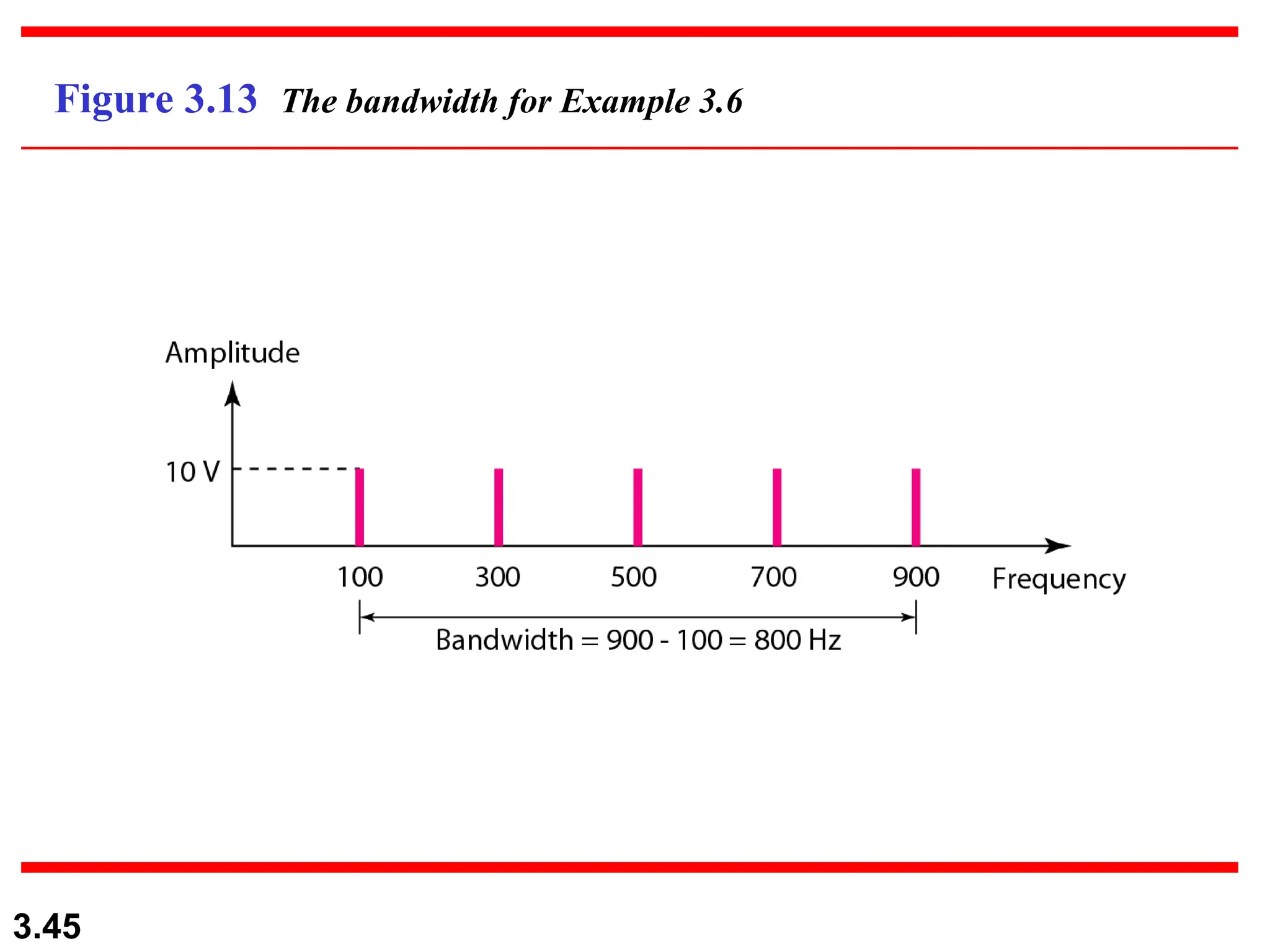
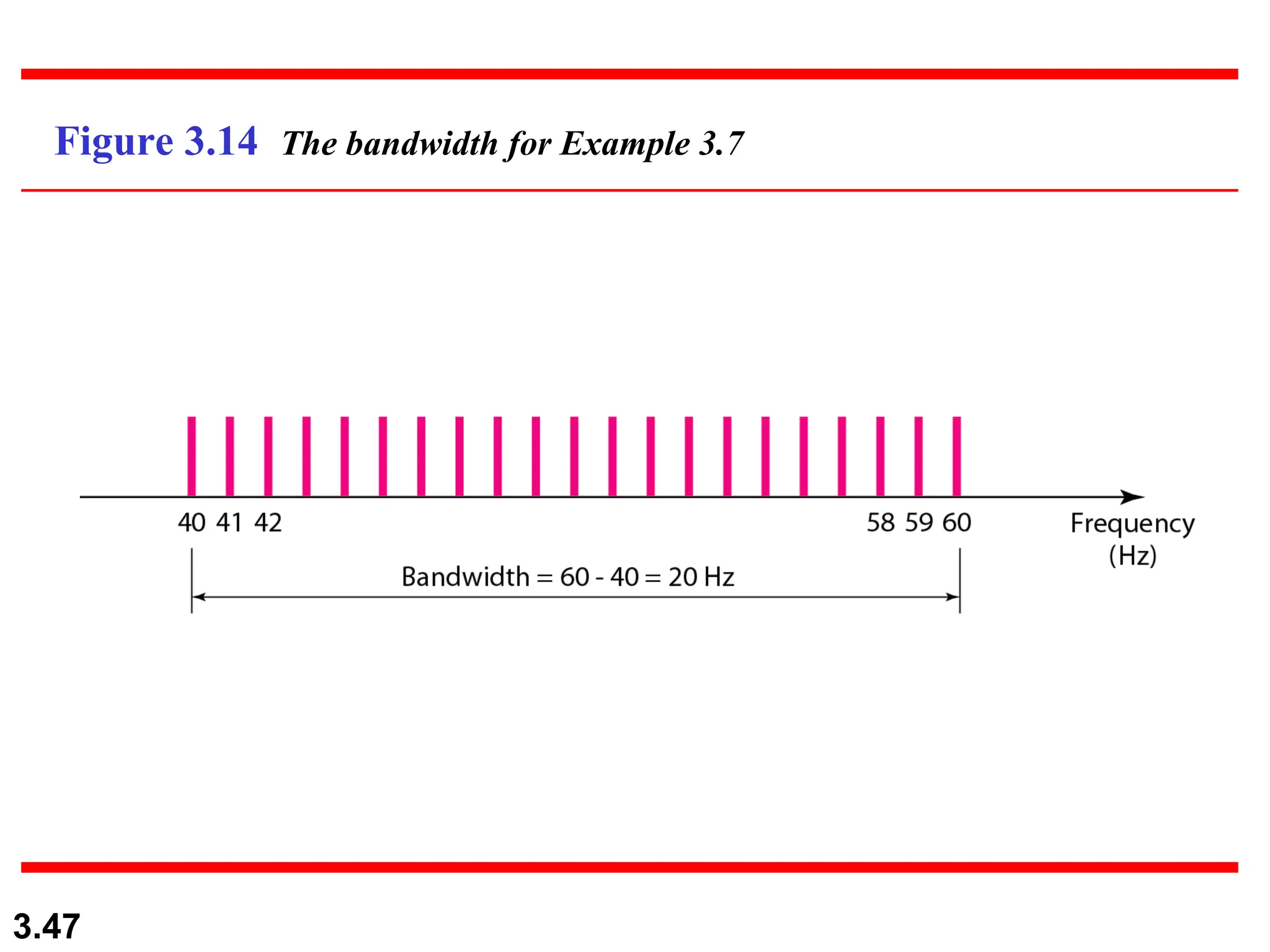
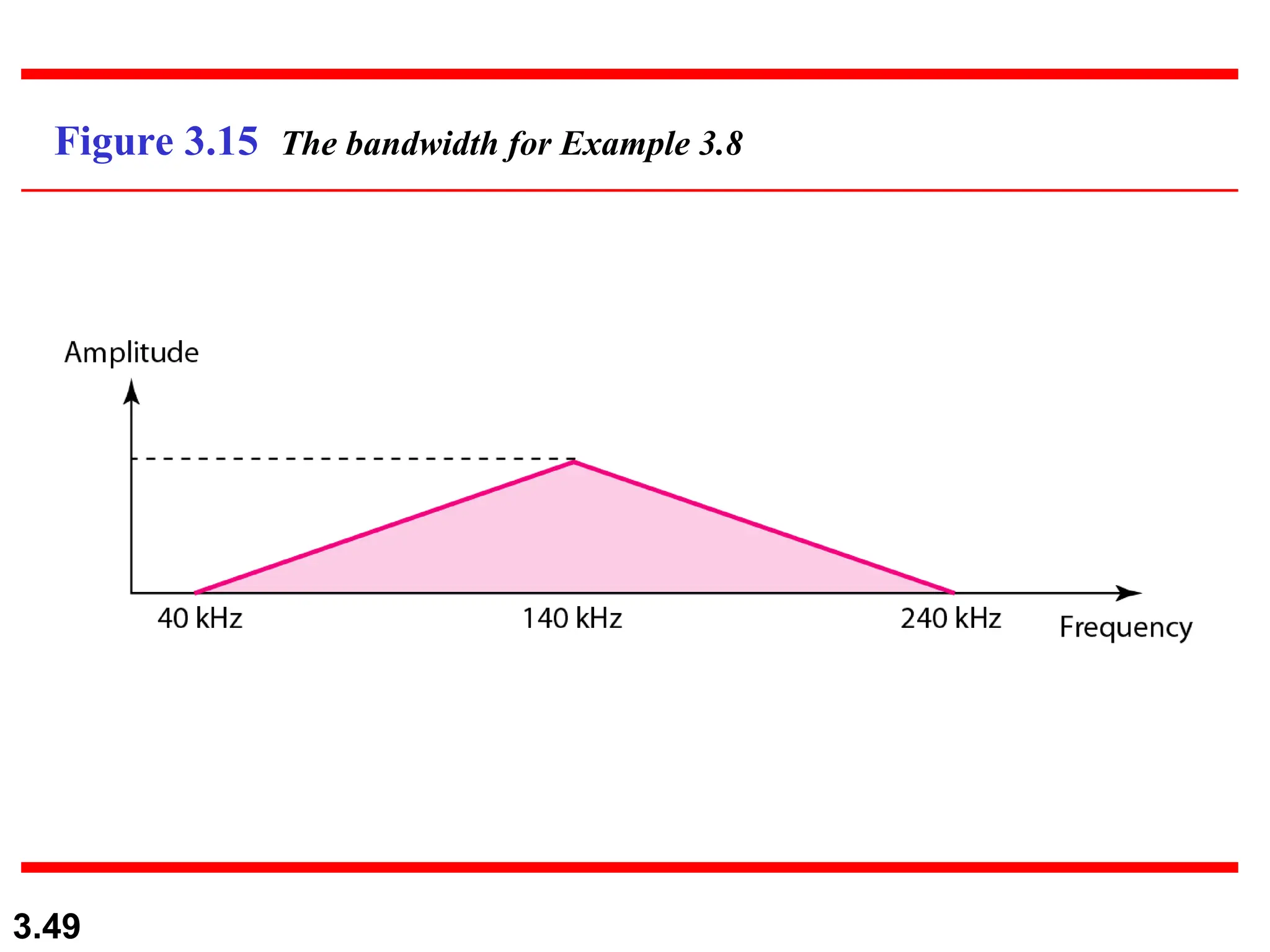
The document discusses data communication systems, focusing on point-to-point and multipoint connections, as well as various network topologies. It explains the elements of communication protocols, including syntax, semantics, and timing, and differentiates between analog and digital signals and data. Additionally, it covers the frequency and bandwidth characteristics of signals, utilizing figures to illustrate these concepts.