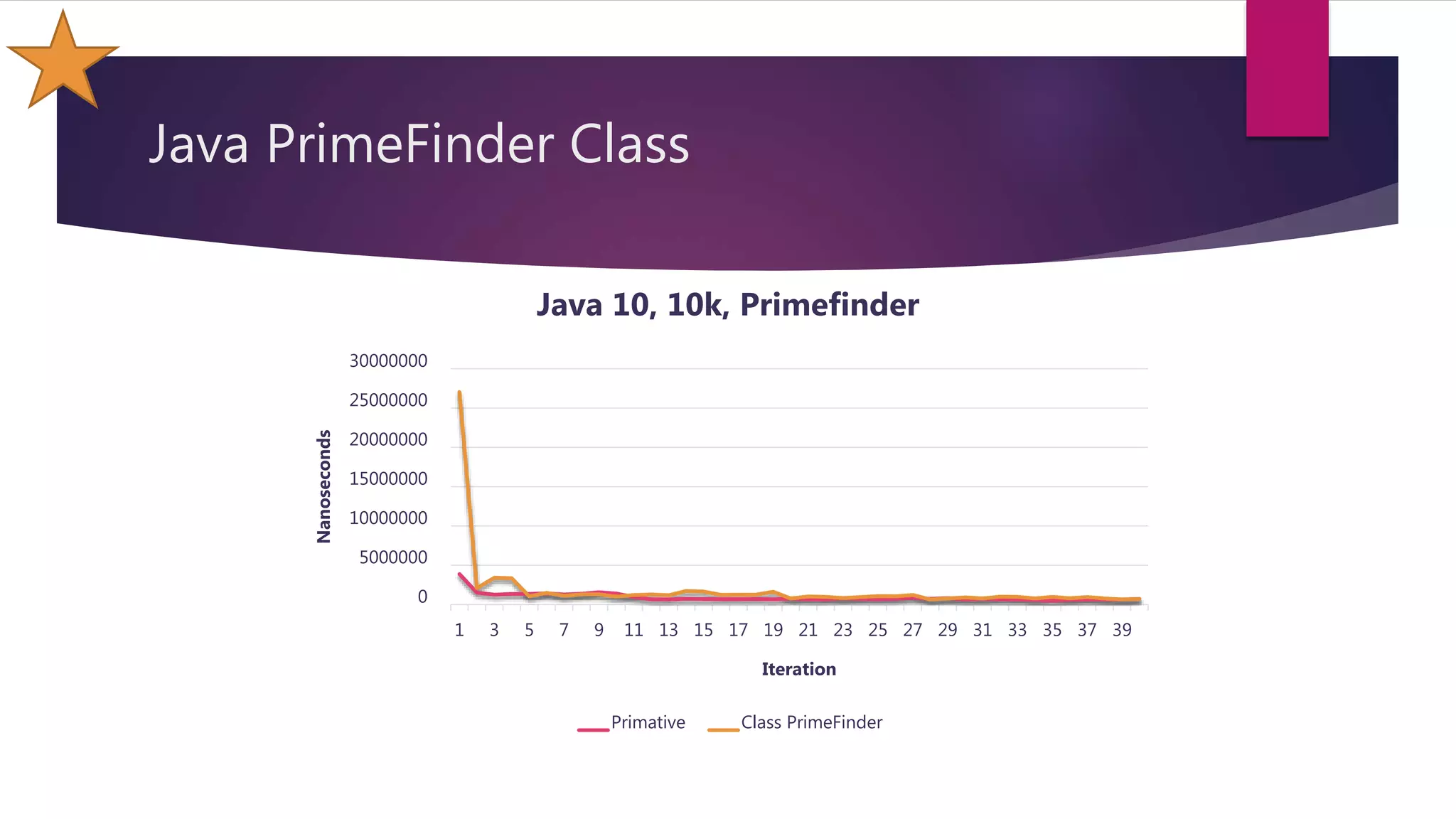
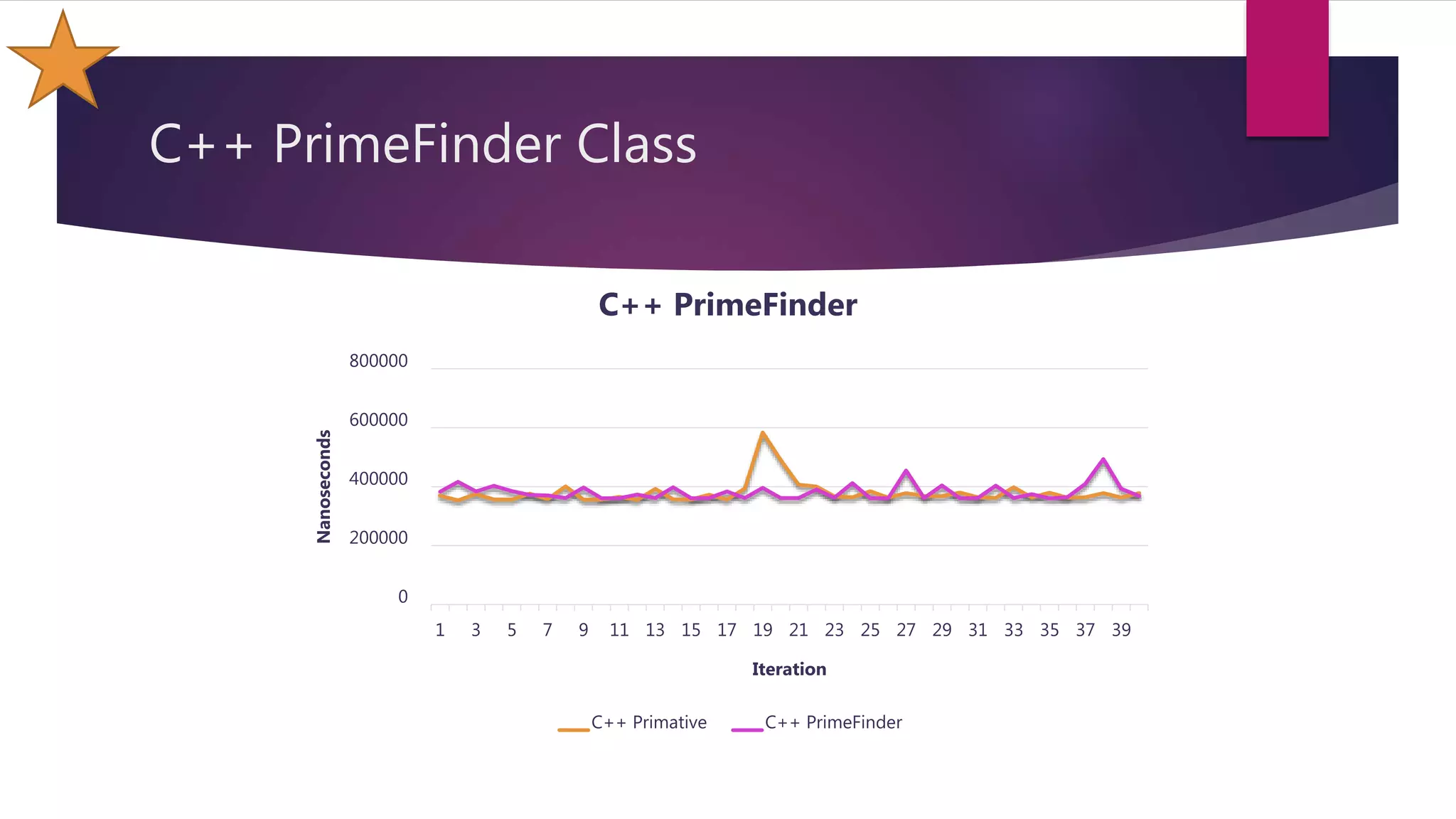
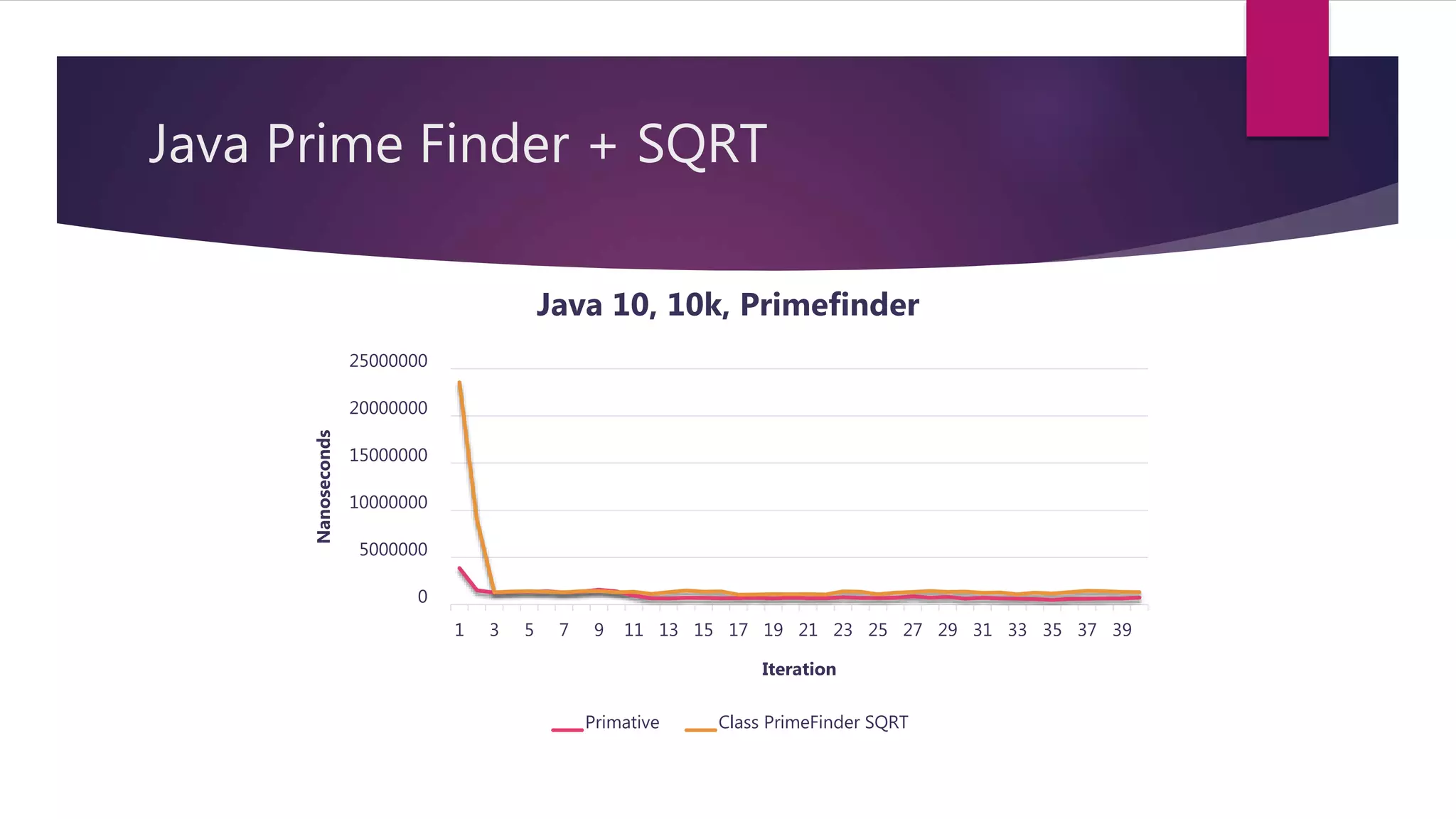
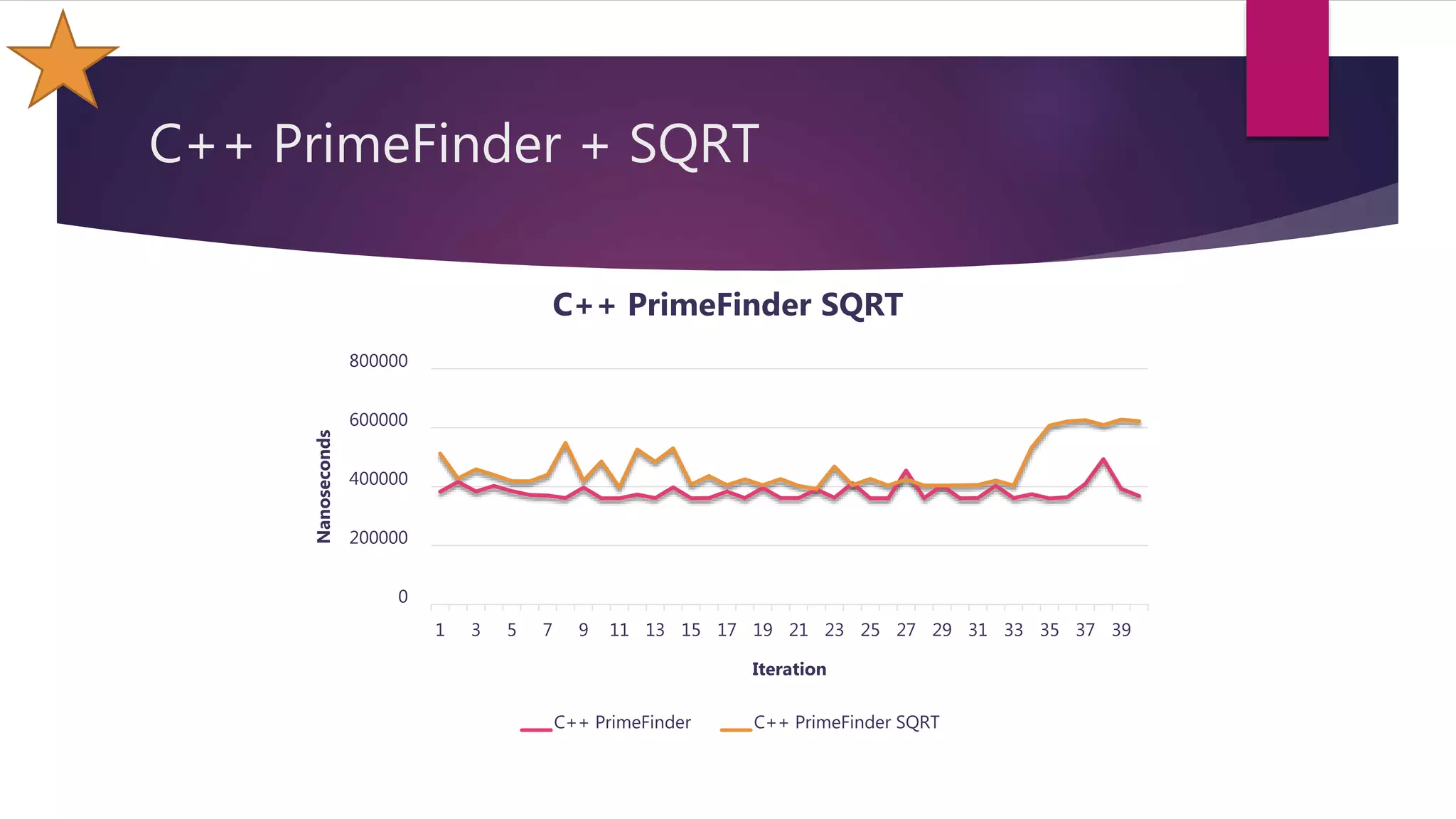
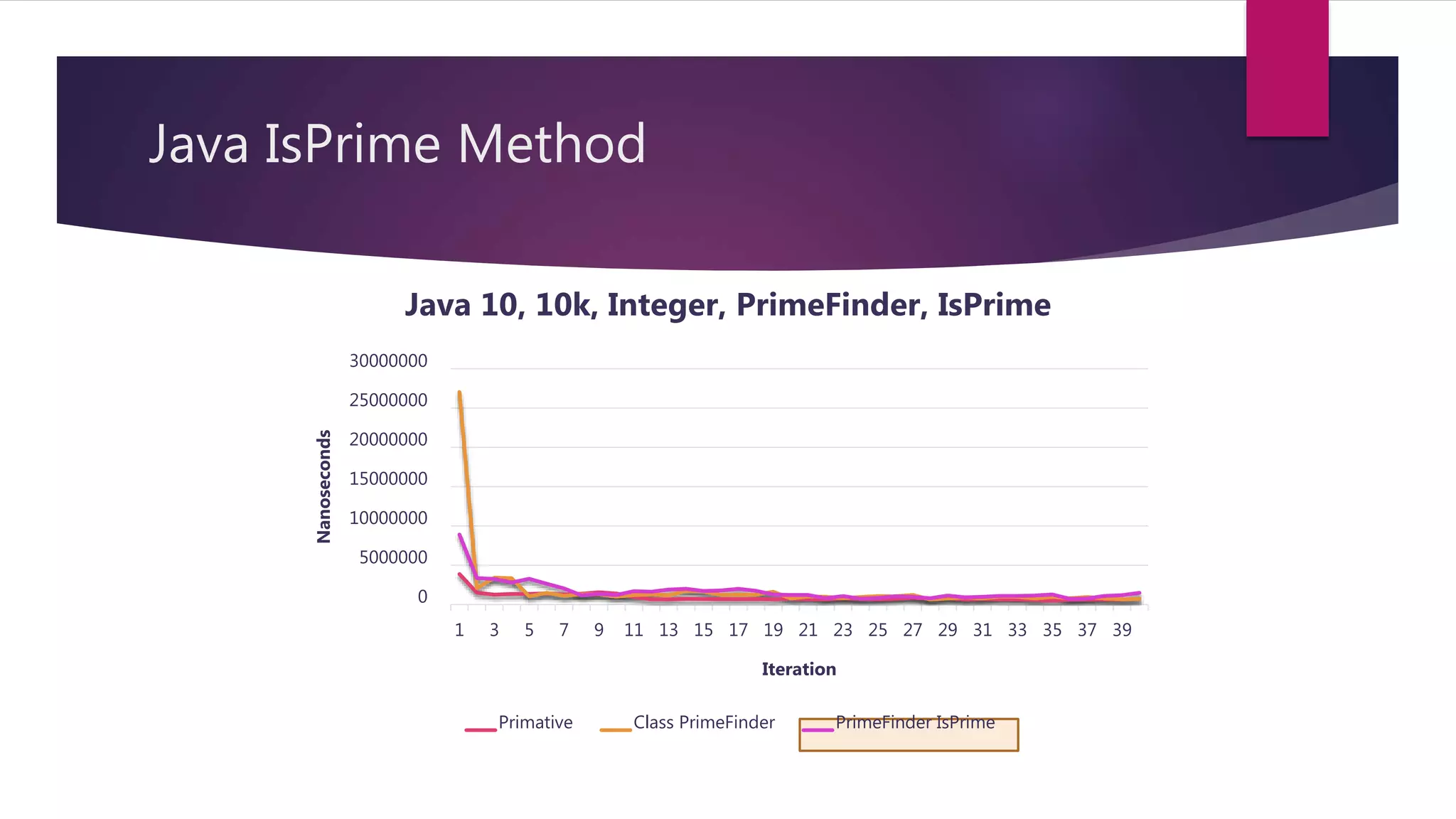
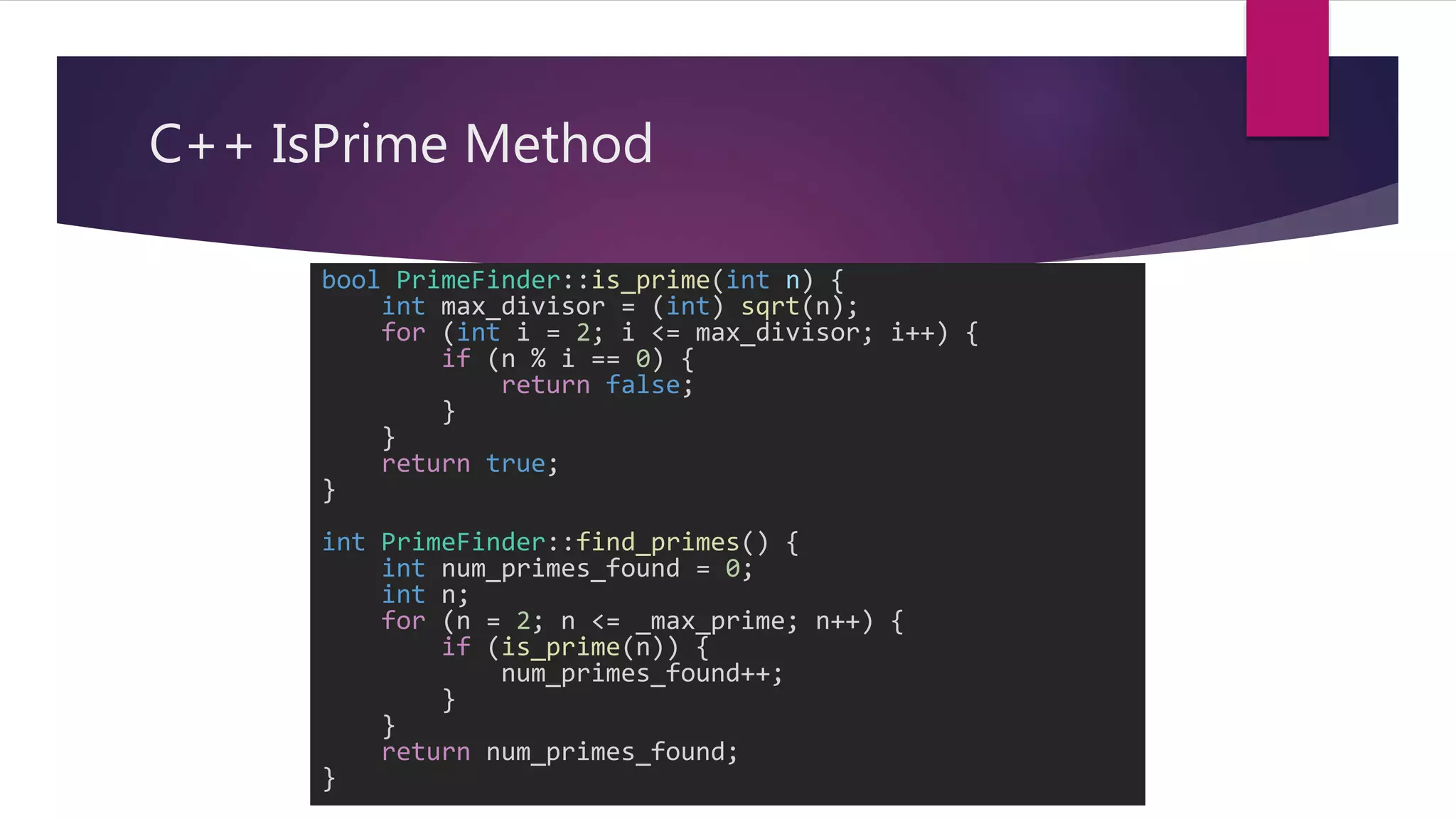
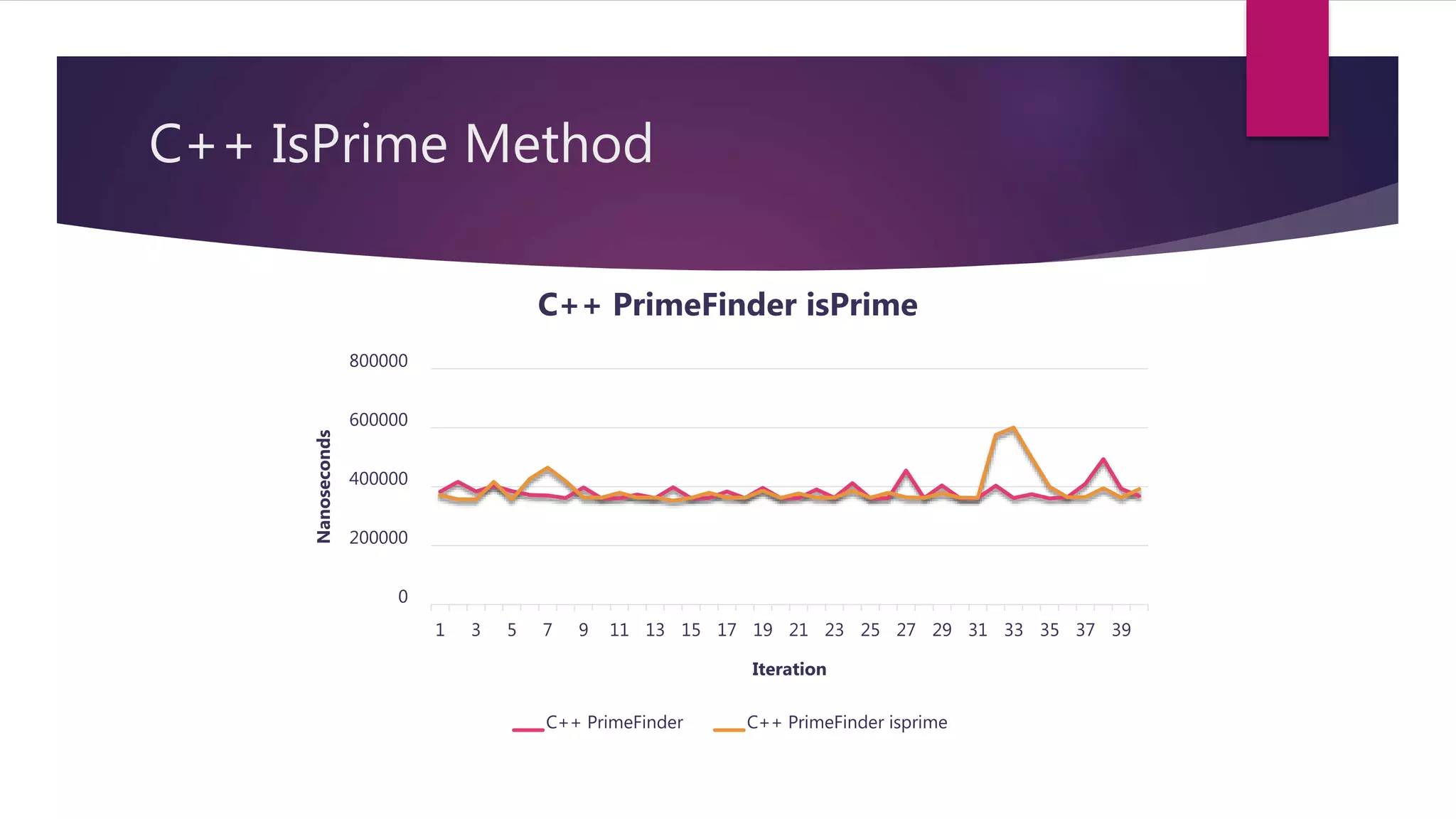
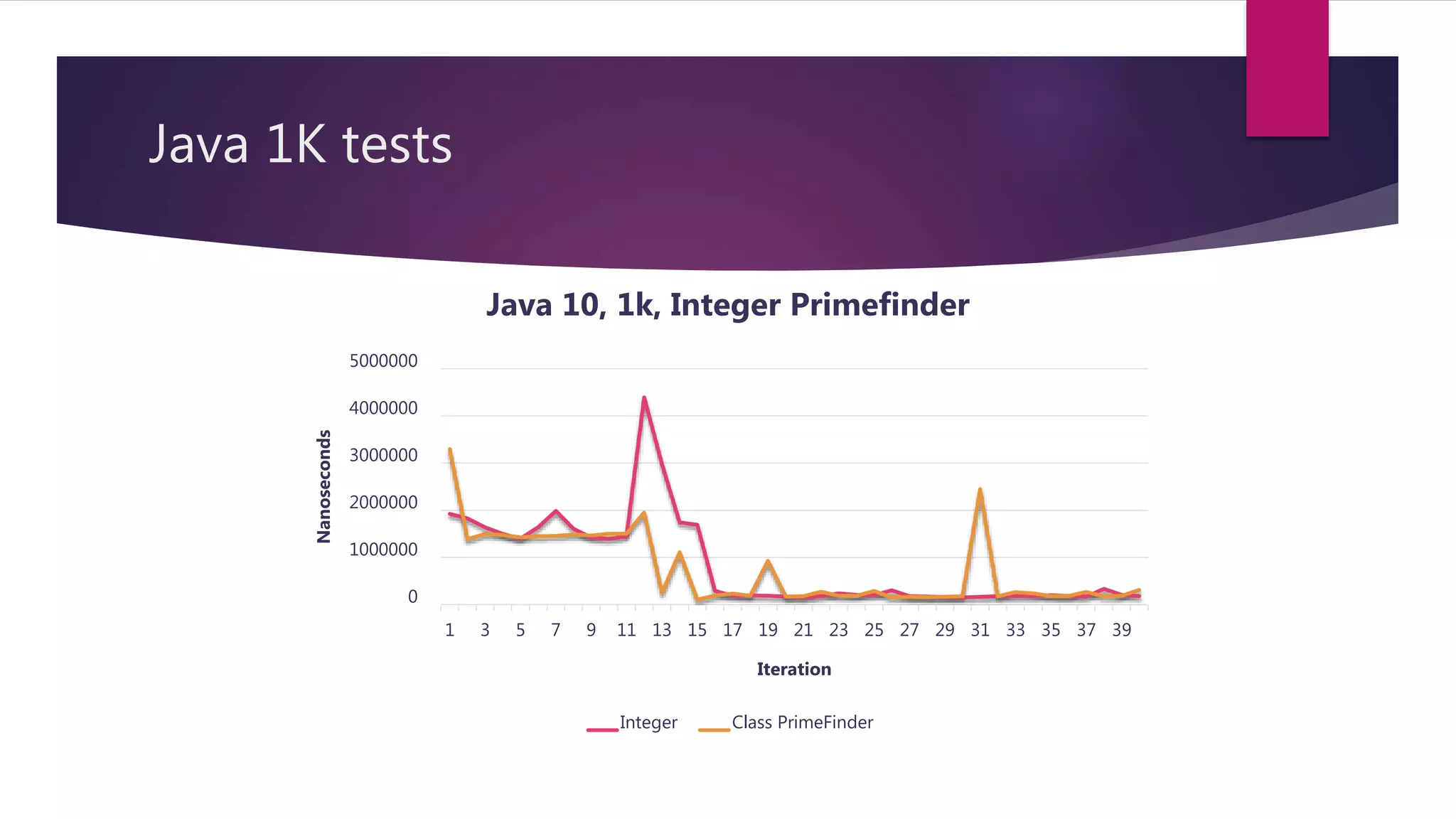
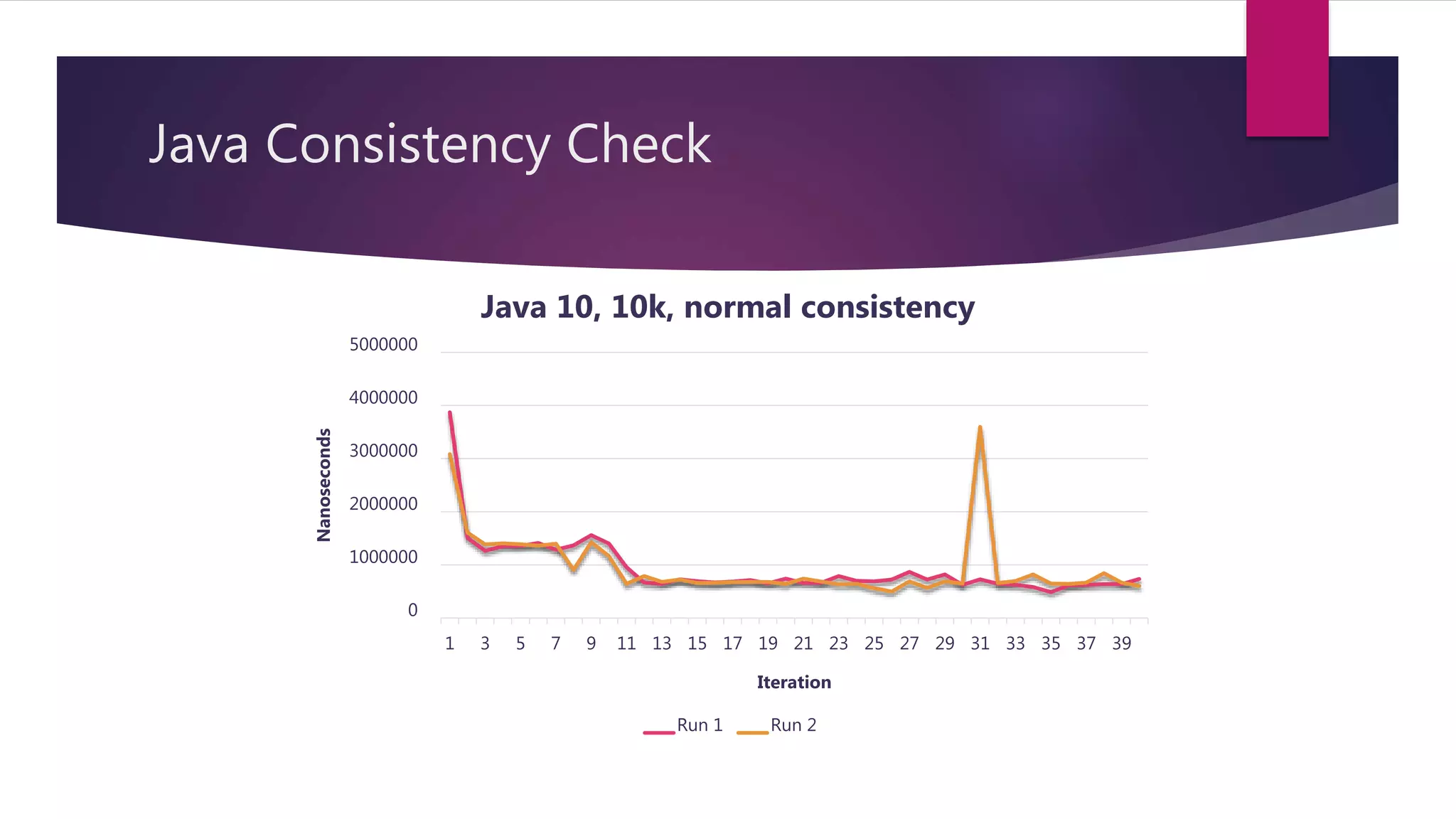
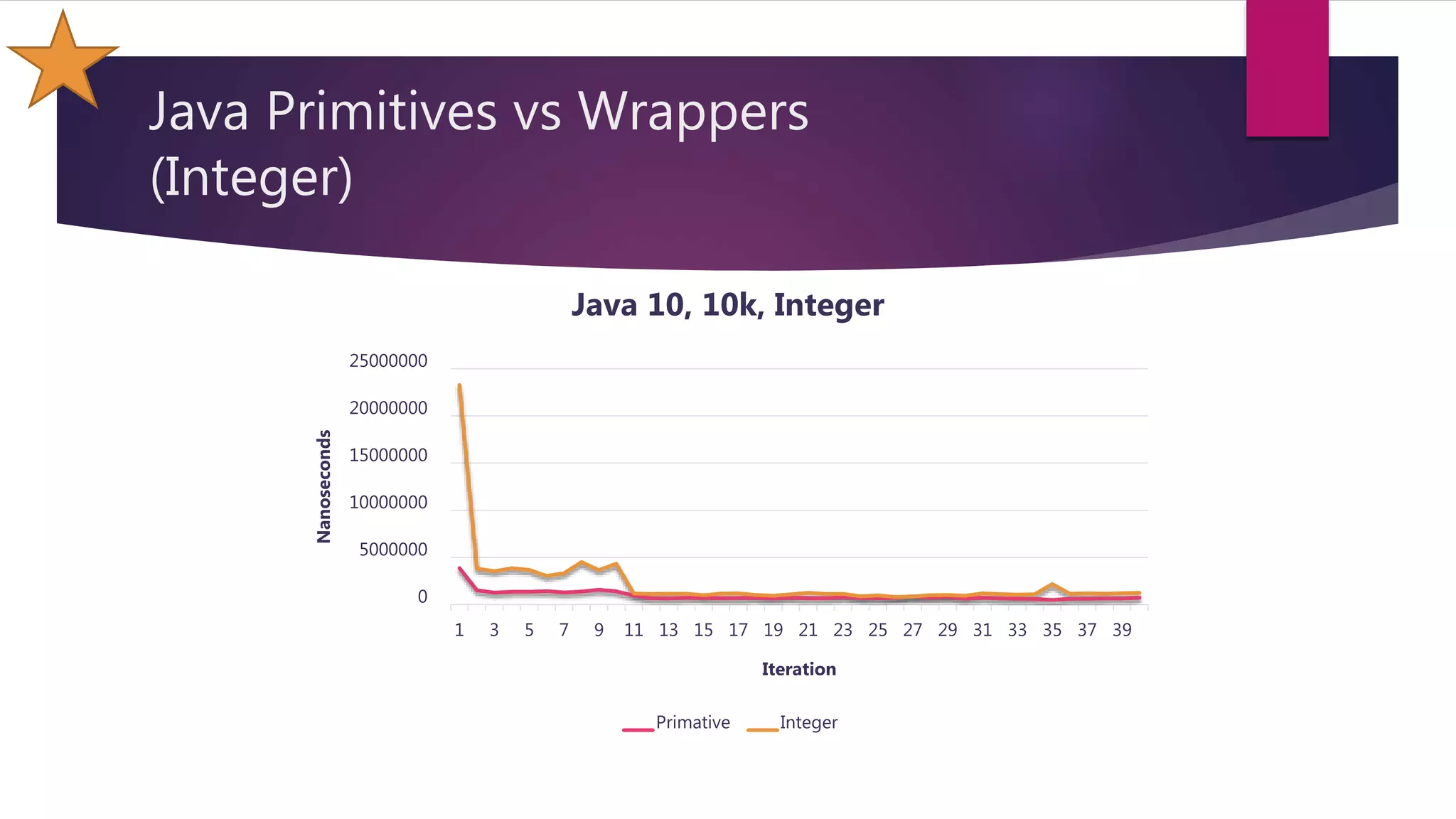
This document discusses optimizations made to code for finding prime numbers in Java and C++. It analyzes performance of different implementations, including using primitives vs wrappers, creating a PrimeFinder class, bringing the square root calculation inside the loop, and adding an is_prime method. Graphs show performance improvements from these changes, with the fastest implementations taking around 2-3 million nanoseconds to find primes up to 10,000.



![Java PrimeFinder Class
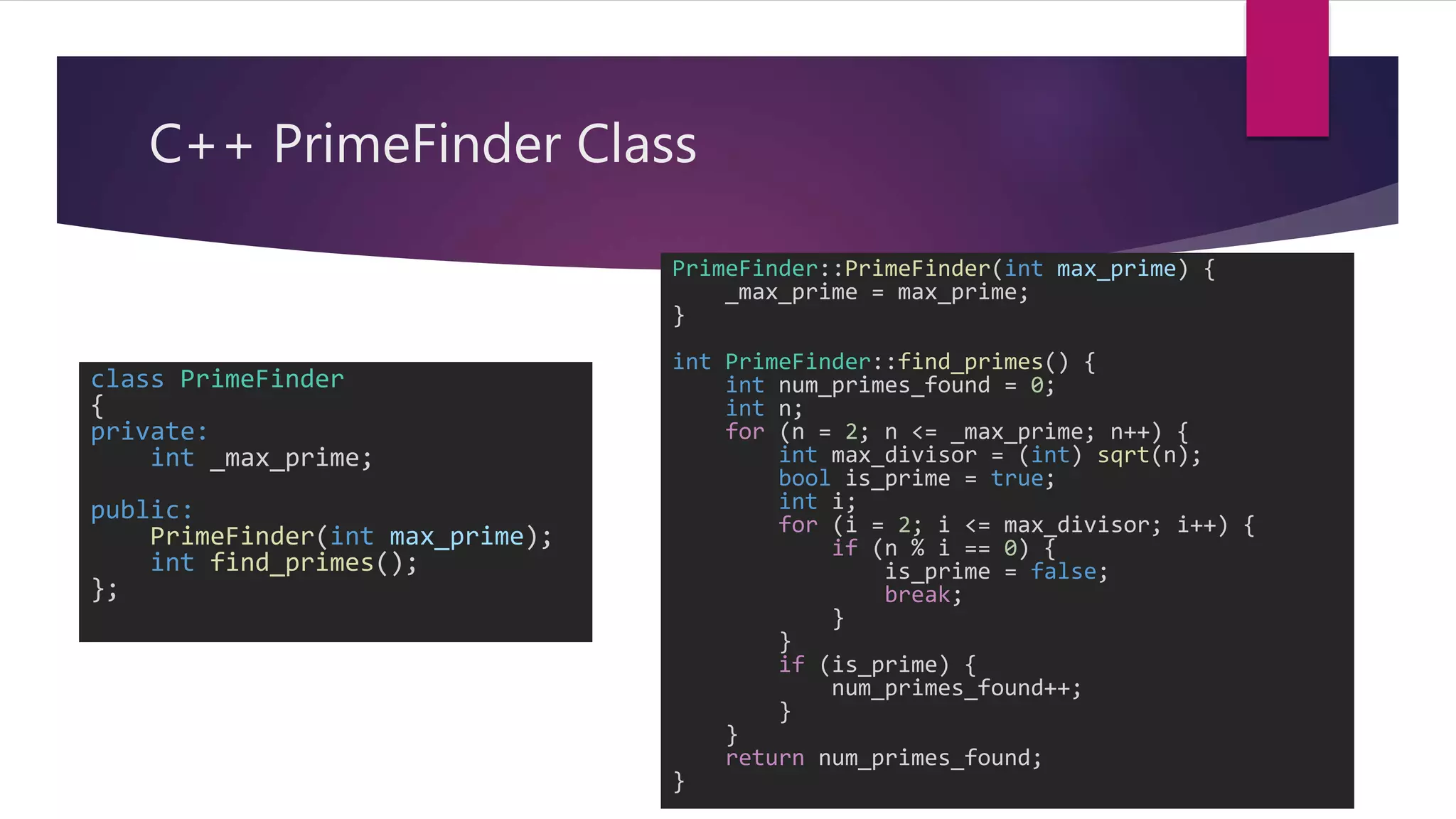
public class PrimeFinder {
private Integer max_prime;
public PrimeFinder(Integer max_prime) {
this.max_prime = max_prime;
}
public Integer find_primes() {
Integer num_primes_found = 0;
for (Integer n = 2; n <= max_prime; n++) {
Integer max_divisor = (int) sqrt(n);
Boolean is_prime = true;
for (Integer i = 2; i <= max_divisor; i++) {
if (n % i == 0) {
is_prime = false;
break;
}
}
if (is_prime) {
num_primes_found++;
}
}
return num_primes_found;
}
}
public static void main(String[] args) {
for (Integer iter = 0; iter < max_iter; iter++) {
//Start Timer
PrimeFinder primeFinder = new PrimeFinder(iter, max_prime);
num_primes_found = primeFinder.find_primes();
//End timer & Print
}](https://image.slidesharecdn.com/primeresultsobjects-191201184225/75/C-Java-JIT-Optimizations-Finding-Prime-Numbers-7-2048.jpg)