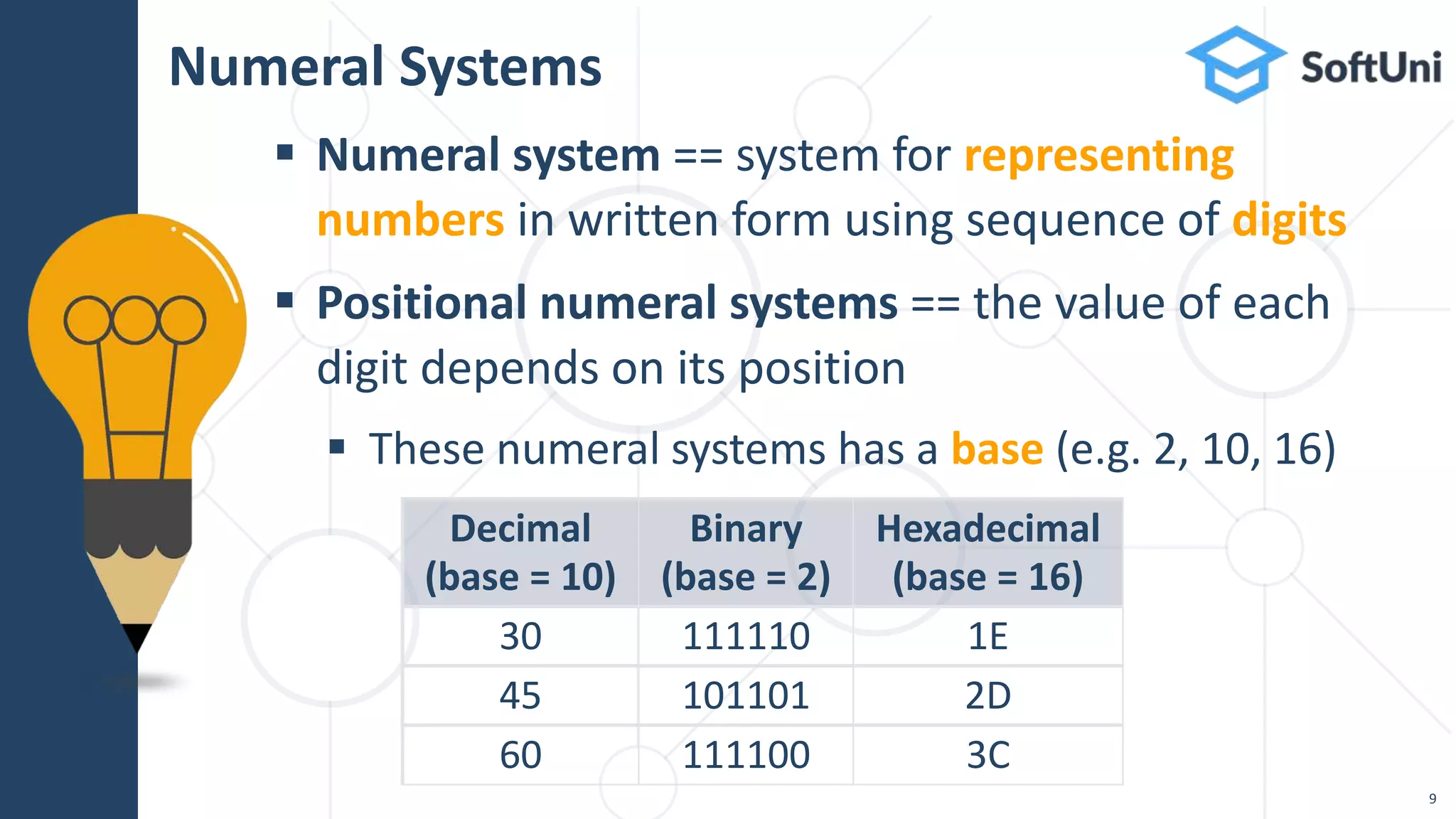
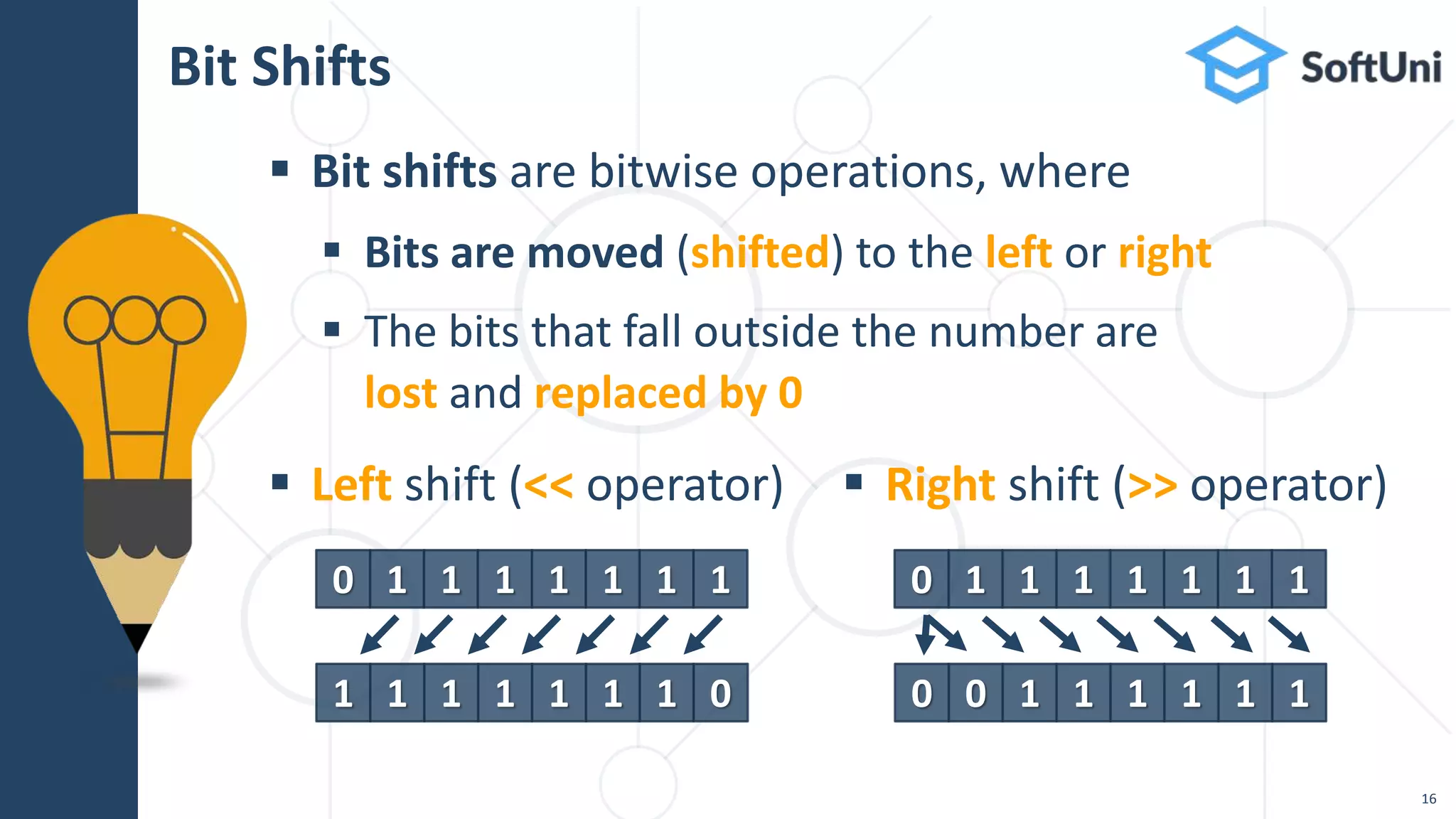
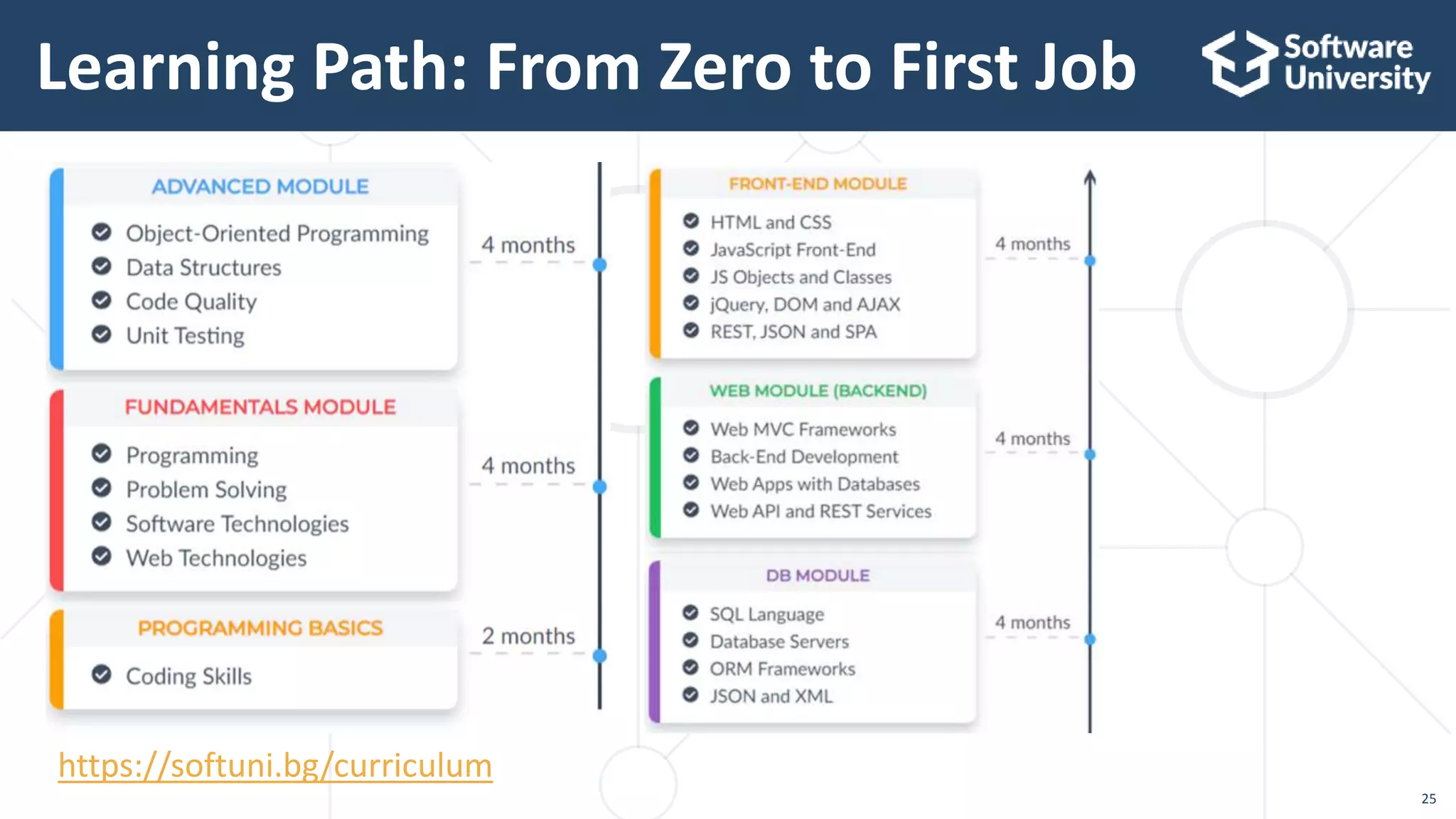
The document outlines essential skills and knowledge required for becoming a software developer, including coding, algorithms, and bitwise operations. It explains numeral systems, such as binary, decimal, and hexadecimal, along with their conversions and bit manipulation techniques. Additionally, it emphasizes the importance of practice and commitment, recommending extensive study and the completion of practical coding projects.