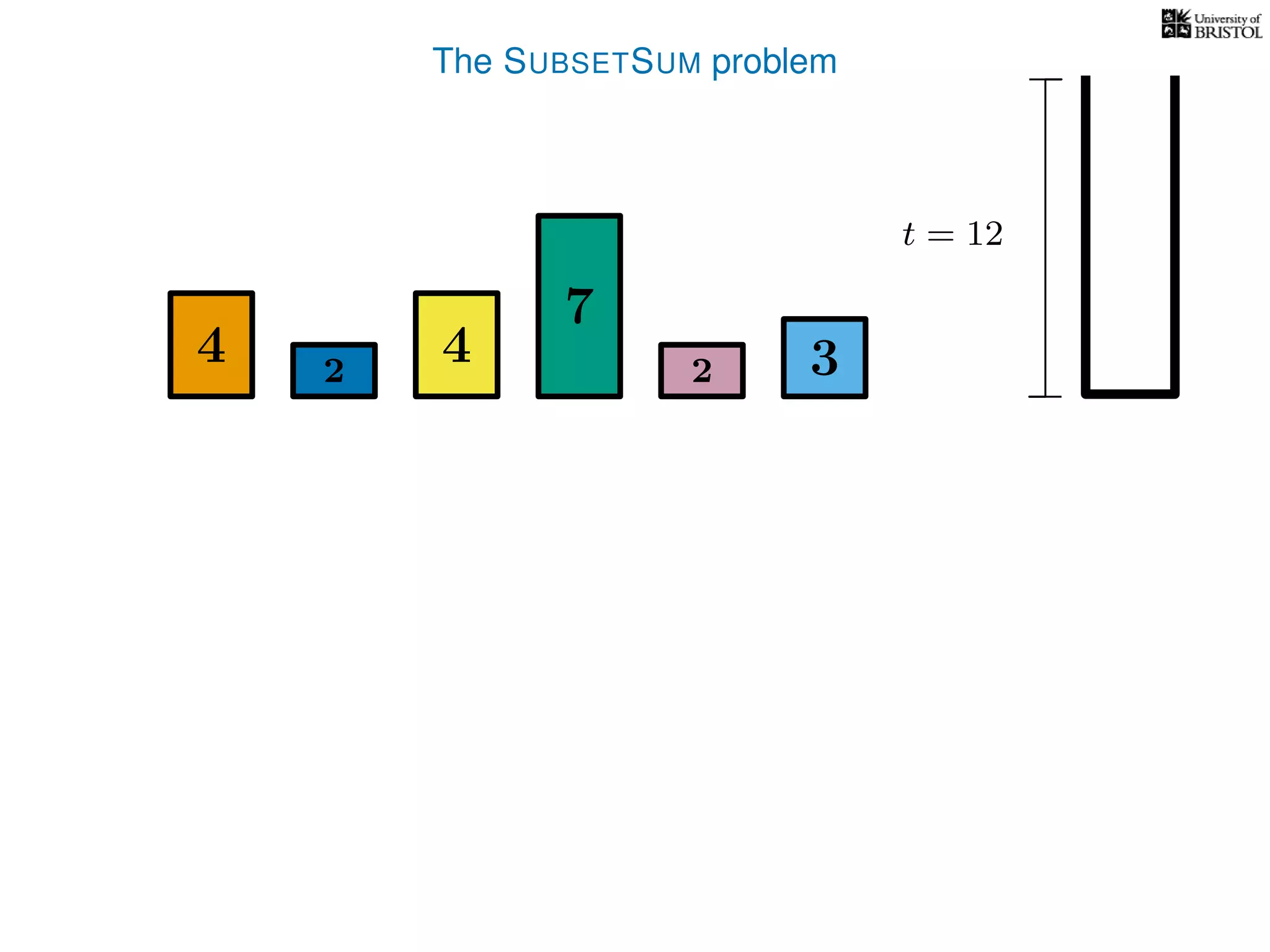
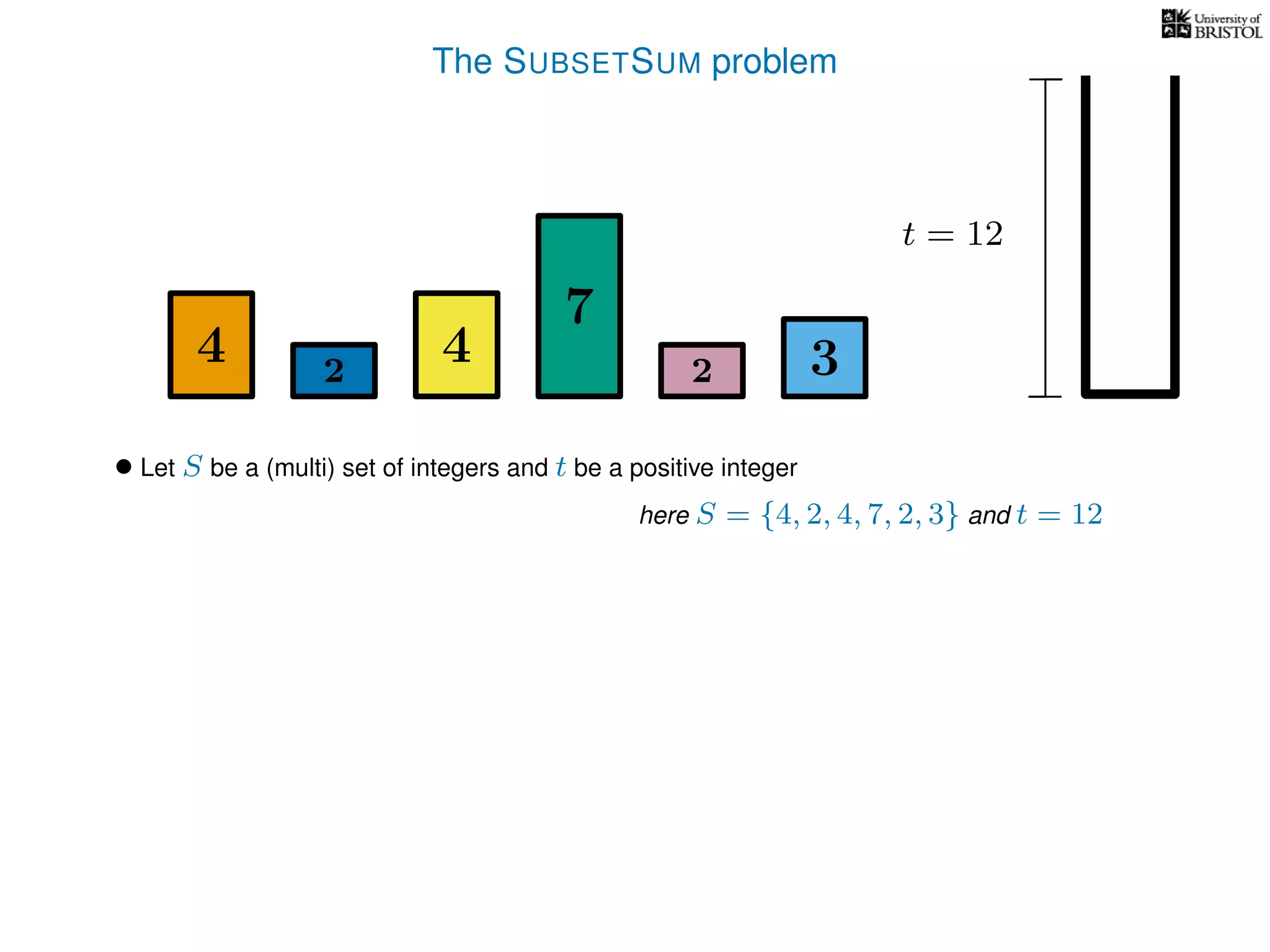
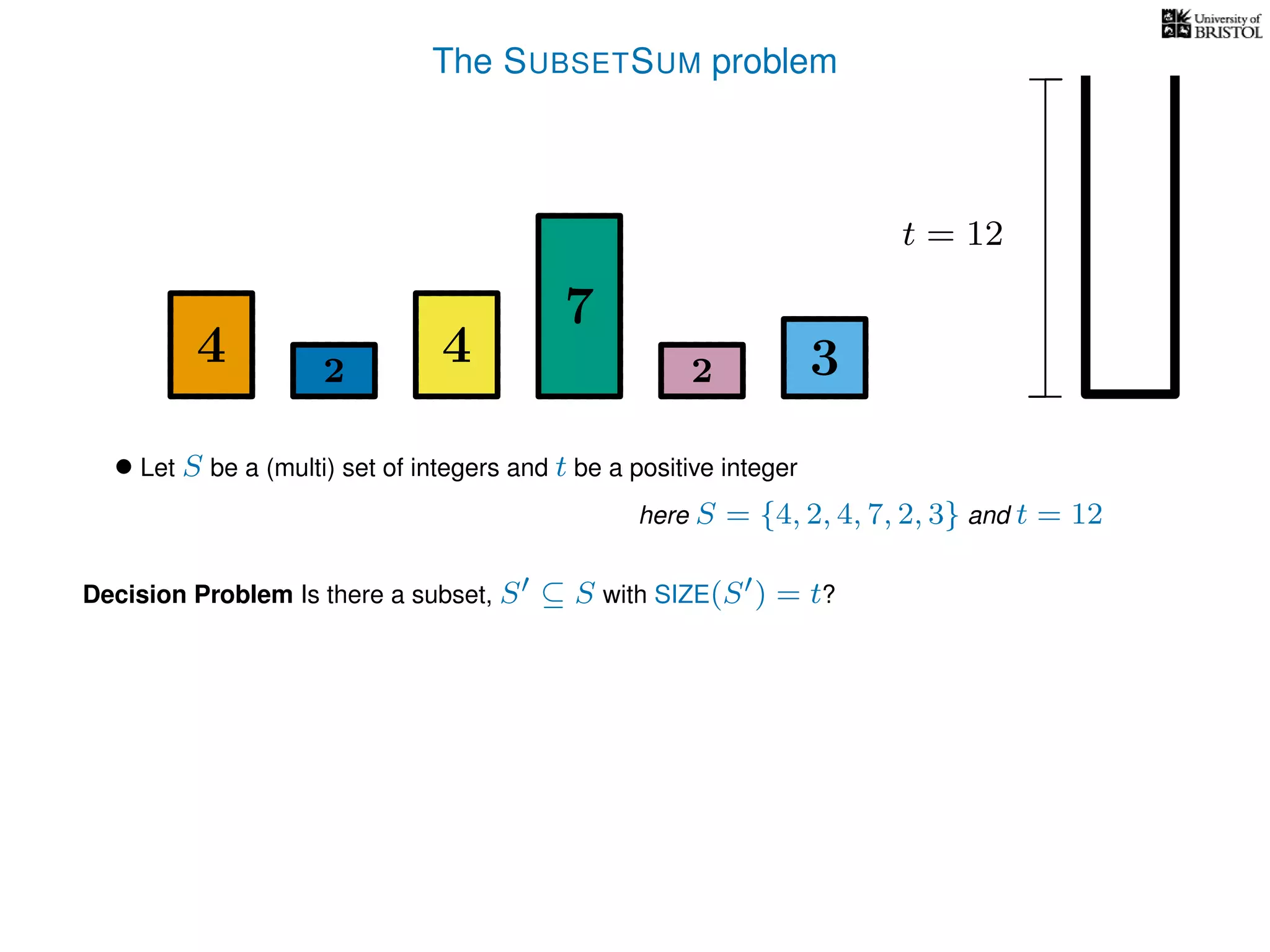
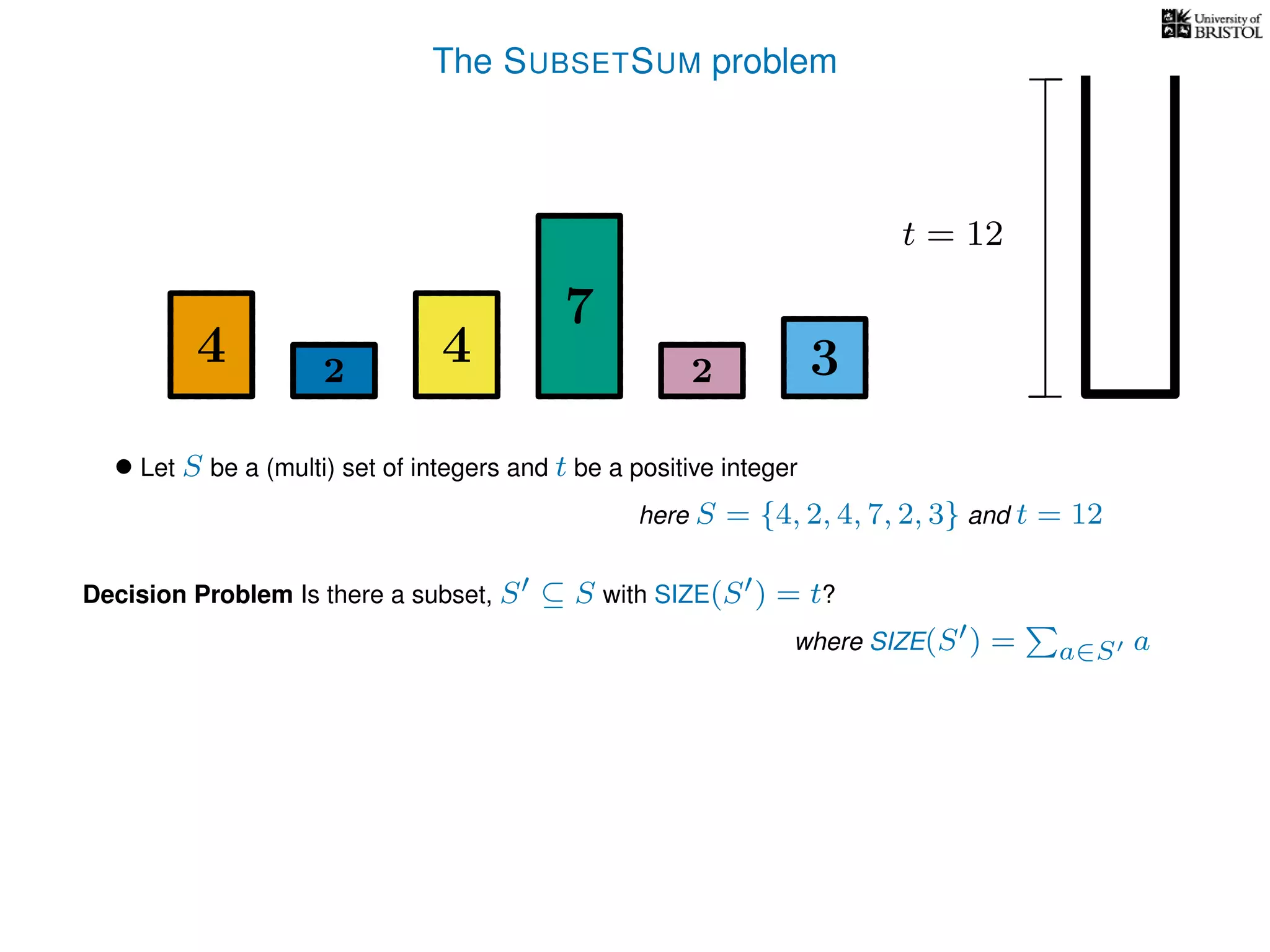
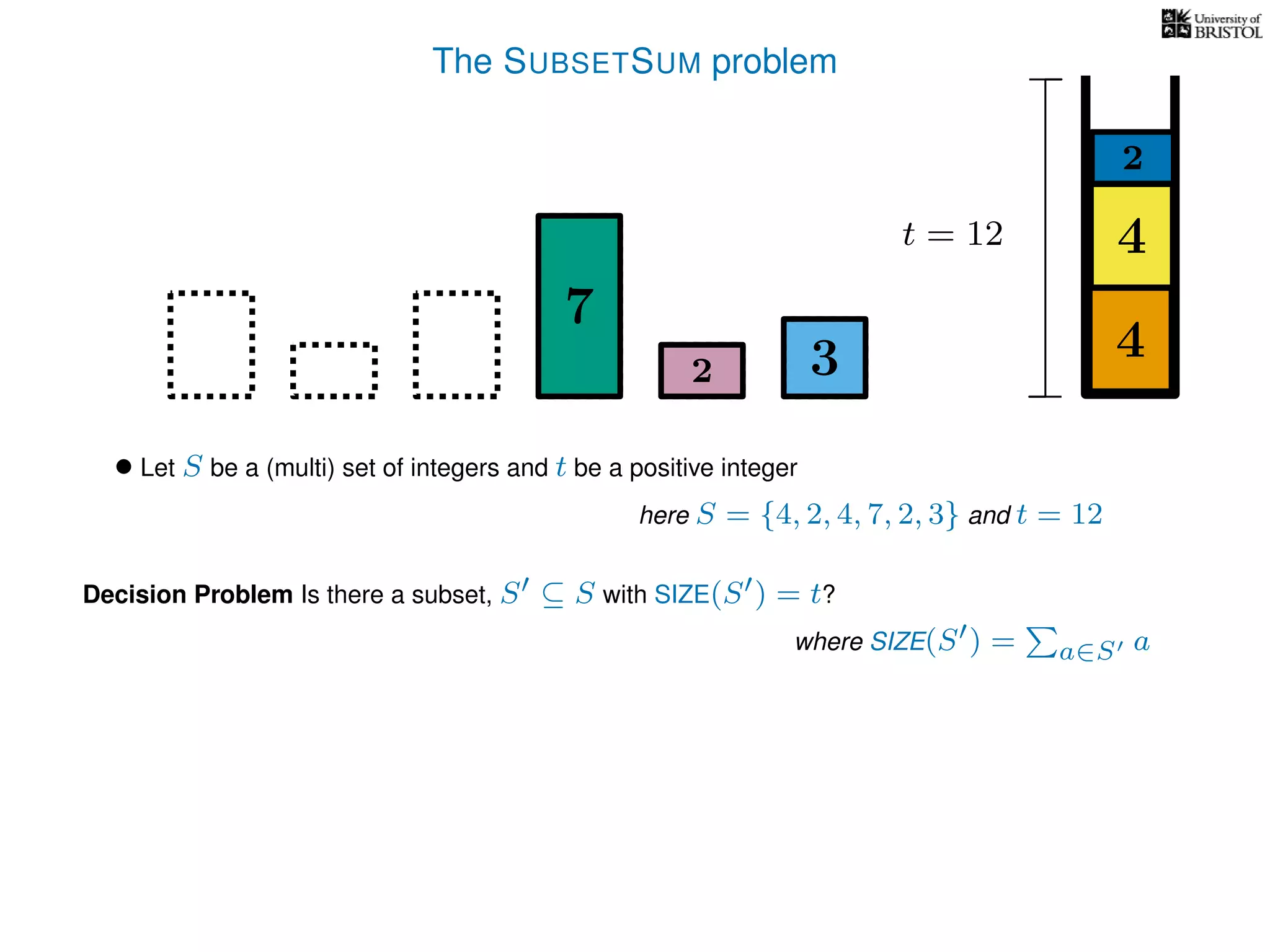
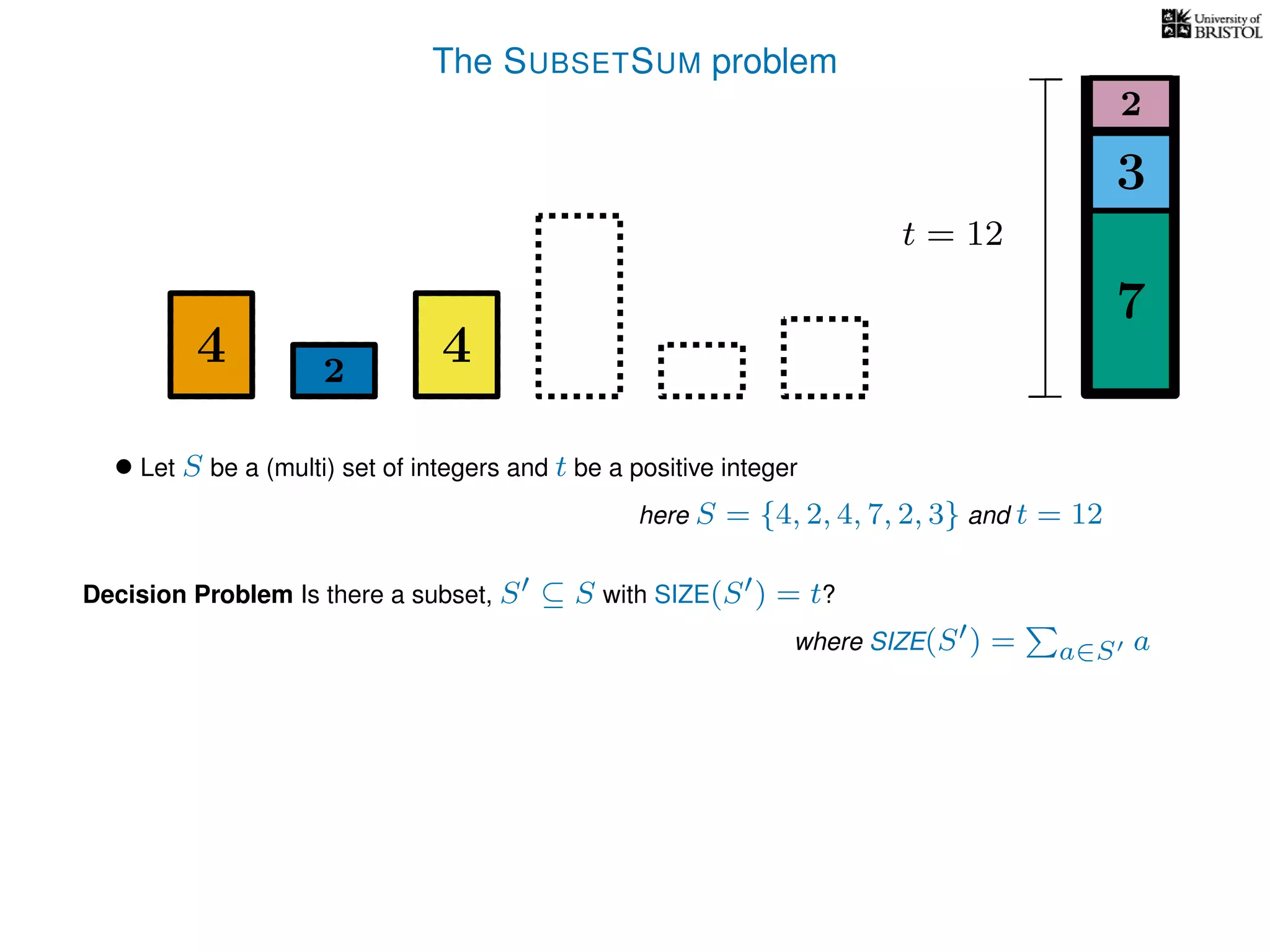
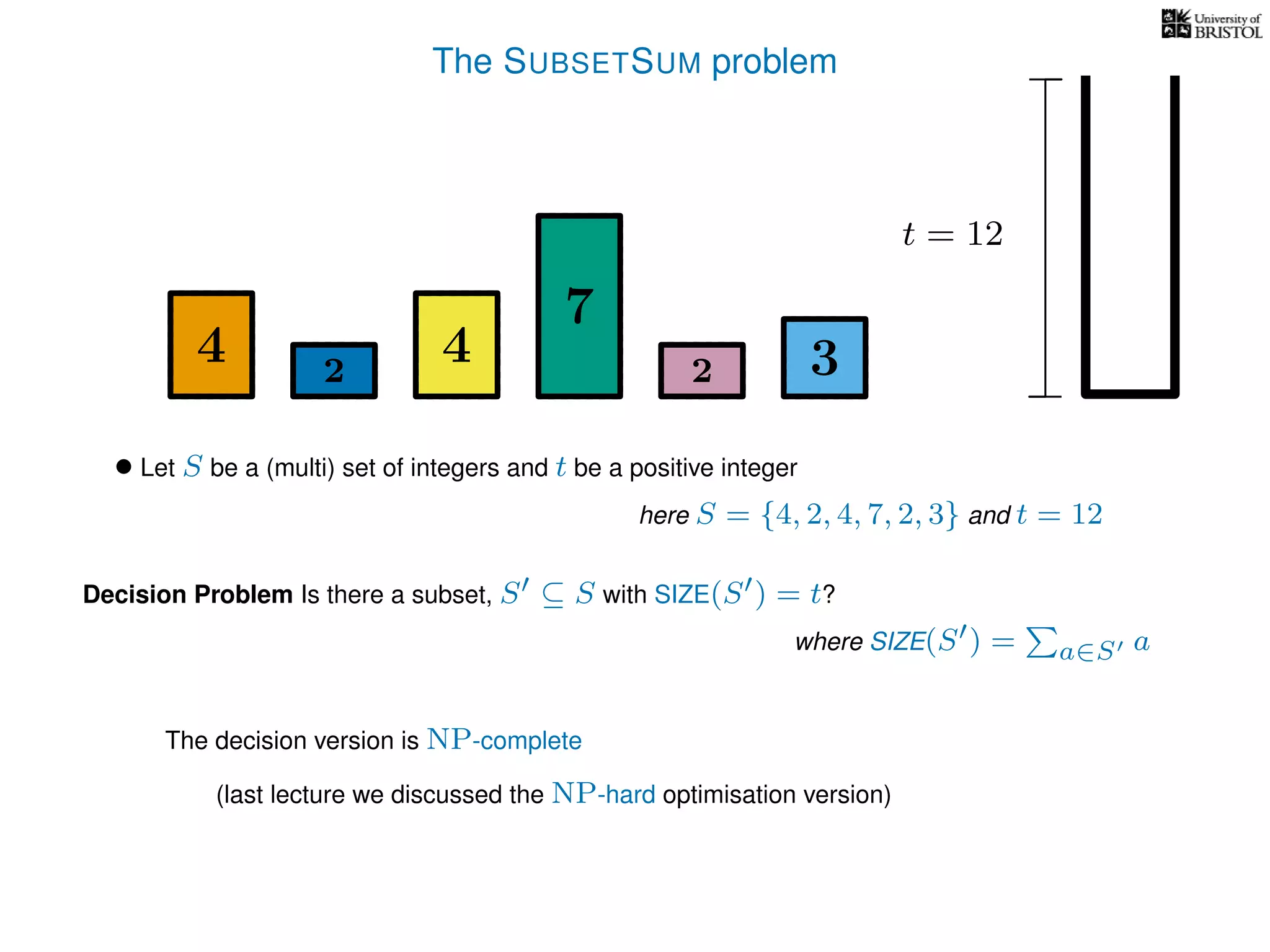
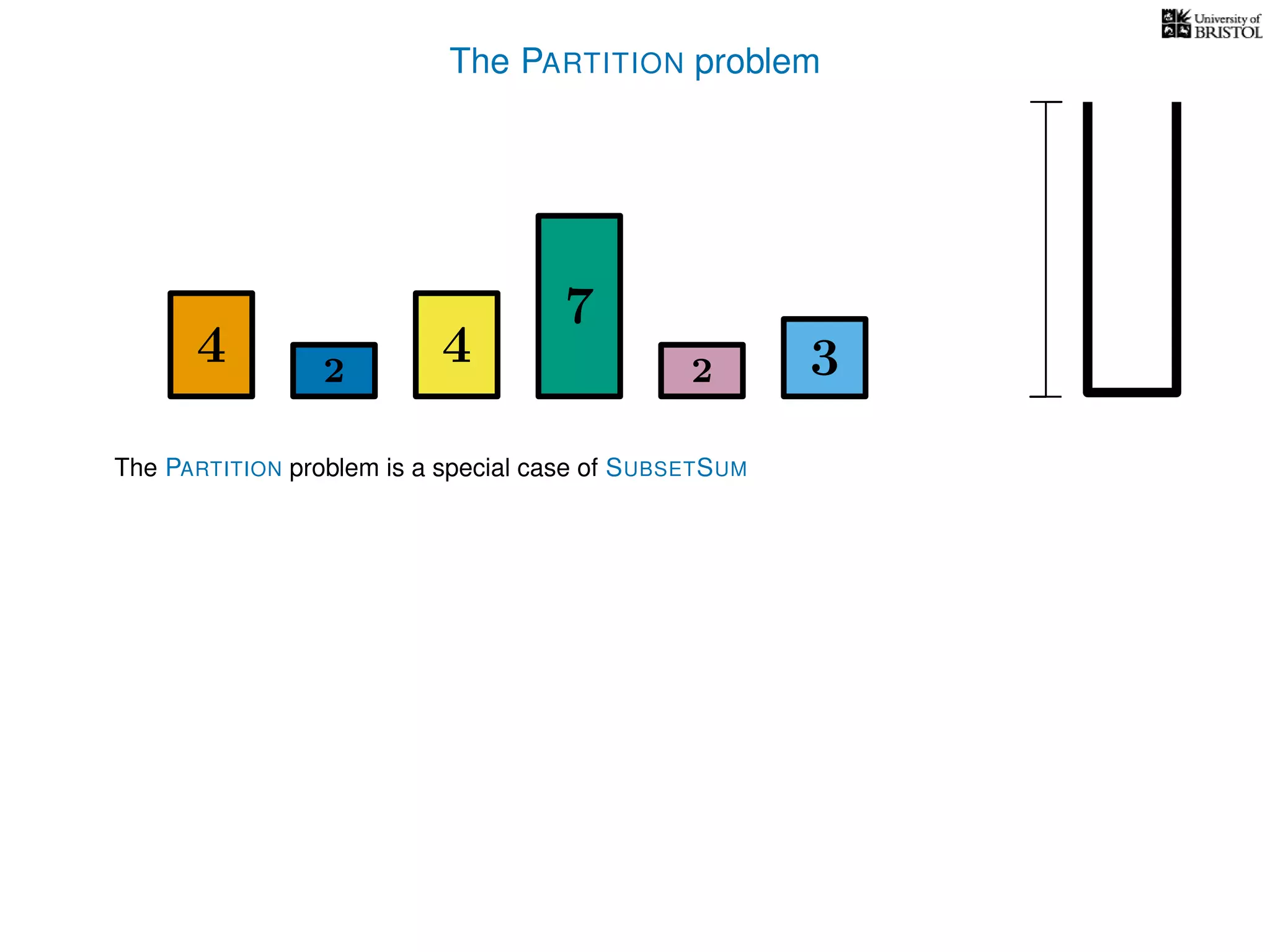
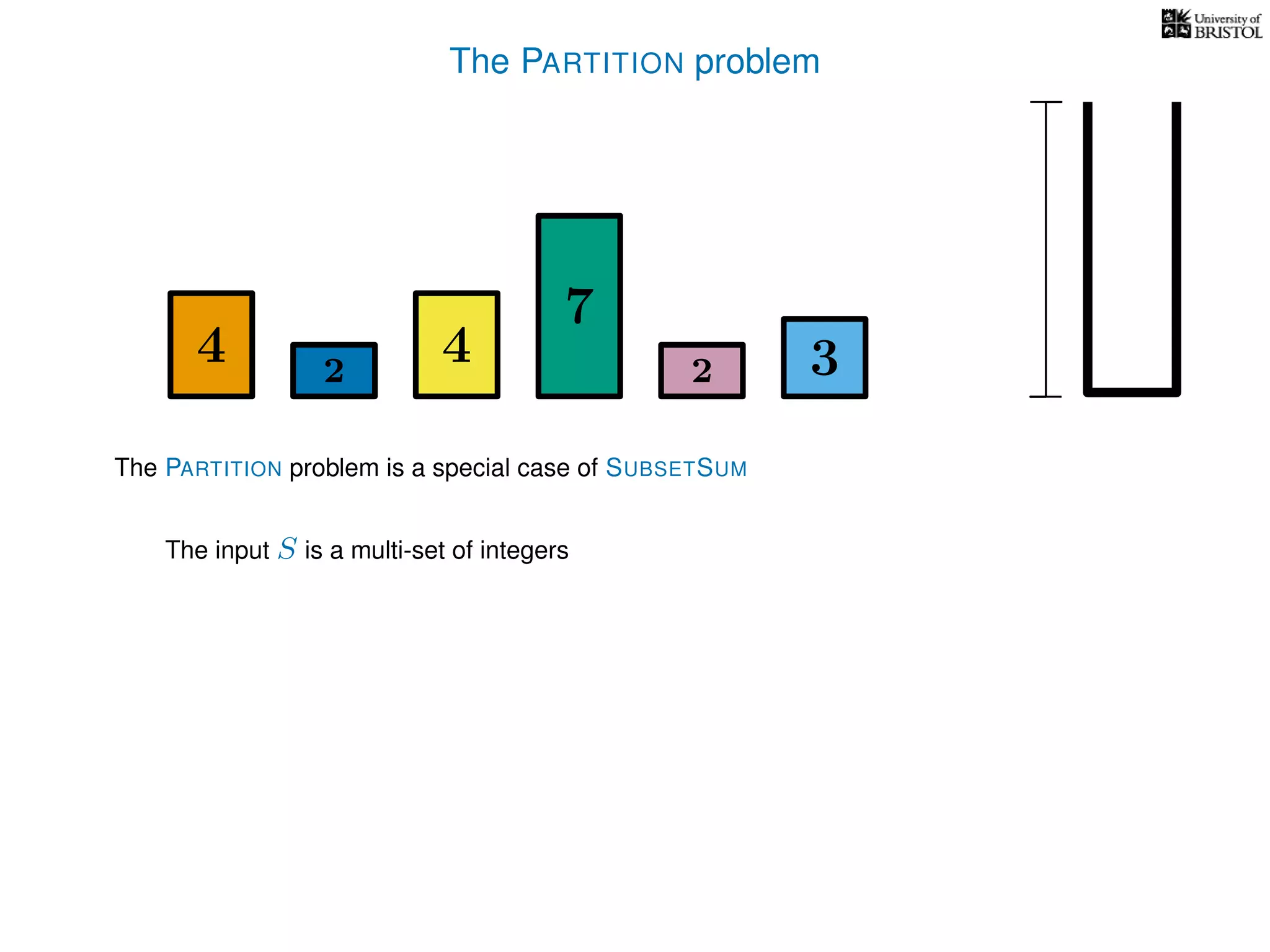
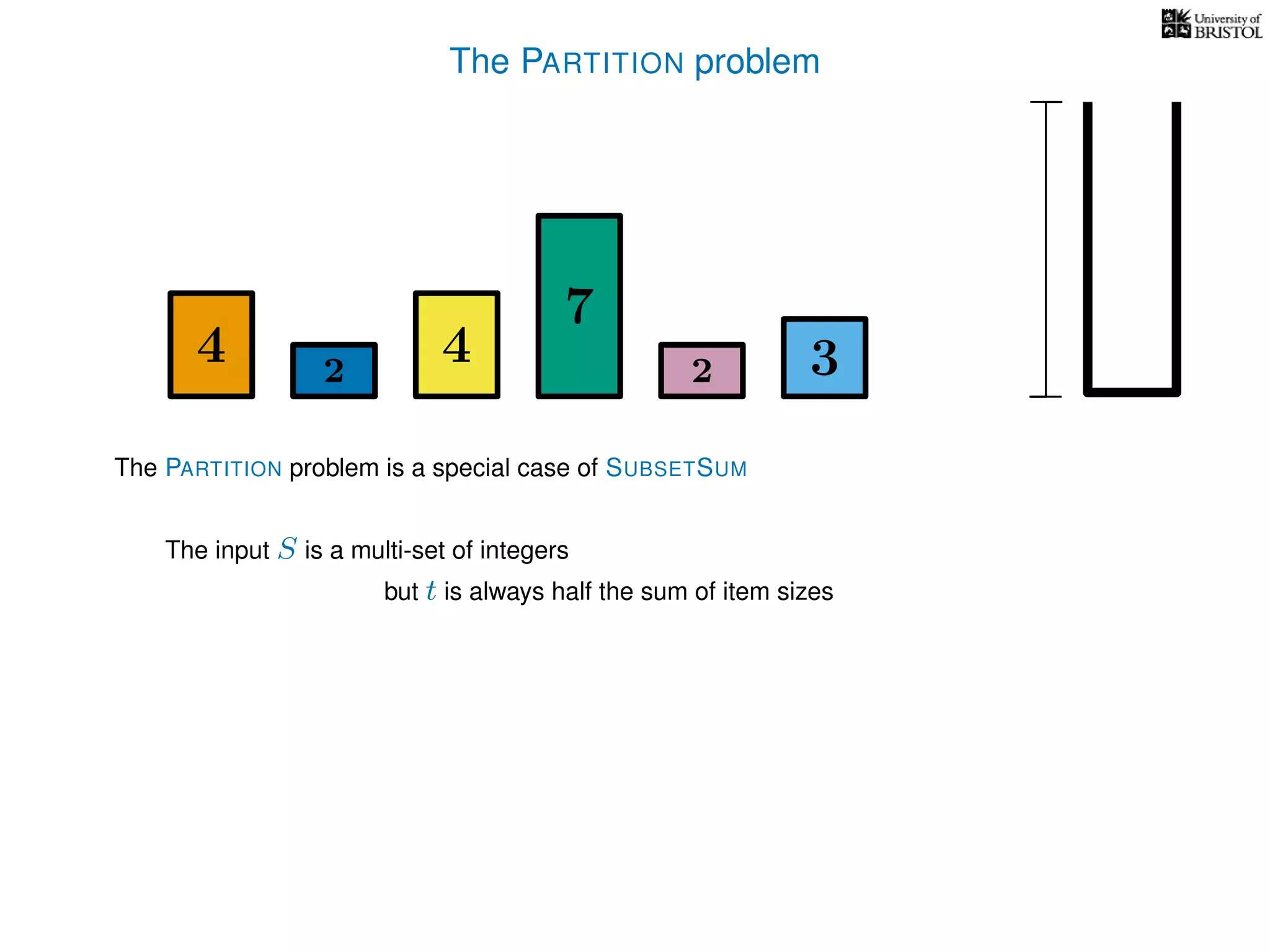
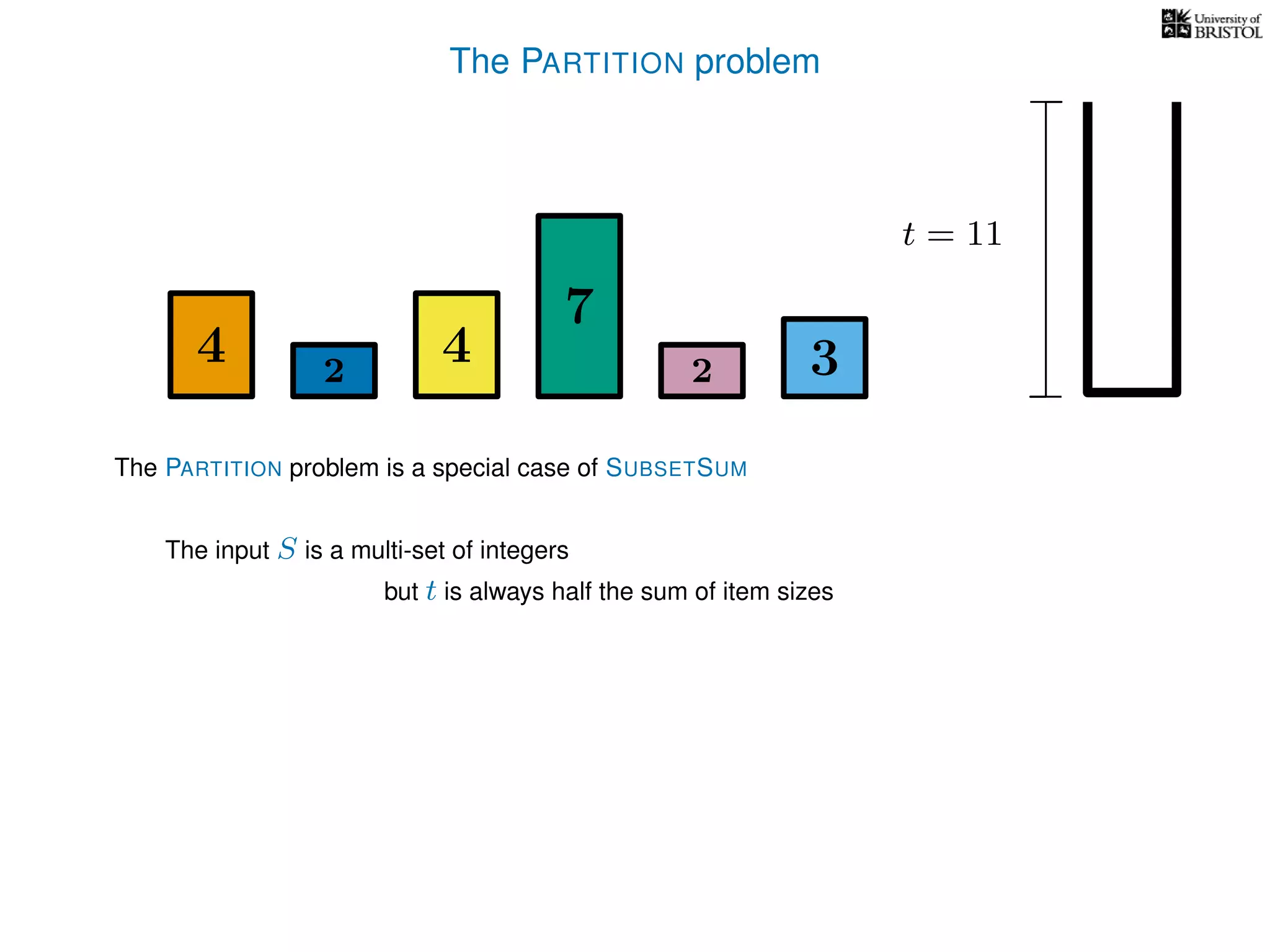
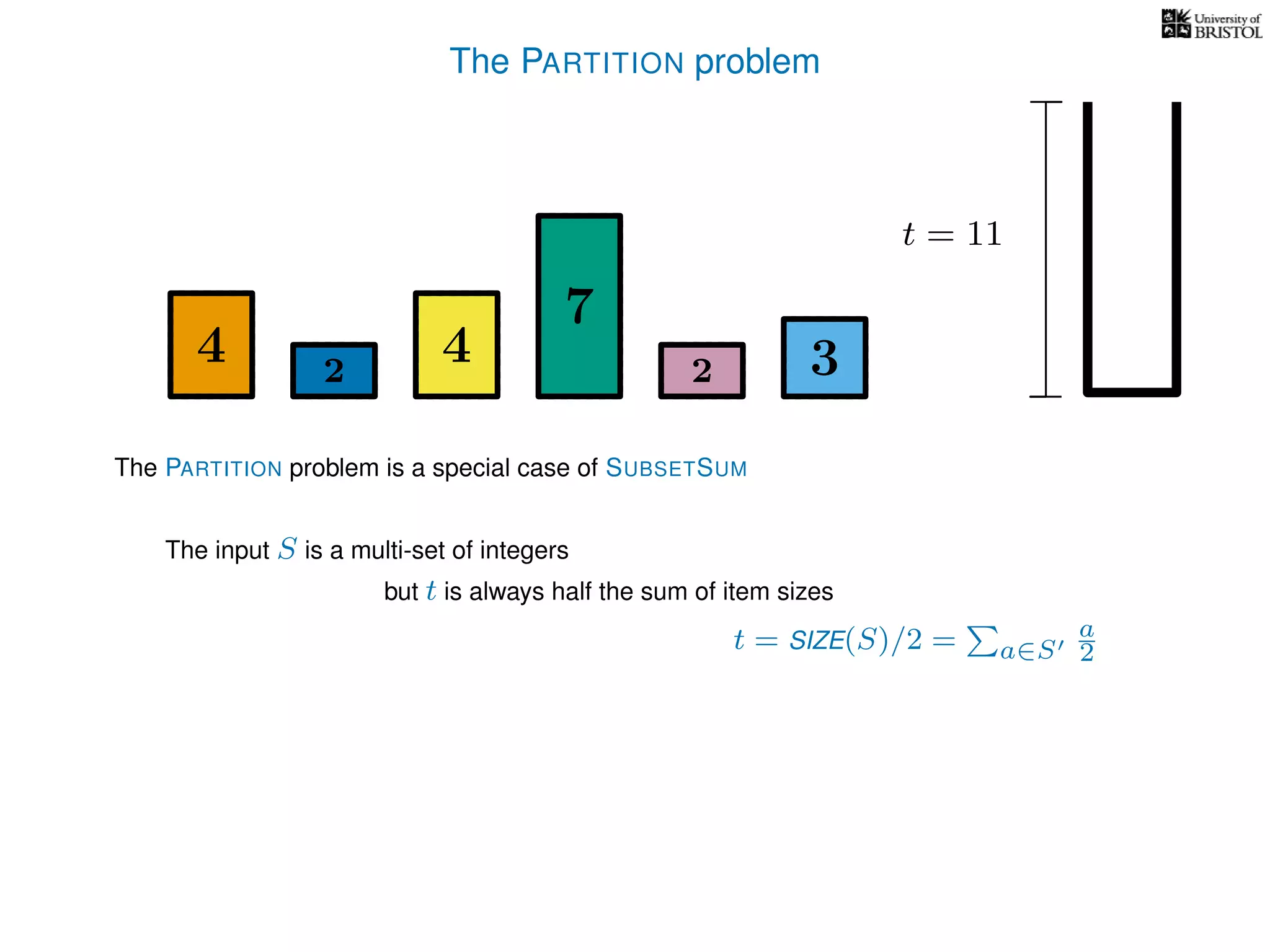
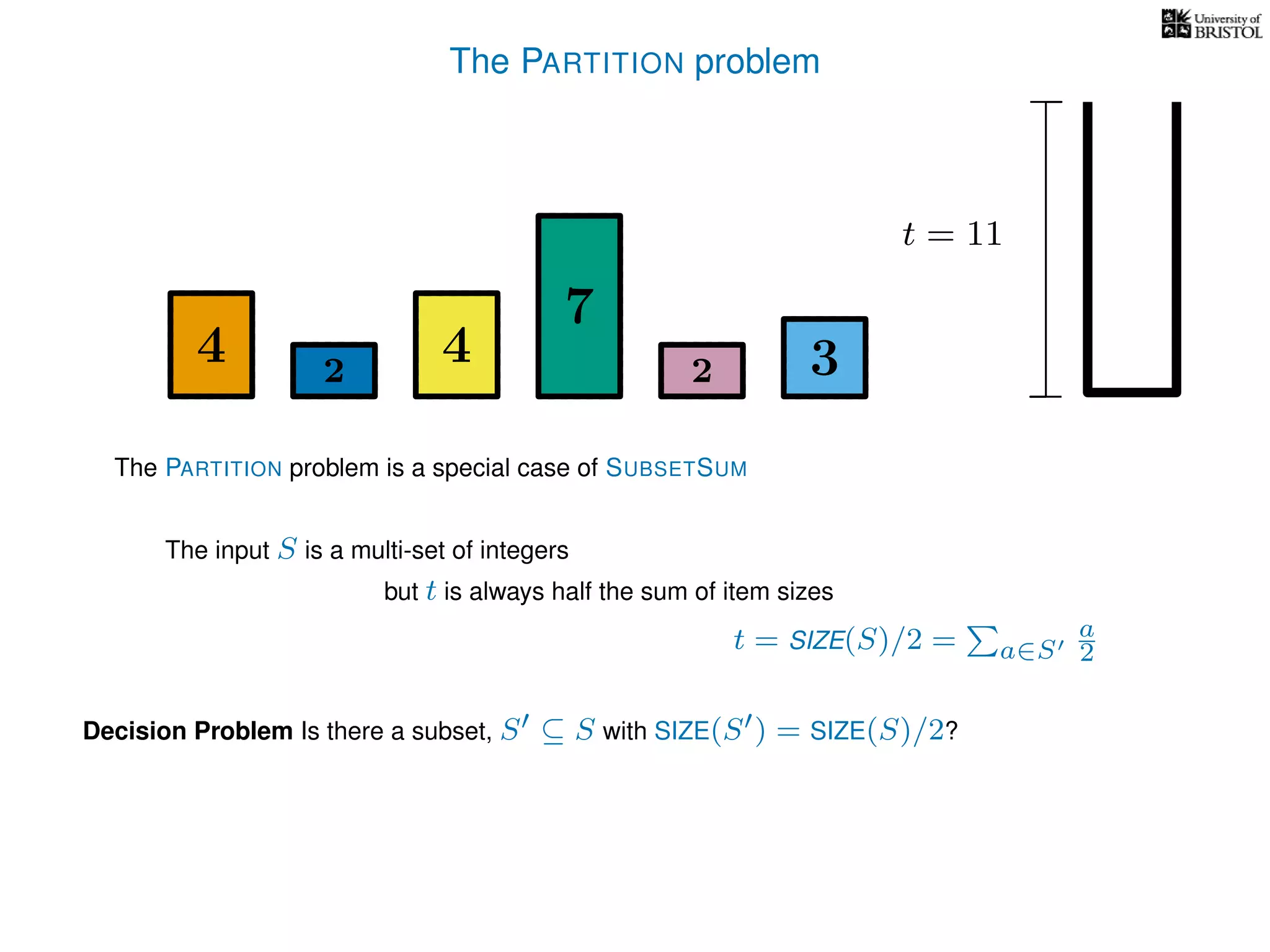
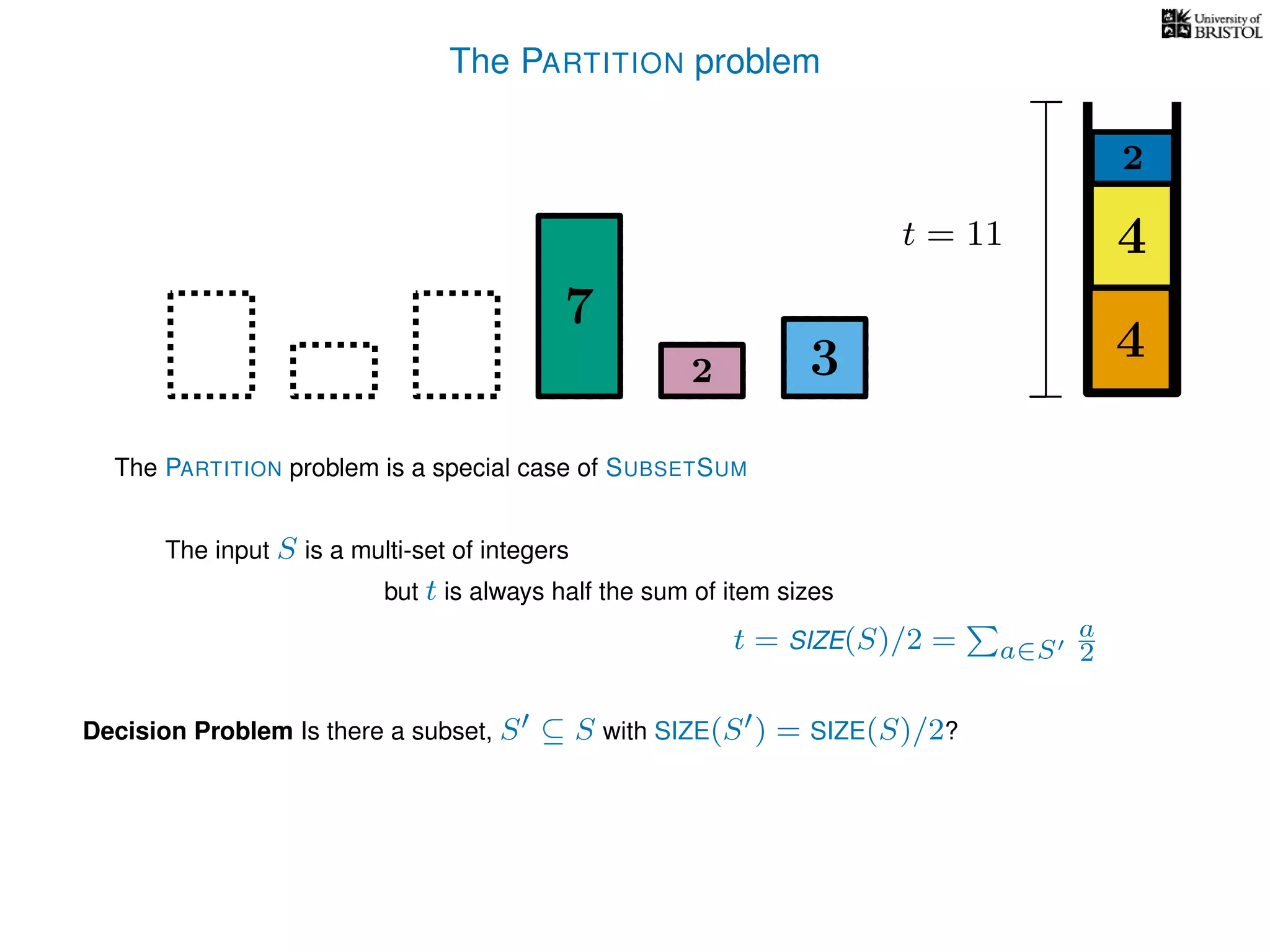
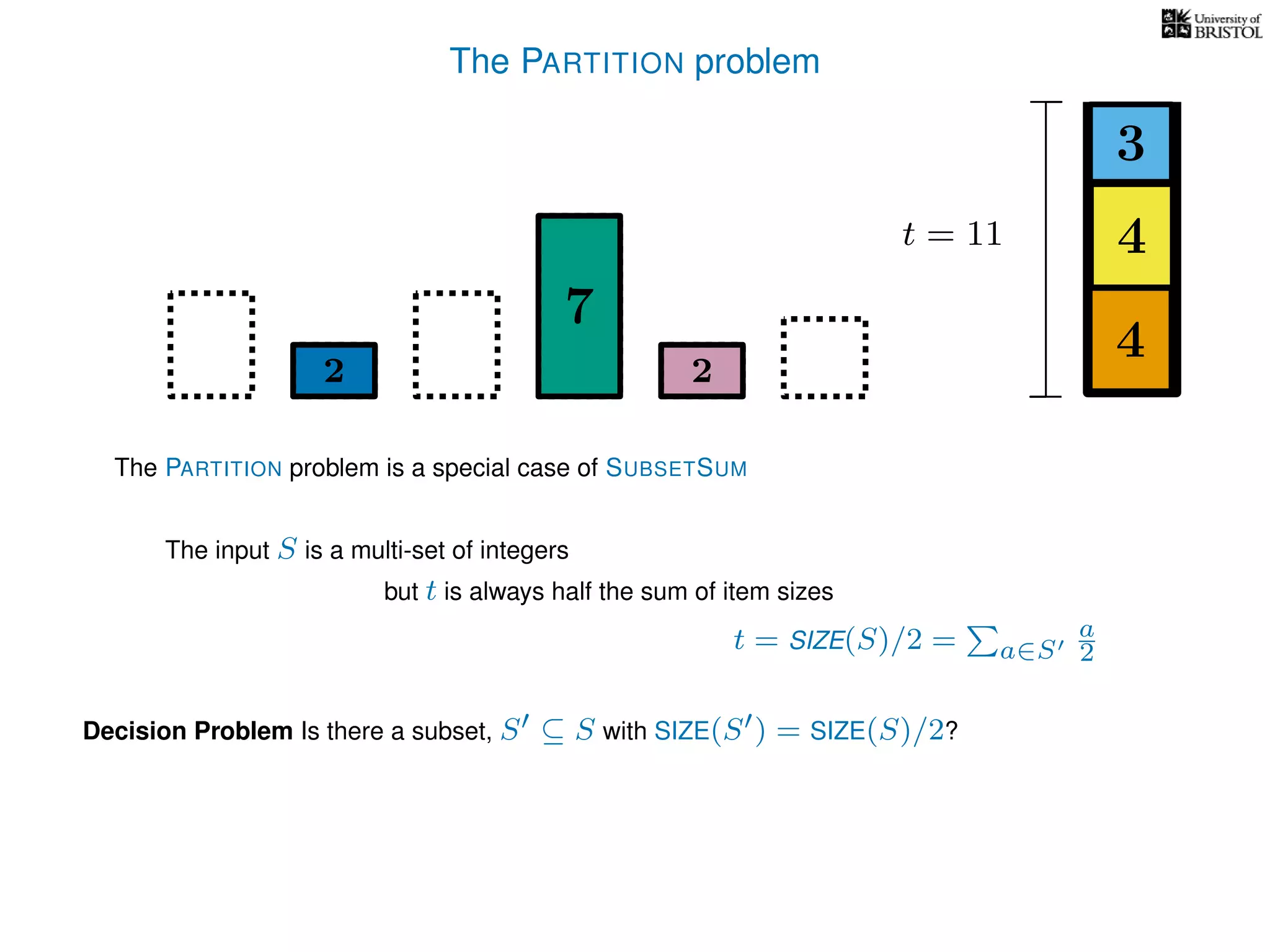
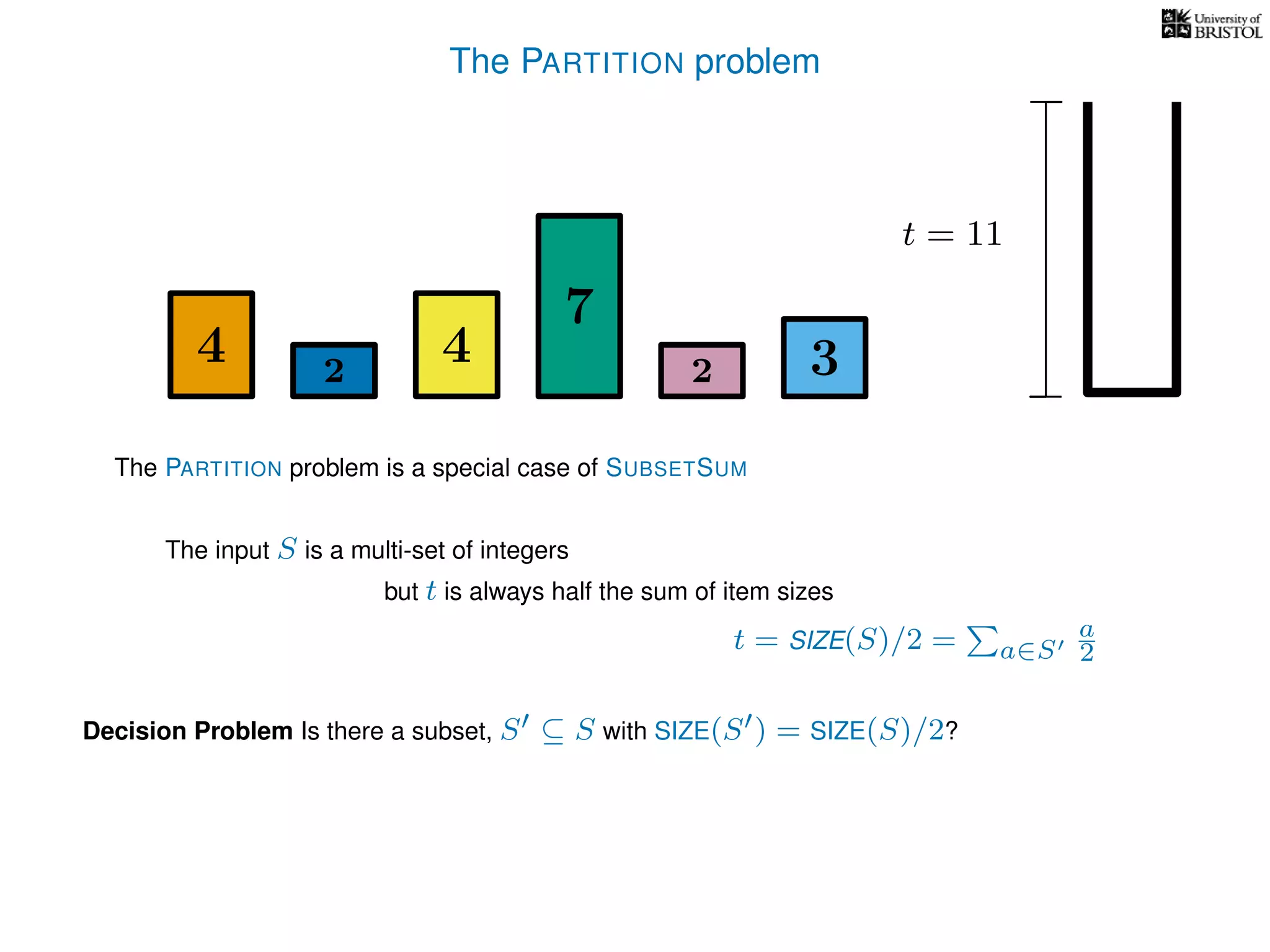
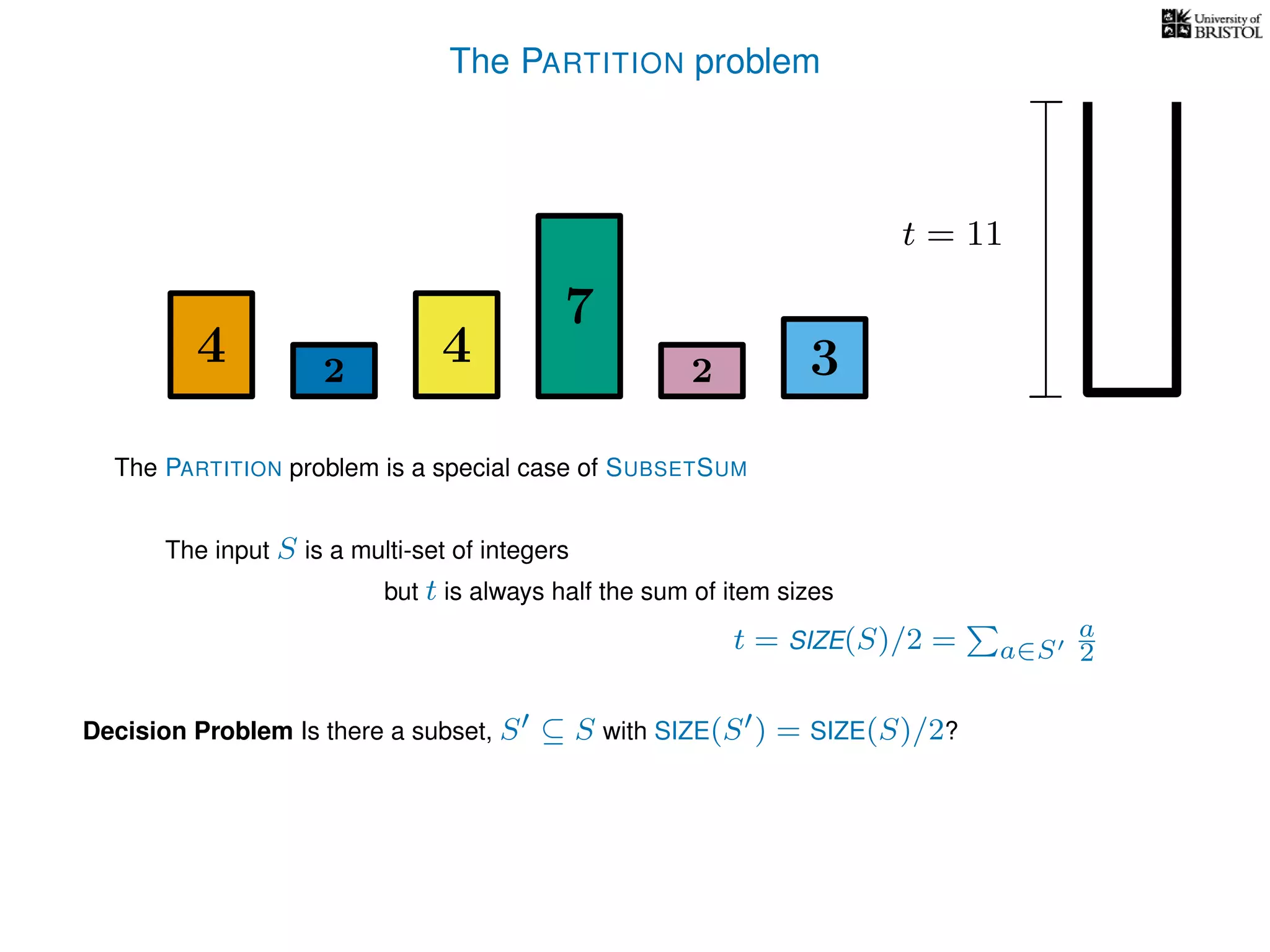
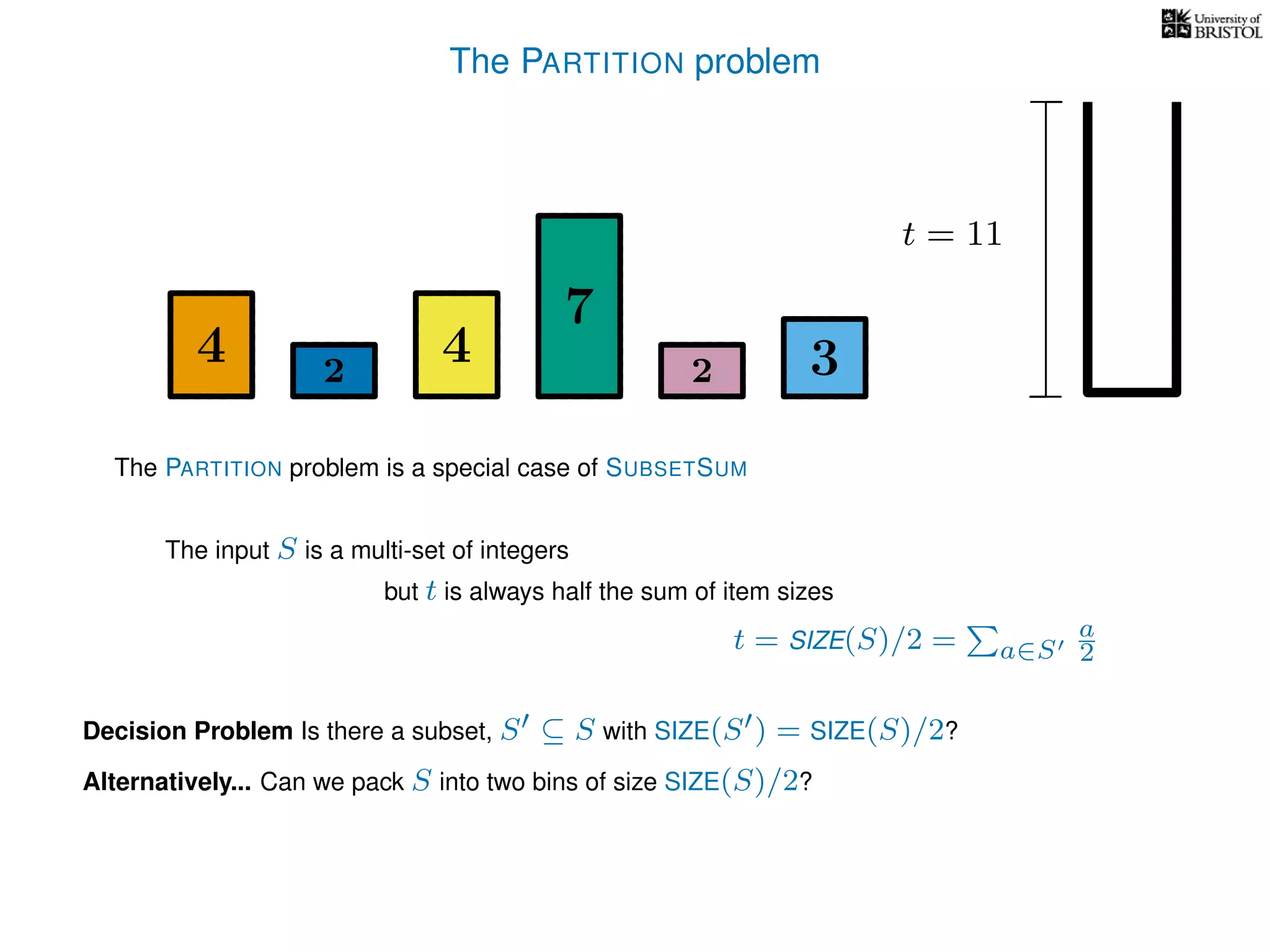
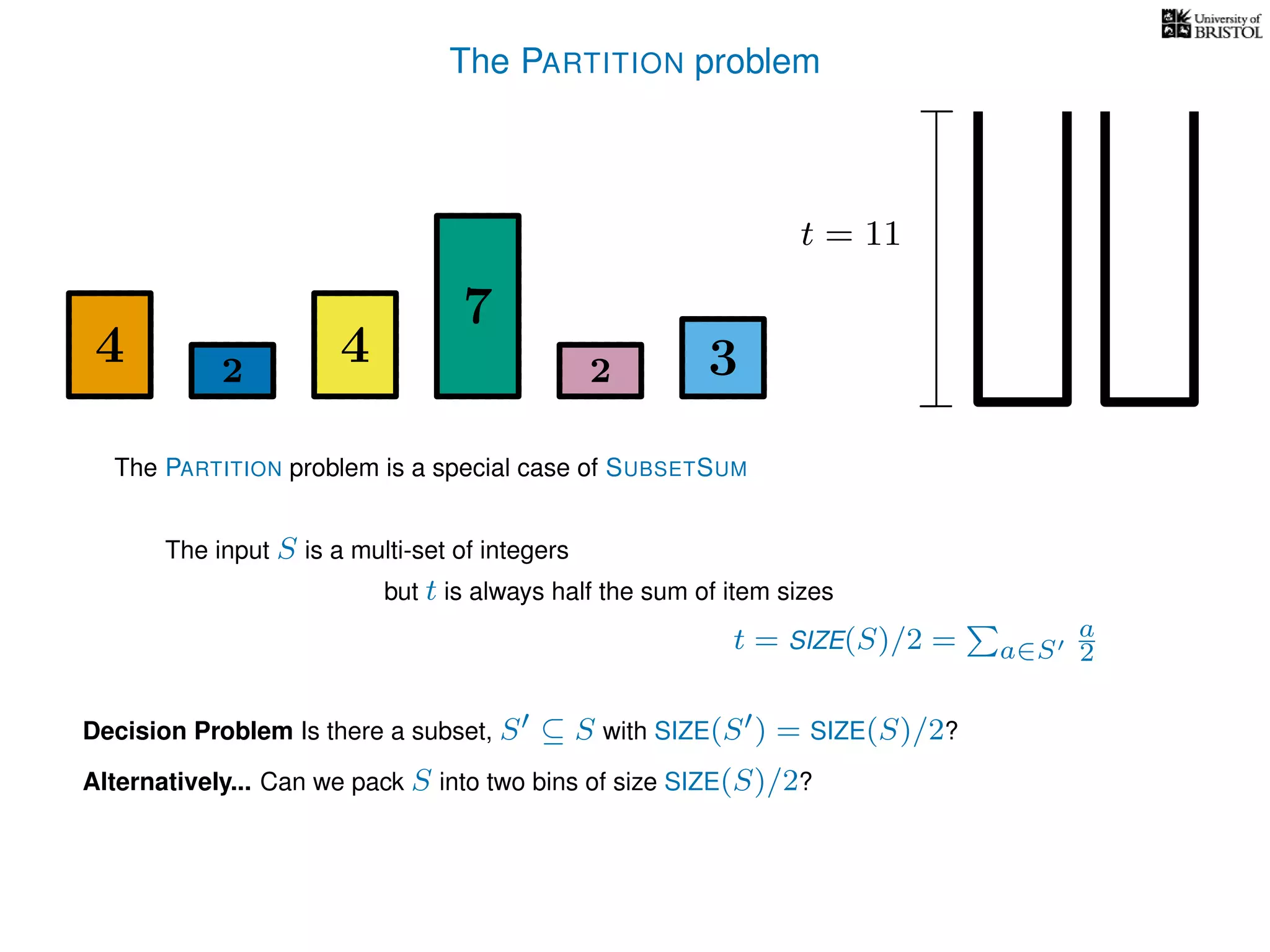
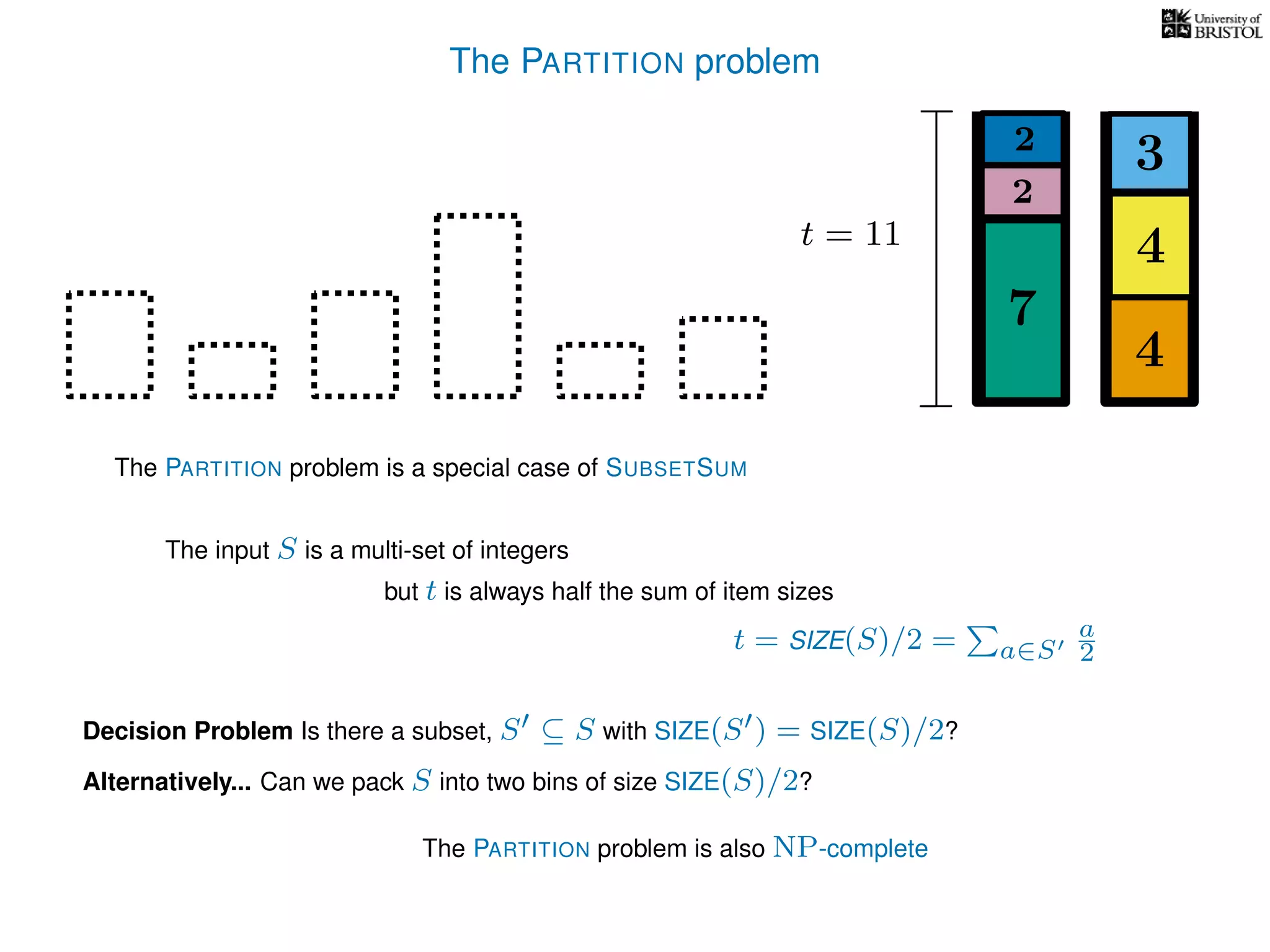
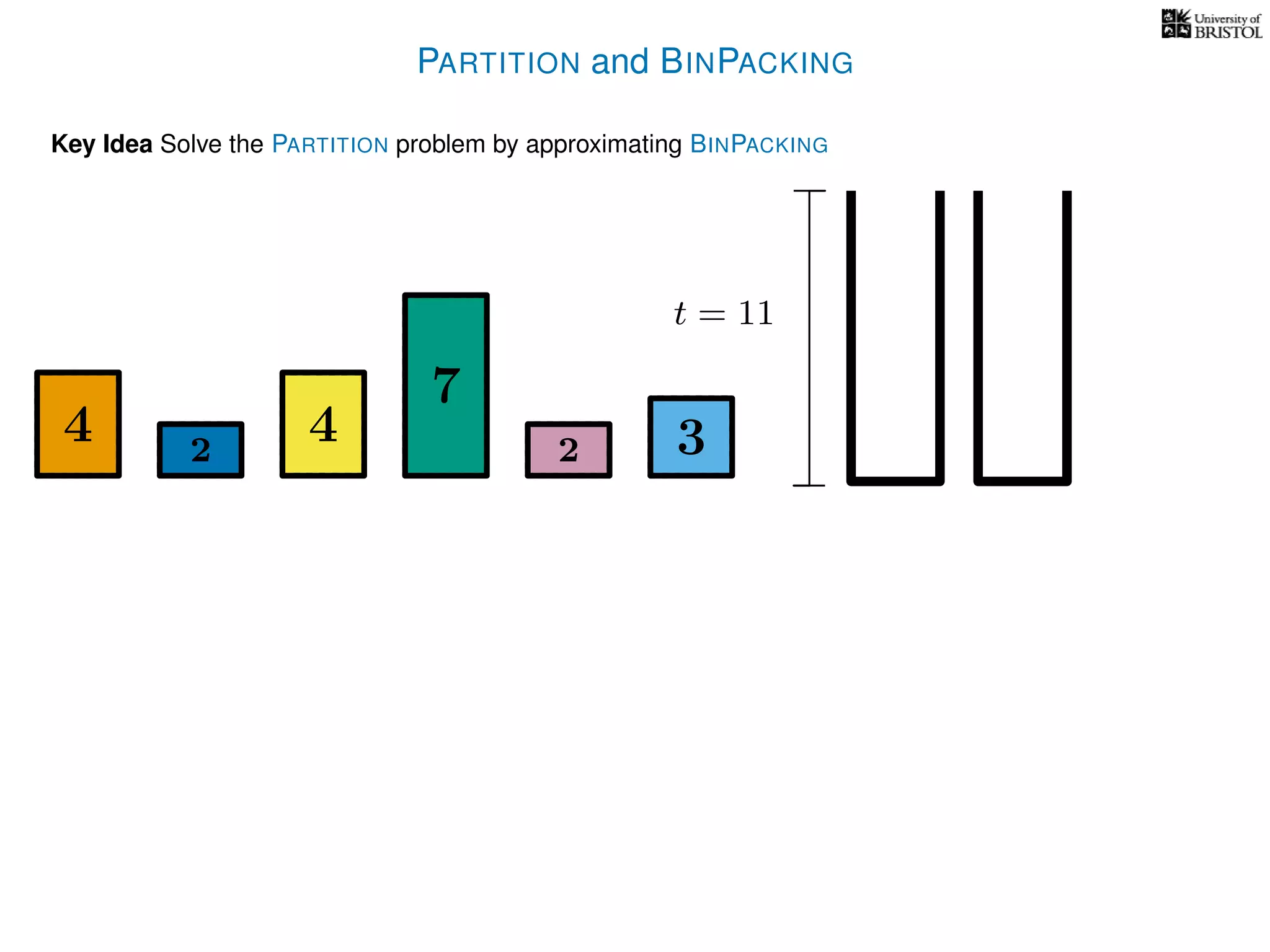
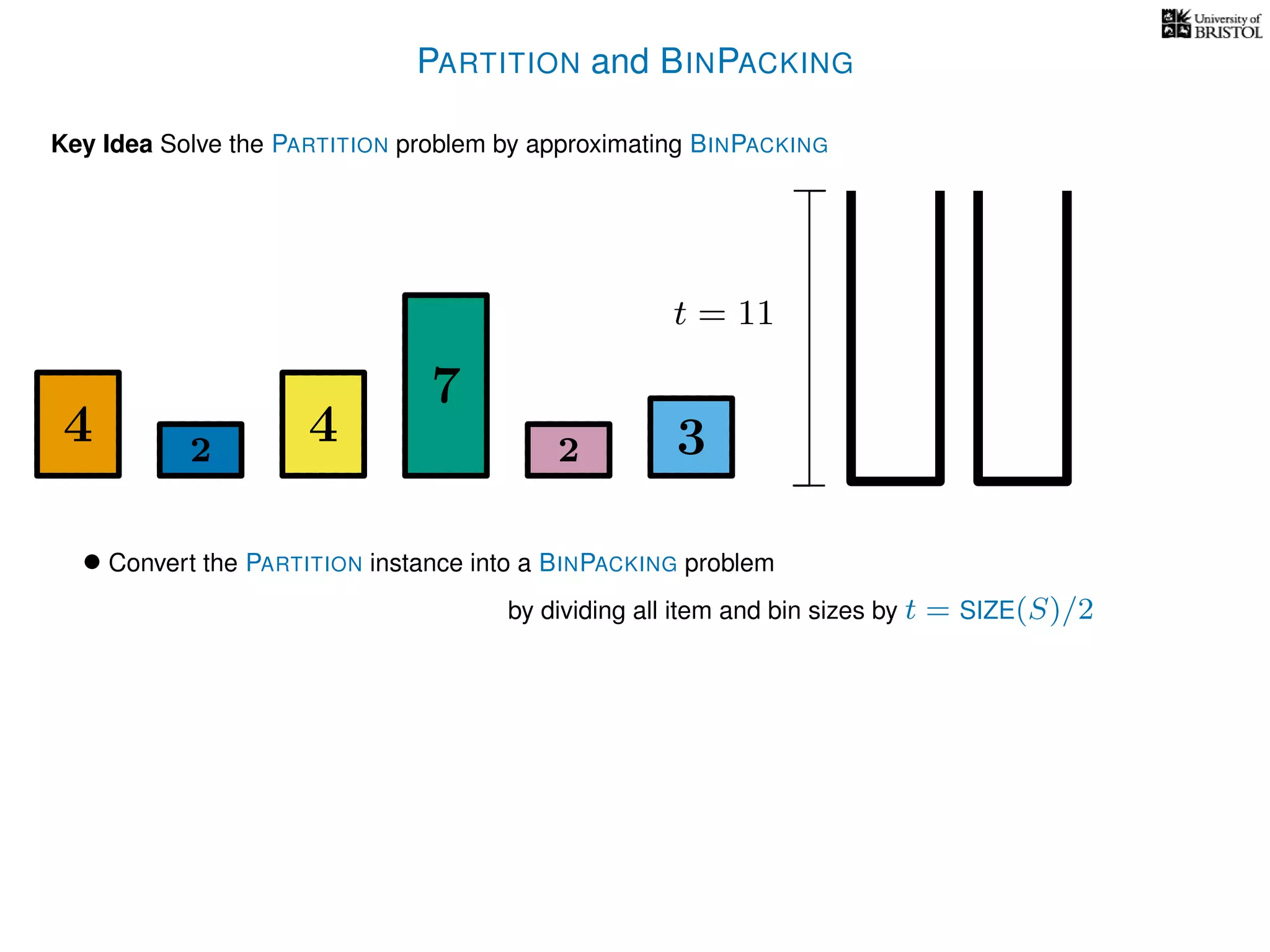
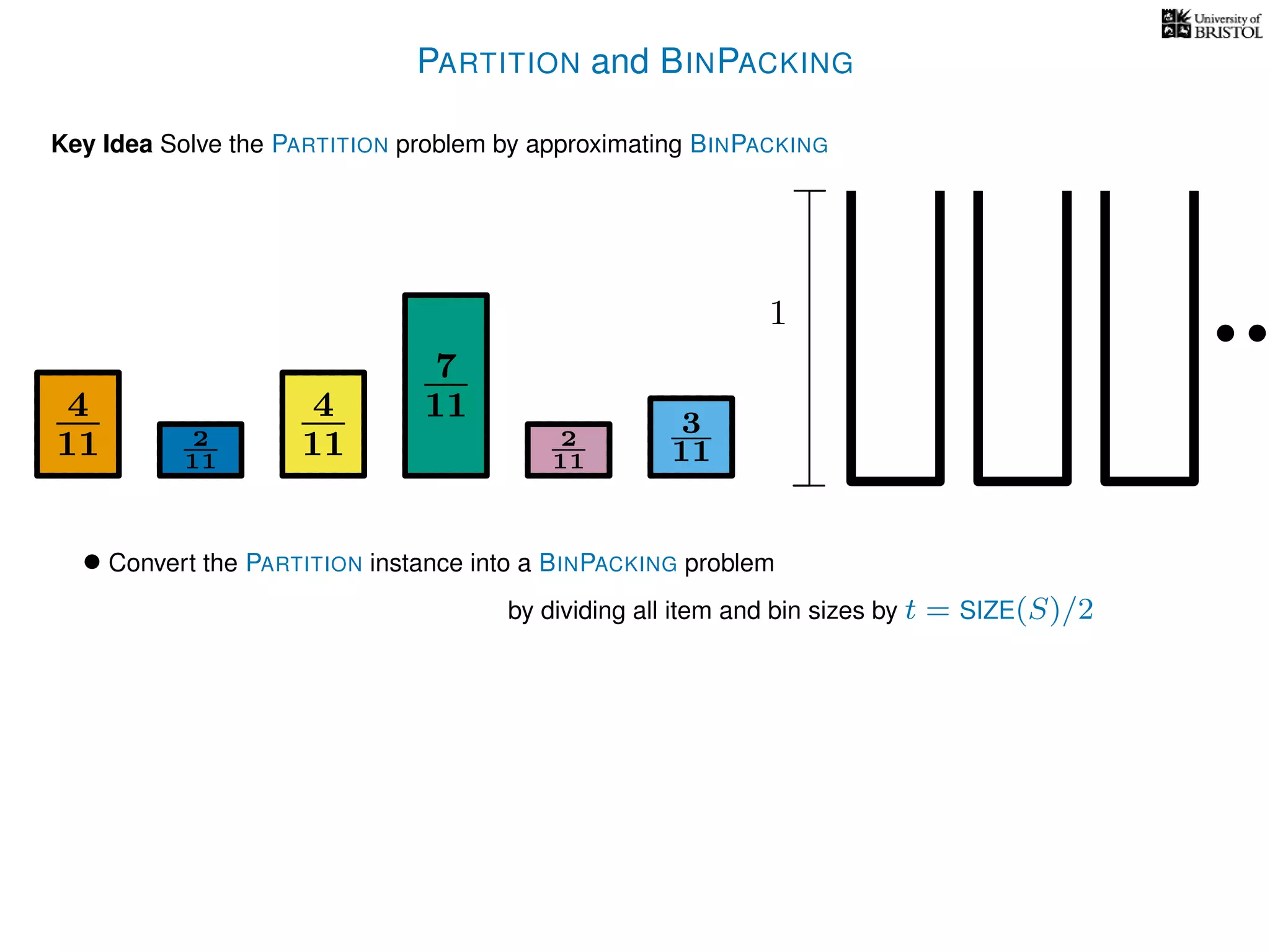
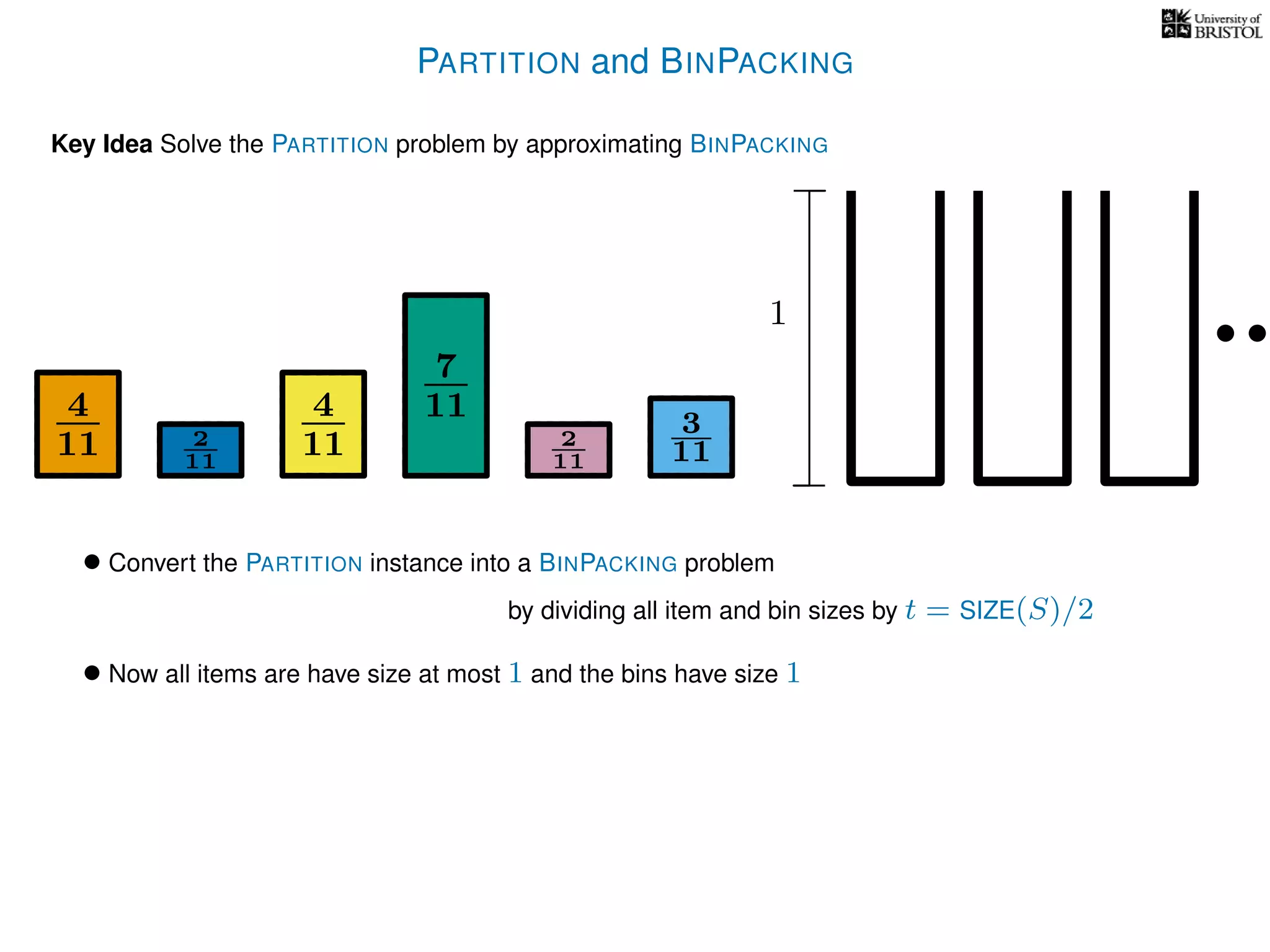
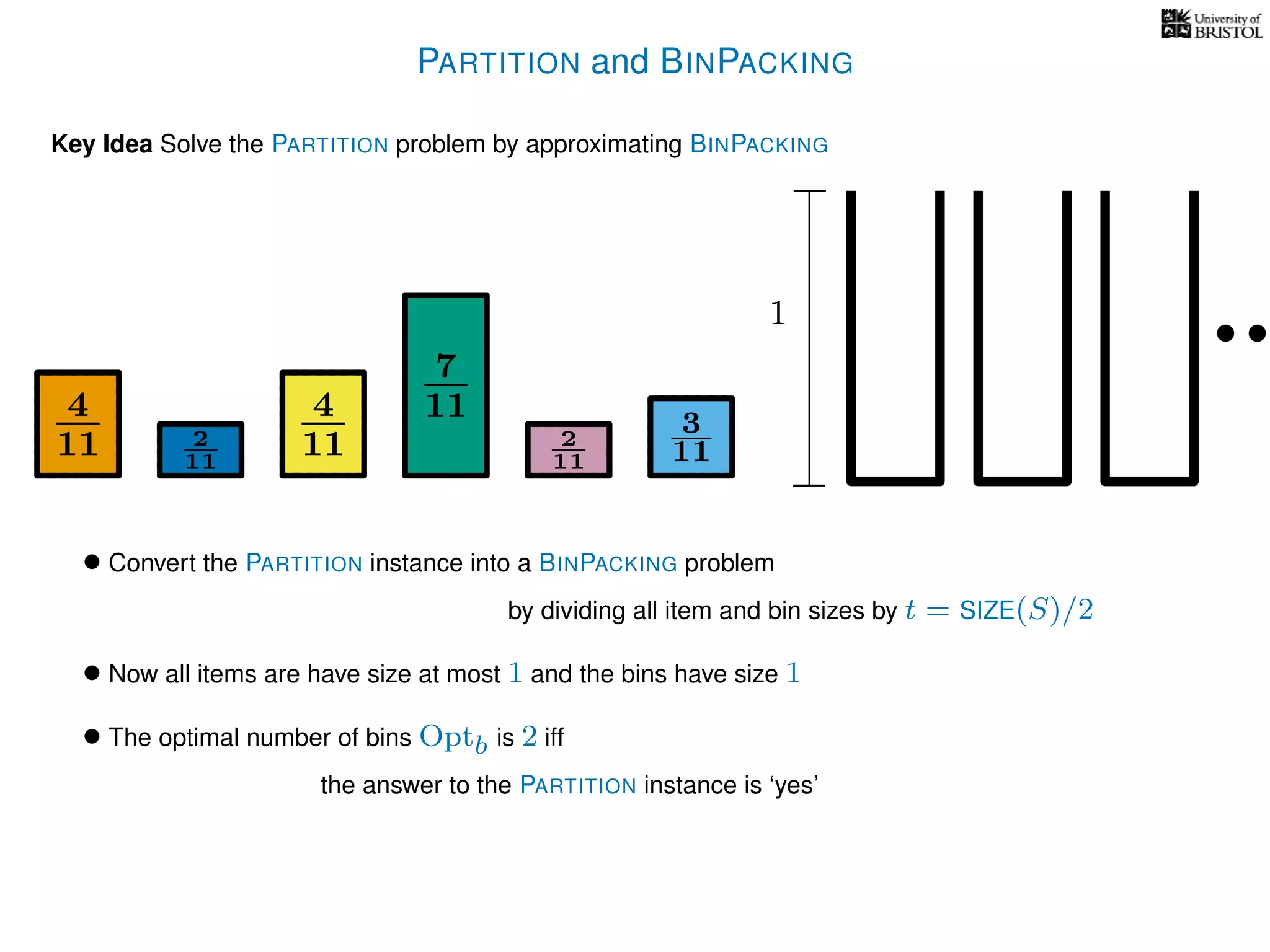
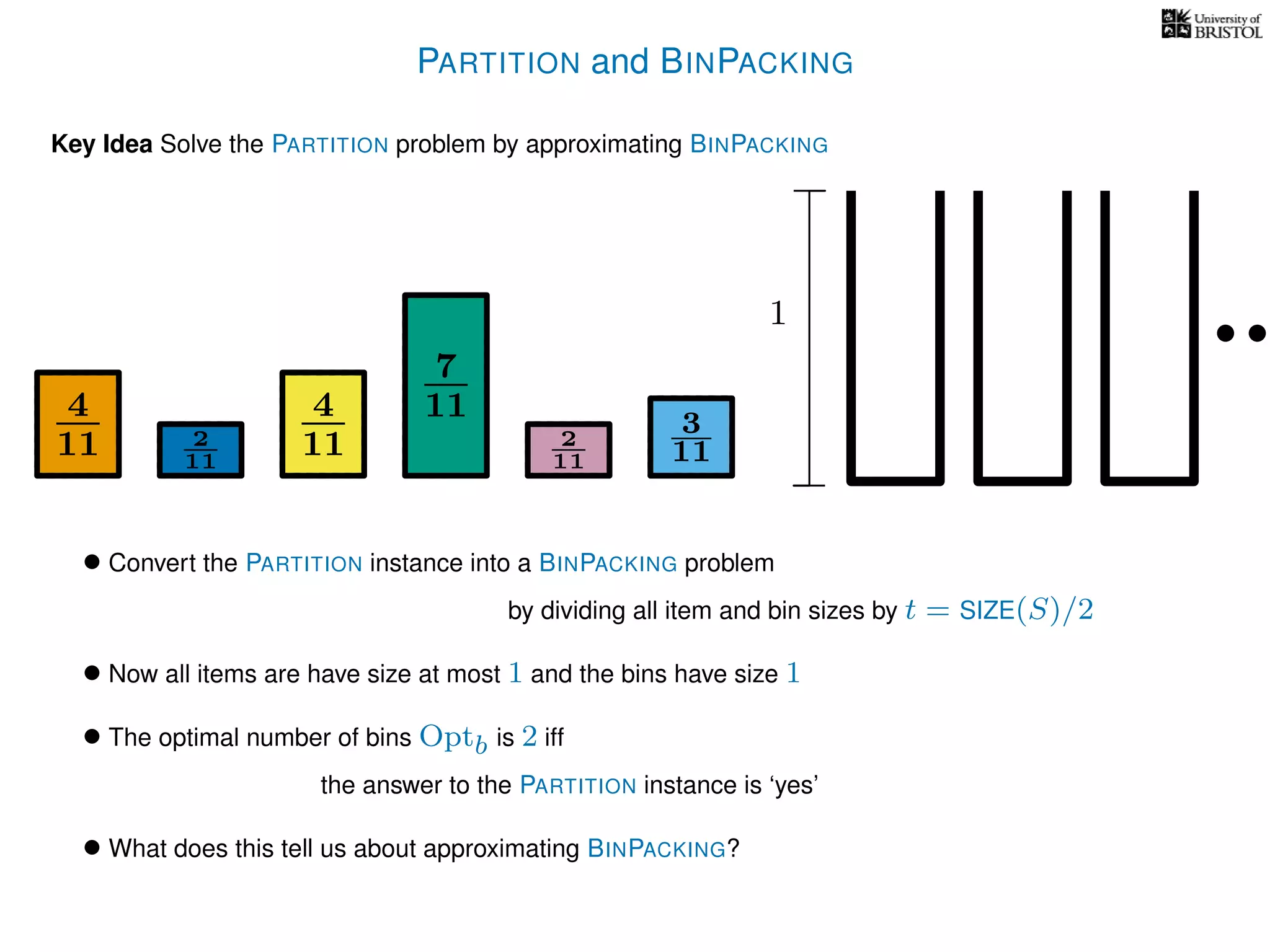
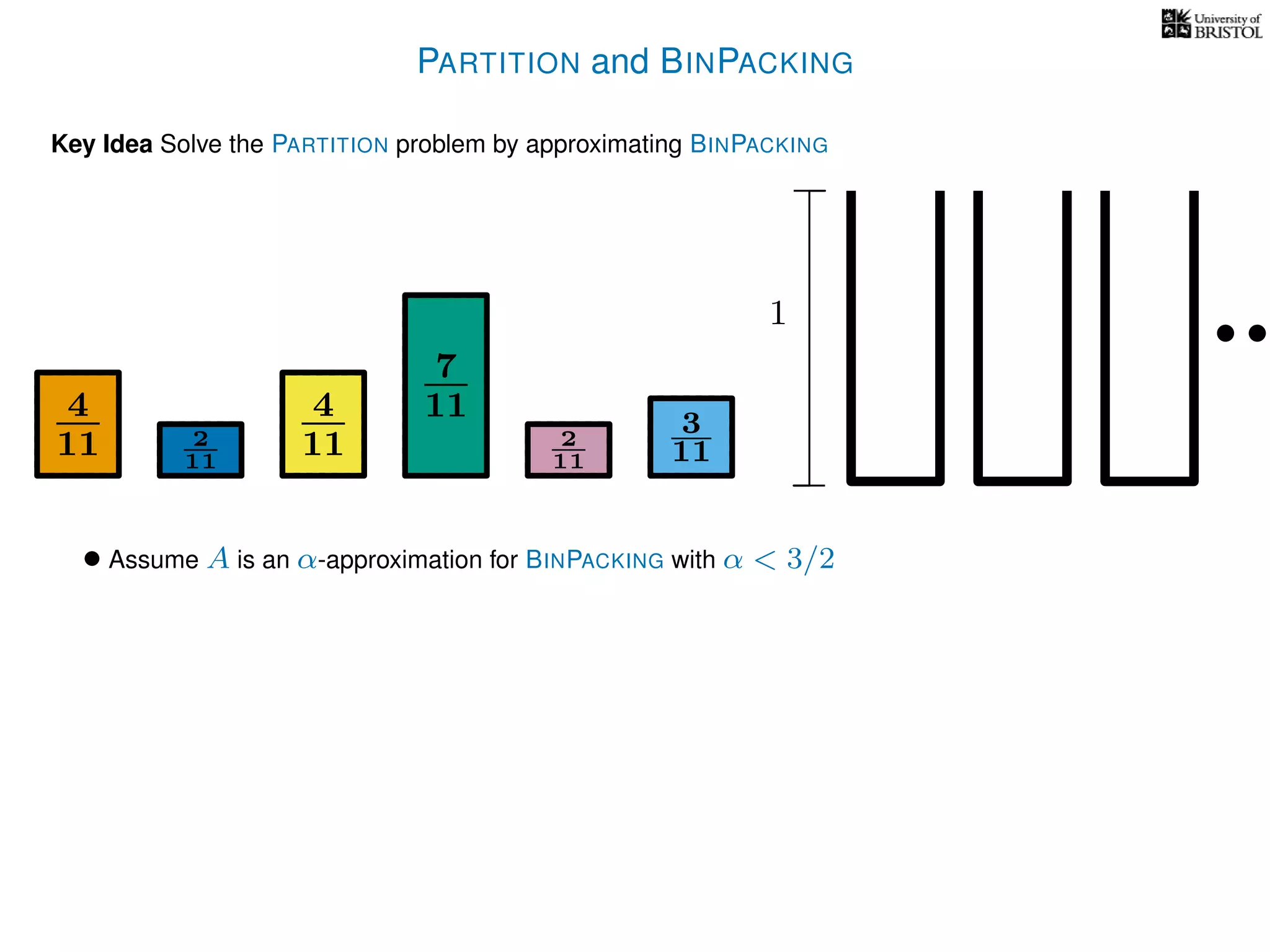
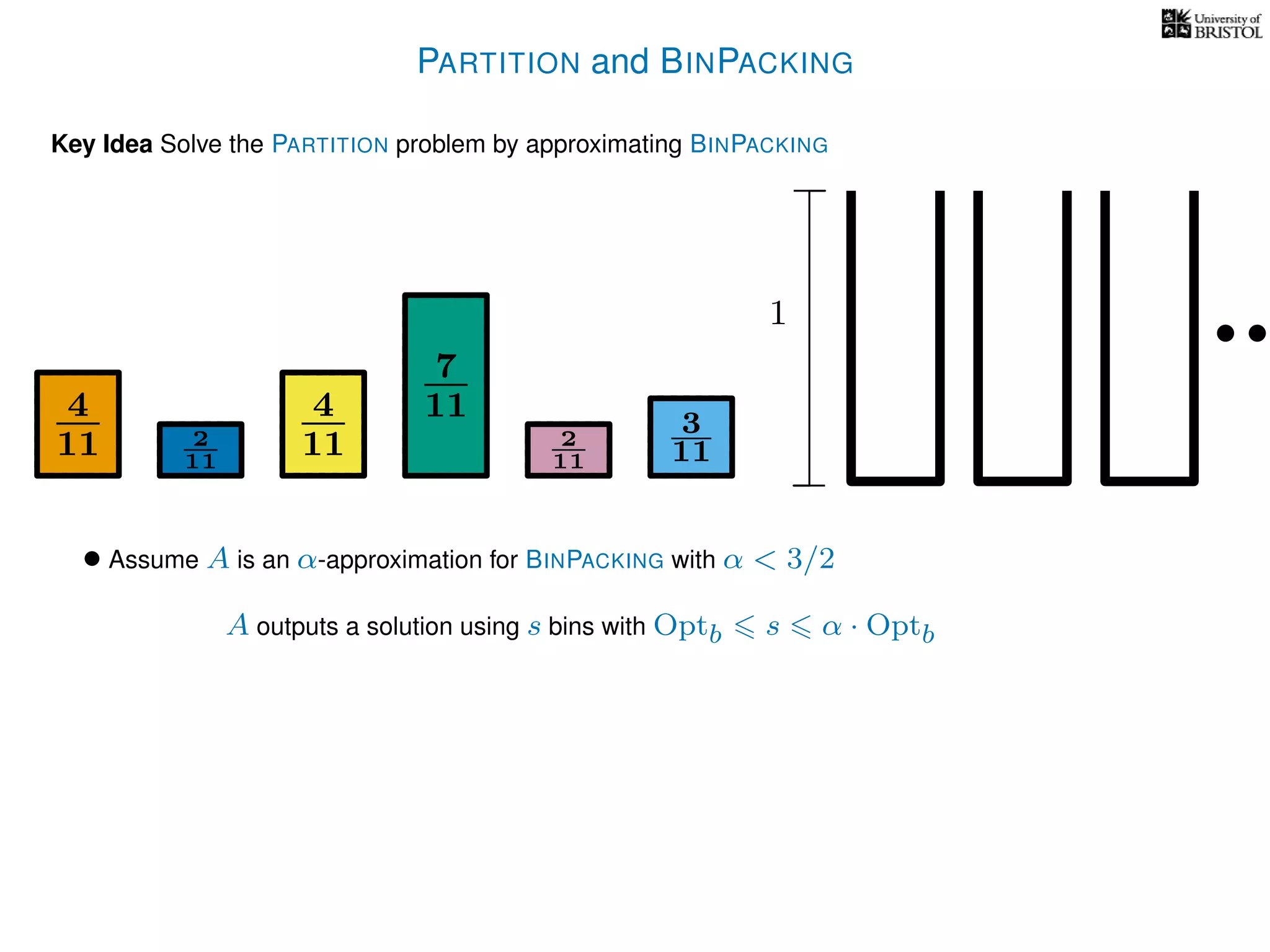
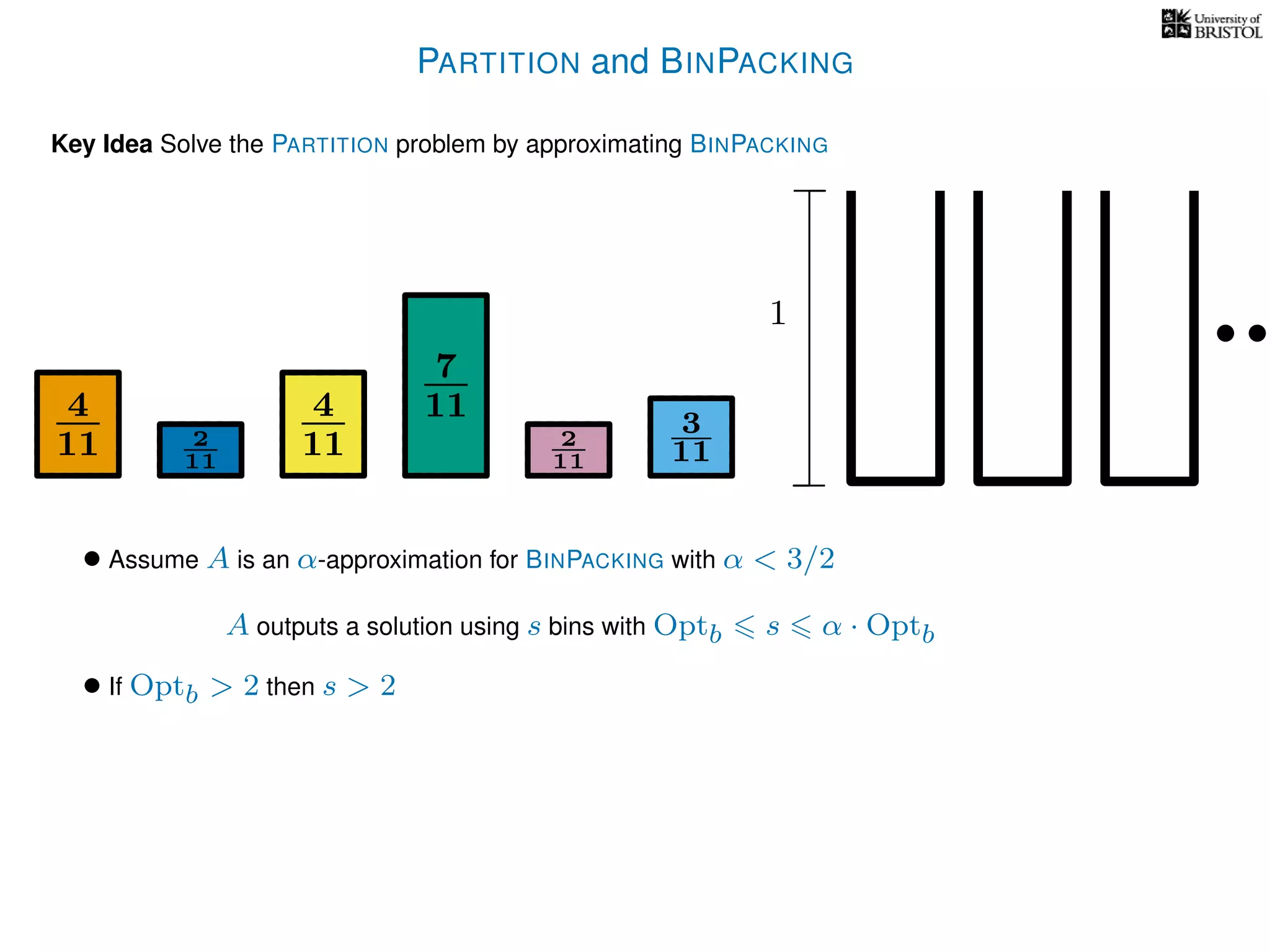
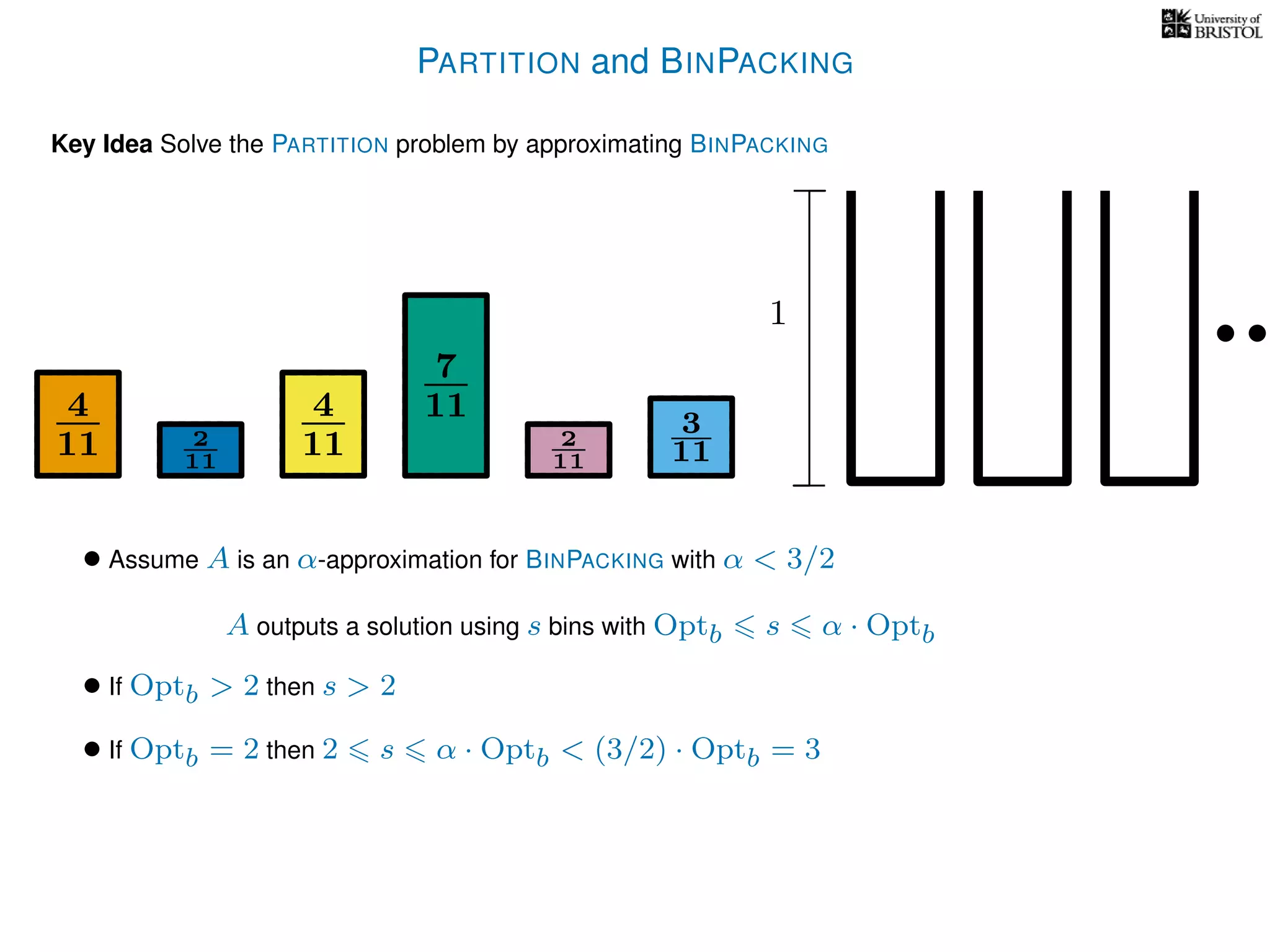
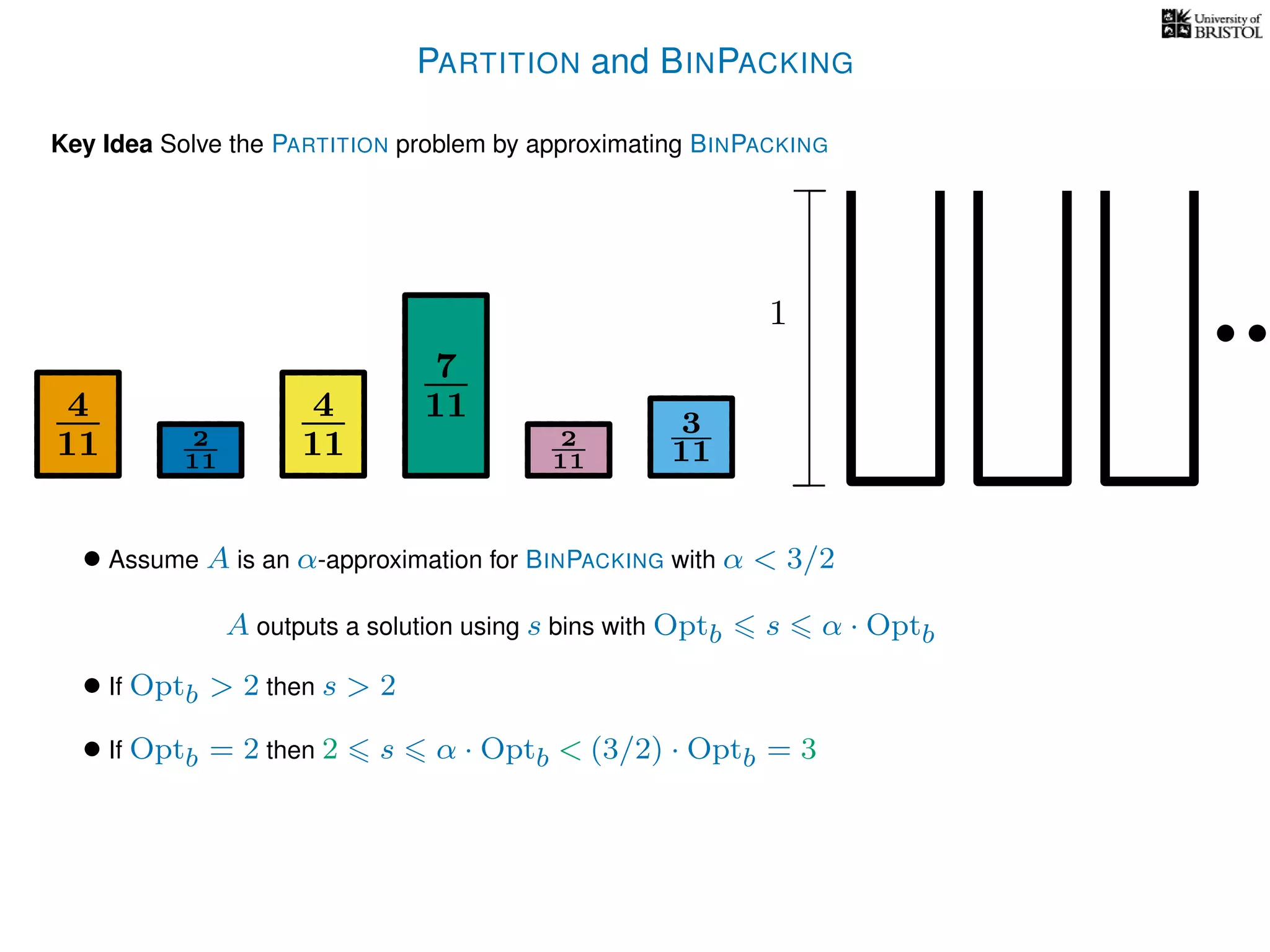
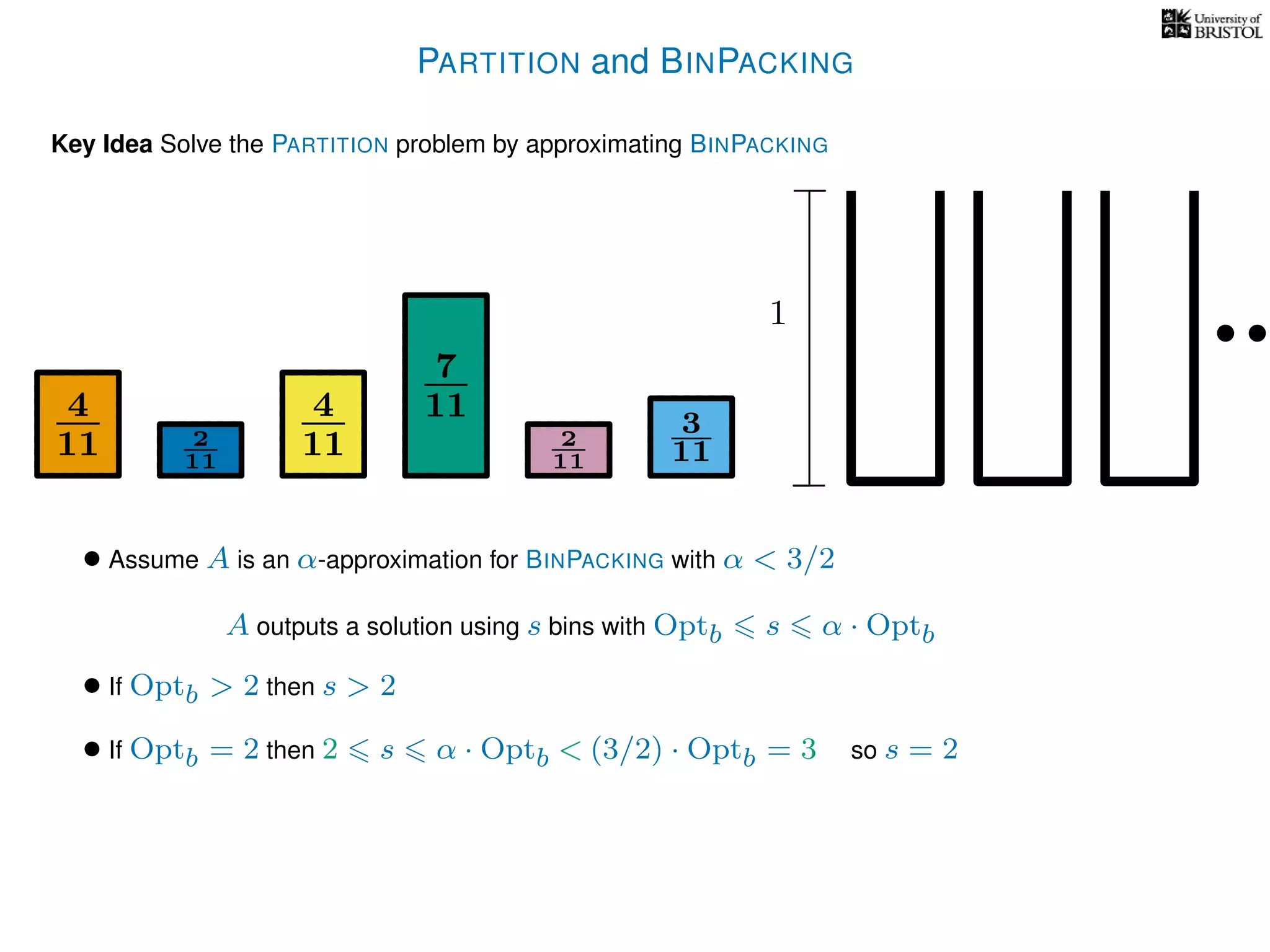
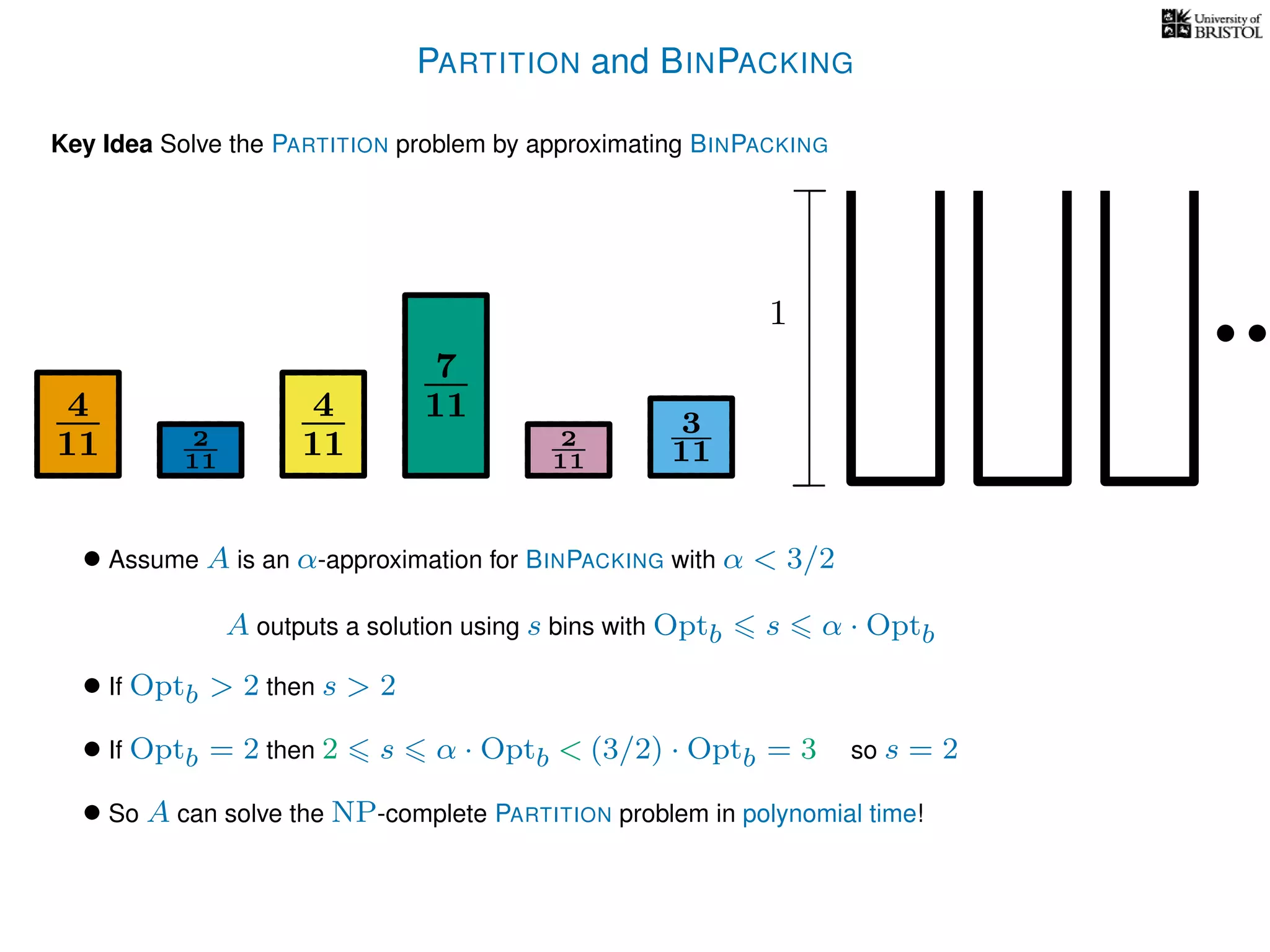
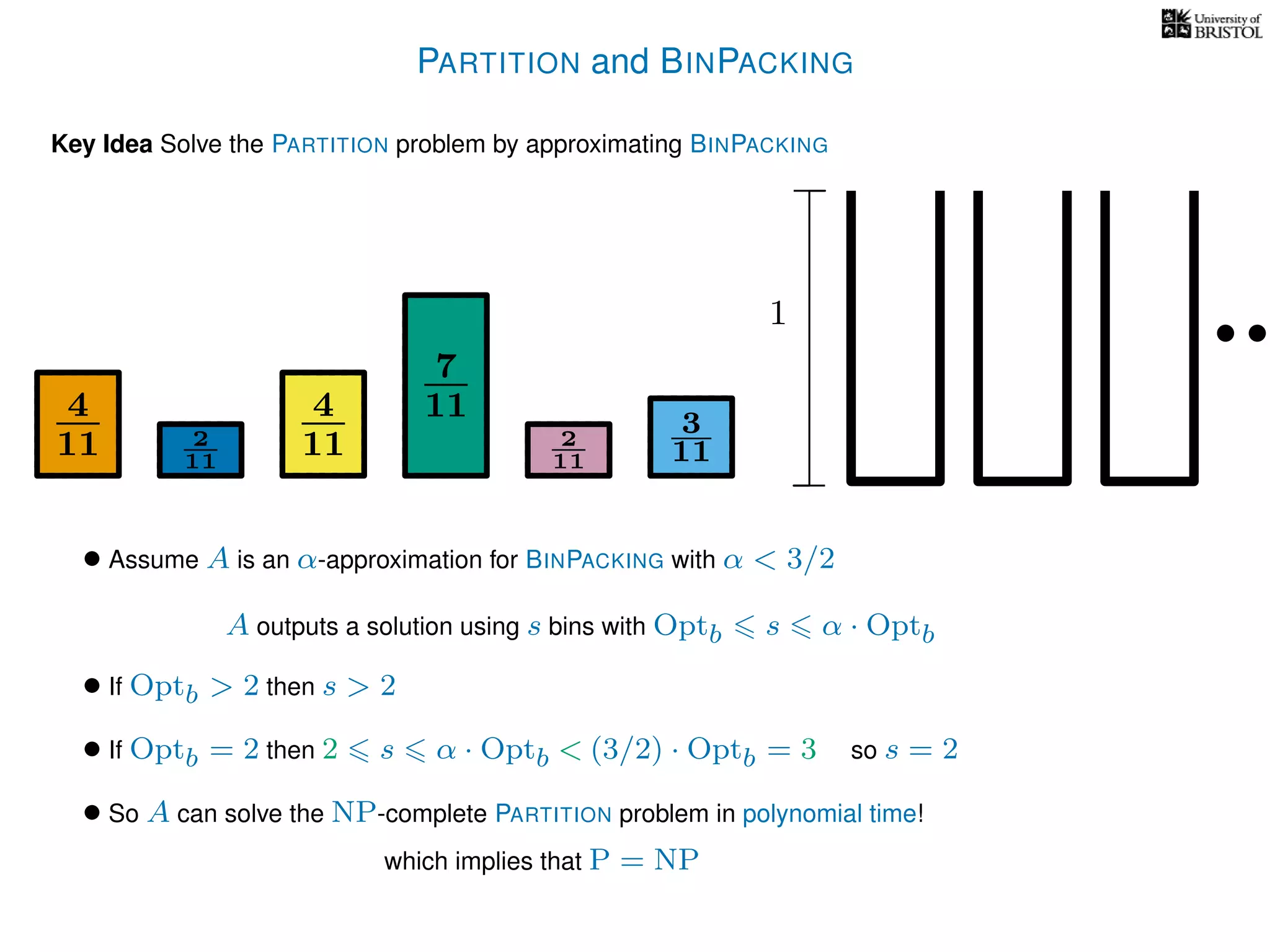
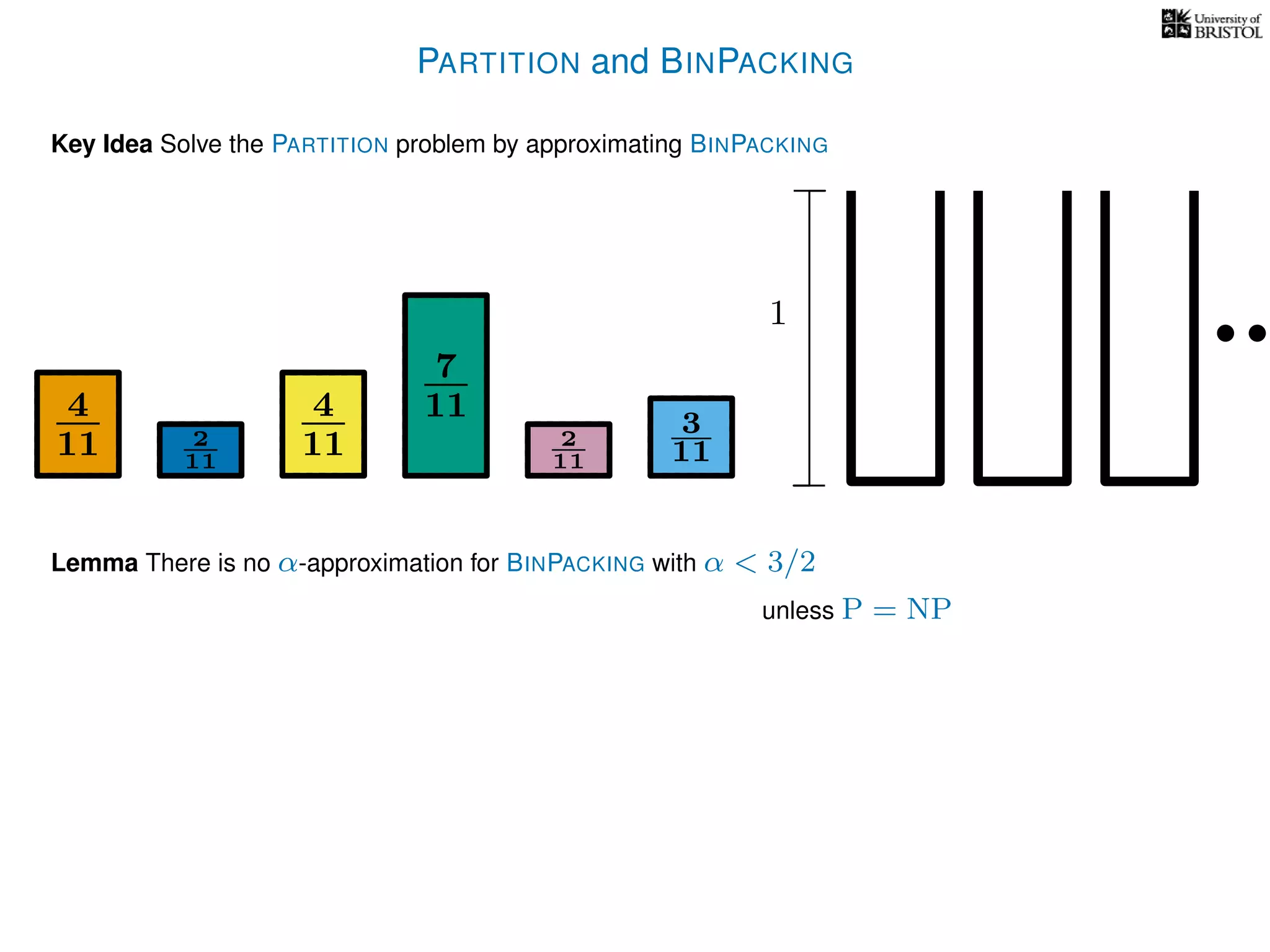
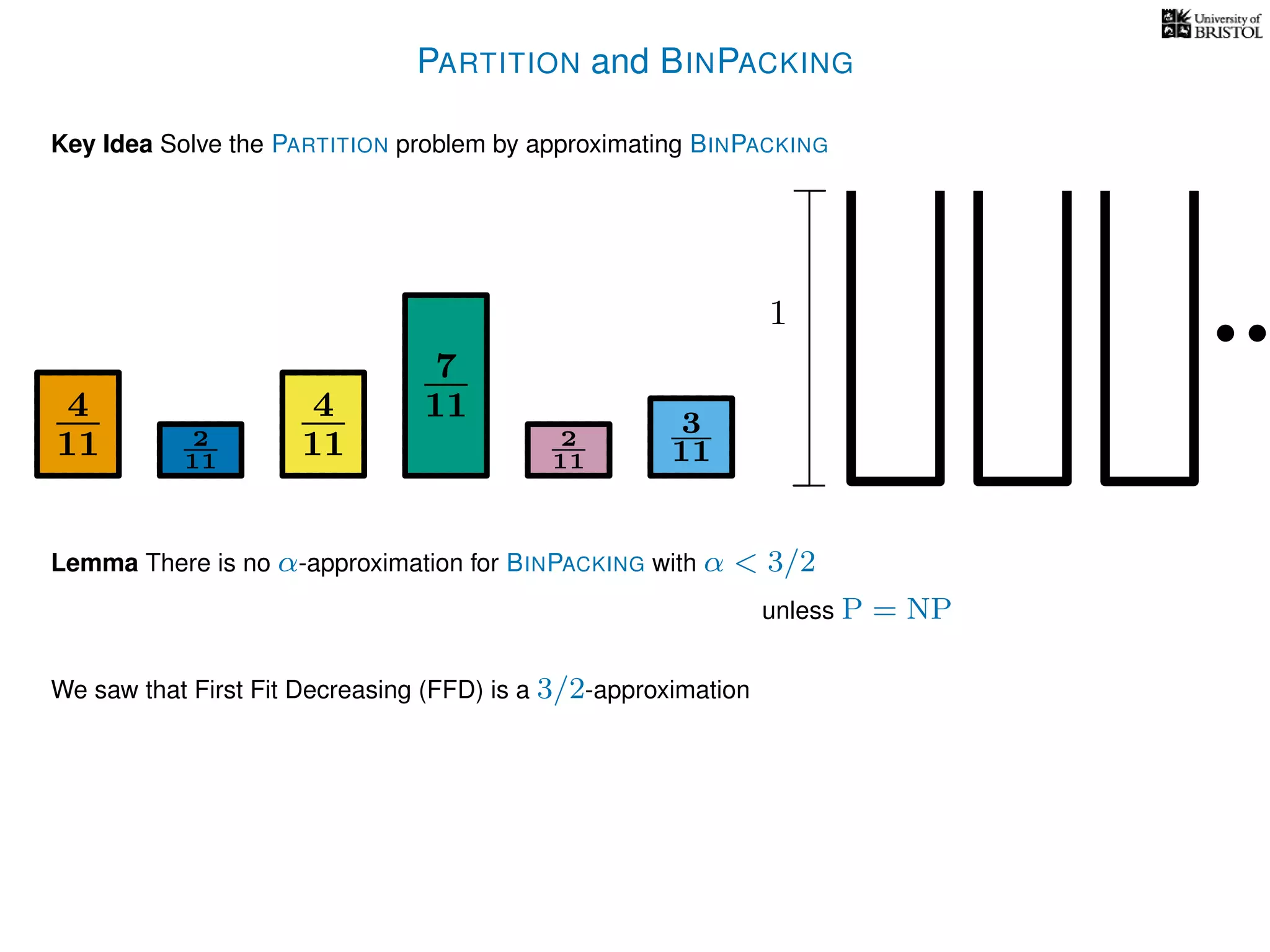
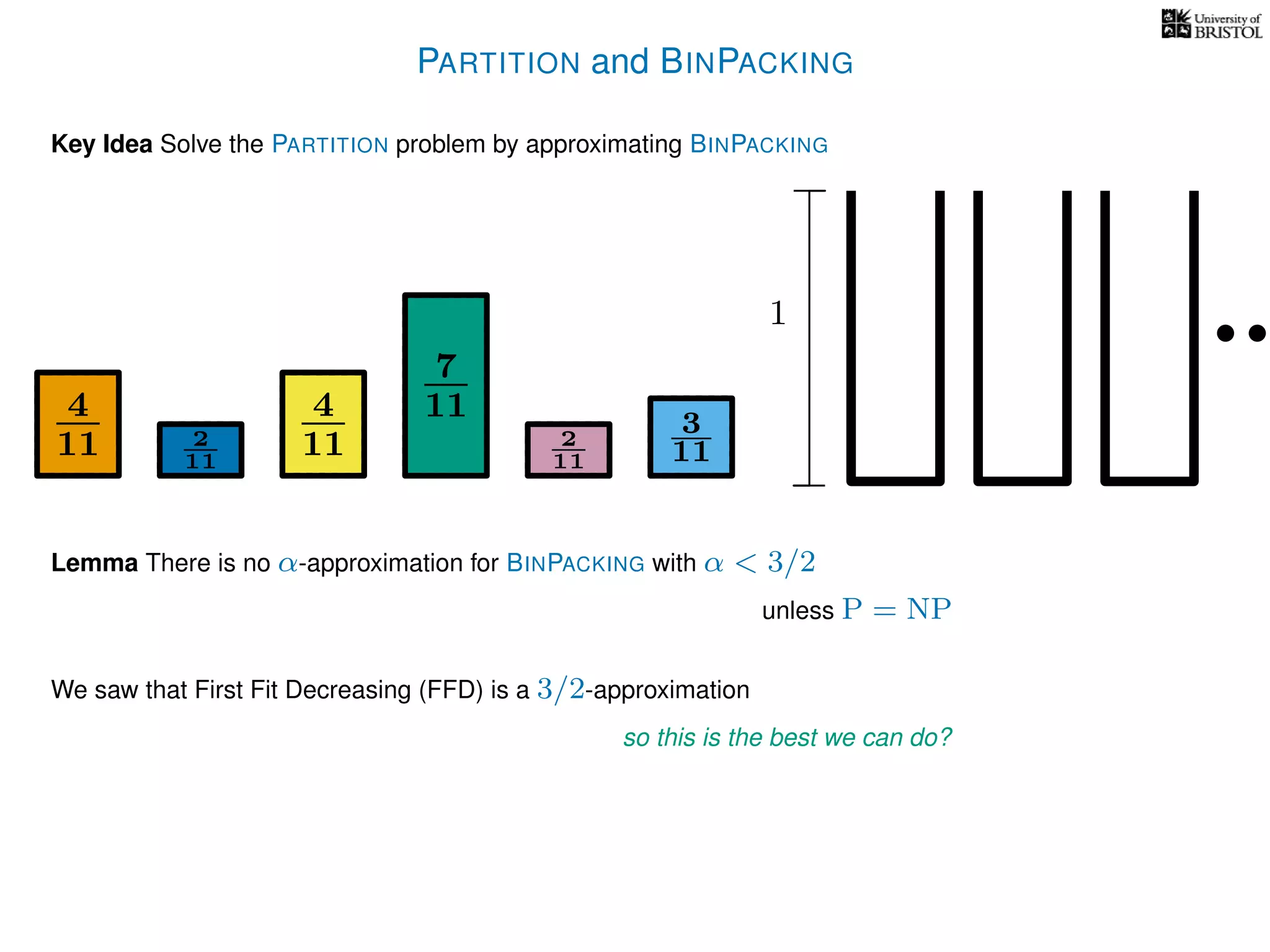
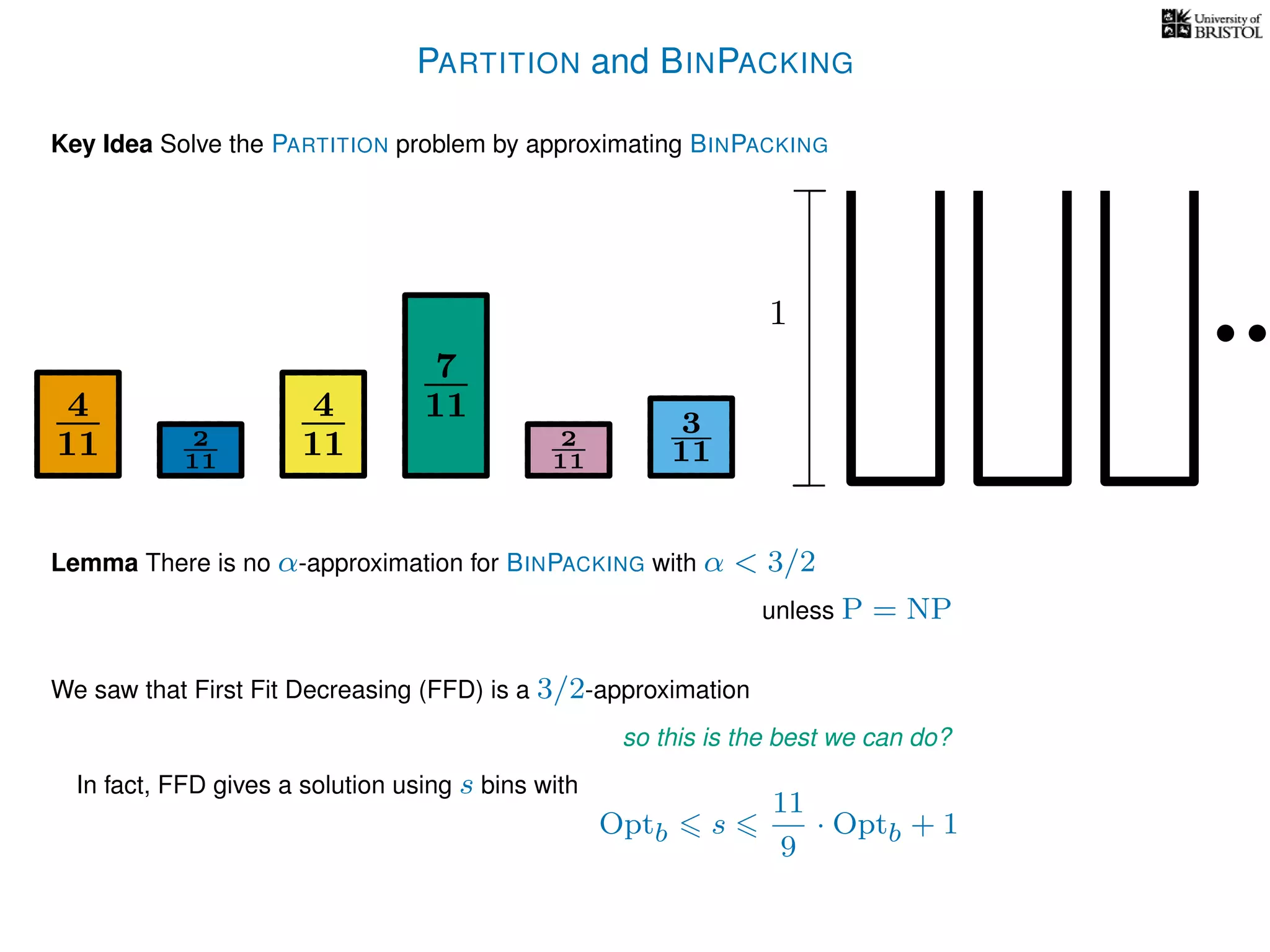
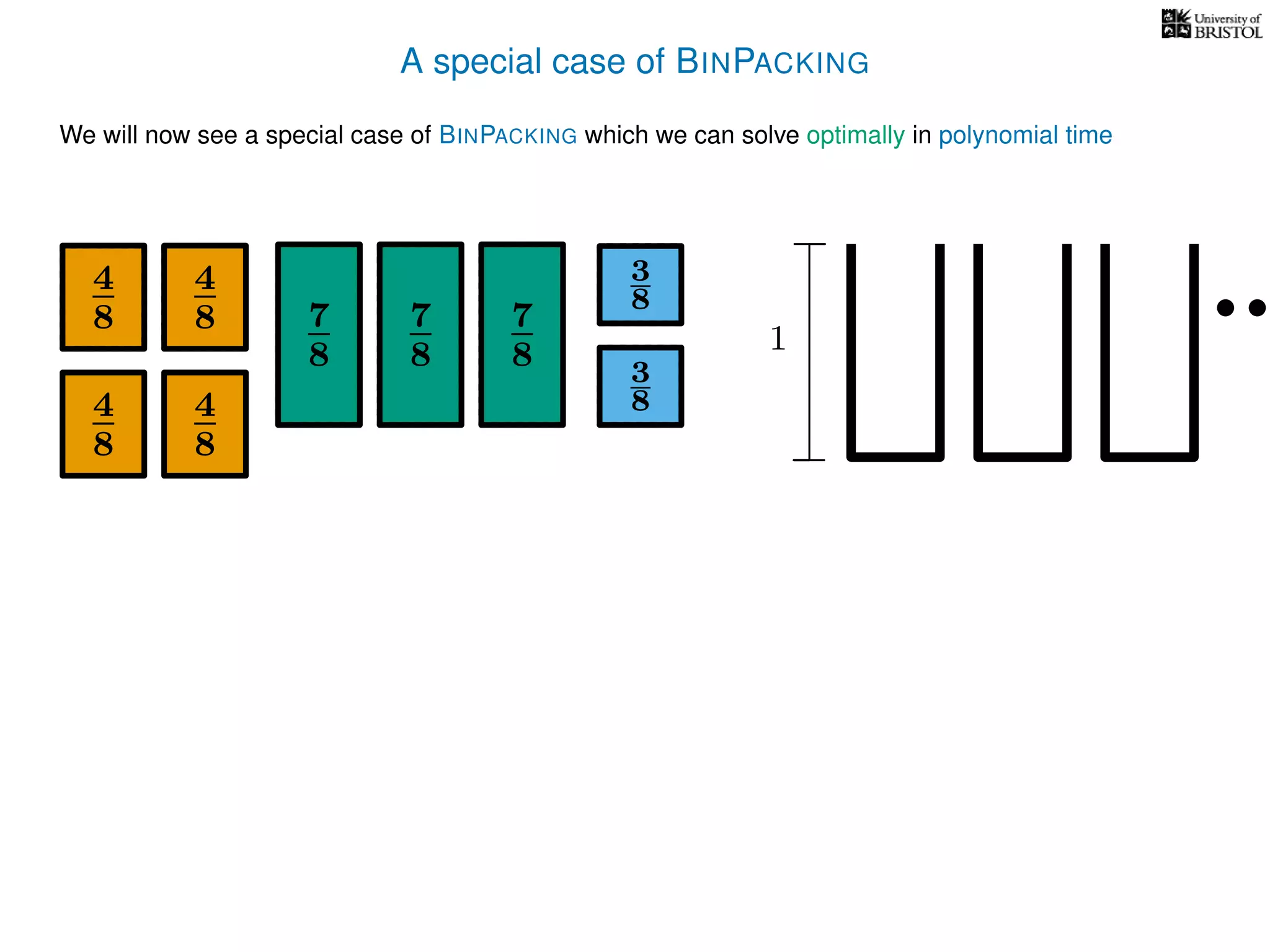
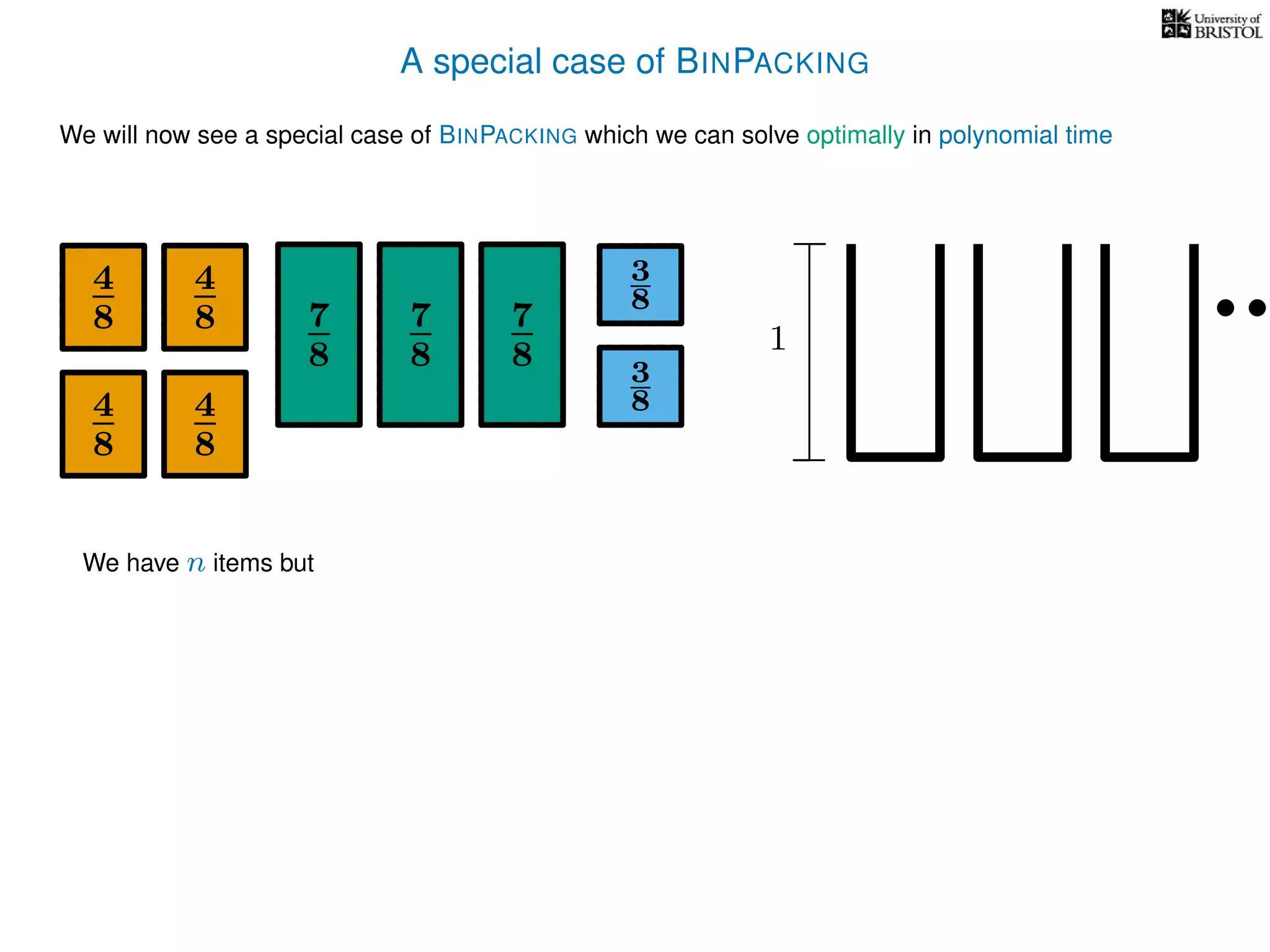
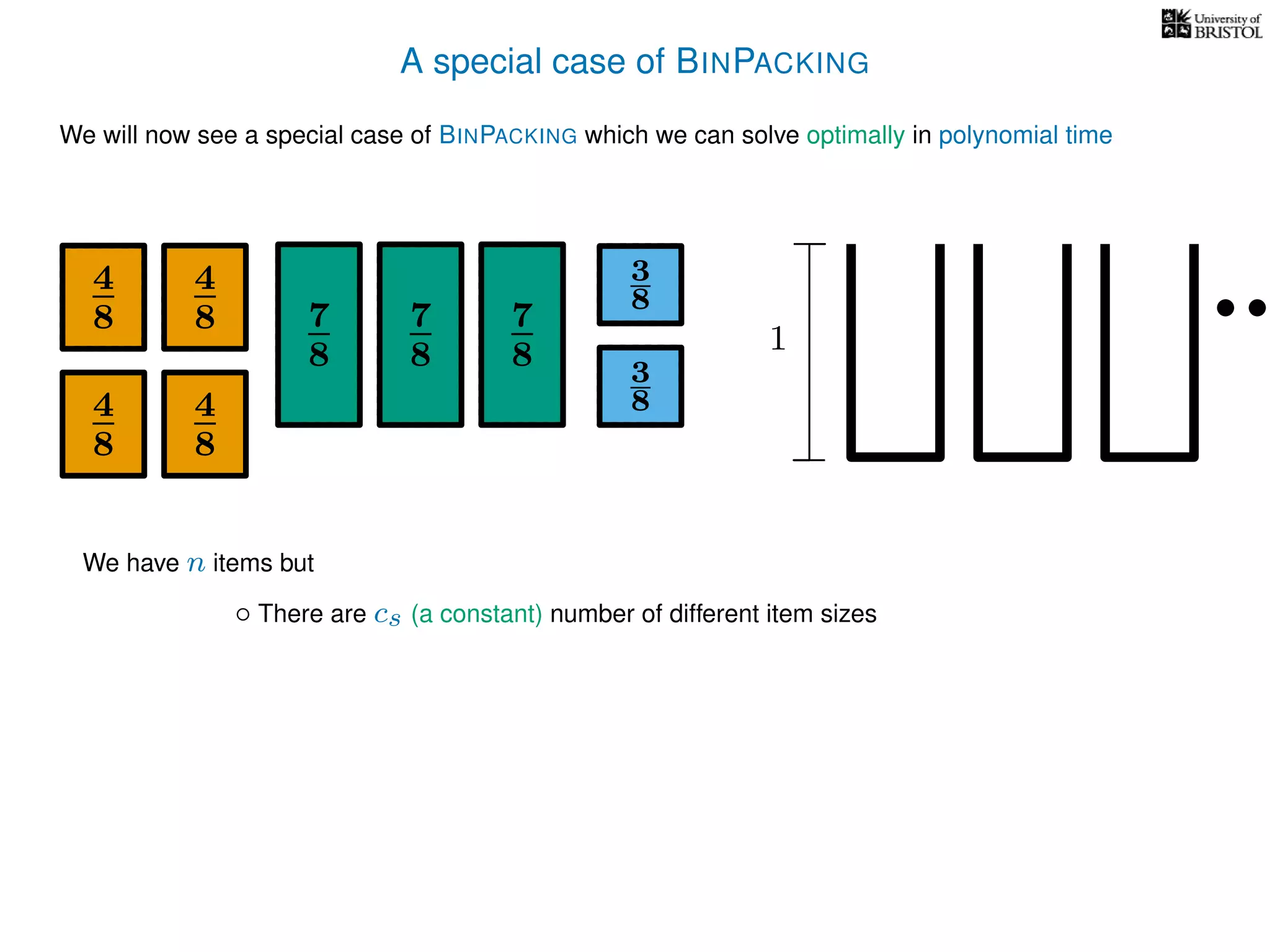
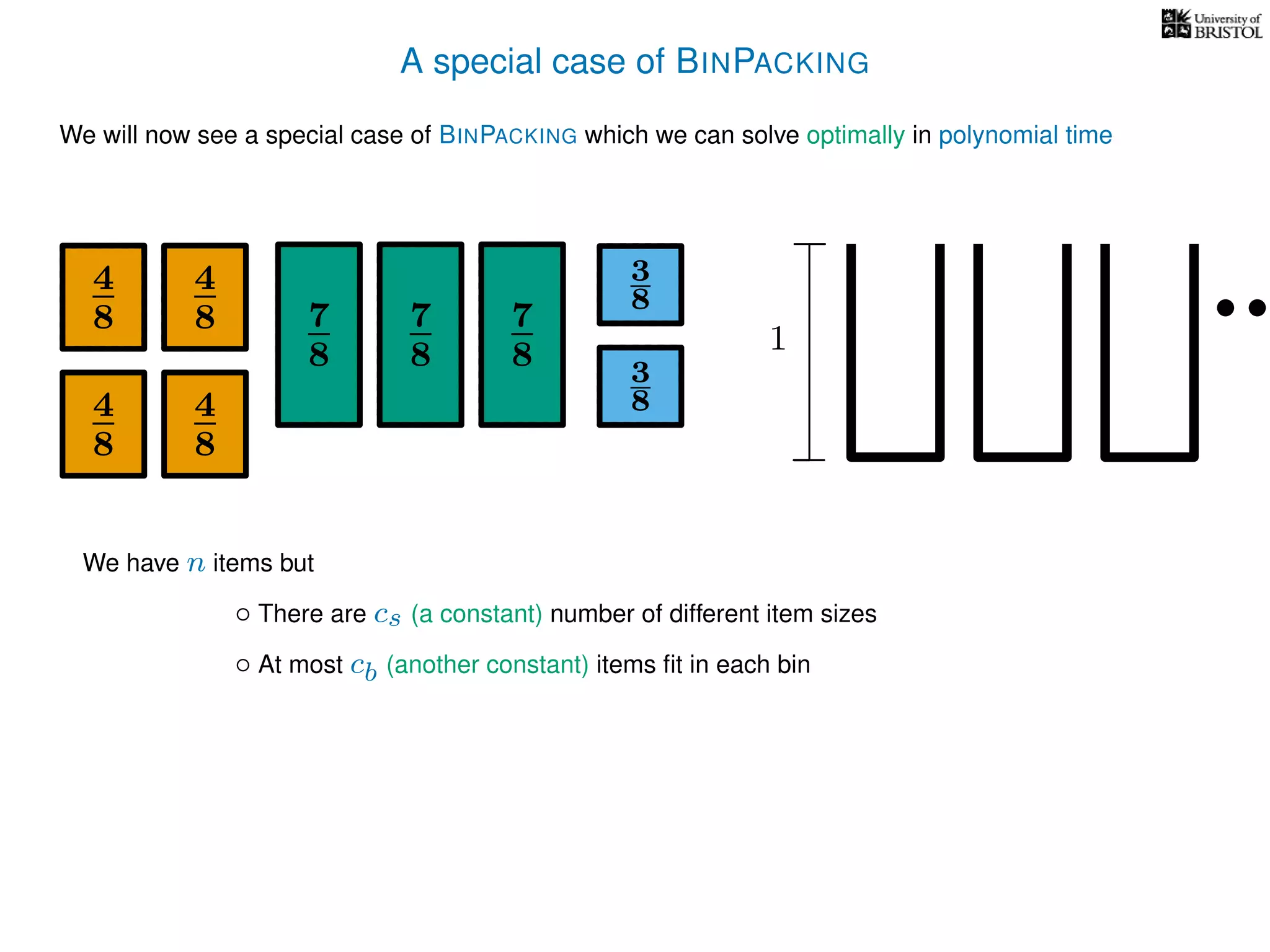
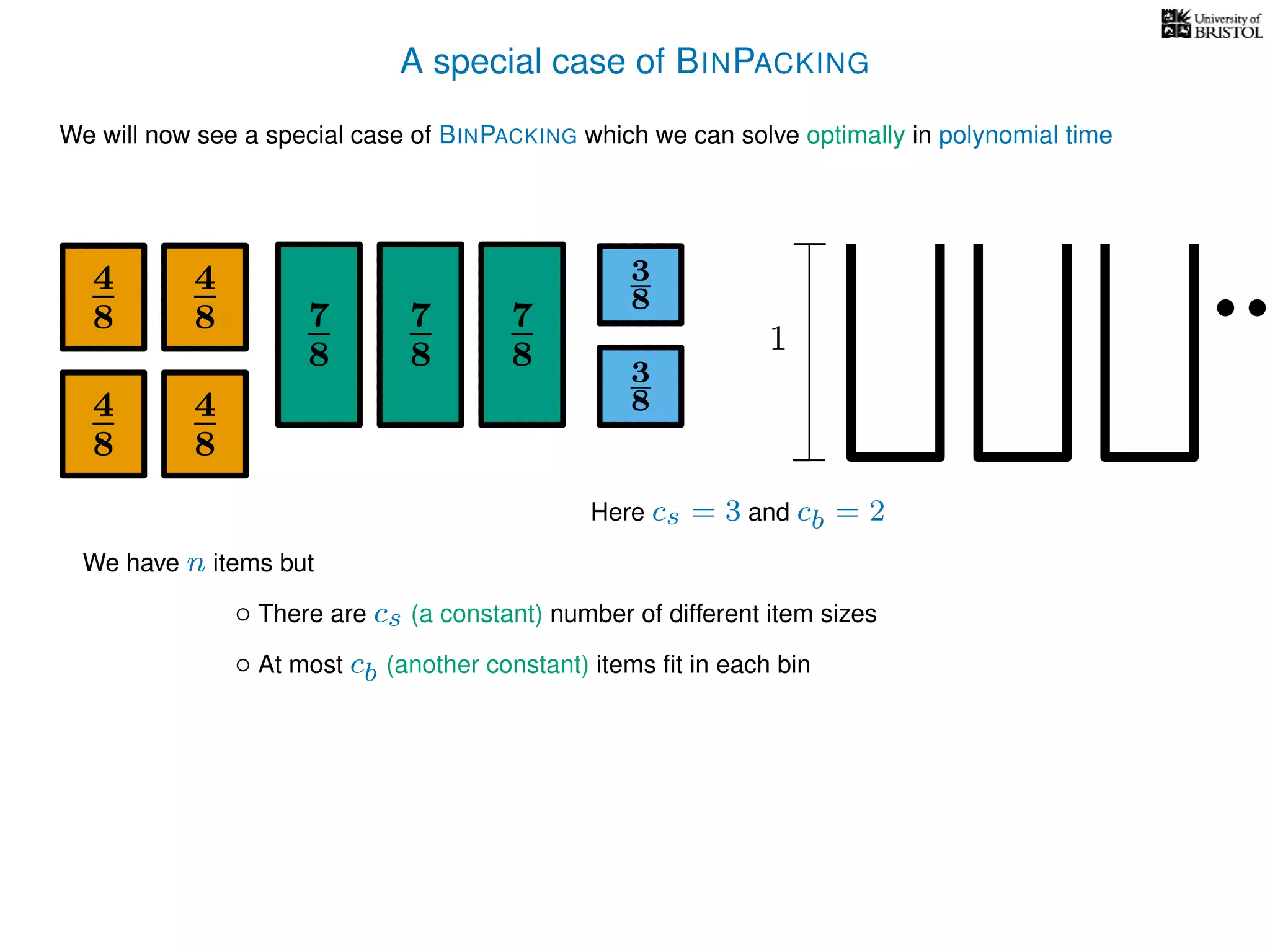
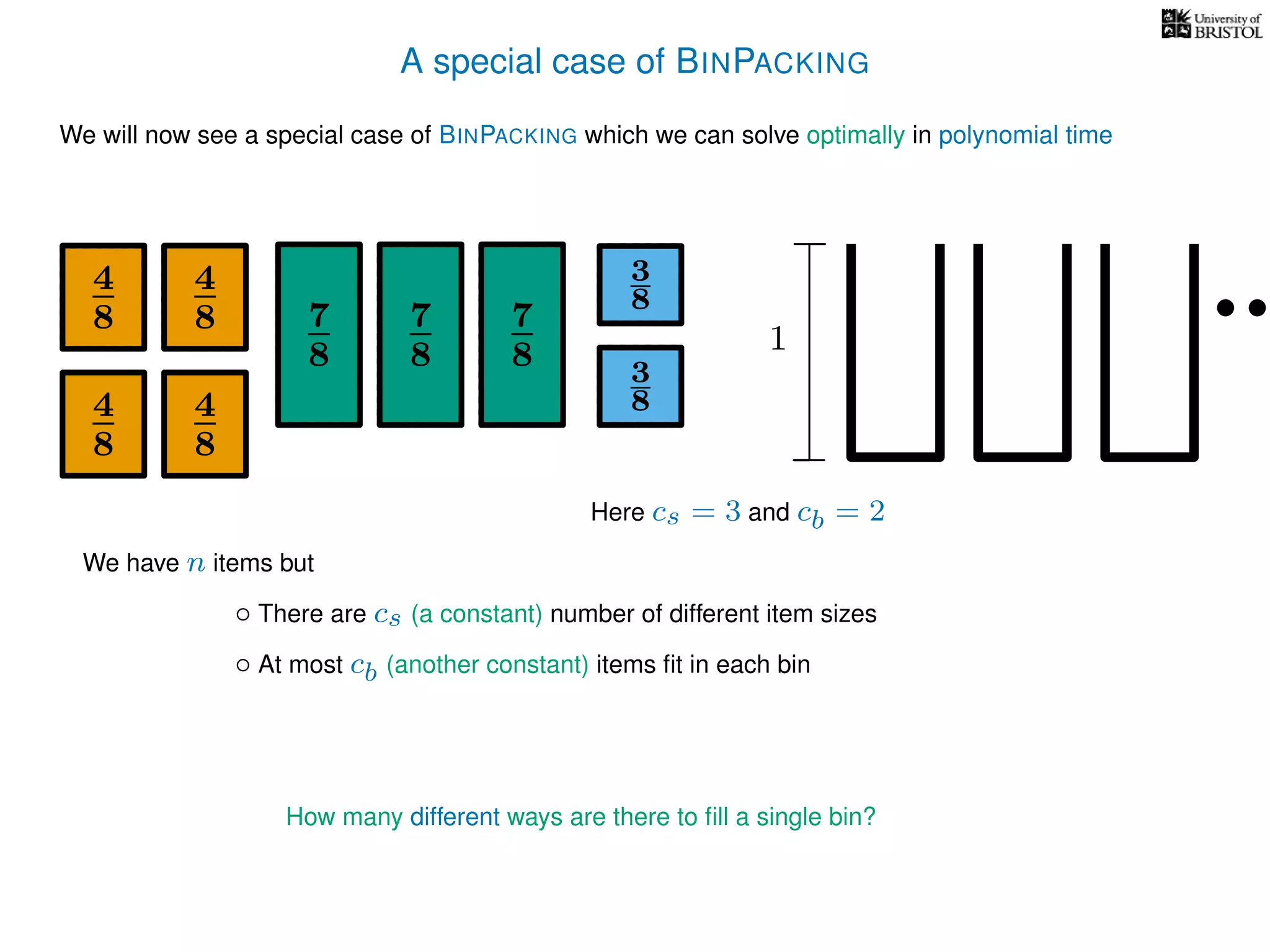
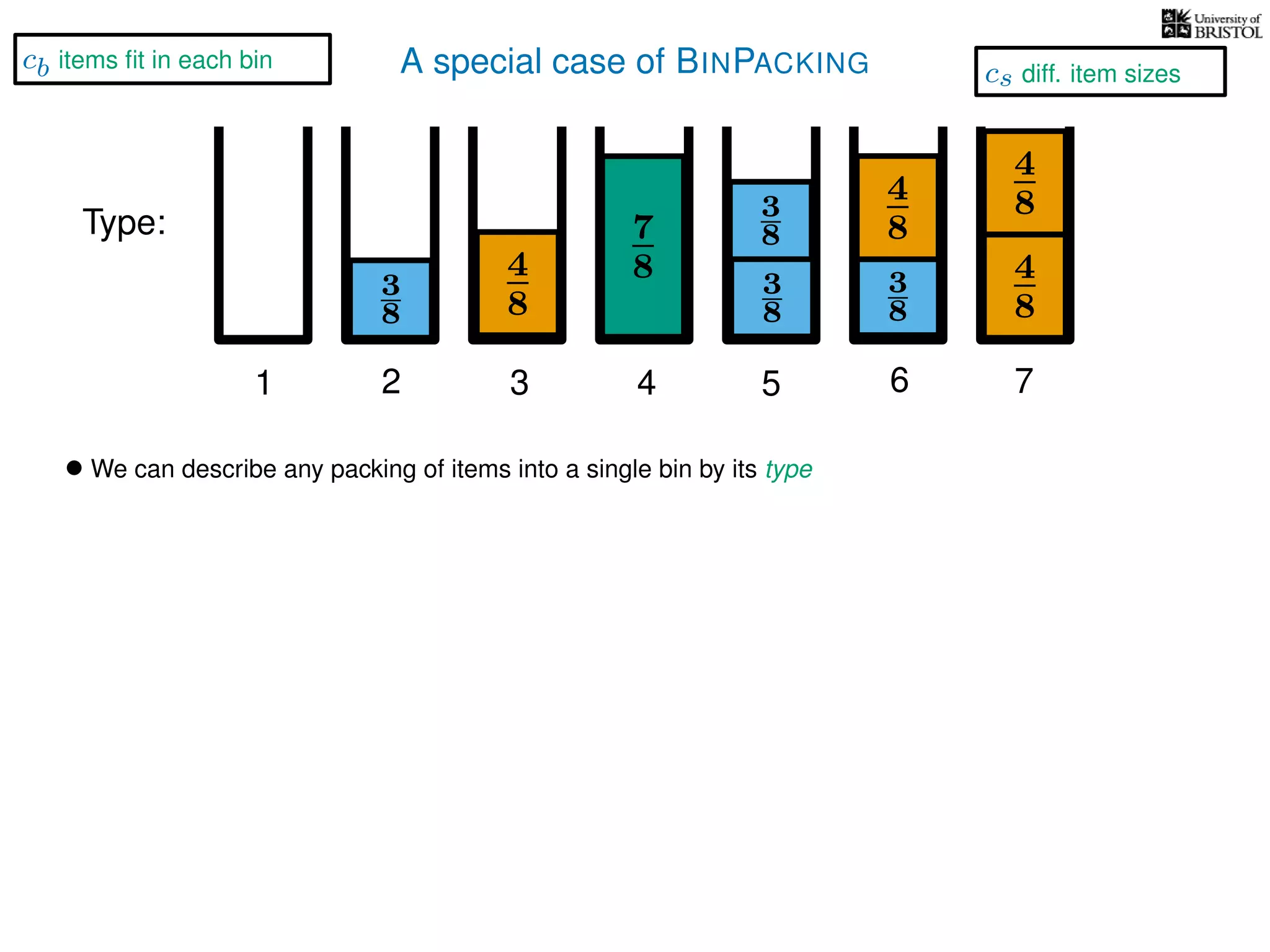
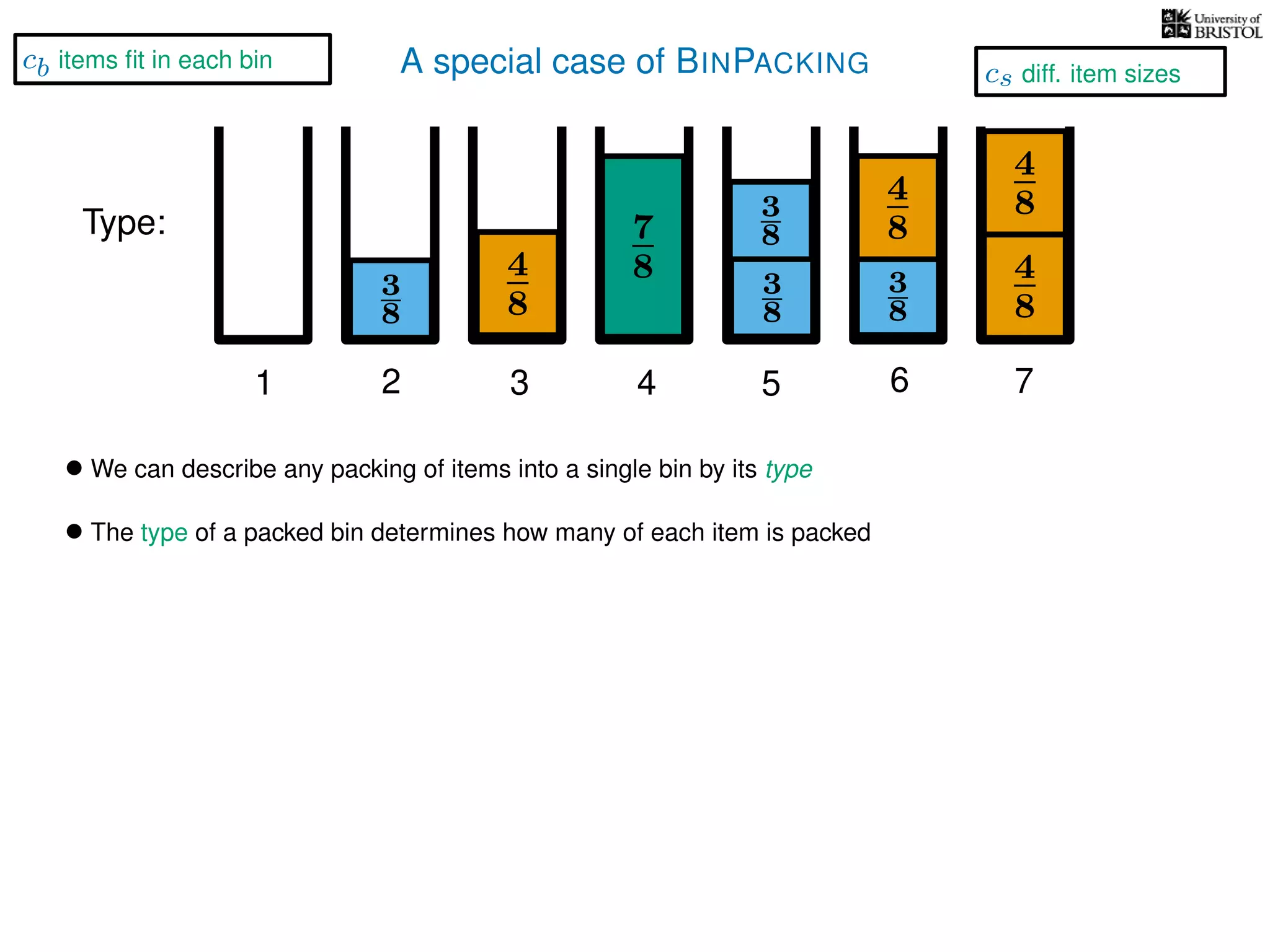
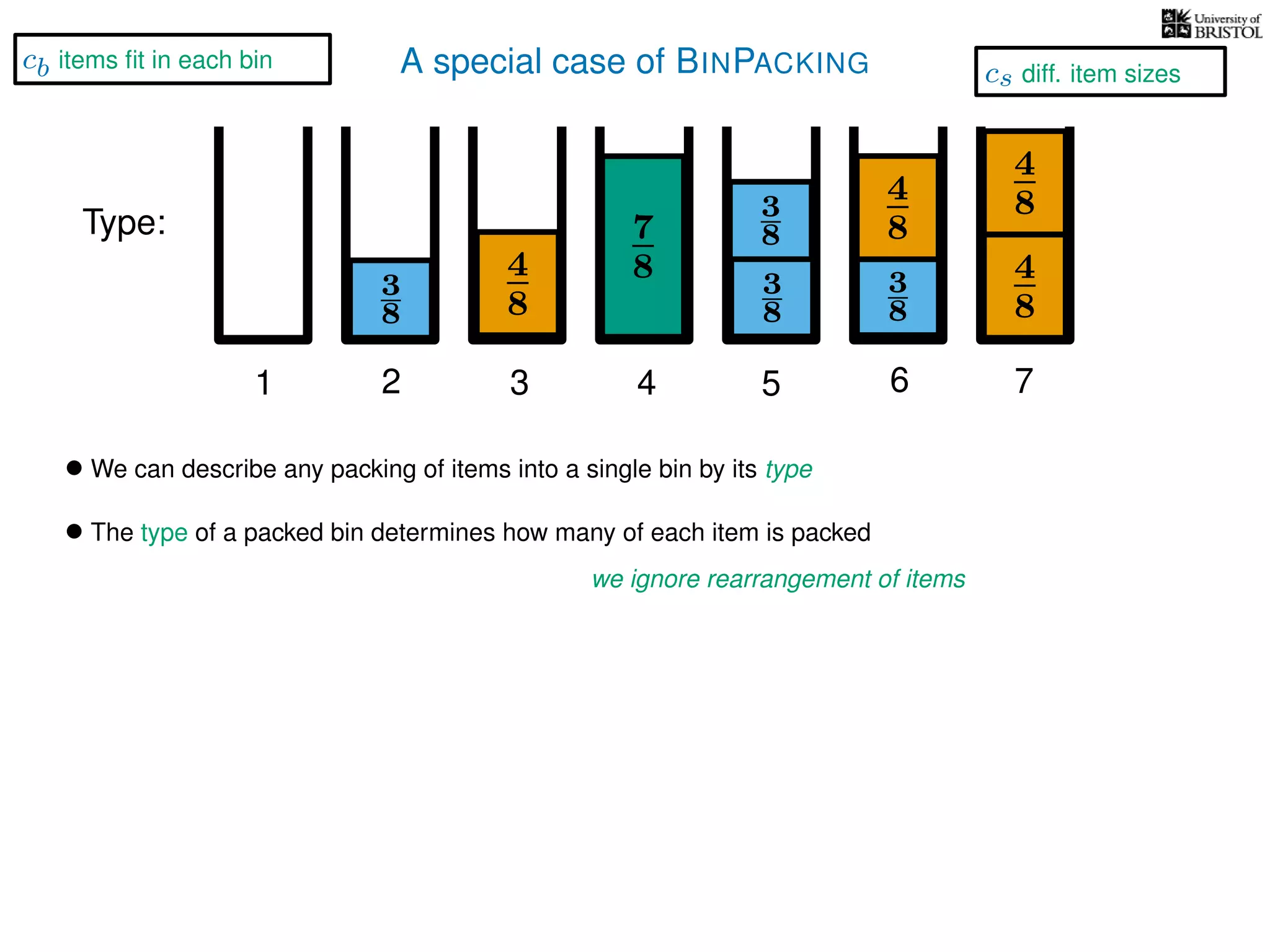
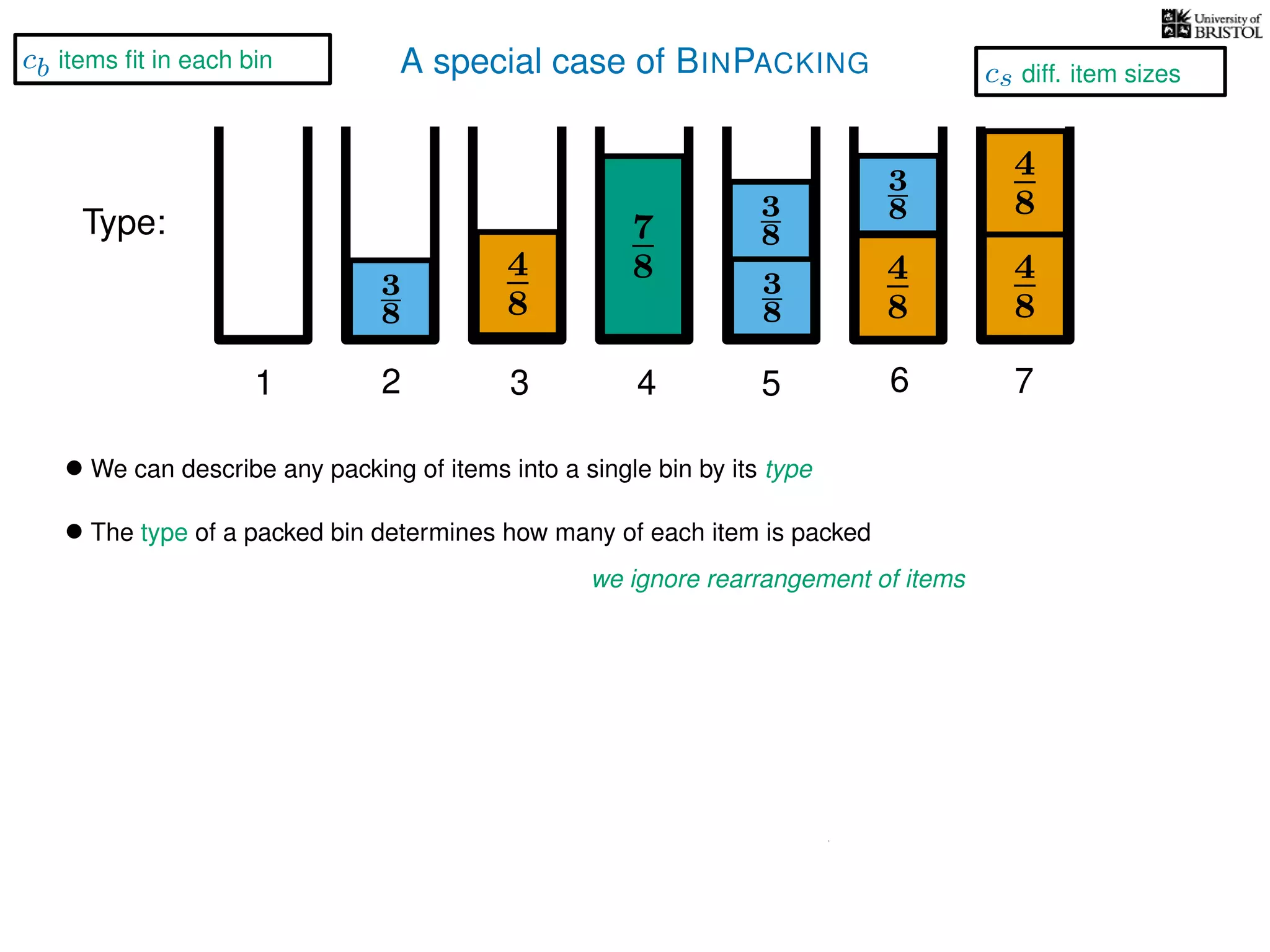
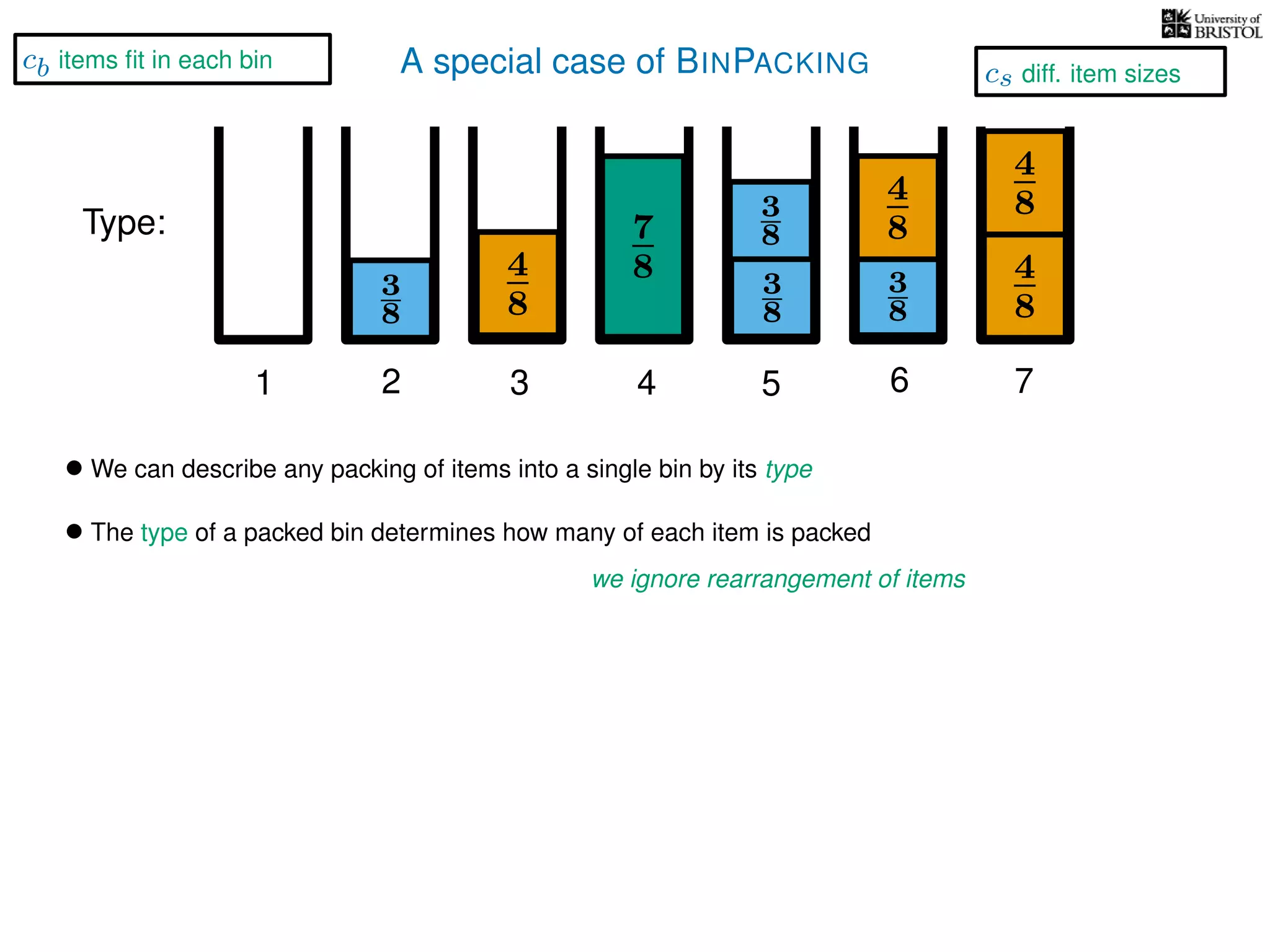
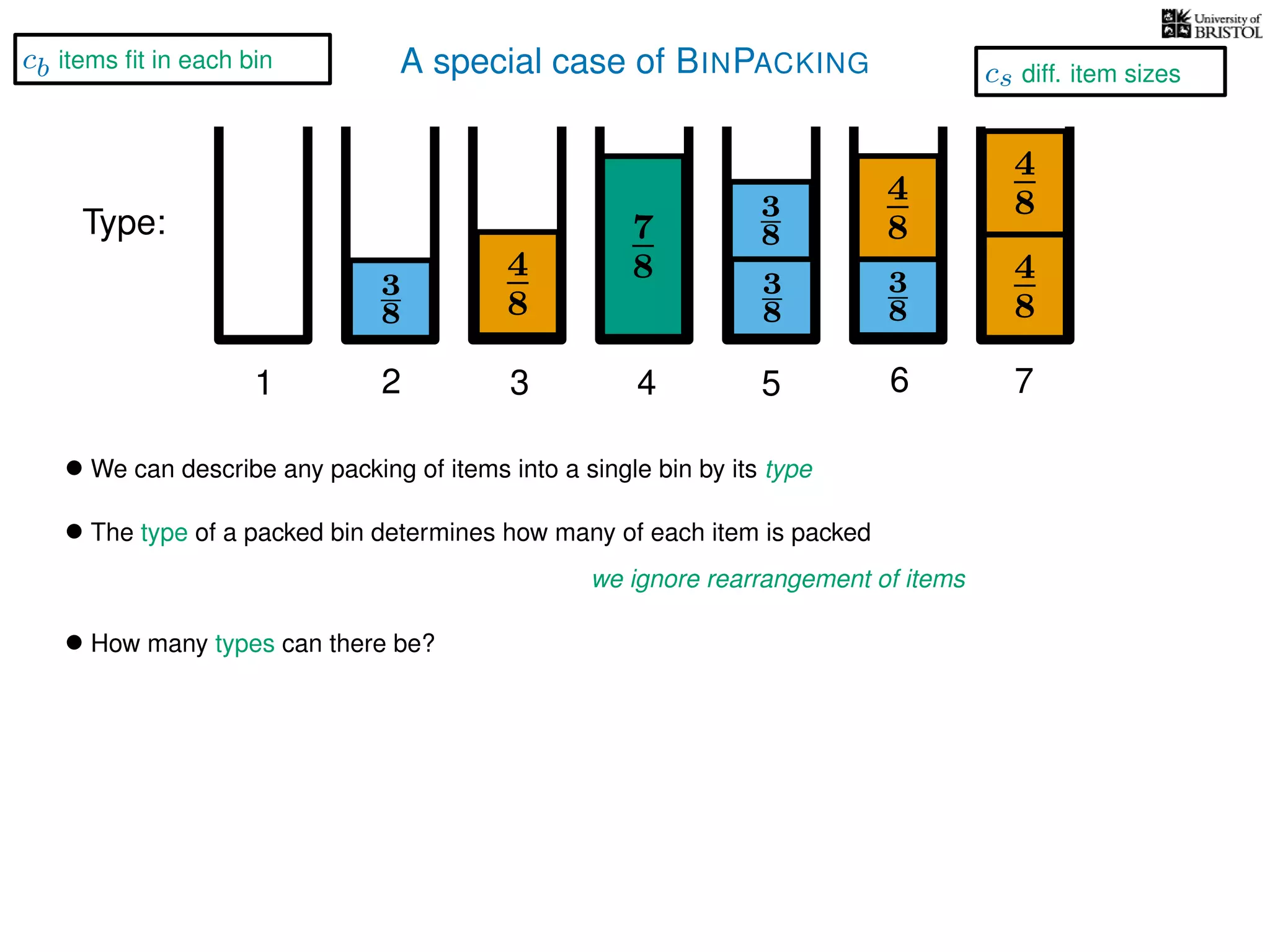
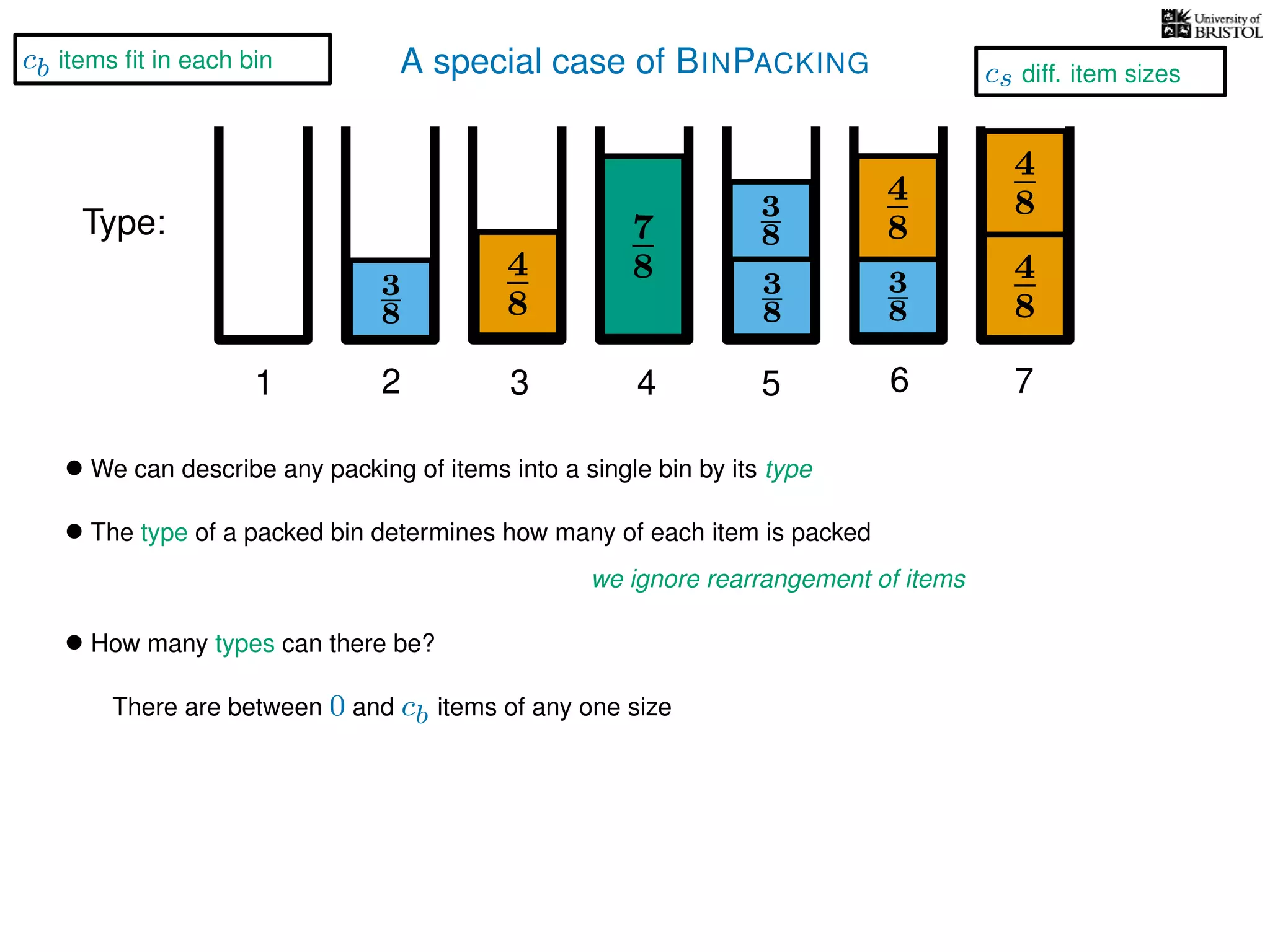
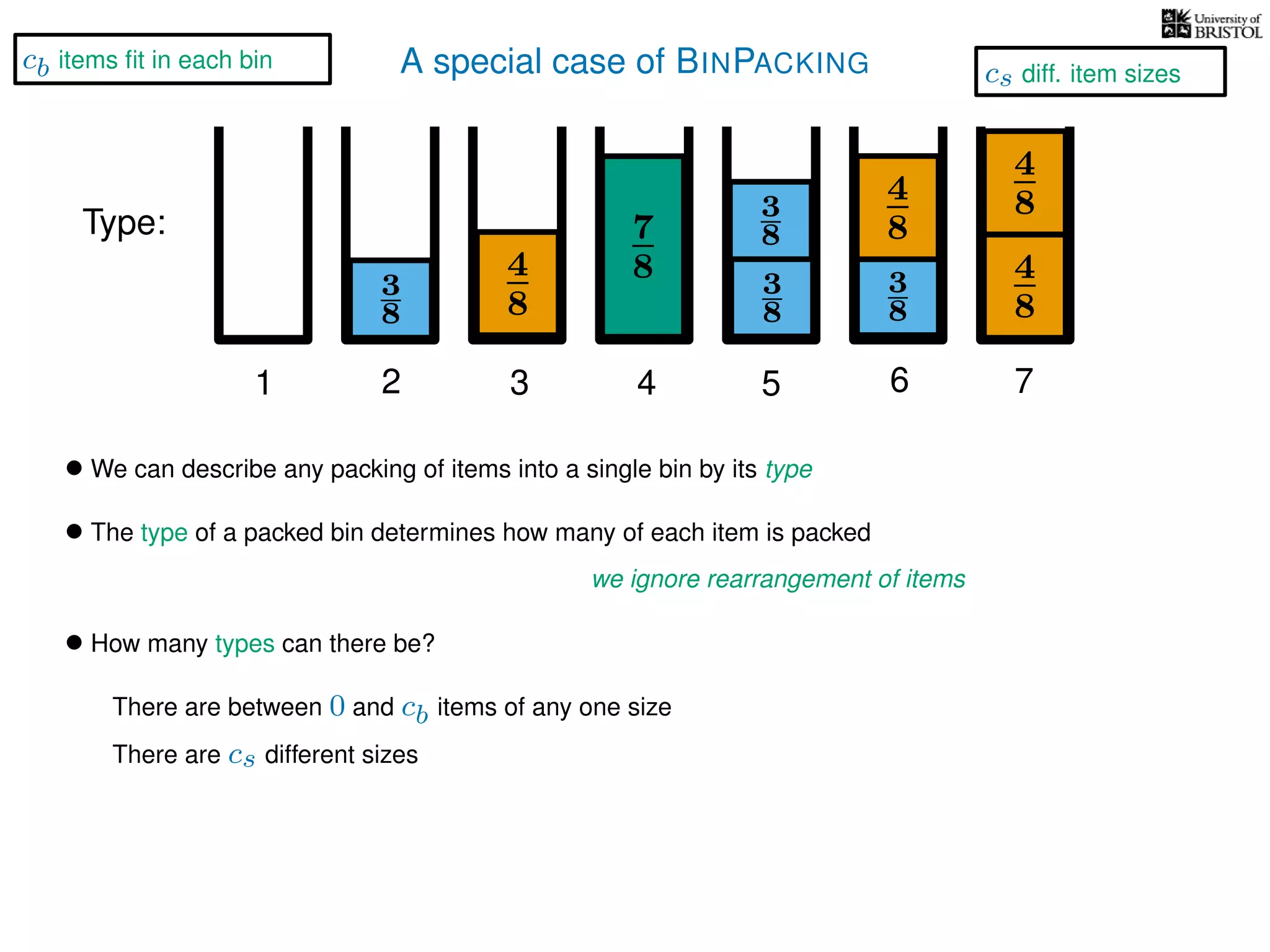
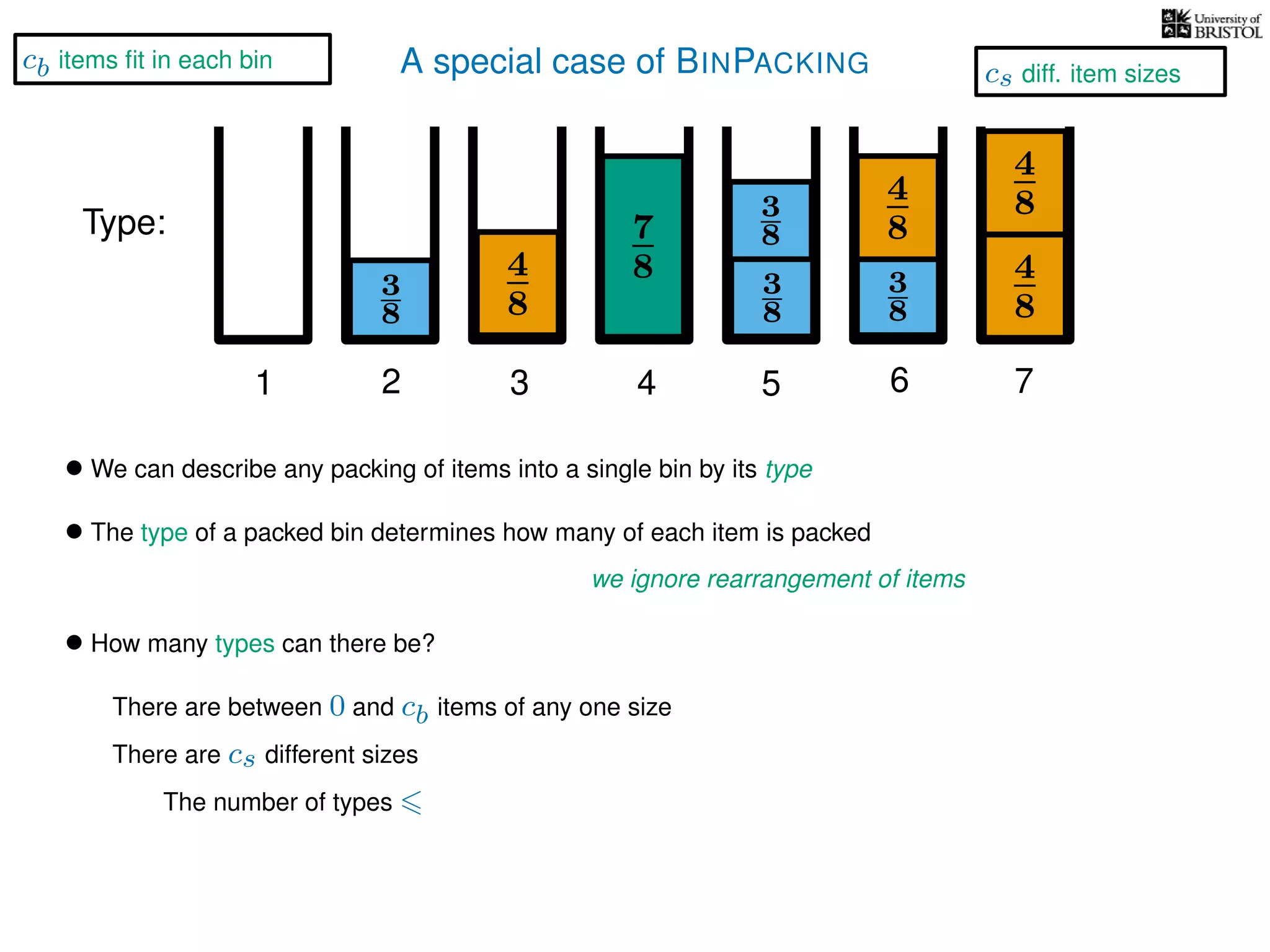
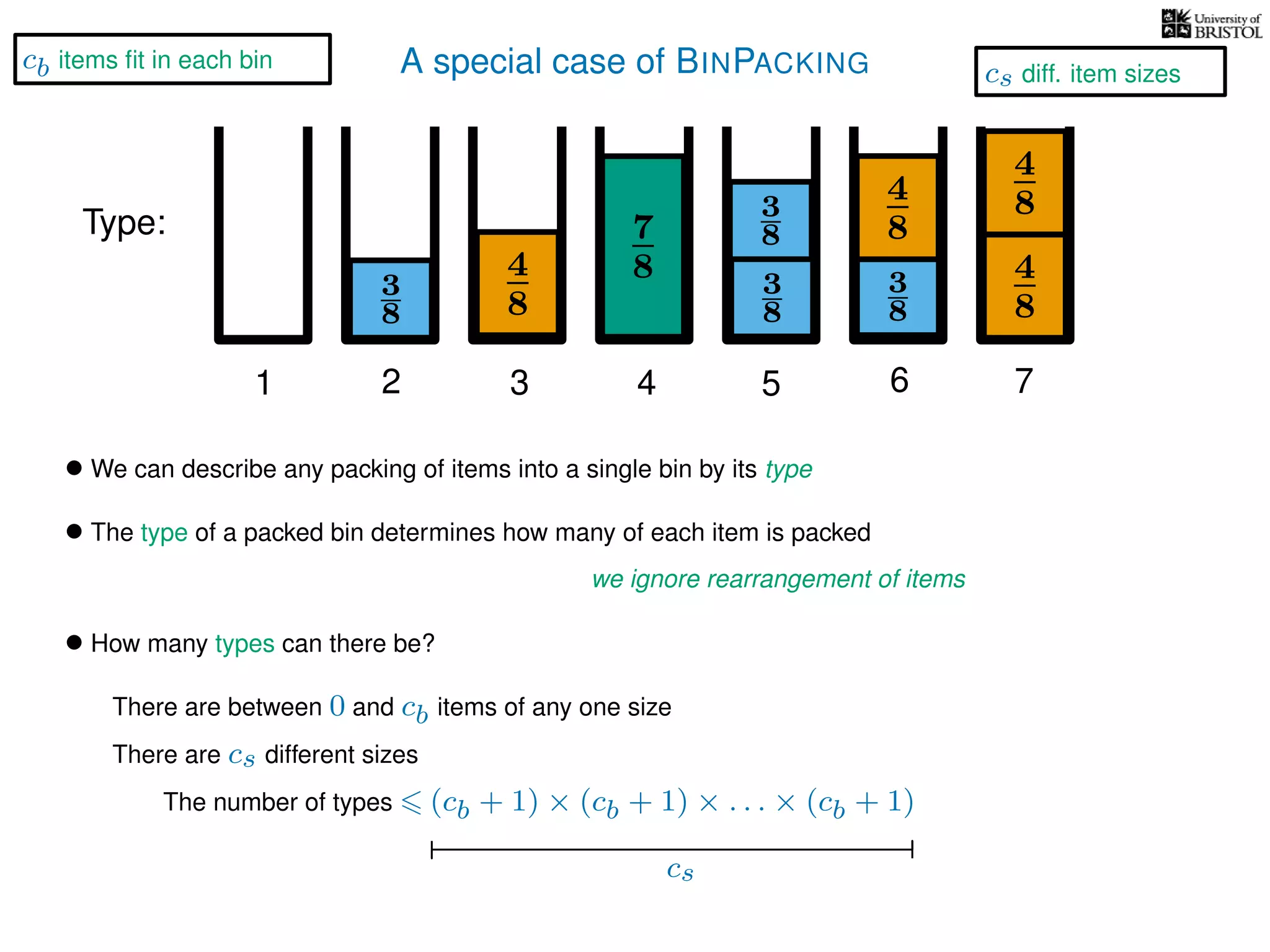
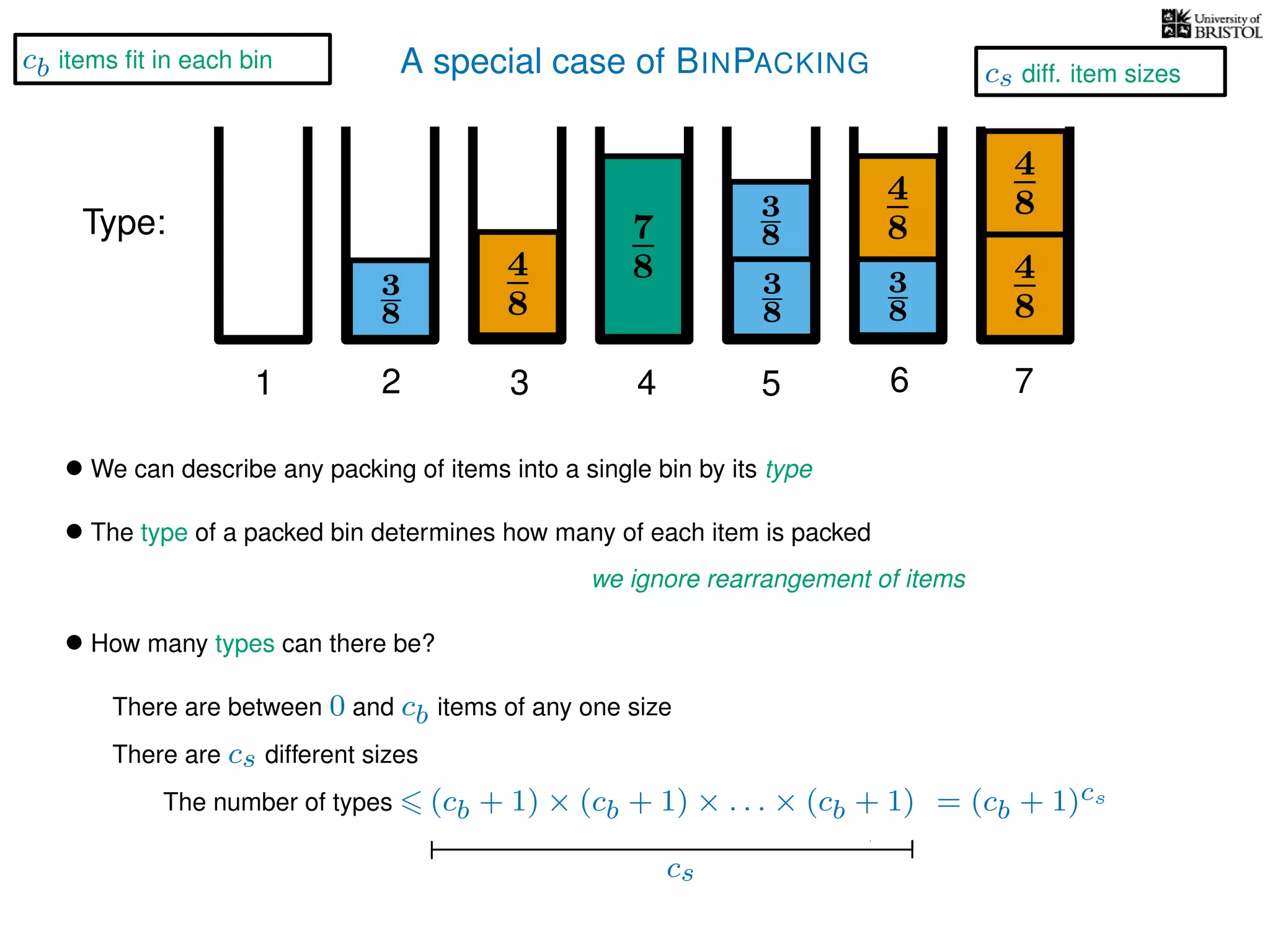
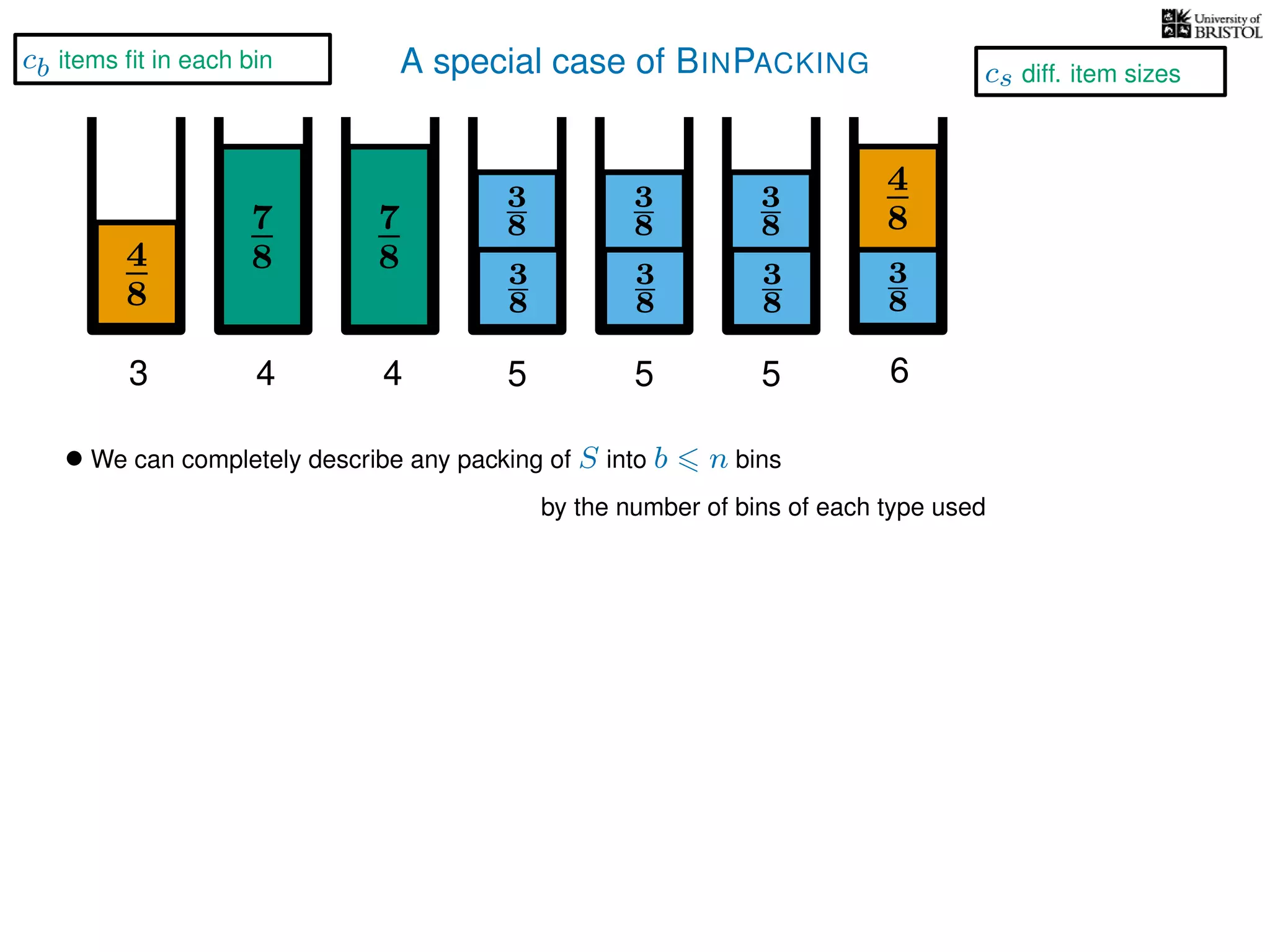
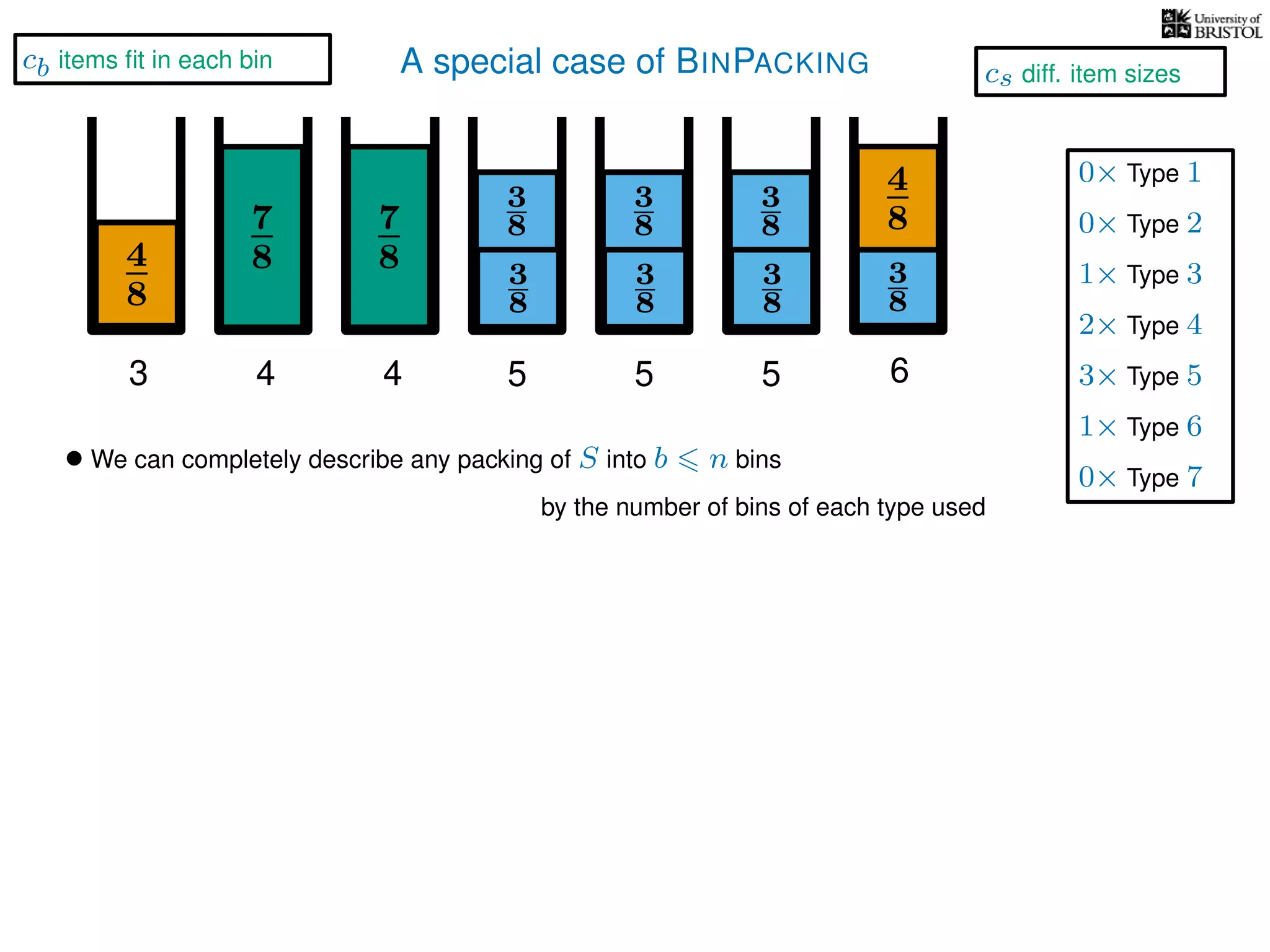
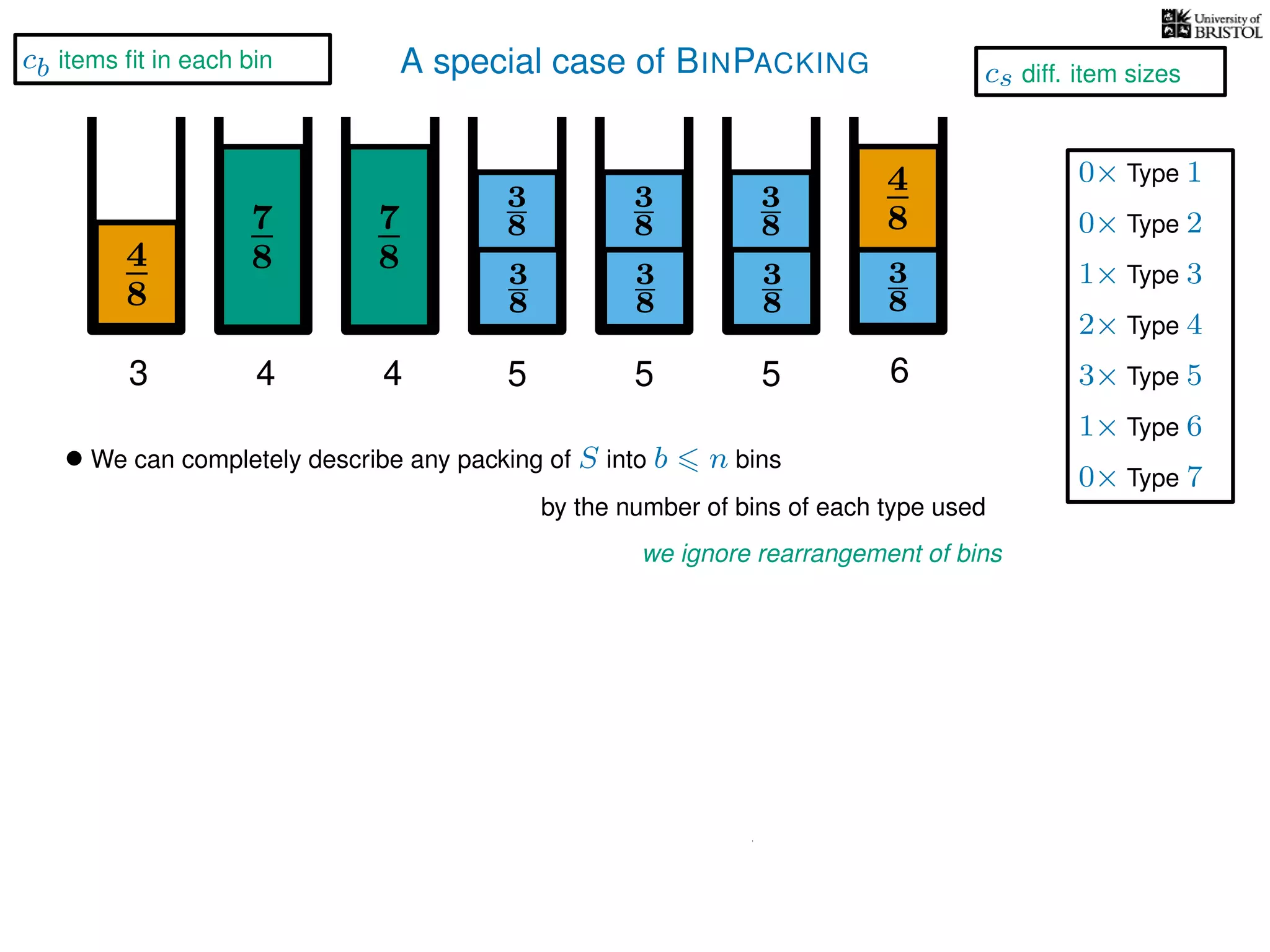
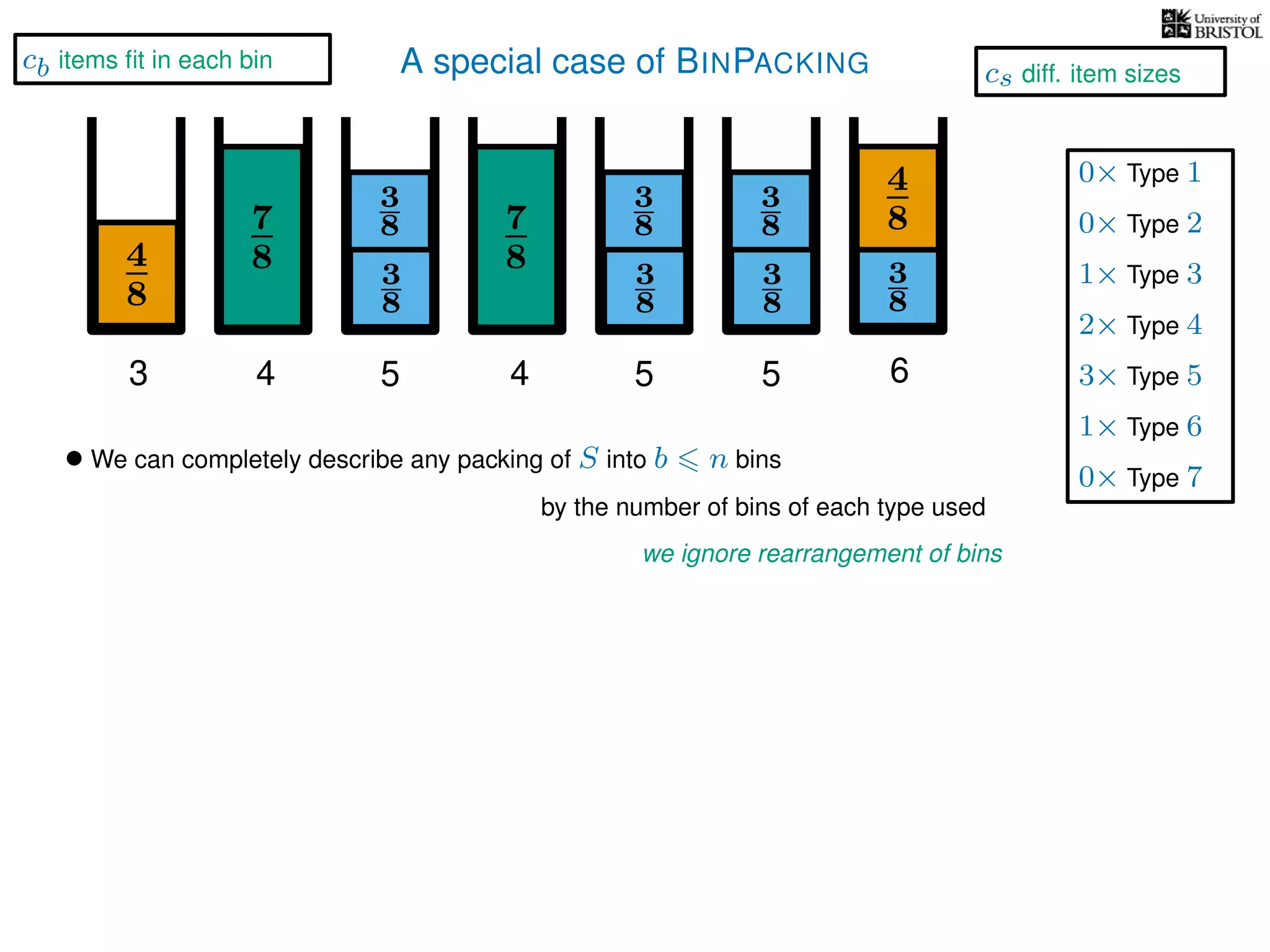
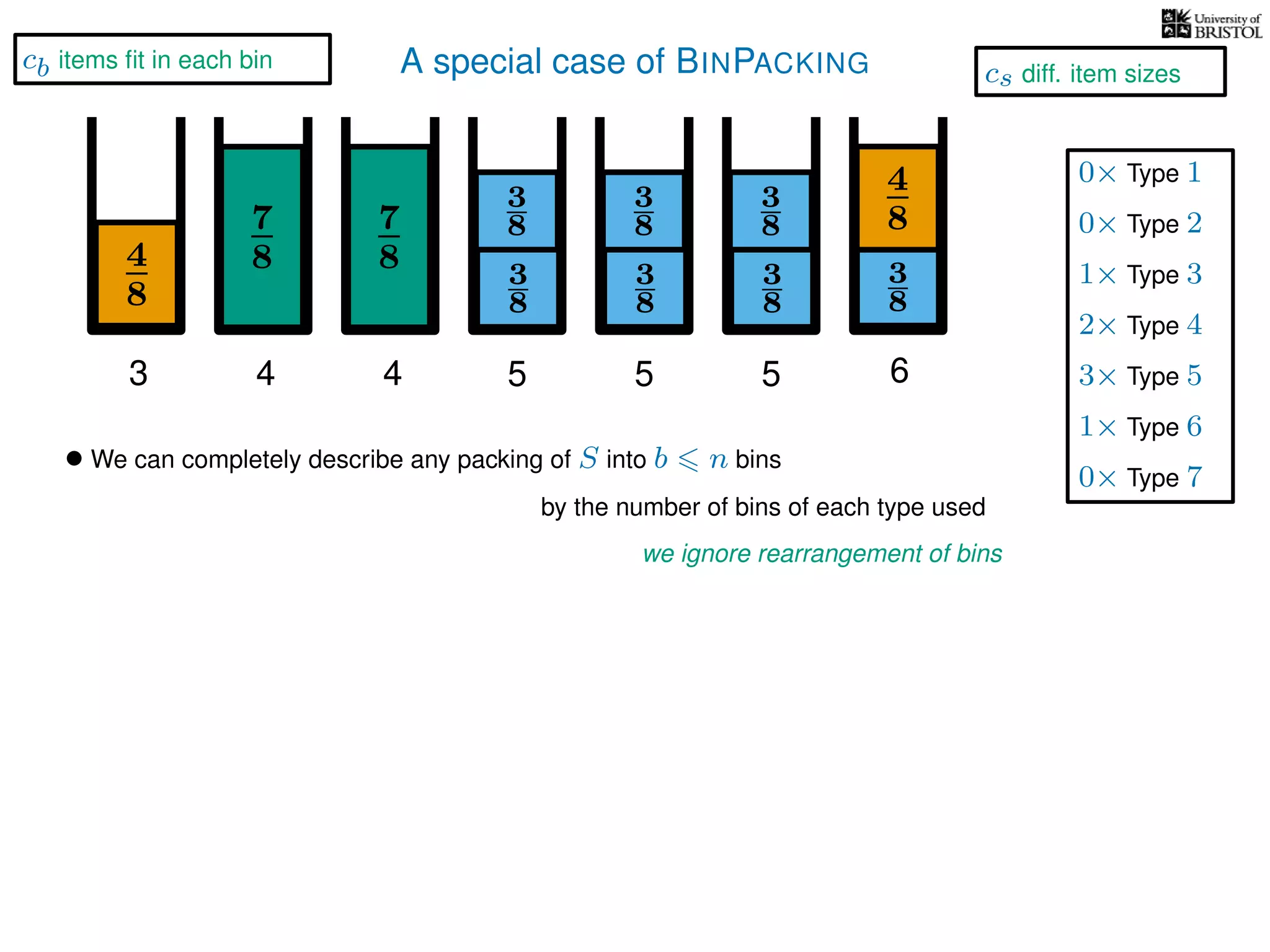
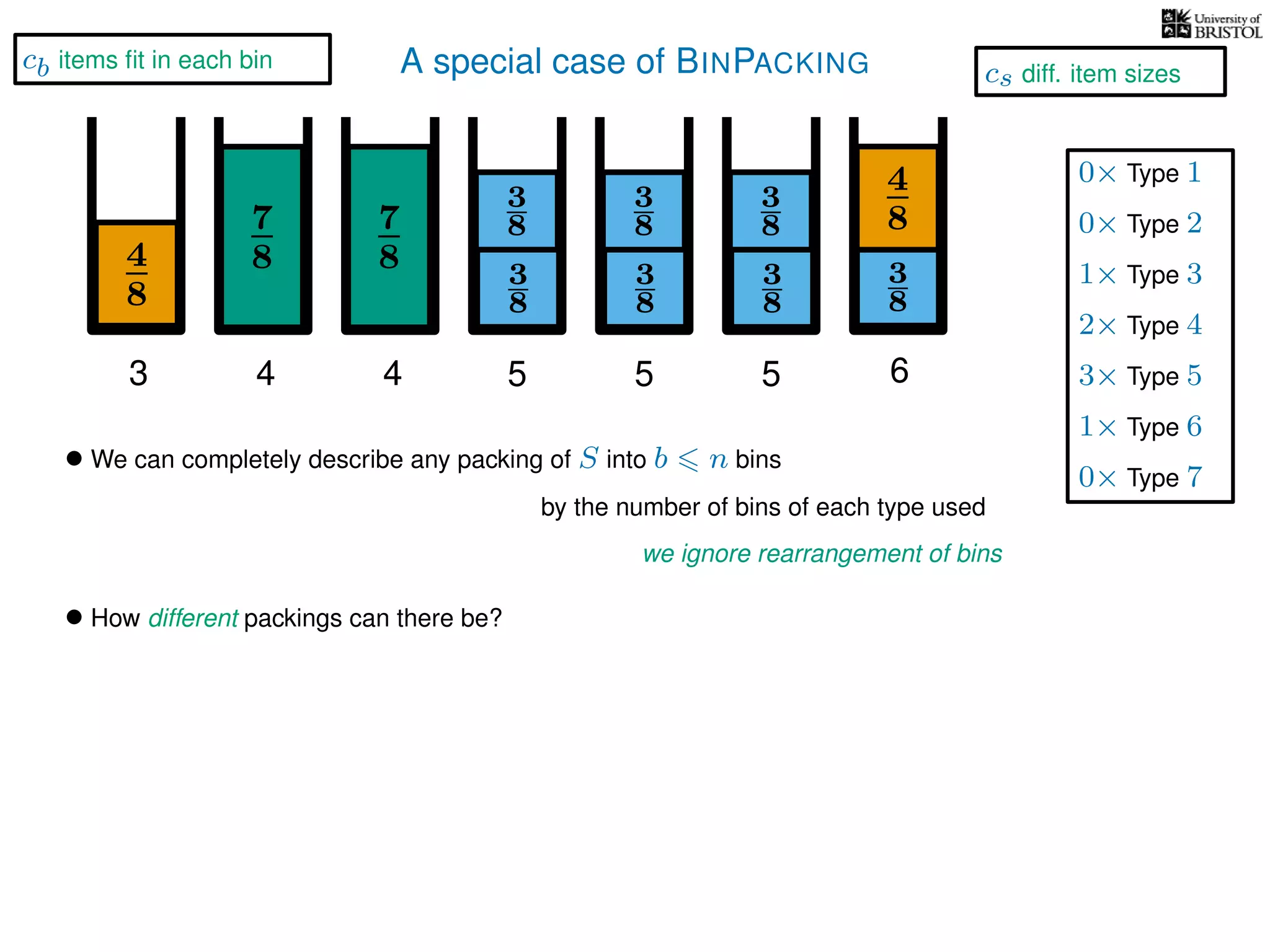
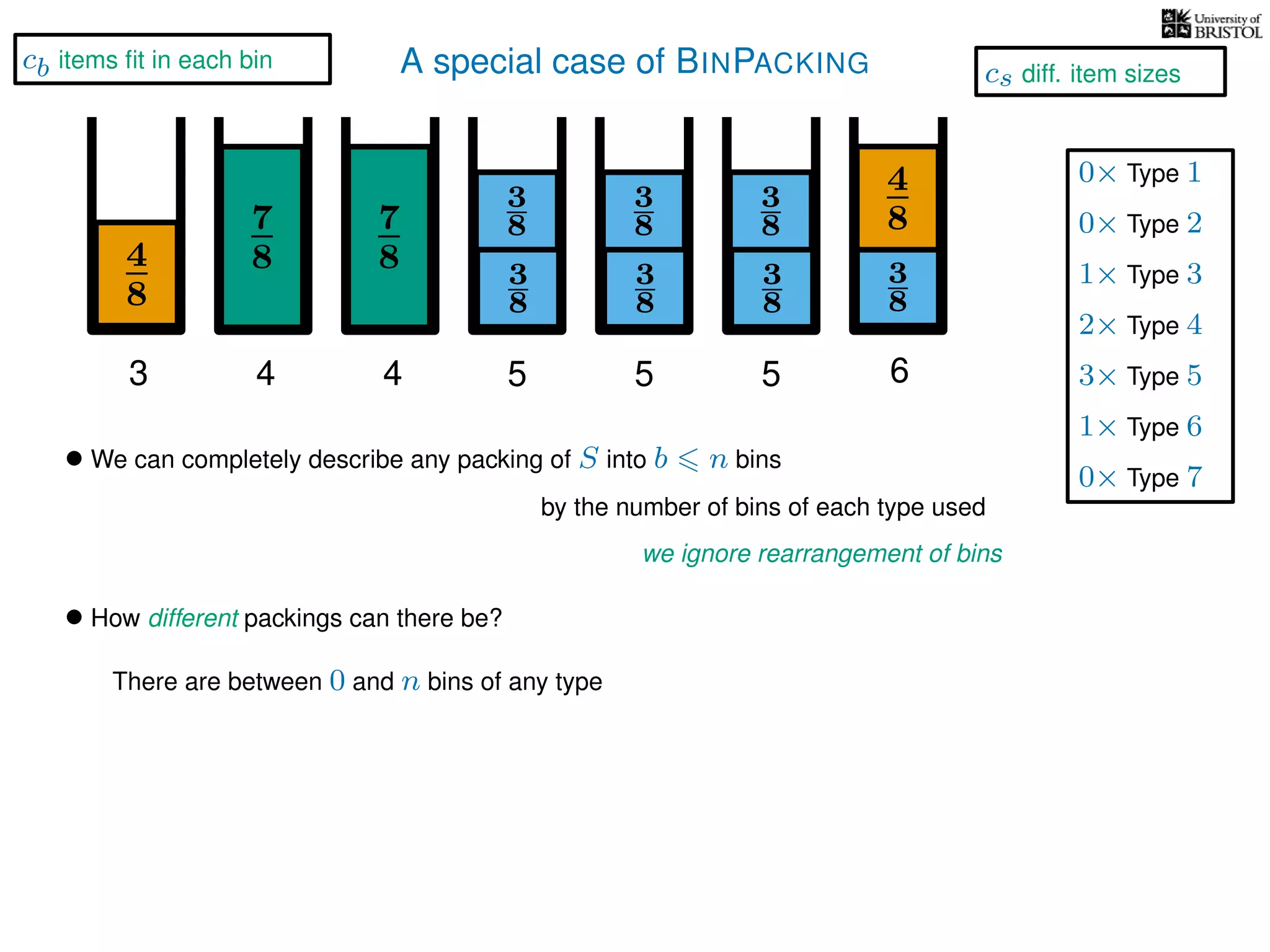
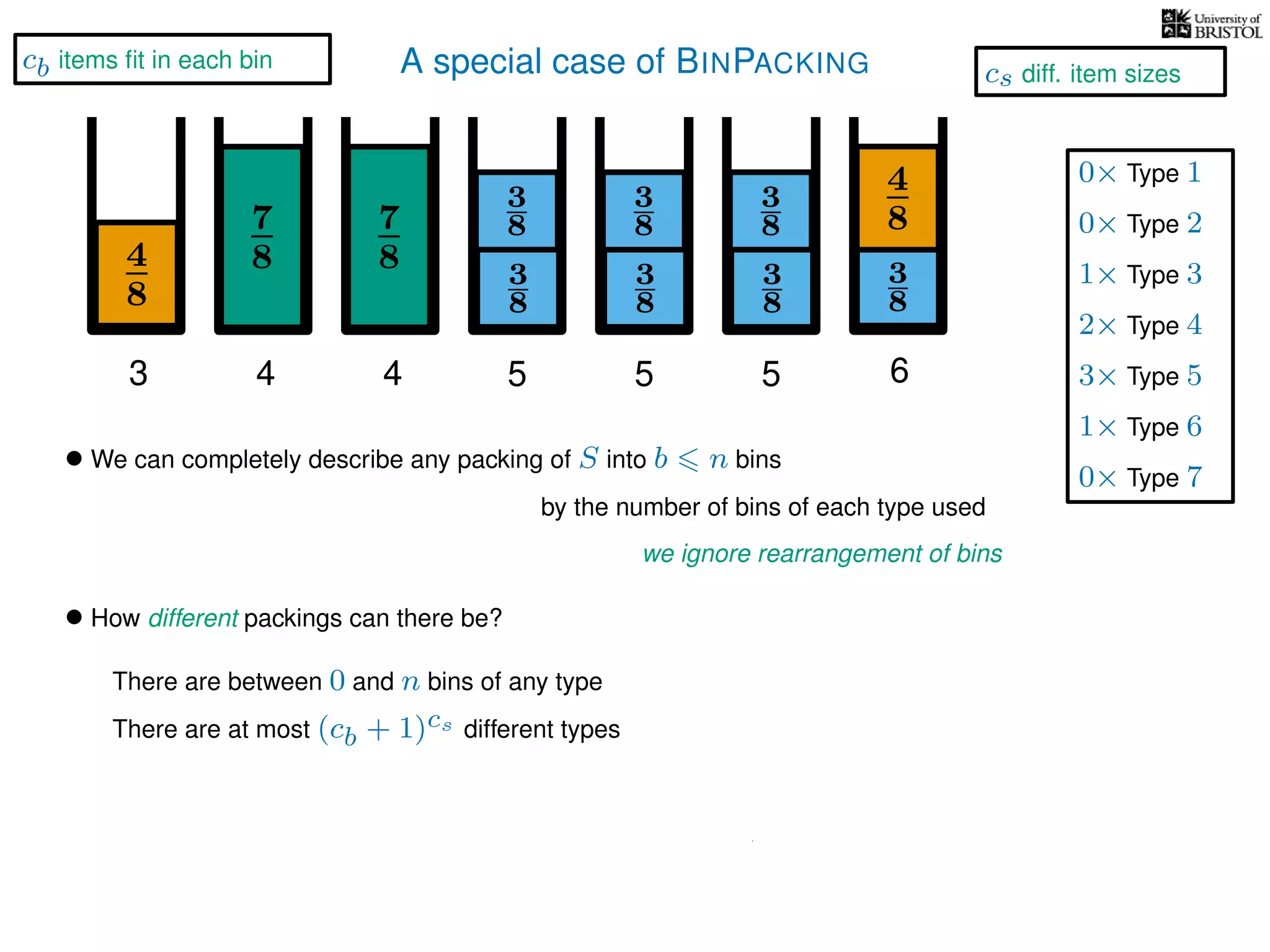
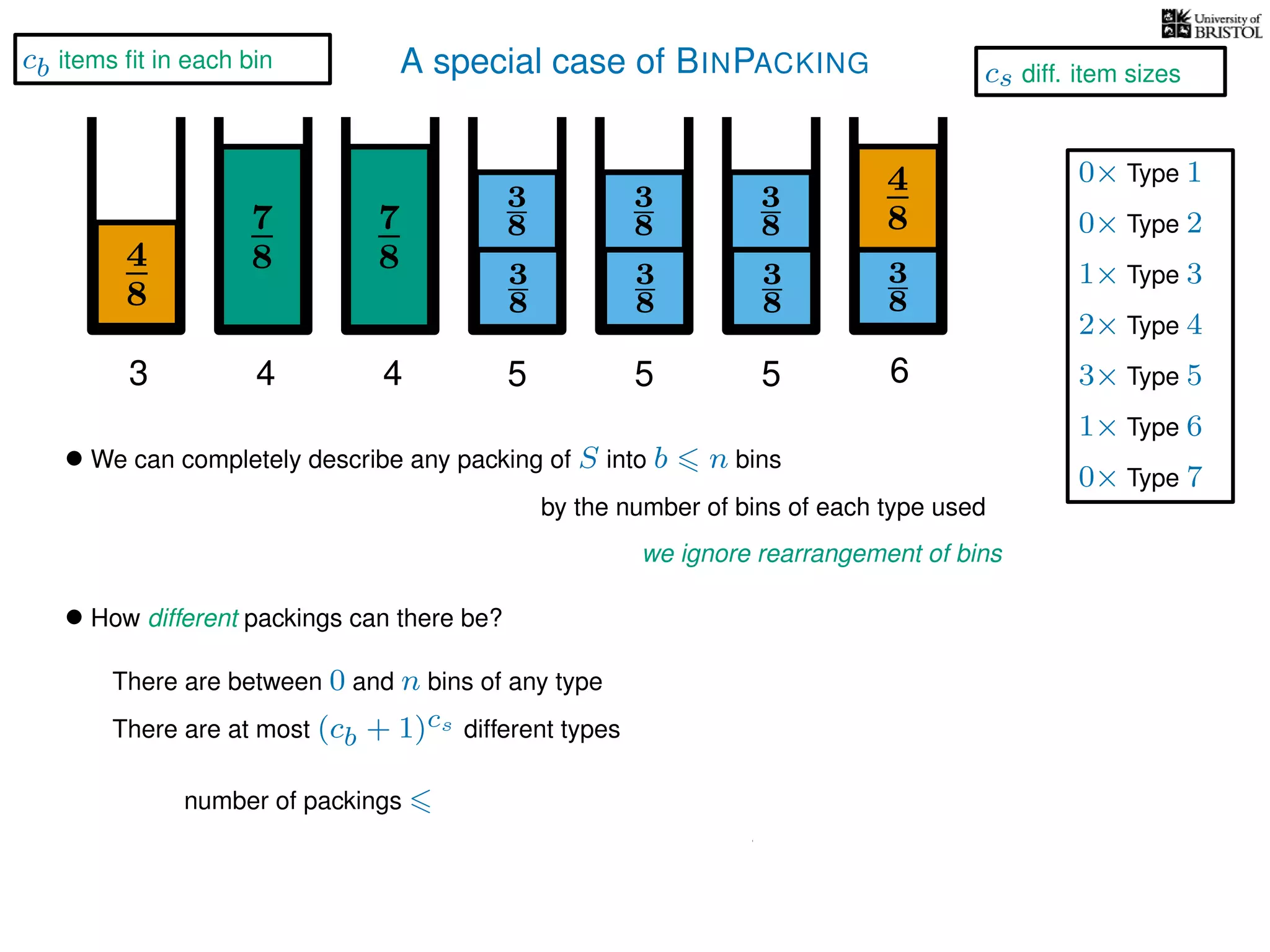
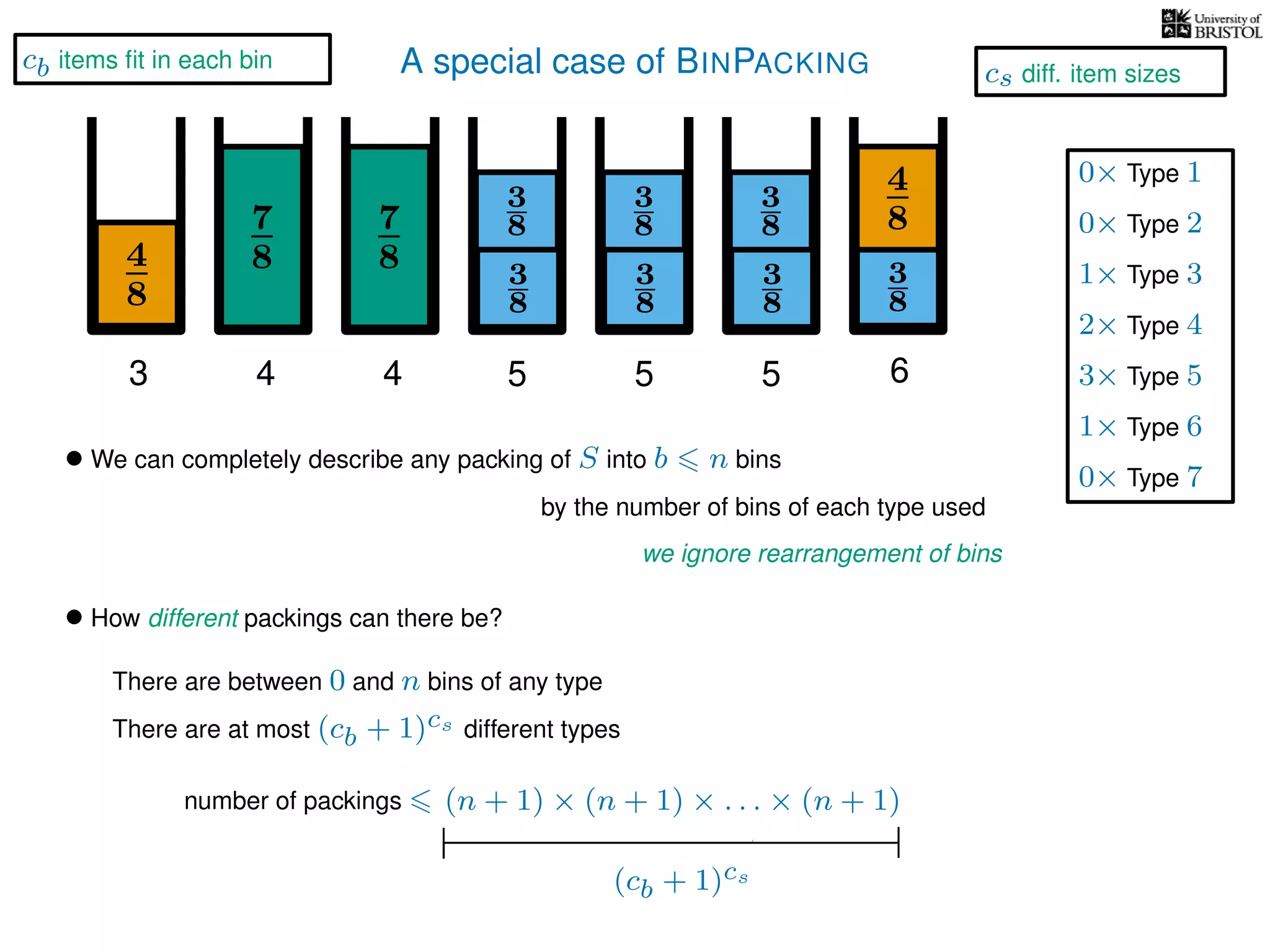
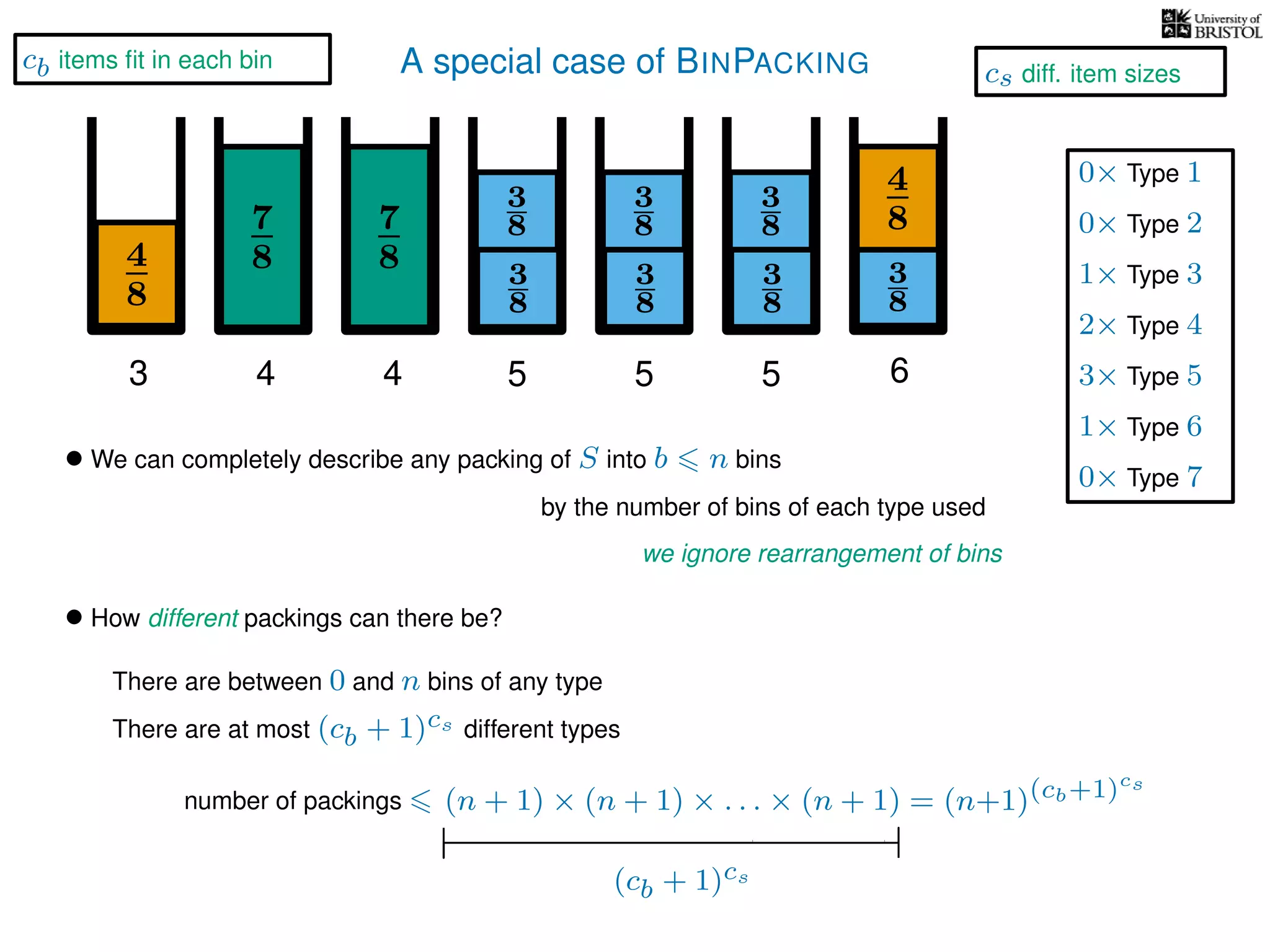
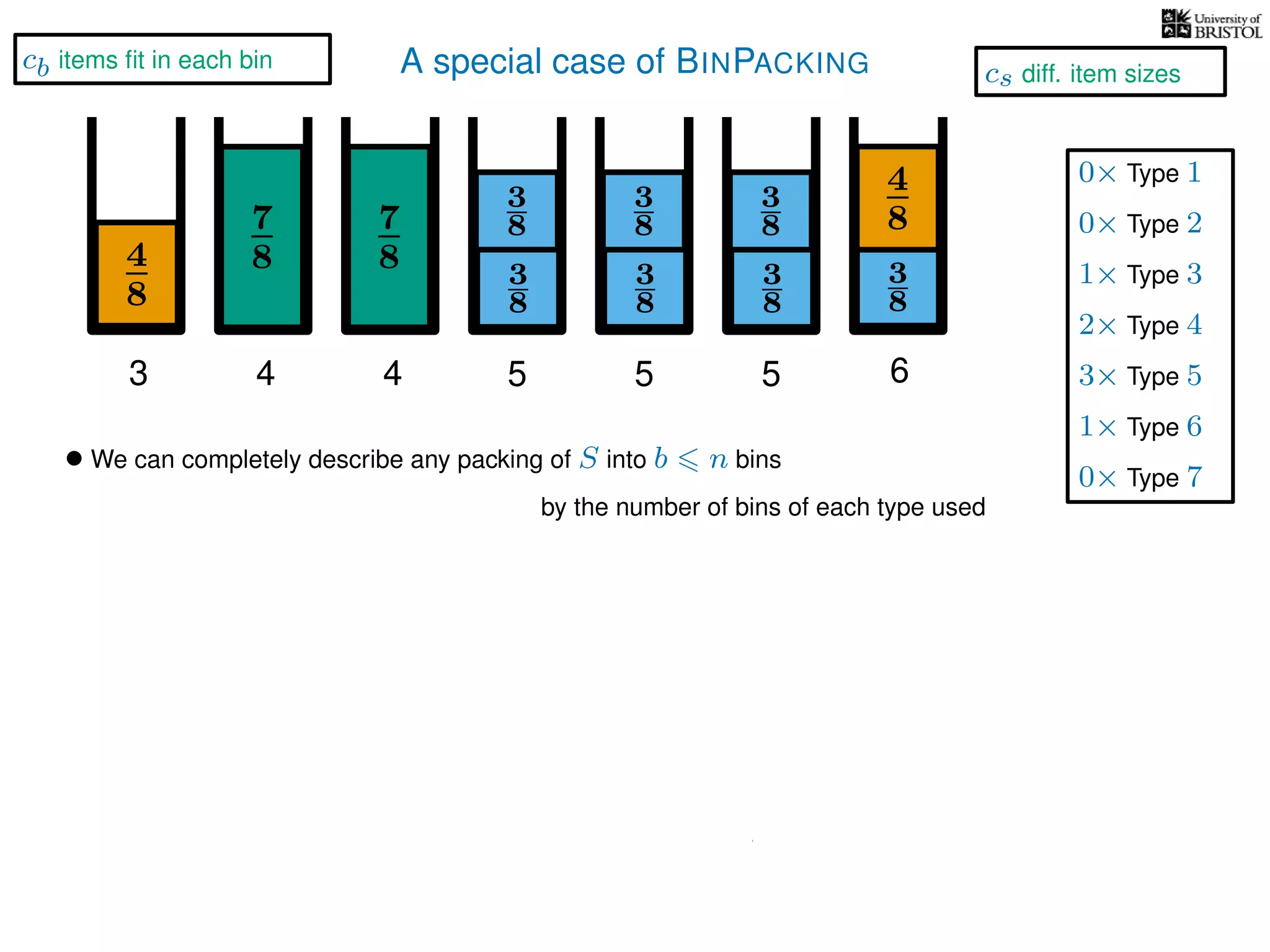
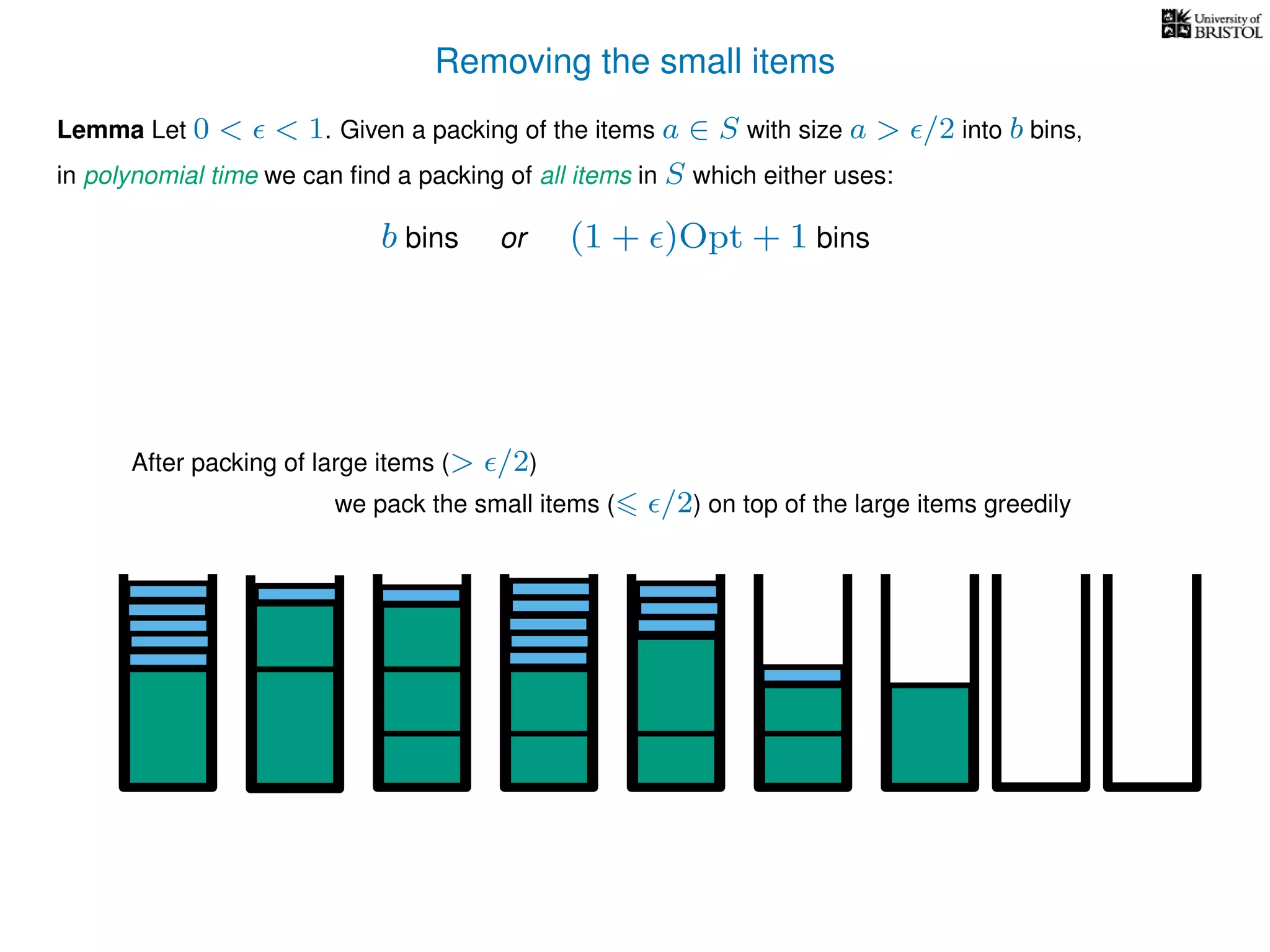
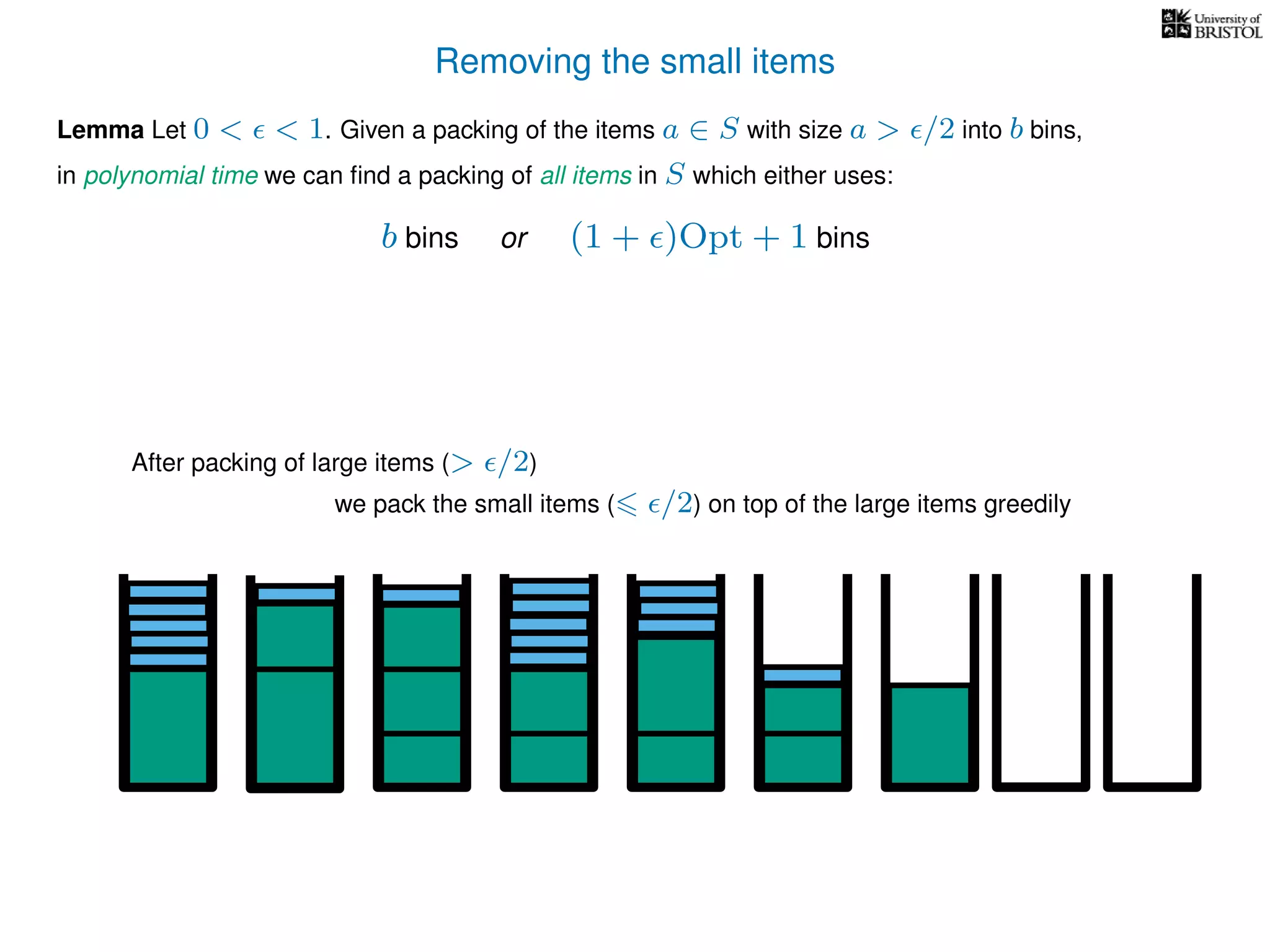
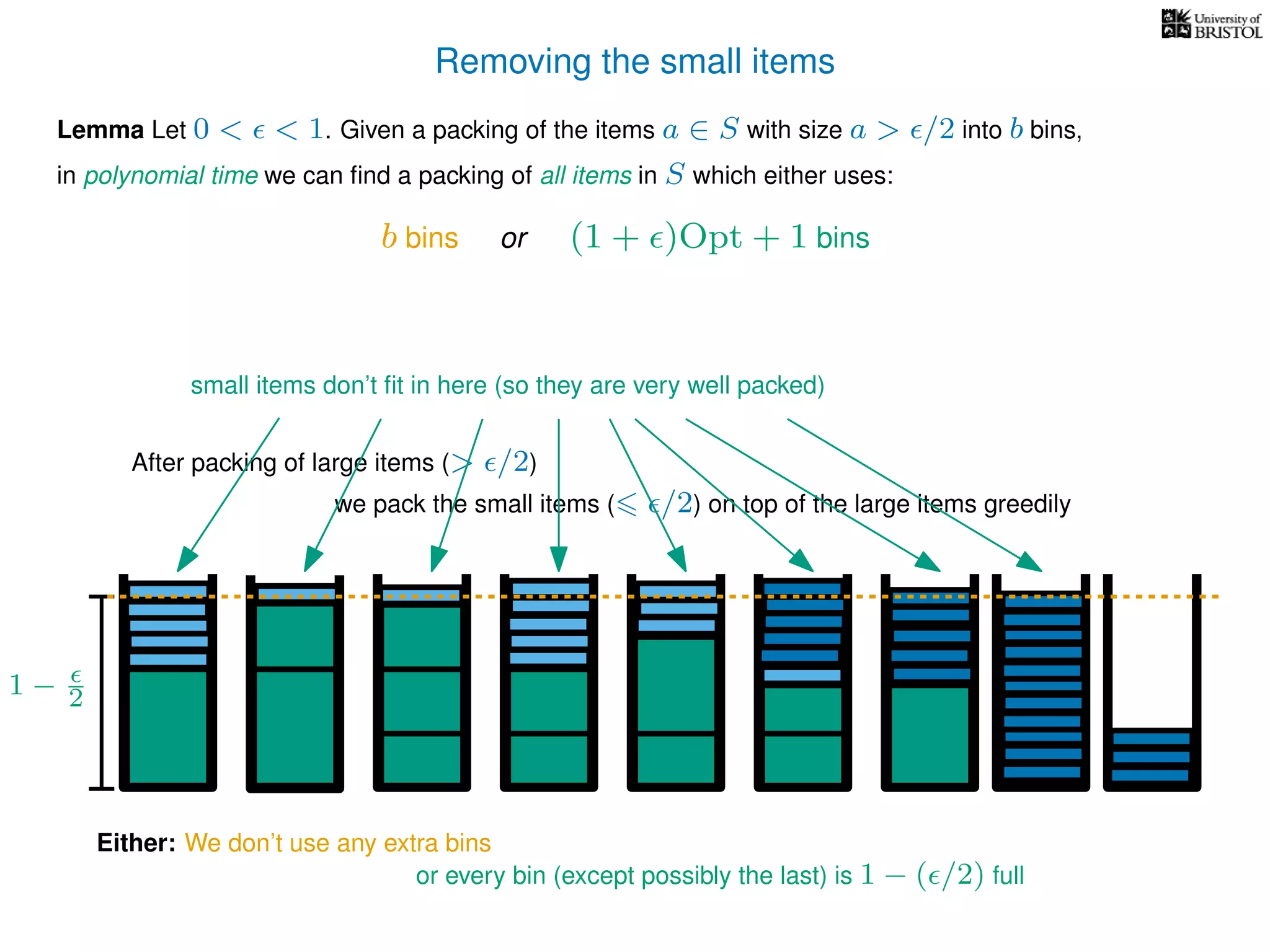
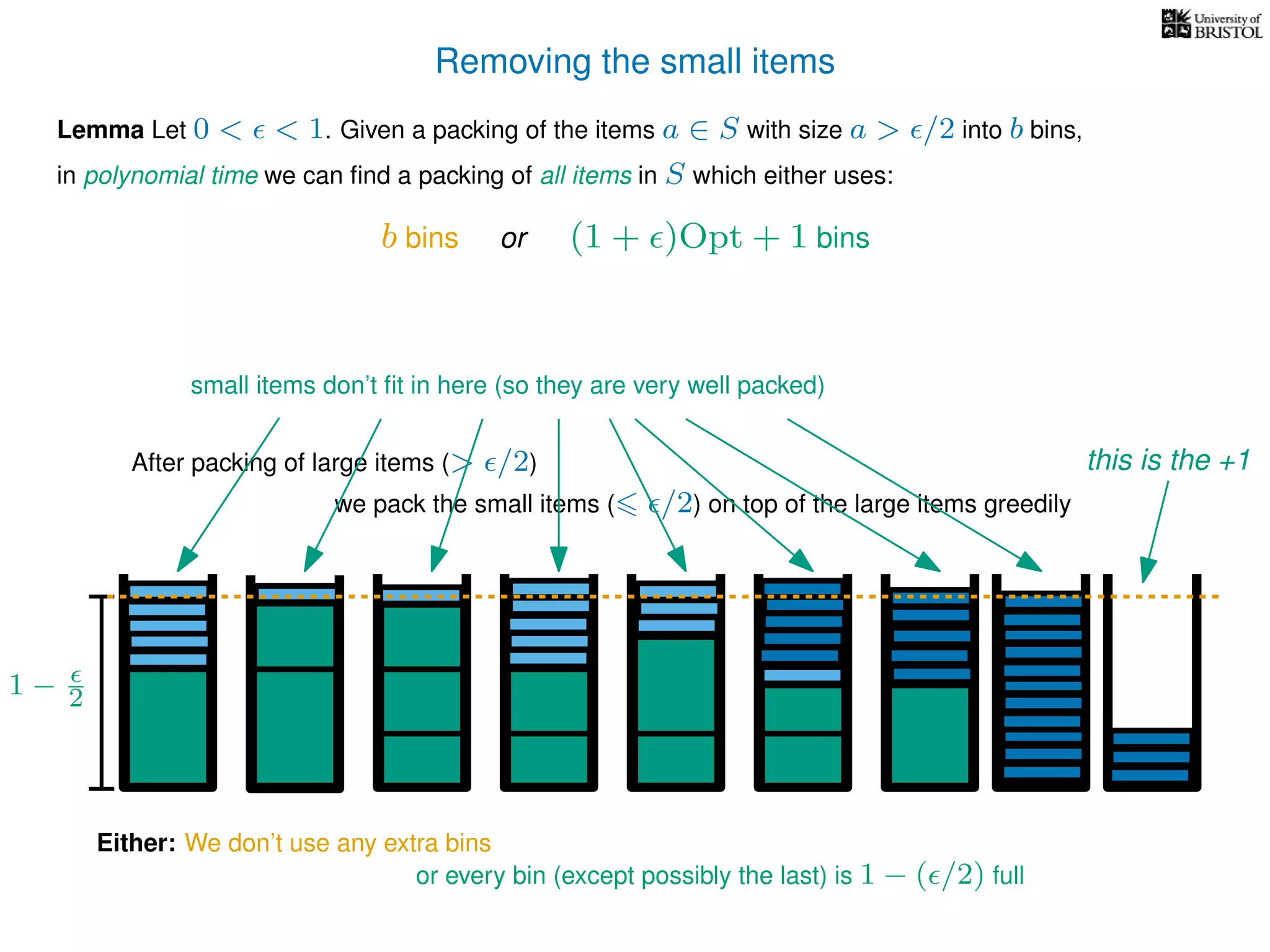
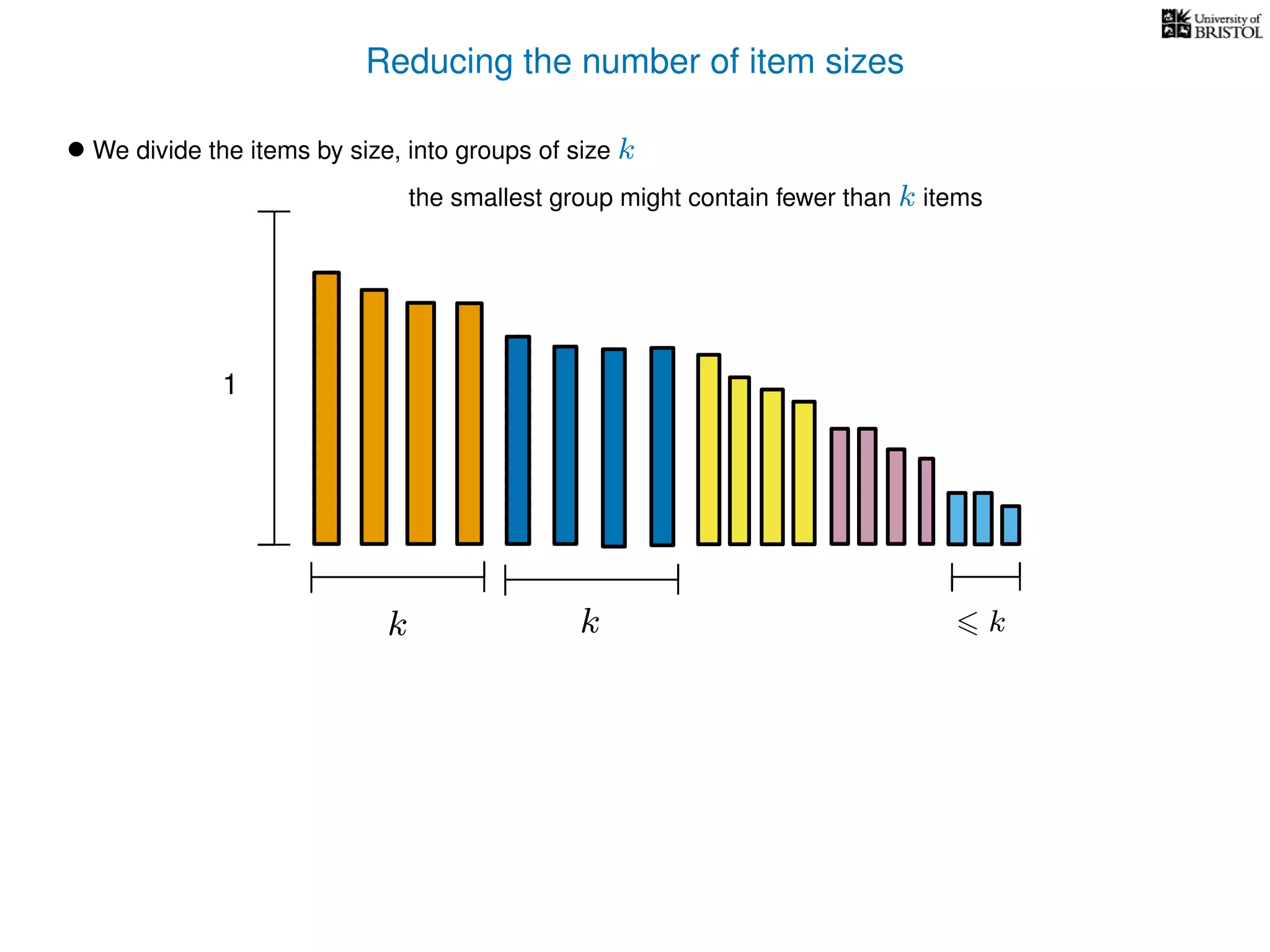
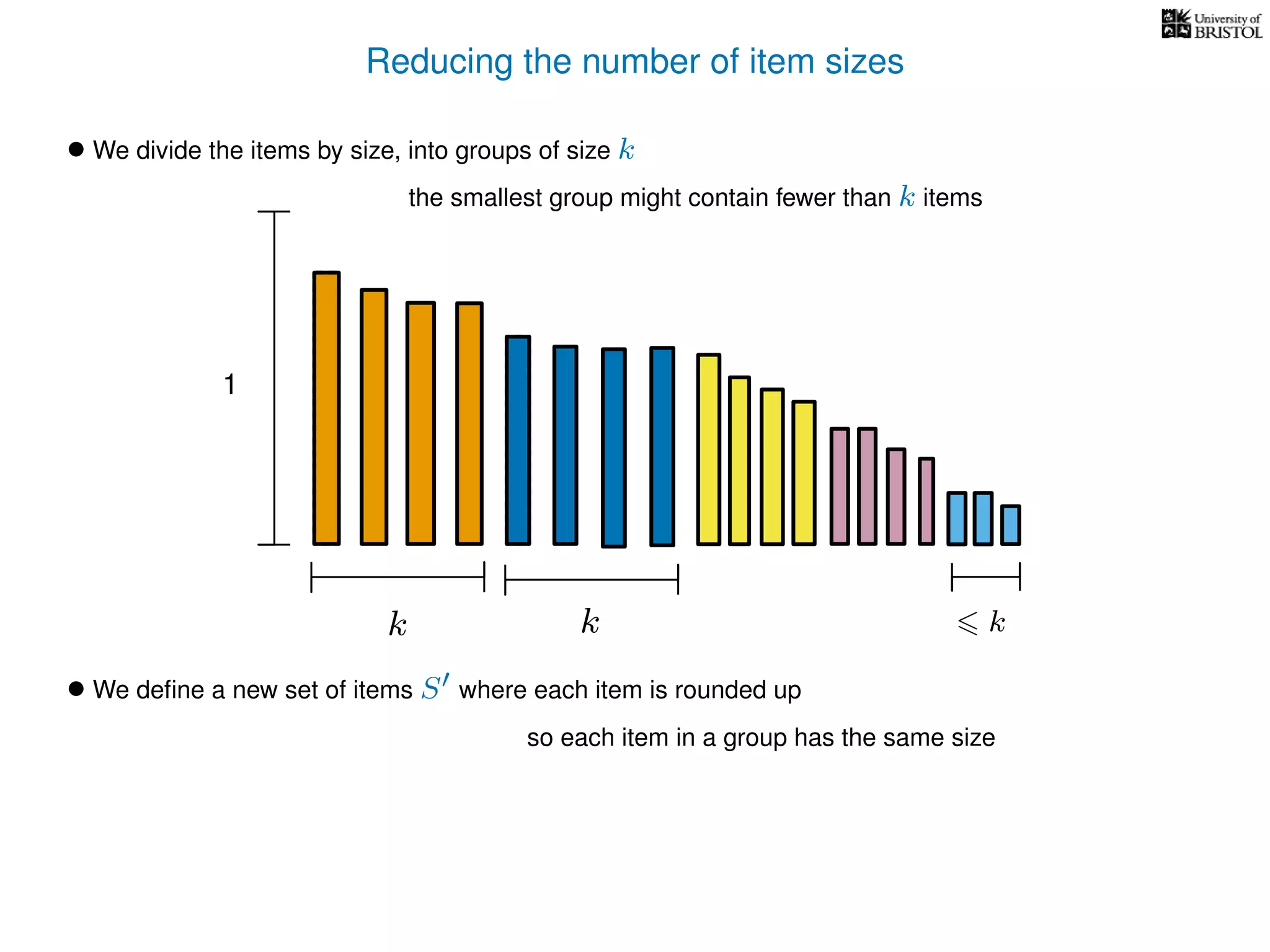
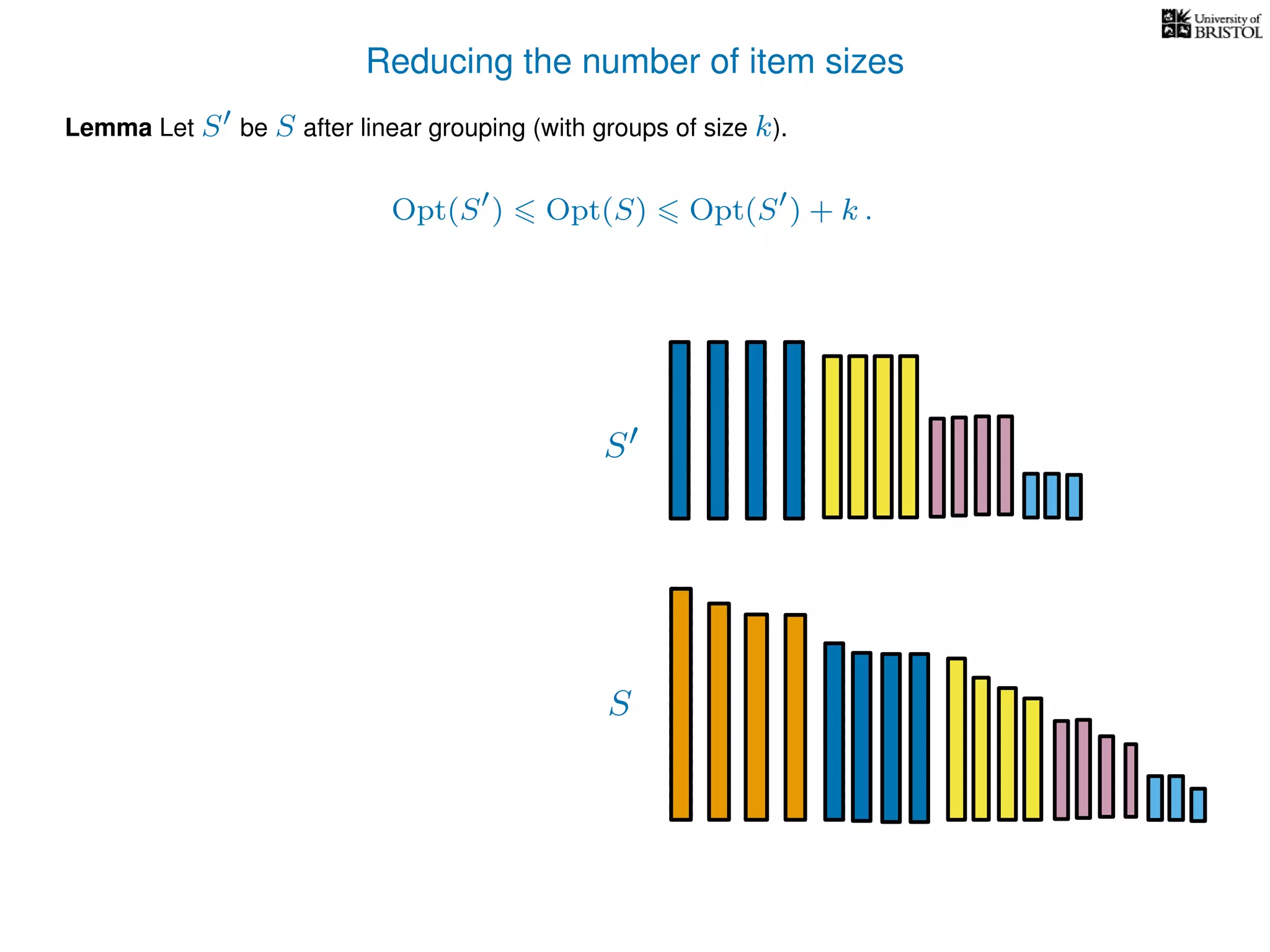
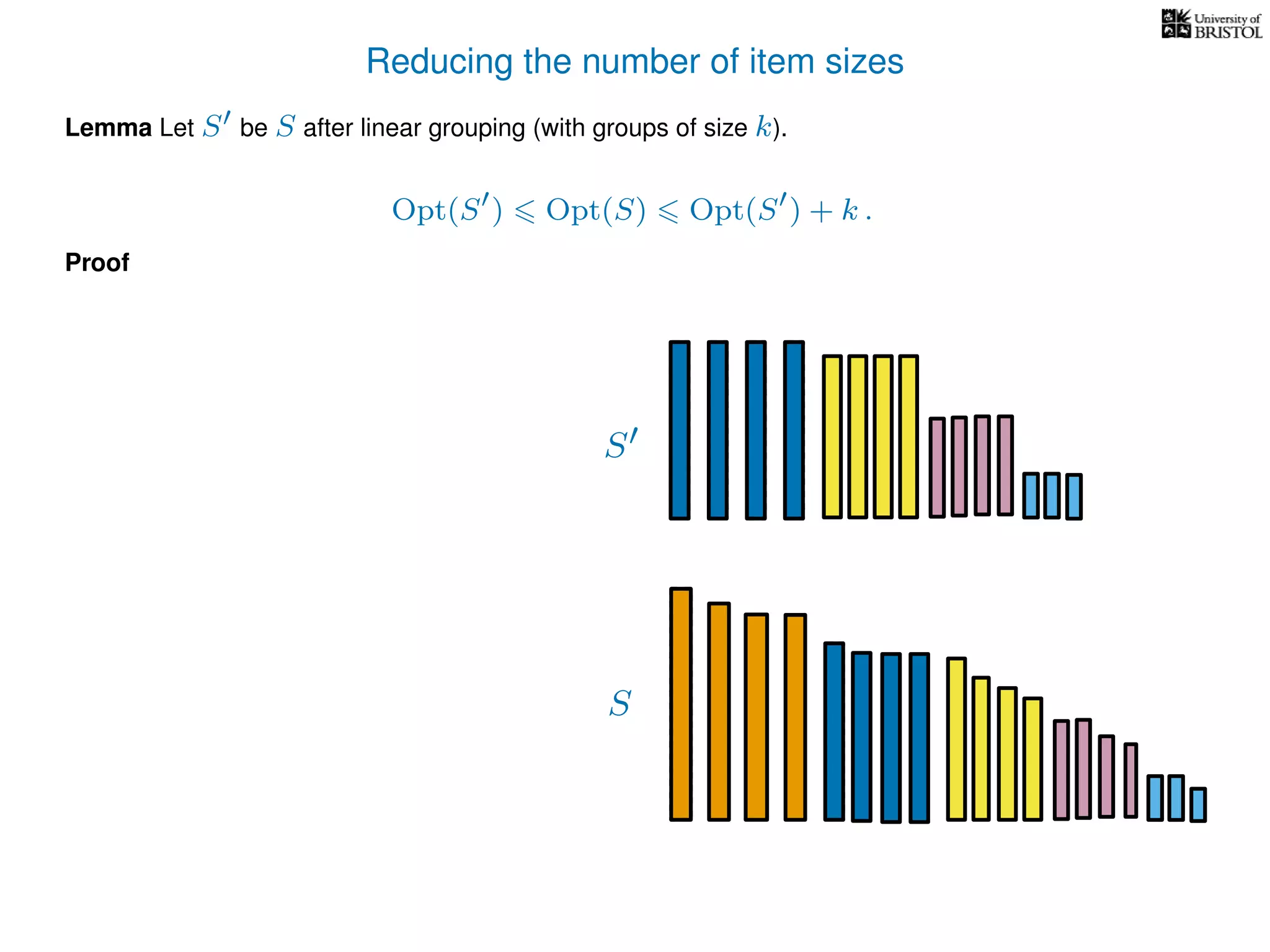
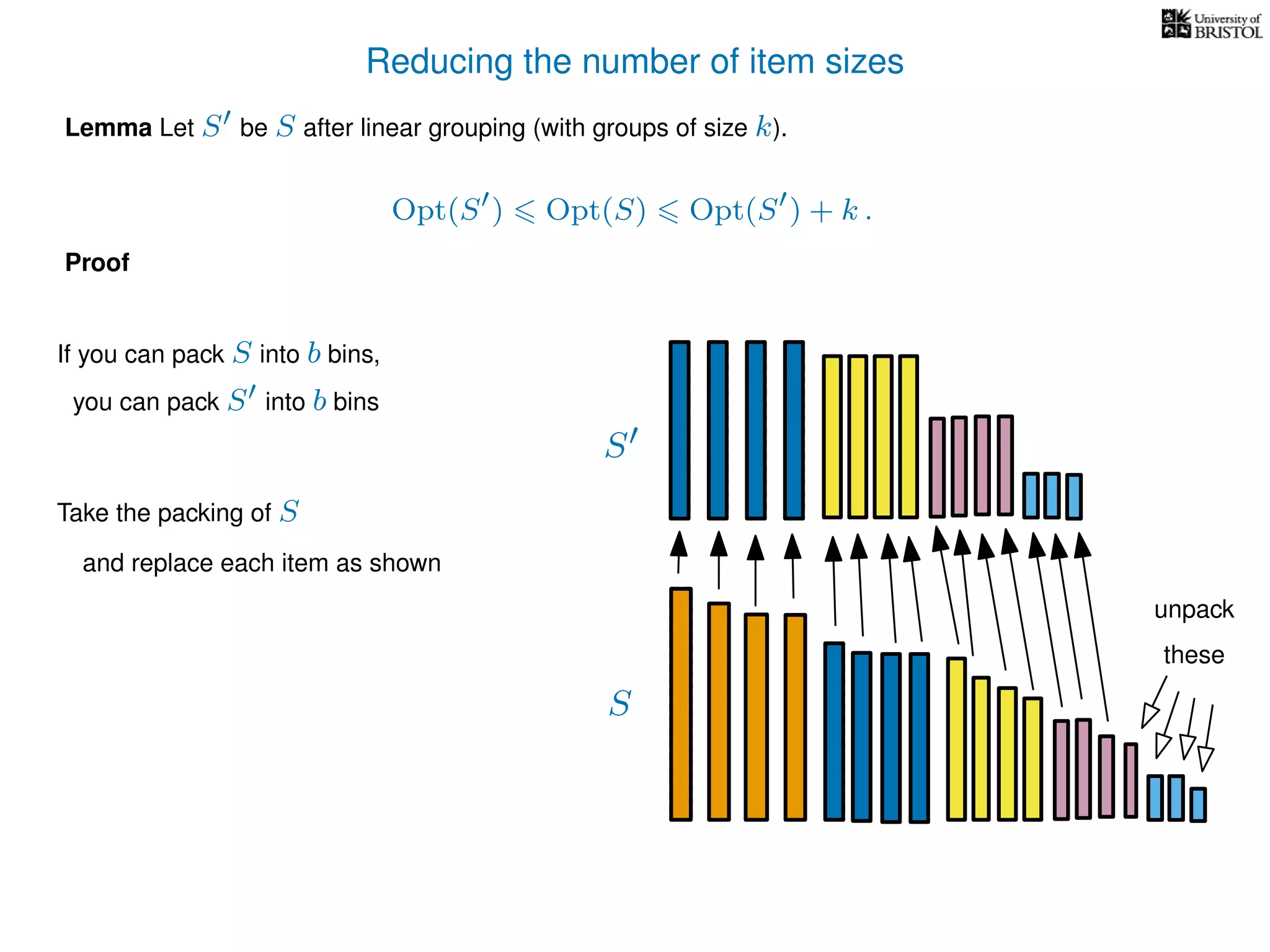
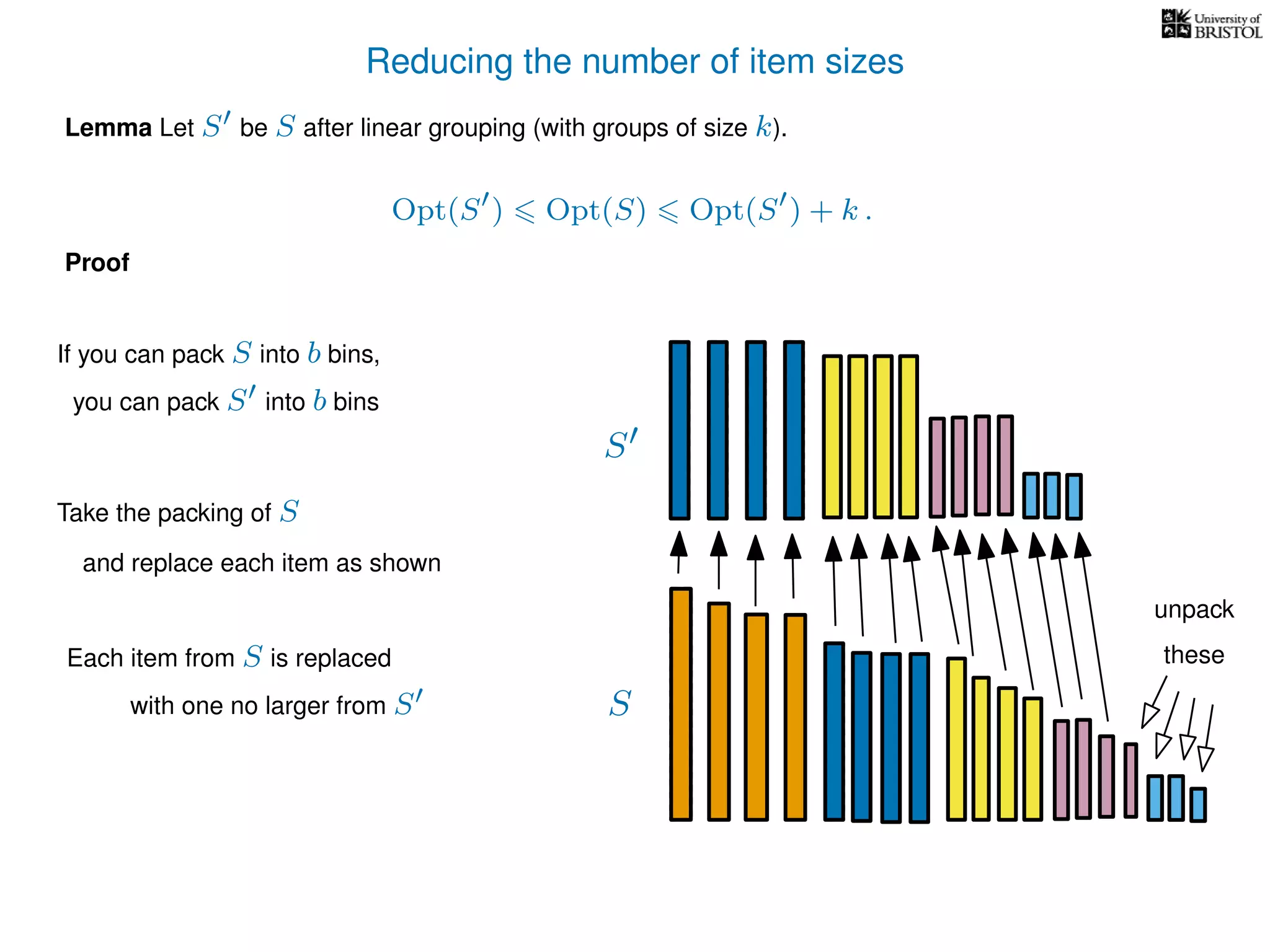
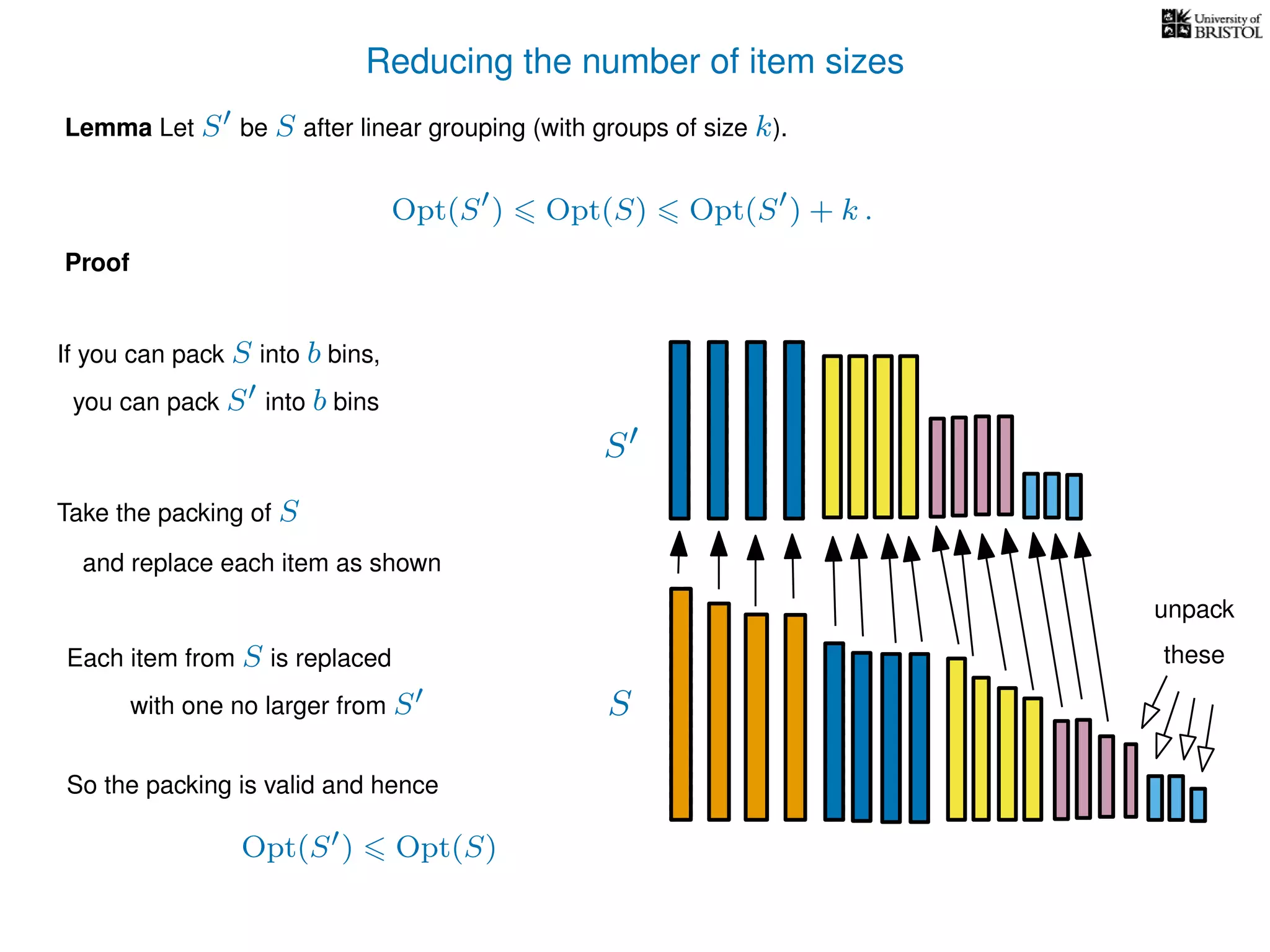
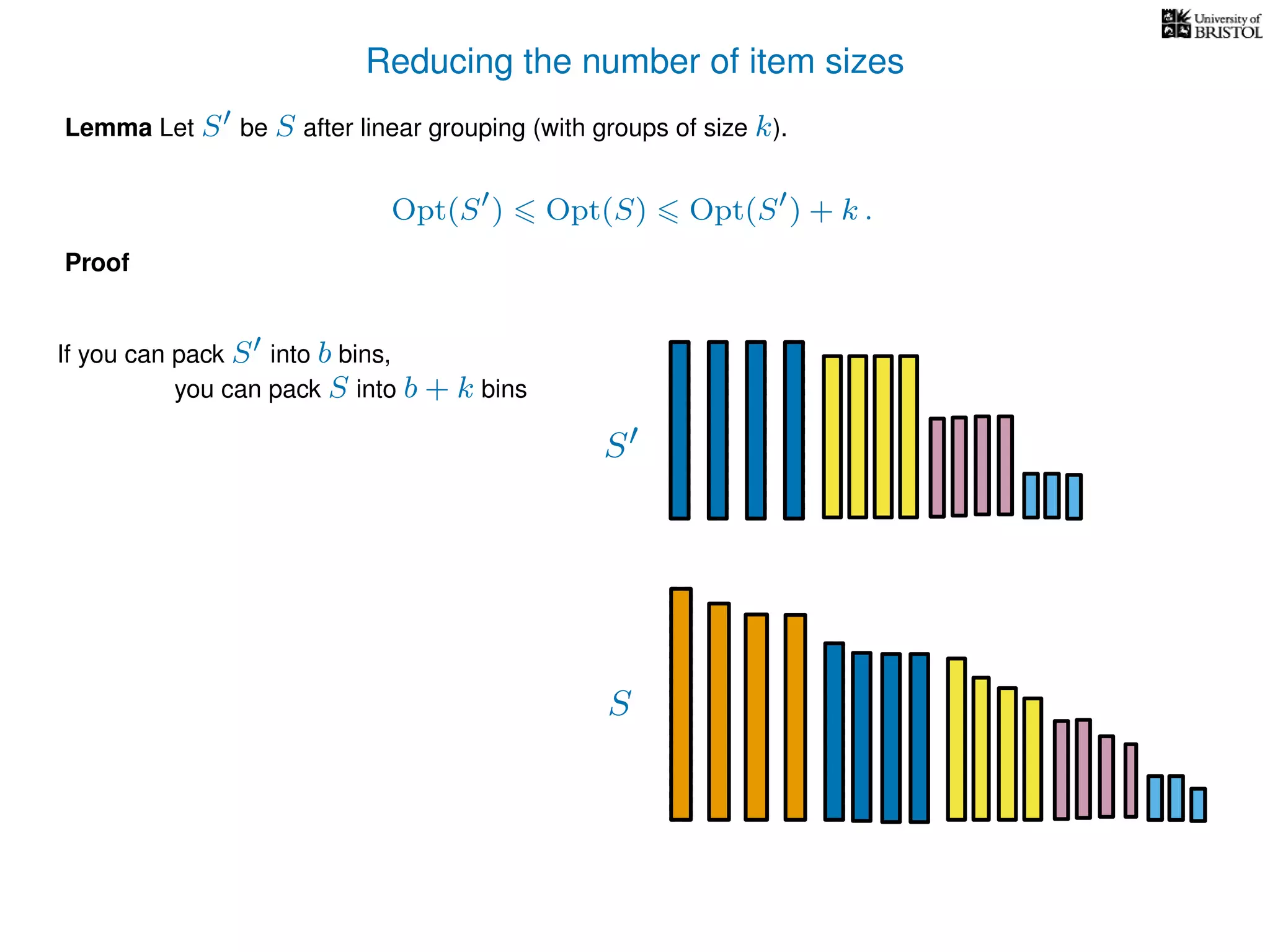
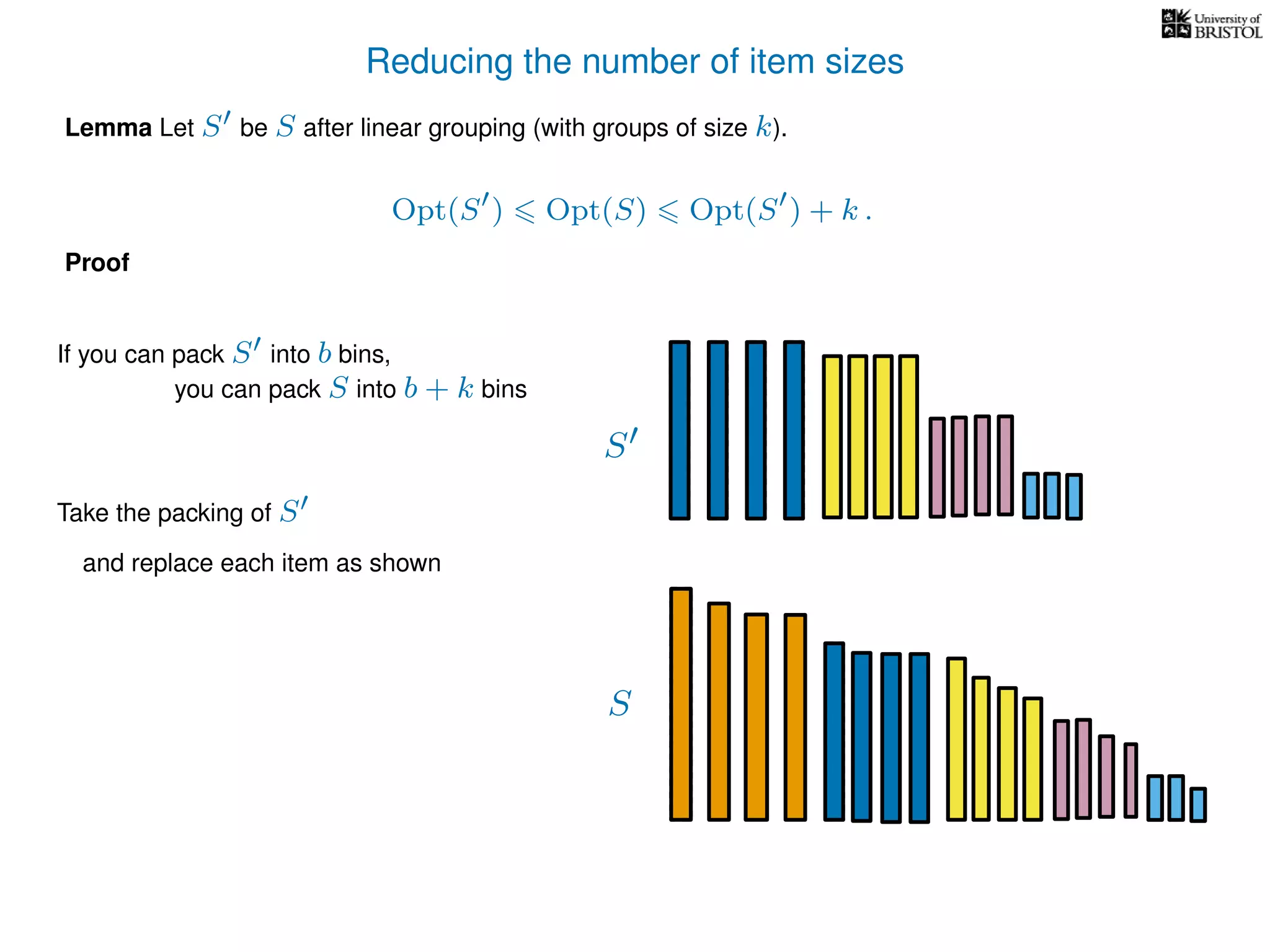
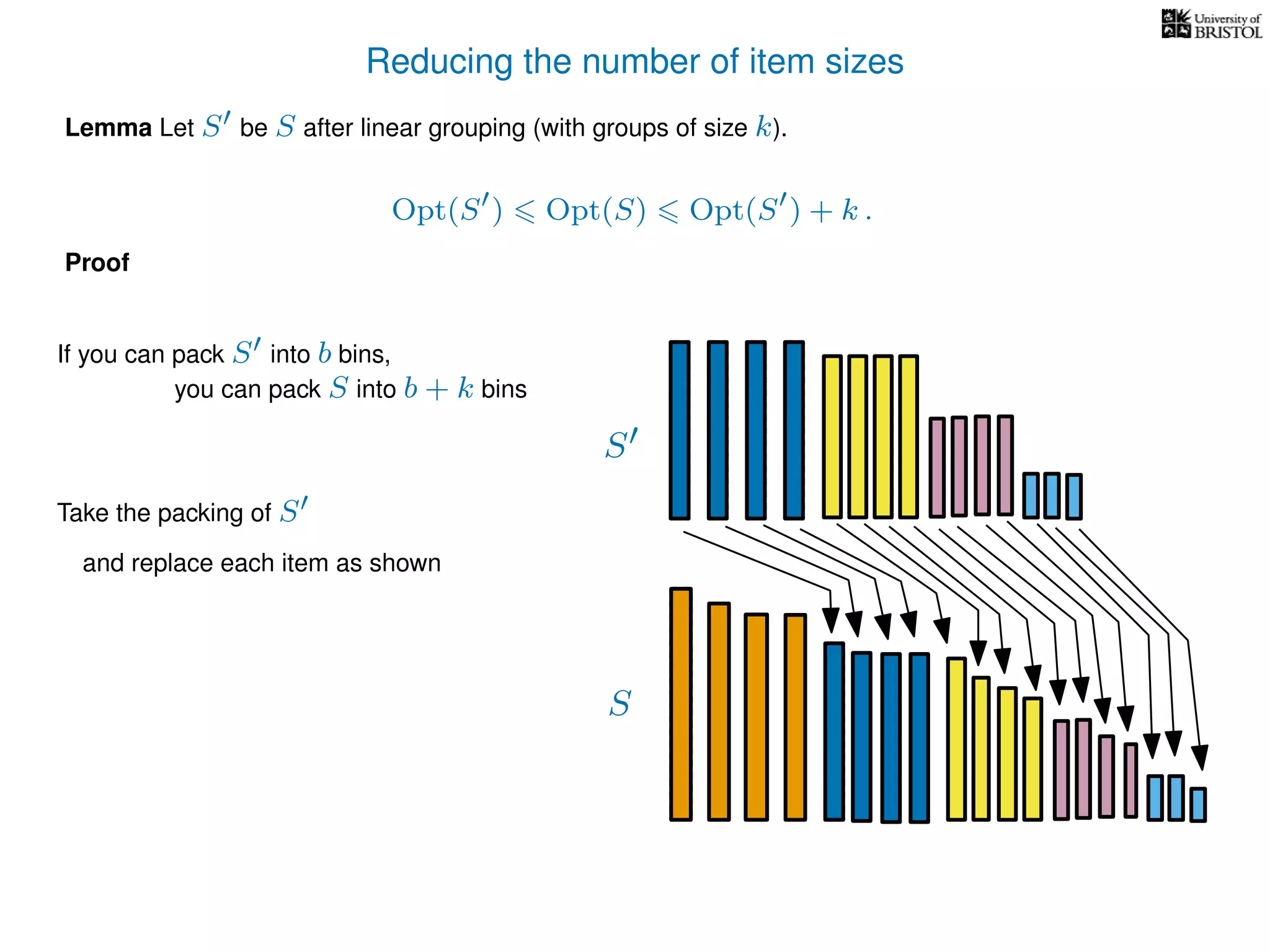
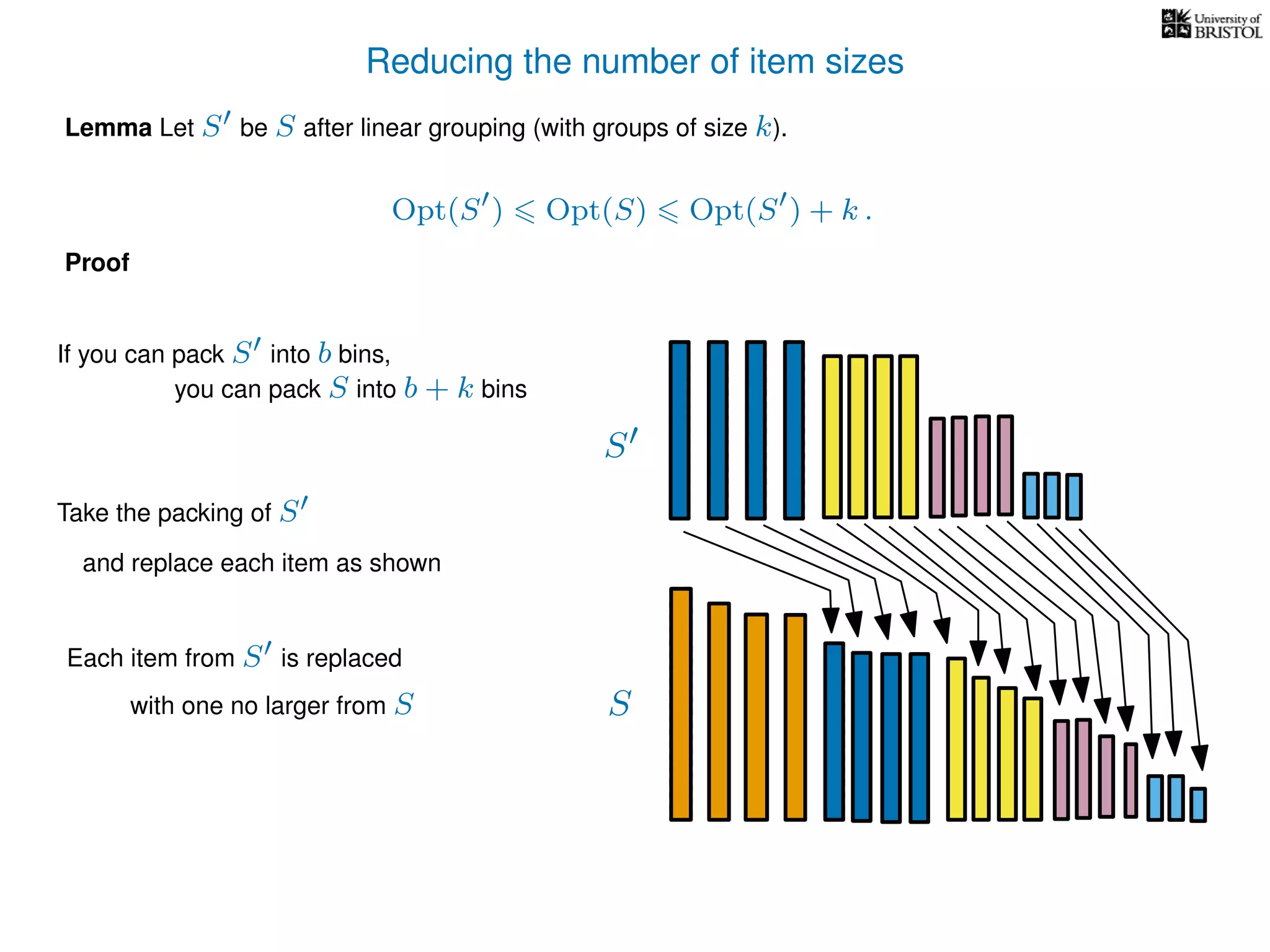
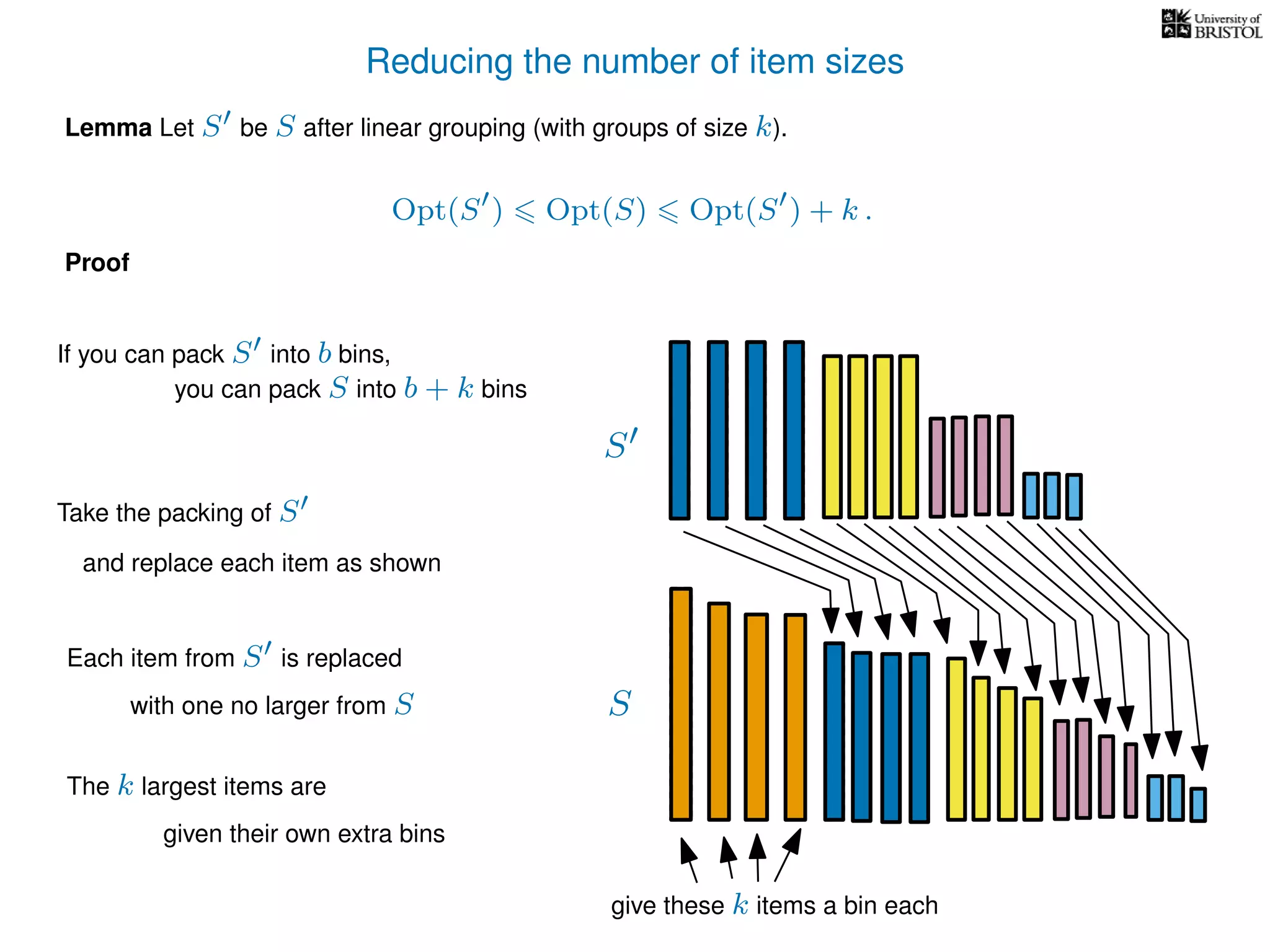
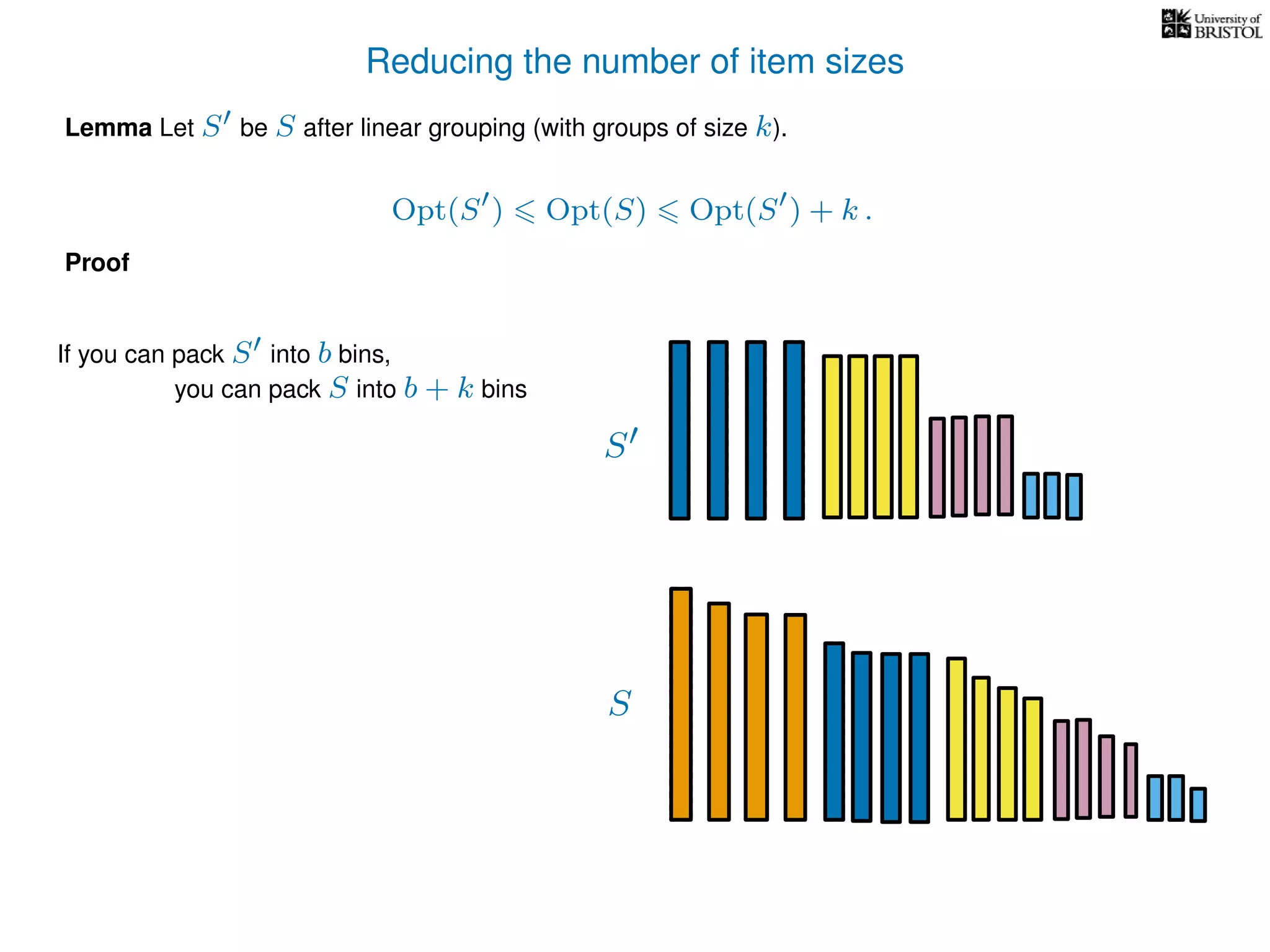
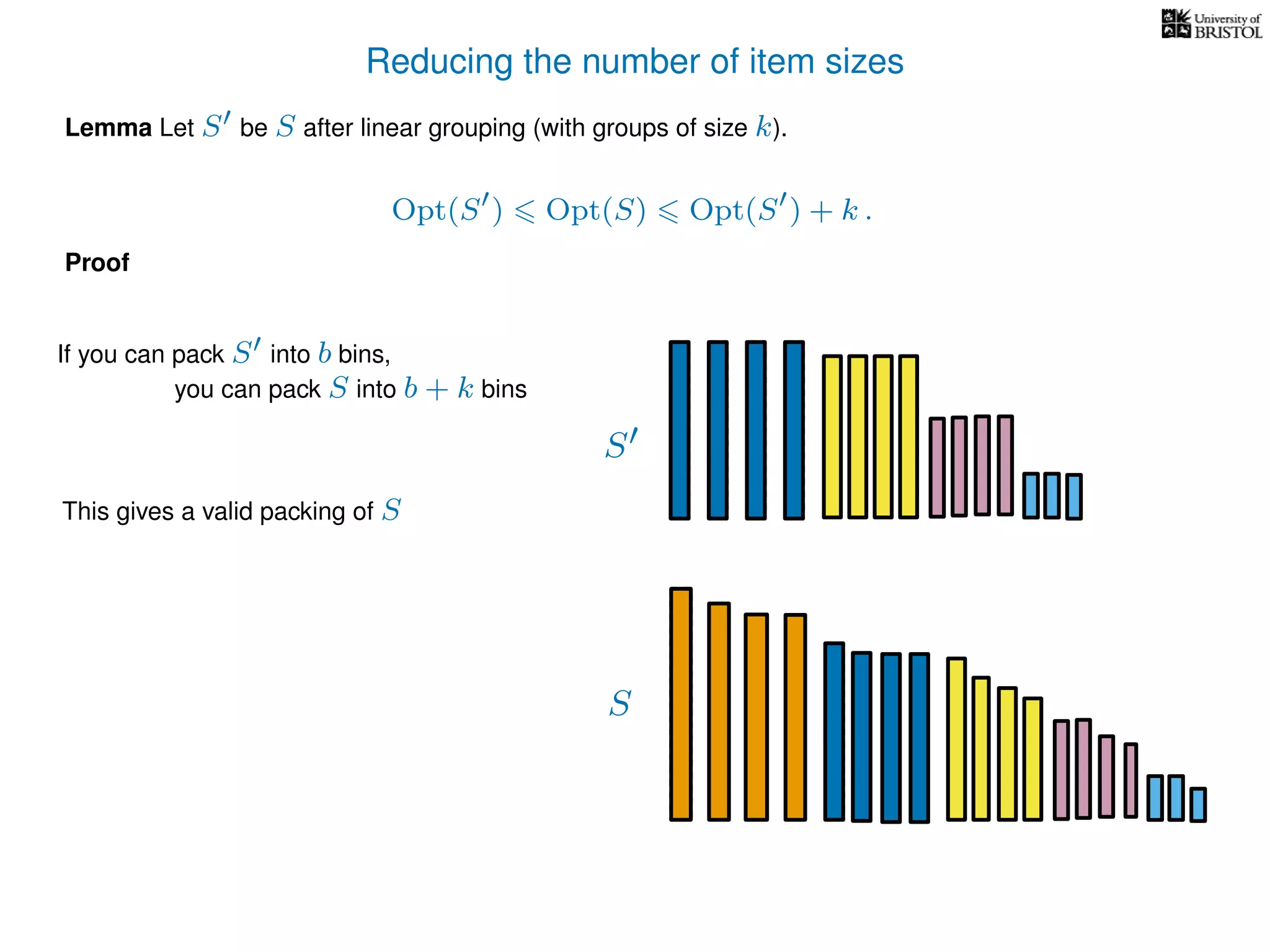
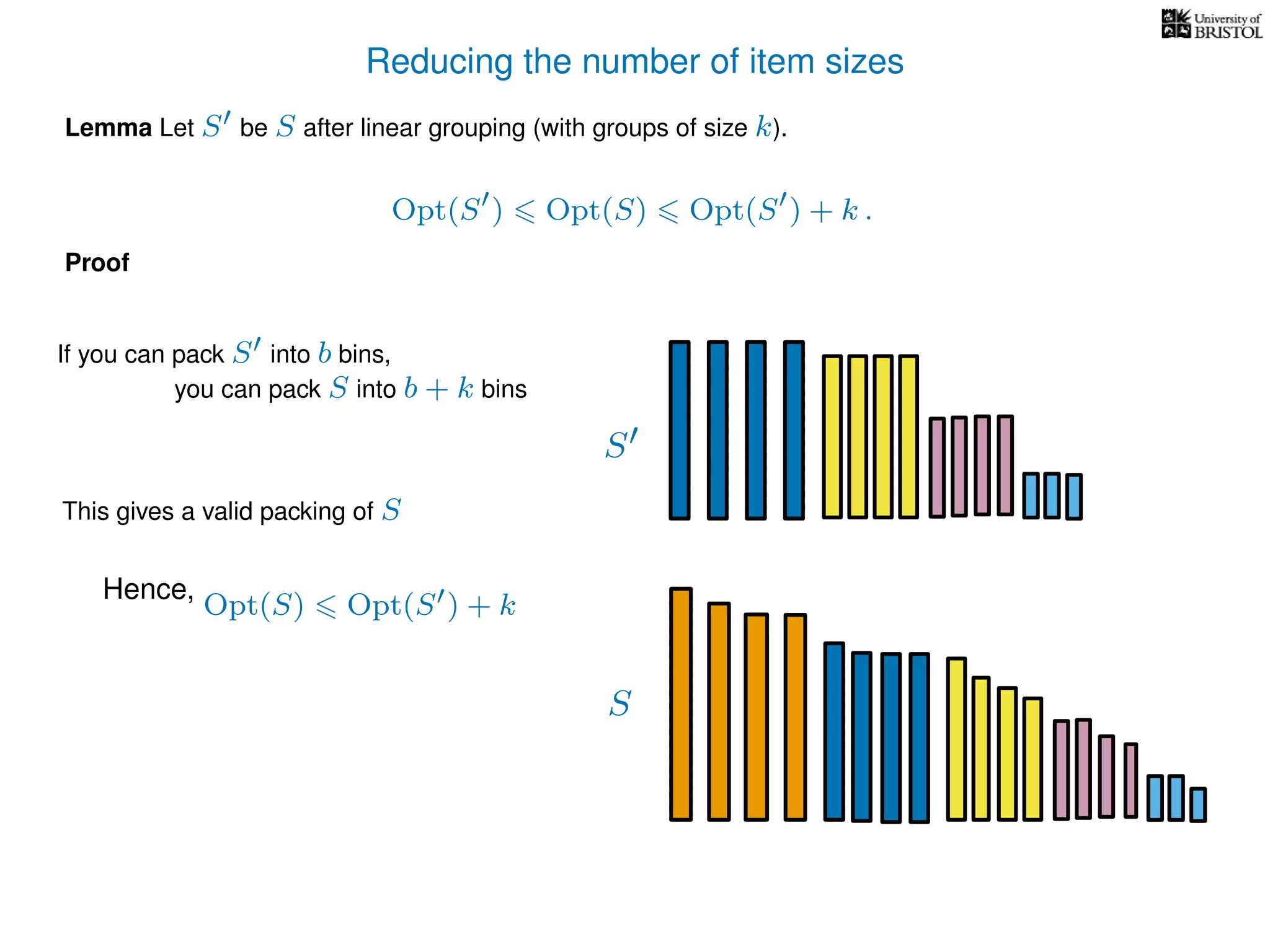
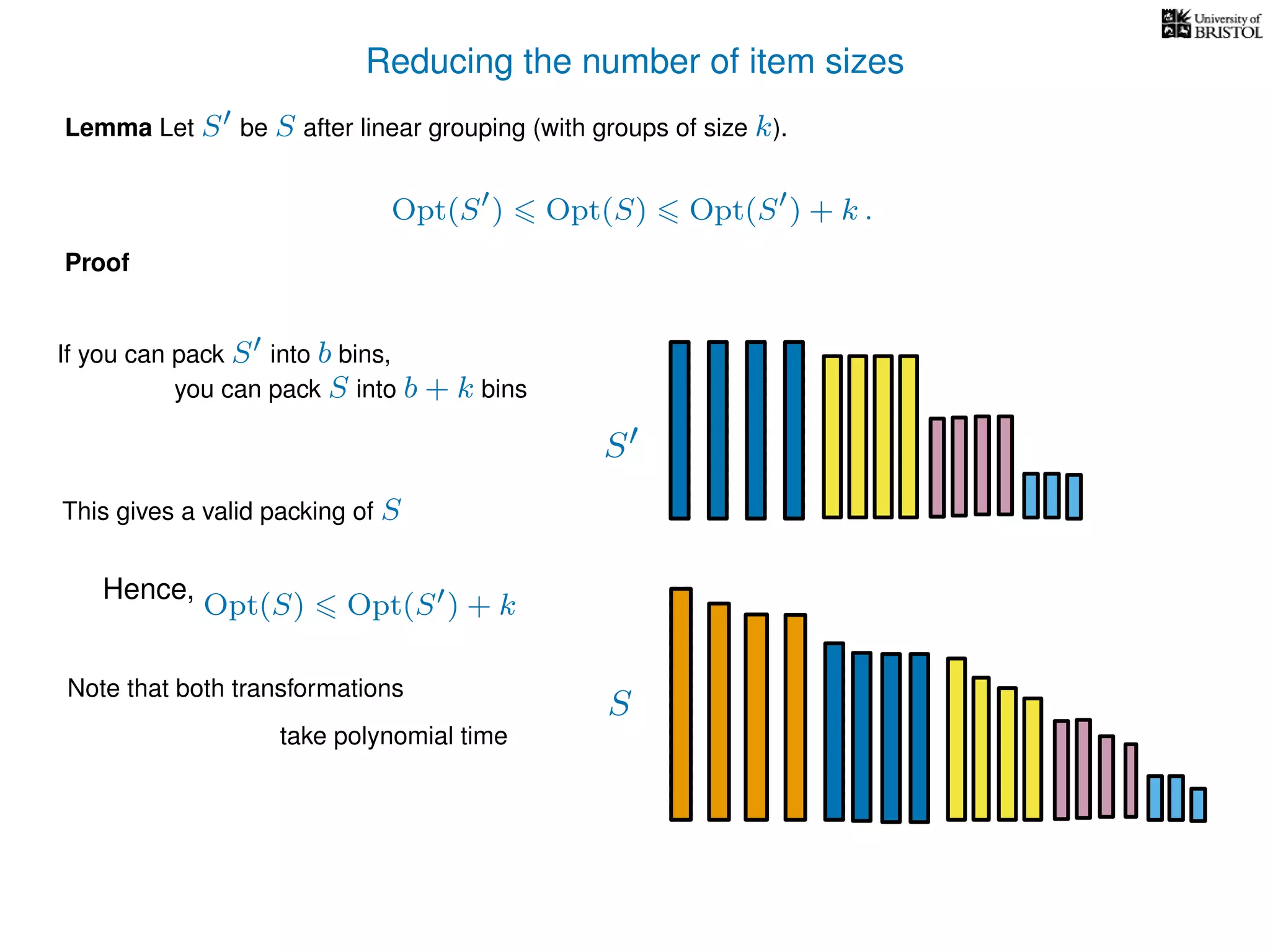
The document discusses approximation algorithms, particularly focusing on polynomial time approximation schemes (PTAS) and fully polynomial time approximation schemes (FPTAS). It also delves into specific problems like the subset sum and partition problems, defining decision problems related to these and exploring their NP-completeness. Lastly, it addresses the nuances of approximation guarantees and the implications of achieving better than 3/2 approximations in relation to whether P equals NP.