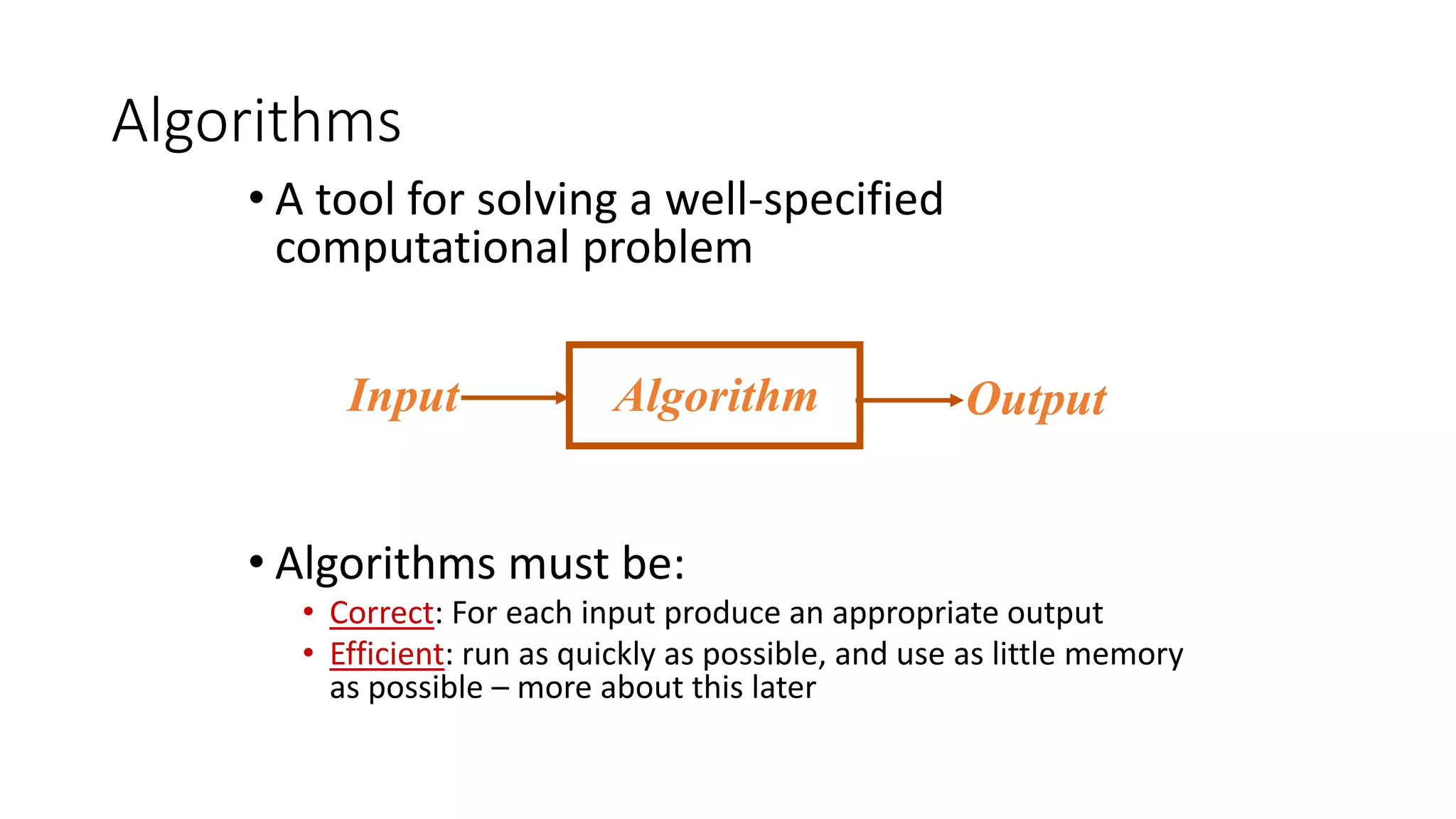
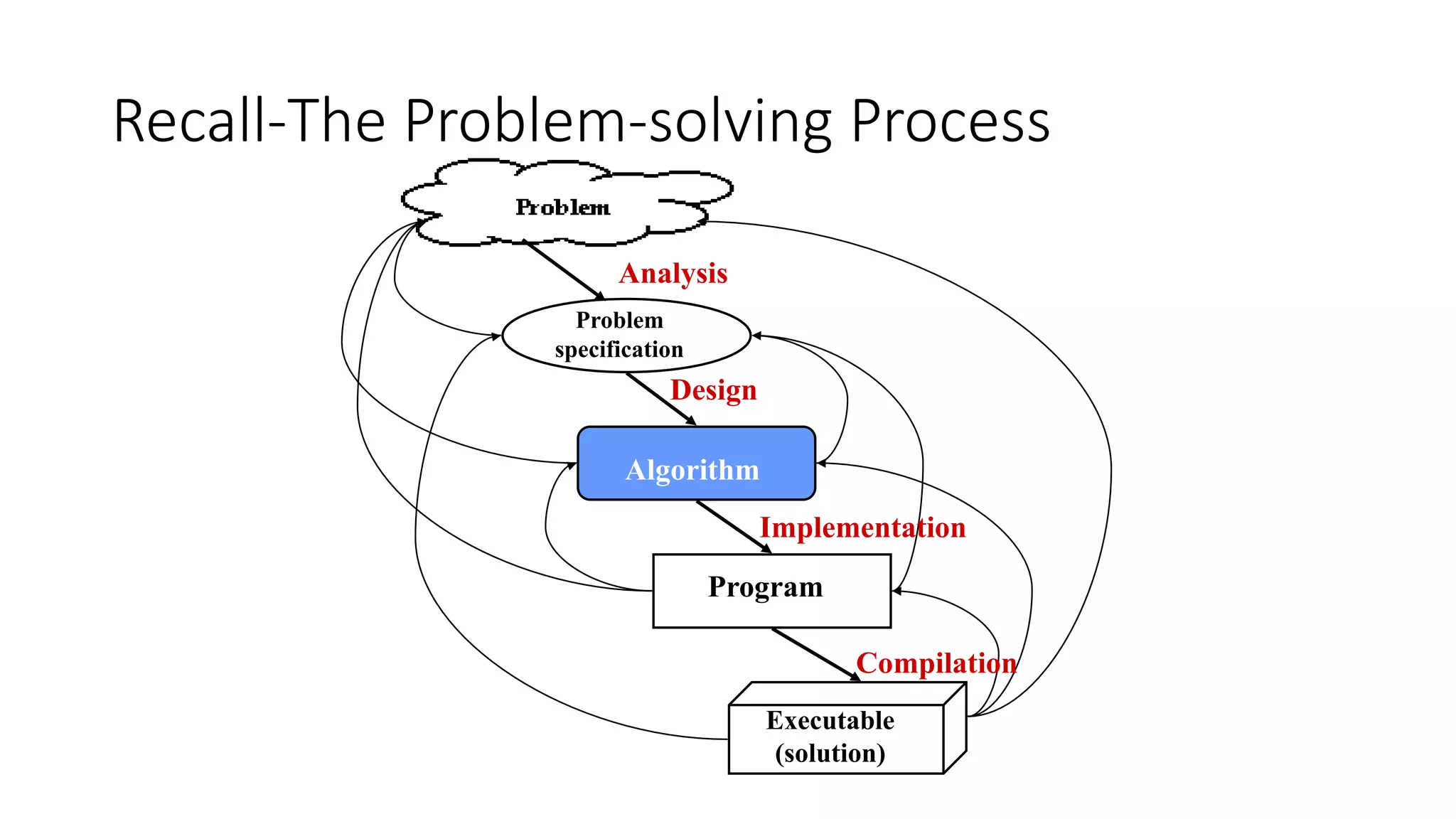
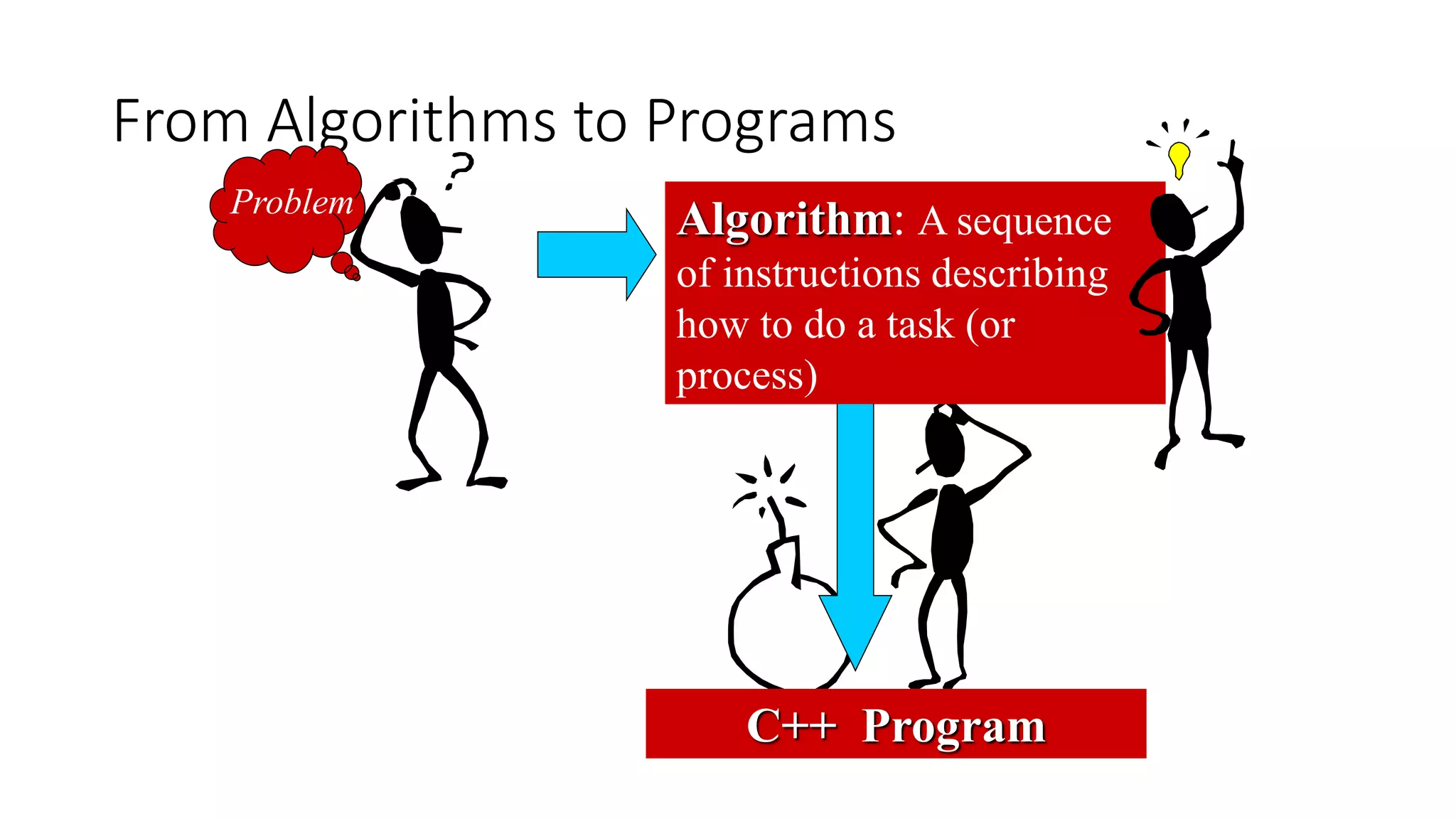
The document discusses algorithms and their role in computing. It defines an algorithm as a well-defined computational procedure that takes input and produces output. Algorithms must be correct, producing the right output for each input, and efficient. It presents examples of computational problems and their algorithms. The document also discusses pseudo-code for writing algorithms and the divide-and-conquer technique for algorithm design, which breaks problems into smaller subproblems.






![Pseudo-code conventions
• Variables ( such as i, j, and key) are local to the given procedure. We
shall not us global variables without explicit indication.
• Array elements are accessed by specifying the array name followed by
the index in square brackets. For example, A[i] indicates the ith element
of the array A. The notation “…" is used to indicate a range of values
within an array. Thus, A[1…j] indicates the sub-array of A consisting of
the j elements A[1], A[2], . . . , A[j].
• A particular attributes is accessed using the attributes name followed by
the name of its object in square brackets.
• For example, we treat an array as an object with the attribute length
indicating how many elements it contains( length[A]).](https://image.slidesharecdn.com/algorithmsandproblemsolving-230814090311-2632bf78/75/Algorithms-and-problem-solving-pptx-10-2048.jpg)




