A taste of Functional Programming

A Taste of Functional
Programming with Haskell
Mohammad Ghabboun Functional→
Programming

Functional Programming
Languages
● Haskell
● Standard ML
● OCaml
● Scheme
● Clojure
● F#
● Scala
● Erlange

What is a function?
● Functions that fail (Null, exceptions...)
● Functions that go into infinite loop
● Functions that do IO
● Function that have side effects (change state)
● ...

What is a function?
● Functions that fail (Null, exceptions...)
● Functions that go into infinite loop
● Functions that do IO
● Function that have side effects (change state)
● Those are not functions but actually procedures
● So...

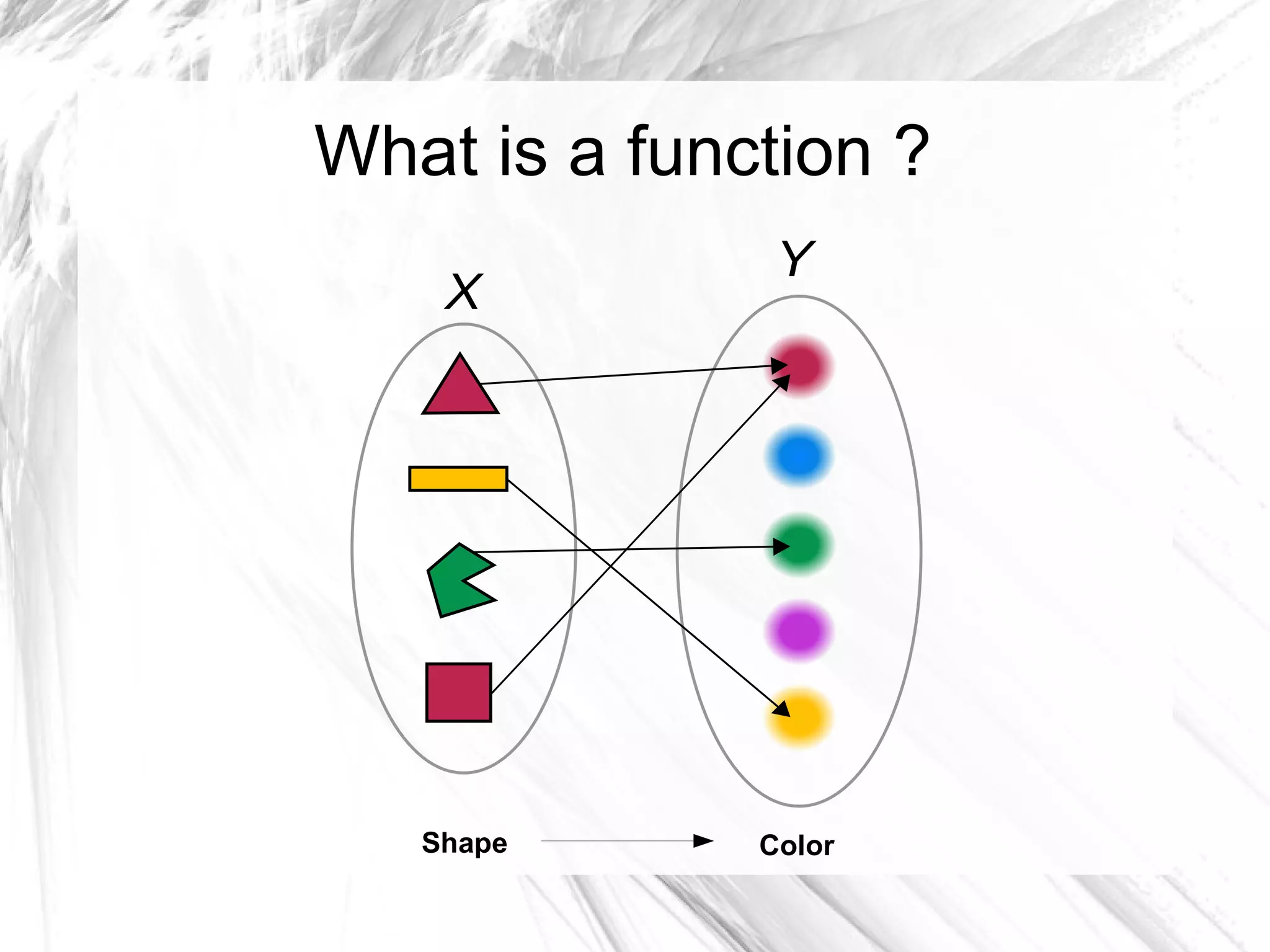
What is a function ?
X
Y
Shape Color

What is a function ?
Pure functions in Haskell, as math functions,
is mapping between two values
int add ( int x, int y )
{
return x + y;
}
Add :: Int → Int → Int
Add x y = x + y

No assignments, only equality!
● Let x = 4
● x = 6 (error!)
● x is 4 it cannot be changed
● Left equals Right
● Let y = 5
● y = y + 1 (error!)
● (y-y) = 1
● 0 = 1 wrong!!

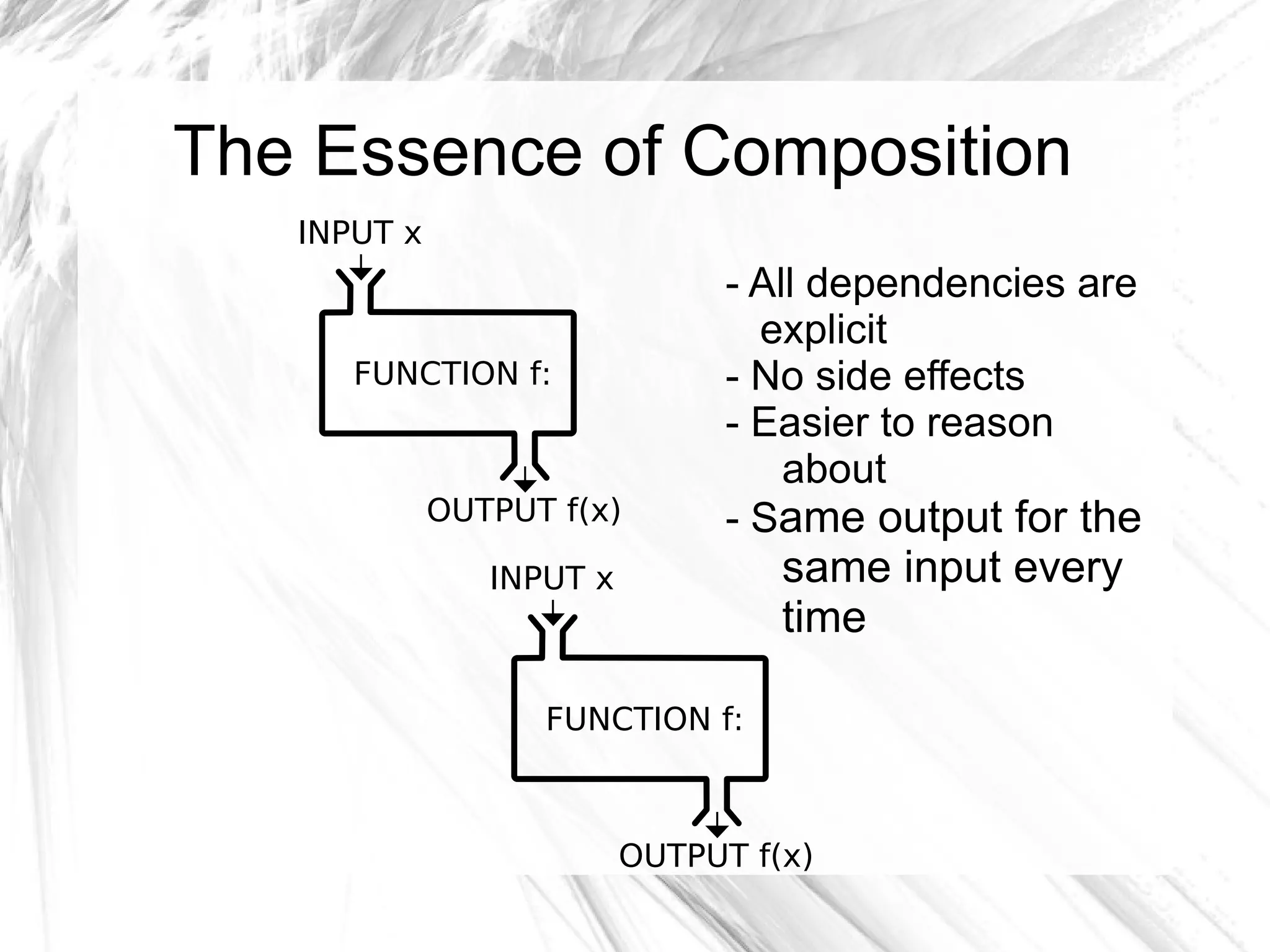
The Essence of Composition
INPUT x
FUNCTION f:
OUTPUT f(x)
INPUT x
FUNCTION f:
OUTPUT f(x)
- All dependencies are
explicit
- No side effects
- Easier to reason
about
- Same output for the
same input every
time

What is Functional
Programming (FP) ?

FP is about focusing on the
solution
It's about computing results and not
performing actions..

Motivational Example
bool isPrime(int n)
{
if (n <= 1)
return false;
if (n == 2)
return true;
for (unsigned int i = 2; i < n; ++i)
if (n % i == 0)
return false;
return true;
}

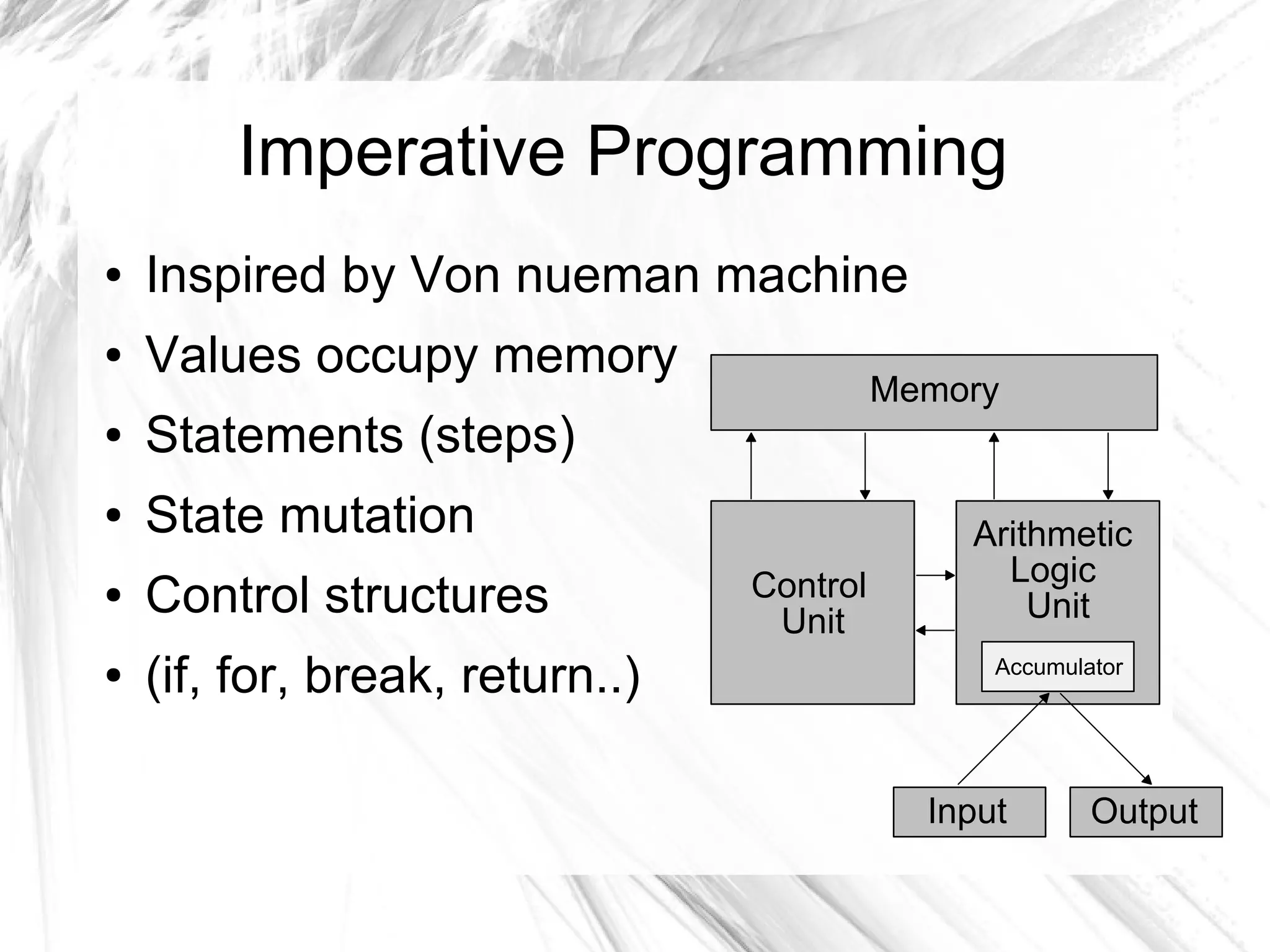
Imperative Programming
● Inspired by Von nueman machine
● Values occupy memory
● Statements (steps)
● State mutation
● Control structures
● (if, for, break, return..)
Arithmetic
Logic
Unit
Control
Unit
Memory
Input Output
Accumulator

Motivational Example
● isPrime :: Int → Bool
● isPrime n = not (any (divides n) [2..n-1])
● A prime number is a natural number greater than 1 that has no
positive divisors other than 1 and itself. - wikipedia

Functional Programming (Haskell)
● Haskell is the purest FP language
● General purpose
● Functions as first class values
● Strongly Typed
● Based on Lambda Calculus and Category
Theory

Real World Applications of FP
● Haxl Project (Facebook)
● Financial Applications (Standard Chartered )
● Algebird Library for Big Data Patterns (e.g.
Map, Reduce, Monoids, Monads )
● Compilers (Perl Compiler and many DSLs)
● Static Analysis (Galois)

Quick, Sort, Example
● sort [] = []
● sort (x:xs) = sort (filter (<x) xs) ++ [x] ++
sort (filter (>=x) xs)

FP Is Building Higher Level
Abstractions
Less boilerplate code Less bugs→

There is a pattern hiding
somewhere...
int Sum ( array<int> v )
{
int sum = 0;
for (int i = 0; i < v.size(); ++i )
{
sum += v[i];
}
return sum;
}

How can we transform it into pure
function ?
int Sum ( array<int> v )
{
int sum = 0;
for (int i = 0; i < v.size(); ++i )
{
sum += v[i];
}
return sum;
}

Recursion ?
int Sum ( vector<int> v, int i )
{
if ( i >= v.size())
return 0;
return v[i] + Sum ( v, i+1 );
}

Recursion ?
int Sum ( vector<int> v, int i )
{
if ( i >= v.size())
return 0;
return v[i] + Sum ( v, i+1 );
}
sum :: [Int] → Int
sum [] = 0
sum (head:rest) = head + sum rest

Recursion ?
sum [] = 0
sum (x:xs) = x + sum xs

Recursion ?
sum [] = 0
sum (x:xs) = x + sum xs
product :: [Int] → Int
product [] = 0
product (x:xs) = x * product xs

Higher Order Functions
fold :: [Int] → Int
fold [] = 0
fold (x:xs) = x + fold xs

Higher Order Functions
fold :: [Int] → Int
fold [] = 0
fold (x:xs) = x + fold xs
fold :: (b → a → b) → b → [a] → b
fold f acc [] = acc
fold f acc (x:xs) = f acc (fold f x xs)

We just introduced a universal
operator
● sum :: [Int] → Int
● sum = foldl (+) 0
● product :: [Int] → Int
● product = foldl (*) 1
● length :: [Int] → Int
● length = foldl (x → x+1) []

Quick Look at Maps
● Maps are very popular operator in programming languages and
especially functional languages
● It applies a function on every element of a list
● map (x → x*2) [0,1,2,3,4,5]
● [0,2,4,6,8,10]

Quick Look at Maps
● map :: (a → b) → [a] → [b]
● map _ [] = []
● map f (x:xs) = f x : map f xs
● Do you recognize this pattern ?

Quick Look at Maps
● map :: (a → b) → [a] → [b]
● map _ [] = []
● map f (x:xs) = f x : map f xs
● Do you recognize this pattern ?
● It turns out this is a Fold pattern
● map f = foldl (x xs → f x : xs) []

FP Is about Controlling Effects
Everytime I see a Null I kill a cat
-Anonymous
“Null is the billion dollar mistake”
-Tony Hoare

J language example
● class HashMap {
public V get ( Object key );
}

J language example
● class HashMap {
}
● Returns the value to which the specified key is mapped, or null if
this map contains no mapping for the key.

J language example
● class HashMap {
}
● Returns the value to which the specified key is mapped, or null if
this map contains no mapping for the key.
● More formally, if this map contains a mapping from a key k to a
value v such that (key==null ? k==null : key.equals(k)), then this
method returns v; otherwise it returns null. (There can be at most
one such mapping.)
● A return value of null does not necessarily indicate that the map
contains no mapping for the key; it's also possible that the map
explicitly maps the key to null. The containsKey operation may be
used to distinguish these two cases.

How to capture effects ?
● If all we have is pure function
● Type Type→
● How can we capture effects..
– Failure?
– Returning multiple values?
– IO ??
– States ???

Capturing Effects
● lookup :: a -> [(a, b)] -> b
●
But this function can't capture failure if a was not in the dictionary
● Let's solve this problem...

Algebraic Data Types
● But First...
● Let's define some data types
● data Bool = True | False
● data Point = (Float,Float)

Algebraic Data Types
● But First...
● Let's define some data types
● data Bool = True | False
● data Point = (Float,Float)
● Let's introduce a type that capture failures
● data Maybe a = Nothing | Just a

Capturing Effects
● lookup :: a -> [(a, b)] -> Maybe b
● Now failure is captured by type
● Your code have to check for failure
● Failure is explicit
● Problem solved...

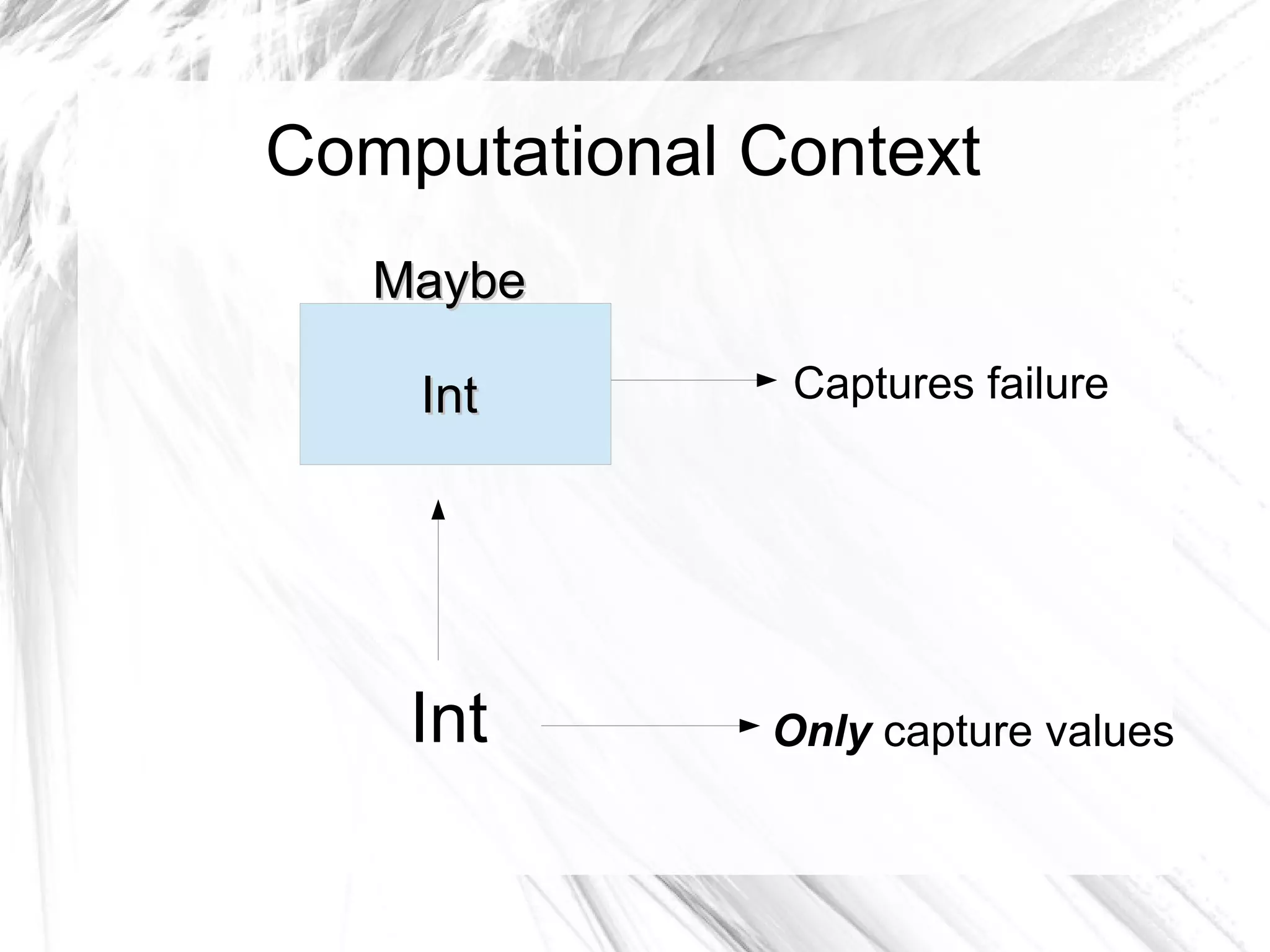
Computational Context
Int
MaybeMaybe
IntInt
Only capture values
Captures failure

Int
ListList
IntInt
Only capture values
Capture Collections
and Non-determinism

Int
IOIO
IntInt
Only capture values
Capture Actions

Map and Lifting
● There is more to map than meets the eye..
● map (x → x*x) [1,2,3,4]
● [1,4,9,16]
● map :: (a → b) → [a] → [b]
● map :: (a → b) → ([a] → [b])

Map Generalization
● Map took a function that works on Int
● returned a function that works on [Int]
● map :: (a → b) → ([a] → [b])
● fmap :: (a → b) → (t a → t b)

Map Generalization
● Map took a function that works on Int
● returned a function that works on T<Int>
● map :: (a → b) → ([a] → [b])
● fmap :: (a → b) → (t a → t b)
● So what is this t we are talking about ?
● t is any computational context we talked about
(Maybe, IO, Lists)

What we have so far..
● A data type, that takes a type and returns another
● Maybe takes Int → Maybe Int
● It's also called a type constructor
● A function that takes a function and returns a lifted function
● fmap :: (a → b) → (t a → t b)
● Any data type that have those two properties is called Functor

Solving Real Problems With Lifting
array< pair<int,int> > CartesianProduct ( array<int> a,
array<int> b )
{
array result;
for (int i=0; i < a.size(); ++i)
{
for (int j=0; j < b.size(); ++j)
{
result.add( make_pair(a[i],b[j]) );
}
}
return result;
}

Solving Real Problems With Functors
● (,) :: a -> b -> (a,b)
● We want to apply it on lists..
● We can lift it to work on lists
● let lifterPair = fmap (,) [1,2,3,4]
● :t lifterPair :: [b -> (Integer, b)]
● lifterPair <*> [5,6,7,8]

Solving Real Problems With Functors
● Even better
● cartProd :: [a] -> [b] -> [(a, b)]
● cartProd = liftA2 (,)

Conclusion
● FP is about focusing on the problems
● FP is about higher level abstractions
● FP is about reducing bugs
● FP is about precise thinking

A taste of Functional Programming

More Related Content

What's hot

Viewers also liked

Similar to A taste of Functional Programming

More from Jordan Open Source Association

Recently uploaded

A taste of Functional Programming