Python - find zero of a function with scipy

Question

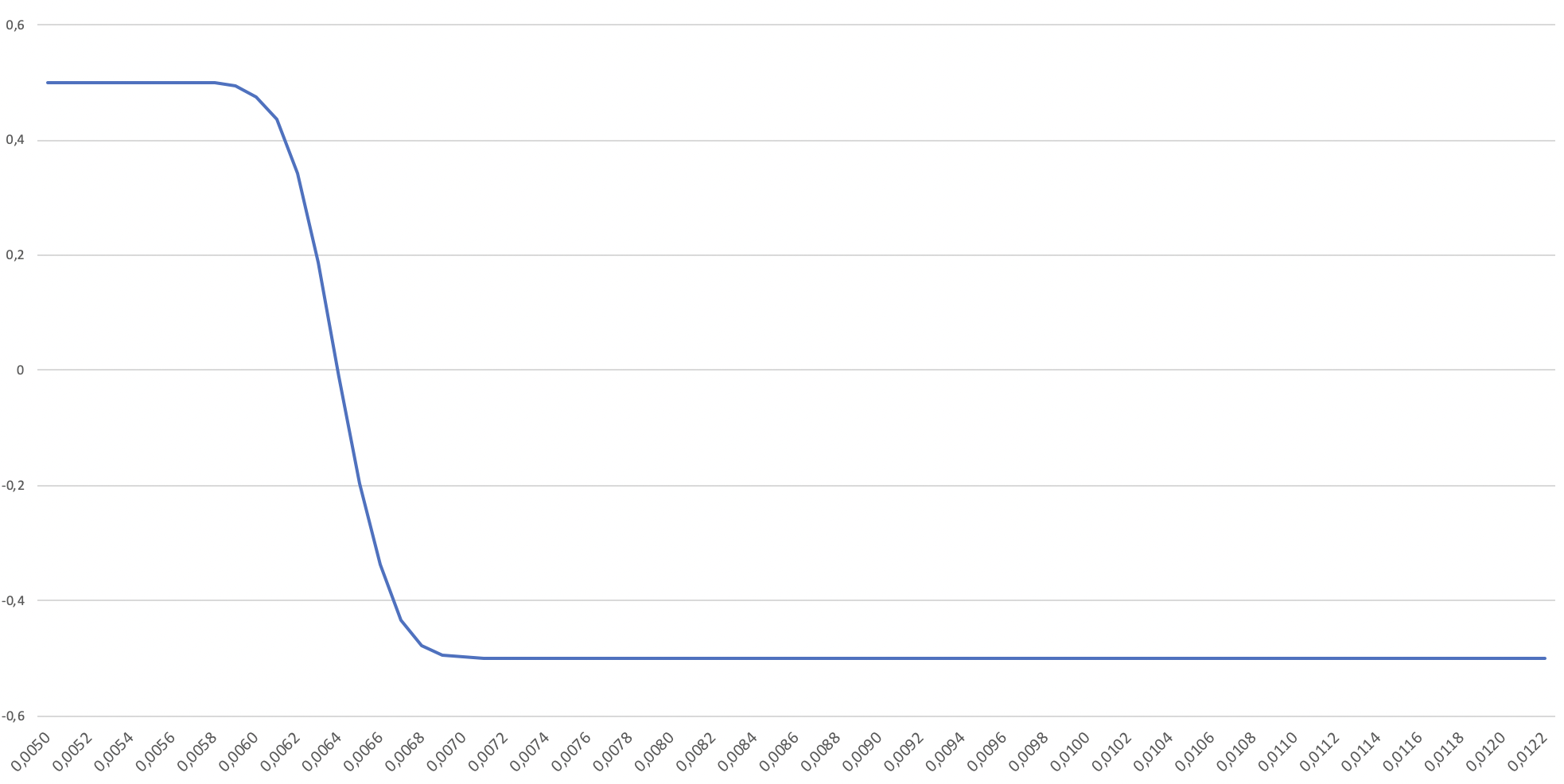
I am having a hard time finding the zero of (I think) a relatively simple function with the following form (also check attached image):

    import numpy as np
    from numpy.random import RandomState
    from scipy import stats, optimize

    state = RandomState()

    def objective_function(x):
        initial = np.ones(10000)
        withdrawal = np.round(x, 4)

        for idx in range(175):
            sim_path = state.normal(1.001275, 0.004267, 10000)
            initial = initial - withdrawal
            initial[initial < 0] = 0
            initial = initial * sim_path

        percentile_cleared = 10000-sum(initial > 0)
        return (5000-percentile_cleared) / 10000

I've been trying to use scipy.optimize.newton with minimal inputs:

solution = optimize.newton(objective_function, x0=0.0075)

but am actually surprised that it is so much sensitive to x0 provided. Small differences in x0 actually determine if a solution could be found or not. The solution is close to 0.0064 in that specific case, but I don't have a good way of determining it in general. And even here, providing x0 of 0.006 will not result in a correct solution.

Do you have any idea if I should provide more inputs to the solver or perhaps express my function in a different way to make it easier for the solver? Thanks a lot in advance!

Can you provide a minimal reproducible example, i.e. your objective function? — joni
– joni, Commented Jul 16, 2021 at 8:19
The variable initial_fv is not defined, so it isn't a working example. — joni
– joni, Commented Jul 16, 2021 at 8:32

joni · Accepted Answer · 2024-12-12 21:10:11Z

3

First of all, note that your objective function is not differentiable in x due to np.round(x, 4), and Newton's method assumes that the function is differentiable. However, even if your function were differentiable, it's hard for the algorithm to converge since the derivative is near zero except for a very tiny interval.

Long story short, use scipy.optimize.root_scalar to find the root of a scalar function. When passing the interval bracketing the root, it uses a derivative-free method by default, i.e.

from scipy.optimize import root_scalar

root_scalar(objective_function, bracket=[0.0, 0.1])

yields

      converged: True
           flag: 'converged'
 function_calls: 38
     iterations: 36
           root: 0.006350000000384172

edited Dec 12, 2024 at 21:10

answered Jul 16, 2021 at 8:58

joni

7,1972 gold badges16 silver badges23 bronze badges

Sign up to request clarification or add additional context in comments.

2 Comments

Nikowhy Over a year ago

The derivative-free method really did it for me. Thanks for your help!

Eric Duminil Over a year ago

Excellent, thanks. 'brentq' method is so good that it seems magical. It's easier to understand how 'bisect' works.

Collectives™ on Stack Overflow

Python - find zero of a function with scipy

1 Answer 1

2 Comments

Your Answer

Hot Network Questions

Collectives™ on Stack Overflow

1 Answer 1

2 Comments

Your Answer

Sign up or log in

Post as a guest

Related