Another Butterfly theorem — Conway like circle

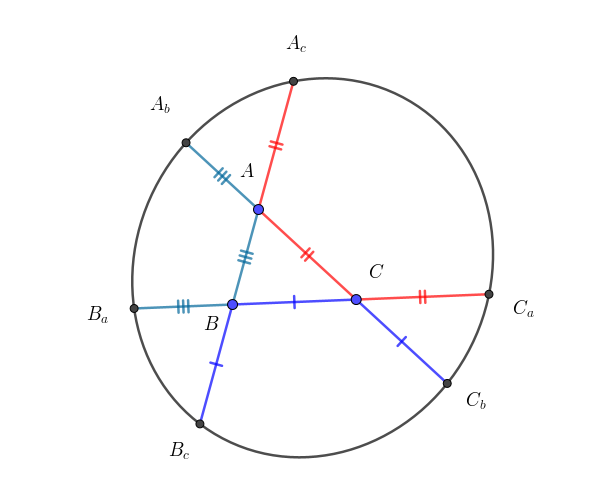
Have You seen these result as follows before?

• In Figure 1: $AA'=BB'=tAB$; $CC'=DD'=tCD$, where t is real number then $ABCD$ is a cyclic quadrilateral iff $A'B'C'D'$ is a cyclic quadrilateral.

• In the Figure 2: $B_a, C_a, C_b, A_b, A_c, B_c$ lie on a conic.

See also:

• Butterfly theorem
• Conway circle theorem