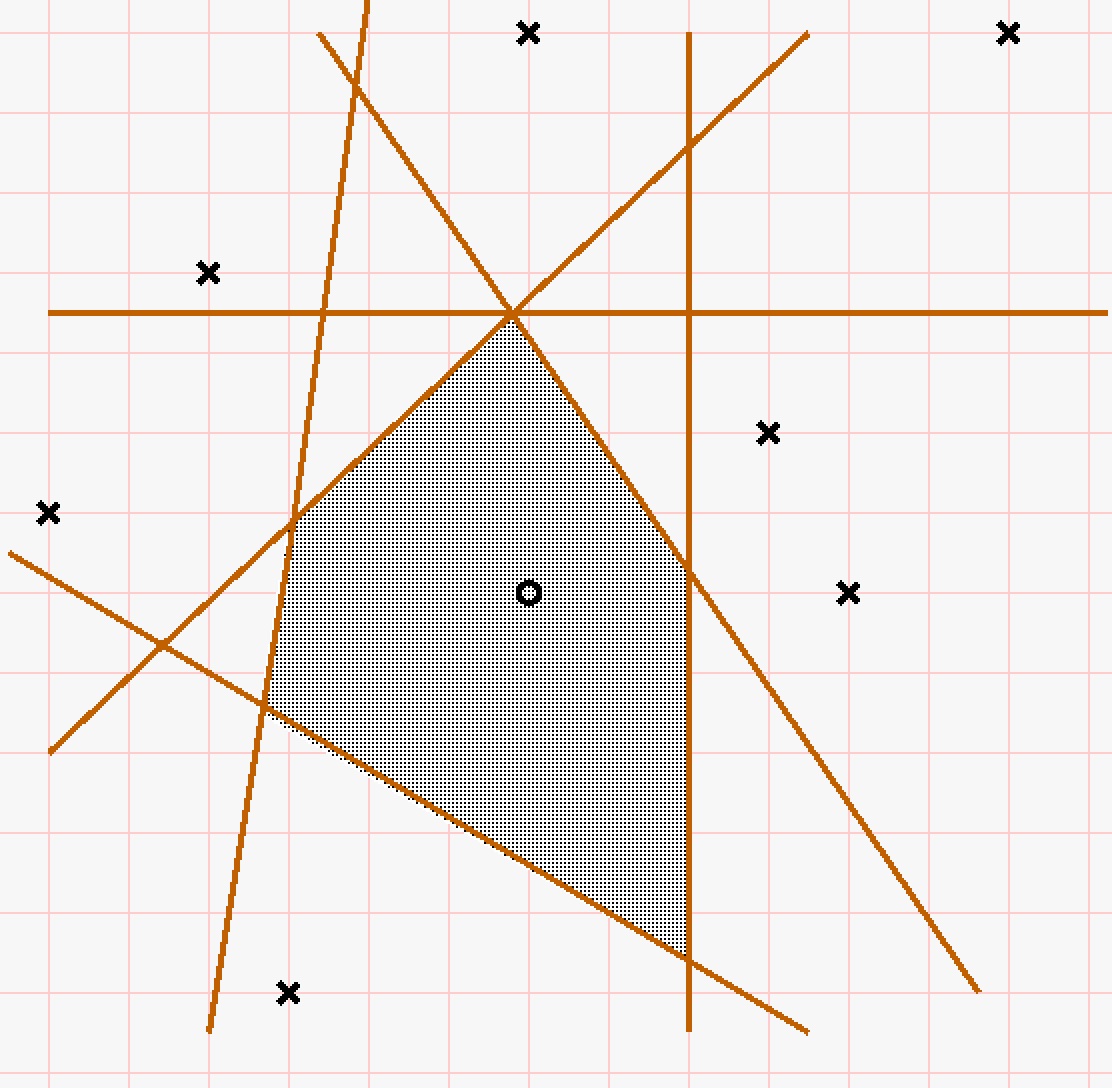
I am working on a problem in dynamical systems where I need to count Voronoi cells arising from nearest neighbours to a subset of the lattice. (See the picture below for an example: the shaded region consists of the points closer to the origin than any of the other centres).
If $S$ is a subset of $\mathbb Z^d$ containing the origin, let $\Lambda_S=\{n\in\mathbb Z^d\colon d(n,0)\le d(n,m)\text{ for all }m\in S\}$. I am hoping for a bound $M(N)$ on the number of possible $\Lambda_S$'s (for different subsets $S$ of $\mathbb Z^d$) such that the cardinality of $\Lambda_S$ is $N$.
Does anyone know if this or similar problems (e.g. a bound on the number of Voronoi cells with given volume) have appeared in the literature? Or does anyone know a way to obtain a bound. Even the case $d=2$ would be of interest.