-
Notifications
You must be signed in to change notification settings - Fork 603
Description
Hello,
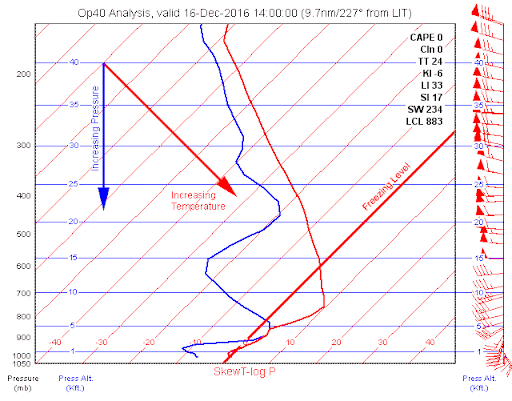
I'd like to inquire about and offer to help add a feature I'd like to be able to use but I'm not quite sure where to start with implementing it. There's a scientific chart I'd like to make called a Skew-T Log-P diagram. The Y axis (Pressure as a vertical coordinate) is in logarithmic space, which thankfully core-plot already does! The strange part is that the X-axis is skewed (Temperature) anywhere from 33-45 degrees to the right of the vertical axis. I noticed that there is a not-yet implemented ScaleType identifier called 'angular', which sounds like it would be a good direction for being able to implement such a transformation. Here's an example plot below. The solid red line highlighted as the freezing level is an example of how a constant X axis value is represented by a slanted line.
The Charts library for iOS has the ability to apply a matrix transform in which the underlying data can be skewed, but there's nothing for the axis lines. Awkwardly, Charts also doesn't support logarithmic data spaces easily. I would also prefer to use core-plot since it leverages the GPU more than Charts. I'd also prefer to be able to keep things in data-space coordinates and implement this at a lower level.
I've implemented this a little more directly before using Qt Widgets using the following functions to transform from data space to pixel space. I understand that implementing this would be required at a lower level than what's done in Qt here, but if I can be directed to a good starting place I think I could figure out the rest and make a pull request.
Any suggestions on where to start?
def initUI(self):
## These are some padding variables for axis drawing, and data-space limits on the graph
self.lpad = 30; self.rpad = 65
self.tpad = 20; self.bpad = 20
self.tlx = self.rpad; self.tly = self.tpad
self.wid = self.size().width() - self.rpad
self.hgt = self.size().height() - self.bpad
self.brx = self.wid ; self.bry = self.hgt
self.pmax = 1050.; self.pmin = 100.
self.barbx = self.brx + self.rpad / 2
self.log_pmax = np.log(self.pmax); self.log_pmin = np.log(self.pmin)
self.bltmpc = -50; self.brtmpc = 50; self.dt = 10
self.xskew = 100 / 3.
self.xrange = self.brtmpc - self.bltmpc
self.yrange = np.tan(np.deg2rad(self.xskew)) * self.xrange
self.clip = QRect(QPoint(self.lpad, self.tly), QPoint(self.brx + self.rpad, self.bry))
self.originx = 0. # self.size().width() / 2
self.originy = 0. # self.size().height() / 2
self.scale = 1.
def pres_to_pix(self, p):
scl1 = self.log_pmax - self.log_pmin
scl2 = self.log_pmax - np.log(p)
return self.bry - (scl2 / scl1) * (self.bry - self.tpad)
def tmpc_to_pix(self, t, p):
scl1 = self.brtmpc - (((self.bry - self.pres_to_pix(p)) /
(self.bry - self.tpad)) * self.yrange)
return self.brx - (((scl1 - t) / self.xrange) * (self.brx - self.lpad))