|
1 | 1 |
|
2 | | - |
3 | | -## 前言 |
4 | | -在上一个章节xxx,本章节接下来将主要介绍xxxx的相关知识。如有错误还请大家及时指出~ |
5 | | - |
6 | | ->本文已同步至 [GitHub](https://github.com/CoderMerlin/coder-programming)/[Gitee](https://gitee.com/573059382/coder-programming)/公众号,感兴趣的同学帮忙点波关注~ |
7 | 2 |
|
8 | | -问题: |
| 3 | + |
| 4 | + |
9 | 5 |
|
10 | | -- xxxxx? |
11 | | -- xxxxx? |
| 6 | +>每章一点正能量:人的一生可能燃烧也可能腐朽。 |
| 7 | +## 前言 |
| 8 | +相信大家在面试或者工作中偶尔会遇到递归算法的提问或者编程,我们今天来聊一聊`从数学归纳法到理解递归算法`。如有错误还请大家及时指出~ |
12 | 9 |
|
| 10 | +>本文已同步至 [GitHub](https://github.com/CoderMerlin/coder-programming)/[Gitee](https://gitee.com/573059382/coder-programming)/公众号,感兴趣的同学帮忙点波关注~ |
13 | 11 |
|
14 | 12 | ## 1. 数学归纳法 |
15 | 13 |
|
16 | 14 | ### 1.1 简介 |
17 | 15 |
|
18 | 16 | > **来源百度百科** |
19 | 17 |
|
20 | | -数学归纳法(Mathematical Induction, MI)是一种数学证明方法,通常被用于证明某个给定命题在整个(或者局部)自然数范围内成立。除了自然数以外,广义上的数学归纳法也可以用于证明一般良基结构,例如:集合论中的树。这种广义的数学归纳法应用于数学逻辑和计算机科学领域,称作结构归纳法。在数论中,数学归纳法是以一种不同的方式来证明任意一个给定的情形都是正确的(第一个,第二个,第三个,一直下去概不例外)的数学定理。虽然数学归纳法名字中有“归纳”,但是数学归纳法并非不严谨的归纳推理法,它属于完全严谨的演绎推理法。事实上,所有数学证明都是演绎法。 |
| 18 | +**数学归纳法**(Mathematical Induction, MI)是一种数学证明方法,通常被用于证明某个给定命题在整个(或者局部)自然数范围内成立。除了自然数以外,广义上的数学归纳法也可以用于证明一般良基结构,例如:集合论中的树。这种广义的数学归纳法应用于数学逻辑和计算机科学领域,称作结构归纳法。在数论中,数学归纳法是以一种不同的方式来证明任意一个给定的情形都是正确的(第一个,第二个,第三个,一直下去概不例外)的数学定理。虽然数学归纳法名字中有“归纳”,但是数学归纳法并非不严谨的归纳推理法,它属于完全严谨的演绎推理法。事实上,所有数学证明都是演绎法。 |
21 | 19 |
|
22 | | -自然数是指表示物体个数的数,即由0开始,0,1,2,3,4,……一个接一个,组成一个无穷的集体,即指非负整数。 |
| 20 | +**自然数**是指表示物体个数的数,即由0开始,0,1,2,3,4,……一个接一个,组成一个无穷的集体,即指非负整数。 |
23 | 21 |
|
24 | 22 | ### 1.2 推演步骤 |
25 | 23 |
|
|
73 | 71 | ``` |
74 | 72 |
|
75 | 73 | 1+2+3+...+(n-1) = (n-1)n/2 |
76 | | - |
| 74 | + |
77 | 75 | ``` |
78 | 76 |
|
79 | 77 |
|
|
85 | 83 | ``` |
86 | 84 |
|
87 | 85 | 1+2+3...+(n-1)+n = (n-1)n/2+n |
88 | | - |
| 86 | + |
89 | 87 | ``` |
90 | 88 |
|
91 | 89 | 化简右边得:`n(n+1)/2`,那么我们最后证明的结果就是成立的! |
|
114 | 112 |
|
115 | 113 | 满足条件: |
116 | 114 |
|
117 | | -- 1. 严格定义递归函数作用,包括参数,返回值,其他变量。 |
118 | | -- 2. 先一般情况,后特殊情况。 |
119 | | -- 3. 有退出条件。在一般情况下,能让递归正常退出的条件。 |
120 | | -- 4. 每次调用必须缩小问题规模,且新问题与原问题有着相同的形式,即规律。 |
| 115 | +1. 严格定义递归函数作用,包括参数,返回值,其他变量。 |
| 116 | +2. 先一般情况,后特殊情况。 |
| 117 | +3. 有退出条件。在一般情况下,能让递归正常退出的条件。 |
| 118 | +4. 每次调用必须缩小问题规模,且新问题与原问题有着相同的形式,即规律。 |
121 | 119 |
|
122 | 120 | 上面的条件一环扣一环,也可以缩减成两个主要条件:`有规律`,`有退出条件`。我们以上面的条件,来结合案例进行理解。 |
123 | 121 |
|
@@ -268,7 +266,7 @@ System.out.println("公众号:Coder编程:3的阶乘:" + factorial(3)); |
268 | 266 |
|
269 | 267 | `斐波那契数列` 我想大家同样熟悉了解,下面我们继续回顾一下斐波那契数列到底是什么? |
270 | 268 |
|
271 | | -![斐波那契数列图]() |
| 269 | +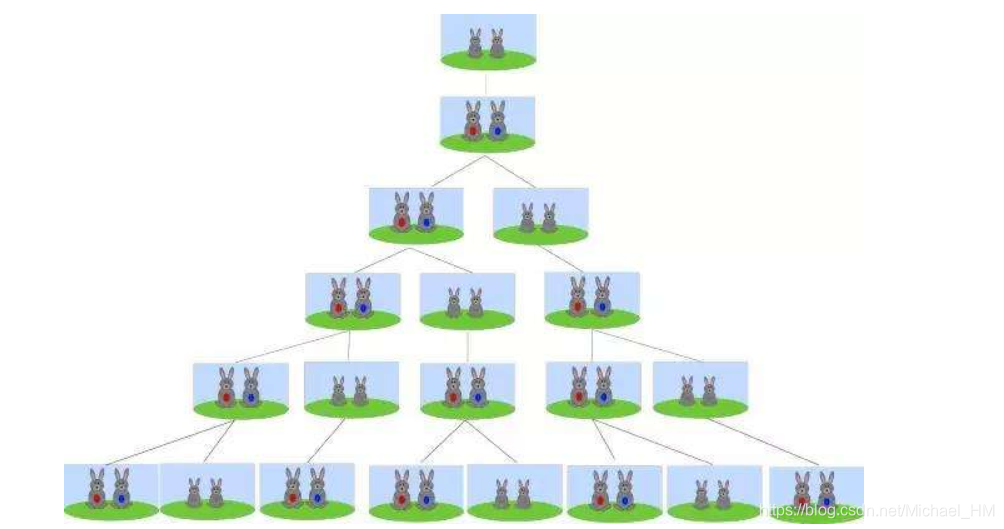 |
272 | 270 |
|
273 | 271 | 斐波那契数列: 1、1、2、3、5、8、13、21..... |
274 | 272 |
|
@@ -300,26 +298,26 @@ System.out.println("公众号:Coder编程:斐波那契数列:" + fib(3)); |
300 | 298 |
|
301 | 299 | 操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。 |
302 | 300 |
|
303 | | -![汉诺塔图]() |
| 301 | +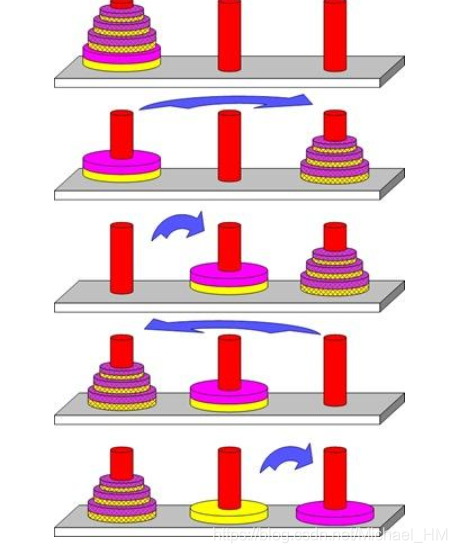 |
304 | 302 |
|
305 | 303 | 在总结规律和写代码之前,我们先来玩几把简单的(**先一般后特殊**): |
306 | 304 |
|
307 | 305 | > 注:我们以数字的大小作为盘子的大小。 |
308 | 306 |
|
309 | | -- 1. 一个盘子的情况: |
| 307 | +1. 一个盘子的情况: |
310 | 308 |
|
311 | 309 | 1.1 将A柱子的1号盘子直接移动到C柱子中。 |
312 | 310 | 1.2 结束。 |
313 | 311 |
|
314 | 312 |
|
315 | | -- 2. 两个盘子的情况: |
| 313 | +2. 两个盘子的情况: |
316 | 314 |
|
317 | 315 | 2.1 将A柱子的1号盘子移动到B柱子。 |
318 | 316 | 2.2 将A柱子的2号盘子移动到C柱子。 |
319 | 317 | 2.3 将B柱子的1号盘子移动到C柱子。 |
320 | 318 | 2.4 结束。 |
321 | 319 |
|
322 | | -- 3. 三个盘子的情况: |
| 320 | +3. 三个盘子的情况: |
323 | 321 |
|
324 | 322 | 3.1 将A柱子的1号盘子移动到C柱子。 |
325 | 323 | 3.2 将A柱子的2号盘子移动到B柱子。 |
@@ -359,48 +357,70 @@ System.out.println("公众号:Coder编程:斐波那契数列:" + fib(3)); |
359 | 357 |
|
360 | 358 | ``` |
361 | 359 |
|
| 360 | +move(3,"A","B","C"); |
| 361 | +
|
362 | 362 | /** |
363 | 363 | * 汉诺塔问题 |
364 | 364 | * @param dish 盘子个数(也表示名称) |
365 | | - * @param from 初始塔座 |
366 | | - * @param temp 中介塔座 |
367 | | - * @param to 目标塔座 |
| 365 | + * @param from 初始柱子 |
| 366 | + * @param temp 中介柱子 |
| 367 | + * @param to 目标柱子 |
368 | 368 | */ |
369 | 369 | public static void move(int dish,String from,String temp,String to){ |
370 | 370 | if(dish == 1){ |
371 | | - System.out.println("将盘子"+dish+"从塔座"+from+"移动到目标塔座"+to); |
| 371 | + System.out.println("将盘子"+dish+"从柱子"+from+"移动到目标柱子"+to); |
372 | 372 | }else{ |
373 | | - move(dish-1,from,to,temp);//A为初始塔座,B为目标塔座,C为中介塔座 |
374 | | - System.out.println("将盘子"+dish+"从塔座"+from+"移动到目标塔座"+to); |
375 | | - move(dish-1,temp,from,to);//B为初始塔座,C为目标塔座,A为中介塔座 |
| 373 | + move(dish-1,from,to,temp);//A为初始柱子,B为目标柱子,C为中介柱子 |
| 374 | + System.out.println("将盘子"+dish+"从柱子"+from+"移动到目标柱子"+to); |
| 375 | + move(dish-1,temp,from,to);//B为初始柱子,C为目标柱子,A为中介柱子 |
376 | 376 | } |
377 | 377 | } |
378 | 378 |
|
379 | 379 | ``` |
380 | 380 |
|
| 381 | +- move(dish-1,from,to,temp);//A为初始柱子,B为目标柱子,C为中介柱子 |
| 382 | +这里需要将n-1之前的盘子都放到B柱子上,最后第n个盘子放到C柱子。 |
| 383 | + |
| 384 | +- move(dish-1,temp,from,to);//B为初始柱子,C为目标柱子,A为中介柱子 |
| 385 | +这时候B变为了初始柱子,A成为了目标柱子。将之前n-1个盘子放到C目标柱子中。 |
381 | 386 |
|
| 387 | +打印结果: |
382 | 388 |
|
| 389 | + |
383 | 390 |
|
384 | 391 | ## 文末 |
385 | 392 |
|
386 | | -本章节主要简单介绍了xxx 的相关知识,后续我们将会继续xxx。 |
| 393 | +本章节主要简单介绍了数学归纳法与递归算法的一些思想。希望对大家有所帮助! |
| 394 | +今后我会在每张文章开头增加 **每章一点正能量** ,文末增加5个编程相关的英语单词 **学点英语**。希望大家和我一样每天都能积极向上,一起学习一同进步! |
| 395 | + |
| 396 | +### 学点英语 |
| 397 | + |
| 398 | +- JRE Java Runtime Environment(Java运行环境),运行 JAVA程序所必须的环境的集合,包含JVM标准实现及Java核心类库。 |
| 399 | +- JSDK Java Software Development Kit,和JDK以及J2SE 等同。 |
| 400 | +- JDK Java Development Kit(Java开发工具包):包括运行环境 、编译工具及其它工具、源代码等,基本上和J2SE等同。 |
| 401 | +- J2ME Java 2 Micro Edition(JAVA2精简版)API规格基 于J2SE ,但是被修改为可以适合某种产品的单一要求。J2ME使JAVA程序可以很方便的应用于电话卡、寻呼机等小型设备,它包括两种类型的组件,即配置 (configuration)和描述(profile)。 |
| 402 | + |
387 | 403 |
|
388 | 404 | >欢迎关注公众号:**Coder编程** |
389 | 405 | 获取最新原创技术文章和相关免费学习资料,随时随地学习技术知识! |
390 | 406 |
|
391 | | -参考文章: |
392 | 407 |
|
393 | | -xxxxx |
394 | 408 |
|
395 | | -xxxxx |
| 409 | +参考文章: |
| 410 | + |
| 411 | +https://www.cnblogs.com/ysocean/p/8005694.html |
396 | 412 |
|
| 413 | +http://www.nowamagic.net/librarys/veda/detail/2314 |
397 | 414 |
|
398 | | - |
| 415 | + |
399 | 416 |
|
400 | 417 | ## 推荐阅读 |
401 | 418 |
|
402 | | -xxxxx |
403 | 419 |
|
404 | | -xxxxx |
| 420 | +[一篇带你读懂TCP之“滑动窗口”协议 ](https://mp.weixin.qq.com/s?__biz=MzIwMTg3NzYyOA==&mid=2247483706&idx=1&sn=8eed9d160013bd8ed6203ad511711553&chksm=96e67029a191f93fdd1543af2bf06025397d9c3bd0f0692c7fe247ab9c139cd869d69ab05498&token=1104592742&lang=zh_CN#rd) |
| 421 | + |
| 422 | +[带你了解数据库中JOIN的用法 ](https://mp.weixin.qq.com/s?__biz=MzIwMTg3NzYyOA==&mid=2247483713&idx=1&sn=d61ad0aed42dc36d64d17732db352288&chksm=96e67052a191f9445bbe3d5825ce547ad3171c3874b571a93b97977d0668413e37a164c3e0bc&token=1144933717&lang=zh_CN#rd) |
| 423 | + |
| 424 | +[ 深入浅出了解“装箱与拆箱” ](http://mp.weixin.qq.com/s?__biz=MzIwMTg3NzYyOA==&mid=100000124&idx=1&sn=3e6cda3aef95f2dd609dd96963094da6&chksm=16e6706f2191f97972ca1b674034d0fb55026521d1418d1c069f1367b5ada38455ed2f4e2fcf#rd) |
405 | 425 |
|
406 | | -xxxxx |
| 426 | + |
0 commit comments