Sticks expectation

Question

This was originally a question from interviewstreet.com over a decade ago

You are given an array (or whatever - your choice of input) of positive integers \$y_1,\ldots,y_n\$ that represents \$n\$ line segments, where segment \$i\$ has endpoints \$(i, 0)\$ and \$(i, y_i)\$. Imagine that from the top of each segment a horizontal ray is shot to the left, and this ray stops when it touches another segment or it hits the \$y\$-axis. Construct an array of \$n\$ integers, \$v_1,\ldots,v_n\$, where \$v_i\$ is equal to the length of ray shot from the top of segment \$i\$. Define \$V(y_1,\ldots,y_n)=v_1+\cdots+v_n\$.

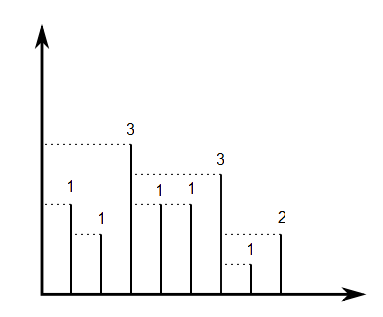
For example starting with \$3,2,5,3,3,4,1,2\$, then \$v_1,\ldots,v_8=1,1,3,1,1,3,1,2\$ as shown in this picture, and so \$V(3,2,5,3,3,4,1,2)=1+1+3+1+1+3+1+2=13\$ here.

sticks

For each permutation \$p\$ of \$1,\ldots,n\$, you can calculate \$V(y_{p_1},\ldots,y_{p_n})\$. You can then take the average across all possible permutations.

Write a program or function that gives the expected value of \$V(y_{p_1},\ldots,y_{p_n})\$ for a uniformly random permutation \$p\$ of \$1,\ldots,n\$. Include a complexity measure for your approach, such as \$O(n)\$ or \$O(n!)\$ and explain why.

This is code-golf, so the shortest answer in bytes wins. Standard rules apply and default loopholes are forbidden.

Test examples include

Input y             Output E[V]
3,2,5,3,3,4,1,2     15.25
1,2,3               4.333333
3,3,3               3
2,2,3               4
10,2,4,4            6
10,10,10,5,10       5.8
1,2,3,4,5,6         11.15

@doubleunary Those three steps would give an answer, but perhaps there might be shorter calculations that combine some steps. — Henry
– Henry, Commented Nov 1 at 16:20
Welcome to Code Golf and nice first challenge! Please note that for code-golf most answers are likely to use the worst possible time complexity. (Or even worse than the worst, if that saves a byte.) — Arnauld
– Arnauld, Commented Nov 1 at 16:44
@Arnauld It was on interviewstreet.com in 2012. The web archive has it on HackerRank only in 2021 — Henry
– Henry, Commented Nov 1 at 17:58
The HackerRank TOS states that all materials are copyrighted. — doubleunary
– doubleunary, Commented Nov 1 at 18:33

Jonathan Allan · Accepted Answer · 2025-11-01 22:08:52Z

Jelly, \$O(n \log n)\$ 13 bytes or \$O(n^2)\$ 12 bytes

\$O(n \log n)\$ 13 bytes

ĠẈṚÄ‘÷@ƊS×L‘$

A monadic Link that accepts a list of heights and yields the expected total visible distance.

Try it online! Or see the test-suite.

How?

Note that the actual height values are irrelevant; what matters is the count of each distinct height and for each of these how many lines are equal or greater in value.

By linearity of expectation, we can compute the contribution each line has by what could be in the gaps between it and other lines of equal or greater height.

If the number of lines is \$n\$, and there are \$m\$ distinct heights with ordered counts \$C\$ with suffix-sums \$S\$ then:

$$\Bbb E[V] = (n + 1) \sum_{i=1}^{m}\frac{C_i}{S_i + 1}$$

ĠẈṚÄ‘÷@ƊS×L‘$ - Link: list of positive integers, Heights
Ġ             - group indices by ascending value (O(n log n))
 Ẉ            - length of each -> C
  Ṛ           - reverse -> Rev(C)
       Ɗ      - last three links as a monad - f(Rev(C)):
   Ä          -   cumulative sums {Rev(C)} (O(n)) -> Rev(S)
    ‘         -   increment each of {those}
     ÷@       -   divide {Rev(C)} by {those} (vectorises)
        S     - sum {those}
            $ - last two links as a monad - f(Heights):
          L   -   length {Heights} -> n
           ‘  -   increment -> n+1
         ×    - {sum result} multiplied by {n+1}

\$O(n^2)\$ in 12 bytes

L‘ɓ>€`§ạ⁹÷@S

TIO

How?

As above, but summing all individual contributions found by a cross-product of comparisons.

L‘ɓ>€`§ạ⁹÷@S - Link: list of positive integers, Heights
L            - length {Heights} -> n
 ‘           - increment -> n+1
  ɓ          - start a new dyadic chain - f(Heights, n+1)
     `       - use {Heights} as both arguments of:
    €        -   for each:
   >         -     greater than? (vectorises)
      §      - sums
       ạ⁹    - absolute difference with {n+1} (vectorises)
         ÷@  - {n+1} divided by each of {those}
           S - sum

Wouldn't group indices by ascending value amount to a sort so \$O(n \log n)\$? — Henry
– Henry, Commented Nov 1 at 18:07
Ah, yes, it needs to sort by the m keys - interpreter function. — Jonathan Allan
– Jonathan Allan, Commented Nov 1 at 18:14

Jonathan Allan · Accepted Answer · 2025-11-01 23:31:51Z

3

Python 3, \$O(n^2)\$ 55 bytes

lambda a:sum(-~len(a)/-~sum(h<=v for v in a)for h in a)

An unnamed function that accepts a list of positive integers, a, and returns the expected total visible distance.

Try it online!

Python 3.8+ \$O(n \log n)\$, 104 bytes

lambda a,s=1:(c:=Counter(a))and sum(c[v]/(s:=s+c[v])for v in sorted(c)[::-1])*s
from collections import*

TIO

edited Nov 1 at 23:31

answered Nov 1 at 21:22

Jonathan Allan

115k8 gold badges68 silver badges293 bronze badges

Add a comment |

Arnauld · Accepted Answer · 2025-11-02 07:57:59Z

2

JavaScript (ES6), 56 bytes, \$O(n^2)\$

The much more clever algorithm used by Jonathan Allan.

a=>a.map(h=>t+=a.map(H=>q+=++n&&h<=H,n=q=1)&&n/q,t=0)&&t

Try it online!

JavaScript (ES6), 104 bytes, \$O(n!)\$

A naive implementation that processes all permutations of the input array and computes the rays for each of them.

f=(a,q=t=n=0,p=[f])=>a.map((v,i)=>f(a.filter(_=>i--),p.findIndex(V=>V<v^1)-~q,[v,...p]))+a?t/n:t+=++n&&q

Try it online!

edited Nov 2 at 7:57

answered Nov 1 at 20:34

Arnauld

205k21 gold badges186 silver badges670 bronze badges

Add a comment |

Kevin Cruijssen · Accepted Answer · 2025-11-03 08:05:01Z

05AB1E, 11 bytes, \$O(n^2)\$

g>IDδ›≠O>/O

Port of @JonathanAllan's Python answer, so make sure to upvote that answer as well.

Try it online or verify all test cases.

Explanation:

g          # Push the length of the (implicit) input-list - O(n)
 >         # Increase it by 1 - O(1)
I          # Push the input-list again - O(1)
 D         # Duplicate it - O(1)
  δ        # Pop both lists, and apply double-vectorized: - O(n²)
   ›≠      #  <= check (or technically an > check with invert after it) - 2O(1)
     O     # Sum each inner list together - O(n²)
      >    # Increase each sum by 1 as well - O(n)
       /   # Divide the length+1 by each of these sum+1s - O(n)
        O  # Then sum everything together - O(n)
           # (after which the result is output implicitly)

Combined complexity:
$$O(n)+O(1)+O(1)+O(1)+O(n^2)+2O(1)+O(n^2)+O(n)+O(n)+O(n) = \\ 2O(n^2)+4O(n)+5O(1) → \\ O(n^2)$$

Neil · Accepted Answer · 2025-11-02 00:45:43Z

Charcoal, O(n²), 15 bytes

ＩΣＥθ∕⊕Ｌθ⊕ＬΦθ÷λι

Try it online! Link is to verbose version of code. Explanation: Port of @JonathanAllan's Python 3 answer, except replacing sum(h<=v for v in a) with len(v for v in a if v//h).

   θ            Input array
  Ｅ             Map over positive integers
       θ        Input array
      Ｌ         Length
     ⊕          Incremented
    ∕           Divided by
           θ    Input array
          Φ     Filtered by
             λ  Inner positive integer
            ÷   Is not less than
              ι Outer positive integer
         Ｌ      Length
        ⊕       Incremented
 Σ              Take the sum
Ｉ               Cast to string
                Implicitly print

M-- · Accepted Answer · 2025-11-02 07:01:24Z

1

Julia, \$O(n^2)\$, 44 bytes

sum((length(y)+1)/(sum(i.<=y)+1) for i in y)

Attempt This Online!

edited Nov 2 at 7:01

answered Nov 2 at 6:37

M--

9566 silver badges13 bronze badges

Add a comment |

Henry · Accepted Answer · 2025-11-02 02:38:24Z

0

R, 43 bytes \$O(n\log n)\$

a=table(-y)
(sum(a)+1)*sum(a/(cumsum(a)+1))

Try it online!

R, 47 bytes \$O(n^2)\$

sum((length(y)+1)/(rowSums(outer(y,y,"<="))+1))

Try it online!

answered Nov 2 at 2:38

Henry

2095 bronze badges

New contributor

\$\begingroup\$ This is the correct count: R, 49 bytes: \(y){a=table(-y) (sum(a)+1)*sum(a/(cumsum(a)+1))}. Similarly, for the 2nd solution, you need to count 6 more bytes. \$\endgroup\$

M--
– M--

2025-11-02 03:49:57 +00:00
Commented Nov 2 at 3:49
\$\begingroup\$ Also, please see this: codegolf.meta.stackexchange.com/a/12104 \$\endgroup\$

M--
– M--

2025-11-02 04:06:36 +00:00
Commented Nov 2 at 4:06
\$\begingroup\$ Your first solution can be shorter by 2 bytes: \(y,a=table(-y),?=sum)(1+?a)*?a/(cumsum(a)+1) \$\endgroup\$

M--
– M--

2025-11-02 06:44:05 +00:00
Commented Nov 2 at 6:44
\$\begingroup\$ And the second solution can be shortened by 1 byte: \(y)sum((sum(y|1)+1)/(rowSums(outer(y,y,"<="))+1)) \$\endgroup\$

M--
– M--

2025-11-02 06:52:37 +00:00
Commented Nov 2 at 6:52
\$\begingroup\$ 44 bytes for the first: ato.pxeger.com/… \$\endgroup\$

pajonk
– pajonk

2025-11-02 12:14:31 +00:00
Commented 2 days ago

Add a comment |

Stack Exchange Network

Sticks expectation

7 Answers 7

Jelly, \$O(n \log n)\$ 13 bytes or \$O(n^2)\$ 12 bytes

\$O(n \log n)\$ 13 bytes

How?

\$O(n^2)\$ in 12 bytes

How?

Python 3, \$O(n^2)\$ 55 bytes

Python 3.8+ \$O(n \log n)\$, 104 bytes

JavaScript (ES6), 56 bytes, \$O(n^2)\$

JavaScript (ES6), 104 bytes, \$O(n!)\$

05AB1E, 11 bytes, \$O(n^2)\$

Charcoal, O(n²), 15 bytes

Julia, \$O(n^2)\$, 44 bytes

R, 43 bytes \$O(n\log n)\$

R, 47 bytes \$O(n^2)\$

Your Answer

Hot Network Questions

Sticks expectation

7 Answers 7

Jelly, \$O(n \log n)\$ 13 bytes or \$O(n^2)\$ 12 bytes

\$O(n \log n)\$ 13 bytes

How?

\$O(n^2)\$ in 12 bytes

How?

Python 3, \$O(n^2)\$ 55 bytes

Python 3.8+ \$O(n \log n)\$, 104 bytes

JavaScript (ES6), 56 bytes, \$O(n^2)\$

JavaScript (ES6), 104 bytes, \$O(n!)\$

05AB1E, 11 bytes, \$O(n^2)\$

Charcoal, O(n²), 15 bytes

Julia, \$O(n^2)\$, 44 bytes

R, 43 bytes \$O(n\log n)\$

R, 47 bytes \$O(n^2)\$

Your Answer

Sign up or log in

Post as a guest

Related

Hot Network Questions